Systematic assessment of the sex ratio at birth for all countries and estimation of national imbalances and regional reference levels

Significance

This study provides information on sex ratio at birth (SRB) reference levels and SRB imbalance. Using a comprehensive database and a Bayesian estimation model, we estimate that SRB reference levels are significantly different from the commonly assumed historical norm of 1.05 for most regions. We identify 12 countries with strong statistical evidence of SRB imbalance: Albania, Armenia, Azerbaijan, China, Georgia, Hong Kong (SAR of China), India, Republic of Korea, Montenegro, Taiwan (Province of China), Tunisia, and Vietnam.

Abstract

The sex ratio at birth (SRB; ratio of male to female live births) imbalance in parts of the world over the past few decades is a direct consequence of sex-selective abortion, driven by the coexistence of son preference, readily available technology of prenatal sex determination, and fertility decline. Estimation of the degree of SRB imbalance is complicated because of unknown SRB reference levels and because of the uncertainty associated with SRB observations. There are needs for reproducible methods to construct SRB estimates with uncertainty, and to assess SRB inflation due to sex-selective abortion. We compile an extensive database from vital registration systems, censuses and surveys with 10,835 observations, and 16,602 country-years of information from 202 countries. We develop Bayesian methods for SRB estimation for all countries from 1950 to 2017. We model the SRB regional and national reference levels, the fluctuation around national reference levels, and the inflation. The estimated regional reference levels range from 1.031 (95% uncertainty interval [1.027; 1.036]) in sub-Saharan Africa to 1.063 [1.055; 1.072] in southeastern Asia, 1.063 [1.054; 1.072] in eastern Asia, and 1.067 [1.058; 1.077] in Oceania. We identify 12 countries with strong statistical evidence of SRB imbalance during 1970–2017, resulting in 23.1 [19.0; 28.3] million missing female births globally. The majority of those missing female births are in China, with 11.9 [8.5; 15.8] million, and in India, with 10.6 [8.0; 13.6] million.

We describe a method for probabilistic and reproducible estimation of the sex ratio at birth (SRB; ratio of male to female live births) for all countries, with a focus on assessing the SRB reference levels (which we henceforth term “baseline level”) and SRB imbalance due to sex-selective abortion.

Under normal circumstances, SRB varies in a narrow range around 1.05, with only a few known variations among ethnic groups (1–13). For most of human history, SRB remained within that natural range. However, over recent decades, SRBs have risen in a number of Asian countries and in eastern Europe (14–30). The increasing imbalance in SRB is due to a combination of three main factors that lead to sex-selective abortion (22, 24). Firstly, most societies with abnormal SRB inflation have persisting strong son preference, which provides the motivation. Secondly, since the 1970s, prenatal sex diagnosis and access to sex-selective abortion have become increasingly available (31–35), providing the method. Thirdly, fertility has fallen to low levels around the world that resulted in a “squeezing effect”: attaining both the desired small families and the ideal sex composition by resorting to sex selection (22). Consequently, sex-selective abortion provides a means to avoid large families while still having male offspring. Necessary conditions for the occurrence of sex-selective abortions include a large tolerance for induced abortion from both the population and the medical establishment, available techniques for early sex detection, and legal medical abortion for several weeks after onset of pregnancy (36).

Estimation of the degree of SRB imbalance is complicated by the amount of uncertainty associated with SRB observations due to data quality issues and sampling errors. While the United Nations (UN) Population Division publishes estimates for all countries in the World Population Prospects (WPP), its estimates are deterministic and depend on expert-based opinions which are not reproducible (37). Although modeling and simulation studies of the SRB have been carried out for selected countries (38–40), these studies did not estimate the SRB and its natural fluctuations; instead, SRB estimates were taken from the UN WPP. A recent assessment by the Global Burden of Disease Study 2017 (41) produced estimates for 195 countries based on 8,936 country-years of data but does not assess baseline values or imbalances. An up-to-date systematic analysis for the SRB—one of the most fundamental demographic indicators—for all countries over time using all available data with reproducible estimation method is urgently needed.

To fill the research void, we develop model-based estimates for 212 countries (referring to populations that are considered as “countries” or “areas” in the UN classification) from 1950 to 2017. Our analyses are based on a comprehensive database on national-level SRB with data from vital registration (VR) systems, censuses, and international and national surveys. In total, we have 10,835 observations, equivalent to 16,602 country-years of information, in our database from 202 countries. We implement two Bayesian hierarchical models to estimate SRBs in two types of country-years: (i) those that are not affected by sex-selective abortion and (ii) those that may be affected by sex-selective abortion that leads to SRB imbalances.

In the model for country-years not affected by sex-selective abortion, the SRB is given by the product of a baseline value and a country-year-specific multiplier that accounts for natural fluctuation around the baseline value. We allow baseline values to differ across countries within a region, and across regions, to incorporate SRB differences due to ethnic origin (1–13). Hence, for this purpose, regions refer to groupings of countries based on their dominant ethnic group (SI Appendix, Table S17). For example, we group countries in Europe, North America, Australia, and New Zealand to refer to the regional grouping of countries with a majority of Caucasians. Within each country and region, we assume that the baseline value is constant over time.

The model for natural fluctuations in the SRB is fitted to the global database after excluding data from country-years that may have been affected by masculinization of the SRB. We use inclusive criteria to identify such country-years, based on a combination of qualitative and quantitative approaches. We select countries with at least one of the following manifestations of son preference: (i) a high level of desired sex ratio at birth (DSRB), (ii) a high level of sex ratio at last birth (SRLB), or (iii) strong son preference or inflated SRB suggested by a literature review. The earliest start for the sex ratio inflation is set to 1970, which is when sex-selective abortions first became available.

We parametrize SRB inflation during a sex ratio transition using a trapezoid to allow for consecutive phases of increase, stagnation, and a decrease back to zero. We incorporate the fertility squeeze effect by using the total fertility rate [TFR, obtained from the UN WPP 2017 (37)] into the model to inform the start year of SRB inflation. Parameters are estimated with a Bayesian hierarchical model (42) to share information across countries about the inflation start year, the maximum inflation, and the length of inflation period during the three phases.

To quantify the effect of SRB imbalance due to sex-selective abortion, we calculate the annual number of missing female births (AMFB) and the cumulative number of missing female births (CMFB) over time. AMFB is defined as the difference between the number of female live births based on SRB without inflation and the number of female live births based on SRB with inflation. CMFB for a certain period is the sum of AMFB over the period. We define countries with strong evidence of SRB inflation to be those countries with at least 1 y with at least 95% probability of a positive number of missing female births (AMFB $>$ 0).

Results

The compiled database, annual estimates for national, regional, and global SRB during 1950–2017, and national AMFB during 1970–2017 are available in Datasets S1–S4. The SRB estimates for selected years by country are in SI Appendix, Table S20.

Global and Regional SRB Estimates.

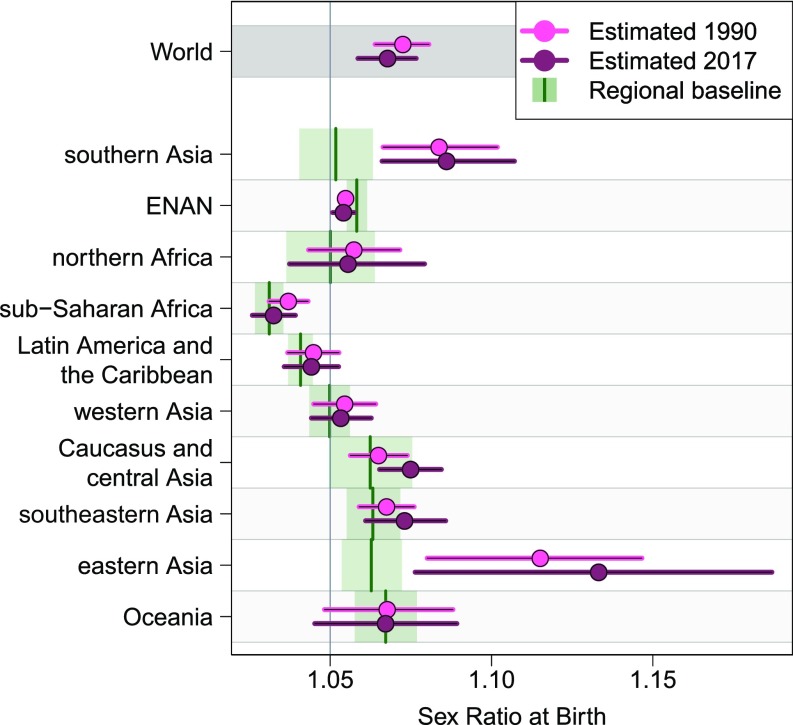
The global and regional SRB median estimates and 95% uncertainty intervals in 1990 and 2017 are presented in Fig. 1 and Table 1. Globally, the SRB in 2017 is 1.068 (95% uncertainty interval, [1.059; 1.077]). Levels and trends vary across regions. In 2017, the regional-level estimated SRBs range from 1.032 [1.026; 1.039] in sub-Saharan Africa to 1.133 [1.076; 1.187] in eastern Asia.

Fig. 1.

Global and regional SRB estimates in 1990 and 2017, and regional baseline values of SRB. Dots indicate median estimates, and horizontal lines refer to 95% uncertainty intervals. Regional baseline values are in dark green, where the vertical line segments refer to median estimates, and green shaded areas are 95% uncertainty intervals.

Table 1.

Global and regional SRB in 1990, 2000, and 2017

	SRB				Change of SRB
World, region	Baseline value	1990	2000	2017	1990–2000	2000–2017	1990–2017
World	—	1.073	1.078	1.068	0.005	−0.010	−0.005
		[1.064; 1.081]	[1.071; 1.085]	[1.059; 1.077]	[−0.001; 0.013]	[−0.018; −0.002]	[−0.014; 0.005]
southern Asia	1.052	1.084	1.097	1.086	0.014	−0.011	0.002
	[1.040; 1.063]	[1.066; 1.102]	[1.079; 1.116]	[1.066; 1.107]	[0.005; 0.022]	[−0.024; 0.003]	[−0.011; 0.017]
ENAN	1.058	1.055	1.055	1.054	0.001	−0.001	−0.001
	[1.055; 1.061]	[1.054; 1.056]	[1.054; 1.056]	[1.051; 1.057]	[−0.001; 0.002]	[−0.005; 0.002]	[−0.004; 0.003]
northern Africa	1.050	1.057	1.056	1.056	−0.002	−0.001	−0.002
	[1.036; 1.064]	[1.043; 1.072]	[1.042; 1.070]	[1.037; 1.079]	[−0.009; 0.006]	[−0.013; 0.020]	[−0.015; 0.019]
sub-Saharan Africa	1.031	1.037	1.035	1.032	−0.002	−0.002	−0.005
	[1.027; 1.036]	[1.031; 1.043]	[1.029; 1.041]	[1.026; 1.039]	[−0.007; 0.002]	[−0.007; 0.003]	[−0.010; 0.001]
Latin America and	1.041	1.045	1.045	1.044	0.000	−0.001	−0.001
the Caribbean	[1.037; 1.045]	[1.037; 1.053]	[1.036; 1.053]	[1.036; 1.053]	[−0.007; 0.007]	[−0.009; 0.008]	[−0.009; 0.008]
western Asia	1.050	1.055	1.056	1.053	0.002	−0.003	−0.001
	[1.044; 1.056]	[1.045; 1.064]	[1.048; 1.064]	[1.044; 1.063]	[−0.006; 0.009]	[−0.011; 0.006]	[−0.011; 0.008]
Caucasus and central Asia	1.062	1.065	1.077	1.075	0.012	−0.003	0.010
	[1.050; 1.075]	[1.056; 1.074]	[1.070; 1.085]	[1.065; 1.084]	[0.005; 0.020]	[−0.011; 0.006]	[0.001; 0.019]
southeastern Asia	1.063	1.067	1.068	1.073	0.001	0.005	0.006
	[1.055; 1.072]	[1.059; 1.076]	[1.060; 1.077]	[1.061; 1.086]	[−0.008; 0.010]	[−0.007; 0.017]	[−0.007; 0.018]
eastern Asia	1.063	1.115	1.157	1.133	0.042	−0.024	0.018
	[1.054; 1.072]	[1.080; 1.147]	[1.128; 1.189]	[1.076; 1.187]	[0.009; 0.083]	[−0.081; 0.029]	[−0.043; 0.079]
Oceania	1.067	1.068	1.068	1.067	0.000	0.000	−0.001
	[1.058; 1.077]	[1.048; 1.088]	[1.046; 1.089]	[1.045; 1.089]	[−0.014; 0.014]	[−0.017; 0.016]	[−0.019; 0.017]

Median estimates are numbers before the brackets. Numbers in the brackets are 95% uncertainty intervals. —, the model does not estimate a global baseline value.

Between 1990 and 2017, the change in the global SRB is not statistically significant. For the same period, none of the regional estimated SRBs have significant reductions, while Caucasus and central Asia have an increase at 0.010 [0.001; 0.019]. Between 1990 and 2000, the increase in global SRB is at 0.005 [−0.001; 0.013]. During 1990–2000, the increases on regional SRB are significantly above zero in eastern Asia at 0.042 [0.009; 0.083], southern Asia at 0.014 [0.005; 0.022], and Caucasus and central Asia at 0.012 [0.005; 0.020]. Between 2000 and 2017, the changes of SRB are not significant for any regions. However, on a global level, the decrease of SRB during 2000–2017 is significantly below zero at −0.010 [−0.018; −0.002].

The regional SRB baseline values range from 1.031 [1.027; 1.036] in sub-Saharan Africa to 1.063 [1.055; 1.072] in southeastern Asia, 1.063 [1.054; 1.072] in eastern Asia, and 1.067 [1.058; 1.077] in Oceania (Table 1 and Fig. 1). When comparing to the conventional value of 1.05 for SRB baseline adopted by the UN WPP (37), the regional baseline values differ significantly from 1.05 for 6 out of 10 regions: significantly above 1.05 for “ENAN” (the combination of countries in Europe, North America, Australia, and New Zealand), southeastern Asia, eastern Asia, and Oceania and significantly below 1.05 for sub-Saharan Africa and Latin America and the Caribbean. In 2017, the aggregated SRB in three regions (southern Asia, Caucasus and central Asia, and eastern Asia) are significantly above their corresponding regional baseline median estimates. In 1990, the aggregated regional-level SRB in southern Asia and eastern Asia are significantly above their regional baseline median estimates.

National SRB Estimates Case Studies.

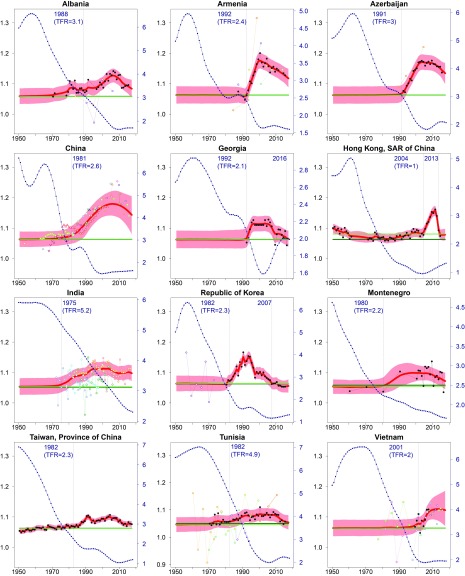
We illustrate SRB estimates for 12 countries which are identified to have strong statistical evidence of SRB inflation. The SRB median estimates and 95% uncertainty intervals for the 12 countries are shown in Table 2 and Fig. 2. TFR estimates are overlaid onto SRB estimates in Fig. 2, to illustrate the relationship between the start year of SRB inflation period and fertility decline, as incorporated into the model to estimate the start year of inflation period.

Table 2.

SRB results for countries with strong statistical evidence of SRB inflation

		SRB			Year
Country	Region	Start year	Max	2017	Start inflation	Max
India	southern Asia	1.061	1.113	1.098	1975	1995
		[1.035; 1.087]	[1.090; 1.137]	[1.071; 1.124]	[1970; 1981]
Albania	ENAN	1.079	1.127	1.083	1988	2006
		[1.058; 1.101]	[1.104; 1.150]	[1.054; 1.113]	[1973; 1997]
Montenegro	ENAN	1.056	1.099	1.072	1980	1997
		[1.031; 1.084]	[1.067; 1.130]	[1.045; 1.100]	[1971; 1991]
Tunisia	northern Africa	1.057	1.085	1.054	1982	2000
		[1.034; 1.080]	[1.061; 1.108]	[1.028; 1.081]	[1976; 1989]
Armenia	Caucasus and central Asia	1.059	1.176	1.117	1992	2000
		[1.034; 1.084]	[1.150; 1.203]	[1.087; 1.149]	[1990; 1993]
Azerbaijan	Caucasus and central Asia	1.068	1.171	1.134	1991	2003
		[1.041; 1.095]	[1.145; 1.197]	[1.097; 1.168]	[1988; 1994]
Georgia	Caucasus and central Asia	1.063	1.115	1.065	1992	2003
		[1.034; 1.098]	[1.090; 1.141]	[1.039; 1.092]	[1977; 1994]
Vietnam	southeastern Asia	1.076	1.126	1.122	2001	2012
		[1.052; 1.099]	[1.089; 1.171]	[1.070; 1.186]	[1991; 2005]
China	eastern Asia	1.073	1.179	1.143	1981	2005
		[1.047; 1.103]	[1.141; 1.221]	[1.079; 1.205]	[1972; 1989]
Hong Kong, SAR of China	eastern Asia	1.082	1.157	1.078	2004	2011
		[1.066; 1.098]	[1.140; 1.174]	[1.059; 1.098]	[2002; 2005]
Republic of Korea	eastern Asia	1.072	1.151	1.056	1982	1990
		[1.052; 1.092]	[1.131; 1.171]	[1.034; 1.078]	[1978; 1984]
Taiwan, Province of China	eastern Asia	1.069	1.100	1.076	1982	2004
		[1.060; 1.079]	[1.090; 1.110]	[1.065; 1.087]	[1972; 1987]

Countries are presented by region. Median estimates are numbers before brackets. Numbers in brackets are 95% uncertainty intervals. SRB “Max” refers to the maximum SRB after inflation starts. Year “Max” refers to the year in which the maximum SRB is after inflation starts.

Fig. 2.

SRB estimates during 1950–2017 for countries with strong statistical evidence of SRB inflation. The scale on the left y axis refers to SRB, and the scale on the right y axis refers to TFR. Red lines and shaded areas are country-specific SRB median estimates and their 95% uncertainty intervals. Dark green horizontal lines are median estimates for regional SRB baselines. Light green horizontal lines are median estimates for national SRB baselines. Observations from different data series are differentiated by colors, where VR data are black solid dots. The blue square dots are the UN WPP 2017 TFR estimates. Blue vertical lines indicate median estimates for start and end years (if before 2017) of SRB inflation period. TFR values in the start years of SRB inflation periods are shown.

Among the 12 countries, 9 are from Asian regions (Caucasus and central Asia, eastern Asia, southeastern Asia, and southern Asia). TFR values at the start of sex ratio transitions vary across countries. As shown in Fig. 2, India is a country with a high TFR value of 5.2 at the start of its inflation period in 1975, while SRB inflation is estimated to start in Vietnam in 2001 when its TFR declined to 2.0 and in Hong Kong, SAR of China in 2004 with a TFR at 1.0. Since the start of the inflation, SRBs reached their maximum before 2017 for all 12 countries. During the sex ratio transitions, SRB reached its maximum after 2000 in 9 countries. The earliest maximum occurred in Republic of Korea in 1990, and the latest occurred in Vietnam in 2012. The highest median estimates of in-country maximum SRB since the start of inflation are in China (1.179 [1.141; 1.221] in 2005), Armenia (1.176 [1.150; 1.203] in 2000), Azerbaijan (1.171 [1.145; 1.197] in 2003), Hong Kong, SAR of China (1.157 [1.140; 1.174] in 2011), and Republic of Korea (1.151 [1.131; 1.171] in 1990). The SRBs have converged back to the range of natural fluctuations in 2007 for Republic of Korea, in 2013 for Hong Kong (SAR of China), and in 2016 for Georgia. By 2017, the lowest SRBs among the 12 countries are 1.054 [1.028; 1.081] in Tunisia and 1.056 [1.034; 1.078] in Republic of Korea, while the highest are 1.134 [1.097; 1.168] in Azerbaijan and 1.143 [1.079; 1.205] in China.

Missing Female Births Estimates.

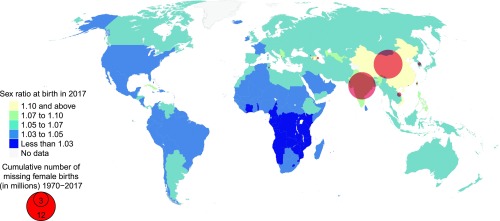
From 1970 to 2017, the total CMFB for the 12 countries with strong statistical evidence of SRB inflation is 23.1 [19.0; 28.3] million (Table 3 and Fig. 3). The majority of CMFB between 1970 and 2017 are concentrated in China, with 11.9 [8.5; 15.8] million, and in India, with 10.6 [8.0; 13.6] million. The CMFB between 1970 and 2017 in China and India made up 51.40% [41.28%; 61.28%] and 45.94% [36.09%; 55.83%], respectively, of the total CMFB.

Table 3.

CMFB for periods 1970–1990, 1991–2000, 2001–2017, and 1970–2017, for countries with strong statistical evidence of SRB inflation

	CMFB (thousands)				Proportion of the total CMFB, %
Country (region)	1970–1990	1991–2000	2001–2017	1970–2017	1970–1990	1991–2000	2001–2017	1970–2017
India	2,190	3,379	5,062	10,632	56.58	47.22	41.79	45.94
(S.A.)	[1,058; 3,736]	[2,426; 4,362]	[3,488; 6,667]	[7,972; 13,597]	[28.97; 94.09]	[36.51; 58.53]	[31.46; 53.06]	[36.09; 55.83]
Albania	0	4	7	11	0.00	0.05	0.06	0.05
(ENAN)	[0; 7]	[1; 7]	[5; 9]	[6; 21]	[0.00; 0.20]	[0.01; 0.11]	[0.04; 0.08]	[0.03; 0.09]
Montenegro	0	1	1	2	0.01	0.01	0.01	0.01
(ENAN)	[0; 1]	[0; 1]	[1; 2]	[1; 4]	[0.00; 0.05]	[0.00; 0.02]	[0.00; 0.01]	[0.01; 0.02]
Tunisia	5	13	19	37	0.13	0.19	0.15	0.16
(N.A.)	[0; 13]	[6; 20]	[9; 29]	[20; 56]	[0.01; 0.43]	[0.08; 0.30]	[0.07; 0.26]	[0.08; 0.25]
Armenia	0	6	14	19	0.00	0.08	0.11	0.08
(C.C.A.)	[0; 0]	[5; 7]	[11; 16]	[16; 23]	[0.00; 0.00]	[0.06; 0.11]	[0.08; 0.15]	[0.07; 0.11]
Azerbaijan	0	15	56	72	0.00	0.21	0.47	0.31
(C.C.A.)	[0; 1]	[10; 22]	[47; 66]	[59; 85]	[0.00; 0.03]	[0.13; 0.33]	[0.36; 0.63]	[0.24; 0.40]
Georgia	0	6	6	12	0.00	0.08	0.05	0.05
(C.C.A.)	[0; 5]	[4; 8]	[4; 10]	[8; 19]	[0.00; 0.13]	[0.05; 0.12]	[0.03; 0.09]	[0.03; 0.09]
Vietnam	0	0	254	254	0.00	0.00	2.10	1.10
(S.E.A.)	[0; 0]	[0; 47]	[140; 400]	[143; 409]	[0.00; 0.00]	[0.00; 0.64]	[1.13; 3.50]	[0.60; 1.82]
China	1,617	3,622	6,656	11,895	41.76	50.60	54.95	51.40
(E.A.)	[81; 3,899]	[2,426; 4,800]	[4,423; 8,953]	[8,504; 15,780]	[3.13; 69.42]	[38.99; 61.27]	[43.25; 65.33]	[41.28; 61.28]
Hong Kong, SAR of China	0	0	7	7	0.00	0.00	0.06	0.03
(E.A.)	[0; 0]	[0; 0]	[5; 9]	[5; 9]	[0.00; 0.00]	[0.00; 0.00]	[0.04; 0.08]	[0.02; 0.04]
Republic of Korea	50	91	14	155	1.30	1.27	0.12	0.67
(E.A.)	[36; 82]	[73; 111]	[5; 31]	[122; 206]	[0.68; 3.06]	[0.94; 1.73]	[0.04; 0.27]	[0.49; 0.95]
Taiwan, Province of China	9	21	17	47	0.22	0.29	0.14	0.20
(E.A.)	[2; 25]	[10; 30]	[7; 29]	[23; 73]	[0.04; 0.73]	[0.13; 0.45]	[0.06; 0.25]	[0.10; 0.33]

Countries are presented by region. Median estimates are the numbers before the brackets. Numbers inside the brackets are the 95% uncertainty intervals. Proportions may not sum up to 100%, due to rounding. S.A., southern Asia; N.A., northern Africa; C.C.A., Caucasus and central Asia; S.E.A., southeastern Asia; E.A., eastern Asia.

Fig. 3.

SRB in 2017 and the CMFB during 1970–2017, by country. Countries are colored by the levels of their SRB median estimates. Radii of circles are proportional to CMFB for countries. For high-resolution plot of Fig. 3, see SI Appendix, section 11.

Discussion

Our study is a systematic analysis of SRB for all countries that produces annual estimates from 1950 to 2017 and assesses baseline levels and imbalances. We have compiled an extensive SRB database to include all available data from national VR systems, international surveys on full birth history, censuses, and national-level surveys and reports. These are synthesized using a Bayesian hierarchical model for estimation, which allows sharing of information between data-rich country-years and neighboring country-years with limited information or without data.

The SRB baseline value is related to individual-level factors including maternal or paternal age at conception, birth order, sex of the preceding child, maternal weight, family size, socioeconomic conditions, environment condition for mother during pregnancy, that is, the Trivers–Willard hypothesis, and ethnic origin (1–13, 43–51). Most of the aforementioned information is not available for all country-years of interest. Two exceptions are TFR (as a proxy of parity) and gross domestic product (GDP) per capita. We do not find a consistent relation between the observed SRB and TFR and GDP per capita at the regional level (see SI Appendix, section 4 for detailed analyses). We do estimate the differences in SRB due to ethnic origin, which we approximate by grouping countries from similar regions or with similar ethnic origins due to European colonization. Further refinements of the grouping are possible, for example, to divide sub-Saharan Africa into smaller regions since there is additional heterogeneity in the biological SRB levels within the region (3, 4, 9), or to divide Latin America and the Caribbean into two subregions because of the majority of African ancestry in the Caribbean countries. However, in the absence of unanimously agreed regional groupings, we opt for larger aggregations in this study. We compare the model-based baseline estimates with information from studies on SRB differences by ethnicity (SI Appendix, section 6) and find that our results are consistent with those studies. Previous analyses of time trends in SRB in several industrial countries found that changes were explained by country-specific circumstances rather than changes in ethnic baseline values (2, 12, 46, 52–54). Hence, we model the SRB baseline values as constant over time and add in a time series component to capture temporal fluctuations around baseline values.

We highlight the necessity to acknowledge the baseline difference in SRB across regions and across countries within regions. The estimated regional baseline values differ significantly from 1.05 for the majority of the regions we study. In addition, almost half (88 out of 212) of the estimated country-level baseline values, accounting for ethnic difference across countries within a region, are significantly different from 1.05. The resulting baseline values provide a better reflection of observed heterogeneity than the widely adopted value 1.05 which is typically used in population estimation (37, 55–59). Based on the estimate of 38.2 million total births in sub-Saharan Africa in 2017 (37), an estimated SRB of 1.03 would result in 183,400 more female births than 1.05 would. When using 1.05 instead of the regional baseline value as a reference in sub-Saharan Africa, potential deviations that would signify the early stage of SRB inflation would be more likely to be misjudged as natural fluctuations, and the severity of prenatal sex discrimination would be more probable to be underestimated. Note, however, that this is a hypothetical statement; we find no significant evidence of SRB inflation in sub-Saharan African countries to date.

We find that, during 1970–2017, missing female births occurred mostly in China and India, resulting in CMFB of 11.9 [8.5; 15.8] million and 10.6 [8.0; 13.6] million, respectively. Details on data preprocessing for China and India are in SI Appendix, section 1. Our estimates of AMFB for China and India are similar, albeit slightly lower than those by other studies on missing female births (60, 61); see SI Appendix, section 7.

There are limitations to our modeling of the SRB imbalance. Firstly, in the SRB inflation model, we incorporate fertility decline as a covariate. The other necessary conditions for sex-selective abortion, for example, the intensity of son preference, the tolerance for induced abortion, the accessibility of the technology of early sex detection, and legality of medical abortion (36), are not included due to the lack of information for all country-years of interest. An analysis of the relation between son preference—as measured through the DSRB—and the severity of the SRB imbalance does not suggest that son preference is predictive of the intensity (SI Appendix, section 4). Secondly, the functional form used for the inflation is a simple trapezoid one. Attempts to fit more-flexible models were unsuccessful due to identifiability issues between natural fluctuations and the actual inflation. If more detailed information regarding predictors and/or sex-selective abortion becomes available, the model can be expanded to incorporate it and provide more detailed insights into SRB inflation. Thirdly, some countries may have limited data before 1970, the year when sex-selective abortion became possible. Consequently, for such countries, the national SRB baselines are mostly informed by region, albeit with uncertainty that captures the cross-country variability in national baselines.

We introduce the concept of being at risk for SRB inflation, which refers to populations where masculinization of the SRB may be (but is not necessarily) present. We identify countries at risk for SRB inflation using a combination of qualitative and quantitative measures. For the quantitative selection criteria, we identify countries with high SRLB/DSRB using universal cutoff values suggested by Bongaarts (15), regardless of ideal family size (62). Out of the 212 countries considered in this study, we obtain information on son preference in the form of SRLB/DSRB and/or the literature on 90 countries. We also identify an additional 65 countries with VR coverage for the period 1970–2017 for which no SRB inflation has been suggested. Fifty-seven countries have no information available to establish whether they are at risk for SRB inflation (given in SI Appendix, Table S18). For these countries, we assume that they are not at risk for SRB inflation. This is a study limitation, as a sex ratio bias may go unnoticed. The limitation is mainly for the affected countries only; the countries without information contribute only 3.2% to the total number of births globally in 1970–2017.

To identify countries with strong statistical evidence of SRB inflation among countries at risk for SRB inflation, we assess the uncertainty of AMFB and select countries with inflation probability of at least 95%. Twelve countries are identified, including one country (Tunisia) for which SRB inflation has not been reported in the articles obtained in the literature review. A lower cutoff of the inflation probability would have resulted in a larger set of countries being identified as having inflation. In particular, Singapore and Morocco have probabilities higher than 80% of having inflation. We present the uncertainty regarding the SRB inflation for these countries (see SI Appendix, section 2). We do not highlight the measured SRB inflation in countries with greater uncertainty, because there is a higher probability that the measured inflation is just a natural fluctuation. In addition, we find that, for countries with greater uncertainty about possible inflation, the estimation of the start year of inflation is sensitive to model assumptions (see SI Appendix, section 5 for a sensitivity analysis). In-depth analyses are needed to confirm the existence or nonexistence of the SRB inflation for such countries.

We focus on assessing the SRB imbalance due to sex-selective abortion. Other factors like war, famine, natural disaster, and economic depression are reported to result in rapid and transient changes in SRB (49, 51, 63, 64). Analyzing how these crises affect the level and trend of SRB is beyond the scope of our study. Moreover, data quality issues during crises are common. We adopt procedures from the UN Inter-agency Group for Child Mortality Estimation (IGME) (65) to exclude data from country-periods with national conflicts and natural disasters.

Our study analyzes national-level SRB, which may mask SRB disparities at the subnational level or SRB imbalances for subgroups of births. For example, sex-selective abortion has been reported for higher-order births in Nepal (66), and geographical differences in SRB have been documented for Indonesia (67). The national-level SRB imbalance depends on the proportion of births affected. If the proportion of birth with imbalanced sex ratio is small enough, the subgroup-specific imbalances may not be flagged as a statistically significant imbalance on the national level and may not be distinguishable from a natural fluctuation. Future work should assess subnational divisions to better understand where female births are most discriminated against in the prenatal period.

The findings of our study underscore the importance of the assessment of the sex ratio at birth and its natural variation over time and across countries, as well as the gap in data needed to provide more precise assessments.

Materials and Methods

Details on the database and model are provided in SI Appendix and summarized in this section.

Model Inputs.

We produce SRB estimates for 212 countries with total population size greater than 90,000 as of 2017. Due to data availability and inclusion criteria, we construct a database with data from 202 countries. The database includes 10,835 data points on national-level SRB, corresponding to 16,602 country-years of information. On average, 82.2 country-years of data are available for each of the 202 countries with data.

In the SRB database, we compile VR data from the UN Demographic Yearbook and the Human Mortality Database, sampling registration system data for India, Pakistan, and Bangladesh from annual reports, international survey data from microdata or reports (Demographic and Health Surveys, World Fertility Surveys, Reproductive Health Survey, Multiple Indicator Cluster Surveys, Pan Arab Project for Family Health, and Pan Arab Project for Child Development), and census and national-level survey data from reports. For survey data with available microdata files, we use a jackknife method to calculate sampling errors for observations with varying reference periods (SI Appendix, section 1). We conduct data quality checks for VR data before inclusion (SI Appendix, section 1). We exclude data from country-periods where national-level conflict and natural disasters occur. The crises are identified using the UN IGME criteria (65). Additional information on data processing for China and India is given in SI Appendix, section 1. Detailed information on data sources is in SI Appendix, Table S19.

Estimates of TFR and number of births for all countries are obtained from the UN WPP 2017 version (37); we use the annual estimates from 1950 to 2017.

Selection of Countries at Risk for SRB Inflation.

We generate DSRB in 220 Demographic and Health Surveys from 73 countries and generate the SRLB in 283 Demographic and Health Surveys from 83 countries. We follow the steps described in Bongaarts (15) to compute DSRB and SRLB. We identify 11 countries with high DSRB and 13 countries with high SRLB. We also conduct a systematic literature review to identify countries with empirical evidence of SRB inflation, as well as countries with populations that are considered to have a son preference or to be a patrimonial society. Twenty-three countries are identified by the literature review. In total, out of the 212 countries considered, there is information on DSRB/SRLB criteria and/or literature for 90 countries, and we identify 29 countries at risk for SRB inflation using the three selection criteria. We assume that the remaining 122 countries without information on DSRB/SRLB and literature are not at risk for SRB inflation. This includes 65 countries with VR coverage during 1970–2017, which we assume would have been identified in the literature search if SRB imbalance or son preference were present. The remaining 57 countries without information cover only 3.2% of all births globally in 1970–2017. SI Appendix, section 2 explains the selection in detail.

Model of Country-Years Without SRB Inflation.

We model SRB in country-years without inflation as a product of two components: (i) a national baseline value, which is assumed to be constant over time, and (ii) a country-year–specific multiplier that captures the natural fluctuation of the country-specific SRB around its respective baseline value over time. We allow for baseline values to differ across countries within the same region, to incorporate SRB differences due to ethnic origin on a national level in a region. The national baselines are pooled toward the same regional baseline. The regional baselines are to capture the ethnic difference across regions. We assign independent uniform priors to each of the regional baseline values. The country-year–specific multiplier is modeled with an autoregressive time series process of order 1 within a country. For countries without any data or with very limited information, the multiplier is equal to (or shrunk toward) 1, such that the estimated SRBs without inflation are given by (or close to) their corresponding national baselines. For countries where the data suggest different levels or trends, the multipliers capture these natural deviations from national baselines.

To estimate SRB for country-years without inflation, and to estimate baseline values, we fit the model to a reduced database by excluding data from the 29 countries at risk for SRB inflation with reference year from 1970 onward. We keep the data with reference year before 1970 for the 29 countries, since sex-selected abortion technology was not widely available or affordable before 1970.

Model of Country-Years with Potential SRB Inflation.

We model SRB in the 29 countries at risk for SRB inflation as the sum of two parts: (i) the inflation-free SRB level, given by the model of country-years without SRB inflation as described above, and (ii) a nonnegative SRB inflation factor. The country-year–specific SRB inflation factor is modeled from 1970 onward for those countries. The parametrization of inflation factor is described in the introduction. The hierarchical distributions for the start year of SRB inflation follow a truncated $t$ distribution to capture start years with outlying TFR levels. Normal distributions are used for the other parameters of the trapezoid function, with lower truncations at zero. We assign vague priors to the mean and SD of these truncated distributions, with the exception of the mean of the start year of SRB inflation. The mean for the start year is determined by an analysis of the relation between fertility levels and the start as observed in countries with high-quality VR data (SI Appendix, section 2).

Out of the 29 countries at risk for SRB inflation, we identify 12 countries with strong statistical evidence of SRB inflation (as listed in Table 2). These countries are selected based on the AMFB: a country is identified as having SRB inflation if the probability of AMFB greater than zero is at least 95% for at least 1 y during 1970–2017.

Data Quality Model.

We construct a data quality model to account for varying data quality from VR systems, surveys, and censuses. We account for differences in error variance across observations, where error variance is given by stochastic errors for VR data and the sum of sampling and nonsampling errors for non-VR data. Sampling errors are computed to reflect the sampling design. Nonsampling errors are estimated within the model by data source type. Errors—and hence the error variance—associated with non-VR data tend to be larger than errors associated with VR data, and this is reflected in the model fitting, as the weight assigned to a data point increases as its error variance decreases. Resulting model-based estimates are more strongly weighted by observations with smaller errors, and uncertainty ranges are narrower for country-periods with more observations with smaller error variance. The details are in SI Appendix, section 2.

Model Validation.

We use two out-of-sample and in-sample validation exercises, and a simulation to assess model performance.

In the first out-of-sample validation exercise for countries without SRB inflation, we leave out all data that are collected after 2004, corresponding to 20% of the global reduced database. We fit the model without the inflation factor to the remaining training database, and obtain median estimates, projections, and uncertainty intervals that would have been constructed in the year 2005 based on available data at that time. We also conduct an in-sample validation to test the performance of the model without the inflation factor. We randomly leave out 20% of the global reduced database and fit the model with the training database. We repeat this process 30 times.

In the second out-of-sample exercise, we focus on the 29 countries at risk for SRB inflation and leave out all data in these countries collected after 2009, corresponding to approximately 20% of the data for these countries. We fit the model with the inflation factor to the training set to obtain median estimates and projections for the SRB and inflation. We also assess the performance of the inflation model by simulating the SRB for each country after 1970 based on the median estimates of the global parameters of the inflation model (and not the country-specific data).

We calculate various validation measures to assess model performance, including prediction errors and coverage. The error for each left-out observation is defined as the difference between the left-out observation and the posterior median of the predictive distribution based on the training database. Coverage refers to the percentage of left-out data points falling above or below their corresponding 95% or 80% prediction intervals. For the 30 rounds of in-sample validations, we compute the averages of these measures. The model validation results suggest that the models are reasonably well calibrated (SI Appendix, section 3).