Hemodynamic Variables in Aneurysms are Associated with Thrombotic Risk in Children with Kawasaki Disease

Abstract

Background

Thrombosis is a major adverse outcome associated with coronary artery aneurysms (CAAs) resulting from Kawasaki disease (KD). Clinical guidelines recommend initiation of anticoagulation therapy with maximum CAA diameter (D_max) ≥8mm or Z-score ≥10. Here, we investigate the role of aneurysm hemodynamics as a superior method for thrombotic risk stratification in KD patients.

Methods and Results

We retrospectively studied ten KD patients with CAAs, including five patients who developed thrombosis. We constructed patient-specific anatomic models from cardiac magnetic resonance images and performed computational hemodynamic simulations using SimVascular. Our simulations incorporated pulsatile flow, deformable arterial walls and boundary conditions automatically tuned to match patient-specific arterial pressure and cardiac output. From simulation results, we derived local hemodynamic variables including time-averaged wall shear stress (TAWSS), low wall shear stress exposure, and oscillatory shear index (OSI). Local TAWSS was significantly lower in CAAs that developed thrombosis (1.2±0.94 vs. 7.28±9.77 dynes/cm², p=0.006) and the fraction of CAA surface area exposed to low wall shear stress was larger (0.69±0.17 vs. 0.25±0.26 %, p=0.005). Similarly, longer residence times were obtained in branches where thrombosis was confirmed (9.07±6.26 vs. 2.05±2.91 cycles, p=0.004). No significant differences were found for OSI or anatomical measurements such us D_max and Z-score. Assessment of thrombotic risk according to hemodynamic variables had higher sensitivity and specificity compared to standard clinical metrics (D_max, Z-score).

Conclusions

Hemodynamic variables can be obtained non-invasively via simulation and may provide improved thrombotic risk stratification compared to current diameter-based metrics, facilitating long-term clinical management of KD patients with persistent CAAs.

1. Introduction

Thrombosis is the primary risk associated with coronary artery aneurysms (CAAs) resulting from Kawasaki disease (KD). However, factors that predict thrombus formation in these patients remain incompletely known. A major clinical decision in the management of KD patients with CAAs is when to initiate systemic anticoagulation therapy and when to discontinue it after remodeling has occurred. Current American Heart Association (AHA) guidelines are based on limited evidence and rely solely on anatomical measurements, with recommended initiation of systemic anticoagulation for CAA with a maximum diameter ≥8mm or Z-score≥10 [1]. We hypothesize that hemodynamics might provide improved thrombotic risk stratification metrics for KD patients.

Simulations based on computational fluid dynamics (CFD) can now non-invasively provide patient-specific hemodynamic information from vascular imaging data. CFD and finite element methods, originally developed to provide predictive simulation capabilities in traditional engineering fields, including the aerospace, turbomachinery, and naval industries, have been translated to healthcare applications in recent decades. Recent clinical trials have confirmed the utility of CFD for assessing severity of coronary stenosis, leading to the first FDA approval of CFD technology for clinical use. CFD simulations can also provide variables such as wall shear stress (WSS), the frictional force exerted by the blood on the arterial wall, and residence time, a measure of flow stagnation, which are known to contribute to thrombus formation but are not otherwise clinically available. Numerous studies have used computational simulations to relate hemodynamic quantities to thrombus formation in atherosclerotic coronary artery disease [2,3], abdominal aortic aneurysms [4,5] and medical devices [6–8], suggesting that abnormal flow conditions induce a pro-coagulant state. The fluid forces on endothelial cells and blood components such as platelets can trigger activation and play an important role in platelet adhesion and clustering [9–11]. Secondary flows generated by complex geometries such as aneurysms can also result in recirculation and entrapment of particles, facilitating thrombus initiation and growth [4,5].

Previous computational and experimental studies in KD have suggested that CAA hemodynamics may play an important role in thrombus formation [12–16]. We investigated multiple hemodynamic variables and retrospectively evaluated their sensitivity and specificity for thrombosis risk stratification, compared to anatomical measurements, for a subset of KD patients. This is the first study to directly correlate hemodynamic data with patient outcomes, with the aim of providing information that could ultimately improve CAA thrombosis risk stratification and facilitate more informed clinical decisions regarding initiation of anticoagulation therapy.

2. Methods

2.1. Patient population

We retrospectively identified 10 KD patients followed at The Hospital for Sick Children (SickKids) and who underwent a Cardiac Magnetic Resonance Imaging (CMRI) study as part of their routine clinical care. This study was approved by the Institutional Review Board at Stanford University and The Hospital for Sick Children, University of Toronto.

Our cohort included KD patients with at least one CAA, 5 patients who had developed thrombosis during the course of their disease, and 5 non-thrombosed patients with no confirmed thrombosis up to the last follow-up clinical visit. Imaging data were all collected post-thrombotic event and the scan dated closest to thrombus detection was selected for the study. The thrombosis group included only patients with no significant changes in coronary anatomy between the time of thrombosis and the CMRI study; this anatomical evaluation was based on longitudinal echocardiographic measurements of CAA diameter and Z-scores [17]. In three out of the five patients with confirmed thrombosis, the thrombus was still visible in the CMRI. In those cases, a patent lumen without thrombus was considered to construct the anatomical model. Patients with incomplete clinical history or insufficient image data quality, which precluded anatomical model construction, were not selected for the study. This cohort of ten patients included 32 total aneurysms (5 thrombosed), defined as the coronary artery regions where Z-score>5. All patients but one were on systemic anticoagulation at the time of thrombosis, or the imaging study if no thrombotic event was reported (Table 1). The start date of oral anticoagulation with enoxaparin was subsequent to the acute phase of disease. One patient presented with thrombus on admission to SickKids hospital so no anticoagulation therapy had been administered prior to thrombosis detection. Only one patient was receiving dual-antiplatelet therapy.

Table 1.

Demographic and clinical characteristics of patients

Patient ID	Age at KD diagnosis [years]	Age at CMRI [years]	Sex	BSA	Cardiac Output [l/min]	Pressure Sys/Dias [mmHg]	Thrombosis	Thrombosis Location	Medication at time of thrombosis/ CMRI
									Aspirin	Clopidogrel	Enoxaparin	Warfarin
1	0.4	6.8	M	0.99	3.79	106/48	+	RCA	+	−	−	+
2	8.4	16.7	M	1.75	3.42	102/56	+	LAD	+	−	+	−
3	3.0	3.5	M	0.66	2.31	82/39	+	RCA	+	+	+	−
4	5.4	6.9	M	0.90	4.13	99/54	+	RCA	+	−	−	+
5	0.5	0.6	F	0.63	1.85	76/40	+	LAD	+	−	−	−
6	7.9	14.9	M	1.44	7.86	115/67	−	NA	+	−	−	+
7	12.1	16.7	F	1.64	5.69	102/47	−	NA	+	−	−	+
8	8.7	9.1	M	1.34	6.53	128/68	−	NA	+	−	+	−
9	11.0	17.6	M	1.41	4.21	120/72	−	NA	+	−	−	+
10	0.1	11.1	M	1.15	4.93	111/53	−	NA	+	−	−	+

KD=Kawasaki disease; BSA=body surface area; RCA=right coronary artery; LAD=left anterior descending; CCX=circumflex coronary artery; CMRI=cardiac magnetic resonance imaging, NA=Not Applicable

2.2. Cardiac magnetic resonance imaging protocol

CMRI imaging was performed on a Siemens 1.5T MRI scanner (Siemens Medical Solutions, Erlangen, Germany). The protocol included magnetic resonance angiography of the heart and the coronary arteries performed after the injection of gadolinium-based contrast (Gadovist), using a cardiac and respiratory-gated 3D TrueFISP sequence. Phase contrast MRI imaging was performed in the ascending aorta, in orthogonal planes distal to the aortic valve, using an encoding velocity of 150 cm/s.

2.3. Computational simulations

Patient-specific modeling and simulation was performed using the SimVascular [18] open source software, proceeding from image data to temporal and spatially resolved pressure and velocity fields (Figure S1).

2.3.1. Patient-specific 3D modeling

We used SimVascular modeling tools to construct patient-specific anatomical models of the main coronary arteries (right, left main, left anterior descending and circumflex) and the aorta, as well as the aortic arch branches (brachiocephalic artery, left common carotid artery and left subclavian artery).

2.3.2. Finite element mesh

To prepare for simulations, we generated a finite element mesh using the open source package TetGen [19] included in SimVascular. To ensure mesh convergence and achieve local accuracy near the wall, which is necessary to adequately resolve WSS, we constructed a boundary-layer mesh and used local mesh refinement in the aneurysmal regions.

2.3.3. Fluid-solid equations solver

We used the stabilized finite element solver included in SimVascular to solve the time-dependent Navier-Stokes equations, which govern blood flow. Blood was modeled as an incompressible Newtonian fluid (density=1.06 g/cc, dynamic viscosity=0.04 dynes/cm²). Solver numerics have been adapted for cardiovascular applications and included backflow stabilization [20], implicit boundary condition coupling [21], and a specialized linear solver [22].

Fluid-structure interaction, required to efficiently model vessel wall deformability, was achieved using the coupled momentum method [23]. We assigned wall material properties (elasticity, Young’s modulus) and wall thickness to each independent vessel. In this study, we used Phase Contrast MRI to estimate patient-specific aortic elastic modulus from changes in the cross-sectional area over the cardiac cycle; E_aorta=kE_p, where E_p is a modified Peterson’s elastic modulus [24], computed based on cross-sectional distensibility instead of diameter (E_p=A_d(p_s-p_d)/(A_s-A_d)), and k=10 was derived from the thin wall assumption (t<r/10). Patient aortic pressures (ps, pd) were acquired during the clinical visit previous to the CMRI study. This method allowed us to incorporate patient-specific arterial properties (E_aorta=0.25±0.1 MPa) in our models and therefore obtain patient-specific aortic compliance. The elastic modulus for the coronaries and aortic branches was set to literature values [24–27] (E_cor=1.15 MPa, E_neck=0.7 MPa). Arterial wall thickness for the aorta was calculated from previously reported radius-thickness ratios [27] and coronary artery thickness was assigned based on literature morphometric measurements [28].

2.3.4. Boundary conditions

A closed-loop Lumped Parameter Network (LPN) was used to model the heart and the distal vasculature. LPNs provide a means of representing distal vascular resistance and capacitance using an electrical analogy and have been used previously for single ventricle and coronary artery bypass graft (CABG) patients [29–36]. During systole, the distal coronary resistance increases substantially due to increasing intra-myocardial pressure resulting from myocardial contraction, causing the coronary flow to be out of phase with the systemic flow. Specialized boundary conditions that couple the intra-myocardial pressure to the coronary flow are required to replicate this complex physiology in the numerical model. A schematic of the closed-loop LPN used to represent the coronary and systemic downstream circulation in a KD patient is shown in Figure S1.

We employed an automated parameter tuning method [37] to estimate patient-specific LPN parameters so our model matched patient systolic/diastolic pressure and cardiac output (Table 1). Parameters were normalized to patient stroke volume and body surface area to facilitate the automatic tuning process. Using this framework, we matched patient-specific targets systematically with an average error of 5.4±4.1%, which is well within the error range associated with the clinical measurements.

2.4. Hemodynamic variables and patient classification

Simulated pressure and velocity fields were used to derive hemodynamic quantities presumed to be clinically relevant to thrombus formation. We computed time-averaged wall shear stress (TAWSS), time-averaged wall shear stress gradient (TAWSSg), and oscillatory shear index (OSI). These quantities were temporally averaged over one cardiac cycle and spatially averaged over each aneurysm surface. Additionally, we defined low wall shear stress exposure (A_WSS) as the non-dimensional ratio of area below a specific value of TAWSS and total aneurysm surface area. To compute residence time (RT) we solved a transport equation, using a finite element method [38]. We selected a region of interest in the model (i.e. branch) and calculated the average time a parcel of fluid spends in that specific region based on the pre-computed velocity field.

In addition to hemodynamic variables, we included anatomical measurements in our analysis, specifically maximum aneurysm diameter (D_max), Z-score and total aneurysm surface area (S_a), extracted directly from the constructed anatomical models.

To determine potential guidelines for thrombotic risk stratification based on our simulation results, data-driven cutoff values for hemodynamic variables were obtained from receiver operating characteristic (ROC) curves. The optimal cutoff was selected as the threshold that maximized the distance to the identity line, and a patient was considered at high-risk of thrombosis if one CAA or branch met classification criterion. Threshold values to compute low TAWSS exposure were also derived from TAWSS ROC curve analysis.

2.5. Statistical analysis

We used Wilcoxon rank test to compare local hemodynamics (TAWSS, TAWSSg, OSI, A_WSs) and geometric variables (D_max, Z-score, S_a) between the thrombosed and non-thrombosed CAAs, with p values <0.05 considered to be significant. Residence times were analyzed on a per branch basis also using Wilcoxon rank test. Correlations between hemodynamics and CAA geometry were evaluated using Pearson’s linear correlation coefficient.

3. Results

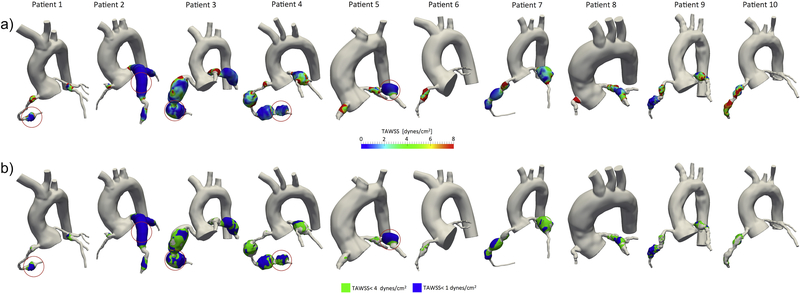
Patient demographics and clinical data are summarized in Table 1. Ten patient-specific coronary models were constructed for this study (Figure 1) and a total of 32 CAAs (19 RCA, 10 LMCA/LAD, 3 CCX; 5 thrombosed) were identified and analyzed; in some cases multiple aneurysms existed in a single branch. Spatial distribution of relevant hemodynamic quantities such as TAWSS or A_WSS, demonstrated qualitative correlation with thrombosis (Figure 1). In particular, areas of low TAWSS generally occurred in areas of confirmed thrombus formation.

Figure 1.

a) Local coronary artery aneurysm spatial distribution of time-averaged wall shear stress (TAWSS) obtained from computational simulations. Thrombosed coronary artery aneurysms are circled in red, showing correspondence between localized low TAWSS and thrombosis. b) Low wall shear stress exposure computed locally at each coronary artery aneurysm. Thrombosed coronary artery aneurysms are circled in red, larger aneurysm surface area exposed to low wall shear stress (TAWSS < 3 dynes/cm², TAWSS < 1 dynes/cm²) is correlated with thrombosis locations.

3.1. Local hemodynamic variables identify aneurysmal regions at higher risk of thrombosis

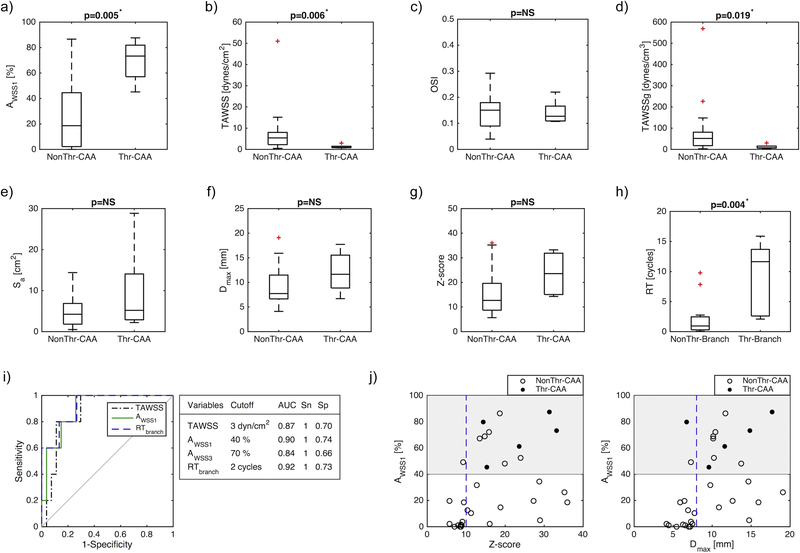
Quantitative analysis of the hemodynamic variables revealed significant differences between CAAs free of thrombosis and those with confirmed thrombosis (Figure 2). Local TAWSS corresponding to thrombus locations was significantly lower than for other CAAs where no thrombosis occurred (1.2±0.94 vs. 7.28±9.77 dynes/cm², p=0.006) and so was TAWSSg (11.83±10.66 vs. 75.63±112.34 dynes/cm³, p=0.019). The fractions of CAA surface area exposed to low TAWSS were also significantly larger for both threshold values considered: 3 dynes/cm², A_WSS3 (0.90±0.1 vs. 0.51±0.33, p=0.016) and 1 dyne/cm², A_WSS1 (0.69±0.17 vs. 0.25±0.26, p=0.005). Similarly, RT was significantly increased in branches with CAAs where thrombosis occurred (9.07±6.26 vs. 2.05±2.91 cardiac cycles, p=0.004). No significant differences were found for OSI (0.14±0.05 vs. 0.15±0.06, p=0.880) or geometric variables: S_a (9.70±11.04 vs. 4.75±3.50 cm², p=0.361), D_max (12.09±4.32 vs. 9.40±3.78 mm, p=0.213), Z-score (23.58±8.78 vs. 15.58±8.99, p=0.077).

Figure 2.

Analysis of hemodynamic and geometric parameters for thrombosed and non-thrombosed CAAs and branches: a) low wall shear stress exposure (A_WSS1 = area exposed to TAWSS < 1 dyne/cm²), b) time-averaged TAWSS, c) oscillatory shear index (OSI), d) time-averaged wall shear stress gradient (TAWSSg), e) aneurysm surface area (S_a), f) maximum aneurysm diameter (D_max,) g) Z-score and h) residence time (RT), i) ROC curves and cutoff values for time-averaged wall shear stress (TAWSS) (AUC = 0.87), low wall shear stress exposure (A_WSS1) (AUC = 0.9), and residence time (RT) (AUC = 0.92), j) Comparison between low shear stress exposure (A_WSS1) and geometric variables. CAA = Coronary artery aneurysm; NonThr = No confirmed thrombosis; Thr = Confirmed thrombosis; AUC=Area under the curve, Sn = Sensitivity; Sp = Specificity

Pearson correlation coefficients computed for TAWSS vs. Z-score (r²=−0.35, p=0.047), TAWSS vs. D_max (r²=−0.36, p=0.044), A_WSS1 vs. Z-score (r²=0.39, p=0.028), A_WSS1 vs. D_max (r²=0.45, p=0.011) indicated low correlation between hemodynamic and geometrical variables. A large spread in TAWSS and A_WSS was observed across the range of D_max and Z-scores.

3.2. Patient thrombotic risk stratification was improved using hemodynamic variables

Area under the ROC curves (AUC) showed good accuracy of the proposed hemodynamic variables for thrombosis risk stratification (AUC_tawss=0.87, AUC_AWSS1=0.9, AUC_AWSS3=0.84, AUC_Rt=0.92). Resulting thresholds and associated sensitivities and specificities are presented in Figure 2. Patient-specific assessment of thrombotic risk (Table 2) according to the hemodynamic cutoff values had 100% sensitivity and improved specificity, TAWSS (specificity=0.6), A_WSS1 (specificity=0.6), A_WSS3 (specificity=0.6), RT (specificity=0.8), compared to standard clinical metrics, D_max (sensitivity=0.8, specificity=0.4) and Z-score (sensitivity=1, specificity=0.2).

Table 2.

Patient classification according to coronary artery aneurysm thrombosis risk

Patient ID	1	2	3	4	5	6	7	8	9	10
Confirmed Thrombosis	+	+	+	+	+
Dmax > 8 mm	•	•	•	•			•	•	•
Z-score >10	•	•	•	•	•		•	•	•	•
TAWSS < 3 dynes/cm2	•	•	•	•	•		•		•
AWSS3 > 70%	•	•	•	•	•		•		•
AWSS1 > 40%	•	•	•	•	•		•		•
RT > 2 cycles	•	•	•	•	•		•

+ Confirmed thrombosis; •Positive predicted thrombosis risk; TAWSS=time-averaged wall shear stress; A_WSS3=area exposed to TAWSS < 3 dyne/cm²; A_WSS1=area exposed to TAWSS < 1 dyne/cm²; RT=residence time; D_max=maximum aneurysm diameter

4. Discussion

This study defines associations of hemodynamic data with patient outcome data regarding thrombosis in patients with persisting CAAs post-KD. While previous studies analyzed flow conditions in the CAAs for KD patients and reported abnormal flows characterized by low velocities and recirculation [15,16], results were not statistically associated with confirmed thrombotic events. Prior studies also showed that the presence of an aneurysm leads to abnormal hemodynamics quantified by WSS and residence time [13,14]. Here for the first time we used a multi-scale approach that includes deformable wall capabilities and a closed-loop LPN to characterize KD coronary artery hemodynamics. Our results suggest that these hemodynamic variables are able to identify regions at highest risk of thrombosis (Figure 1). Based on our analysis, using hemodynamic variables for thrombotic risk stratification reduces the number of false positives while retaining a similar true positive rate, thus improving specificity (Table 2).

We reported five KD cases with confirmed thrombosis, and in four of these, thrombus location corresponded to aneurysms with lowest TAWSS values (1^st quartile) and largest A_WSS (4^th quartile). For the remaining patient (patient 1) TAWSS and A_WSS were in the 2^nd and 3^rd quartile respectively. Aneurysms adjacent to those where thrombus developed also presented moderately low TAWSS values (lower-half), suggesting that multiple aneurysms or complex geometries may contribute to flow conditions that favor thrombus initiation and growth. Among all patients who experienced thrombosis, except patient 2, the lowest TAWSS values were located in the thrombosed aneurysm. For patient 2, we obtained comparable TAWSS in LAD and LCX aneurysms, although thrombosis was reported only in the LAD. Although there were no statistically significant differences in average OSI values between the thrombosed and non-thrombosed aneurysms, qualitative analysis shows local concentration of high OSI (>0.25) in some regions.

Our findings associating hemodynamic variables with thrombotic risk are supported by prior experimental studies, which have established links between adverse flow conditions and endothelial cell function. Under healthy shear stress conditions endothelial cells release signaling molecules such us NO or PGI₂ that maintain an anticoagulant state [39,40], while, exposure to oscillatory shear stress may induce a pro-coagulant phenotype that increases expression of tissue factor [41]. Our results suggest that a combination of flow stasis, low TAWSS, and high OSI may promote a pro-thrombotic state. All aneurysms where thrombosis occurred presented regions where both TAWSS<1 dyne/cm² and OSI>0.25 were co-located.

In addition to the effect of pathological blood flow on the endothelium, hemodynamics can influence thrombus formation by mediating platelet activation and aggregation [11]. At low shear stress, coupled with high RT, conditions may favor deposition of activated platelets [5,42]. In our simulations RT was over ten cardiac cycles in some thrombosed arteries. Recirculation zones can trap platelets and facilitate platelet aggregation. In addition, accumulation of activated platelets can raise local concentration of platelet agonists such as ADP that reinforce platelet activation. Future work could leverage our advection-diffusion simulation methods to investigate transport of blood components involved in the thrombus formation process, including agonist concentration thresholds for platelet activation. These might provide insight into thrombus initiation and identify components with a dominant role in KD thrombosis.

Because platelets can be activated by either mechanical (shear-induced activation) [11,43] or biochemical stimuli, via the extrinsic or intrinsic pathway, our results suggest different potential targets for thromboprophylaxis in KD patients. Even if thrombin production is inhibited by administration of anticoagulants, flow-mediated platelet activation and aggregation can still occur. Thus, hemodynamic analysis might be useful to decide who would most benefit from dual-antiplatelet therapy. Among the five patients who developed thrombosis in our cohort, two were on warfarin and two were on enoxaparin at the time of thrombosis, while only one patient was on dual-antiplatelet therapy. AHA guidelines recommend triple-therapy (anticoagulation and dual-antiplatelet therapy) for selected patients with very severe/complex aneurysms or history of previous thrombosis [1]. In our cohort, all but one patient started dual-antiplatelet therapy after thrombosis was detected. Patients 1–5 and 7 were classified as high-risk according to all hemodynamic indices reported. This suggests that use of the proposed hemodynamic metrics might help determine which patients would benefit from dual-antiplatelet therapy that targets both TXA2 and ADP receptors, in addition to systemic anticoagulation, even before there is a thrombotic event. Patients with unfavorable hemodynamics might also be candidates for treatment with the direct thrombin inhibitors or oral anti-Factor Xa anticoagulants. Up to the last follow up no additional thrombotic events for patients 1–5, and no signs of thrombosis in patient 7 were reported. In some cases in our cohort, the hemodynamic analysis is suggestive of a pro-thrombotic environment, but no thrombosis has been detected; in these patients genetic factors and the possibility of a less pro-coagulant phenotype should be considered.

Low correlations were observed between hemodynamic variables, in particular TAWSS, A_WSS and RT, and geometric variables Z-scores and D_max. Also, patient classification according to Z-score and D_max produced very low specificity, despite being the currently accepted clinical metric for anticoagulation initiation. Representing the complex geometry of KD aneurysms with a single measurement is problematic. More complex and advanced analysis of the aneurysm geometry, such as statistical shape analysis, is needed in order to obtain geometric quantities that are comparable to hemodynamic variables. Nevertheless, from this study we can infer some qualitative factors that relate geometry and risk of thrombosis. First, our results suggest that more distal aneurysms may be more prone to thrombosis than proximal, and risk is increased when multiple aneurysms develop adjacent to each other. Flow conditions observed in the presence of an aneurysm were distinct in proximal and distal sections of the artery, with lower TAWSS found in distal aneurysms. Also, we observed that proximity of multiple aneurysms substantially increases RT.

To the best of our knowledge, this study is the first to incorporate deformable wall capabilities with a closed-loop multi-scale model to simulate KD coronary artery aneurysm hemodynamics. Comparison of rigid and deformable wall simulation results, for this patient cohort, showed that despite the differences in local WSS, TAWSS sensitivity to changes in coronary arteries Young’s modulus and thickness is small, and trends are conserved between rigid and deformable simulations. Nevertheless, additional information regarding patient-specific wall structure and composition, as recently reported using optical coherence tomography [44,45], could improve local assessment of aneurysm wall stress and strain. We did not have evidence of abnormal perfusion as a result of KD for any of the patients in this cohort, so normal myocardial perfusion was considered for all patients. However, our model would allow to add perfusion defects if measured in the clinic, as observed in some recent studies [46].

4.1. Limitations of the study

The number of patients included in this study is modest; however, it should be noted that it is difficult to identify well-characterized KD patients with both anatomic and outcomes data. Due to the small positive samples size (5 thrombosed CAAs), it was not possible to perform a mixed-effects analysis to compare the two groups of CAAs and account for the fact that a single patient could have multiple aneurysms in either one or both of the coronary arteries. Evaluation of mixed-effects of multiple aneurysms will require a larger cohort of patients. A general limitation related to the use of MRI imaging in the coronaries is the relatively low image resolution for very young patients, which could potentially introduce geometric uncertainty in the model. Prospective studies focused on this patient population should take this into consideration and include hemodynamic variables uncertainty quantification methods. There remain limitations regarding the clinical use of our computational models since they require labor-intensive model construction and high-performance parallel computing. However, the steady increase in computer power, together with recent advances in machine learning methods for automatic image segmentation, and increasingly efficient computational methods, will certainly improve the turn-around time for simulations to ultimately enable their routine clinical use. There are recent precedents for the adoption of patient-specific computational modeling in the clinical setting, for example fractional flow reserve estimated using computed tomography (FFR-CT) [47,48] to assess functional significance of coronary stenoses, suggesting that there is clinical translational potential for the hemodynamic analysis presented here.

4.2. Conclusion

We determined associations of hemodynamics with patient outcome data for CAA thrombosis and provided a detailed analysis (per aneurysm, per branch and per patient) demonstrating that hemodynamic variables were more predictive of thrombotic risk than aneurysm geometry alone, albeit in a limited cohort. Hemodynamic variables can be obtained non-invasively via simulation and provide valuable information on the local risk of thrombosis. Our results suggest that hemodynamic data could ultimately be incorporated into clinical decision-making to help guide long-term management of KD patients with CAAs, including selection of patients for systemic anticoagulation as well as identifying those patients who would benefit from the addition of dual-antiplatelet therapy. However, future prospective studies in larger cohorts of KD patients should validate these findings. Finally, the metrics proposed in this study could be directly extended to other diseases that involve the presence of aneurysms, or other anatomic alterations, and where thrombus formation may be a potential risk, such as abdominal aortic aneurysm, aortic dissection, or atherosclerotic coronary and carotid arteries.

Highlights.

• Computational simulations provide patient specific hemodynamics non-invasively.

• Hemodynamic variables are superior to anatomical measurements for KD aneurysms assessment.

• Local hemodynamic variables identify aneurysmal regions at higher risk of thrombosis.

• Patient thrombotic risk stratification was improved using hemodynamic variables.

• Hemodynamic variables may improve clinical decision-making regarding anticoagulation therapy.

Glossary

KD

Kawasaki Disease

CAA

Coronary Artery Aneurysm

CMRI

Cardiac Magnetic Resonance Imaging

RCA

Right Coronary Aneurysm

LAD

Left Anterior Descending

LCX

Left Circumflex

TAWSS

Time-Averaged Wall Shear Stress

OSI

Oscillatory Shear Index

RT

Residence Time