Nonlinearity and Amplification in Cochlear Responses to Single and Multi-Tone Stimuli

Abstract

Mechanical displacements of the basilar membrane (BM) and the electrophysiological responses of the auditory outer hair cells (OHCs) are key components of the frequency tuning and cochlear amplification in the mammalian cochlea. In the work presented here, we measured the responses of (1) the extracellular voltage generated by OHCs (V_OHC) and (2) displacements within the organ of Corti complex (OCC) to a multi-tone stimulus, and to single tones. Using optical coherence tomography (OCT), we were able to measure displacements of different layers in the OCC simultaneously, in the base of the gerbil cochlea. We explored the effect of the two types of sound stimuli to the nonlinear behavior of voltage and displacement in two frequency regions: a frequency region below the BM nonlinearity (sub-BF region: f < ~ 0.7 BF), and in the best frequency (BF) region. In the sub-BF region, BM motion (X_BM) had linear growth for both stimulus types, and the motion in the OHC region (X_OHC) was mildly nonlinear for single tones, and relatively strongly nonlinear for multi-tones. Sub-BF, the nonlinear character of V_OHC was similar to that of X_OHC. In the BF region X_BM, V_OHC and X_OHC all possessed the now-classic nonlinearity of the BF peak. Coupling these observations with previous findings on phasing between OHC force and traveling wave motions, we propose the following framework for cochlear nonlinearity: The BF-region nonlinearity is an amplifying nonlinearity, in which OHC forces input power into the traveling wave, allowing it to travel further apical to the region where it peaks. The sub-BF nonlinearity is a non-amplifying nonlinearity; it represents OHC electromotility, and saturates due to OHC current saturation, but the OHC forces do not possess the proper phasing to feed power into the traveling wave.

1. Introduction

In the mammalian cochlea a fluid/tissue traveling wave carries sound energy from the base towards the apex of the cochlea. This cochlear wave is tonotopic: depending of the frequency of the stimulus, the wave peaks at a specific location along the longitudinal axis of the cochlea – the best frequency (BF) place for that tone – high frequencies in the base, low frequencies in the apex. The sensory tissue of the cochlea, the organ of Corti complex (OCC), moves with the wave and the relative motion between the reticular lamina (RL) and the tectorial membrane (TM) leads to the mechano-electric transduction of auditory hair cells. This differential motion pivots the stereocilia of the hair cells, varying the conductance of the mechano-electric transducer (MET) channels and leading to current and voltage variations within the hair cells. The voltage variations cause inner hair cells (IHCs) to release neurotransmitter to auditory neurons and outer hair cells (OHCs) to create mechanical force, driven by electro-mechanic transduction (Frank et al., 1999; Kalinec et al., 1992). The OHC forces enhance the pressure at the BM, and BM motion by a factor of up to 1000 for low sound pressure level (SPL) sounds in the BF region but do not affect the BM response to high SPL sounds, or sub-BF sounds (below ~ 0.7 BF) at any SPL (Olson, 1999; Rhode, 2007). The increased and frequency-sharpened BM response in the BF region is the fundamental expression of the mechanism termed “cochlear amplification”. Studies have explored the physical mechanism that leads to the separation of sub-BF and BF regions that are so clearly delineated in the nonlinear character of X_BM. In experimental work in which both V_OHC and mechanical responses (X_BM and pressure at the BM) were measured, a phase shift of V_OHC relative to the mechanical responses occurred at a frequency ~ 0.7 × BF, close to the frequency where X_BM became nonlinear (Dong and Olson, 2013). Analysis of OHC mechanics showed that this phase shift would produce a separation into non-amplifying (sub-BF) and amplifying (power generating, BF) regions. Analytical models have been able to produce the regional separation by various means, for example tectorial membrane resonance (Nankali, et al., 2018), traveling wave mode shifts (van der Heijden, 2014; Lamb and Chadwick, 2011) and feed-forward produced by longitudinal coupling (Yoon, et al., 2011).

Recent OCT-based displacement measurements have shaken up the field of cochlear mechanics by observing sub-BF nonlinearity in the motions within the OCC, which we term X_OHC (Lee et al., 2016, He et al., 2018, Cooper et al., 2018). Sub-BF nonlinearity has also been observed in local measurements of OHC extracellular voltage, V_OHC (Dong and Olson, 2016). In this study we attempt to place these new findings, particularly the findings of sub-BF X_OHC nonlinearity, into the context of cochlear amplification. We used an OCT system to simultaneously measure X_BM and X_OHC, and measured V_OHC in separate preparations. We measured these responses to two different types of stimuli, single tones and Zwuis multi-tone complexes.

In the sub-BF region we observed boosting of X_OHC and V_OHC that saturated at high SPL; X_BM was linear in the sub-BF region, in keeping with previous findings. The difference in sub-BF responses when using the single versus the multi-tone stimulus was helpful in exploring sub-BF nonlinearity. In previous measurements of X_BM the two stimulus types gave rise to qualitatively similar behavior (Versteegh and van der Heijden, 2012). Our X_BM data was consistent with those findings. In contrast, in our X_OHC and V_OHC measurements the sub-BF responses to the two stimulus types differ. We explored the stimulus-dependent difference with a Boltzmann saturation model of the V_OHC results. In the sub-BF region, the phase difference between V_OHC (approximately proportional to OHC force) and X_BM or X_OHC was not the phasing needed for OHC force to impart power into the traveling wave.

In the BF region, X_BM, X_OHC and V_OHC all showed an enhanced and sharpened nonlinear peak at low and moderate SPLs. (The high SPL BF-region behavior was more complicated, as described below.) A phase shift occurs in the transition between the sub-BF and BF regions, resulting in BF-region phasing in which OHC forces would impart power into the traveling wave -- power that feeds forward with the wave to grow the peak.

Based on these observations and observations of others discussed below, we propose the following characterization: the sub-BF region is a region of “non-amplifying nonlinearity” whereas the BF region is a region of “amplifying nonlinearity”.

2. Methods

2.1. Basic preparation

The animal studies were approved by the Institutional Animal Care and Use Committee (IACUC) of Columbia University. Gerbils were anesthetized throughout, and euthanized by pentobarbital anesthetic overdose at the end of the experiments. A tracheotomy was performed to maintain a clear airway and a regulated heating blanket maintained the body temperature at ~ 37°C. The left pinna was removed and the bulla was opened to view and access the cochlea.

2.2. Sound stimulus

The sound stimuli were generated by a Tucker Davis Technologies (TDT) System and presented closed-field to the ear canal (EC) by a Radio Shack dynamic speaker. A Sokolich ultrasonic microphone (WGS & Associates, Newport Beach, CA) was coupled to the speaker tube for sound calibration just inside the EC. Displacement and extracellular voltage experiments were performed on separate days and animals. In both sets of experiments two types of acoustic stimulation were used, “Zwuis” multi-tone complexes and single tones between 1 kHz – 32 kHz, with frequency spacing of 500 Hz for the voltage measurements and larger for the displacement measurements. For single tone measurements the stimulus duration was ~ 1s per recording. For the multi-tone, because of the constraints of the Zwuis stimulus frequencies (Eq. 1) the total duration was longer, ~ 5s (voltage measurements) and ~ 10s (OCT measurements). For both stimulus types frequencies were chosen so that their periods fit an even number of times into the stored data set in order to avoid line broadening in the Fourier transformed data.

2.3. Zwuis Multi-tone stimulus

Zwuis tone complexes were developed by van der Heijden and Joris (2003) as a method to measure the response to many frequencies at the same time. The distinct stimulus frequencies f₁, f₂, … , f_N are chosen such that there is no overlap between the second and third order distortion products and the primary frequencies. In this way, output distortion products were separable from primary tones. A random phase between -p and p was chosen for each tone. Including a random phase kept the total voltage sent to the speaker low since the sine waves were never “all in phase” and the random phase also let us say that the stimulus amplitude was ~ √N x amplitude of each frequency component. Eq. 1 presents the multi-tone Zwuis stimulus used in this work. We used 40 tone complexes (N = 40) for the V_OHC measurements and 60 tone complexes for the displacement measurements. (The different number for the two measurements was due to the need for long data acquisition times to reduce the noise level in the OCT measurements and did not influence the results.)

$$\begin{gathered} V_{Zwuis}(t)={\sum }_{i=1}^{N}A\text{cos}\left(2\pi f_{i}t+{\phi }_i\right) \\ {f}_k\pm f_l\ne f_n \\ {f}_k\pm f_l\pm f_m\ne f_n\text{ for all k},1,\text{m},\text{n}=1,\dots ,\text{N} \\ {\phi }_i=random variable \end{gathered}$$ (1)

2.4. OHC extracellular voltage

A hand-drilled hole of diameter ~ 100 μm (termed cochleostomy) was made in the bony wall of the cochlea, to access the scala tympani (ST) in the first turn of the cochlea (Fig. 1A&B). To ensure the preparatory surgery did not damage the cochlea, compound action potentials (CAPs) were measured with an electrode at the round window before and after the cochleostomy (Fig. 1C). A tungsten microelectrode, insulated to its tip, with ~ 1 μm tip diameter (FHC Inc. Bowdoin, ME) was inserted into the hole and advanced ~ 250 – 300 μm to be positioned close to the BM, to measure local V_OHC. This distance was based on measurements made in the same location with a pressure sensor that detects the BM surface, both previously published (Olson, 1999, Dong & Olson, 2013) and also performed by the first author of this report. A reference electrode was placed in the neck muscle. When the cochlear electrode is close to the BM, the local traveling wave becomes apparent in the presence of phase delay through several cycles and a peak emerges at frequencies close to the BF. By varying the location of the cochleostomy and angle of the electrode, locations with BF from ~ 16.5 to 25 kHz were probed in different experiments. The V_OHC measurements were performed with a sampling rate of 195312.5 Hz. The recordings were averaged in the time domain, in order to reduce the size of the stored data sets. The final traces were subjected to Fourier analysis to find the amplitude and phase of the responses at stimulus frequencies.

Figure 1:

A) view of the gerbil cochlea from the bulla opening (drawing by Vanessa Cervantes). V_OHC responses were measured via a hand-drilled hole (~ 100 μm) in ST in the base of cochlea. Displacement responses were measured through the intact round window membrane. B) Cross-section of the cochlea, showing the electrode positioned close under the organ of Corti complex (OCC) in the first turn. The OCC spirals around the cochlea, and some of its main parts are labeled in the section on the left. TM: tectorial membrane, RL: reticular lamina, BM: basilar membrane, OHCs: outer hair cells. C) Compound action potential (CAP) thresholds before (solid lines) and after (dashed lines) the cochleostomy for eight extracellular voltage experiments.

2.5. Displacements in the organ of Corti complex

A commercial ThorLabs Telesto III spectral domain optical coherence tomography (SD-OCT) system was used to measure the vibrations of the OCC through the intact round window membrane. Spectral domain phase microscopy (SDPM), a functional extension of OCT, simultaneously measures the time-locked displacements at multiple locations along the instrument’s optical path. Gerbil bullae were narrowly opened and the animals were placed under the OCT. Distortion product otoacoustic emissions (DPOAEs) were measured at the beginning of the experiment and between runs to gauge cochlear condition. Two-dimensional scans, termed B-scans, were taken across the radial direction of the organ of Corti and used to identify regions of interest for SDPM vibrometry. Once the cochlea was positioned, the OCT system acquired a series of time-locked one-dimensional A-scans, termed an M-scan. Each pixel in the A-scan corresponds to 2.7μm in the axial direction, for measurements in saline-rich tissue where the index of refraction is assumed that of water (n = 1.33). In an OCT system, the pixel size that defines axial resolution is derived from the light source bandwidth. The lateral resolution of the Telesto’s objective lens, the Thorlabs LSM03, was specified by the manufacturer as 13 μm. In the M-scan, the time-dependent phase of each pixel is proportional to the instantaneous displacement of the structure at that pixel (Lin et al., 2017, 2018). The signal-to-noise ratio of the OCT measurements depends on the reflectivity of the tissue within the organ of Corti, which varies across experiments. In preparations of relatively high reflectivity we could achieve a noise floor of ~ 50 pm.

The Telesto was controlled using custom software written in C++ and based on the ThorLabs Software Development Kit. The Tucker Davis Technologies system described above was used to generate the acoustic stimuli and perform the EC pressure measurements. The clock signal from the Tucker Davis zBus was modified to give a high-duty-cycle square wave (90% high 10% low) which was used to trigger each OCT scan, thus synchronizing the OCT with the acoustic stimulus and responses measured in the EC. OCT recordings were taken with a sampling rate of 97656.25 Hz. The raw OCT spectra were first converted to maps of intensity vs. depth (axial position) termed “A-scans” and then selected pixels were chosen for extraction of the displacement vs. time. For the single tone measurements, after extracting displacement, the recordings were averaged 511 times in the time domain, in order to reduce the size of the stored data sets. The duration required for a set of single tone OCT measurements was ~ 30 minutes, mainly due to the ~ 40 seconds needed to store each recording from the OCT system to disk. No averaging was used in the multi-tone recordings because the time traces of the multi-tone stimuli never repeated. The final traces were subjected to Fourier analysis to find the amplitude and phase of the responses at stimulus frequencies. The response at each frequency was included in the results if its amplitude was three standard deviations above the mean noise floor measured with ten neighboring points in the Fourier Transform. (This screening was usually adequate but sometimes additional screening was applied, when data points passed the screen but were in the noise on visual inspection.) Image processing and analysis scripts were written in custom software in Matlab (R2016b).

2.6. Boltzmann Model

To explore the observations of V_OHC with the two stimulus types, the sub-BF region V_OHC was modeled by a two-state Boltzmann model. This basic sigmoidal function is often used to describe the OHC MET channel operation (Equation 1 in Fettiplace and Kim, 2014). The nonlinearity of the OHC MET channel is the dominant factor that contributes to nonlinearities of the OHC mechanical and electrical responses (Santos-Sacchi, 1993). The input/output (I/O) equation is as below:

$$y=B/\left[1+e^{-a_3\left(x-x_0\right)}\right]$$ (2)

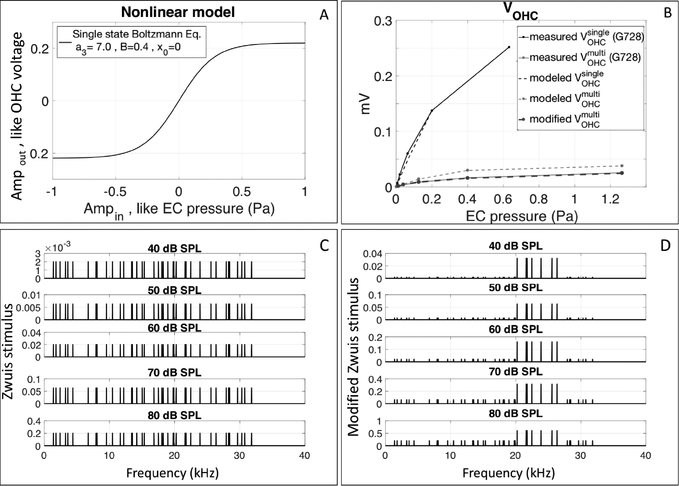
In this work, the output y corresponds to the amplitude of the fundamental component of V_OHC and x represents the input sound pressure in the EC, in Pascals. B was the maximum output value (the maximum extracellular voltage) and a₃ is the slope factor. X₀ allows an offset. To understand our observations, the output of this nonlinear function was explored with the following inputs: (i) a single tone in the form V(t) = A cos (2πft + φ), (ii) a 40-component Zwuis tone complex as in Eq. 1 and (iii) a modified 40-component Zwuis tone complex, described in the discussion of Fig. 10.

Figure 10:

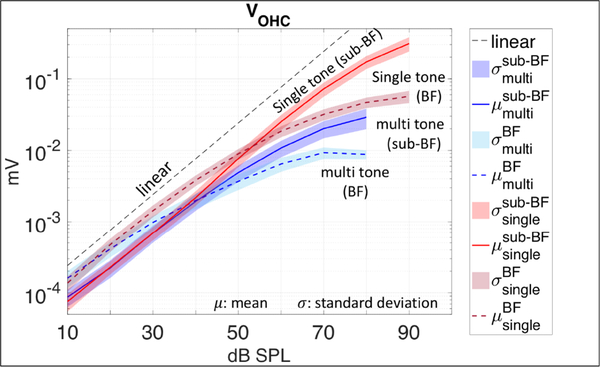
A) Two-state Boltzmann function used to model the saturation of the OHC MET channels in the sub-BF region. B) Input/output curves of experimentally measured V_OHC responses with single tones (black solid line, #728 run10) and multi-tone stimuli (gray solid line, #728 run 11), compared to the V_OHC results from the Boltzmann model with single tones (black dashed line), Zwuis equal 40-tone stimulus (gray dashed line) and with modified Zwuis unequal 40-tone stimulus (gray bold dashed line on top of the gray solid line). C) Spectra of the Zwuis equal 40-tone stimuli. D) Spectra of the modified Zwuis unequal 40-tone stimuli.

3. Results

3.1. OHC extracellular voltage

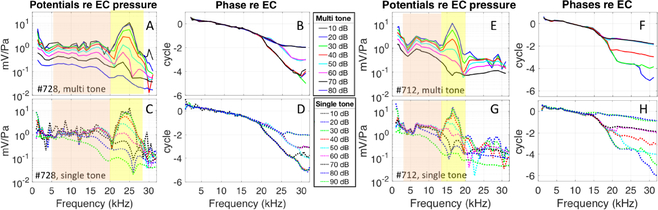
For the present study, V_OHC measurements were made on eight gerbils. Responses from two preparations are emphasized (Figs. 2, 3, 8, 9) and grouped data are also shown (Fig. 4). The two preparations were chosen for illustration because they had BFs at the maximum and minimum of our experiments, #728 ~ 25 kHz, #712 ~ 16.5 kHz. BFs were found as the peak frequency at the lowest SPL. Fig. 2 shows these basic V_OHC results, with the responses to single-tones below and multi-tone stimuli above. The sub-BF and BF regions are coded by the colored vertical bands: orange = sub-BF and yellow = BF. The sub-BF region was chosen from ~ 3 kHz (well below the BF) up to ~ 0.75 × BF (the onset of BM nonlinearity). A notch was often observed in V_OHC responses at ~ 0.75 × BF, for both single and multi-tone stimuli. Such a notch occurred at ~ 20 kHz for #728 and ~ 12.5 kHz for #712. The notch was used to separate sub-BF and BF regions in V_OHC data.

Figure 2:

A,E) Normalized V_OHC for multi-tone Zwuis stimuli. B,F) Corresponding phase re: EC pressure. C&G) Normalized V_OHC for single-tone stimuli. D&H) Corresponding phase re: EC pressure. The nonlinear analysis in this manuscript was done on two frequency regions: 1: sub-BF (orange band) and 2: BF region (yellow band). A-D) #728, runs 10,11, E-H) #712 runs 18,19.

Figure 3:

Amplitude and phase of V_OHC re: EC pressure, in response to multi-tone Zwuis (blue) and single-tone stimuli (red, dotted). #728 runs 10 and 11.

Figure 8:

Comparison of the responses of V_OHC (dashed bold lines), X_BM (solid lines) and X_OHC (solid bold lines) with A) Single tone stimuli at three frequencies in the sub-BF region. B) Multi-tone stimuli at three frequencies in the sub-BF region. C) Single tone stimuli at 1–2 frequencies in the BF region. D) Multi-tone stimuli at 1–2 frequencies in the BF region. VOHC responses from #728: run10 (single tone), run 11 (Zwuis multi-tone). X_BM & X_OHC responses from #733: run27 (single tone), run 26 (Zwuis multi-tone).

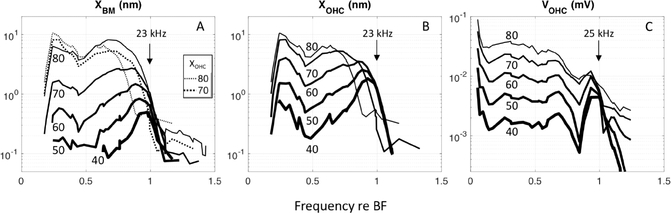
Figure 9:

A) X_BM amplitudes to multi-tone stimulus B) X_OHC amplitudes to multi-tone stimulus (#733 run 26, BF = 23 kHz). C) V_OHC amplitudes to multi-tone stimulus (#728 run 11, BF = 25 kHz). The x axis is plotted normalized to BF, the y-axis units are in the panel titles.

Figure 4:

Input/output curves for V_OHC data in response to Zwuis multi-tones (blue), and single tones (red) in sub-BF and BF regions. Grouped results from eight preparations. In the sub-BF region V_OHC responses to single tones were linear to ~ 70 dB SPL, while in V_OHC responses to multi-tones began to be compressed much earlier (~ 50 dB SPL). In the BF region V_OHC responses to both stimuli were more compressed than in the sub-BF region. I/O curves were derived from data averaged across the eight preparations in Fig.1C.

In response to single tones (lower panels of Fig. 2), V_OHC grew linearly through 70 dB SPL in the sub-BF region. In the BF-region V_OHC showed compressive nonlinearity throughout almost the entire SPL range, but scaled linearly from 10–30 dB SPL. Contrary to the single tone responses, when the multi-tone Zwuis stimulus was applied (upper panels of Fig. 2), the V_OHC nonlinearity in the sub-BF region started at a much lower stimulus level, ~ 50 dB SPL. For both stimulus types the degree of nonlinearity was larger in the BF region, and started at 30 dB SPL. The phase of V_OHC relative to the phase of the sound pressure in the EC is in Fig. 2 D&H (single tone data) and Fig. 2 B&F (Zwuis multi-tone data). Steep phase accumulation in the BF region at low-moderate SPL evinced the traveling waves in the cochlea and was present for both types of acoustic stimuli. At the highest SPLs (80–90 dB) the V_OHC phase flattened considerably, and the remaining slope could be attributed mainly to middle ear delay (~ 25 μs, Olson, 1998). At that point the OHC currents contributing to V_OHC cannot be attributed to local OHC responses alone.

In Fig. 3 the V_OHC responses to the multi- and single tone stimuli are shown together at each SPL (#728). These are the data in Fig. 2A–D, plotted to directly compare the responses to the two stimulus types. The responses are approximately identical at 10 and 20 dB SPL, but at 30 dB SPL compression was apparent in the BF region of the multi-tone response. At 50 dB SPL there was substantially more compression in the multi-tone response, and this difference extends to sub-BF frequencies. The notch at ~ 20 kHz is plainly seen for both stimulus types, and is accompanied by a ripple in the phase that, due to phase unwrapping, can either push the phase down (10–40 dB SPL) or up (50–60 dB SPL).

Experimentally measured input/output curves for V_OHC data representing the sub-BF and BF regions are shown in Fig. 4 (grouped data from eight preparations). The sub-BF curves were generated by averaging responses in the sub-BF region (orange band in Fig. 2) of an individual animal and then averaging these across the eight preparations, and similarly for the BF region (yellow band in Fig.2). The observations regarding nonlinearity noted when describing Fig. 2 are reinforced by the I/O curves. V_OHC was nonlinear in both frequency regions, but showed more compression in the BF region. V_OHC compression was larger in response to Zwuis stimuli (blue curves) than in the responses to single tone stimuli (red curves).

3.2. Displacements in the organ of Corti complex

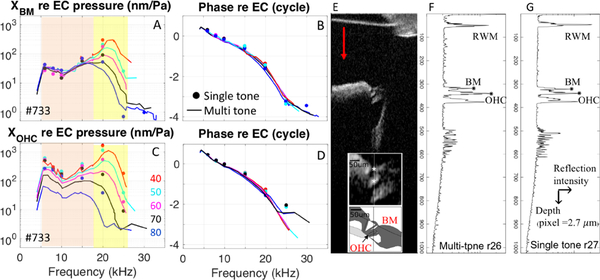
Displacements of the OCC were measured in six gerbils. Fig. 5 shows representative responses from one preparation that illustrate the main points. Due to the long OCT data collection and processing time, displacements in response to single tones were collected from only 6–7 frequencies, which gave enough information to compare to the multi-tone responses. The amplitude and phase of displacements of the BM and a location ~ 50 μm inside the OCC, close to the OHCs are shown in Fig. 5. (Zwuis responses = solid lines, single tone responses = solid dots). Responses were normalized to the stimulus pressure. Fig. 5E shows the B-scan for these displacement data, with the inset an enlarged view showing the locations where we measured displacement. These locations corresponded to the BM and the OHC location, identified in the cartoon depiction of the OCC. The reflection intensity of structures was collected from an axial line (vertical line in Fig. 5E inset), and created a depth profile (A-scan). The magnitude of the A-scans of two consecutive runs, with Zwuis multi-tone (run 26) and single tone (run 27) stimuli are shown in Fig. 5F and 5G, respectively. The A-scan magnitudes looked similar as they should, and small differences in the A-scan magnitudes indicate slight shifting of the preparation between runs. As described in the methods, the time dependent phase of the A-scan is proportional to displacement.

Figure 5:

A) Amplitude of X_BM re: EC pressure, in response to single tones (solid dots) and multi-tones (solid lines). B) Corresponding phase re: EC pressure. C) Amplitude of X_OHC ~ 50 μm inside the organ of Corti re: EC pressure, in response to single tones (solid dots) and multi-tones (solid lines). D) Corresponding phase re: EC pressure. E) Structural B-scan of the organ of Corti taken by OCT system, with expanded view of organ of Corti and a cartoon depiction in the inset. F) A-scan magnitude, averaged over all the A-scan magnitudes in the M-scan, of Zwuis run 26. G) Averaged A-scan magnitude of singletone run 27. #733, Zwuis run 26: BM (pixel 321), OHC (pixel 340), single tone run 27: BM (pixel 318), OHC (pixel 341). The positive displacement direction was defined as indicated by the red arrow in E.

X_BM responses to both the multi-tone and single tone stimuli were linear in the sub-BF region and nonlinear in the BF region (Fig. 5A). This result is consistent with basal BM data going back decades (Robles and Ruggero, 2001; Versteegh and van der Heijden, 2012). No significant difference was seen in the phase of X_BM responses to the single and multi-tone stimuli (Fig. 5B). X_BM single tone responses were slightly larger than multi-tone responses in the BF region. X_OHC responses to the multi-tone and single tone stimuli were nonlinear in the BF region, and larger than X_BM responses (Fig. 5C compared to Fig. 5A). X_OHC in the sub-BF region was more complicated. With single tone stimuli X_OHC was nearly linear, becoming mildly compressively nonlinear at 80 dB SPL. With multi-tone stimuli X_OHC was nonlinear starting at ~ 50 dB SPL. No significant difference was seen in the phase of X_OHC responses to the single and multi-tone stimuli (Fig. 5D). The behavior of X_OHC was in many ways similar to that of the V_OHC responses in Fig. 2, although the highest SPL responses cut off at a lower frequency in X_OHC than in V_OHC, as will be described further below. Displacement results from three additional preparations are shown in Fig. 6, and show repeatability with these observations.

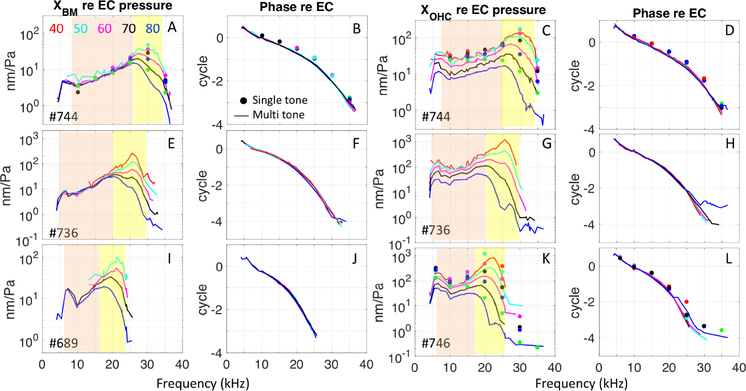
Figure 6:

Four additional displacement dataset show repeatability. A,E,I) Amplitude of X_BM re: EC pressure in response to single tones (solid dots) and multi-tones (lines). B,F,J) Corresponding phase re: EC pressure. C,G,K) Amplitude of X_OHC re EC pressure in response to single tones (solid dots) and multi-tones (solid lines). D,H,L) Corresponding phase re: EC pressure. #744: Zwuis run 23: BM (pixel 167), OHC (pixel 181), single tone run 21: BM (pixel 169), OHC (pixel 182), #736: Zwuis run 18: BM (pixel 244), OHC (pixel 256), #689: Zwuis run 25: BM (pixel 262), #746: Zwuis run 16: OHC (pixel 307), single tone run 17: OHC (pixel 308).

Fig. 7 shows the experimental input/output curves for A) X_BM and B) X_OHC responses to the multi-tone Zwuis stimulus (grouped results from six preparations.) The curves were obtained by averaging responses in the sub-BF region (orange regions in Figs. 5 & 6) of an individual animal and then averaging these across the six preparations, and similarly for the BF (yellow) regions. These curves reinforce the observations above. At the BM (Fig. 7A), the sub-BF region displacements scaled linearly with stimulus level and the BF region scales nonlinearly. At the OHC location (Fig. 7B), in the sub-BF region, multi-tone displacements were compressed starting at 40–50 dB SPL. In the BF region, X_OHC peaked at ~ 70 dB SPL and then actually decreased with increasing SPL. This “hyper-compression” was also seen in single tone X_OHC (Fig. 8C). These observations of hyper-compression in motion responses within the organ of Corti confirmed other recent measurements (Cooper et al., 2018).

Figure 7:

Grouped input/output curves for A) X_BM and B) X_OHC, in response to Zwuis multi-tone stimuli. Compression was seen in X_OHC responses from ~ 40–50 dB SPL (black solid line in 7B), while X_BM remained linear (black solid line in 7A). In the BF region, X_OHC showed hyper-compression. (#707,733,736,739,744,746).

3.3. V_OHC, X_BM and X_OHC

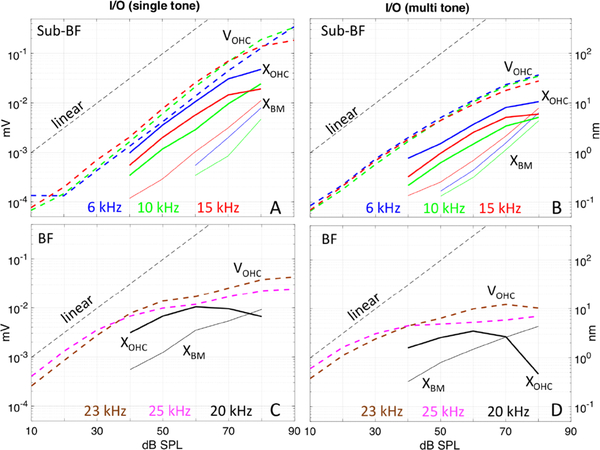
In Fig. 8, experimentally measured input/output curves for X_BM (solid lines) and X_OHC (solid bold lines), are compared to the input/output curves for V_OHC (dashed bold lines). Illustrative data from two preparations is shown and each panel includes all three quantities. The left panels, Fig. 8A&C, are single tone responses and the right panels, Fig. 8 B&D, are multi-tone responses. The top row compares V_OHC, X_BM and X_OHC results at three frequencies in the sub-BF region (6,10 and 15 kHz, #728,733). The bottom row compares V_OHC results at two frequencies in the BF region (23 and 25 kHz, #728) to X_BM and X_OHC results at a frequency close to the BF (20 kHz, #733). This figure reinforces observations from above: In the sub-BF region, the magnitude of X_OHC was greater than X_BM, and X_OHC and V_OHC were compressively nonlinear, while X_BM was linear. In the sub-BF region with single-tone stimulation, V_OHC and X_OHC responses were compressed only at high SPL, ~ 80 dB (Fig. 8A), whereas with multi-tone stimulation V_OHC and X_OHC responses were compressed from ~ 40–50 dB SPL (Fig. 8B). In the BF region (Fig. 8C&D), V_OHC, X_BM and X_OHC all showed nonlinear compression. Hyper-compression was observed in X_OHC at SPLs above 60 dB SPL, and was more pronounced with the multi-tone stimulus (Fig. 8D). V_OHC became very compressed above ~ 40 dB SPL with the multi-tone stimulus, but did not become hyper-compressed.

To gain a better understanding of the hyper-compression, unnormalized V_OHC, X_BM and X_OHC frequency responses to multi-tone stimuli are shown in Fig. 9. With increasing SPL, X_BM nearly saturated in the BF region, and the BF peak moved to lower frequencies. At 80 dB SPL the peak shifted to a value ~ 0.7 times the BF, a frequency low enough such that X_BM scaled nearly linearly there throughout the SPL range (Fig. 9A). This is the X_BM “passive” peak, uninfluenced by OHCs. In contrast, sub-BF X_OHC was nonlinear and showed substantial saturation at ~ 80 dB SPL (Fig. 9B). In the BF region, X_OHC responses from 40–60 dB SPL were fully saturated and at 70 dB hyper-compression was evident, and was substantial at 80 dB SPL, for which the response dropped off steeply above ~ 0.6 BF. The 70 and 80 dB SPL X_OHC responses from Fig. 9B are included in the X_BM panel (Fig.9A) as dotted lines, to show that X_OHC, which was substantially greater than X_BM at low and moderate SPLs, dropped beneath X_BM when hyper-compressed. Like X_OHC, sub-BF V_OHC was nonlinear and showed substantial saturation at ~ 80 dB SPL (Fig. 9C). In the BF region V_OHC is fully saturated but only showed a hint of hyper-compression at 80 dB SPL. However, as mentioned when describing Fig. 2, at high SPL V_OHC responses can no longer be attributed solely to local OHCs, and the contribution from distant OHCs might be filling in a hyper-compressed local response.

4. Discussion

OCT technology allowing for motion measurements within the OCC is opening new views to excitation of hair cells and cochlear amplification. Two groups have made measurements in the gerbil base, and their results differed for motion measured close to the OHCs in the sub-BF region. However, the two groups used different stimuli, Zwuis multi-tone or single tone. The multi-tone stimulus led to compression in the sub-BF OHC-region motion (Cooper et al., 2018), while with the single-tone stimulus, compression in the sub-BF region was nearly absent (He et al., 2018). We measured X_OHC with both stimulus types and repeated the findings of both groups, thus the different results are attributable to the different stimuli. Our first discussion point below explores the reason for the differing degrees of sub-BF compression with the two stimuli. The newly-discovered sub-BF nonlinearity opens questions about cochlear amplification, which for measurements in the cochlear base had previously been confined to the BF region. Our second discussion point combines displacement and extracellular voltage data to explore the question of the relationship between nonlinearity and amplification.

4.1. Comparison of V_OHC responses to single and multi-tone stimuli

V_OHC compression was larger in response to multi-tone than to single tone stimuli. To first order, this can be explained by the fact that the multi-tone stimulus has a magnitude at the EC that is greater than a single tone stimulus by a factor of √N, where N is the number of tones in the multi-tone stimulus. Hair cell responses have been modeled with a compressive Boltzmann type I/O function, and to get insight into our results we used a Boltzmann model (Fig. 10A) to predict the sub-BF I/O curves to multi-tone stimuli, starting with the sub-BF I/O curves from single tone stimuli. We restricted the analysis of this section to the sub-BF region because in this region the nonlinear compression could (hypothetically) be attributed simply to OHC MET saturation, without having to consider amplification. This is important because our input is ear canal pressure, whereas the input to the hair cell is stereocilia deflection. In the simple saturation case, the stimulus at the hair cell would be linearly related to the stimulus pressure at the ear canal. V_OHC measured in the sub-BF region in response to single tones was used to find the parameters for the Boltzmann function described in the methods section. After the Boltzmann I/O function was found, the Zwuis 40-tone stimulus that was used in our experiments was used as input. Initially we used a simple Zwuis set, with equal levels at all frequencies (Fig. 10C). The predicted output, gray dashed line in Fig. 10B, showed less compression than what was measured experimentally (gray solid line in Fig. 10B). This is not surprising because we considered the sub-BF region, and with the multi-tone stimulus, BF tones will also be present and due to cochlear tuning they will provide a relatively larger stimulus to the local OHCs, and thus play a larger role in saturating the local MET channels. Thus, as a second approximation we weighted the BF region tones in our Zwuis stimulus to a reasonable degree as shown in Fig. 9D (40 dB = x16 , 50 dB = x10 , 60 dB = x8, 70 dB = x5, 80 dB = x3). These weightings were roughly drawn from the #733 OHC location data set. With this reasonable adjustment the Boltzmann I/O was successful at predicting the sub-BF V_OHC responses as shown in the gray bold dashed line in Fig. 10B.

Nonlinearities can produce non-intuitive behavior; as an example, when two tones are input to a Boltzmann type nonlinearity, the tone with the larger amplitude linearizes the smaller-amplitude tone -- so that the smaller-amplitude tone no longer shows compressive behavior (Fahey et al., 2000, Dong and Olson, 2016.) It was useful to find that in the exploration illustrated in Fig. 10, our reasonable and intuitive modification to the input of a Boltzmann function was successful in predicting the observed compressive output.

4.2. Comparison of V_OHC , X_BM and X_OHC

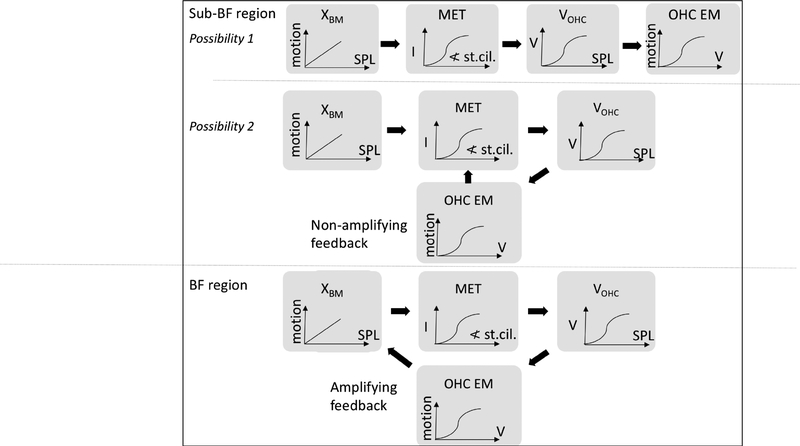
Recent measurements in the basal cochlea (or much of the cochlea in mouse) by others and ourselves (Figs. 5 and 6) have shown that in the sub-BF region, the displacement response within the organ of Corti (here termed X_OHC) is boosted in-vivo, and scales nonlinearly with stimulus level (He et al., 2018, Cooper et al., 2018, Lee et al., 2016). This is different from BM motion, which is linear and unboosted (passive) in the sub-BF region. We suggest that it is appropriate to think of the sub-BF nonlinearity as a “non-amplifying nonlinearity”. Non-amplifying nonlinearity corresponds to OHC stereocilia being stimulated by BM motion, producing receptor current which then produces V_OHC, causing the OHCs to move via electromotility (Brownell et al., 1985), but without injecting energy into the traveling wave. The injection of energy into the traveling wave is the mechanism that allows the traveling wave to travel robustly to its best-place region, where it slows, grows and peaks (de Boer and Nuttall, 2000). In the extreme form of non-amplifying nonlinearity (Fig. 11 possibility 1), this OHC motion does not feed back to enhance stereocilia motion, and the nonlinearity observed in X_OHC is simply the OHC electromotile response to the saturating transducer current. In a less extreme form of non-amplifying nonlinearity (Fig. 11 possibility 2), the OHC motion does feed back to increase stereocilia motion, and thus increase V_OHC and OHC electromotility, but without the proper phasing to inject power into the cochlear traveling wave.

Figure 11:

Diagram of the possibilities for nonlinearity in sub-BF and BF region. In possibility 1 of the sub-BF region, X_BM is linear and drives OHC stereocilia, producing an OHC electromotile response that is compressed due to saturation of the OHC MET channel. There is no feedback in possibility 1. In possibility 2, the OHC electromotile response does increase OHC stereocilia motion but OHC electromotility is not phased properly to inject energy into the traveling wave. In the BF region, OHC electromotility is phased correctly to exert power-injecting forces, and traveling wave amplification is present.

One way to decide between the extreme and less extreme forms of the sub-BF non-amplifying nonlinearity is to look quantitatively at the saturation. For single tone measurements, at sub-BF frequencies, saturation of V_OHC and X_OHC occurred at a stimulus level of ~ 80 dB SPL. 80 dB SPL corresponds to a displacement of ~ 30–50 nm at the OHC location and of ~ 2–10nm at the BM (Fig. 8). Peng et al. (2013), found that saturation in OHCs occurred for stereocilia tip displacements of ~ 30–50 nm. If the stereocilia were being driven by BM motion (possibility 1) with some geometric factor between BM and stereocilia which is assumed less than a factor of 2, SPLs would have to be larger than 80 dB SPL before OHC responses became saturated. On the other hand, if the stereocilia were being driven by OHC motion (possibility 2), saturation is expected to occur at ~ 80 dB SPL. Thus, possibility 2 is supported: in this scenario, OHC electromotility does feed back to enhance stereocilia motion in the sub-BF region. In further support of possibility 2, Jia and He (2005) directly observed that OHC electromotility caused stereocilia motion in a passive hemicochlea.

Now that we have accepted possibility 2, that OHC electromotility has a positive feedback on stereocilia motion in the sub-BF region, in what sense we can justify the sub-BF nonlinearity as “non-amplifying”?

Firstly, the results showed substantial quantitative and qualitative differences between BF-region responses and the sub-BF-region responses: Both V_OHC and X_OHC had different gains and degrees of nonlinearity in the different frequency regions; X_BM showed nonlinearity only in the BF-region.

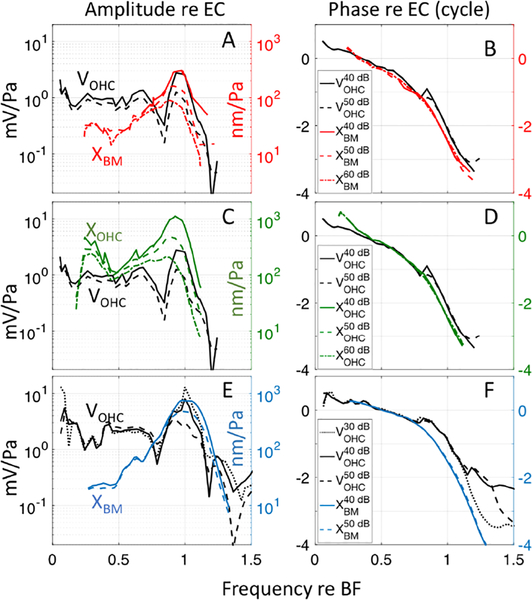
Secondly, Dong and Olson (2013) described an underlying basis for the transition of OHC forcing from “non-amplifying” to “amplifying”. With simultaneous measurements, they measured the phase of V_OHC relative to X_BM (or pressure at the BM, which has a phase very similar to X_BM) and observed a phase shift in V_OHC relative to X_BM that developed at ~ 0.7 × BF, close to where the sub-BF meets the BF region. Their data analysis, based on known OHC mechanics, in particular that OHC force is in phase with V_OHC (Frank, et al., 1999), showed that the phase shift moved the energetics to a condition where OHCs pump energy into the traveling wave at frequencies above the shift and through the BF peak. Although the present measurements of V_OHC and X_OHC were not made simultaneously, we had data with similar BFs with which to do a comparison. Fig. 12 compares V_OHC to X_BM and X_OHC responses. In Fig. 12 A&B, the amplitude and phase of V_OHC in response to a multi-tone stimulus (black lines) were compared to X_BM (red lines). V_OHC responses are from #728 (as in Fig. 2 A&B) with BF = 25 kHz; X_BM responses are from #733 (as in Fig. 5 A&B) with BF = 23 kHz. The x-axis is plotted normalized to BF. Fig. 12 C&D is the comparison of V_OHC and X_OHC in the same preparations as Fig. 12 A&B. Fig. 12 E&F is a similar comparison in the lower BF region. In this case, for V_OHC we used #712, BF = 16.5 kHz and for the BM motion we used published data from Ren et al., (2011), their Fig. 1 D&F, with BF = 15.3 kHz. (Ren et al. showed velocity, not displacement, and the phase reference was stapes velocity. To compare with our data, their BM velocity was replotted as displacement with phase relative to ear canal pressure; see figure caption for details.) The amplitude results in Fig. 12 A&C&E show V_OHC, X_BM and X_OHC peaking at the BF at low SPL. The V_OHC notch and corresponding phase ripple that were noted when describing Fig. 2 are apparent. For this discussion, the most important aspect of the comparison between X_BM, X_OHC and V_OHC is in the phase. At the frequency of the amplitude notch, ~ 0.7 × BF, a phase shift of V_OHC relative to X_BM and X_OHC of between 1/4 to 1/2 cycle occurs. When V_OHC leads X_BM and X_OHC by 1/4 cycle, OHC somatic force leads X_BM and X_OHC by ~ 1/4 cycle. Velocity always leads displacement by 1/4 cycle, thus OHC force is in phase with BM (or OHC) velocity. When velocity and force are in phase, power is imparted and amplifies the traveling wave. This amplification occurs in the BF region. On the other hand, in the sub-BF region, V_OHC, X_BM and X_OHC are approximately in phase, thus, velocity and OHC somatic force are not in phase: the sub-BF region, and thus sub-BF nonlinearity is “non-amplifying”. This is the phase shift first noted in Dong and Olson (2013), and those findings are confirmed and extended to a lower frequency region by these results.

Figure 12:

A) Comparison of normalized amplitudes of V_OHC in response to multi-tone stimuli (#728 run 10, BF = 25 kHz, black line = 40 dB SPL, black dashed line = 50 dB SPL) to multi-tone BM displacement (#733 run 27, BF = 23 kHz, red solid line = 40 dB SPL, red dashed line = 50 dB SPL, red dashed/dotted line = 60 dB SPL). B) Phase of these quantities re: EC pressure. C) Comparison of normalized amplitudes of V_OHC in response to multi-tone stimuli (#728 run 10, BF = 25 kHz, black line = 40 dB SPL, black dashed line = 50 dB SPL) to multi-tone OHC displacement (#733 run 27, BF=23 kHz, green solid line = 40 dB SPL, green dashed line = 50 dB SPL, green dashed/dotted line = 60 dB SPL). D) Phase of these quantities re: EC pressure. E) Comparison of normalized amplitudes of V_OHC in response to single tone stimuli (#712 run 19, BF = 16.5 kHz, black dotted line = 30 dB SPL, black solid line = 40 dB SPL & black dashed line = 50 dB SPL) to single-tone BM displacement measured by Ren, et al. (2011) (blue solid line = 40 dB SPL & blue dashed line = 50 dB SPL). To make the Ren et al BM velocity comparable to our BM displacement data, velocity magnitudes were divided by 2π x stimulus frequency and plotted normalized to the EC pressure. F) Phase of these quantities re: EC pressure. To make the Ren et al phase comparable to the phase of the present study, a 25ms middle ear delay was added to the Ren et al. data (Olson, 1998) and the phase was shifted by −0.25 cycle so that it represents BM displacement.

Thirdly, a recent experiment using OCT studied suppression of X_BM and X_RL (displacement of the reticular lamina; similar to our X_OHC, a region with sub-BF nonlinearity) with a second tone (Dewey et al, 2019). In keeping with previous findings, in the sub-BF region, X_BM was not affected by the second tone (e.g. Rhode, 2007). With the probe frequency near the BF, both X_BM and X_RL were maximally suppressed by tones slightly higher in frequency than the BF probe tone. The authors’ interpretation was that in the BF region the amplification “accumulated” as the traveling wave reached its peak place, and tones that peaked slightly basal were most effective in suppressing this accumulating amplification. With the probe tone in the sub-BF region, X_RL could be suppressed, but the suppression was relatively tightly tuned to frequencies around the local BF. This is as would be expected by suppression in a simple saturating I/O function, since the BF responses will be relatively large and thus more suppressive. The authors interpreted this sub-BF as a local nonlinearity, not involved in the accumulation of amplification. Our terminology is different than that of Dewey et al (2019) but the conceptualization is similar: the sub-BF nonlinearity boosts responses locally, but it is only in the BF region that energy is supplied to the traveling wave, allowing the wave to enter the region where it slows, peaks, and finally drops sharply.

5. Conclusion

To summarize, our results showed strong similarity between sub-BF XOHC and VOHC, suggesting that XOHC is primarily due to OHC electromotility-derived motion. Our Fig. 9 observation that XOHC, much greater than XBM at low-moderate SPL, fall beneath XBM at high SPL, and observations of large reduction in sub-BF XOHC post-mortem even at high SPL (He, et al., 2018) support this interpretation. The phasing between XBM and VOHC (Fig. 12) confirms previous findings showing a phase shift that occurs at a frequency separating BF and sub-BF regions (Dong and Olson, 2013). Applying known OHC electro-mechanics, the BF-region phasing is as needed for OHC energy input into the cochlear traveling wave. Finally, recent suppression experiments (Dewey et al, 2019) showed that only BF-region nonlinearity contributes to the accumulation of amplification. Taken together, these findings support a conceptual division in which the sub-BF nonlinearity is non-amplifying and the BF region nonlinearity is amplifying.

• At frequencies below the best frequency the outer hair cell extracellular voltage is mildly nonlinear in response to single tones and relatively strongly nonlinear in response to multi-tone stimuli.

• At frequencies below the best frequency the nonlinear behavior of the displacement of the outer hair cell region is similar to that of the outer hair cell extracellular voltage.

• A phase shift occurs in the outer hair cell extracellular voltage relative to both the basilar membrane and outer hair cell region motion, and leads to cochlear amplification.