Theoretically meaningful models can answer clinically relevant questions

Abstract

This scientific commentary refers to ‘The ease and sureness of a decision: evidence accumulation of conflict and uncertainty’, by Mandali et al. (doi:10.1093/brain/awz013).

This scientific commentary refers to ‘The ease and sureness of a decision: evidence accumulation of conflict and uncertainty’, by Mandali et al. (doi:10.1093/brain/awz013).

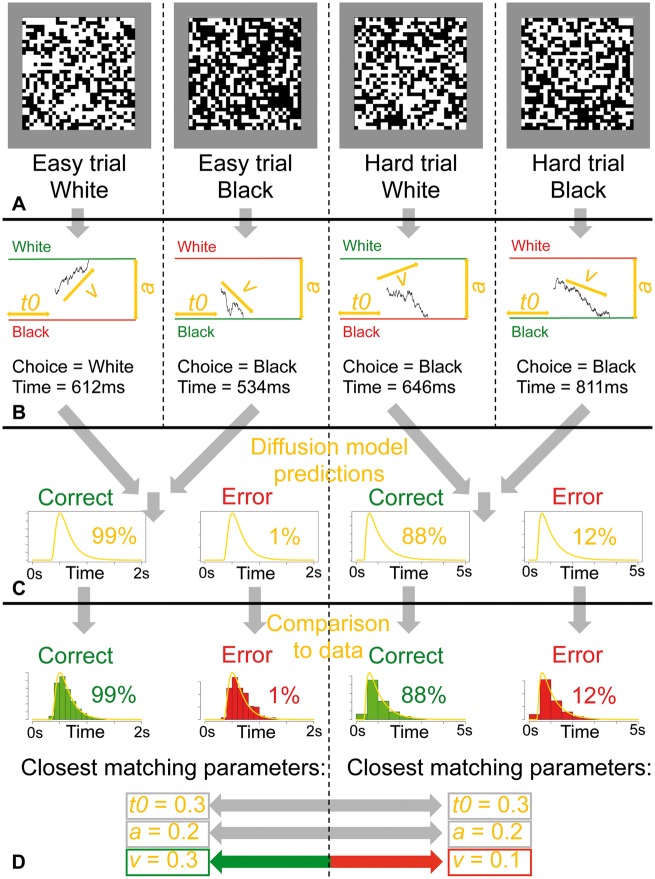
One of the most dominant models of human decision-making over the past decades has been the diffusion model (Ratcliff, 1978; Ratcliff et al., 2016). However, the diffusion model may not be familiar to all readers of Brain, as the model has primarily been applied within the field of cognitive psychology. The diffusion model proposes that decision-making results from an internal process of sequential evidence accumulation, where each potential choice alternative accumulates evidence from the environment over time, until the evidence for one alternative reaches some threshold level of evidence that triggers a decision. Importantly, the diffusion model can decompose the accuracy and time taken for each decision into latent parameters from the underlying decision-making process, most notably drift rate, decision threshold, and non-decision time. The drift rate parameter is the rate of evidence accumulation, with faster accumulation indicating better ability. The decision threshold parameter is the amount of evidence required to trigger a decision, with higher decision thresholds indicating greater caution. The non-decision time parameter represents the time taken up by processes such as perceptual encoding and motor responding. These latent parameters allow researchers to directly assess changes in the components of the underlying cognitive process, rather than attempting to indirectly infer changes from the raw observed variables, such as accuracy and mean response time. A schematic overview of the diffusion model is provided in Fig. 1.

Figure 1.

A schematic depiction of the diffusion model, and how the latent parameters relate to the raw data from decision-making tasks. (A) A typical experiment for applying the diffusion model, where participants decide whether the display of pixels contains greater numbers of white or black pixels. The first and second panels show easy trials, where the display is clearly dominated by white, or by black. The third and fourth panels show hard trials, where the display is less clearly dominated by white, or by black. (B) The diffusion process underlying the decision. Decisions for easier trials are generally faster and more accurate, as the drift rate (v) is larger. Note that a refers to the decision threshold, and t0 refers to the non-decision time. (C) The diffusion model predictions for the choice response time distributions—formed by combining the choices and times for each decision across the experiment—shown separately for easy and hard trials. (D) The process of estimating the latent parameters using the diffusion model, where the diffusion predictions are compared to the actual data. In this case, all parameters are the same for easy and hard trials, except for drift rate, which is larger for easier trials.

In this issue of Brain, Mandali and co-workers present a clear example of how the diffusion model can provide additional insight into the differences between clinical groups in various components of an underlying cognitive process (Mandali et al., 2019). Specifically, Mandali et al. compared healthy controls to participants with obsessive-compulsive disorder (OCD) and participants with alcohol dependence in an experimental task where participants made repeated two-alternative choices between different symbols, with each symbol providing a £1 reward with some probability, and the probability of reward for each symbol changing over the course of the experiment. This task separates two different elements of incoming evidence, which are often conflated: the difference between the alternatives in the probability of a reward (i.e. difficulty/conflict), and the uncertainty of whether or not a reward would occur for each alternative (i.e. the variance of a Bernoulli random variable). A standard analysis of mean response time and accuracy proved difficult to interpret. Participants with OCD were slower than healthy controls in easy trials with moderate uncertainty, and less accurate than healthy controls in difficult trials with high uncertainty, whereas participants with alcohol dependence were slower than healthy controls in hard trials with low uncertainty, and both slower and less accurate than healthy controls in easy trials with moderate uncertainty. In contrast, a diffusion model analysis yielded more interpretable results. Both clinical groups were more cautious (i.e. higher thresholds) overall in the task than healthy control subjects, and showed poorer performance (i.e. lower drift rate) than healthy controls under certain conditions. Participants with OCD were poorer than healthy controls in difficult trials that were uncertain, which Mandali et al. link back to the compulsive checking behaviours of these patients; participants with alcohol dependence were poorer than healthy controls in easy trials, and showed no improvement in task performance for easy trials over hard trials. As pointed out by Mandali et al., these findings have importance in terms of how these clinical conditions are viewed and potentially how they are treated.

Mandali et al. should be commended for using the diffusion model to make direct inferences about the underlying components of the cognitive process, rather than indirect inferences based only on observed variables. Many studies involving human decision-making continue to perform statistical analyses on observed variables, such as mean response time, and infer that changes in these observed variables reflect changes in specific underlying cognitive components, such as mental processing speed (i.e. drift rate). However, as discussed in Mandali et al., the response choices and times may be generated by an intricate combination of several different latent parameters. One classic example of response time providing a poor proxy for drift rate is in the literature on ageing, where older participants are slower at many cognitive tasks than younger participants. Salthouse (1996) suggested that this reflected a cognitive slowdown, where older participants were slower because cognitive abilities decrease with age. However, a diffusion model analysis revealed that in many tasks older participants had equal cognitive abilities to younger participants (i.e. equal drift rates), and that the slower responding of older participants was caused by a combination of increased caution (i.e. higher thresholds) and longer non-decision times (Ratcliff et al., 2001). In sum, the work of Mandali et al. provides a key example of the importance of making direct assessments on the latent parameters, rather than indirect inferences that use observed variables as a proxy for cognitive constructs.

However, we also believe that the analysis of Mandali et al. can be improved by taking into account the recent literature on statistical methods for cognitive models. First, Mandali et al. use a two-step approach, where the parameters are first estimated for each individual using a Bayesian hierarchical model, and then placed into a subsequent statistical analysis (e.g. an ANOVA) to assess differences between conditions or groups. However, as shown by Boehm et al. (2018), this intuitive approach creates a systematic bias towards finding effects. Specifically, the individual parameter estimates are subject to shrinkage in the initial hierarchical estimation, which reduces the within-group variance in the subsequent statistical analyses, and therefore inflates the effect sizes. This may be particularly problematic in Mandali et al.’s experimental condition with hard trials and high uncertainty, as all participants had fewer than 15 trials within the condition, and many participants had fewer than five trials. When applying a hierarchical model to data this sparse, the individual parameter estimates become strongly drawn to the group mean.

Second, Mandali et al. had to make a series of analysis choices, but did not explore or report whether reasonable alternative choices would leave the results qualitatively unaffected. For example, they used null-hypothesis significance testing for the observed variables, Bayes factors for the latent parameters, and the deviance information criterion for the hierarchical model. This methodological variety may be driven in part by pragmatic considerations, but it would nevertheless be good to learn the extent to which the qualitative conclusions are robust to the different analysis choices (Evans, in press). Another example is the choice to exclude trials with response times under 50 ms. Usually, response times <150 ms or 200 ms are excluded as anticipatory responses. The choice of this response time lower-bound exclusion criteria can be highly influential, as the non-decision time parameter estimate is constrained by the fastest responses included in the data, which can then influence the estimated values of the other parameters. To address this issue one may perform a multiverse analysis, where a researcher chooses a range of possible exclusion criteria and assesses how these choices affect the results (Steegen et al., 2016).

To conclude, Mandali et al. should be commended for using a modern framework (hierarchical drift diffusion model; Wiecki et al., 2013) for applying the diffusion model in order to learn about the latent cognitive processes that cause performance differences between clinical groups. As in most other empirical work, alternative analyses are possible and may or may not support the same conclusion. As a general solution, anonymized data could be shared in a public repository, allowing other researchers to conduct reanalyses and examine the robustness of the conclusions. Although the diffusion model is a powerful weapon in the arsenal of cognitive science, researchers unacquainted with state-of-the-art modelling may find it difficult to wield. This difficulty in application has frustrated the model’s broader adoption. In the future, we hope to implement a framework for applying the diffusion model within the program JASP (JASP Team, 2018), which will incorporate the most recent, robust methodologies within a simple point-and-click interface, allowing researchers to make robust inferences on the latent parameters of the diffusion model.

Competing interests

The authors report no competing interests.

Glossary

Bayesian hierarchical model: Bayesian parameter estimation involves estimating a distribution of possible values for each parameter, rather than only a single point estimate, taking into account uncertainty in the true value. Adding a hierarchical structure to the model means that latent parameter values are estimated for each individual participant, with all individual parameter values constrained to follow a group-level distribution.

JASP: An open-source statistical software package, catering to a similar audience as SPSS, which implements common statistical analyses using both frequentist and Bayesian methods. JASP also implements more advanced statistical methods, such as structural equation models and network analyses, and within the near future will aim to implement cognitive models, such as the diffusion model. More information can be found at https://jasp-stats.org/.

Shrinkage: A phenomenon that occurs within hierarchical models where the estimated parameter values for each individual become more alike to one another than when estimated independently, due to the constraint of all individuals having to follow the group level distribution. Although shrinkage is generally seen as a positive, making estimation more robust when there are few data per participant, shrinkage also decreases the heterogeneity in parameter estimates for participants within the same group, which becomes problematic in the case of two-step analysis approaches.