Morphological Differentiation of the Skull in Two Closely-related Mustelid Species (Carnivora: Mustelidae)

Abstract

Alexei V. Abramov, Andrey Yu. Puzachenko, and Igor L. Tumanov (2016) A morphological differentiation (i.e., the amount of morphological space occupied) in two polecat species, Mustela putorius and M. eversmanii, has been studied. These closely related species are similar in the body size, the age of origin, and many aspects of their natural history. We have used cranial characters to estimate some parameters of morphological diversity, to compare ‘morphological niche breadth’ occupied by polecats in the morphological space and their overlap, assuming that variation in the characteristics of morphological diversity could be reflected in the extent of adaptive diversification. A comparison of diversity based on 23 cranial characters shows that the polecats occupied distinct areas of the morphospace. Both skull ‘size’ and ‘shape’ characters are important components of the morphological differentiation between M. putorius and M. eversmanii. It seems that the difference between these polecat species is accounted for the ecological pattern rather than the phylogenetic one. Resource partitioning and the lessening of their ecological niches’ overlap in two sympatric carnivores could apparently explain the observed differences of their morphospaces. The morphological diversity of the European polecat is higher than that of the steppe polecat. A possible explanation of this phenomenon is likely to lie in the differences between prey ranges of these species. The morphological diversification in M. putorius could be facilitated by its adaptations to forest habitats of the temperate zone with a wide range of potential prey, whereas M. eversmanii could have evolved under more severe conditions of arid Eurasian habitats with a possible prey specialization.

BACKGROUND

The common trait of adaptive radiation is the occupation of a great number and a wide variety of ecological niches (Simpson 1953). General ecological observations testify that the natural selection acts to reduce both morphological and behavioral similarities between competing animals, thus lessening their niche overlap. The diversification of morphological characters (body size, cranial and dental characters) is often the first- order response to competitive situations among mammals, notably among carnivores (Dayan et al. 1989, 1990; Brown 1995; McDonald 2002). The structure of morphological disparity is often used for estimation of interspecific competition within multi-species guilds (Davies et al. 2007; Meloro 2011; Abramov and Puzachenko 2012). Another aspect of this estimation is comparison of the sister taxa that originated at the same time and under the same initial conditions (Brooks and McLennan 1993). By comparison of closely related taxa of similar age, it is possible to determine whether a particular taxon has diversified to a greater extent than another one with similar ecology and for the same period of time.

In order to analyze the morphological differentiation, we have examined two closely related species of the Palaearctic polecats (Carnivora, Mustelidae) which overlap in their morphology, are roughly similar in their natural history and diet requirements, and appear to have originated at roughly the same time.

Three polecat species of the subgenus Putorius, the European polecat M. putorius L., 1758, the steppe polecat M. eversmanii Lesson, 1827 and the black-footed ferret M. nigripes (Audubon et Bachman, 1851), appear to belong to the most reliably defined species group of the genus Mustela (Youngman 1982; Abramov 2000). Two polecat species are widespread in the Palaearctic Region. The European polecat occurs throughout the forest European zone, except for northern Scandinavia, from British Isles to the Ural Mountains, whereas the steppe polecat is distributed from the southern regions of central and eastern Europe in the west throughout southern Russia (including southern Siberia) and Middle Asia to Mongolia and northern and western China in the east (Heptner et al. 1967; Wozencraft 2005). Almost a half of the range of European polecat lies within the range of steppe polecat (Stroganov 1962). The endangered black-footed ferret exists in few populations in North America (Hillman and Clark 1980).

Morphological differences between polecat species are poorly defined, so that the reality of a true species split was even debated (see Blandford 1987). Several authors have considered M. putorius, M. eversmanii, and M. nigripes conspecific to be viewed as one Holarctic species (Ellerman and Morrison-Scott 1951; Anderson 1977; Anderson et al. 1986). The European and steppe polecats are occasionally reported to hybridize where they overlap in their distribution (Stroganov 1962; Heptner et al. 1967). Experimental hybridization among M. putorius and M. eversmanii was shown to be possible, and all hybrids were fertile (Ternovsky 1977). The black-footed ferret and the steppe polecat can also produce fertile hybrids in captivity (Williams et al. 1996; Biggins et al. 2011). Recent molecular phylogenetic analyses have placed all the polecats in the separate polecat group within Mustela (Davison et al. 1999; Kurose et al. 2000, 2008; Sato et al. 2009; Abramov et al. 2013). Genetic studies have shown a very close phylogenetic relationship between the polecat species. The divergence among M. putorius and M. eversmanii was estimated to have occurred within one Myr ago (Kurose et al. 2000, 2008; Sato et al. 2003, 2012). The polecat fossil records are poorly known, probably due to the limited use of mustelids in biostratigraphy, and their overall paucity in the Late Pleistocene sites. However, the available paleontological data on M. putorius and M. eversmanii also suggest a recent origin of these species (Wolsan 1993).

There have been several studies on the morphological characteristics of M. putorius and M. eversmanii analyzing the interspecific differences or sex, population and age variation within each species (Pocock 1936; Ashton and Thomson 1955; Heptner 1964; Buchalczyk and Ruprecht 1977; De Marinis 1995; Ansorge and Suchentrunk 2001). However, these studies have not addressed the analysis of morphological diversity and morphospace occupation. In the present study, we have used cranial characters to estimate some parameters of morphological diversity, to compare ‘morphological niche breadth’ occupied by polecats in the morphological space and their overlap, assuming that variation in the characteristics of morphological diversity could be reflected in the extent of adaptive diversification. For that, we have introduced an easy-to-use probabilistic model of morphospace and morphological disparity.

MATERIALS AND METHODS

Description of samples and skull measurements

We have examined 235 complete skulls of the two polecat species: M. putorius (126 males and 36 females), M. eversmanii (57 males and 16 females). The studied specimens are deposited in Institute of Animal Systematics and Ecology of the Siberian Branch of the Russian Academy of Sciences, Novosibirsk, Russia; B.M. Zhitkov All- Russian Research Institute of Game Management and Fur Farming, North-Western Branch, Saint-Petersburg, Russia; Zoological Institute of the Russian Academy of Sciences, Saint- Petersburg, Russia. In order to minimize the effect of heterogeneous sample collection, we have analyzed only homogeneous samples consisting of the polecat skulls collected from the same area during a short period of time. All specimens of M. putorius were collected in neighboring districts of Leningrad and Pskov Regions, the European part of Russia, during 1976-1985; all specimens of M. eversmanii were collected in the central part of the Baraba forest-steppe (West Siberia, Novosibirsk Region, Russia) during the 1960-1961 hunting season.

Additional materials studied include the Siberian weasel Mustela sibirica Pallas, 1773 (99 males, 93 females), the ermine Mustela erminea Linnaeus, 1758 (25 males, 35 females), and the European mink Mustela lutreola (Linnaeus, 1761) (48 males, 38 females).

Only adult specimens were used. The age classes were defined by scoring morphological features of skull structure, such as the development of crests, the obliteration of sutures, tooth wear, and dentition (see Buchalczyk and Ruprecht 1977).

Twenty-three variables (see Abramov and Puzachenko 2009 for the scheme of measurements) were taken for each skull using digital caliper to the nearest 0.1 mm. We defined craniodental variables representing the size and shape of major structures of the mustelid skull, which were selected as descriptors of the key skull dimensions: condylobasal length (CbL), neurocranium length (NcL), viscerocranium length (VcL), palatal length (PL), maxillary tooth-row length (MxtL), upper carnassial teeth Pm4 length (Pm4L), greatest length between oral border of the auditory bulla and aboral border of the occipital condyles (BcL), length of the auditory bulla (AbL), zygomatic width (ZyW), mastiod width of skull (MW), postorbital width (PoW), interorbital width (IW), width of rostrum (RW), greatest palatal width (GpW), width of the auditory bulla (AbW), width of upper molar M1 (M1W), cranial height (CH), total length of the mandible (ML), length between the angular process and infradentale (AL), mandibular tooth-row length (MatL), length of lower carnassial teeth M1 (m1L), height of mandible in the vertical ramus (MaH), minimal palatal width (MpW).

Model of morphological space and morphological diversity

In the model of morphological space introduced below, the ‘morphological system’ (or morphosystem) is defined as a set (sample set) of skulls (elements of system) defined on a set of all possible variables - measurements of the skull. The relationship between elements of the morphosystem is set by a metric - a specific method for measuring morphological distances between individuals. ‘Morphological space’ (or morphospace) is a model of a multidimensional, usually Euclidean space constructed to compact representation of morphological distances between individuals’ skull. Each coordinate of the morphospace should contain independent information about the position of morphosystem elements - ‘microstates’ of the morphosystem. The microstates of morphosystem with a unique set of coordinate values uniquely define the position of each microstate in relation to all other microstates in the morphospace. There is a mutually unambiguous correspondence between a microstate in the morphological space and an element of the morphosystem, so that the Euclidean distances between microstates are proportional to the initial morphological distances between elements of the morphosystem.

The whole set of pair-wise distances between microstates sets the ‘morphospace structure.’ Then morphospace is divided by the n equal parts (in general, n is proportional to logN, where N is sample size: n = 1, 2, 3,...k). Further, for any i we can define a sample probability pk = nk/N, where nk is a number of microstates in k-th part of

morphospace (pk ∈ [0;1],

$${\sum }_{i=1}^k\mathrm{pi}=1$$

), and hence our morphospace is defined as a probability space. The mammalian skull is regarded as a highly specialized multifunctional complex skeletal system with a limited ability to change in the relationship between its parts (skull subsystems) (Romer and Parsons 1977; Trainor et al. 2003) and therefore that ‘limitations’ should limit a potential morphological diversity. The distribution of microstates in morphospace reflects these ‘limitations’. Because, many distributions of skull measurements are close to normal, in practice, we can purpose the normal distribution as a most common occurrence (typical) class of microstates distribution by the parts of morphospace when other things being equal.

The concept of ‘morphological diversity’ in the proposed model includes a full set of properties of the morphological space structure and is described by a set of special variables - macroparameters. Macroparameter of the morphological diversity is a function of the morphospace structure, particular of distribution of a microstate in the morphospace, that characterizes it in general; consequently, it may be (according to the conditions of the model) a function that could be used in the statistical mechanics, and, primarily, in the information theory.

Data processing

Before the main statistical analysis, all measures were standardized to exclude the impact of the ‘scale’ of the different measurements according to the following transformation:

$$\widehat{x_i}=\frac{x_i-x_{\min }}{x_{\max }-x_{\min }}$$

, in which xi is the standardized variable, x_i, x_min, and x_max are observed, minimum, and maximum values of the i-th variable, respectively.

The square dissimilarity matrix contained both the Euclidean distances matrix and the matrix of Kendall’s tau-b (corrected for ties) rank- order coefficients (Kendall 1975) among all pairs of skulls that were calculated. The Euclidean metric generates common Euclidian space with the orthogonal Cartesian coordinate system. As a simple geometric distance in a multidimensional space, the Euclidean metric describes a disparity in skull ‘sizes’ between specimens. D. G. Kendall (Kendall 1984) introduced a theoretical base of the specific spherical “Shape Space” for describing (dis)similarities between objects by their shapes per se. The metric based on Kendall’s coefficients causes a curvilinear surface from a Riemann manifold to project on the Euclidian space as a segment (one dimension), a circle (two dimensions), or a multidimensional sphere (three and more dimensions). On the other hand, Kendall’s nonparametric rank coefficient is a difference between the probabilities that the observed rank data are in the same order for the two specimens versus the probability that they are in a different order. Hence, this metric describes a concordance in the variation of different measurements between two comparing specimens. Thus, the Kendall’s coefficient can be interpreted as an integrated metric that describes the variability of skull ‘shape’.

For developing the morphological space described above we used a Nonmetric Multidi- mensional Scaling (NMDS) procedure (Shepard 1962; Kruskal 1964; Davison and Jones 1983; James and McCulloch 1990) based on the matrix of morphological distances: Euclidean distances and the matrix of Kendall’s coefficients (Abramov et al. 2009; Abramov and Puzachenko 2009, 2012; Baryshnikov and Puzachenko 2011; Puzachenko and Korablev 2014). This approach is a nonparametric version of the methods that are aimed at reducing the dimensionality of a data set, so that one can start with many original variables but end up with only a few meaningful virtual axes. It should be noticed that generally, the axes do not exactly coincide with any of the original variables, but any of them can be reproduced as linear combinations of the axes. The ‘best-minimum’ dimensionality of NMDS model was estimated on the basis of the ‘stress formula 1’ (Kruskal’s stress) according to the procedure described by Abramov and Puzachenko (2005) (see also Kupriyanova et al. 2003; Abramov et al. 2009).

NMDS provides the Euclidian space with d coordinates (NMDS axes or dimensions) that hold the main information on the geometrical position of each specimen in this space. The coordinates for a NMDS model based on the Euclidean distances matrix we marked as E1, E2... and coordinates based on Kendall’s rank correlation matrix - as K1, K2... Shape diversity morphospace is presented in the polar coordinate system, which is more suitable for the image of curved space.

In order to create the ‘joint’ size and shape’ diversity morphospace we used principal components analysis where NMDS axes E1, E2... and K1, K2... were as variables. Principal components analysis (PCA) is well-known parametric method reducing the dimensionality of a data set (Legendre and Legendre 1998). We have used it for reducing potential correlations between the NMDS axes of ‘size’ and ‘shape’ morphospaces.

Parameters of morphological diversity

The conditions of modeled space developed by NMDS satisfy the conditions for morphological space as they were described above. Space coordinates (NMDS axes) are orthogonal and the distance for any pair of specimens (microstate of a morphosystem) is proportionally to the morphological distance between them. The coordinates of modeled morphospace can also be interpreted as a pairwise independent “order parameter” or a “degree of freedom” in synergetic sense (Haken 1983). Therefore, morphospace dimensionality (d) is the first acceptable macroparameter of morphological diversity. According to probabilistic conditions of the morphospace model and by analogy with the thermodynamics, we have used information functions in the capacity of parameters of morphological diversity.

A specific morphological niche (James 1982) is part of the morphospace, which is occupied by microstates of one or another species’ morphosystems. Within the framework of this approach, the information Shannon-Weaver entropy (Shannon and Weaver 1949; Hutcheson 1970) may estimate a ‘niche breadth’ or a ‘niche volume’:

$$H=-\sum _{j=1}^d\sum _{i=1}^k{p}_i{\log }_2{p}_i;\sum p_i=1;k=1+{\log }_{2}N$$

,where the p_i - frequency of the values of d-th NMDS axis of a morphospace within fixed k-th interval (according to Sturges’ formula: k = 1 + log₂N), N - sample size. H is the second macroparameter of morphological diversity, obviously, because it is function of the morphospace structure. In this case, structure is set by the distributions of microstates along dimensions of the morphospaces.

The statistical error of H estimated according to the following formula (Kramarenko 2005):

$$m_H=\sqrt{\frac{{\sum }_{i=1}^k[p_i{({\log }_2{p}_i)}^2]-H^2}{2N}}$$

Because H strongly depends on morphospace dimensionality then next macroparameter is H_d= H/d - specific entropy or average entropy.

Fourth introduced information macroparameters of morphological diversity is measure of organization of morphosystem:

$$\mathrm{MO}=\frac{H_{\max }-H}{H_{\max }}=1-\frac{{\sum }_{i=1}^d{H}_i}{d{\log }_2{k}^2}$$

, where H_max calculated on the assumption that p_idistribution is uniform (H/H_max – evenness, information redundancy (Shannon 1948; Pielou 1966)). Von Foerster (1960) was the first who proposed to use the degree of information redundancy as an estimate of the order or organization of a complex system. In this study, we use it as an estimate of potential diversity limitations. MO varies from 1 (extremely strong limitation, full deterministic system) to 0 (limitations are absent, nondeterministic stochastic chaotic system).

A sample size (N) may be significantly affects the value of macroparameters based on entropy. On a logarithmic scale, this dependence on N is written as a linear function. The calibration in this case consists of doing the same thing in accordance with the following transformation:

$$H_i^{\mathrm{cal}}=[H_i-(a-b{\log }_{10}{n}_i)]+(a+b{\log }_{10}\overline{n})$$

The first term of the sum in square brackets corresponds to the subtraction of the linear trend. The second term of the sum is the scale constant, which returns the original scale of H after subtracting the trend; n is the median value of the sample size. Random subsamples with different numbers were selected from the samples i (i = 7-10). For each subsample, we have calculated entropy and then, if necessary, fulfilled a calibration of H.

An overlap of morphological niche

Morphological niche overlapping (James 1982) between two species j and l in multispecies morphospace was estimated by the modified (for multidimensional case) Pianka’s index (1973, 1974):

$$O_{j.l}^d=\frac{{\prod }_1^d{\sum }_1^k{p}_{k_j}{p}_{k_l}}{{\prod }_1^d\sqrt{({\sum }_1^k{p_{k_j}}^2{\sum }_1^k{p_{k_l}}^2)}}$$

, where p_kj and p_kl are the frequency of occurrence of the values of d-th NMDS axis (coordinates of a morphospace) in the k-th interval for species j and l respectively (

$$O_{j.l}^d$$

∈ [0; 1](Abramov and Puzachenko 2012). Any two niches are non-overlapping (

$$O_{j.l}^d$$

= 0) if they are non-overlapping along any single dimension of a morphological space.

Static multivariate allometry

We have used static multivariate allometry coefficients (MAC) (Jolicoeur 1963; Klingenberg 1996) for the comparison of the studied species. We have PCA of the variance-covariance matrix of log-transformed skull measurements. The first principal component PC1 corresponds to the ‘base of size variation’ within a set of measures (most of the variation in a multivariate data set). The coefficient (loading) of a given measure on PC1 divided by 1 / √M (M is the number of measures) is a multivariate allometric coefficient and thus MAC corresponds to slope angle of regression line to the PC1 axis. MAC values > 1.0 indicate positive allometry, whereas MAC = 1.0 indicate isometry, MAC values < 1.0 indicate negative allometry. If MAC = 0, this indicates that a variation of a given measure is completely independent from a general skull size (no allometry or isometry).

Sexual size dimorphism index

Diversity parameters calculated for the polecats were compared with these parameters for some other mustelids (M. sibirica, M. erminea, M. nivalis, M. lutreola, Neovison vison).

As a measure of sexual size dimorphism (SSD) we chose the ratio of male size to female size because they are intuitively simple and easily interpretable:

$$\mathrm{SSD}=\frac{M_{\mathrm{male}}-M_{\mathrm{female}}}{M_{\mathrm{male}}+M_{\mathrm{female}}}\times 100$$

, where M is sample mean for the males or females;

$$\mathrm{ASSD}=[100\times {\sum }_{i=1}^n\frac{M_{\mathrm{male}}-M_{\mathrm{female}}}{M_{\mathrm{male}}+M_{\mathrm{female}}}]/n$$

is average SSD (ASSD), n - number of the skull measures.

RESULTS

Two-species morphospaces and morphological niche overlapping.

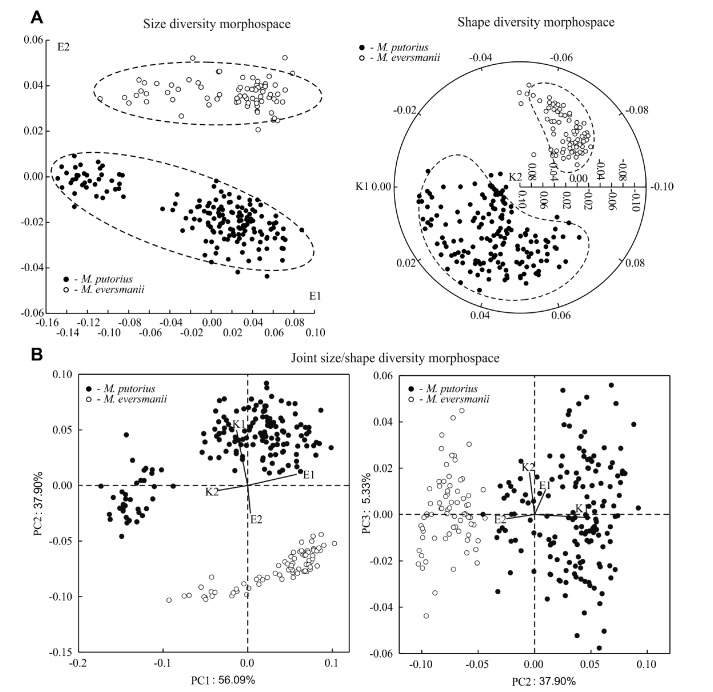
The two-dimensional morphospace is optimal for both ‘size’ and ‘shape’ skull variation in NMDS models (Fig. 1A). The first axis E1 (size variation) is associated with the majority of cranial characters, whereas the second axis E2 negatively correlates with two variables only - the length of the auditory bulla, the postorbital width and the width of M1 (Appendix Table S1, S2). The joint ‘size-shape’ model has three principal components (Fig. 1B), where in PC1 the NMDS axis E1 is partially correlated with the axis K2 and in PC2 the axis E2 is partially correlated with K1. Third component PC3 is correlated with the axis K2.

Fig. 1.

Fig. 1. Two-species (M. putorius, M. eversmanii) morphospace models: (A) skull size morphospace based on NMDS axes E1, E2, and skull shape morphospace based on NMDS axes K1, K2; (B) three-dimensional joint ‘size/shape’ diversity morphospace based on principal components PC1-PC3.

For the ‘shape’ diversity model, the first axis K1 demonstrates a correlation with the length of the auditory bulla, the postorbital width, and the second axis K2 correlates well with most of the characters. Some characters (the neurocranium length, the greatest length between oral border of the auditory bulla and aboral border of the occipital condyles, the width of upper molar M1, and the minimal palatal width) are well associated with two dimensions of the morphospace. Therefore, their total variance is a sum of two independent components. Variation of the skull size in polecat (axis E1) is almost completely determined by SSD as indicated by an analysis of the variance components (Table 1). The variance of axis K2 is also associated with SSD. Species-specific difference depends only on a few characters, which correlate with the axes E2 and K1. A contribution of the species-specific SSD to morphological disparity is low but statistically significant.

Table 1.Spearman Rank Order Correlation coefficient for skull measures and NMDS axes for two polecat species.

Variables	Size diversity model		Shape diversity model		r2
	E1	E2	K1	K2
CbL	0.9	-0.34	0.13	-0.73	0.96
NcL	0.63	-0.48	0.3	-0.49	0.6
VcL	0.85	-0.12	-0.05	-0.69	0.83
PL	0.86	-0.17	0	-0.74	0.91
MxtL	0.88	0.1	-0.32	-0.56	0.93
Pm4L	0.72	0.29	-0.47	-0.42	0.88
BcL	0.62	0.45	-0.56	-0.47	0.93
AbL	0.27	-0.86	0.72	-0.27	0.91
ZyW	0.91	-0.07	-0.11	-0.75	0.91
MW	0.92	-0.08	-0.08	-0.77	0.93
PoW	0.25	-0.93	0.75	-0.14	0.88
IW	0.85	-0.25	0.11	-0.69	0.85
RW	0.92	-0.03	-0.17	-0.66	0.93
GpW	0.87	-0.23	0.01	-0.49	0.91
AbW	0.82	-0.25	0.07	-0.61	0.76
M1W	0.56	-0.63	0.4	-0.24	0.76
CH	0.84	0.01	-0.15	-0.64	0.97
ML	0.96	-0.13	-0.08	-0.78	0.83
AL	0.93	-0.23	0.02	-0.79	0.97
MatL	0.9	-0.06	-0.18	-0.58	0.92
m1L	0.74	-0.06	-0.14	-0.35	0.82
MaH	0.9	-0.18	0.02	-0.8	0.93
MpW	0.65	-0.46	0.24	-0.39	0.71
Analysis of NMDS axes variance
Components of variance, %					Wilks tests
Factor: “species”	7.1	88.4	93.1	0	0.13 (p < 0.01)
Factor: “sex”	67.1	3.5	1.7	62.7	0.26 (p < 0.01)
Joint affect: “species” ×	12.6	5	0.5	13.2	0.76 (p < 0.01)
“sex”
Unexplained variance	13.2	3.1	4.8	24.1

r² – coefficient of multiple regression in the linear multiple regression models for measurements, y=a₁E1+a₂E2+b₁K1+b₂K2+const

Two polecat species occupy an isolated morphospaces along the axes E2 and K1 (Fig. 1A). Morphological niche overlaps (

$$O_{j.l}^d$$

) are 76% along the axis E1 and 85% along the axis K2. In the joint ‘size/shape’ three-dimensional morphospace, polecat morphological niches are separated due to their distribution along the second axis PC2 that correlates with the axes E2 and K1 (Fig. 1B).

The individual morphological niche breadth in M. putorius is almost twice as large as that of M. eversmanii in both size- and shape-diversity morphospaces (Table 2). It means that the morphological diversity of the European polecat is significantly higher than that of the steppe polecat. An interspecific difference in the diversity level is more pronounced in the skull shape (Fig. 1, Table 2).

Table 2.Estimations of the morphological niche breadth (H, bit/microstate) for European and steppe polecats in the two-species morphospaces .

Species	Size diversity morphospace	Shape diversity morphospace
M. putorius	4.53 ± 0.07	4.89 ± 0.05
M. eversmanii	2.50 ± 0.12	2.30 ± 0.11

Species morphospaces

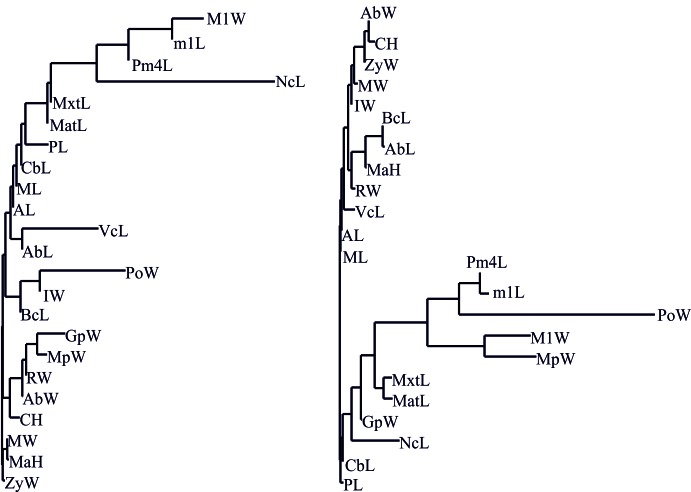
Dimensions of a single species morpho- spaces are higher than those of a joint model. Four-dimensional morphospaces is optimal for reproducing both the size and the shape variation of the M. putorius skull (Table 3). The first axis E1 (general size variation of the skull) is associated with most of the characters, except for the neurocranium length, the width of upper molar M1, the length of lower carnassial teeth M1 and the upper carnassial teeth Pm4 length (Fig. 2). Full variances of all the aforementioned characters are composed of a few independent variance components of different (more than one) dimensions of the morphospace.

Fig. 2.

Fig. 2. NJ trees of skull measurements in M. putorius and M. eversmanii based on the absolute values of Spearman Rank Order Correlation coefficients from Tables 3-4.

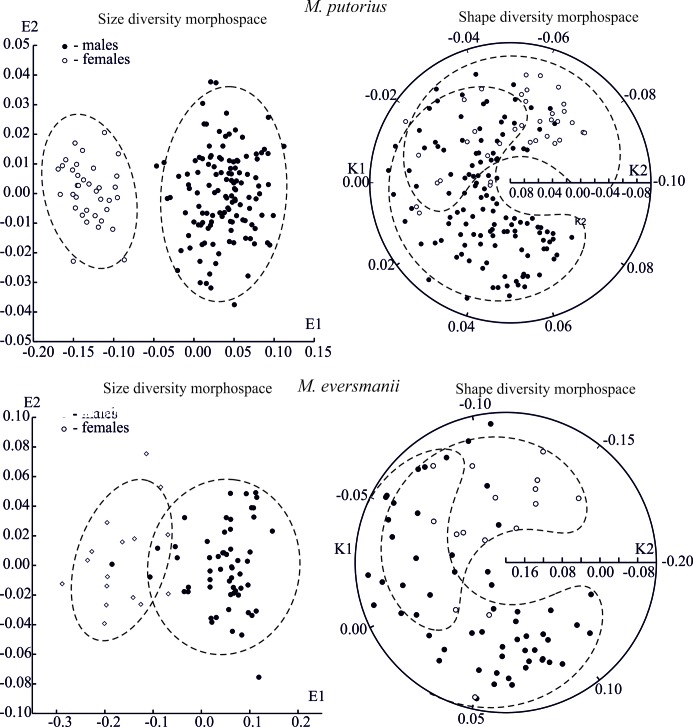
The ‘size’ diversity in the European polecat skull (axis E1) is determined by SSD (Fig. 3, Table 3). Morphological niches of males and females are not overlapped in the size diversity morphospace; however, in the ‘shape’ morphospace they are partly overlapped (Fig. 3).

Fig. 3.

Fig. 3. Projections specific (M. putorius and M. eversmanii) morphospace models on first two coordinates E1-E2 and K1-K2.

Table 3. Spearman Rank Order Correlation coefficients for cranial variables and morphospace axes (E1-E4, K1-K4) in M. putoriu.

Variables	Size diversity model					Shape diversity model				r2
	E1	E2	E3		E4	K1	K2	K3	K4
CbL	0.95	0.18	-0.04		0.14	0.70	0.16	-0.33	-0.08	0.98
NcL	0.68	-0.17	-0.62		0.16	0.38	-0.39	-0.59	-0.05	0.96
VcL	0.84	0.26	0.30		0.02	0.67	0.44	-0.10	-0.17	0.95
PL	0.86	0.19	0.00		0.25	0.71	0.24	-0.39	-0.01	0.95
MxtL	0.89	-0.01	0.12		0.20	0.49	0.32	-0.41	-0.12	0.93
Pm4L	0.80	-0.26	0.07		0.22	0.28	0.23	-0.54	-0.12	0.89
BcL	0.81	0.16	-0.09		-0.12	0.55	0.02	-0.10	0.16	0.92
AbL	0.83	0.16	-0.07		-0.10	0.56	0.05	-0.13	0.09	0.94
ZyW	0.89	0.12	-0.06		-0.02	0.63	0.05	-0.28	-0.29	0.92
MW	0.92	0.15	-0.12		-0.01	0.66	-0.01	-0.29	-0.20	0.95
PoW	0.73	-0.23	-0.16		-0.36	0.28	-0.02	-0.23	-0.34	0.87
IW	0.84	0.12	0.00		-0.20	0.57	0.09	-0.15	-0.35	0.90
RW	0.91	0.00	0.04		0.02	0.52	0.17	-0.35	-0.25	0.93
GpW	0.86	-0.22	0.02		-0.05	0.32	0.16	-0.40	-0.29	0.93
AbW	0.83	-0.06	-0.05		0.02	0.46	0.08	-0.37	-0.20	0.78
M1W	0.70	-0.50	0.15		0.06	0.11	0.30	-0.56	-0.16	0.91
CH	0.82	0.02	-0.21		-0.09	0.52	-0.09	-0.29	-0.17	0.87
ML	0.95	0.17	-0.04		0.13	0.70	0.16	-0.32	-0.16	0.98
AL	0.94	0.19	-0.08		0.13	0.72	0.11	-0.33	-0.17	0.98
MatL	0.90	-0.04	0.05		0.20	0.50	0.29	-0.45	-0.12	0.95
m1L	0.76	-0.35	0.14		0.11	0.21	0.29	-0.48	-0.14	0.88
MaH	0.90	0.19	-0.14		0.04	0.72	0.01	-0.32	-0.21	0.95
MpW	0.75	-0.11	0.12		-0.09	0.34	0.25	-0.22	-0.26	0.82
Analysis of NMDS axes variance
Components of variance, %										Wilks tests
Factor: “sex”	94.0	0	0	0		54.9	1.5	42.0	4.3	0.14 (p< 0.001)
Unexplained variance	6.0	100	100	100		45.1	98.5	58.0	95.7

r²– coefficient of multiple determination in the linear multiple regression model: y=a₁E1+a₂E2+a₃E3+a₄E4+b₁K1+b₂K2+b₃K3+b₄K4+const

The six-dimensional morphospace is optimal for the size diversity model for M. eversmanii and the three-dimensional one for the ‘shape’ diversity morphospace (Table 4). The first axis E1 is associated with most of the characters, except for the postorbital width (Fig. 2) which is correlated with the axis E3. Yet, the sizes and proportions of teeth are not correlated with general skull sizes. SSD determines up to 85% of the size variation of the steppe polecat skull. Morphological niches of males and females are overlapped both in the size diversity and in shape diversity morphospaces (Fig. 3).

Table 4 Spearman Rank Order Correlation coefficients for cranial variables and morphospace axes (E1-E6, K1-K3) in M. eversmanii.

Variables	Size diversity model							Shape diversity model				r2
	E1		E2	E3	E4	E5	E6	K1	K2	K3
CbL	0.93		-0.09	-0.14	0.09	0.05	-0.12	0.48	-0.32	-0.09		0.98
NcL	0.71		0.22	0.20	0.30	-0.13	-0.29	0.27	-0.09	0.01		0.93
VcL	0.83		-0.28	-0.13	-0.18	0.07	-0.02	0.64	-0.36	-0.06		0.95
PL	0.85		-0.10	-0.15	-0.11	-0.02	-0.14	0.48	-0.39	0.05		0.90
MxtL	0.83		0.09	-0.14	-0.14	-0.20	-0.16	0.32	-0.54	0.00		0.94
Pm4L	0.66		0.39	-0.27	0.01	-0.20	0.04	0.05	-0.49	0.08		0.82
BcL	0.82		-0.10	-0.01	0.40	0.01	0.06	0.43	-0.07	-0.23		0.96
AbL	0.80		-0.12	-0.03	0.36	0.03	0.02	0.40	-0.07	-0.29		0.93
ZyW	0.89		-0.12	0.24	-0.07	0.07	0.02	0.63	-0.05	0.17		0.94
MW	0.85		-0.25	0.09	-0.16	0.12	0.05	0.70	-0.15	0.12		0.93
PoW	0.27		0.27	0.80	-0.16	-0.15	-0.10	0.12	0.24	0.28		0.95
IW	0.87		-0.16	0.10	-0.18	0.14	-0.12	0.65	-0.23	0.13		0.90
RW	0.90		0.08	0.01	-0.06	0.09	0.08	0.47	-0.21	0.24		0.93
GpW	0.83		0.22	0.00	-0.03	-0.09	0.11	0.31	-0.23	0.22		0.89
AbW	0.83		-0.07	0.18	0.05	0.11	0.11	0.58	0.00	0.11		0.80
M1W	0.56		0.48	-0.08	0.11	0.08	0.44	0.01	-0.12	0.26		0.89
CH	0.74		-0.15	0.30	-0.07	-0.09	0.22	0.59	0.03	0.16		0.90
ML	0.92		-0.08	-0.06	-0.04	0.03	-0.11	0.54	-0.30	-0.02		0.97
AL	0.92		-0.07	-0.07	-0.08	0.04	-0.08	0.54	-0.32	0.04		0.96
MatL	0.82		0.17	-0.17	-0.17	-0.09	-0.13	0.24	-0.53	0.19		0.94
m1L	0.66		0.35	-0.31	-0.05	-0.35	-0.07	0.02	-0.56	0.08		0.90
MaH	0.83		-0.09	0.09	-0.32	0.05	0.05	0.63	-0.28	0.27		0.91
MpW	0.57		0.56	0.00	-0.04	0.46	-0.15	0.05	-0.17	0.28		0.96
Analysis of NMDS axes variance
Components of variance, %												Wilks tests
Factor: “sex”		85.3	0	0	0	0.6	0	52.9	15.3		0	17.7 (p < 0.01)
Unexplained variance		14.7	100	100	100	99.4	100	47.1	84.7		100

r2– coefficient of multiple determination in the linear multiple regression model: y=a₁E1+a₂E2+a₃E3+b₁K1+b₂K2+b₃K3+const

Morphological diversity

The morphospace dimensionality (d) defines an amount of linear independent variables of morphological diversity and makes a major con- tribution to the value of Shannon-Weaver entropy (H). According to that, the diversity of skull size is lower in M. putorius compared to M. eversmanii, whereas the diversity of skull shape is higher in M. putorius compared to M. eversmanii (Table 5). The normalized parameters of diversity (Hd) are higher in M. putorius for both morphospaces models and this corresponds to the difference in morphological niche widths occupied by polecat species in the joint morphospace (see above). The limitations of morphological diversity of skull (MO) were slightly higher in M. putorius compared to M. eversmanii. However, the differences in macroparameters of the morphological diversity are not significant for the polecats.

Table 5.Macroparameters of morphological diversity of skull in European and steppe polecats and other small mustelids (calibrated values).

Species	Diversity of skull’ size				Diversity of skull’ shape
	d	H	Hd	MO	d	H	Hd	MO
M. putorius	4	8.99 ± 0.06	2.25	0.25	4	10.0 ± 0.09	2.50	0.17
M. eversmanii	6	13.0 ± 0.11	2.17	0.23	3	7.06 ± 0.06	2.35	0.16
M. sibirica	5	10.4 ± 0.08	2.08	0.31	3	7.54 ± 0.05	2.51	0.16
M. erminea	2	4.40 ± 0.08	2.20	0.22	2	4.35 ± 0.06	2.17	0.23
M. lutreola	6	12.7 ± 0.10	2.12	0.25	4	9.23 ± 0.06	2.31	0.18

The comparison of polecats with other mustelid species (M. sibirica, M. erminea, M. lutreola) has revealed a species-specific variation in dimensions (d) of the morphospaces and, respectively, the values of H (Table 5). At the same time, the normalized macroparameters of diversity (Hd, MO) are more stable and vary in different species in a narrow range of values.

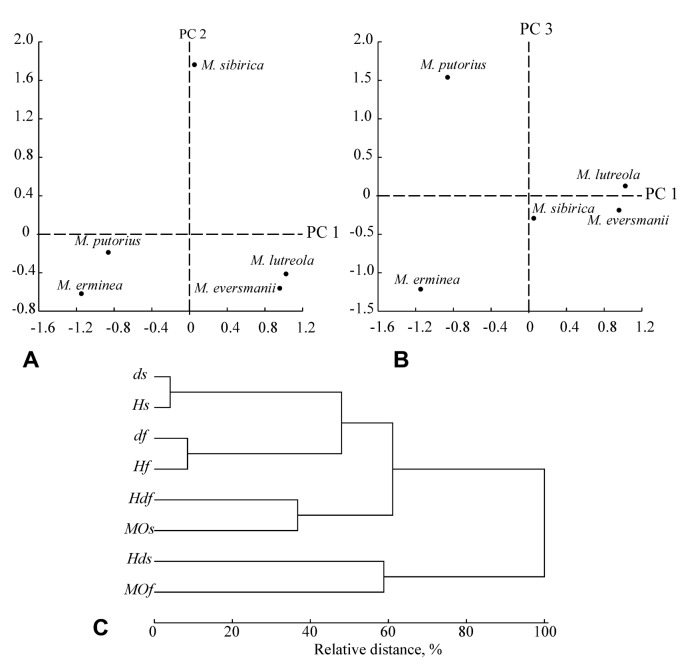
Results of PCA analysis of diversity macroparameters are shown in figures 4A, B and table 6. The first axis PC 1 can be interpreted as a ‘general size diversity’ since ds and Hs are positively highly correlated with it. The second axis PC 2 can be interpreted as an ‘organization of size diversity’ (MOs), and the PC 3 can be interpreted as a ‘general shape diversity’ (Table 6). Several macroparameters (Hds, Hdf and MOf) are correlated with more than one PCs. A cluster analysis based on the factor loadings (Fig. 4C) allows distinguishing three groups of macroparameters: 1) dimensionality and general entropy (ds, Hs, df, Hf) and 2-3) average entropy, measure of order (Hdf, MOs; Hds, MOf). It should be noticed that the macroparameters of shape and size diversity of the skull are correlated with each other stronger than with other macroparameters.

Fig. 4.

Fig. 4. Scatterplots of PC1 vs. PC2 (A) and PC1 vs. PC3 (B) showing the relative positions of the European and steppe polecats and other mustelines species. (C) UPGMA dendrogram of morphological diversity macroparameters based on factor loadings from Table 6: ds, df - dimensionality of the morphospace models, Hs, Hf - entropy, Hds, Hdf - the average entropy, MOs, MOf - the measures of morphosystem organization; abbreviations s and f mark the macroparameters of ‘size’ diversity and ‘shape’ diversity of the skull correspondently.

Table 6. Factor loadings (after varimax normalized rotation) for skull morphological diversity macroparameters in five mustelids species.

Macroparameters	PC 1	PC 2	PC 3
ds	0.921	0.144	0.357
Hs	0.904	0.097	0.404
Hds	-0.628	-0.633	0.369
MOs	0.137	0.968	0.167
df	0.338	0.005	0.885
Hf	0.268	0.123	0.926
Hdf	0.048	0.674	0.704
MOf	-0.563	-0.446	-0.603
Eigenvalue	4.85	1.56	1.16
Total variance, %	60.7	19.5	14.5

According to the result of species ordination in PC1-PC2 space, the steppe polecat is close to the European mink but differs considerably from the European polecat (Figs. 4A, B). The European polecat has a specific combination of the macroparameters as well as the stoat (Fig. 4A), but these species occupies distinct positions in the PC1-PC3 projection of the morphospace in relation to the other species. Thus, both M. putorius and M. eversmanii significantly differ by their parameters of the morphological diversity, particularly by the parameters of the range of skull sizes.

Static multivariate allometry

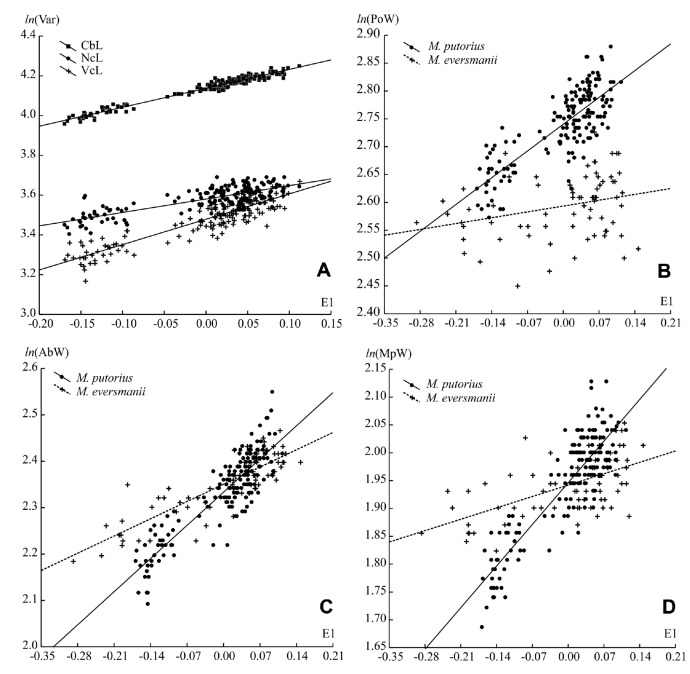
In the European polecat, at least eight cranial measurements are scaled with a positive allometry, 12 with a negative allometry and the rest of them were isometric. In the steppe polecat, 10 measurements are scaled with a positive allometry, 12 with a negative allometry and others were isometric. A comparison of multivariate allometric coefficients (MAC) of the cranial length characters (CbL, NcL, VcL) has revealed that the skull enlarging mostly depends on the length of its visceral part (positive allometry) (Fig. 5A). The width characters (zygomatic width, mastiod width of skull and interorbital width) are scaled with a positive allometry to the skull length. A negative allometry is characteristic of the postorbital width and the skull height.

Fig. 5.

Fig. 5. (A) Allometry of (CbL), the neurocranium length (NcL), the viscerocranium length (VcL) in M. putorius. (B-D) allometry of the postorbital width (PoW), width of auditory bulla (AbW) and the minimal palatal width (MpW) in M. putorius and M. eversmanii. First coor- dinate of the morphospaces (E1) is a general size factor of the skull.

Some characters are species-specific - the level of negative allometry in the postorbital width is higher in the European polecat (Fig. 5B), the level of positive allometry in interorbital width is higher in the steppe polecat. The width of the auditory bulla and minimal palatal width show an isometric allometry in the European polecat but a negative allometry in the steppe polecat (Figs. 5C, D). A significant interspecies difference has been found in the cranial height, the zygomatic width, and the mastiod skull width (Table 7).

Table 7.Multivariate allometric coefficients for M. putorius and M. eversmanii.

Variables	M. putorius	M. eversmanii	M. putorius		M. eversmanii
			females	males	females	males
CbL	0.9 (-)	0.9 (-)	0.8 (-)	0.9 (-)	0.9 (-)	0.9 (-)
NcL	0.6 (-)	0.6 (-)	0.4 (-)	0.5 (-)	0.3 (-)	0.5 (-)
VcL	1.3 (+)	1.4 (+)	1.1 (+)	1.5 (+)	1.5 (+)	1.5 (+)
PL	1.0 (0)	1.1 (+)	0.7 (-)	0.9 (-)	0.8 (-)	1.1 (+)
MxtL	0.8 (-)	0.8 (-)	1.0 (0)	0.9 (-)	0.8 (-)	0.8 (-)
Pm4L	0.8 (-)	0.7 (-)	1.2 (+)	0.7 (-)	1.3 (+)	0.6 (-)
BcL	0.8 (-)	0.8 (-)	1.1 (+)	0.9 (-)	0.8 (-)	0.9 (-)
AbL	0.8 (-)	0.8 (-)	1.0 (0)	0.8 (-)	0.7 (-)	0.9 (-)
ZyW	1.1 (+)	1.2 (+)	0.9 (-)	1.2 (+)	0.8 (-)	1.2 (+)
MW	1.1 (+)	1.2 (+)	0.9 (-)	1.1 (+)	0.9 (-)	1.2 (+)
PoW	0.7 (-)	0.3 (-)	0.6 (-)	0.7 (-)	0.0	0.3 (-)
IW	1.1 (+)	1.4 (+)	1.0 (0)	1.2 (+)	1.4 (+)	1.4 (+)
RW	1.4 (+)	1.3 (+)	1.2 (+)	1.3 (+)	1.4 (+)	1.4 (+)
GpW	0.9 (-)	1.0 (0)	1.1 (+)	0.8 (-)	0.8 (-)	0.9 (-)
AbW	1.0 (0)	1.1 (+)	1.3 (+)	1.2 (+)	1.1 (+)	1.0 (+)
M1W	0.9 (-)	0.7 (-)	1.2 (+)	0.7 (-)	1.3 (+)	0.7 (-)
CH	0.8 (-)	0.9 (-)	0.4 (-)	0.7 (-)	0.7 (-)	0.7 (-)
ML	1.1 (+)	1.1 (+)	0.9 (-)	1.2 (+)	0.9 (-)	1.1 (+)
AL	1.1 (+)	1.1 (+)	0.9 (-)	1.1 (+)	0.9 (-)	1.0 (0)
MatL	0.9 (-)	0.9 (-)	1.0 (0)	0.9 (-)	1.0 (0)	0.9 (-)
m1L	0.9 (-)	0.8 (-)	1.2 (+)	0.7 (-)	1.2 (+)	0.6 (-)
MaH	1.5 (+)	1.4 (+)	1.1 (+)	1.4 (+)	1.2 (+)	1.3 (+)
MpW	1.0 (0)	0.6 (-)	1.3 (+)	0.9 (-)	0.7 (-)	0.8 (-)

(-) negative allometry, (+) positive allometry, (0) close to isometry, a variation of measure is independent from a general size of skull.

The difference of allometric patterns between males and females is higher than that between two polecat species (Table 7). This sexual dimorphism is more pronounced in the European polecat than in the steppe polecat. For example, the females of European polecat have a positive allometry for the Pm4 length, whereas the males show a negative allometry. The reversed situation occurs in the steppe polecat: the females show a negative allometry (zygomatic width) while the males a positive one.

Sexual size dimorphism

Both species exhibit a striking SSD, with males being larger than females in all cranial measurements (Table 8). The SSD level of the European polecat is higher than that of the steppe polecat. This result is in agreement with the analysis of morphospaces for males and females (see above). The SSD patterns of both species are similar; the correlation between SSD values is 0.81 (see Table 8). There are some differences in the manifestation of dimorphism in two species. The sexual dimorphism in zygomatic width, interorbital width and cranial height of the steppe polecat is much higher than that predicted by the regression model (6.8 vs 5.8, 7.0 vs 5.7 and 5.5 vs 4.35, accordingly). At the same time, the SSD for minimal palatal width, postorbital width and width of upper molar M1 are smaller than their predicted values (2.5 vs 5.6, 1.7 vs 3.1 vs and 3.5 vs 4.5, accordingly).

Table 8. SSD of the skull measurements in M. putorius and M. eversmanii.

Variables	M. putorius	F	p	M. eversmanii	F	p
CbL	8.0 ± 0.27	686.0	0 < 0.000001	4.9 ± 0.46	117.1	0 < 0.000001
NcL	5.8 ± 0.42	169.3	0 < 0.000001	3.2 ± 0.35	48.7	0 < 0.000001
VcL	10.6 ± 0.52	306.3	0 < 0.000001	7.5 ± 0.80	86.3	0 < 0.000001
PL	9.0 ± 0.29	585.0	0 < 0.000001	5.8 ± 0.48	104.7	0 < 0.000001
MxtL	7.0 ± 0.32	389.3	0 < 0.000001	4.4 ± 0.45	94.2	0 < 0.000001
Pm4L	6.7 ± 0.39	315.8	0 < 0.000001	3.5 ± 0.67	36.2	0 < 0.000001
BcL	6.4 ± 0.42	232.5	0 < 0.000001	4.1 ± 0.57	52.5	0 < 0.000001
AbL	7.1 ± 0.37	379.0	0 < 0.000001	4.2 ± 0.64	45.7	0 < 0.000001
ZyW	9.4 ± 0.31	459.8	0 < 0.000001	6.8 ± 0.46	135.1	0 < 0.000001
MW	9.6 ± 0.32	562.3	0 < 0.000001	6.4 ± 0.58	112.8	0 < 0.000001
PoW	5.7 ± 0.39	171.7	0 < 0.000001	1.7 ± 0.69	4.9	0.029
IW	9.3 ± 0.47	358.0	0 < 0.000001	7.0 ± 0.75	81.5	0 < 0.000001
RW	11.7 ± 0.39	601.3	0 < 0.000001	6.9 ± 0.69	101.5	0 < 0.000001
GpW	8.1 ± 0.32	579.5	0 < 0.000001	5.3 ± 0.51	100.8	0 < 0.000001
AbW	8.3 ± 0.46	246.1	0 < 0.000001	5.7 ± 0.64	68.3	0 < 0.000001
M1W	7.6 ± 0.46	211.4	0 < 0.000001	3.5 ± 0.89	20.6	0.000022
CH	7.4 ± 0.34	461.1	0 < 0.000001	5.5 ± 0.44	116.8	0 < 0.000001
ML	9.8 ± 0.30	684.8	0 < 0.000001	6.0 ± 0.47	141.6	0 < 0.000001
AL	9.6 ± 0.28	690.8	0 < 0.000001	5.8 ± 0.46	144.8	0 < 0.000001
MatL	7.7 ± 0.30	477.9	0 < 0.000001	5.0 ± 0.51	91.7	0 < 0.000001
m1L	7.5 ± 0.42	299.9	0 < 0.000001	4.1 ± 0.71	43.5	0 < 0.000001
MaH	12.6 ± 0.40	550.1	0 < 0.000001	7.7 ± 0.75	109.9	0 < 0.000001
MpW	9.0 ± 0.46	298.7	0 < 0.000001	2.5 ± 0.74	12.9	0.00059

F represents the F-ratio and p – the significance level for the test for difference in means of males and females for each measurement

The European polecat has a higher SSD than that of the steppe polecat, however, the average ASSD in both polecats lie within the range of other small mustelids (Table 9).

Table 9.Average sexual size dimorphism (ASSD) of skull in small mustelids.

M. putorius	M. eversmanii	M. sibirica	M. erminea	M. nivalis	M. lutreola	N. vison
8.4; 6.71; 6.95	5.1	5.9; 6.6; 9.3	7.3; 6.76	11.02	5.1	2.53; 6.94

The Table includes our data and literature-based data: 115 variables, data from De Marinis (1995); 213 variables, data from Schmidt (1992); 321 variables, farm American mink, data from Jakubowski et al. (2008); 416 variables, feral American mink, data from Wiig (1982); 515 variables, data from Smetanová (2011); 630 variables, data from Yurgenson (1933).

Morphological differentiation between European polecat and steppe polecat

The skulls of European and steppe polecats look very similar. Most of the cranial measurements overlap and do not significantly differ especially in the consideration of SSD (Table 10). The greatest length between the oral border of auditory bulla and the aboral border of the occipital condyles (BcL) is the only skull measurement that allows one to distinguish clearly the polecat species regardless of the sex. Other three characters (Pm4L, AbL, PoW) also allow one to separate both species, however, without a hiatus. The discriminant functions (D) have been calculated for random 100 individuals of both species selected from our sample: the M. putorius function is D=13.17Abl-1.15BcL-132.63; the M. eversmanii function is D=61.29BcL-37.29AbL-357.02. These functions allow to correctly identifying the 135 remaining individuals from the studied samples.

Table 10. Skull measurements of the studied samples of the European and steppe polecats.

Variables	M. putorius				M. eversmanii				Mann-Whitney U-test
									p-level
	M	SD	min	max	M	SD	min	max
CbL	62.8	4.46	52.4	70.0	63.1	3.19	54.4	68.2	0.67
NcL	36.0	2.33	30.1	40.1	35.6	1.48	32.8	39.3	0.07
VcL	32.6	3.34	23.8	39.4	33.5	2.72	27.1	38.2	0.05
PL	29.8	2.42	24.7	33.5	30.5	1.84	25.4	33.3	0.08
MxtL	18.7	1.25	15.2	20.9	19.9	0.94	17.4	21.3	< 0.001
Pm4L	7.0	0.47	5.7	7.9	7.8	0.38	6.7	8.6	< 0.001
BcL	16.2	1.09	13.3	18.5	21.8	1.12	19.2	24.2	< 0.001
AbL	21.4	1.45	17.4	24.1	16.9	0.92	14.5	18.7	< 0.001
ZyW	36.9	3.19	30.0	43.8	38.7	2.62	32.4	45.0	< 0.001
MW	33.9	2.92	27.5	38.7	35.3	2.31	29.6	38.6	< 0.001
PoW	15.5	1.00	13.1	17.8	13.4	0.75	11.6	15.3	< 0.001
IW	16.3	1.45	13.2	19.2	16.7	1.28	13.8	18.9	0.12
RW	15.1	1.55	11.7	18.0	16.0	1.16	13.2	17.7	< 0.001
GpW	22.4	1.63	18.4	25.2	22.9	1.29	19.3	25.2	0.01
AbW	10.4	0.88	8.1	12.8	10.5	0.69	8.9	11.8	0.19
M1W	5.7	0.46	4.6	6.6	5.5	0.33	4.6	6.2	< 0.001
CH	23.3	1.60	19.3	26.8	24.5	1.38	21.2	26.4	< 0.001
ML	38.5	3.33	31.1	44.1	39.9	2.38	33.5	43.3	< 0.001
AL	38.0	3.22	30.7	43.1	38.8	2.22	32.9	42.0	0.13
MatL	23.0	1.63	19.3	25.4	23.9	1.28	20.6	25.8	< 0.001
m1L	7.9	0.58	6.4	9.1	8.2	0.44	7.1	9.2	< 0.001
MaH	18.8	2.10	14.3	22.3	19.5	1.54	15.8	22.1	0.02
MpW	7.0	0.63	5.4	8.4	7.0	0.37	6.2	7.8	0.08

Mean (M), standard deviation (SD), and min–max values of skull measurements (in millimeters) of the studied specimens.

DISCUSSION

An analysis of the multivariate morphospace patterns in Mustelidae by Werdelin and Wesley- Hunt (2014) revealed some subfamily phylogenetic patterns. These authors considered the phylogeny to be a dominant pattern in the carnivoran morphospace mapping. According to this conception, two closely related polecat species should have similar patterns of the morpho- space occupation. Nevertheless, the polecats have a significantly different structure of the morphospaces and morphological niche breadth. It seems that the difference between two polecat species found in the present study could be accounted for the ecological pattern rather than for the phylogenetic one. On the other hand, sympatric and phylogenetically-distant species, such as the least weasel and the ermine can share very similar morphological niches (Abramov and Puzachenko 2012). Resource partitioning and the lessening of their ecological niches’ overlap in two sympatric carnivores could apparently explain the observed disparity of their morphospaces. A study of species co-existence and morphological divergence in the guild of Siberian mustelids revealed that species occupy the morphological space quite evenly, suggesting apparently that resource partitioning is involved (Abramov and Puzachenko 2012).

An analysis of the morphospace occupation in two guilds of the sympatric mustelines - “western” (M. putorius, M. erminea, M. lutreola) and “eastern” (M. eversmanii, M. sibirica, M. erminea) has revealed that the species tend to occupy distinct niches. A morphological divergence can bear a competitive gradient where species can turn aside direct competition (Bowers and Brown 1982).

The two studied polecat species show a clear separation in the morphological space. Characters of both the skull ‘size’ and of the skull ‘shape’ constitute important components of the morphological differentiation between M. putorius and M. eversmanii. The morphological diversity of the European polecat is higher than that of the steppe polecat. A possible explanation for this phenomenon is likely to lie in the difference of the prey range in two polecat species. A diet of the European polecat includes a wider range of prey than that of the steppe polecats (Heptner et al. 1967). In the case of sympatric distribution, the diets of polecat species were similar, but the steppe polecat had the narrower trophic niche breadth, which is evidence of its specialization in hunting and habitat use (Lanszki and Heltai 2007). Kurten (1968) assumed that some cranial characteristics of M. eversmanii that distinguished it from M. putorius probably should have evolved as an adaptation to the lifestyle of the steppe polecat in the habitats that differ significantly from those of the European polecat. It is likely that some of the observed morphological differences between species are determined by a degree of their predatory specialization (e.g., the size of premolar Pm4 and the zygomatic width) and partly by adaptations to different environmental conditions (e.g., such as the size of auditory bullae).

The static allometric trends of cranial characters in two polecat species are in accordance with the ontogenetic skull shape change in small mustelids (Buchalczyk and Ruprecht 1977; Schmidt 1992; Suzuki et al. 2012). Similar allometric patterns found in the polecats may reflect a similarity in ontogenetic changes of the skull; yet the difference of allometric patterns between the males and the females is higher than that between two species.

Both polecat species show a strong SSD. It is more pronounced in the European polecat than in the steppe polecat. Sexual size dimorphism is a typical phenomenon in the mustelids. The main hypotheses attempting to explain the pronounced SSD in Mustelidae include resource partition, sexual selection and bioenergetics (see Holmes and Powell 1994; King and Powell 2007). The observed differences in SSD level can hardly be explained by a more generalist behavior (i.e., the reduction of intra-specific competition) of M. eversmanii. Most of the available data suggest a specialist foraging behavior and habitat selection of this species contrary to M. putorius (Stroganov 1962; Heptner et al. 1967; Lanszki and Heltai 2007). According to the aforementioned hypotheses, the differences in SSD could be explained by sexual selection or by discrepancies in the polygynous mating systems of two species, but we have no data on that. A direct consequence of the higher SSD level in M. putorius population seems to be a broader morphological niche.

A high variation of the average SSD in small mustelids (Table 9) could depend on different set of characters, a geographic variation of SSD or species-specific patterns (see also Abramov and Puzachenko 2009). The observed difference in the SSD level in the polecats may partly be a characteristic of the studied populations rather than a species-specific pattern. A geographic variation of SSD in the polecats will be considered by us in more detail later.

The sexual dimorphism is a result of differences in the scale and allometry of cranial characters in males and females. Therefore, it should reflect the features of male-female allometric ontogenetic patterns. An intraspecific variation of ASSD in the polecats could be an indirect evidence for sensitivity of the mechanisms regulating the skull growth to environmental conditions.

CONCLUSIONS

An analysis of morphological differentiation of the skull in two polecat species has demonstrated their clear separation in the morphological space, with M. putorius being much more diverse than M. eversmanii. The morphological diversification of M. putorius could be facilitated by its adaptations to forest habitats of the temperate zone with a wide range of potential prey. Contrarily, M. eversmanii should have evolved under severe conditions of arid Eurasian habitats, being forced to specialize to certain prey.

Supplementary materials

Table S1.

Spearman Rank Order Correlation coefficients for cranial variables and morphospace axes (E1-E4, K1-K4) in M. putorius (males and females separately)

Table S2.

Spearman Rank Order Correlation coefficients for cranial variables and morphospace axes (E1-E4, K1-K4) in M. eversmanii (males and females separately)