Predicting Need for Advanced Illness or Palliative Care In A Primary Care Population Using Electronic Health Record Data

Abstract

Timely outreach to individuals in an advanced stage of illness offers opportunities to exercise decision control over health care. Predictive models built using Electronic health record (EHR) data are being explored as a way to anticipate such need with enough lead time for patient engagement. Prior studies have focused on hospitalized patients, who typically have more data available for predicting care needs. It is unclear if prediction driven outreach is feasible in the primary care setting.

In this study, we apply predictive modeling to the primary care population of a large, regional health system and systematically examine the impact of technical choices, such as requiring a minimum number of health care encounters (data density requirements) and aggregating diagnosis codes using Clinical Classifications Software (CCS) groupings to reduce dimensionality, on model performance in terms of discrimination and positive predictive value. We assembled a cohort of 349,667 primary care patients between 65 and 90 years of age who sought care from Sutter Health between July 1, 2011 and June 30, 2014, of whom 2.1% died during the study period. EHR data comprising demographics, encounters, orders, and diagnoses for each patient from a 12 month observation window prior to the point when a prediction is made were extracted. L1 regularized logistic regression and gradient boosted tree models were fit to training data and tuned by cross validation. Model performance in predicting one year mortality was assessed using held-out test patients.

Our experiments systematically varied three factors: model type, diagnosis coding, and data density requirements. We found substantial, consistent benefit from using gradient boosting vs logistic regression (mean AUROC over all other technical choices of 84.8% vs 80.7% respectively). There was no benefit from aggregation of ICD codes into CCS code groups (mean AUROC over all other technical choices of 82.9% vs 82.6% respectively). Likewise increasing data density requirements did not affect discrimination (mean AUROC over other technical choices ranged from 82.5% to 83%). We also examine model performance as a function of lead time, which is the interval between death and when a prediction was made. In subgroup analysis by lead time, mean AUROC over all other choices ranged from 87.9% for patients who died within 0 to 3 months to 83.6% for those who died 9 to 12 months after prediction time.

Graphical abstract

Introduction

Evidence indicates that when individuals are in an advanced stage of illness and also have control of care decisions, they often choose home-based, comfort-oriented care [1–4]. Such control is only possible, however, when care preferences are known and documented. This often occurs late in the illness course or not at all, often due to the difficulty of engaging in discussions about end-of-life care wishes [5–8]. Timely outreach by care providers experienced with these kinds of discussions could make it possible for better care alignment with personal preferences, potentially avoiding the loss of control that can occur when urgent clinical interventions are required (see Bernacki et al [9] for a discussion of issues surrounding the timing of goals of care conversations). The growth in availability and use of both hospice and inpatient palliative care programs is consistent with patient preferences; between 2000 and 2013, the percentage of hospitals offering palliative care increased from 25% to 72%, and the use of hospice services among Medicare beneficiaries increased from 22% in 2000 to 42.2% in 2009 [10]. However, outreach offering such support services is largely confined to inpatient care, usually following a serious acute event. As a consequence, care at the end of life continues to be aggressive because the option to choose is unnecessarily delayed or simply not offered. Typically, three to four months are required after an initial contact for individuals to decide on options they want to exercise [11]. Therefore, effective outreach should occur roughly six months or more before end of life care decisions have to be made.

Electronic health records (EHRs), now widely adopted in U.S. healthcare, have opened a unique era in medicine where population-level data on patients can be used in real time to predict and potentially improve outcomes for a given patient [12–14]. Studies conducted in the inpatient setting have been able to effectively predict the need for end-of-life care [15]. Prediction within the non-hospitalized population could allow for patient outreach and support earlier in the advanced illness course, ideally in advance of critical events that result in hospitalization. Data collected in the non-inpatient setting, however, can be very sparse. This could cause the performance of any predictive model to suffer within patient populations with lower frequencies of health care utilization.

The purpose of this study is to examine the effectiveness of end-of-life care prediction in the primary care context, and to determine the extent to which technical choices made during model development impact model performance. Specifically, we examine the impact of data density requirements (requiring patients to have a minimum number of health care encounters before making a prediction) and dimensionality reduction by grouping of ICD diagnosis codes into Clinical Classifications Software code groups on model performance. We also conduct sub-group analysis to examine model performance as a function of lead time, which is the interval between the prediction and time of death and quantifies the extent of “early warning” offered by the model.

Related Work

Mortality and morbidity models have a long history in medical informatics; the venerable Charlson Index [16], for instance, is still widely used to quantify disease and morbidity burden in health services research. However, it is not clear that such simple indexes are suitable for use in population-wide surveillance and needs-assessment monitoring. They often have poor discriminative ability [17] and rely on the accurate scoring of presence or absence of various disorders; computationally phenotyping these disorders in EHR or claims data for these purposes is often problematic [17–20]. In addition, efforts to update the parameters of the Charlson index have yielded mixed results, with slightly improved performance in some datasets and unchanged or worse performance in others [21]. Thus, recent work on mortality models takes a statistical learning approach using observed patient characteristics (from patient-reported outcomes [22,23], administrative claims data [24–26], survey data [27,28], or EHRs [15]) without assuming much about the semantics of the presence or absence of the data elements. Unlike the present study, this prior work largely focuses on specific patient populations, such as patients with end-stage renal disease [29], acute ST-elevated myocardial infarction [30], dementia [31], or recent episodes of critical care [32]. Recent studies also primarily center upon hospitalized patients, in-hospital mortality, or very short or long timeframes for mortality [23,33–45]. These studies do not systematically examine the tradeoffs between model performance and applicability resulting from technical choices, such as data density requirements. Our experiments were thus conceived specifically to address the feasibility and elucidate the tradeoffs in monitoring a primary care population for advanced illness or end-of-life care using statistical learning methods.

Methods

Problem Formulation

We developed predictive models with the intention of identifying patients sufficiently far in advance of death that patients could decide what type of care they would prefer by e.g., facilitating goals of care conversations between patients and providers and completing advanced directives. We approached this as a supervised learning problem using EHR data. Our dataset spans three years from July 1, 2011 and July 1, 2014, and for each patient we pick a random date between July 1, 2012 and July 1, 2013 as their prediction time. We examine model performance for subgroups of patients who died 0 to 3, 3 to 6, 6 to 9, and 9 to 12 months after prediction time. Identifying patients with end-of-life care needs farther ahead of time (within limits) presumably benefit patients and families by providing more time in which to explore care options. In this analysis, we labeled those who died as positive cases, while other patients are labeled as negative cases.

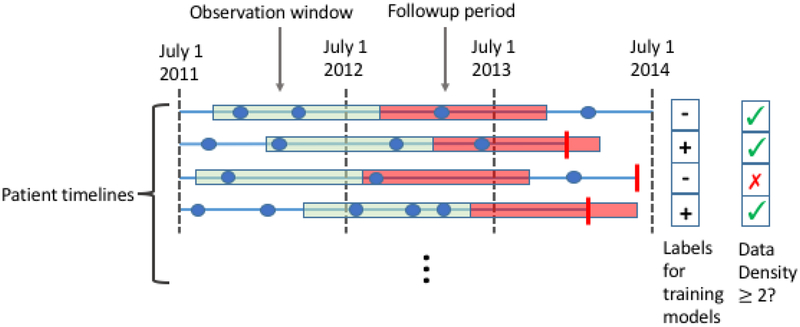
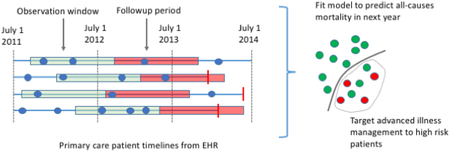
Because this is a retrospective study, we must also decide for each patient when in their timeline we make the prediction; we refer to this time point as the prediction time. For each patient, we pick a random date in the second year of the study period as their prediction time. We do so because in real life we never know exactly when someone is going to die; the final model will be applied to the patient’s record at some time, and some will die in the following 12 months, while others will not. Our models use as input the EHR data from the twelve months prior to each patient’s randomly chosen prediction time; we refer to these prior 12 months as the observation window. Thus, for a given patient, our task is to predict, at the patient’s prediction time, whether the patient will die within the next 12 months given the EHR data available in their observation window (Figure 1). Patients who died prior to their prediction time were removed from analysis.

Figure 1.

We construct a supervised learning problem for the task of predicting all causes mortality within a year. The dataset comprises patient level EHR data from July 1, 2011 through July 1, 2014. We represent each patient’s timeline as a horizontal line, with events shown as blue dots (for clinical encounters) or vertical red bars (for mortality). We construct a supervised learning problem as follows. For each patient we pick a random time in the second year of the study period. We then use the data from the year prior to these times (green segments) to predict the probability of mortality in the follow-up period (red segments). Positive cases are patients whose timelines end during their follow-up period (2nd and 4th rows). Data density requirements may exclude patients from the study. For instance, using a data density requirement of 2 encounters, the patient represented by the 3rd row would be excluded because they have only 1 encounter during in the year preceding their prediction time.

Source Population

The study, completed as a retrospective cohort analysis of Sutter primary care patients, was approved by the Sutter Health Institutional Review Board. Sutter Health (www.sutterhealth.org) is a not-for-profit open health system with a network of more than 5,000 physicians, 24 hospitals, and other healthcare services serving 23 counties in northern California, and uses a single instance of EpicCare across all of its health care delivery facilities. We used patient data from July 1, 2011 through June 30, 2014. Patients were included in the study if they: (1) had a primary care (PC) relationship with Sutter Health, defined as having at least two encounters with a primary care physician (Family Medicine, Internal Medicine or Obstetrics-Gynecology) during the study period; and (2) were 65 to 89 years of age throughout the study period. Death dates were obtained from a combination of EHR, Medicare records, California Department of Public Health records, and the Social Security Death Index. Individuals were randomly partitioned once prior to analysis into training and test sets, with 70% of patients assigned to the training set. In the combined training and test sets, 90.8% of patients who died in the year following after their prediction time had no hospital encounters during their observation windows, and 93.1% of these patients had no inpatient admissions during the same period. Furthermore, only 1.6% of these patients were assigned an ICD-9CM code for palliative care (V66.7) or had an encounter encoded as “Palliative Medicine”. These statistics highlight the need for timely outreach to these patients and also demonstrate why inpatient mortality prediction is insufficient to reach the majority of patient that might benefit.

Data and Features

EHR data from each patient’s observation window was processed into features as follows. The data comprised demographics (age, gender and race) and counts of individual ICD diagnosis codes, procedure CPT codes, medication pharmacy subclasses, encounters, and hospital visits. Features were not created for ICD and CPT codes occurring in fewer than 200 patients, or for pharmacy subclasses occurring in fewer than 10 unique patients. Intuitively, patients with complex medical histories including many distinct diagnoses, procedures and medication orders are more likely to be seriously ill. We therefore characterize the complexity of each patient’s medical history by computing - separately for diagnosis, procedure, and pharmacy subclasses - the maximum and minimum count of distinct codes occurring in any single day of their respective observation periods. Thus, if a patient has three encounters during their observation period, with 3, 8, and 5 diagnosis codes for those encounters, the values of these features would be 8 and 3. The number of distinct medical specialties seen during the observation window was also computed, along with the mean and maximum number of office visits and of distinct medical specialties seen on each day (excluding days with zero counts). Supplementary Materials Table 1 lists the full set of features used.

Experimental Design

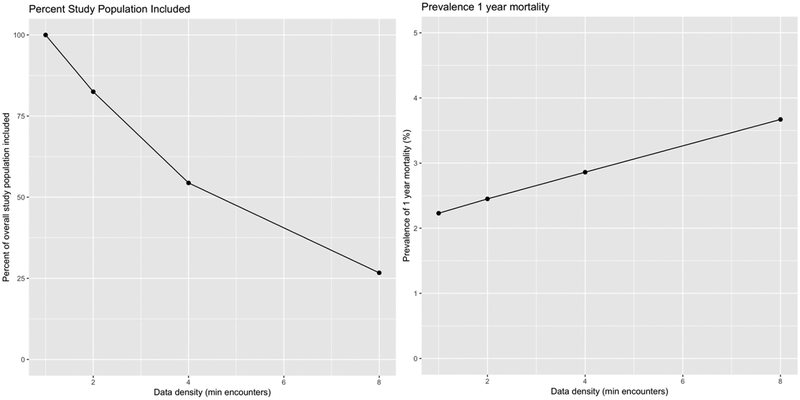
Many choices made during model development interact with each other to influence model performance and utility [46,47]. We thus performed experiments systematically varying important factors. The most important factor is the data density requirement for patient inclusion, where data density is defined as the number of clinical encounters occurring during the patient’s observation window. Clinical encounters are defined as any patient interaction with a provider and may include ambulatory care office visits, virtual visits, ED visits, hospitalizations, and prescription orders. Although patients with higher data density have more information on which to base a prediction, requiring many encounters as an inclusion criterion reduces the eligible population for the study. As we increase the data density requirement from 1 encounter to 8 encounters, the eligible population decreases by 73% and the prevalence of 1 year mortality increases from 2.1% to 3.8% (Figure 2). The choice directly influences the amount of data available for training and, separately, the patient population on which the model may eventually be used [48]. Such patients are also more likely to be seriously ill than the general population [49,50]. We varied the minimum number of encounters required in the observation window between 1, 2, 4, and 8 encounters. Motivated by recent work [51] we also explored the effect of reducing dimensionality of the data by grouping ICD codes into coarser categories as defined by the Healthcare Cost and Utilization project (HCUP) single level Clinical Classifications Software, or CCS, categories (see https://www.hcup-us.ahrq.gov/toolssoftware/ccs/ccs.jsp).

Figure 2.

Impact of data density on eligible population and prevalence. As data density requirements increase, the fraction of the population included (and for whom the model would be applicable later) falls. Because patients with higher data density tend to be sicker, as data density increases, the prevalence of the outcome (death) increases.

For each combination of the above choices, we fit two types of models – L1 regularized logistic regression [52] and gradient boosted trees [53] – yielding a total of 16 experimental conditions under which models were built. Regularized logistic regression models are widely used because they are easy to interpret, straightforward to tune, and often yield performance that is close to that of more complex models; gradient boosted trees can automatically model non-linearities and interactions between features. We used the glmnet [54] and gbm [55] R packages, respectively. Note that, in contrast to related work whose aim was to maximize predictive performance using neural nets for hospitalized patients [15], our current study focused instead on exploring the impact of technical decisions in a new setting - monitoring a primary care population for advanced illness or end-of-life care needs. This requires systematic exploration of the space of choices, rendering extensive tuning of neural nets problematic. In addition, we note that simple models with reasonable features have proven to be quite competitive with neural nets [43].

Model fitting

We subsampled the training datasets for each experimental condition such that the prevalence of the positive class was 10% in order to avoid convergence problems when fitting linear models (without subsampling, many experimental conditions yielded linear models that contained only an intercept term due to the very low prevalence of positive cases). Subsampling for each experimental condition was performed by retaining all positive cases and subsampling the negative cases to a 9:1 ratio to the positive cases. Note that the test data retained the natural prevalence of positive cases. Hyper-parameters for each model were tuned as follows. For logistic regression, the regularization hyper-parameter was tuned by 10-fold cross validation on the training data using the 1-s.e.m. rule [56]. For gradient boosting, we fixed the maximum depth of the base models at 6 and learning rate to 0.005, and tuned the number of trees by performance on 30% of the training data reserved for this purpose. The final models were then fit on all of the training data with the optimal number of trees.

Evaluation

Models were evaluated on the held-out test set using the area under the receiver operating characteristic curve (AUROC) and area under the precision-recall curve (AUPRC). Each model was evaluated for performance on four subpopulations of the validation set patients, defined by the lead time provided on each subpopulation. The subpopulations were those who died within 3 months, between 3 and 6 months, between 6 to 9 months, and between 9 and 12 months after prediction time. Note that we do not subsample the test set to increase the prevalence of positive cases, i.e., the test set has the prevalence of death at 2.1% to represent realistic usage scenarios in the primary care setting.

Results

Our results are summarized in Figures 3 (AUROC) and 4 (AUPRC). AUROC measures the ability to discriminate between positive (i.e., patients who died within one year of prediction time) and negative (all others) cases, and does not account for the change in the prevalence of the positive class induced by data density requirements. AUPRC measures the average Precision or Positive Predictive Value (PPV) across all possible decision thresholds, and takes positive class prevalence into account. These performance measures are complementary to each other, and together provide a more complete picture of model performance than either alone, particularly when there is significant class imbalance [57]. In addition, in order to make the tradeoffs under the different experimental conditions more concrete, we also report the positive predictive value (PPV), negative predictive value (NPV), specificity, recall (sensitivity), and F1 at a posterior probability threshold of 0.5. In the following sections, we first discuss the characteristics of the study and analytic populations and then present our results, focusing on one technical choice at a time.

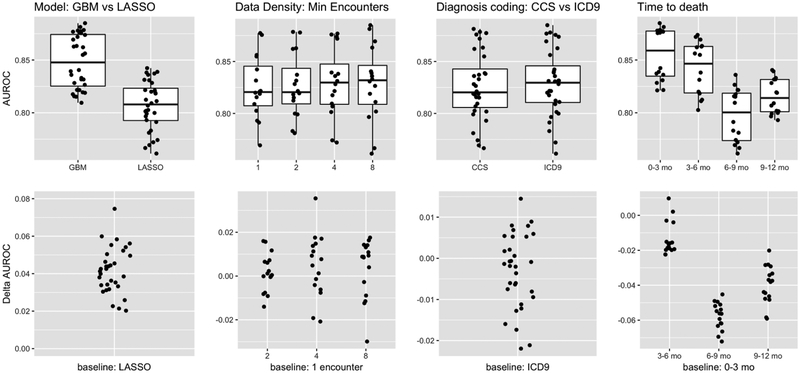
Figure 3.

Performance measured by AUROC, which emphasizes ability to discriminate between positive (patients who died within one year) and negative cases (all others). Our experiments manipulated three factors -- model type (GBM = gradient boosted model; LASSO = L1 regularized logistic regression), data density (minimum number of encounters during the observation period), and coding of the diagnoses (CCS vs ICD codes). The first three columns compare performance as one factor at a time is varied, with the performance across all other settings of the other factors shown. The fourth column shows the subgroup analysis evaluating model performance in various intervals. The top row plots shows the absolute AUROCs, whereas the plots below show the change in AUROC relative to the indicated baseline on the x-axis. These results show that: a) There is substantial, consistent benefit to modeling interactions and non-linearities, b) There is no consistent benefit in discrimination ability by imposing data density requirements, c) There is no benefit to aggregating diagnosis codes from ICD to CCS, and d) As expected it is more difficult to discern positive cases who die further in the future.

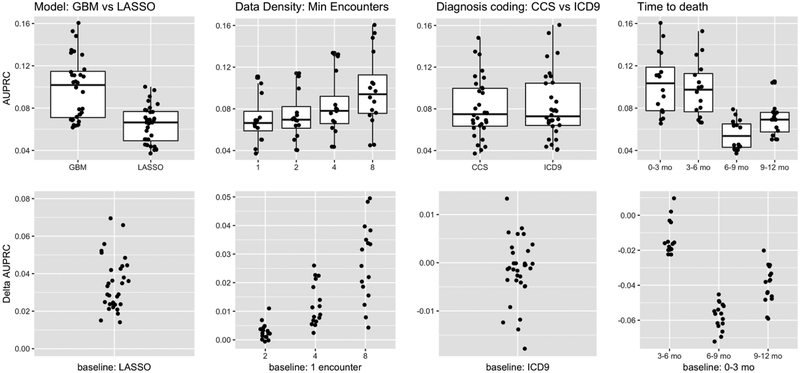
Figure 4.

Performance measured by AUPRC, which takes into account the prevalence of the positive class (i.e., patients who died within one year of the prediction time). We show how performance compares as we vary one experimental factor at a time, across all other settings of the other factors (first three columns). We also show how performance varies with respect to how far in the future the positive cases die. The top row shows absolute AUPRC while the bottom row shows the change in AUPRC relative to the indicated baseline. These results indicate that: a) Again there is consistent benefit to modeling non-linearities and interactions, b) Although models do not discriminate between positive and negative cases more accurately as we increase data density requirements, the AUPRC still increases due to increasing prevalence of the positive class, c) There is again no benefit to coding diagnoses as CCS vs ICD-9 codes, and d) As expected it is easier to discern positive cases when death occurs farther in the future.

Study and Analytic Populations

A total of 349,667 patients met inclusion criteria for the study; 2.1% died during the one year follow-up period after their prediction times. Figure 2 summarizes the impact of different data density requirements on the size of the applicable population as a fraction of the overall study population, and on prevalence of the outcome. As expected, more stringent data density requirements reduce the size of the population to which the model can be applied, with a reduction of 73% as we increase the requirement from 1 encounter to 8 encounters. In addition, because patients who are seriously ill tend to have more encounters with the healthcare system than healthy patients, prevalence also increases with data density requirements, from 2.1% to 3.7%. We emphasize that only a small fraction of the overall study population have any hospital encounters (3.2%), and an even smaller fraction (1.9%) were admitted as inpatients, during their observation period. Among patients who died within a year of their prediction time, only 9.2% had a hospital encounter and 6.9% had an inpatient encounter. These statistics highlight the main difference between the general primary care population and the hospitalized, generally very ill patients that have been the focus of most prior work on mortality and morbidity prediction. Supplementary Materials Table 2 details the characteristics of the eligible population as we vary the data density requirement.

Model Class

We fit gradient boosted trees and L1 regularized logistic regression models for each experimental condition. Under all 16 experimental conditions, gradient boosted trees were superior to logistic regression, suggesting that modeling interactions and non-linearities is beneficial. As measured by AUROC (Figure 3, first column), boosted trees had an average advantage of 4.1% over logistic regression, with a minimum of 2% and a maximum of 7.5%. Across all experimental conditions, the mean AUROC of boosted trees was 84.8% and the mean AUROC of logistic regression was 80.7%. As measured by AUPRC (Figure 4, first column), which takes prevalence into account, the gap between boosted trees and logistic regression was smaller but still significant and consistent, with boosted trees outperforming logistic regression by 3.4% on average. The smallest gap in performance by AUPRC was less than 1.4%, while the largest gap in performance was 7%, and the mean AUPRC across all experimental conditions was 9.7% for boosted trees versus 6.4% for logistic regression. At a posterior probability threshold of 0.5, the logistic regression models on average had higher specificity and lower recall than gradient boosted trees (PPV: 40.1% vs 38.5%, NPV: 95.7% vs 94.7%, specificity: 99.6% vs 98.5%, recall: 6.89% vs 23.3% for logistic regression vs gradient boosting respectively, averaged across other experimental conditions). The mean F1 measure, which captures the balance between PPV and recall, at this threshold and averaged across all experimental conditions was 0.117 vs 0.290. On average, gradient boosted trees provide a much better balance of PPV vs recall.

Diagnosis Code Grouping

The features for our models are high-dimensional and sparse. It has been observed previously that grouping ICD diagnosis codes improved the performance of models predicting CHF [51]. However, in our study, code grouping had little impact on model performance. Models using CCS diagnosis code groupings versus individual ICD codes had average AUROCs of 82.6% versus 82.9% (Figure 3, second column), and AUPRCs of 8.1% versus 8.2% (Figure 4, second column), respectively. At a threshold of 0.5, aggregating ICD codes into CCS code groups does not significantly change PPV, NPV, specificity, recall or F1 (39.3% vs 39.4%, 95.2% vs 95.2%, 99.1% vs 99.0%, 14.9% vs 15.3%, and 0.204 vs 0.203 respectively). Thus, it appears that for this application there is little benefit to using grouped codes.

Data Density Requirements

Intuitively, one might expect that higher data density in the observation window (i.e., more encounters or more utilization of health care resources) would improve predictive accuracy due to increased information on which to base predictions. Furthermore, because more seriously ill patients are likely to have more encounters than healthy patients, we might expect that higher data density requirements would increase prevalence (Figure 2).

As we varied the minimum number of encounters required for patient inclusion in the study cohort from 1 to 8, we found that there was little variation in mean model performance as measured by AUROC (Figure 3, third column), which varied in a relatively narrow range from 82.%5 to 83.0%. This suggests that it is not significantly easier to discriminate between positive and negative cases when higher data density requirements are enforced.

However, requiring increased data density did have a significant impact on the eligible patient population, with a 73% reduction in the size of that population as the minimum number of encounters increased from 1 to 8. In addition, the prevalence increased from 2.1% for a requirement of 1 encounter to 3.7% for a requirement of 8 encounters (Figure 2). The mean AUPRC varied from 7.1% under the 1 encounter requirement to 9.8% under the 8 encounter requirement (Figure 4, third column). In light of our previous results showing that the ability to discriminate between positive and negative cases does not vary dramatically when increasing data density requirements, this increase is likely due to the increasing prevalence of the positive class. At a threshold of 0.5, we find that specificity is unchanged as we vary data density requirements (99.0% at both 1 and 8 encounters), while PPV, NPV, and recall vary from 36.6% to 43.4%, 95.7% to 94.4%, and 16.0% to 14.8%, respectively as we increase the requirement from 1 encounter to 8. However, the F1 measure remains relatively constant, ranging from 0.209 to 0.201, indicating that the increase in PPV driven by increasing prevalence of the positive class is cancelled out by a drop in recall.

Sub-group Analysis

We performed a subgroup analysis to evaluate model performance in various intervals (0–3 months, 3–6 months, 6–9 months, and 9–12 months) after a certain prediction time. We would expect it to be more difficult to discriminate patients who die farther from their prediction times. Lead time, or how far in advance we can predict an outcome, is a critical aspect of model performance. Longer lead times generally make the prediction task more difficult, but also offer more room for effective interventions. For patients who died within 3 months of their prediction times, the mean AUROC for gradient boosted trees using ICD codes was 87.9%, falling slightly to 83.6% for patients who died between 9 and 12 months after their prediction times (Figure 3, fourth column). The AUPRC varied more dramatically, falling from a high of 13% for the 0–3 month group to 8.3% for the 9–12 month group even though the prevalences were roughly equal (Figure 4, fourth column).

Important Features

Regularized logistic regression and gradient boosted trees automatically select relevant features. Examining the features selected by each model class can provide insight into both their utility and the observed difference in their performance. To these ends, we summarized feature importance for both model classes by averaging across data density requirements and using ICD coding of diagnoses. For logistic regression, we used the absolute value of the model coefficients for each feature. For gradient boosted trees, we used the relative influence of each feature. We provide feature importance data in Supplementary Materials 3–5. There are two main findings from this analysis.

First, each model class utilizes feature that indicate that the patient in question has already been identified as in need of end-of-life care, e.g., encounters coded as SPECIALTY.Palliative Medicine and ICD-9 code V49.86 (Do not resuscitate status). Gradient boosted tree models also utilize ICD-9 code V66.7 (Encounter for palliative care). However, only 2.6% of patients who died within a year of their prediction time had an encounter with Palliative Medicine or were assigned V66.7 or V49.86 codes. Ablation experiments in which we remove these three features results in drops in AUROC of 0.29% and 0.028% and drops in AUPRC of 0.43% and 0.46% for logistic regression and gradient boosted trees respectively. We therefore do not anticipate that this the use of (or censoring of) these features is a critical issue in these models.

Second, there is substantial agreement between the model classes that certain diagnoses, medications, and procedure orders are indicative of high mortality risk, e.g., patients with cancer or taking antipsychotic medications are at high risk. However, there are also substantive differences between the model classes. For instance, the single most important feature for gradient boosted trees is Age, which is only the 30^th most important feature for logistic regression. In addition, the gradient boosted trees use features that summarize patient complexity and health care utilization such as the total number of encounters and the number of different medical specialties seen during the observation period, while logistic regression assigns zero weight to these features. One important difference between gradient boosted trees and logistic regression is that the former can automatically model interactions between features. This suggests that such features are most informative in interaction with other features and help explain why gradient boosted trees outperform logistic regression; in isolation, they are equivocal regarding one year mortality.

Discussion

The purpose of this study was to determine whether the need for advanced illness or end-of-life care can be accurately predicted outside of the hospital setting, in a general primary care population, and to examine the impact of technical choices on predictive performance. In this population, only 9.2% of patients who died during the one year follow up period after their prediction time had a hospital visit during the prior year, and only 6.9% had an inpatient visit. Thus, over 90% of the patients who died did not have an inpatient encounter, highlighting the opportunity for a predictive model for advanced illness or end-of-life care needs to guide outreach to these patients in an outpatient setting. We formulated the prediction problem using the surrogate outcome of all-cause mortality. Models were evaluated using AUROC, which measures the ability to discriminate between positive and negative cases regardless of prevalence, and AUPRC, which is sensitive to prevalence and may thus be more relevant when there is significant class imbalance [57,58]. In addition, we calculated the PPV, NPV, specificity, recall, and F1 measure at a threshold of 0.5. Each model was evaluated on the basis of its ability to identify patients who died in three month intervals after their prediction times. In contrast to related work [15], in this study we employ linear models and gradient boosted trees instead of neural nets, which are more easily tunable with limited computation than neural nets. In our experience, there is usually little performance difference between well-tuned gradient boosted tree models and neural nets for problems using EHR data [43]. We systematically varied model class, diagnosis code groupings, and data density requirements to examine the impact on each of these factors on model performance and utility.

We found that the most important of these factors was model class, followed by data density requirements. Gradient boosted trees consistently outperformed regularized logistic regression by significant margins, suggesting that non-linearities and interactions are important for this application. At a threshold of 0.5, logistic regression has higher PPV and specificity, but significantly lower recall. The F1 measures at this threshold, averaged over the experimental conditions, were 0.117 vs 0.290 for logistic regression and gradient boosting respectively. Increasing the data density requirement significantly restricted the population to which the model could be applied and increased the prevalence of positive cases. We found that the AUROC varied only slightly over the range of data densities examined, while the AUPRC varied more, suggesting that any gains in performance were due primarily to the increased prevalence of positive cases among patients with many encounters. At a threshold of 0.5, increasing the data density requirement led to a small gain in PPV, but this was balanced out by a concomitant decrease in recall, resulting in no significant change in F1 measure. We further observed, consistent with intuition, that it is harder to discriminate patients who died farther in the future. However, reasonable discrimination was possible even 9 months in advance of death. Finally, dimensionality reduction by aggregation of ICD diagnosis codes into CCS categories did not prove to be beneficial in this setting. However, it is important to note that these conclusions may not apply to other problems using EHR data or to other health systems, and different tasks may benefit more or less from the various approaches evaluated in this study. This may be especially relevant in health systems which have more complete data.

These results suggest that predictive models using EHR data can be applied to a broad patient population, and can effectively identify the need for advanced illness or end of life care far enough in advance for effective interventions outside of the inpatient setting where such models are usually employed.

Surveillance is typically considered when an important health need is identified for which there is a solution available. When individuals who are in an advanced stage of illness have control of care decisions, they often choose home-based, comfort-oriented care [1–4]. Despite recent progress translating conceptual definitions of serious illness into effective operational criteria using administrative data [59–60], conducting surveillance of a large population for patients who are approaching end-of-life remains challenging. Hence, accurate predictive models such as those we have developed create opportunities to proactively reach individuals in need.

Our work has important limitations with respect to addressing these needs. There are a host of cultural issues with predicting end of life including, but not limited to, ethical challenges as to how such models might be used, communication challenges around how providers, patients, and families are contacted and engaged to discuss options, and management challenges to ensure that patient autonomy is not usurped and that fairness and patient control of care access is maintained [61]. Fortunately it has been shown that mortality predictions are not useful for controlling spending [62] thus reducing the likelihood of one potential nefarious use. Data quality remains challenging - Sutter Health is an open health care system, meaning that patients may utilize non-Sutter facilities and health care services, resulting in an incomplete picture of healthcare utilization and gaps in ascertainment of the death outcome for model training. Even after pooling information from multiple sources, there may still be under-ascertainment of the outcome in the training data. With more complete outcome ascertainment and healthcare utilization data, model performance would likely increase. Furthermore, there are challenges in operationalizing such a predictive model, especially given that a physician must ultimately decide whether and what actions are warranted, recognizing that models are imperfect and mitigating potential harms that could arise from their blind use [63]. Decisions must therefore be balanced with caution in managing false positives, the benefits of patient control in care decision-making, and the risks from future care that offers little benefit.

Conclusion

Constructing and validating a predictive model for end-of-life care needs is the first step in identifying which patients should be a priority for timely advanced illness or end-of-life care outreach. We have shown that EHR-based predictive models can function well within a primary care population, and can accurately predict the need for end-of-life care 9 months or more prior to death. We systematically varied model class, diagnosis code groupings, and data density requirements to examine the impact on each of these factors on model performance and utility. Our results suggest that predictive models using EHR data can be applied to a primary care population, and can effectively identify the need for advanced illness or end of life care far enough in advance for effective interventions outside of the inpatient setting, where such models are usually employed. This work also finds significant benefit to modelling non-linearities and interactions, which is easily achieved using off-the-shelf models such as gradient-boosted trees. Data density requirements induce a tradeoff between wide applicability and accuracy of the model. Finally, we found no benefit to reducing dimensionality of the problem by aggregating diagnosis codes into CCS groups.

Highlights.

• Outreach to patients with an advanced illness is an important unmet medical need.

• Predictive models identify eligible patients with sufficient lead time and accuracy.

• Non-linearities and interactions are important for model performance.

• Data density requirements affect model performance and applicability.

• Grouping of diagnosis codes to CCS code categories did not affect performance.