Analysis of facial skeletal asymmetry during fetal development using μCT imaging

Abstract

Objectives:

Asymmetry has been noted in the human craniofacial region in several pathological conditional and growth abnormalities, often with a directional predilection. Physiological asymmetry has also been reported in normal adults and adolescents, with certain regions of the cranioskeleton, such as the mandible, displaying prevalent asymmetry. However, the timing at which such asymmetries arise has not been evaluated. The objectives of this study were to assess the degree of asymmetry in facial bones during the fetal stages of human development.

Material & Methods:

Twenty-one preserved conceptuses from the Congenital Anomaly Research Center at Kyoto University, between ages 15–20 weeks of gestation, were studied using high resolution μCT imaging. Asymmetry analysis was performed on digitally segmented facial bone pairs, using geometric morphometric (GM) approaches as well as adapted deformation-based asymmetry (DBA) methods.

Results:

GM analysis revealed that the developing facial bones display statistically significant fluctuating and directional asymmetry. DBA methods suggest that the magnitude of asymmetry in facial bones is low and does not appear to be correlated to the estimate of overall size of conceptus. Additionally, the patterns of asymmetry are highly variable between individual specimen.

Conclusions:

The developing fetal facial skeleton displays variable patterns of low magnitude asymmetry. GM and DBA methods offer unique advantages to assess facial asymmetry quantitatively and qualitatively.

Introduction

A key feature of vertebrate/human morphogenesis is bilateral symmetry. Yet small amounts of asymmetry in morphological and functional traits are considered the norm. Studying craniofacial asymmetry is pertinent for many different scientific fields including developmental biology, comparative biology, evolutionary biology as well as clinical fields such as maxillofacial surgery and orthodontics.

Directional asymmetry (DA) is a consistent difference in a trait(s) or a metric(s), between the right and left sides of an organism (e.g. left temporal areas of the human brain are larger than right). In contrast, random deviations (right or left) from normal symmetry is termed as fluctuating asymmetry (FA). Strong DA in certain pathological conditions affecting the craniofacial region have been identified, such as greater incidence of right-sided coronal synostosis and left-sided cleft lips [1]. Altered patterns of DA have also been found in conditions where facial changes accompany abnormal brain development, such as autism spectrum disorder and schizophrenia [2, 3]. Existence of physiologic DA in craniofacial structures has been debated [4, 5]. Utilization of 3D data have uncovered that seemingly symmetrical dental and facial traits exhibit subtle, yet significant levels of DA [6, 7]. Findings suggest that the left side is slightly, but systematically larger than the right when analyzing the normal human dental arch [8], as well as the certain metrics of the human face [9, 10]. Existence of FA in mandibular retrusion has also been suggested [11].

The timing at which asymmetries develop in facial structures is unknown, since most studies evaluate postnatal stages and reflect cumulative effects of developmental processes through ontogeny, including postnatal bone remodelling. The few studies that evaluated prenatal stages have historically relied on the use of photos, 2-dimensional (2D) x-rays, ultrasound images, or measurements made from dissected and disarticulated post-mortem skeletons. 3D images (μCT, CBCT, MRI, 3D-photogrammetry) overcomes many of limitations inherent to 2D data. Conventional asymmetry analyses compare bilateral distance and/or angles between landmarks annotated on 3D images [12–14]. Geometric Morphometrics (GM) offers certain advantages over traditional morphometric methods. GM analyses maintain the geometry of configurations by combining multiple landmarks into one analysis and permits a comprehensive evaluation of craniofacial shape and morphology [15]. GM has been applied to quantitatively assess asymmetry [16, 17]. However, results obtained from GM analyses can be challenging to interpret and visualize. Additionally, GM uses sparse landmarks (or semi-landmarks) to assess shape and asymmetry in complex structures. In this regard, newer Deformation Based Asymmetry (DBA) methods show particular promise, due to their independence from the plane of symmetry and ability to provide dense shape information across the entire surface of the image. Hence, DBA methods permit interpretation of local and global asymmetry distribution [18–21].

Given the prevalence of facial asymmetries in the population and lack of information about when they arise, we sought to assess the degree of asymmetry in developing facial bones at fetal stages. Our study focused on second trimester fetuses when craniofacial form is being established. We use high-resolution 3D computed microtomography (μCT) coupled with GM and DBA analyses to quantify asymmetry in facial bones.

Materials and Methods

Specimens

The Congenital Anomaly Research Center at Kyoto University, Japan has maintained a large collection of human conceptuses since 1961, collected under the Maternity Protection Law of Japan [22, 23]. Specimens have been fixed in formalin upon collection, preserving soft and hard tissues. Conceptuses without any distinct congenital anomalies and artificial deformities of the face were selected for the present study (n=21, crown rump length 98–198 mm, ~15 – 20 weeks of gestation). Their use was approved by the Ethics Committee at Kyoto University Graduate School and Faculty of Medicine, Kyoto, Japan (R0316, R0347, and R0989).

Imaging and segmentation

μCT imaging was performed at 120 kVp, 180–200 μA at a range of 35 – 66 micrometers using TOSCANER-30000 μFD-ZⅡ(Toshiba, Tokyo Japan). Scans were reconstructed into 3D volumes and digitally segmented using the Amira®6.0 software to isolate select paired craniofacial bones (frontal, maxillary, palatal, zygomatic, petrous temporal and mandibular). Threshold based semi-automated segmentation was accomplished by selecting voxels with an intensity exceeding a specified minimum masking value, kept constant between the left and right antimeres for each specimen. Subsequently, surface meshes were generated and utilized for landmark annotation.

Landmark annotation and error measurements

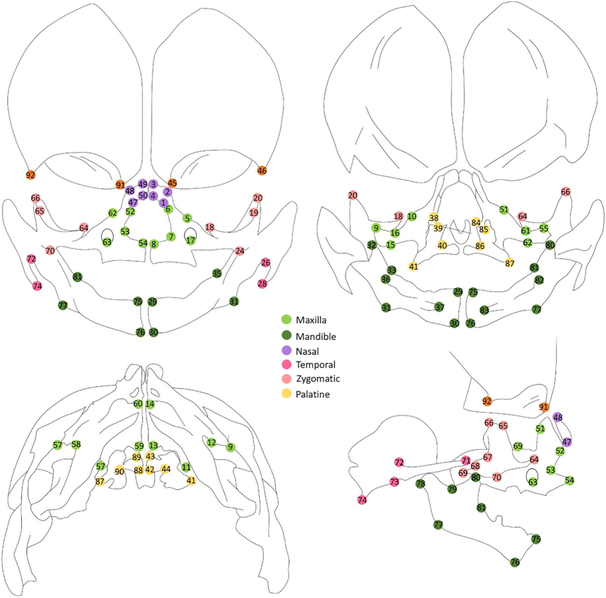
Manual landmarks (Table 1, Fig 1) were annotated on the 3D surface files of each specimen using Checkpoint™ (Stratovan Corporation, Davis, CA, USA) using a combination of the multiplanar (boundary) and 3D rendering views. Repeat landmarks were placed on all the specimen by the same investigator (SRB) 1 week apart. Intra-investigator error was calculating by measuring the Euclidean distance between the Cartesian coordinates from the original and repeated landmarking attempts for all specimen.

Table 1.

Landmark description and errors

Landmark #	Description	Error (mm)
		Mean	Std dev
1 /47	the most anterior-lateral point of the nasal bone	0.079	0.045
2 /48	the most anterior-medial corner point of the nasal bone	0.124	0.086
3 /49	the most posterior-medial corner point of the nasal bone	0.129	0.087
4 /50	the most posterior-lateral corner point of the nasal bone	0.093	0.059
5 /51	the lacrimal groove	0.368	0.276
6 /52	the most anterior-superior point ofthefrontal process of the maxilla	0.114	0.096
7 /53	the greatest concavity of the nasal aperture of the maxilla	0.173	0.130
8 /54	the tip oftheanterior nasal spine	0.084	0.062
9 /55	the most posterior-superior point ofthezygomatic process of the maxilla	0.141	0.216
10 /56	the notch on the orbital surface of the maxilla superior to the infraorbital formen	0.327	0.284
11 /57	the posterior-superior corner of the palatal process of the maxilla	0.186	0.266
12 /58	the medial groove on the inferior surface ofthezygomatic process of the maxilla	0.232	0.231
13 /59	the most posterior-medial-inferior point on the palatal process of the maxilla	0.122	0.103
14 /60	the most anterior-medial-inferior corner of the palatal process of the maxilla	0.132	0.100
15 /61	the greatest convexity on the inferior surface ofthezygomatic process	0.157	0.110
16 /62	the greatest concavity of the superior surface of the zygomatic process (opposing 17/74)	0.264	0.138
17 /63	The most inferior point of the infraorbital foramen	0.151	0.084
18 /64	the most anterior point on the orbital surface of the maxillary process ofthezygomatic bone	0.075	0.040
19 /65	the most anterior-superior point ofthefrontal process of the zygomatic bone	0.159	0.149
20 /66	the most superior point of the marginal process of the zygomatic bone	0.122	0.139
21 /67	the greatest concavity on the posterior aspect of the zygomatic bone	0.158	0.119
22 /68	the most superior-posterior point of the temporal process ofthezygomatic bone	0.099	0.130
23 /69	the most inferior-posterior peakofthetemporal process ofthezygomatic bone	0.097	0.069
24 /70	the most anterior-inferior point of the maxillary process ofthezygomatic bone	0.125	0.082
25 /71	the most anterior point ofthezygomatic process of the temporal bone	0.095	0.060
26 /72	thegreatest concavity ofthejunction ofthezygomatic process and squamoustemporal bone	0.204	0.153
27 /73	the greatest concavity ofthejunction ofthezygomatic process and squamoustemporal bone	0.311	0.227
28 /74	the most posterior-inferior point on the ossifying temporal bone	0.090	0.082
29 /75	the most superior-medial point ofthesymphysis of the mandible	0.104	0.099
30 /76	the most inferior-medial point of the symphysis of the mandible	0.213	0.178
31 /77	the greatest convexity on the inferior surface of the angle of the mandible	0.391	0.209
32 /78	the most superior-posterior point of the ossifying condyle	0.252	0.230
33 /79	the deepest point on thesigmoid notch of mandibular ramus	0.223	0.203
34 /80	the most superior point of the coronoid process	0.123	0.077
35 /81	the anteriorjunction oftheramusand body ofthemandible	0.402	0.235
36 /82	the most posterior point of the lingual tuberosity process ofthemandible	0.139	0.081
37 /83	the tip oftheantero-medial projection ofthelingual plateofthemandible	0.392	0.240
38 /84	the most anterior-superior point on the vertical plate of the palatal bone	0.244	0.217
39 /85	the notch on the superior crest of the vertical palte of the palatal bone	0.282	0.241
40 /86	the inferior point on thespheno-palatine notch	0.252	0.167
41 /87	the most postero-lateral point on the pyramidal process of the palatal bone	0.259	0.164
42 /88	the most posterior-medial point of the horizontal plate of the palatal bone	0.102	0.059
43 /89	the most anterior-medial point of the horizontal plate of the palatal bone	0.188	0.224
44 /90	the most posterior-lateral point ofthejunction of the horizontal and vertical plate of the palatal bone	0.242	0.134
45 /91	the most inferior point of the maxillary process ofthefrontal bone	0.203	0.234
46 /92	the most posterior-inferior-lateral point on the orbital ridge ofthefrontal bone	0.283	0.337

Fig. 1. Landmarks.

Schema of landmarks used in study (top left = anterior view, top right = intra cranial, bottom left = inferior view, bottom right = right lateral view)

Landmark based geometric morphometric (GM) analysis of asymmetry

Analysis of DA and FA was performed by combining GM methods which identify patterns of covariation among landmarks, with a two-way MANOVA (referred to as Procrustes ANOVA), as described by Klingenberg and McIntyre [17]. Briefly, 3D coordinates from each sample were mirrored. Next, the original and mirrored configurations were superimposed using Generalized Procrustes Analysis (GPA). GPA achieves optimal fit by removing scale, rotation and translation during registration and iteratively minimizing the distances between the landmarks in the configurations, resulting in new landmark coordinates (Procrustes coordinates). Deviation of corresponding Procrustes coordinates between the original and mirrored configurations was measured as asymmetry. Shape variation was decomposed into variation across individuals, variation among right and left sides across the sample (DA), variation due to an individual-side interaction (FA), and measurement error (Table 2). Measurement error was quantified by the variation over replicates for each individual and side. The main effect of FA was tested against measurement error and that of individuals, while DA was tested against FA. For testing the statistical significance, permutation tests with 10,000 resampling was performed. DA component was calculated as the deviation between the average shapes of the right and left side. FA components were calculated as deviations of each sample from the mean shape, subtracting the overall DA component. Principal component (PC) analysis was performed on FA components. For visualization of GM results, radial basis function interpolation was used for warping a mean surface mesh, followed by applying an arbitrarily scaled color gradient which describes the distribution of DA and FA [7]. GPA and Procrustes ANOVA were performed using Geomorph package [24], in R 3.4.1 [25]. Visualization was performed using MATLAB 9.0.1 (Mathworks, Natick, MA, USA).

Table 2.

Procrustes ANOVA of craniofacial landmarks

Effect	Df	Sum of squares	Mean Sum of squares	F	p (value)
Individual	20	0.428475684	0.021423784	11.1448323	0.0027
Side	1	0.003780501	0.003780501	1.96664831	0.0109
Ind * Side	20	0.038446131	0.001922307	3.80250181	1.00E-04
Error	42	0.021232567	0.000505537	NA	NA

Deformation Based Asymmetry (DBA) analysis using surface meshes

We have previously developed voxel-based DBA methods to quantifying 3D facial development in animal models [26, 27]. In this study we implemented a surface-based version of our method to assess asymmetry, using the Visualization Toolkit (www.vtk.org).Calculation of dense point correspondences, as described by Hutton et al. [28] was adapted to find direct left/right correspondences, without mapping to a symmetric mean template. This direct comparison provides appropriate information for individual samples, where asymmetry is expected to be within normal ranges and the variation between individuals is relatively high.

Briefly, each specimen mesh was mirrored and rigidly aligned to the original mesh using our annotated landmarks. This is followed by a thin plate spline (TPS) deformation and a closest-point deformation (CPD) to obtain point correspondences at each mesh node. For each point, an asymmetry flow vector was defined by the difference in position between the corresponding points on the mirror and original images, representing the transformation due to asymmetry. We assessed our TPS warping accuracy [18] on a representative image and found it to be 0.029 mm, which is very low and suggests that the CPD step is likely to identify the correct point correspondences. Two properties of local morphology were calculated at each point to capture independent aspects of facial asymmetry- magnitude and angle of deformation. These quantify the positional difference and direction of the transformation between an image and its mirrored copy at each corresponding point, respectively. We also repeated these steps for the two independent landmarking attempts and the vector between the corresponding points at each mesh node was used as the estimated measurement error and subtracted from the asymmetry feature values. This incorporates knowledge about the potential error in measurement, for either an individual or spatial location, hence deemphasizing asymmetry found in regions with high uncertainty. An adjusted magnitude of asymmetry was calculated for each specimen by averaging the asymmetry feature scores at each node.

Results

We measured the intra-investigator error for each landmark and found good repeatability. Table 1 shows mean and standard deviation of errors for individual landmarks. The overall average error for all landmarks was 0.189 mm.

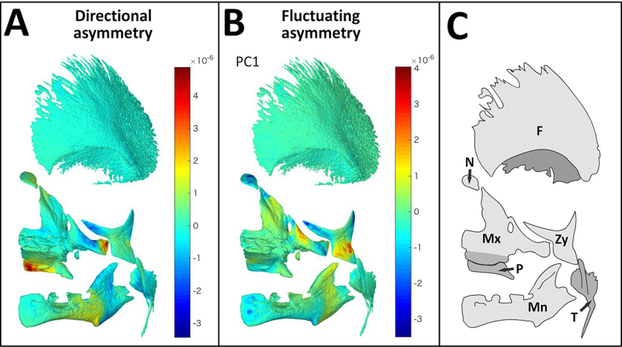
Procrustes ANOVA suggests that fetal facial bones demonstrate significant DA and FA (p=0.0109 and p<0.001 respectively, Table 2), as the mean sum of squares for each are larger than the error represented by the residuals. Although statistically significant, the overall magnitudes of landmark shifts obtained from the GPA superimposition were very low. These shifts were visualized by interpolation to a mean surface mesh and application of a scaled color gradient depicting areas of DA and FA (Fig 2A and B respectively). Our GM analyses indicates very small, but statistically significant DA and FA in facial bones during the fetal period of growth. The postero-medial region of the palatine bone and the zygomatic process of the maxillary bone appear larger on the left when compared to the right side of the face, while the lateral body of the maxilla, maxillary process of the zygomatic bone and the ramal areas of the mandible were larger on the right compared to the left side of the face (Fig 2A, 2C). Lateral areas of the zygomatic bone, infraorbital region of the maxilla, the nasal bone and ramal areas of the mandible demonstrates FA (Fig 2B, 2C).

Fig. 2. GM analysis of asymmetry.

Mean surface mesh of facial bones (tilted frontal view) with color maps indicating areas of asymmetry assessed by GM. (A) Visualization of DA components, positive values (warm colors) represent areas that are larger on the left, while negative values (cold colors) represent areas which are large on the right side of the cranioskeleton. (B) Visualization of FA components (PC1). Values close to zero (green) represents symmetric areas while positive and negative values (warm and cold colors, respectively) represent asymmetric areas, as compared to mean shape along PC1. (C) Schema with key of facial bones: Mx=maxilla, Mn= mandible, P=palatal, Zy=zygoma, T= temporal, N=nasal, F=frontal)

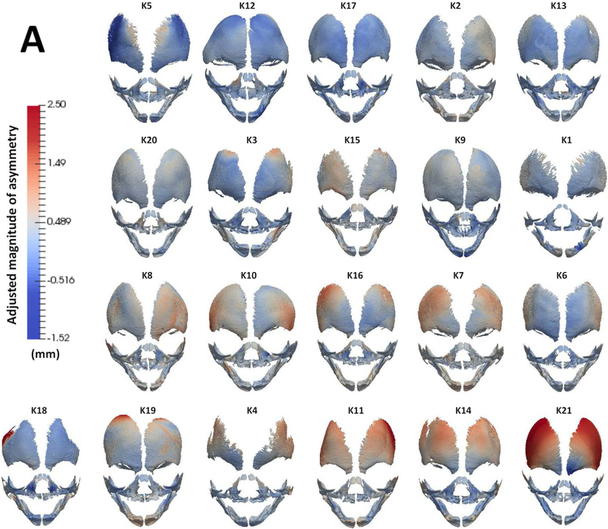
To assess local areas of asymmetry over the entire surface of facial bones, we utilized an adapted DBA analysis. Figure 3A shows the frontal view of the color-maps depicting magnitude of asymmetry for each specimen. A score for adjusted magnitude of asymmetry was calculated and demonstrates overall low magnitude of asymmetry for each specimen (Fig 3B). The correlation between crown rump length (CRL) of each specimen to adjusted magnitude of asymmetry was 0.51, indicating that asymmetry estimates do not change with size of the conceptuses between 15 – 20 weeks of gestation. Some of the meshes display increased asymmetry in the infraorbital areas of maxillary bone (Fig 3A; K7, K8, K10, K11, K16, K20), similar to the FA distribution seen using GM analysis (Fig 2B). However, the magnitude of asymmetry in these localized regions is small and notably, the distribution of asymmetry is highly variable between specimens.

Fig 3. DBA analysis of asymmetry (A).

Frontal view of surface meshes of all specimens analyzed in this study. A color map (left, mm) was applied to the surface which depicts magnitude of asymmetry score at each node of the mesh. Red and blue colors indicate areas of high and low asymmetry, respectively. (B) Graph depicts all specimens (x-axis) ordered by increasing crown rump length (left vertical axis) and their adjusted magnitude of overall asymmetry (right vertical axis). Note that specimens in (A) have been isometrically scaled and are arranged (top to bottom, left to right) by increasing order of adjusted magnitude of asymmetry reported in (B).

Discussion

Conventional asymmetry analyses using 3D CBCT images utilizes sagittal, axial and coronal planes to obtain linear distances and angles and assess craniofacial asymmetry [7]. Given that most bones in our specimen do not display midline ossification at the fetal stage, we were unable to dependably locate the midsagittal plane. Reliance on bilateral landmarks to mathematically attain a midsagittal plane would confound the subsequent assessment of asymmetry at those landmarks. Additionally, small changes in plane angle designations can magnify projected distance measurements, hence confounding quantification of asymmetry [7]. Hence, we utilized GM and DBA analyses for asymmetry assessment.

GM analyses demonstrated small but significant areas of asymmetry in the developing fetal facial skeleton, and reveal that FA predominated over DA (Table 2). FA noted in the maxillary and zygomatic bones (Fig 2B) may reflect the ontogenetic allometry in these structures during this period, where antero-lateral expansion seems to predominate (unpublished data). Notably, our data does not reflect the magnitude or directionality of facial skeletal asymmetries that have been reported in in adolescents and adults. [7, 9, 10, 12]. One possible reason is that adult tissues display cumulative effects of developmental, environmental and functional processes. The stages studied here captures the initial ossification events in these bones. With growth and interconnection established by sutures and synchondroses, patterns of asymmetries may change, especially with continued bone remodelling.

Studies have indicated that the mandible displays significant asymmetry. Hujoel et al. [11] evaluated lower face asymmetry in ~6500 adolescents, utilizing dental markers as a surrogate for jaw size. They reported lower face asymmetry in ~25% of the population. Unilateral retrognathia was more common than unilateral prognathia (~17% and ~8% respectively). Interestingly, the former display FA while the later displays DA, occurring more often on the left than the right side [11]. The authors also found that the prevalence of symmetric, i.e. bilateral retrognathia and prognathia, changes with age. However, the prevalence of asymmetric i.e. unilateral retrognathia or prognathia, does not increase or decrease after age 12. A similar lack of age-related changes in mandibular and facial asymmetry in adolescent patients has been reported [29, 30]. However, Melnik has reported improvement in asymmetry from age 6–12 yrs and also found left side dominance in mandibular size at young ages [31]. In our fetal specimen, the mandible does not appear to be a site where significant DA or FA is evident (Fig 2). Several individual specimens did reveal asymmetric areas in the mandible when analyzed using DBA methods (Fig 3A; K3, K7, K11, K15, K14, K16, K18, K19). However, the distribution of this asymmetry is highly variable, and of low magnitude. Once again, this suggests that the prevalent asymmetries reported in the mandible develop later in ontogeny.

Results from our DBA analysis demonstrates a large amount of variability in asymmetric areas in individual specimen (Fig 3A). Visualizing such variability is difficult using GM methods which are restricted to regions around annotated landmarks, highlighting the advantages DBA methods provide. Although some specimens displayed similar distribution of asymmetry based upon DBA and GM analyses, the results obtained are not categorically homologous. For example, DBA analyses demonstrate relatively higher asymmetry distributed to areas of the frontal bone (Fig 3A). However, GM analysis does not depict any asymmetry in this region (Fig 2). This may be related, in part, to sparse sampling limitation inherent to GM analysis. Another source of difference may be derived from the superimposition methods utilized by the two analyses or the way in which error is measured.

Our study has certain limitations. 1) The gender distribution within our sample is difficult to determine. A lack of sexual dimorphism pertaining to cranioskeletal asymmetry has been reported [32, 33], hence it is unlikely that stratification of our specimen based on sex would have altered our findings. 2) Genetic information is not available and hence we cannot entirely rule out the absence of diseases which may impact craniofacial symmetry. However, if some of the conceptuses analyzed here did have a genetic disorder influencing asymmetry, it would further reduce our asymmetry estimations. 3) Our analysis utilized aborted conceptuses from a geographically and presumably ethnically discrete population. 4) Our sample size is relatively small. 5) The samples utilized in this study have been preserved for many years. However, historical comparisons between fresh fetuses and formalin-fixed fetuses have shown a very slight but uniform distortion [34], permitting analysis of asymmetry [35].