Isolation and Identification of Listeria monocytogenes Utilizing DC Insulator-based Dielectrophoresis

Abstract

Foodborne pathogens pose one of the greatest challenges facing public health in the modern day. One important pathogen, Listeria monocytogenes, is known to be challenging to detect and identify. Three serovars cause most of the Listeria related food-borne illnesses, which the Centers for Disease Control currently utilizes a combination of pulsed-field gel electrophoresis and whole genome sequencing for identification and the determination of clusters and outbreaks. There is a potential method for rapid collection of epidemiological information by exploiting the electrokinetic and dielectrophoretic properties of the L. monocytogenes serovars. Using dielectrophoresis, the three most commonly identified serovars of L. monocytogenes can be distinguished from each other. The electrokinetic and dielectrophoretic mobilities of each serovar was determined through a combination of electrokinetic velocity and dielectrophoretic trapping assessments, in conjunction with finite element multi-physics modeling. A mathematical model of the data, which defines the various factors of dielectrophoretic trapping, is utilized and verified based on the behavior of L. monocytogenes in the microchannel. The trapping condition for the serovars were evaluated as 2.8 ± 0.2 × 10⁹, 2.2 ± 0.2 × 10⁹, and 2.2 ± 0.3 × 10⁹ V m^–2 and the electrokinetic mobility was assessed to be 19 ± 0.7, 17 ± 0.7, and 9.2 ± 0.3 × 10^–9 m²V^–1s^–1 for the L. monocytogenes serovars 1/2a, 1/2b, and 4b, respectively.

Graphical Abstract

Introduction:

Listeriosis is an infection caused by Listeria monocytogenes, and while infrequent, is one of the deadliest foodborne illnesses. In the United States alone each year, 48 million new cases of illness can be associated with foodborne origins, which has been increasing in frequency and coming from a broader number of food sources. They result in around 128,000 hospitalizations and 3,000 deaths, of which 19% of the deaths are caused by L. monocytogenes[1, 2]. Listeria monocytogenes is unique and hard to contain as it is able to grow and thrive in refrigeration and can also survive heating and drying remarkably well[3]. Furthermore, outbreaks of L. monocytogenes are notoriously difficult to detect as the organism has a long incubation time[4] and obtaining complete food histories can be challenging to impossible as patients are often extremely ill or deceased[5].

Listeria monocytogenes is a rod-shaped gram-positive bacterium and is approximately 0.4–0.5 × 0.5–2.0 µ m in size. There are thirteen serovars (serotypes), although 95% of outbreaks can be linked to three serovars, 1/2a, 1/2b, and 4b, where 4b causes more than half of these outbreaks[6–8]. A unique combination of expression of O-somatic and H-flagellar antigens defines the designation of each serovar[9–11]. The variable gene content in L. monocytogenes is described by three lineages I, II, and III, where serovars 1/2a is a part of lineage I and 1/2b and 4b are part of lineage II[12, 13]. These serovars represent broadly distinct phylogenetic groups[8]. There are several methods to detect L. monocytogenes and they can be categorized as culture-based techniques, immuno-based techniques, molecular methods for identification and confirmation, and ‘other’[14]. Beyond identification and confirmation, subtyping is performed using a variety of techniques including serotyping, phage typing; amplification-based, restriction digest-based, electrophoretic, and sequencing-based methods; along with single nucleotide polymorphism-based analysis[15]. Methods which utilize phenotypic subtyping are generally less sensitive, and therefore have a lower differentiation ability, and are hard to reproduce, while genotypic approaches are more reliable and sensitive[14].

Many of the current techniques used for identification, confirmation, and subtyping of L. monocytogenes face limitations based on their lengthy time for assessment, issues of reproducibility between analysts; need of cold chain reagents, highly specific antisera, or restriction enzymes; and technical expertise[5, 16]. The most commonly used technique for confirmation and speciation of L. monocytogenes is Pulsed Field Gel Electrophoresis (PFGE); a national and international network of the laboratories performing PFGE to detect outbreaks is known as PulseNet.[5, 13, 17–20]. In Europe and the US there has been a push to use PFGE in combination with whole-genome sequencing (WGS), which has greatly improved the ability for accurate speciation of L. monocytogenes and helped minimize the size of outbreaks[5, 13]. There is a well-recognized need for a faster, high resolution, reproducible method of identifying and subtyping L. monocytogenes[5, 10].

Serotyping can be performed as a preliminary method to subtype L. monocytogenes as it allows for comparison of results from different studies and offers context for phylogenetic or phenetic relationships[10, 12, 21]. Furthermore, serotyping gives insight into the epidemiology of L. monocytogenes serovars. However, there is some cross over in that L. monocytogenes and L. seeligeri share some serotypes so the incorrect species identification can occur[22]. Therefore, serotyping alone is not able, in the case of a listeriosis outbreak, to identify a positive correlation between foodborne and clinical isolates or identify an outbreak. However, there is potential to demonstrate a negative correlation between a foodborne and a clinical isolate.

To accomplish serotyping, the traditional method of agglutination is costly and expertise-limited; and is dependent on high-quality sera, which is in turn dependent on standardized strains and antigen prep methods[12, 23, 24]. Alternatively, PCR methods can be more accessible, but they still require sequence-specific primers, and can have difficulties distinguishing some serovars[10, 12, 25–27]. Multi-locus sequence typing (MLST) and multi-locus virulence gene sequencing typing (MLVST) are also used to gain insight into various L. monocytogenes samples, but are time consuming and require technical reproducibility[8]. Recently, MALDI-TOF has been developed for the confirmation of various bacteria, including Listeria, down to the species level[28–30]. For L. monocytogenes lineage level detection has been established, however speciation of the specific serovars has not yet been achieved.

Cell Manipulation Using Dielectrophoresis in Microfluidic Devices

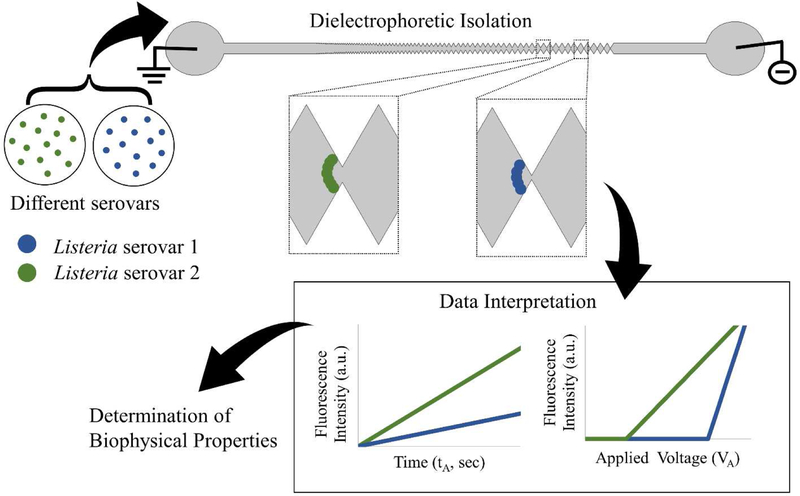
This work proposes a new method of serotyping, which is not dependent on antisera or primers and can eventually be done in a in a cost-effective manner, by minimally trained personnel in a matter of minutes to a few hours based on biophysical properties of cells using microfluidics (Figure 1).

Figure 1–

Representation of dielectrophoretic trapping in a gradient-iDEP microdevice for determination of biophysical properties of serovars. (Top) Two Listeria serovars analyzed using DEP in a microdevice. The microdevice has a sawtooth geometry, where the distance between the triangular insulator tips decreases from left to right. The hybrid device made of PDMS, fabricated with soft lithography, and glass are sealed together using an oxygen plasma treatment. The electrokinetic and dielectrophoretic properties for specific analytes interact uniquely with the microdevice which directly reflects their biophysical properties. The specific location of trapping for an analyte in the microdevice is based on differences in their biophysical properties; the point when the electrokinetic force is balanced by the dielectrophoretic force. (Bottom) The trapping behavior of an analyte can be interrogated and modeled using two methods: 1) based on the time potential has been applied or 2) varying the voltage applied to the system and monitoring signal at given time point.

The explosion of the microfluidics field in recent years is driven by the need for a low sample consumption, easy to use, inexpensive, rapid, precise, and accurate method capable of probing biological samples[31–40]. Microfluidic techniques have been applied to a wide range of analytes, but as a relatively young field there are still many applications to investigate, improvements to be made, and potentially novel methods to explore.

One prominent set of techniques utilizes electrokinetic (EK) forces to interrogate analytes based on their response to an electric field. These techniques are comparatively simple to use and are applied to a wide variety of applications. One prominent EK technique is dielectrophoresis (DEP), which utilizes a non-uniform electric field to manipulate particles in response to their polarizability and can influence both charged and neutral particles.

Dielectrophoresis was first performed in 1951 using a two-electrode system[41]. The field initially developed as electrode-based dielectrophoresis (eDEP) using low voltages, where the size, shape, and positioning of the electrodes defines the distribution of the electric field. This strategy has been used to influence several analytes including, but not limited to: viruses[42, 43], bacteria[44], yeast[45], and mammalian cells[36, 46]. Some limitations to eDEP are that the electrodes are prone to fouling, channels cannot normally be reused, electrolysis (and other electron transfer reactions) can occur at the electrodes creating bubbles and potentially altering the buffers present, and fabrication can be expensive. Additionally, the forces are only effective in the volume near the electrodes where the high gradients are achieved.

An alternative to eDEP is insulator-based dielectrophoresis (iDEP), established in the early 2000s [37–40, 47–54], where electrodes are placed in distal reservoirs and insulating features are used to manipulate the distribution of the electric field. Alternating Current (AC) and Direct Current (DC) fields can be used, where DC fields drive the movement of the analytes with EK transport, while AC fields can be used to refine separations. Properties of the particle, including size, structure, permittivity, surface charge, etc., will affect its behavior in a microchannel. At the constrictions in the microchannel the DEP force is the highest, and this is where the analytes will either be streamed or trapped in response to their individual properties. A significant application of the technique focuses on manipulation of bacterial cells to allow faster identification, isolate them from complex mixtures, and create a better understanding of their biophysical properties[35, 47, 48, 51, 55].

This work uses iDEP to interrogate three serovars of L. monocytogenes by studying their trapping behavior in a microchannel. The trapping behavior of the serovars is quantified using a physical model of trapping which enables the explicit determination of both the electrophoretic and dielectrophoretic mobilities (Figure 1). The technique presented should be capable of identifying a negative correlation between two isolates and preliminary identifying potential positive correlations between two isolates. This system introduces a new technique for serotyping of L. monocytogenes, which is rapid, simple to use, less dependent on proprietary supplies (such as primers and “kits”), and cost effective.

Theory:

The manipulation of analytes using iDEP is possible because of the effects caused by the electrokinetic and dielectrophoretic forces. Further development of the effect of these forces can be found in previous works[51, 52, 56–59].

The electrokinetic mobility $\left({\text{μ}}_{EK}\right)$, combines the effects of the electroosmotic and electrophoretic mobilities ${\text{μ}}_{EOF}$ and ${\text{μ}}_{EP}$ respectively, is a measure of biophysical properties of a given cell.

$${\text{μ}}_{EK}=\left({\text{μ}}_{EO}+{\text{μ}}_{EP}\right)=\frac{-{\epsilon }_m{\zeta }_m}{\eta }+\frac{{\epsilon }_m{\zeta }_p}{\eta }=\frac{-{\epsilon }_m\left({\zeta }_m-{\zeta }_p\right)}{\eta }$$ (1)

Where ε_m is the permittivity of the medium, ζ is the zeta potential of medium (m) and particle (p), and ɳ is the vistocisty of the medium. The electrokinetic velocity $\left({\stackrel{\rightharpoonup }{v}}_{EK}\right)$ is therefore defined by the ${\text{μ}}_{EK}$ and the electric field $\left(\stackrel{\rightharpoonup }{E}\right)$.

Using DC potentials, the electrophoretic (EP) and electroosmotic (EOF) velocities can be combined to define the electrokinetic velocity $\left({\stackrel{\rightharpoonup }{v}}_{EK}\right)$.

$${\stackrel{\rightharpoonup }{v}}_{EK}={\text{μ}}_{EK}\stackrel{\rightharpoonup }{E}$$ (2)

The relationship between ${\stackrel{\rightharpoonup }{v}}_{EK}$ and $\stackrel{\rightharpoonup }{E}$ is linear for a specific analyte as ${\text{μ}}_{EK}$ is considered a constant in this case. The dielectrophoretic velocity can be similarly described using the dielectrophoretic mobility $\left({\text{μ}}_{DEP}\right)$ and the gradient of the electric field squared $\left(\nabla {\left|\stackrel{\rightharpoonup }{E}\right|}^2\right)$.

$${\stackrel{\rightharpoonup }{v}}_{DEP}=-\left(\frac{{\epsilon }_m{r}^2{f}_{CM}}{3\eta }\right)\nabla {\left|\stackrel{\rightharpoonup }{E}\right|}^2=-{\text{μ}}_{DEP}\nabla {\left|\stackrel{\rightharpoonup }{E}\right|}^2$$ (3)

Where, r is the radius of the particle, and ƒ_CM is the Clausius-Mossotti factor. The Clausius-Mossotti factor is dependent on the conductivity of the particle and medium in DC fields, and the resulting sign will result in either positive or negative DEP. Previous work has demonstrated that the µ_DEP is intrinsic to the particle’s properties[60]. The effect of a non-uniform electric field acting on a polarizable particle is known as the dielectrophoretic force, ${\stackrel{\rightharpoonup }{F}}_{DEP}$. For a spherical particle with a single dipole, the force is described as:

$${\stackrel{\rightharpoonup }{F}}_{DEP}=2\pi {\epsilon }_m{r}^3{f}_{CM}\nabla {\left|\stackrel{\rightharpoonup }{E}\right|}^2$$ (4)

Based on the CM factor, positive DEP occurs when the conductivity of the particle is greater than the conductivity of the media. This results in the particle being attracted to areas with high electric field strength. Conversely, negative DEP occurs when the conductivity of the media is larger than the conductivity of particle, which effectively repels the particle from areas with high electric field strength.

In the case of L. monocytogenes, which are rod shaped, when the DEP force is modelled the equation for an ellipsoid particle must be considered, which is described by:[61, 62]

$${\stackrel{\rightharpoonup }{F}}_{DEP}=\frac{4}{3}\pi abc{\epsilon }_m\left(\frac{{\sigma }_p-{\sigma }_m}{Z{\sigma }_p+\left(1-Z\right){\sigma }_m}\right)\nabla {\left|\stackrel{\rightharpoonup }{E}\right|}^2$$ (5)

where the semi-principal axes of the ellipsoid are represented by a, b and c (a > b = c) and Z is the depolarization factor.

Diffusion, advection, and electrokinetic effects control the movement of particles in a microfluidic channel. Advection $\left({\stackrel{\rightharpoonup }{v}}_{Bulk}\right)$ can be ignored since pressure driven flow is absent, and as L. monocytogenes is larger than 1 µm the effects of diffusion can also be disregarded. Particle flow can therefore be described by[63, 64]:

$$\stackrel{\rightharpoonup }{J}=D\nabla \text{C}\hspace{0.17em}\text{+}\hspace{0.17em}C\left({\stackrel{\rightharpoonup }{v}}_{Bulk}+{\stackrel{\rightharpoonup }{v}}_{EK}+{\stackrel{\rightharpoonup }{v}}_{DEP}\right)\approx C\left({\stackrel{\rightharpoonup }{v}}_{EK}+{\stackrel{\rightharpoonup }{v}}_{DEP}\right)$$ (6)

where D is the diffusion coefficient and C is the concentration of particles. The movement of particles is therefore only affected by EK and DEP. The DEP velocity will only have an effect with high gradients of the electric field, which occur at the constriction points in the microchannel. Therefore, particle motion is mostly due to the EK, and the electric field lines approximate the particle movement in the microchannel.

Analytes are trapped in the microchannel when the particle velocity along the field line is zero: $\stackrel{\rightharpoonup }{J}\cdot \stackrel{\rightharpoonup }{E}=0$. This trapping occurs such that ${\stackrel{\rightharpoonup }{v}}_{DEP}$ is equal to ${\stackrel{\rightharpoonup }{v}}_{EK}$. Using the EK and DEP mobilities the trapping of analytes can be described by[56, 64]:

$$\left({\text{μ}}_{EK}\stackrel{\rightharpoonup }{E}-{\text{μ}}_{DEP}\nabla {\left|\stackrel{\rightharpoonup }{E}\right|}^2\right)\cdot \stackrel{\rightharpoonup }{E}\le 0$$ (7)

$$\frac{\nabla {\left|\stackrel{\rightharpoonup }{E}\right|}^2}{E^2}\cdot \stackrel{\rightharpoonup }{E}\ge \frac{{\text{μ}}_{EK}}{{\text{μ}}_{DEP}}$$ (8)

Trapping of particles in the microchannels provides absolute values for both the electrokinetic and dielectrophoretic mobilities which can in turn provide insight into the biophysical properties.

Materials and Methods:

Microdevice Fabrication

A sawtooth microchannel was used for the manipulation of the three serovars of L. monocytogenes, which has been described in detail elsewhere[32, 48, 65–68]. Briefly, the microchannel walls consist of equilateral triangular shaped insulators that are adjoined. Gates in the microchannel occur at the constriction points in the microchannel when the two triangles from the channel walls are closest together in the microchannel. The size of the triangles increases from inlet to outlet, and as a result the gate sizes decrease. A given gate size repeats six times in the microchannel prior to the gate size decreasing. The characteristics of the microchannel are such that the length, width, and depth are 4.2 cm, 1000 µm, and 16.9 ± 1 µm (average between templates), respectively. The gates in the microchannel range in size from the initial 945 µ m gate to the final 27 µm gate. All microchannels were cleaned and bonded on the day of use.

Cell culture and labeling

Three serovars of L. monocytogenes, specifically 1/2a (ATCC 51772), 1/2b (ATCC 51780), and 4b (ATCC 13932) were obtained. Seed stocks of each serovar were stored in Listeria enrichment broth (LEB) and 16.7% glycerol at −80°C. To grow the serovars, 10 mL of sterile LEB was aliquoted into a culture tube, inoculated, and placed in a shaker/incubator over night at 250 rpm (37°C). When cultures reach the late log phase, the approximate concentration of cells is 10⁹ CFU mL^-1. The cultures were stored at 4°C.

Cells were labelled using NHS-rhodamine (excitation/emission wavelength: 552/575 nm). A 1:10 dilution of cultured cells in 2 mM phosphate buffer (PB), pH 7.4 was prepared. The NHS-rhodamine solution (10 mg/mL) was prepared fresh daily in DMSO. A 20 µL aliquot of the dye solution was added to the diluted cell suspension and vortexed and incubated in a water bath (37°C) for 20 minutes. To remove excess dye a wash procedure was repeated thrice with 2 mM PB. The first centrifugation was performed for 10 minutes at 2000 g, while all subsequent centrifugations were done for only 5 minutes. The final suspension of the labeled cell pellet was in 1 mL of 2 mM PB with 4 mg/mL of bovine serum albumin (BSA).

Experimental

A microdevice was filled with 2 mM PB, pipetting 15 µ L into the inlet and outlet reservoirs. The solution was then removed from both inlet and outlet reservoirs and 15 µL of 2 mM PB with 4 mg/mL of BSA was introduced into the inlet reservoir for 10 minutes, providing a static coating of BSA on the channel walls prior to introduction of bacteria to the channel. Platinum electrodes (diameter 0.404 mm; Alfa Aesar, Ward Hill, MA) were inserted into the inlet and outlet reservoirs. The BSA solution was then removed and 15 µL of the labelled bacteria was added to the inlet reservoir and allowed to fill the channel without electrical manipulation for 10 minutes. The outlet reservoir was then filled with 15 µL of 2 mM PB with 4 mg/mL of BSA to eliminate hydrodynamic flow with a resulting conductivity of 3 × 10² µS/cm.

The microchannel was imaged using an Olympus IX70 inverted microscope with a 4× objective. The device was placed on the microscope stage and the platinum electrodes were connected to a HVS448 3000D high voltage sequencer (Labsmith, Inc., Livermore, CA). Illumination was provided by a mercury short arc lamp (H30 102 w/2, OSRAM). Fluorescence microscopy was enabled by an Olympus DAPI, FITC, Texas Read triple band pass filter cube (Olympus, Center Valley, PA). DC potentials across the device ranged from 0–500 V in 50 V increments.

Images were digitally captured with a monochrome QICAM cooled CCD camera (QImaging, Inc., Surrey, BC) using Streampix V image capture software (Norpix, Inc., Montreal, QC). To assess, manipulate, quantify images, generate data, and convert files, Image J (NIH freeware) was used. For the velocity determination, individual bacteria were traced frame to frame at various applied voltages until the particular particle could not be identified in the subsequent frame. This was performed at or near the centerline of the microchannel just prior to the 27 µm gate. Velocity analysis was only done for applied potentials where individual bacterium could be identified from frame to frame, allowing for position tracing over time. For each serovar, the path of ten bacterial cells were traced, determining their starting and ending locations and the time between location measurements. Analysis of particle velocity was done for three trials of each serovar.

Safety Considerations

Organisms used in this experiment were Biosafety Level (BSL) II. Experiments were performed in an approved BSL II laboratory within accordance to the current version of the CDC/NIH BMBL publication.

Physical Modeling:

Multiphysics

The distribution of the electric potential within the microchannel utilized in experiments was modelled using a finite element, multi-physics software (COMSOL, Inc., Burlington, MA). Centerline approximations of these values was used to interpret the behavior of the bacteria in the microchannel. A detailed description of the modeling methods have been published elsewhere[56]. Briefly, an accurately-scaled 2D representation of the channel was built in AutoCAD and imported to COMSOL. A 2D model was used as it simplifies the calculation and decreases computational time, and the electric potential will vary minimally across the relatively small depth. It is noted that the surface charge of glass and PDMS likely differ, which may affect the accuracy of the computations.

Model of the Data

Models of data for the collection of particles in DEP devices have previously been developed and are based on the Fokker-Planck equation (FPE) to describe the behavior of particles in a solution when subjected to an arbitrary external force. The FPE considers space, time, and the concentration of the particles [69, 70]. Similarly, for the data collected in this paper a simplified model was developed to quantify the collection of bacteria in response to the trapping forces in a region of interest (ROI) defined as an 80 × 50 pixel box at the first of the 27 µm gates (see data figures). The changing fluorescence intensity (FI) within this region was assessed with respect to time with a single voltage applied and with respect to the applied voltage at a set time of collection. An assumption was made that the behavior of the particles is approximated as though all the particles are traveling along the centerline of the microchannel. To further understand the parameters effecting trapping, a model of the data, which correlates these factors was utilized[71].

Briefly, the model determines the total number of particles that will arrive and can therefore be trapped at gate of interest. For these methods of data assessment, the distance (d) that a given particle may travel under the experimental conditions must be established[71]. Throughout most of the channel DEP forces are minimal (the exception being at the smaller gates) and the velocity is defined by EK effects[56, 63, 64]. Therefore, the distance a given particle travels to its trapping location can be described by combining ${\stackrel{\rightharpoonup }{v}}_{EK}$ (Eq. 2) and the basic equation for velocity:

$$\stackrel{\rightharpoonup }{d}=\left({\mu }_{EK}{\stackrel{\rightharpoonup }{E}}_{ave}\right)t$$ (9)

where t is time and ${\stackrel{\rightharpoonup }{E}}_{ave}$ is the average applied electric field. The total number of particles (N) in a given volume that can reach their trapping location can be described as:

$$N=n\stackrel{\rightharpoonup }{d}wh=n{\mu }_{Ek}{\stackrel{\rightharpoonup }{E}}_{ave}wht$$ (10)

where and n is the concentration of particles, w is the width, and h is the height of channel. Each particle has an average fluorescence intensity (γ) which will contribute to the total fluorescence intensity (FI). However, the trapped particles cannot all be simultaneously visualized since the depth of the focal plane is smaller than the depth of the channel and particles will overlap with one another. Therefore, to account for the depth of the microchannel, a stacking factor, s, is included, based on the number of particles that can be stacked in the depth of the channel:

$$FI=\frac{\gamma n{\mu }_{Ek}{\stackrel{\rightharpoonup }{E}}_{ave}wht}{s}$$ (11)

The time for which the potential is applied, or the magnitude of the applied potential may be held constant. Holding the ${\stackrel{\rightharpoonup }{E}}_{ave}$ constant gives a time-dependent model. For the microchannel in this study, ${\stackrel{\rightharpoonup }{E}}_{ave}$(V/m) is the applied potential (V_A) divided by the length of the microchannel:

$${\stackrel{\rightharpoonup }{E}}_{ave}=24V_A$$ (12)

For the microchannel used in this paper, the time-based model is:

$$FI=\frac{24V_A\gamma n{\mu }_{Ek}wh}{s}t$$ (13)

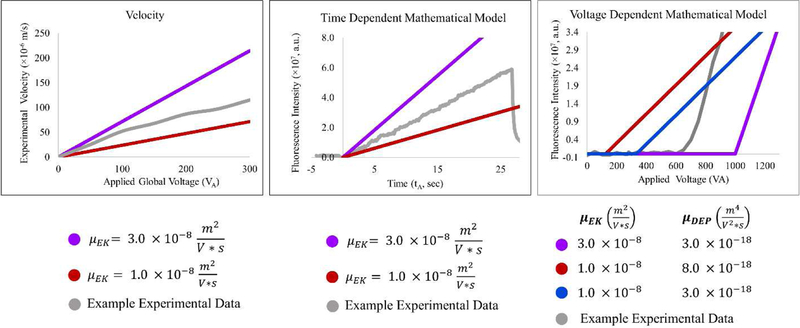
The collection rate is directly proportional to the electrokinetic mobility (Figure 2).

Figure 2–

Illustration showing general structure of model and data. The behavior of analytes is monitored for velocity (left), time-dependent collection (middle) and voltage-dependent collection (right). Purple, red, and blue lines are representative values of biophysical properties and the grey lines are typical experimental behaviors. Velocity is monitored in the open portions of the channel with various applied potentials and is reflective of the electrokinetic properties only (left). Time-dependent data (middle) is a function of the relative fluorescence intensity and the electrokinetic mobility of the particles. For the voltage dependent data (right), both the electrokinetic and dielectrophoretic mobility affect the onset voltage for trapping (correlating to the x-intercept of the line describing the sloped data, the discontinuity in the data structure). The slope is indicative of the amount of bacteria that have been collected given the application of voltage for a set amount of time at each voltage. A detailed description of the models for each data type can be found in the text. For both models the following values are used: $\gamma n=5\times {10}^5\left(a.u.m^{-3}\right),w=0.3\hspace{0.17em}mm,h=17\mu m,s=15$. For time dependent model, the applied potential is 300 V and for the voltage-dependent model t = 10 s was used.

For a voltage-dependent data assessment of FI Equation 9 is rearranged such that, t is held constant at specific time after the initiation of applied potential, while V_A is varied, and a factor, c, relative to the onset of voltage is introduced:

$$FI\left(V_A\right)=\frac{\gamma n{\mu }_{Ek}wht}{s}{\stackrel{\rightharpoonup }{E}}_{ave}\left(V_A\right)+c$$ (14)

The onset of trapping can be correlated to the ratio of mobilities (Eq. 8) for a given analyte of interest.

$$\frac{\nabla {\left|\stackrel{\rightharpoonup }{E}\right|}^2}{E^2}\cdot \stackrel{\rightharpoonup }{E}\left(c\right)\ge \frac{{\text{μ}}_{EK}}{{\text{μ}}_{DEP}}$$ (15)

Values for the electric field and gradient were determined with finite element multi-physics modeling using the centerline and the maximum ratio achieved (Vm^–2) at the first 27 µm gate. Using the specific properties of the channel used in this paper results in the following relationship:

$$\left[\frac{\nabla {{\left|\stackrel{\rightharpoonup }{E}\right|}^2}_{max}}{{E^2}_{max}}\cdot {\stackrel{\rightharpoonup }{E}}_{max}\left(c\right)\right]=1.0\times {10}^7\ast c=\frac{{\mu }_{EK}}{{\mu }_{DEP}}$$ (16)

$$c=\frac{1}{1.0\times {10}^7}\left(\frac{{\mu }_{EK}}{{\mu }_{DEP}}\right)$$ (17)

The signal from the voltage-dependent data is well-described by a piecewise function, with the discontinuity at c:

$$FI\left(V_A\right)=\{\begin{array}{l}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}0,if\hspace{0.17em}{V}_A<\frac{1}{1.0\times {10}^7}\left(\frac{{\mu }_{EK}}{{\mu }_{DEP}}\right)\\ 24\frac{\gamma n{\mu }_{Ek}wht}{s}\left[V_A-\frac{1}{1.0\times {10}^7}\left(\frac{{\mu }_{EK}}{{\mu }_{DEP}}\right)\right],if\hspace{0.17em}{V}_A\ge \frac{1}{1.0\times {10}^7}\left(\frac{{\mu }_{EK}}{{\mu }_{DEP}}\right)\end{array}$$ (18)

When no trapping occurs in the microchannel, the contribution to FI from the trapped analyte is absent.

Results:

The three most common serovars of L. monocytogenes were interrogated using iDEP. Each of the serovars was studied in the V1 microchannel, which has been described in detail.[48, 65] For this work, the behavior of the bacteria was assessed at a consistent gate position in each microchannel.

Determining the Velocity and Electrokinetic Mobilities of the L. monocytogenes serovars

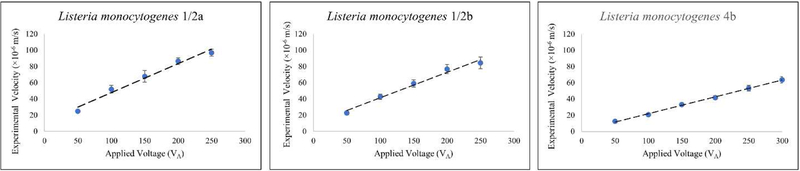
The velocity for all three serovars were determined in the more open portion of the channel, prior to the gate of interest, where no evidence of trapping behavior was observed (Figure 3). The velocity was linear with respect to V_A allowing for an accurate estimate of µ_EK from a range of voltages and velocities. The characteristic value for the serovars of L. monocytogenes (Eq. 2), and their 95% CI, were determined as 19 ± 0.7, 17 ± 0.7, and $9.2\pm 0.3\times {10}^{-9}\frac{m^2}{Vs}$ for serovars1/2a, 1/2b, and 4b, respectively.

Figure 3-.

Plots of the velocity of three serovars at various applied potentials (V_A). All data collected near the first 27 µm gate in the V1 microchannel. Dotted lines are linear fits to the data and error bars are at the 95 % confidence interval. The linear fit is used to determine the electrokinetic mobility for each serovars using ${\stackrel{\rightharpoonup }{v}}_{Ek}={\mu }_{EK}\stackrel{\rightharpoonup }{E}$.

Trapping Experiments

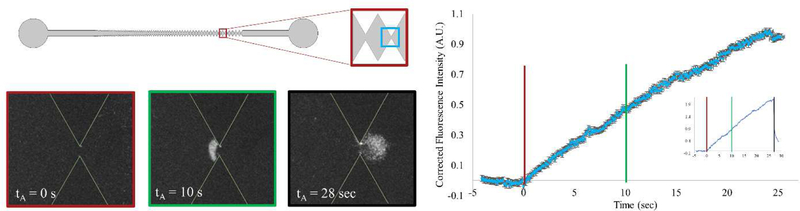
The behavior of the three serovars of L. monocytogenes were studied in an iDEP microchannel where the magnitude of V_A or its duration of application (t_A) were varied. The structure of the data for all three of the serovars was consistent with previous work that used similar methods in a microdevice with comparable geometry. The movement of the analyte toward the outlet with applied potential supports EOF-dominated transport.[47, 48, 54] Trapping behavior of L. monocytogenes was assessed at the first 27 µm gate, where no trapping of the analyte was observed at the 90 µm or larger gates. Characteristically, the fluorescently-labelled bacteria collected in a crescent shape a few microns prior to the first 27 µm gate on the inlet side of the gate (Figures 1 and 4).

Figure 4–

Typical trapping behavior and data in a V1 microchannel at the 27 µm gate (top left illustration, the light blue box represents the area in the images). The data depicted is of Listeria monocytogenes 1/2a with an applied potential of 350 V (85 V/cm). Negative dielectrophoresis results in the collection of the material in a crescent-shaped band on the inlet side of the gate (bottom left). Trapping occurs at applied potentials above a threshold value specific to the serovar. The bacteria are continuously collected when potential is applied. Three time points are shown as images, color coded corresponding to lines on FI vs t plot demonstrating the channel before, during, and after trapping (red = 0 s, green = 10 s, black = 28 s; n = 12, ROI described in the text). The grey region around each data point in plot is the 95% confidence interval. Inset is typical data for a single trial. The reversible nature of capture of the bacteria is demonstrated in the last image, at 28 s, as the bacteria disperse back into the microchannel immediately after the voltage is removed.

The amount of trapped analyte was determined by measuring the FI in a given ROI centered near the point of typical trapping (Figure 4, left, blue box). There are several factors which affect the trapping of material in the microchannel, including the biophysical properties of the analyte of interest, the channel geometry, and the experimental conditions (voltage, buffer properties).

There is a threshold electric potential (c) which meets the trapping ratio that results in bacteria being collected instead of continuing to move past the gate (Eq. 7, 8, &18). The rate at which the bacteria collects is characteristic of the particle transport rate, which is dependent on the ${\stackrel{\rightharpoonup }{v}}_{EK}$. The material continues accumulating in a linear fashion as long as the potential is applied (Figure 4, right).

The trapping behavior of all three serovars were assessed at a consistent time point (t_A = 10 s, Figure 4, green line) at voltages from 50–500 V in increments of 50 V. The FI was then normalized for concentration, and the FI in the ROI prior to the application of voltage. The FI with no applied voltage was measured prior to the application of voltage, specifically 2 seconds after recording was started for the 50 V trials. The threshold value of trapping (when V_A=c) was determined by first determining baseline behavior at low applied potentials where no trapping occurred. The baseline for serovars 1/2b and 4b was determined using the data from 0–150 V applied, while for 1/2a was determined using the data for 0–250V. The background signal limit is denoted by two standard deviations above the average baseline. Statistically significant trapping was considered to be occurring when the FI of the trapped material exceed the background limit. In the case of serovars 1/2a and 1/2b, their respective data points of 300 and 250 V were determined to be significantly different at the 95% CI than the background limit using a 2-tailed t-test. Whereas for serovar 4b, the 250 V data point is not significantly different from the background limit, however if the data point is included in the determination of c, it does not result in a significant difference. Increasing the applied potential resulted in more material being trapped in the 10 second timeframe for applied potential (Figure 4).

All three serovars resulted in a predominantly linear, positive slope at applied potentials greater than their respective values of c. For all three serovars the red data points were utilized to determine c and to calculate the trapping ratio of mobilities (Figure 5). The values of c were determined to be 280 ± 18, 220 ± 15, and 220 ± 31 V for the L. monocytogenes serovars 1/2a, 1/2b, and 4b, respectively. The ratio of mobilities necessary for trapping was then determined, using COMSOL models, to be 2.8 ± 0.2 × 10⁹, 2.2 ± 0.2 × 10⁹, and $2.2\pm 0.3\times {10}^9\frac{V}{m^2}$ for the L. monocytogenes serovars 1/2a, 1/2b, and 4b, respectively.

Figure 5.

Trapping behavior for three serovars (identification noted above each plot) at various applied potentials (V_A). All data was collected at a 27 µm gate in the V1 microchannel after the potential was applied for 10 seconds (t_A). Slope was assessed using signals exceeding the background limit (twice the standard deviation of the baseline data points). Dotted red lines are fitted from the linear part of the data (see text) above the baseline and background limit. The initial trapping voltage is determined by the x-intercept of the linear fit line. The error bars are the 95% confidence interval. Using the linear fits, both the electrokinetic and dielectrophoretic mobilities can be determined using the voltage based physical model (see text).

Modeling of the Data

To verify the efficacy of the data modeling, ${\mu }_{EK}$ for all three serovars was determined using the voltage-dependent data (Eq. 18). Only data beyond the value of V_A where statistically significant trapping occurred were used for the determination of ${\mu }_{EK}$ (Figure 5). The FI for all the trials were taken after 10 seconds of applied potential, the channel height in all cases was 17 µm, and ${\stackrel{\rightharpoonup }{E}}_{ave}$ was determined from Eq. 12. The determination has bracketed variables of the FI observed for trial and the number of trapped particles that can reasonable fit in the trapping zone. The microchannel width, in this study, is between 27 to 1000 µm, however given that the majority of the channel has insulating features a realistic range for the average channel width that the bacteria may be trapped in is 0.25 ± 0.05 mm. As the channel height is 17 µm a maximum of 34 stacked L. monocytogenes cells can be stacked with 1 being the obvious minimum. The actual number of stacked bacterium when trapped is dependent on the size and interactions of individual bacterium. Within this range, the calculated value of ${\text{μ}}_{EK}$ easily falls within the independently measured values (Figure 3 and narrative). Serovars 1/2a and 1/2b fall within the 95% CI interval (19 ± 3.4 × 10^–9 and $17\pm 3.3\times {10}^{-9}\frac{m^2}{Vs}$, respectively) of the ${\mu }_{EK}$ as determined from velocity measurements if 20 bacterial cells are assumed to be stacked and the average channel width is 0.22 µm. For serovar 4b, the data fits within the 95% CI $\left(9.2\pm 1.3\times {10}^{-9}\frac{m^2}{Vs}\right)$ if 12 bacterial particles are stacked with the same average channel width. We recognize that the observed FI provides for a rather generous multiplicative range for stacked bacterium (1–34), but the fact that reasonable values are observed (~12 and ~20), we find this to be supportive of an appropriate treatment and interpretation of these data. This is in spite of some obvious sources of variance which can be attributed to necessarily low number of replicates (n ≤11) for a proof-of-principle study, occasional aggregate formation (changing the trapping location and/or altering the electric field across the device), and small variations in the prototype microdevices. In the case of the serovar 1/2b the data plateaus for the voltage dependent assessment (Figure 5). This is potentially caused by several factors, including reaching the maximum amount of material collected in the ROI after 10 seconds, surpassing the detection limit of the CCD camera, or bacteria starting to collect at the 60 µm gate.

Discussion:

Subtyping, specifically serotyping, in a rapid and reproducible manner is desirable to obtain epidemiological information about L. monocytogenes. This study serves as a proof-of-principle study for a technique that uses microfluidics and electrokinetic forces to rapidly identify, isolate, and serotype L. monocytogenes. The three most common serovars have been demonstrated to have distinct behavior in the microchannel, which is indicative of their electrokinetic and dielectrophoretic properties (Figures 3–6).

Figure 6.

Comparison of the mobilities and their ratio for the three serovars of L. monocytogenes (note vertical axis for each plot). Each serovar possesses a unique set of biophysical properties that can be probed by iDEP. Some serovars pairs have significant statistical overlap in µ_EK and µ_DEP. Including both mobilities, however, allows for differentiation. These differences can be displayed with regard to either the electrokinetic or dielectrophoretic properties without preference in this case. For other serovar or strain comparisons, one plot or the other may allow for the unique differentiation.

The L. monocytogenes serovars tested in this study each behave uniquely according to their biophysical properties (Figure 3). One sub-component which can be independently determined is their ${\stackrel{\rightharpoonup }{v}}_{EK}$, how fast they move in the microchannel when not influenced by DEP, and by extension their ${\mu }_{EK}$. The electrokinetic mobility determination allows insight into the biophysical properties of the cell centered on the concentration and distribution of charge on the surface. Linear electrophoretic approaches have been used to measure ${\mu }_{EK}$ with some success [72–74], consistent with these results. These linear assessments, as practiced, were time consuming, gave broad uneven distributions of ${\mu }_{EK}$, and required pure, well characterized samples. Dielectrophoretic trapping probes the same biophysical properties of the cell as electrokinetic measurements but addresses them in a significantly different format because of the focusing, gradient nature of the technique. Previous work has demonstrated the ability for mixed populations to be assessed[48, 75], however further work is needed to prove the ability for the system to work on clinical or food samples. Mixed populations may be assessed and the ‘distributions’ can be closely examined, quantified, and parsed for biological significance.

Of course, in the DEP experiments, their respective ${\mu }_{DEP}$ is also captured and can be related to several biophysical cell properties[60, 71]. It should be noted that in this case the determination of ${\mu }_{DEP}$ is done based on the trapping condition and ${\mu }_{EK}$ assessed values. The determination of these values are based on centerline approximations. These approximations neglect to account for the complexities of the field changes which occur across the width of the channel and assume that the collection of the bacteria occurs where the maximum electric field is experienced at the given gate of interest. These assumptions are made based on COMSOL modeling of the collection of the bacteria in a characteristic arc shape, which occurs at a consistent ratio of mobilities [56, 76]. Changes in the ${\mu }_{DEP}$ could be attributed to the CM-factor for a classic sphere (Eq. 3), but the origins of the counteracting force in these experiments is far more complex[60, 71]. Specific cell properties that can influence ${\mu }_{DEP}$ include, but are not limited to, the cell’s size and ability for charges to pass through the cell.

The different biophysical properties of the three L. monocytogenes serovars can be displayed in different configurations (Figures 5 and 6). The variations in the slope correlate to the rate of collection, and thus ${\mu }_{EK}$; whereas the variations in c are a result from differences in both ${\mu }_{EK}$ and ${\mu }_{DEP}$ (Figure 5). The necessary trapping conditions can be represented for each of the L. monocytogenes serovars based on the parameters defined in this work and either the ${\mu }_{EK}$ or ${\mu }_{DEP}$. The three serovars of L. monocytogenes studied in this paper can be differentiated using their ${\mu }_{EK}$ and ${\mu }_{DEP}$, even though there is statistical overlap in their trapping ratios. This is indicative of the fact that all the serovars have unique biophysical properties.

Some of the differences between the serovars’ behavior can be attributed to changes on the surface of the cell. For the L. monocytogenes serovars this is with respect to the O-somatic and H-flagellar antigens, which would be expected to alter the surface charge of the cell [77]. Genetic differences between serovars have been defined using the large amount of genetic information collected by PFGE, WGS, MLST, and MLVST. Correlation between various genetic elements and phenotype have been identified, however a direct connection is not always apparent[8, 13, 78].

The use of DEP and microfluidics allows for a new method of rapidly subtyping, specifically serotyping, L. monocytogenes. Unlike current diagnostic methods this strategy should be possible with minimal sample preparation, in less than a few hours, and can be automated allowing for reproducibility between analysts without the need for specialized techniques. Dielectrophoretic trapping could be used as a method to determine positive or negative correlation of a clinical isolate to a known isolate, helping to rapidly determine which serovar is present. Beyond the proof-of-concept presented here, this method will need to be fully characterized for its ability to reliably serotype all strains of L. monocytogenes and identify L. monocytogenes versus other strains of Listeria. Further testing would also need to be performed to confirm that this method can overcome the challenges which PCR faces[10, 12] and to ensure this technique can handle several different food-borne bacteria. Current isolation methods for clinical samples requires growth on selective solid media and the fastidious nature of Listeria means it may take from one to three days for growth with additional testing required for identification[17]. These methods cannot determine specific serovars of L. monocytogenes and is what results in the need for further testing by PFGE and WGS to identify outbreaks. This dielectrophoretic method would allow rapid, straightforward isolation, identification, and subtyping from a single sample.

Beyond applications of identifying strains of Listeria, the combination of finite element multi-physics calculations and the model of the data enables a new understanding of how biophysical differences of analytes result in differing trapping behaviors. Specifically, using the ratio of mobilities and c, unique values for both ${\mu }_{EK}$ and ${\mu }_{DEP}$ can be determined. To verify the accuracy of this model a comparison of the ${\mu }_{EK}$ was determined based on the velocity of the bacterial particles and using the model. For the model of the data, a change in the number of stacked particles can significantly shift the determination of ${\mu }_{EK}$. This is seen for the L. monocytogenes serovars as when all the parameters except the stacking factor are held constant, the respective serovars fall within the 95% CI of the velocity determined measurements for L. monocytogenes 1/2a and 1/2b with 20 stacked particles and for L. monocytogenes 4b with 12 stacked particles. It should be noted that L. monocytogenes 4b has the largest error in c, which will result in less accuracy in the of ${\mu }_{EK}$ determined by the model. To further refine the values determined by the model more trials may be necessary. With more data points that fall in the linear range of the voltage dependent data (Figure 5) an estimate with lower variance for the mobilities should be possible. Furthermore, the assumptions made for the width and stacking factor are bounded independent variables. The width of the channel when trapping occurs will vary slightly with the applied voltage.

Conclusion

This work demonstrates the ability for iDEP to differentiate the three most common serovars of L. monocytogenes, establishing a foundation for a subtyping/serotyping method and a new investigative tool for basic scientific studies of Listeria. The serovars behavior in the microchannel allows for their differentiation, and their electrokinetic and dielectrophoretic mobilities can also be determined. In the future, based on the work presented here, the L. monocytogenes serovars can be separated using gradient-iDEP based on the difference in their biophysical properties. A physical model is employed and verified to assess the DEP trapping behavior and gives insights into the origins of the differing behaviors of the analytes. Using this model may help to better understand the differences both between and within serovars. Changes in some of the experimental parameters, buffer compositions and applied potential (AC vs DC), could potentially help improve this separation capability. An investigation into the limit of detection of this technique and the ability of iDEP to identify variants of the serovars, such a variant of 4b, termed 4bV or IVb-v1, would also be beneficial to further establish this technique[8].

Highlights.

• The biophysical properties of a cell can be interrogated with electrokinetics

• Dielectrophoresis can be used to rapidly speciate Listeria monocytogenes

• A data model quantitates biophysical properties of trapping dielectrophoresis

• Dielectrophoresis can rapidly collect epidemiological information

Abbreviations:

DEP

dielectrophoresis

iDEP

insulator-based dielectrophoresis

EP

electrophoresis

EOF

electroosmotic flow

µ_EK

electrokinetic mobility

µ_EP

electrophoretic mobility

µ_EO

electroosmotic mobility

µ_DEP

dielectrophoretic mobility

ƒ_CM

Clausius-Mossotti factor

${\stackrel{\rightharpoonup }{v}}_{EK}$

electrokinetic velocity

${\stackrel{\rightharpoonup }{v}}_{DEP}$

dielectrophoretic velocity

$\stackrel{\rightharpoonup }{E}$

electric field strength

$\nabla {\left|\stackrel{\rightharpoonup }{E}\right|}^2$

dielectrophoretic gradient factor

L. monocytogenes

Listeria monocytogenes