Gateless and reversible carrier density tunability in epitaxial graphene devices functionalized with chromium tricarbonyl

Abstract

Monolayer epitaxial graphene (EG) has been shown to have clearly superior properties for the development of quantized Hall resistance (QHR) standards. One major difficulty with QHR devices based on EG is that their electrical properties drift slowly over time if the device is stored in air due to adsorption of atmospheric molecular dopants. The crucial parameter for device stability is the charge carrier density, which helps determine the magnetic flux density required for precise QHR measurements. This work presents one solution to this problem of instability in air by functionalizing the surface of EG devices with chromium tricarbonyl -Cr(CO)₃. Observations of carrier density stability in air over the course of one year are reported, as well as the ability to tune the carrier density by annealing the devices. For low temperature annealing, the presence of Cr(CO)₃ stabilizes the electrical properties and allows for the reversible tuning of the carrier density in millimeter-scale graphene devices close to the Dirac point. Precision measurements in the quantum Hall regime show no detrimental effect on the carrier mobility.

Graphical Abstract

1. INTRODUCTION

Due to its advantageous electrical properties, graphene has been the subject of extensive study over more than a decade.^1–3 Among the variety of ways developed to synthesize graphene, epitaxial graphene (EG) on silicon carbide (SiC) displays superior properties for the development of quantized Hall resistance (QHR) standards.^4–11 Developing highly efficient standards using EG requires the long-term stability of electrical properties of millimeter-scale EG devices in ambient conditions, to equal the long-term stability and precision of GaAs-AlGaAs heterostructure QHR devices.¹¹ These properties include the longitudinal conductivity σ_xx, carrier density n, and mobility μ, which are related by the equation σ_xx = neμ.

While initial efforts to realize millimeter-scale EG devices for metrology have been fruitful, electrostatic gating for devices of this size and application is quite difficult. One early and successful process used to reduce the carrier density for QHR devices was photochemical gating, using ZEP-520A electron beam positive tone resist as an electron acceptor, but the process reversibility has inherent limitations based on number of thermal cycles to which a device is exposed.¹² Other methods for carrier density control and conservation have also been explored,^13–14 such as the use of poly-methyl methacrylate (PMMA),^12,15 atomically layered dielectrics,^16–19 Parylene,^20–21 amorphous boron nitride,^22–23 and hexagonal boron nitride.^24–25, but were either unable to achieve metrological usefulness,^20,22 or are irreversible processes.¹⁵

When EG is exposed to ambient atmospheric conditions, it experiences a drift in the carrier density and conductivity because of the physisorption of H₂O and O₂, which are found to be p-doping species because of their oxidizing characteristic.^26–29 Achieving electrical stability is critical for device applications including mass-produced electronics, chemical and biological sensors, and functionalized materials. This motivation holds particularly true for resistance metrology, where a narrow range of carrier densities between 1 × 10¹¹ cm⁻² and 3 × 10¹¹ cm⁻² is needed to produce a resistance plateau of $R_{\text{xy}}=\frac{e^2}{2h}$ at easily accessible magnetic flux densities (B). Generally, lower carrier densities will yield unreliable plateaus and higher carrier densities correlate to a plateau onset at higher magnetic flux densities.¹¹ Thus, gateless control of the carrier density is crucial to improving accessibility of resistance metrology using EG, where this v = 2 plateau can exhibit precise quantization at low magnetic fields (between 2.5 T and 7 T) for carrier densities in the vicinity of 10¹¹ cm⁻².⁴

In this work, we report the gateless and reversible carrier density tunability in EG devices functionalized with chromium tricarbonyl [Cr(CO)₃]. We have observed carrier density stability in air over the course of one year with shifts less than 10¹¹ cm⁻², and by controllable and reversible tuning, achieved metrologically useful values of the QHR, rendering Cr(CO)₃ as a suitable compound for stabilizing electrical devices based on EG. Controllable tuning was demonstrated by annealing the device in vacuum to the desired carrier density while monitoring the device’s room-temperature longitudinal resistivity. Despite exposure to heating in vacuum at up to 363 K (90 °C), EG devices retained full functionalization, and when stored in air for typically 24 h to 36 h following the anneal and measurement, the device’s carrier density drifted back to a low value, on the order of 10¹⁰ cm⁻², with respect to inherent EG doping above 10¹³ cm⁻². These results demonstrated that this functionalization method can be used to stabilize and reversibly tune the carrier density in millimeter-scale EG devices without the need of electrostatic gating, reducing the level of processing required for useful devices. Furthermore, these devices exhibited properties suitable for resistance metrology with proper tuning.

2. SAMPLE PREPARATION

2.1. EG Growth and Device Fabrication

EG is formed during thermal decomposition of the SiC substrate causing an enrichment of the surface with carbon atoms due to the preferential sublimation of silicon atoms. Samples used for this study were grown using 4H-SiC(0001) semi-insulating substrates with a miscut of ≤ 0.10°. Before growth, the substrates were first cleaned by piranha etch, followed by a dip into diluted hydrofluoric acid and a surface treatment with polymer adsorbates for polymer-assisted sublimation growth (PASG) by spin coating a weak solution (approximately 2 ml_[AZ5214E] / l_{[isopropanol]}).³⁰ For graphene growth, the resulting SiC(0001) samples were placed on a polished disk of glassy carbon with the Si face in direct contact with the disk for face-to-graphite growth.⁸ Combining the PASG and face-to-graphite growth methods suppresses the formation of etch pits and high substrate steps as well as related bilayer domains. The annealing process at 1900 °C was performed in argon at atmospheric pressure with a graphite-lined resistive-element furnace. After growth, EG was inspected with confocal laser scanning and optical microscopy to rapidly identify successful growths over large areas.³¹

2.2. EG Functionalization with Cr(CO)₃

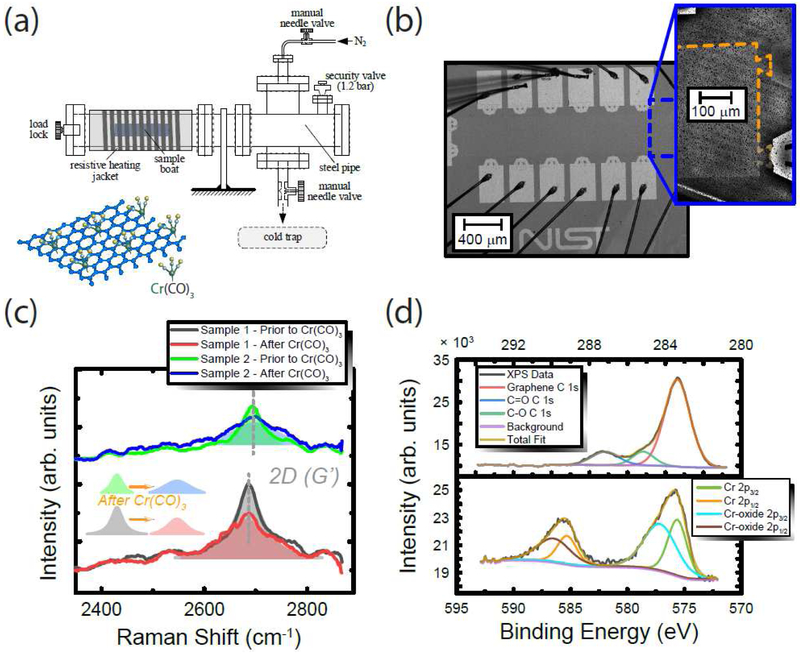
The concept of functionalizing EG with Cr(CO)₃ was motivated, in part, by pursuits to alter the electronic structure of graphene without drastically modifying the in-plane transport properties, and to date, several groups use different forms of graphene to study the mechanisms behind hexahapto functionalization.^32–37 Covalent functionalization by this method does not fully passivate the EG surface, but greatly reduces the level of electron doping in EG devices and helps to limit the long-term drift in carrier density levels. For our method, which follows closely that of Ref. 35, the completed EG device was placed in a phosphor-bronze (Ph-Br) boat and loaded into a small homemade vacuum furnace shown in Figure 1 (a). The chamber was then purged with nitrogen gas and heated slightly above 130 °C for 2 h while keeping the load lock slightly open to remove any lingering adsorbates on the surface of the EG device. After placing approximately 100 mg of crystalline Cr(CO)₆ (chromium hexacarbonyl) in a separate section of the Ph-Br sample boat, the system was closed, and nitrogen flow was stopped. The furnace temperature was then raised to 130 °C, using the optimized conditions set forth by Ref. 36. The Cr(CO)₆ sublimates and reacts with the surface of EG, resulting in the ring-centered Cr(CO)₃ functionalization. An illustration of this mechanism is provided in Figure 1 (a), as well as an optical image of one of the devices in Figure 1 (b). The sample space was then evacuated using a liquid nitrogen cold trap for about 30 minutes before the chamber was cooled down and opened. Out of seven fabricated devices used in this study, six were functionalized using the vacuum furnace method.

Figure 1.

(a) Drawing of the furnace for functionalization processes and rendering of the graphene crystal structure functionalized with Cr(CO)₃. (b) An image of one device, taken at 5 × and 20 × (inset) magnification with a confocal laser scanning microscope, after functionalization. The inset uses a fading orange dashed line to mark the EG edge. Black dots appear on the surface which are clusters of CrO₃, as described by XPS measurements. (c) Raman spectra for two devices, taken both before (green and black curves and areas) and after (blue and red curves and areas) functionalization. (d) XPS spectra for the surface presence of carbon (C 1s) and chromium (Cr 2p) in the top and bottom panel, respectively.

3. SAMPLE CHARACTERIZATION

3.1. Raman Spectroscopy

Raman spectroscopy was utilized to monitor the behavior of the 2D (G’) peak of the EG before and after the functionalization process. Spectra were collected with a Renishaw InVia micro-Raman spectrometer^{[see notes]} using a 633 nm wavelength excitation laser source and a backscattering configuration. The spot size was about 1 μm, the acquisition times were 300 s, the laser power was 1.7 mW power, and the optical path included a 50 × objective and 1200 mm⁻¹ grating. Rectangular Raman maps were collected with step sizes of 20 μm in a 5 by 3 raster-style grid. The presence of Cr(CO)₃ on the EG surface yielded a modified 2D (G’) peak with a smaller intensity, redshifted position, and larger width. The average changes in intensity, position, and width for the case before and after functionalization corresponded to a factor of 0.68 ± 0.05, a redshift of 4 cm⁻¹ ± 0.5 cm⁻¹, and a broadening of 51.3 cm⁻¹ ± 10.5 cm⁻¹, as shown in Figure 1 (c) using two examples (all uncertainties represent 1σ deviations). The effects have been observed with other amorphous materials deposited on EG.²² Only the 2D (G’) peak was used to assess the changes of the EG surface due to the overwhelmingly large SiC response in the G peak region.

3.2. X-Ray Photoelectron Spectroscopy

X-ray photoelectron spectroscopy (XPS) measurements on functionalized EG devices were performed in a commercial instrument equipped with a monochromatic Al Kα excitation photon source and a hemispherical electron analyzer. All XPS measurements were performed at a base pressure of 2.7×10⁻⁷ Pa or less, electron take-off angle of 0° with respect to the surface normal, and an energy resolution of 0.1 eV. The spectra in Figure 1 (d) show the fittings done for the spectral regions relevant to C 1s in the top panel and Cr 2p in the bottom panel. For binding energies near the carbon region, EG and SiC show contributions of carbon around 283 eV, C-O at 285 eV, and C=O at 287 eV. Analyzing the Cr 2p peaks required the fitting to include chromium oxide compounds. The Cr 2p_3/2 peak can be deconvoluted into two peaks at binding energies of 576 eV and 577 eV, assigned to graphene bonded Cr(CO)₃ and CrO₃, respectively. Though the observed components of the functionalization process are expected and reported in the literature, their relative intensities were much higher compared to adjacent atoms like carbon.^{32–34,36,38–39} This observation is explained and resolved in the Supplementary Data.

4. RESULTS AND DISCUSSION

4.1. Gateless and Reversible Tuning of the Carrier Density

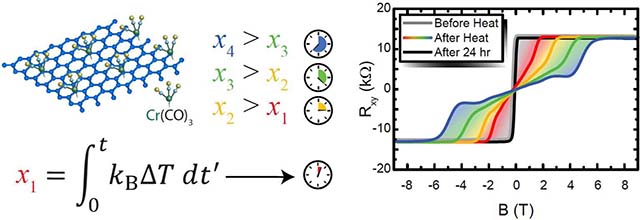
Six functionalized devices and one control device were tested for carrier density stability. By annealing the device at a fixed temperature for a prolonged time in vacuum and within the cryogenic measuring system, ranging from 5 min to 90 min, the carrier density becomes more n-type. The integrated heat exposure (IHE) is a figure of merit used to quantify the applied changes to the device caused by annealing:

$$IHE=\underset{0}{\overset{t}{\int }}{k}_{\text{B}}\left(T_{\text{ applied }}-T_{\text{RT}}\right)d{t}^{\prime }$$ (1)

T_RT is taken to be 300 K, k_B is the Boltzmann constant, and the integral is evaluated over time in seconds. Repeatable annealing was achieved using proportional–integral–derivative (PID) controllers that require some time to reach temperatures as high as 360 K, and so the effects of annealing between room temperature and the desired temperature must be accounted for. While annealing, only the longitudinal resistivity, a quantity that is correlated with the carrier density, was monitored. At room temperature while in vacuum or inert gases such as helium, the longitudinal resistivity shifted by less than 100 Ω overnight, compared to the typical value of up to 10 kΩ, (see Supplementary Data), making it a negligible shift compared with that above room temperature. After annealing, the carrier density and mobility were derived from cryogenic transport measurements in a 9 T superconducting magnet system.

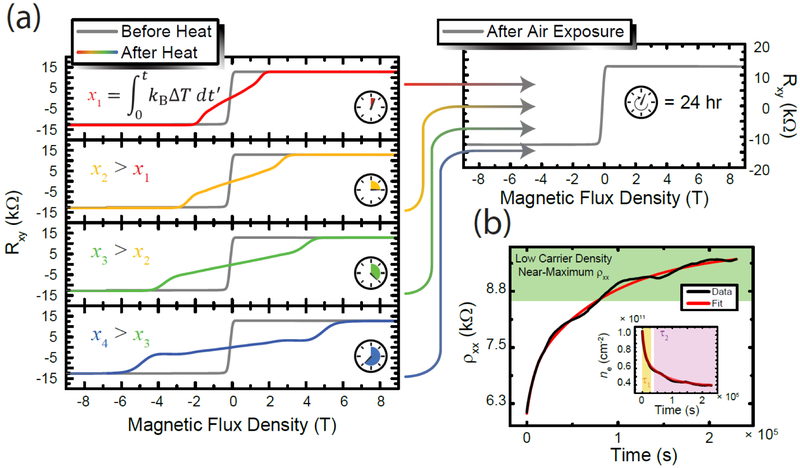
To evaluate a device’s carrier density, one can use the relation $n_{\text{e}}=\frac{1}{e\left(\frac{d{R}_{xy}}{dB}\right)}$, where n_e is the carrier density, e is the elementary charge, B is the magnetic flux density, and R_xy is the Hall resistance, using SI units for all quantities. As shown in the gray curves in Figure 2 (a), before the device was annealed, the Hall resistance data indicated low carrier densities, on the order of 10¹⁰ cm⁻². The carrier density increased as a consequence of annealing at a temperature between 300 K and 360 K for varying periods of time, resulting in an IHE (or x_i as shown abstractly in each panel) on the order of 10⁻¹⁸ J·s. The device was able to retain this carrier density in vacuum or helium at 300 K, before its exposure to air. Once the device was in air, the carrier density returned to its low value as before within roughly 24 hr. During this process, the longitudinal resistivity was monitored with time, and is plotted in Figure 2 (b). Two exponential decay terms were used to describe the device’s asymptotic approach to 15.5 kΩ for reasons that will be explained next. The corresponding time constants, τ₁ and τ₂, were 7600 s and 6.97 × 10⁴ s, respectively.

Figure 2.

(a) The Hall resistance for some devices are shown at 1.6 K, with all gray curves representing data after the device has been left to stabilize in air for 24 h or more, before temperatures above 300 K were applied. Each of the four panels depicts a different measurement where the device was first allowed to chemically equilibrate with air, followed by annealing in vacuum. The total IHE increases with each panel. In all cases, when the device is left in air for a period of at least one day, the device’s carrier density returns to a value on the order of 10¹⁰ cm⁻². (b) When the device is warmed up to room temperature and stored in air, the longitudinal resistivity shifts and asymptotically reaches a maximum over approximately 70 hr, resulting in a Fermi level of EG that is close to the Dirac point. Two exponential decays comprise this behavior, as seen in the inset, and are then used to fit the data.

The physical interpretation of this behavior can best be described by the Langmuir adsorption model for competing species.⁴⁰ To convert the longitudinal resistivity in Figure 2 (b) to a corresponding device carrier density in the inset, the two quantities’ relationship was determined for each device and averaged, as shown in Figure 3. Since the devices were presumed to have a significantly lower population of physical adsorbates (but not of chemically bonded Cr(CO)₃) due to prolonged annealing, the gas species to which the devices presumably were exposed included atmospheric dopants, namely N₂ (78.1 %), O₂ (20.9 %), and Ar (0.93 %) as well as water vapor. Other constituents are several orders of magnitude lower in concentration. Argon and nitrogen were neglected due to weak interactions with graphene compared to other constituents.^41–43 This leaves O₂, but H₂O must also be added in the appropriate amount. At 25 °C and 35 % to 40 % relative humidity, the expected percentage contribution of water vapor to the ambient environment, in terms of mass, is between 0.8 % and 0.9 %. The time-dependent function for the occupancy of one of two competing gaseous species (in this case, oxygen) is:⁴³

$$\frac{d{\theta }_{O_2}}{dt}=k_{O_2,A}{p}_{O_2}\left(1-{\theta }_{O_2}(t)-{\theta }_{H_{2}O}(t)\right)-k_{O_2,D}{\theta }_{O_2}(t)$$ (2)

${\theta }_{O_2}(t)$ and ${\theta }_{H_{2}O}(t)$ are the fractional occupancies of oxygen and water on EG’s available surface sites. The quantities $k_{o_2}$ and $p_{o_2}$ are the rate constants (A for adsorption and D for desorption) and unitless ratio of oxygen’s partial pressure to the total pressure. For the differential equation involving ${\theta }_{H_{2}O}(t)$, the two molecule subscripts need to be swapped. From these coupled first-order ordinary differential equations, one can determine both the final occupancy percentage for each species at equilibrium as well as the form taken by ${\theta }_{gas}(t)$, which includes two exponential decay terms. The final predicted occupancies of oxygen and water are approximately 90 % and 10 %, respectively. More mathematical details are provided in the Supplementary Data.

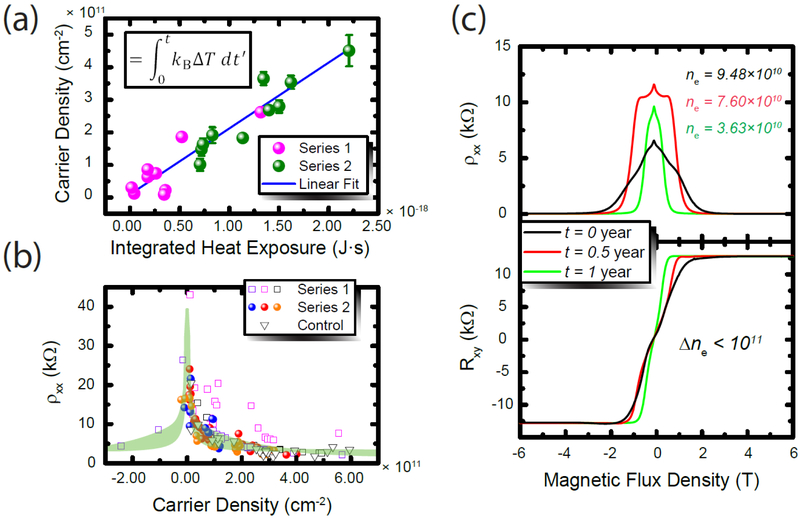
Figure 3.

(a) The correlation between integrated heat exposure and the subsequently-measured carrier density at 1.6 K is shown, with different color data points representing different packages onto which devices were mounted, with Series 1 (pink) and 2 (green) corresponding to the 12-pin and 32-pin packages, respectively. Error bars represent 1σ uncertainties of the average of multiple measurable regions on the device. (b) The relationship between carrier density and longitudinal resistivity, both measured at 1.6 K. (c) The stability of the carrier density is demonstrated to be less than 10¹¹ cm⁻² for the same device exposed to air over the course of one year. This is an indication that Cr(CO)₃ has remained on the EG surface and could be a suitable material for metrological applications.

When the carrier density is fit to the two decay terms from the Langmuir model, the time constants listed earlier provide an optimized reduced chi-squared. Previously reported work indicates that adsorption of oxygen and water on graphene takes place on a similar order of magnitude,^44–48 with oxygen adsorption taking place at slightly slower times at room temperature, assuming that the adsorption follows an Arrhenius behavior. A more detailed analysis of the time-dependency of water adsorption revealed a ${\tau }_{H_{2}O}$. of about 130 min,⁴⁴ which agrees quite well with our first time constant. The second constant requires more careful treatment to justify. With both species of gases occupying roughly equal areas for times below 2 hr, water must undergo significant desorption to accommodate for the equilibrium occupancies. A different study on EG measured a time constant on the same order of magnitude when the device was exposed to room temperature air.⁴⁹ We can make an estimation based on the measured water desorption energy of 360 meV,⁴⁸ and by use of the formula $k_A=v\exp \left[\frac{-E_{\text{ads}}}{k_{\text{B}}T}\right]$, where E_ads is the adsorption energy per molecule, v is an attempt frequency (in this case, the attempt frequency is the vibrational frequency of the molecule, usually approximated as 10¹³ s⁻¹), k_B is the Boltzmann constant, and T is temperature (K), the estimated time constant is on the order of 10⁶ s, which is about 15 times higher than our fit value. Inaccuracies can arise from two factors: (1) the uncertainty of the desorption energy on EG, which can contribute an order-of-magnitude change to the time constant, and (2) the significant increase of hydrophobicity found in EG versus other forms of graphene, which would cause desorption to occur on faster time scales.⁴⁷

4.2. Quantifying the IHE and Determining Long-Term Stability of the Carrier Density

The amount of IHE (shown as x_i in Figure 2) was quantified in Equation 1 and used to shift the carrier density by a desired amount. This correlation is shown in Figure 3 (a). The two data point colors indicate two different types of devices since some devices were older by a year compared with the newer devices. The data in pink come from devices mounted on a 12-pin package, whereas the data in green were acquired with devices mounted on a 32-pin package and allowed for more regions of the millimeter-scale EG to be tested. The error bars correspond to the uncertainties generated by the variation across the device, only present in the 32-pin package since the 12-pin package was only used to monitor one region’s carrier density. There is a clear linear trend within the order of magnitude of carrier density that is most suitable for resistance metrology. Figure 3 (b), as described earlier, is a plot of the relationship between the longitudinal resistivity and carrier density, both measured at 1.6 K using the length of the device as 640 μm and the width as 400 μm for the conversion from a measured resistance. From this plot, we are also able to determine the mobilities of the device regions which span two orders of magnitude, from 10⁴ cm²V⁻¹s⁻¹ to 10⁵ cm²V⁻¹s⁻¹.

Now that the tunability and reversibility of functionalized EG have been explored, the issue of long term stability remains. Figure 3 (c) shows an example device stored in air over the course of one year and exhibits stability such that shifts are less than 10¹¹ cm⁻². Despite the appearance of the Hall plateau as flat at this low carrier density, precision measurements suggest that the plateau is not quantized to within parts in 10⁸. Thus, some additional electrons are needed, but with this level of stability in air coupled with the linear relationship between IHE and carrier density, we can develop resistance standards that have a shelf life longer than one year.

4.3. Tuning EG Devices for Metrological Applications

With the knowledge that devices exposed to air retain a stable, but low, carrier density (less than 10¹¹ cm⁻²), and the method to apply a specific amount integrated heat, we are now able to tune devices to a carrier density which enables metrological access to the quantum Hall effect.¹¹ Device quantization was verified by measuring the longitudinal resistivity ρ_xx =V_xx/I_SD ∗ w/l where V_xx is the voltage drop across the potential contacts, I_SD is the source/drain current and w and l are the width of the Hall bar and the distance between the potential contacts, respectively. If ρ_xx becomes negligibly small, the Hall resistance R_H becomes quantized, for example, at the v = 2 plateau with R_H = V_xy/I_SD = R_k/2, where R_k is the von Klitzing constant. Thus, clear indication of a breakdown of resistance quantization can be identified through changes in the resistivity that depend on the magnetic flux density, temperature, and current.⁵⁰

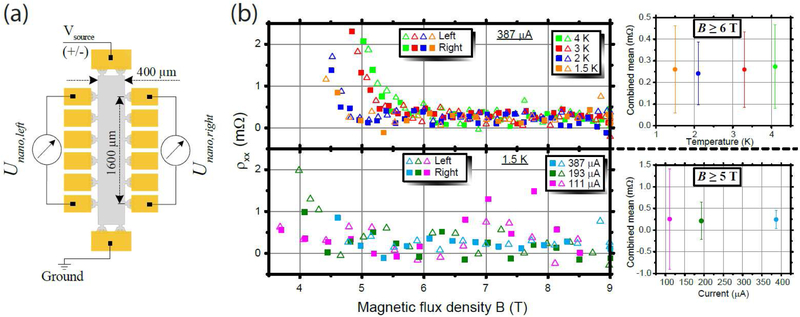
Figure 4 shows resistivity measurements of an EG device of dimensions 1.6 mm × 0.4 mm (Fig. 4 (a)) that were collected using a nanovoltmeter and a ramping voltage source that are both normally used in a two-terminal cryogenic current comparator bridge for high resistance measurements.⁵¹ The voltage source was operated at voltages of ±0.5 V, ±1.1 V and ±5 V, allowing for currents up to about 387 μA in the v = 2 quantum Hall regime. Increasing the temperature from 1.5 K to 4 K at a high current of 387 μA had no measurable impact on the longitudinal resistivity at magnetic flux densities greater than 6 T (Fig. 4 (b), upper panels) and reducing the current only increased measurement noise (Fig. 4 (b), lower panels). In all measurements, an offset of about ρ_xx = 0.25 mΩ (about 10⁻⁸ R_K) was observed, likely to be the result of circuit leakage or nanovoltmeter input leakage in the measurement, since similar offsets were also observed using many functionalized and untreated samples. However, since there is no temperature or current dependent behavior over a wide range of magnetic flux densities, in agreement with the guidelines for reliable dc measurements of the QHR, we expect the devices to be well quantized despite the small offset.

Figure 4.

Resistivity measurements in the QHE regime at the low potential side of the Hall bar. (a) The measurement configuration of the graphene QHR device (1600 μm x 400 μm) for the determination of the resistivity along the right and the left side of the device with polarity reversal. (b) The vanishing of the resistivity on both sides of the Hall bar at high fields indicates resistance quantization at a current of 387 μA and temperatures up to 4 K (upper diagram). Increasing the current from 111 μA to 387 μA at 1.5 K (lower diagram) results in reduced noise but is not corelated with an increase in the resistivity. Also shown are the scatterplots of the corresponding resistivity measurements for increasing temperatures (upper) and increasing currents (lower) summarize the results by taking the mean value of the left and the right side of the Hall bar for B ≥ 6 T and B ≥ 5 T. Error bars represent 1σ uncertainties of the average of all color-coded measurements above the indicated magnetic flux density.

5. CONCLUSION

Chemically functionalized EG has been shown to maintain a low and stable carrier density for at least one year, allowing it to be a promising candidate for the development of QHR standards with a long shelf life. The major difficulty of stabilizing the carrier density under ambient conditions has been solved with Cr(CO)₃ to the point where devices retain metrological usefulness, even after long-term storage and many temperature cycles between 1.5 K to 360 K, by a reversible and easily controllable tuning process. Through precision measurements, we have shown that hexahapto functionalization is suitable for exceptionally robust QHR standards operating at 4 K and 7 T, with applied measurement voltages up to 5 V. Overall, these results show progress toward EG sensors and electronic devices that can achieve long useful lifetimes and predictable characteristics in ambient conditions.