Altered dynamic electroencephalography connectome phase-space features of emotion regulation in social anxiety

Abstract

Emotion regulation deficits are commonly observed in social anxiety disorder (SAD). We used manifold-learning to learn the phase-space connectome manifold of EEG brain dynamics in twenty SAD participants and twenty healthy controls. The purpose of the present study was to utilize manifold-learning to understand EEG brain dynamics associated with emotion regulation processes. Our emotion regulation task (ERT) contains three conditions: Neutral, Maintain and Reappraise. For all conditions and subjects, EEG connectivity data was converted into series of temporally-consecutive connectomes and aggregated to yield this phase-space manifold. As manifold geodesic distances encode intrinsic geometry, we visualized this space using its geodesic-informed minimum spanning tree and compared neurophysiological dynamics across conditions and groups using the corresponding trajectory length. Results showed that SAD participants had significantly longer trajectory lengths during Neutral and Maintain. Further, trajectory lengths during Reappraise were significantly associated with the habitual use of reappraisal strategies, while Maintain trajectory lengths were significantly associated with the negative affective state during Maintain. In sum, an unsupervised connectome manifold-learning approach can reveal emotion regulation associated phase-space features of brain dynamics.

1. Introduction

According to the National Institute of Mental Health, the lifetime prevalence of Social Anxiety Disorder (SAD) among adults in the United States is 12.1% (Kessler et al., 2005). Disruption in regulating emotions has been observed among patients with SAD (Amstadter, 2008) and individual differences in emotion regulation may relate to vulnerability to anxiety and mood disorders (Campbell-Sills and Barlow, 2007). While a few published studies have reported localized connectivity abnormalities in SAD (Etkin et al., 2010; Sladky et al., 2013) during emotion regulation, a systems-level investigation into overall brain network dynamics as measured using electroencephalography (EEG) has not been well explored. Here we utilize a novel manifold learning approach that reconstructs the phase-space of brain network dynamics while patients with SAD and healthy controls perform an emotion regulation task (ERT).

To ensure we have a sufficient connectomes sample for our phase-space construction procedure, we employed EEG for its high temporal resolution and selected a well-validated emotion regulation task (Fitzgerald et al., 2016; Parvaz et al., 2012). Further, informed by our own finding that in healthy individuals, ERT is sensitive to theta activity (4–7Hz) (Xing et al., 2016) as well as findings from other groups suggesting that theta connectivity is related to positive emotional states (Aftanas and Golocheikine, 2001) and cognitive processes (Cavanagh and Frank, 2014; Gruzelier, 2009), we tested our phase-space manifold learning approach on dynamic theta EEG connectomics. The theta connectome data was obtained using the same recording system in an overlapping sample previously reported in (Xing et al., 2017), where we demonstrated that SAD patients had higher overall theta connectivity, averaged over time as well as across all EEG channels, at rest.

The concept of a phase-space, as originally introduced in mathematics and physics, is a multi-dimensional space in which all states of a dynamic system were represented using a combination of a position vector and the corresponding momentum. In the field of quantitative EEG, the closely related term “state-space” has been used variably dependent on the specific applications. For example, it has been used to refer to an auto-regression based s-estimator applied to EEG time series to identify the disconnection topography in source localized schizophrenia brain networks (Jalili et al., 2007), as well as to evaluate EEG signal synchronization (Carmeli et al., 2005) and to estimate the cortical connectivity of healthy brains during movie watching (Cheung et al., 2010). Another related approach is the Taken’s embedding that seeks to find a proper embedding dimension of a dynamical system using a time-delayed construction. This approach has been used to reconstruct a strange attractor of a system in an optimal embedding dimension by examining the behavior of nearest neighbors (Jeong et al., 1998b). Note that the input of the Taken’s embedding is the time series of a scalar quantity and the output is the embedding dimension or another downstream scalar quantity (e.g., the Lyapunov exponent). While a few EEG resting state applications have shown that such embeddings may be sensitive in capturing the temporal dynamic changes in certain disorders (Jeong et al., 1998b) (Jeong et al., 1998a; Stam, 2005), the Taken’s embedding nevertheless is likely only applicable during the resting-state and is computed at each sensor location, yielding a scalar quantity for each sensor instead of a systems-level connectome-type analysis. (Stam et al., 1996). Furthermore, the concept of state space analysis has been used to construct a log likelihood-based EEG time series mapping to yield a “sleep manifold” (Hight et al., 2014).

However, in these studies, recordings from electrodes were mapped onto a multi-dimensional space that was indexed by anatomical regions-of-interest, which are placed with respect to anatomy and thus not with respect to the intrinsic features of brain dynamics as captured by the dynamic EEG connectome graphs. To explore the complex dynamics of human brain in the connectome-level space as opposed to the sensor-based space, our novel phase-space approach constructs a manifold where each position p is instead a dynamic EEG connectome (i.e., any position p in this manifold corresponds to a connectome graph which by itself is a frame or “snapshot” of a dynamic connectome time series that is constantly evolving as a trajectory or orbit in this space). Mathematically a connectome graph is coded as an N by N matrix where N is the number of sensors and each element in the matrix encodes the dynamic EEG relationship between the tracings of the two corresponding sensors.

In order to construct connectome-level phase-space manifold, we leveraged dissimilarity-based graph embedding (Bunke and Riesen, 2011) that allows us to embed each connectome graph “snapshot” in a high-dimensional space. While in our case there is no clear equivalent to the concept of “momentum” (defined as the product of mass and velocity), we nevertheless could estimate the “velocity” of a dynamic EEG connectome time series at any given time point, if this time series has been preprocessed in such a way that consecutive connectome frames are separated by a fixed known time interval and that a very large amount of connectome “snapshots” are available, thus allowing us to estimate the manifold “geodesic” (i.e., the shortest distance on the manifold) between any two connectome graphs.

For the rest of the paper we used this unsupervised connectome-level manifold learning to construct the global geometry of EEG dynamics related to emotion processing, and to explore phase-space features during task performance between healthy controls and a group of participants with social anxiety disorder. As a person’s temporal EEG connectome while performing a task now corresponds to a phase-space “trajectory”, its dynamics can be precisely characterized using intrinsic geometric features of this phase-space. In previous applications, trajectory of the phase space, constructed with temporal power oscillations, showed promising results in predicting emotional state during movie-watching (Nie et al., 2011; Wang et al., 2014). We hypothesized that SAD networks would exhibit abnormal features in a phase space comprising connectomes of all study participants and all task conditions. Furthermore, we hypothesized that phase-space features such as trajectory length per second (i.e., speed) would be associated with anxiety level, self-reported reappraisal tendencies, and ERT-related affective state.

2. Materials and Methods

2.1. Participants

All participants provided written informed consent as approved by the local Institutional Review Board at the University of Illinois at Chicago. Diagnosis was based on the Structured Clinical Interview for DSM-IV (‘SCID-IV’ (First et al., 1995) and the clinician-administered Liebowitz Social Anxiety Scale (“LSAS” (Liebowitz, 1987) and Hamilton Anxiety Rating Scale (Hamilton, 1959) determined symptom severity and general anxiety level, respectively. The Emotion Regulation Questionnaire (‘ERQ’; (Gross and John, 2003)) assessed subjective habitual use of reappraisal. Participants were between 18 and 55 years of age and free of major medical or neurologic illness as confirmed by a board-certified physician. SAD was required to be the primary diagnosis; however, comorbidity was permitted. All participants were free of psychotropic medications and none were engaged in psychotherapy. Healthy control (HC) participants were required to not have an Axis I disorder. Exclusion criteria for all participants were current substance abuse or dependence (within 6 months of study) or history of major psychiatric illness (e.g., bipolar disorder, psychotic disorder, pervasive developmental disorder). Participants were compensated for their time.

2.2. EEG data acquisition

EEG data were collected from 20 participants with SAD and 20 HC using the Biosemi system (Biosemi, Amsterdam, Netherlands) with an elastic cap with 34 recording channels. Each participant underwent ERT (Gross, 1998). Participants viewed pictures from a standardized set (Lang et al., 1997) during continuous EEG recording. Participants were asked to maintain their emotional state when viewing negative images (‘Maintain’), use a cognitive strategy to reduce negative affect when viewing negative images (‘Reappraise’), or view neutral pictures (i.e., ‘Neutral’). Negative and neutral images were displayed on the screen for seven seconds in a random order. EEG data were processed according to the method described in detail in (Xing et al., 2017). Additionally, participants also performed the same ERT during fMRI scans, during which subjective negative affect ratings were collected. At the end of each trial, participants were asked to rate how negative they feel on a five-point rating scale (1= not negative at all, 5 = extremely negative). Greater Maintain and Reappraise affective ratings in generalized anxiety disorder patients have been reported using the same ERT task (Fitzgerald et al., 2017)

2.3. EEG connectome

All EEG data were preprocessed using Brain Vision Analyzer (Brain Products, Gilching Germany) by first segmenting task trials into seven-second segments. A sliding window with a width of 0.5 seconds and a step size of 0.05 seconds was applied to create the dynamic data. The first and last five time points were discarded, resulting in 130-time points per session. (The same framework was performed on a down sampled data with less overlapping (20% overlaps). Main findings of two temporal sampling are consistent. Results of the down sampled data are included in Appendix C.) As functional communications between two brain regions result in synchronized or phase-coupled EEG readouts, in this study we used the weighted phase lag index (WPLI)(Cohen, 2014; Vinck et al., 2011), computed between the time series of two channels to form EEG connectomes (each of which is a symmetric 34-by-34 matrix). This connectivity estimation approach has shown higher sensitivity and reduced the volume conduction contaminations in detecting complex and variable activity patterns (Lau et al., 2012). Mathematically, WPLI is defined as:

$$WPL{I}_{xy}=\frac{n^{-1}{\sum }_{t=1}^n\left|imag\left(S_{xyt}\right)\right|sgn\left(imag\left(S_{xyt}\right)\right)}{n^{-1}{\sum }_{t=1}^n\left|imag\left(S_{xyt}\right)\right|}$$ (Eq. 1)

Where imag(S_xyt) indicate the cross-spectral density at time t in the complex plane xy (t is discretized and ranges from 1 to n), and sgn is the sign function (−1; +1 or 0).

The connectivity matrices were generated with the MATLAB toolbox Fieldtrip (Donders Centre for Cognitive Neuroimaging, Nijmegen, Netherlands). The final output time-dependent 34-by-34 EEG connectome for an individual task of each subject is arranged as [34*34]*50*130 ([channel*channel]*frequency*time). Guided by our recently published paper, we primarily focused on the phase-space informed by the theta frequency band (4–7 Hz) EEG connectomes; thus, for each time point, an averaged connectome from 4–7 Hz was taken to represent the theta connectome.

2.4. Learning the phase-space manifold of EEG dynamics via non-linear dimensionality reduction

Our approach to EEG-based connectomics was to reframe it as a phase-space reconstruction problem. Due to its high temporal resolution, each connectivity matrix graph samples a distinct state of this dynamical system, with the time-dependent dynamic EEG connectivity for a particular participant during a particular ERT condition evolving as a trajectory in this abstract space. In order to yield sufficient data to learn the space comprising states of ‘on-line’ emotion regulation ability, we combined connectomes from all 40 participants (i.e., collapsing across SAD and HC groups) at all time points, as collectively they sample this phase-space “connectome manifold of interest”. As each participant contributed 3 dynamic connectomes (3 ERT task conditions) each of which having 130 time point, thus the total number of samples we have for this connectome manifold is thus 130 * 40 * 3 =15600. To learn any non-linearity, we employed manifold learning via nonlinear dimensionality reduction.

In what follows, we will describe in detail the three computational steps (and one optional step) involved in our novel approach: Step I: graph dissimilarity embedding, Step II: recovery of phase-space nonlinearity via geodesic computation, Step III: phase-space visualization via geodesic-informed minimum spanning tree, and the (optional) prototype graph selection. (Fig. 1)

Fig. 1: Constructing the dynamic phase-space and visualizing the minimum spanning tree.

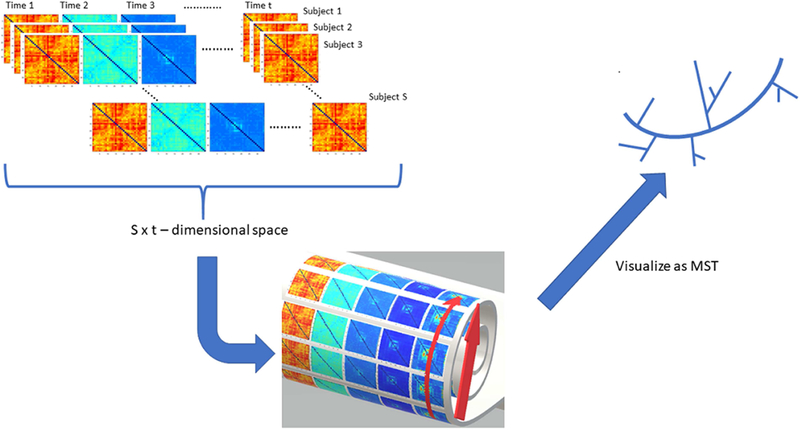
This figure illustrates the basic idea of our phase-space manifold reconstruction framework. Dynamic connectomes are generated from EEG data using a sliding window approach. Each connectome (from all subjects and all time points), mathematically defined as a 34 by 34 matrix, is mapped onto a point on a manifold that is embedded in a high dimensional space (here the manifold is depicted as a Swiss roll, a 2-dimensional structure that is rolled up and embedded in 3D). +-Thus, the distance in the high dimensional space (straight arrow) is not the manifold geodesic distance (curved arrow), which encodes the intrinsic geometric features of the manifold. This distance is used to create the neighborhood graph visualized as minimum

2.4.1. Step I: Graph dissimilarity embedding

Connectomes can be represented as a graph ℊ = (V, E, W). In EEG connectomes, the node set V corresponds to the recording channels, and the weights W of the edge set E in our case are informed by WPLI connectivity. Once the connectome graphs are computed, we used the graph dissimilarity space embedding (DSE) to first embed each connectome in a high-dimensional Euclidean space where each point corresponds to a connectome. As will be seen below, with DSE the dimensionality of this Euclidean space is in the same order as the number of total dynamic EEG connectomes across all subjects (20 HC, 20 SAD), ERT conditions (3 task senarios, neutral, maintain, reappraise), and time points (130 time points), which was (20+20)*3*130=15600.

The graph dissimilarity embedding procedure, first proposed by Bunk and Riesen in 2008(Bunke and Riesen, 2008) (Bunke and Riesen, 2011; Duin et al., 2010), is summarized as follows. Given a graph set G (the set of all possible graphs under consideration) and n “prototype” graph observations ℊ_i ∈ G (i = 1, 2, 3, …n) using which we will embed every element in this graph set (see prototype graph selections in the optional step below) and d a distance metric that can be computed between two graphs d: ℊ × ℊ → [0, ∞) then any graph X ∈ G can be represented using ${\phi }_n^G:G\to R^n$ defined as the n-dimensional vector:

$${\phi }_n^G\left(X\right)=\left(d\left(X,{ℊ}_1\right),\dots d\left(X,{ℊ}_n\right)\right)$$ (Eq. 2)

This way any graph set can be vectorized by a set of n real numbers corresponding to a point in an n-dimensional Euclidean space.

Given two connectome matrices, X and Y in G various choices of dissimilarity metric have been proposed (for a comprehensive review, see (Kessler et al., 2005; PW and Elzbieta, 2005)). A natural choice of d which we adopted here, is the Frobenius norm $d\left(X,Y\right)=\sqrt{{\sum }_{ij}{\left(X_{ij}-Y_{ij}\right)}^2}$ where the subscript indicates the (i, j)-th element of a matrix. Thus, we can compute a straight line Euclidean distance between X and Y in the embedding space as follows:

$$\left|{\phi }_n^G\left(X\right)-{\phi }_n^G\left(Y\right)\right|=\sqrt{{\sum }_{k=1}^n{\left(d\left(X,{ℊ}_k\right)-d\left(Y,g_k\right)\right)}^2}.$$ (Eq. 3)

By iterating through all combinations of X and Y in G, thus forming a matrix that encodes pairwise Euclidean distance between any two EEG connectomes, we proceed to the next step where we reconstruct phase-space manifold properties via geodesic computation, as non-linearity information is encoded using the geodesic distance between any two connectome graphs (each of which is a 34 by 34 matrix).

2.4.2. Step II: Recovery of phase-space nonlinearity via geodesic computation

As elegantly illustrated by the Swiss roll example in the original isomap paper (Tenenbaum et al., 2000), straight line distances in the Euclidean space where a manifold is embedded is not the geodesic distance intrinsic to the manifold. (The non-linear relationship between direct Euclidean distance and geodesic distance of ERT phase space is presented in Fig. A2 of Appendix A) Thus, to preserve the non-linearity of the underlying phase-space, it is crucial to first reconstruct the local neighborhood around each point in this space to construct the manifold geodesic distance. This is because that the Euclidean distance matrix from Step I is computed based on d (which is used to define coordinates in the embedding space, and not intrinsic to the manifold) and thus will not properly inform geodesics (the shortest paths on the “manifold” which is an intrinsic property) except in local neighborhoods. Here the local neighborhood was constructed using the k-nearest neighbors (KNN) procedure (k=60, ~0.4% of total points, see supplementary material in Appendix A that compared our embedding results across a range of k), followed by computing the geodesic distances using the Dijkstra algorithm (Dijkstra, 1959). After Step II, phase-space manifold properties are now encoded using the corresponding geodesic distance matrix (GDM, size 15600 by 15600).

2.5. Minimum Spanning Tree

To visualize this high dimensional phase-space (Fig. 1), we exploited the geodesic-informed minimum spanning tree (MST) by adapting the TreeVis by Qiu and Plevritis (Lee et al., 2011; Qiu and Plevritis, 2013). Note that the phase-space is now represented by a symmetric geodesic distance matrix GDM, where each entry encodes the geodesic distance between any two connectomes; therefore we are able to visualize the phase-space as a network graph (essentially, a network of networks, in which each node is an EEG connectome).

Minimum spanning tree is an optimized graph representation of a network. It simplifies a complex graph by reducing the cycles and minimizing the total edge weight (Graham and Hell, 1985). MST is theoretically advantageous in that it is a sub-network that preserves most fundamental network properties (Tewarie et al., 2015), while simulations and brain network analyses have shown that MST is able to reflect the underlying topology of functional networks, regardless of the scale of edge weights (Stam et al., 2014; Tewarie et al., 2015) (Boersma et al., 2011). TreeVis orders the minimum spanning tree nodes and visualizes them sequentially as follows. TreeVis breaks the tree into chains of nodes. The longest chain is defined as the main chain. Chains that are directly connected to the main chain are defined as the side chains of the main chain. For complex tree structures, each side chain may also have its own lower level side chains. Tree nodes are arranged in an order such that nodes in the main chain come first, followed by nodes in the side chains of the main chain, and then the lower level side chains. The complete workflow of our manifold learning procedure is illustrated in Table 1 (Algorithm 1).

Algorithm 1:

Manifold Learning and visualization of EEG dynamics using graph dissimilarity embedding and geodesic-informed minimum spanning tree

Input: Graph set G, where $G=\left\{{ℊ}_1,{ℊ}_2,\dots {ℊ}_n\right\}$ and each ${ℊ}_i$ is a 34 by 34 EEG connectome

Output: Geodesic distance matrix GDM, where GDM $\in R^{n\times n}$

Minimum Spanning Tree MST of G

1. [Optional] Select Prototype graph set $G_{pro}\subseteq G,G_{pro}=\left\{g_{pro}^1,g_{pro}^2\dots ,g_{pro}^m\right\};m\le n$

2. Construct dissimilarity embedding using Eq. 2

3. for each $g_i,g_j$ in G

4. Construct Euclidean distance matrix $\left(\text{EDM}\right),EDM\in R^{n\times n}$ Euclidean distance between         ${\phi }_n^G\left(g_i\right)\hspace{0.17em}\text{and}\hspace{0.17em}{\phi }_n^G\left(g_j\right)$ is given in Eq. 3

5. end for

6. GDM← Apply Dijkstra algorithm and k nearest neighbors $\left(k=60\right)$ to EDM

7. return GDM

8. MST ← apply TreeV is to GDM to yield geodesic informed minimum spanning tree

9. plot MST

2.6. Optional Step: selection of the prototype graphs

In this section, let us briefly discuss how to determine prototype graphs. In our initial analyses, all the connectomes were used as prototypes (thus, the number of dimensions of the Euclidean space used for DGE is the same as the number of connectome graph matrices in the dataset, i.e., 15600) (Borzeshi et al., 2013; Brühl et al., 2014; Bunke and Riesen, 2011; Zhang et al., 2015). However, one can select a subset of graphs as more representative prototypes during the graph-embedding step (i.e., n, the number of the prototype graphs in Step I is now < 15600). Originally proposed in the context of graph embedding for classification (Nie et al., 2011), an appropriate choice of a class-discriminatory prototype set should provide adequate coverage of the whole graph domain while avoiding redundancies secondary to the inclusion of similar graphs (Borzeshi et al., 2013). In this way, one can obtain an efficient classifier with minimal degradation in classification accuracy and performance.

2.6.1. The spanning prototype selector and the center prototype selector

As two concrete examples, the spanning prototype selector(Bunke and Riesen, 2011) (SPS) was proposed such that each additional prototype selected is the graph that is the furthest away from already selected prototype graphs (with the first graph selected being the median graph, defined as the graph whose sum of geodesic distances to all other graphs is minimum); The center prototype selector (Bunke and Riesen, 2011) (CPS), on the other hand, selected the most central graphs as prototypes, which are recursively defined by the median graph from the remaining graph set.

Mathematically, the median graph median (G) ∈ G of a graph set G is the graph with the minimum sum of distances to all other graphs. In our case, after reconstructing the geodesic distance of the phase-space manifold, the median graph is informed by the GDM, where $\text{median}\hspace{0.17em}(G) ={\text{argmin}}_{g_i\in G}{\sum }_{\mathcal{g}{j}^{\in \hspace{0.17em}G}}GDM\left({\mathcal{g}}_i,{\mathcal{g}}_j\right).$

2.6.2. The modified center prototype selector

In this study, as our overarching goal is precise manifold learning informed by as many available connectome graphs as possible, we further explored the removal of connectomes that may be considered outliers (thus unlikely to be representative prototypes of the underlying manifold), which we call the modified CPS. Similar to CPS, a median graph was first defined as the center; then for all remaining graphs whose geodesic distance to this center are considered outliers by the Hampel identifier (Davies and Gather, 1993) as implemented in Matlab are removed as prototypes. In a data set of scalars X, where X = (x₁, …, x_N). Hampel identifier recognizes x as an outlier, if |x − median(X)| ≥ threshold ∗ MAD(X). The median absolute deviation (MAD) of X is defined as MAD(X) = median(|x₁ − median(X)|, …, |x_N − median(X)|), Here we used the default threshold in Matlab, which is set to 3. (For a detailed description of examples of threshold functions, see Davies & Gather, 1993.) With our data set, 640 graphs were removed from the graph set (14690 graphs remaining). To more fairly compare our modified CPS procedure to the standard SPS and CPS, using the latter two we selected two sets of prototypes with the same size as our modified CPS (14690). This framework is validated with the simulated multi-channel data. The correct manifold structure was recovered in noise free and noisy conditions. (See details of simulation study in Appendix B.)

2.6.3. The MST prototype selector

Last, informed by the MST construction we propose one additional approach to prototype selection which we termed the MST prototype selector. Here, connectome graphs making up the main chain of the MST are defined as the primary prototypes; then the prototype set can be expanded by including connectome graphs from the subsequent lower-level chains. Fig. 7 demonstrated levels of prototypes selected by MST selectors (up to second-level chains).

Fig. 7. MST-based prototype selection.

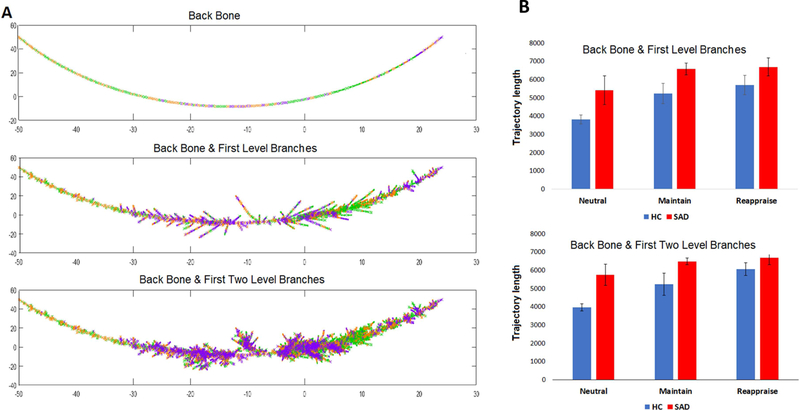
Levels of selected prototypes on the MST (A) and the prototype trajectory Length (B). The first prototype set includes 1956 connectomes from all backbone and all first level branches (middle figure in A); second prototype set includes 4712 connectomes from backbone, first level branches and second level branches (bottom panel in A).

2.7. Trajectory length

The trajectory length of a participant’s brain dynamics in a task condition was estimated by adding up the geodesic distances between consecutive time-dependent EEG connectomes in this phase-space. Let C_t=1, C_t=2, …, C_t=130 ∈ ℝ^34*34 denote the dynamic 130-time point EEG connectome time series of a specific task condition for an individual, then the corresponding trajectory length (L_trajectory) is defined as:

$$L_{trajectory}={\sum }_{t=1}^{130}GDM\left(C_{t+1},C_t\right)$$ (Eq. 4)

We used a repeated measures ANOVA to detect significant task effects, group effects, and task x group interactions for trajectory length in all 3 condition segments of the ERT. Two-tailed Pearson’s correlations were calculated to evaluate relationships between these lengths and symptom measures, affective state, and self-reported reappraisal tendencies.

3. Results

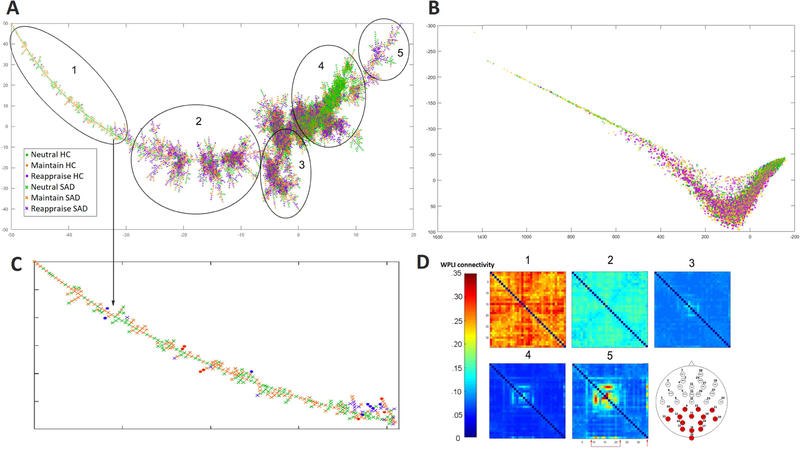
Clinical and demographic data in Table 2 demonstrate that there were no significant differences in age and gender distribution between groups. As expected, SAD participants had higher anxiety scores on the LSAS and HAM-A and they were less likely to use reappraisal as assessed with the ERQ. Fig. 2 A and Fig. 3 A visualize the phase-space manifold using its geodesic-based MST, which reveals highly complex nonlinear dynamics during emotion regulation (note, for example, the cluster comprising mostly neutral connectomes in section 4 in Fig. 2 A). In addition, we provided a two-dimensional isomap representation of the phase space (Fig. 2 B, enlarged 2D isomap in Fig. A1, Appendix A). Overall, no task or groups formed a distinct cluster (Fig. 3 B and Fig. 3 C). In general, the trajectory of a series of connectomes during any ERT condition (130 time-points) traverses along most of the main MST branch. Interestingly, careful inspection revealed that the “left end” of the main branch primarily comprises SAD connectomes during Neutral and Maintain (enlarged view in Fig. 2 C and bar graph in Fig. 3).

Table 2.

Demographic and Task Performance

	Social Anxiety Disorder (N=20)	Healthy Controls (N=20)
	Mean (SD)	Mean (SD)
Demographic
Age	26.80 (8.38)	26.95 (9.64)a
Education in years	15.85 (2.11)	15.70 (2.39)a
Gender (% male)	45%	40%a
Clinical
LSAS	77.30 (14.13)	17.15 (12.25)b
HAM-A	7.50 (4.69)	0.75 (1.21)b
ERQ reappraise	25.15 (5.52)	33.60 (7.05)b
Affective State
	(N=20)	(N=18)
Neutral Condition	1.24 (0.37)	1.13 (0.25)
Maintain Condition	3.10 (0.53)	2.75 (0.77)
Reappraise Condition	2.60 (0.88)	2.25 (0.76)

LSAS, Liebowitz Social Anxiety Scale; HAM-A: Hamilton Anxiety Rating Scale; Two healthy controls participants didn’t select the mood rating before the next session began, thus their performance ratings are not available.

^aThere is no gender (X²(2, N=40), p>0.05), age (two sample t-test, p>0.05) or years of education difference (two sample t-test, p>0.05) between healthy controls and social anxious patients.

^bHealthy controls were less socially anxious (LSAS) and less generally anxious (HAM-A) than SAD participants (two-sample t-test, p < 0.05). Healthy controls more commonly use reappraisal (ERQ reappraise) as a daily emotion regulation strategy (two-sample t-test, p<0.05).

Fig. 2: The reconstructed MST (A) and the corresponding 2D isomap representation (B) of the reconstructed phase-space manifold.

Visually, the “left” MST branch primarily comprises connectomes from SAD subjects while Neutral connectomes appear to form a distinct cluster (sections 1 and 4). Enlarged “left branch” view is in (C). Since each point corresponds to a connectome, we averaged within key sections along the main MST branch and visualized the respective average connectomes in (D). These representative average connectomes exhibit an ordered transition, with emerging connections among parietal and occipital channels (indicated with arrows in section 5 and red channels on the head map) as we move towards the “right branch”.) Two-dimensional isomap representation of the same manifold exhibits similar task and group distribution compared with MST (B).

Fig. 3: Composition of tasks (B) and groups (C) from “left” side to the “right” side of the MST.

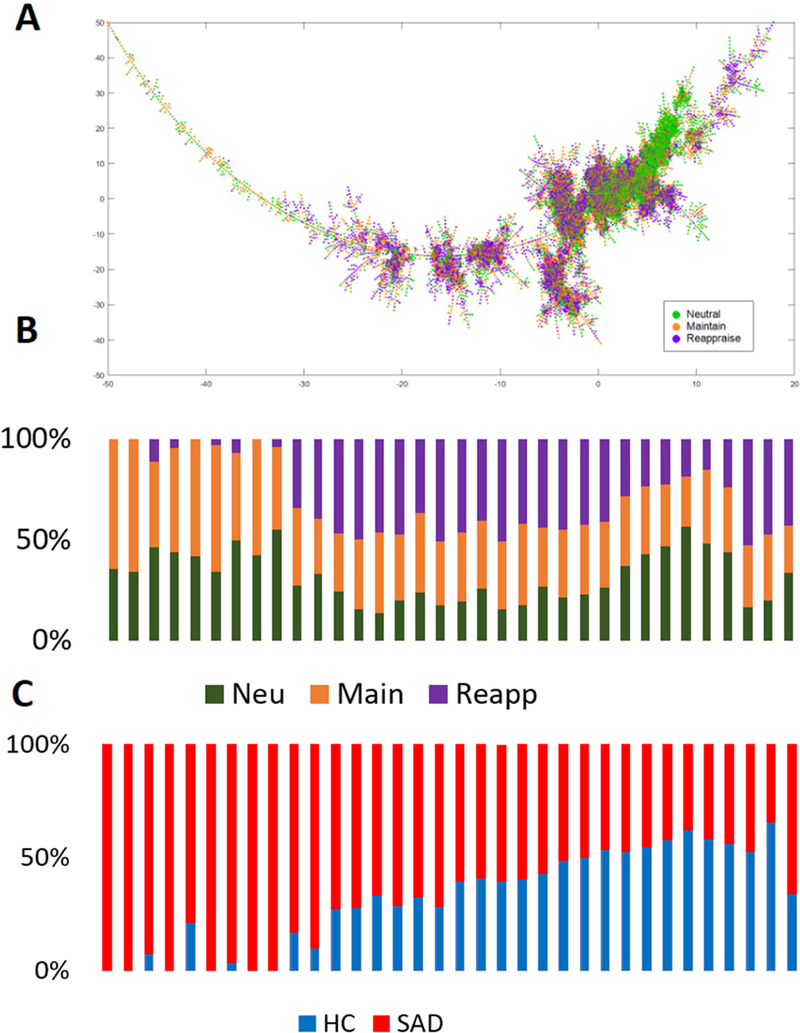
Most of the segment along the tree is occupied by multiple task conditions and groups, indicating that taskand subject-spaces are not completely separate from each other.

To investigate this further, since each point in the MST represents one connectome, we can define a “mean connectome” for different segments of the MST, by averaging element-wise over connectomes within any selected segment. As shown in Fig. 2 D, these mean connectomes along the MST exhibit distinctive patterns, informing the underlying patterns of EEG connectivity typical in this part of the phase-space. Overall, there is a decrease in global EEG connectivity from section 1 to 4, which then increases again from section 4 to 5, in particular over occipital and parietal channels (See Fig A3 in Appendix A for a further demonstration of sensor level connectivity patterns along the MST).

Relating MST findings to anxiety, we further note that participants with SAD had trajectories that more frequently traversed the “left end” of the main branch (Fig. 4 A, B). Repeated ANCOVA analyses were performed to explore the group and task effect of the area under the distribution curve. Indeed, the area under curve analyses for Fig. 4 B revealed a significant condition effect (p = 1.8 × 10–7), a significant group effect (p = .019), and trend level task x group effect (p = .051).

Fig. 4: Neutral connectomes marked by HAM-A scale on MST (A) and Frequency of connectomes to the left of the x-axis threshold (B).

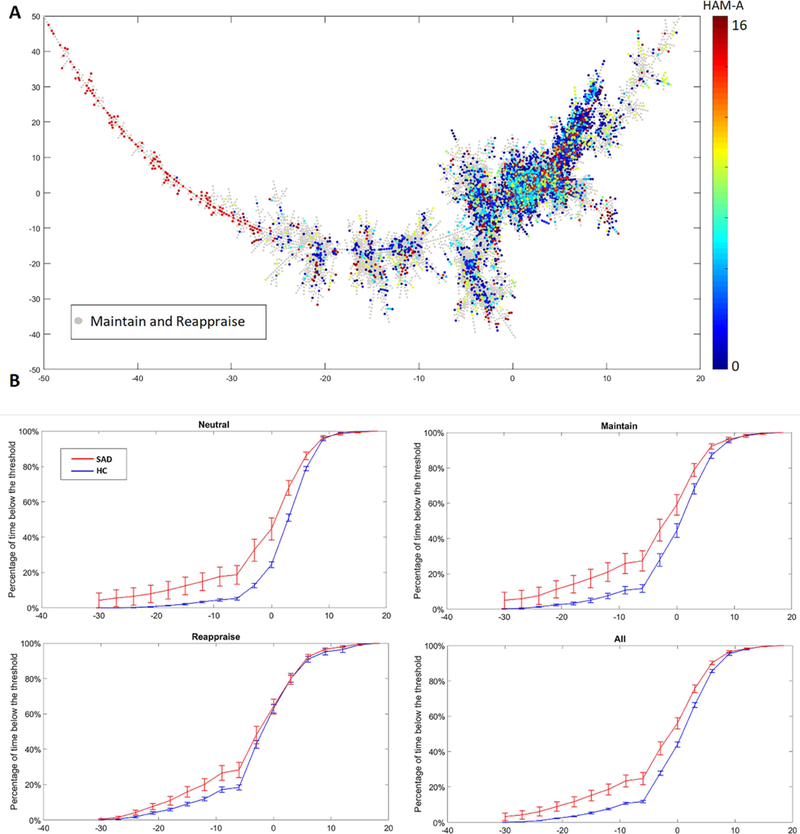
Phase-space trajectories from SAD participants are more likely to visit the “left side” of the MST. With a sliding threshold (x-axis), the frequencies of trajectories (y-axis) crossing to the left of the threshold are computed and compared between SAD participants and healthy controls (HC). Area under the curve analysis revealed a significant task effect (p = 1.8 × 10–7), a significant group effect (p = .019), and trend level task x group effect (p = .051).

Follow-up pairwise analysis for the main effect of condition showed Neutral was significantly different from Maintain (p = 7.7 × 10⁻⁷) and Reappraise (p = 3 × 10⁻⁶), but Maintain and Reappraise did not significant differ from each other (p = .14). Pairwise group differences were reported in Neutral (p = 0.019) and Maintain (p=0.012), such group difference was absent in Reappraise (p=0.112). Similarly, repeated measures ANOVA for trajectory length demonstrated a significant condition effect (p = 7.7 × 10⁻⁸), a significant group effect (p = .024), and a trend level task x group interaction (p = .058). (Fig. 5 A). Follow-up pairwise analysis for the main effect of condition showed Neutral differed from Maintain (p = 7 × 10⁻⁶ and Reappraise (p = 2 × 10⁻⁶) and Maintain was marginally different than Reappraise (p = .049). The main effect of the group showed Neutral and Maintain trajectory are significantly longer in SAD (Neutral: p = 0.018, Maintain: p = 0.043), while Reappraise trajectory length was similar between two groups (p=0.21). Similar analyses using theta power alone failed to yield any significant main effects of task or group, while a permutation analysis using trajectory length confirmed our significant main effect of task condition (Appendix D). Furthermore, ‘on-line’ Reappraise trajectory length was inversely correlated with the tendency to reappraise, as indexed with the ERQ (r=−0.64, p=0.002) (Fig. 5 B). Regarding emotional reactivity, higher negative affective state during the Maintain condition tended to have longer Maintain trajectories (r=0.381, p=0.022) (Fig 5 C). Trajectory lengths for Reappraise or Maintain did not correlate with measures of anxiety.

Fig. 5: Phase-space trajectory metrics of ERT.

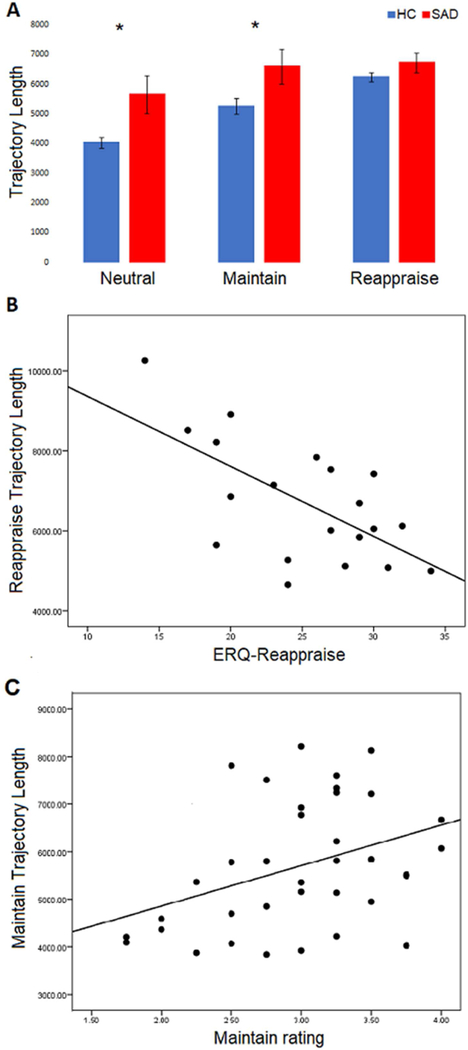
Across all three task scenarios, there was a significant effect of task (p = 7.7 × 10–8), group (p = .024), and trend level interaction effect (p = .058) on phase-space trajectory lengths(A). Reappraise trajectory lengths negatively correlated with Reappraise scores on the ERQ in SAD participants (r=−0.64, p=0.002) (B). Maintain trajectory lengths positively correlated with negative affect ratings during the Maintain task scenario in the total sample (r=0.381, p=0.022) (C).

Additionally, similar group and task differences were reported using three of our alternative prototype sets. (Fig. 6). Trajectory results from CPS, modified CPS and SPS prototype selectors demonstrated consistent task differences (CPS: 5.3 × 10⁻⁸; modified CPS: 1.0 × 10⁻⁶; SPS: 2.2 × 10⁻⁶;) and group differences (CPS: p=0.022; modified CPS: p=0.015; SPS: p=0.020) in the phase-space, with no significant task*group interactions (CPS: p=0.076; modified CPS: p=0.052, SPS p=0.055). For the MST prototype selector, we first included the backbone and the first-level side chain as the initial prototype set (connectomes included =1956), later the second-level of side chains were further included to expand the size of prototypes (connectomes included =4712). Both MST prototype sets exhibit consistent trends in group and task differences, there were significant task effects (backbone with first level side chain: p= 0.001, backbone with first two levels: p=2.1 × 10⁻⁵) and a significant group effect (backbone with first level: p=0.020, backbone with first two levels: p=0.013) (Fig. 7). No statistical analyses were performed at the backbone level due to the number of nodes (only 5% of the total connectomes were represented on the backbone).

Fig. 6: Selecting representative prototype graph set.

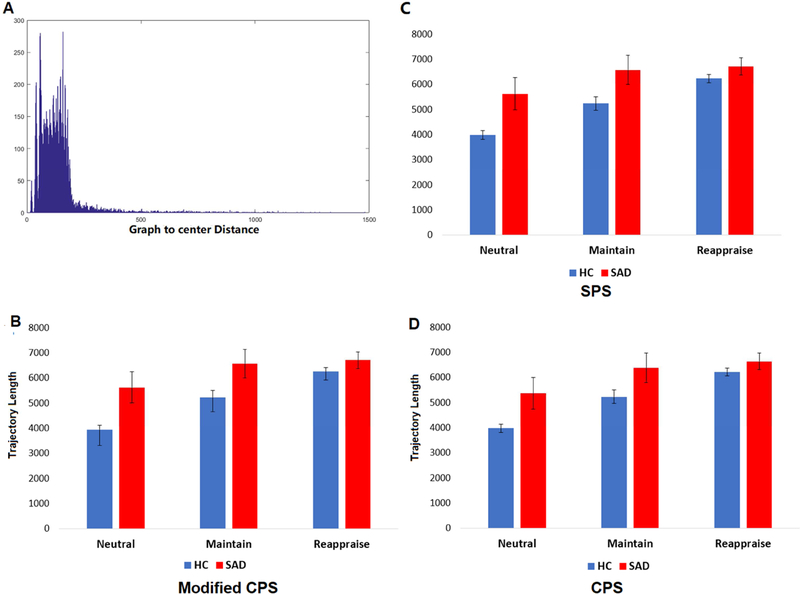
Histogram of graph-to-center geodesic distance (A) and the trajectory length as computed using prototype sets given by modified CPS (B). Results obtained using SPS (C) and CPS (D) showed similar findings as Modified CPS, as well as the original 15600-connectome prototype set (i.e., each connectome is used as a prototype). There were significant group effects of task and group, no interaction effect on phase-space trajectory

4. Discussion

In this paper, we proposed a phase-space connectome manifold reconstruction approach to computational EEG connectomics via unsupervised manifold learning to quantify abnormalities in EEG dynamics during emotion regulation in SAD participants. In this phase-space, intrinsic geometric properties can be encoded using the geodesic distance, thus further permitting a MST-based visualization. Sampling the connectome along the main branch of the MST revealed a pattern of overall increased theta connectivity in the “left-most” part of the branch, which was comprised primarily of SAD participants. This finding replicates our previous study demonstrating increased theta connectivity at rest associated with SAD (Xing et al., 2017). Connectomes sampled from the “right” part of the branch (where the Neutral condition predominated) demonstrated increased theta coupling in parietal and occipital leads, consistent with the visual component of the task. Moreover, the dynamic EEG connectome as a function of time obtained from one participant while performing a specific ERT task corresponded to a phase-space “trajectory”“, also as a function of time. SAD participants had longer trajectories during Neutral and Maintain, while the trajectory length of the latter correlated with negative with negative affective state. Additionally, Reappraise trajectory lengths were inversely correlated with the habitual use of reappraisal as an emotion regulation strategy meaning subjects who were more likely to use reappraisal outside the laboratory setting had reduced trajectory lengths. Thus, our results showed that manifold trajectory length overall separated conditions and diagnoses, and thus can be thought of as a proxy measure for the cognitive load of emotion processing and regulation.

Here we discuss the important potential implications of our novel phase-space manifold approach. In this space, intrinsic manifold properties such as trajectory length per second reflect the underlying cognitive processing. Indeed, given that the complex nonlinearity in EEG dynamics is decomposed in this novel phase-space, where 1) each possible state corresponds to a distinct connectivity pattern, and 2) an isometric mapping (i.e., geodesic distance preserving) is constructed pair-wise across all possible states, we conjecture that the trajectory length normalized over a fixed time interval (i.e., the “normalized” trajectory length or “speed”) reflects the perceived amount of thought transition. Or put more bluntly, we posit that a longer normalized trajectory length is subjectively perceived as a more rapidly-transitioning or “faster” dynamical process (which when occurs at rest may simply relate to the feeling of “racing thoughts”). In this context, given that the trajectory lengths we reported were already “normalized” as all task conditions were seven seconds, our findings can be interpreted very intuitively as follows: People who experience anxiety in general tend to experience higher degrees of thought overactivation (i.e. “racing thoughts” or thought accumulation (Emily and Elana, 2008)), while more cognitively complex tasks require more rapid thought transitions (Fig. 4; order of cognitive complexity: Reappraise > Maintain > Neutral). Further, the habitual use of reappraisal corresponds to less rapid transitioning during Reappraise, suggesting an efficiency resulting from life-long learning and practicing of these strategies. Future studies can explicitly test this hypothesis by examining whether phase-space trajectories are associated with indices of thought over-activation (i.e. the Subjective Thought Overactivation Questionnaire (Keizer et al., 2014)). With graph dissimilarity embedding, we constructed a manifold which captures the underlying phase-space structure of dynamic EEG connectomes insensitive to how the prototype graph sets were selected. Indeed, the average trajectory length of all five prototype sets (selected via CPS, SPS, modified CPS, and two levels of MST) exhibits a consistent trend as in the whole 15600-connectome prototype graph set. Moreover, we proposed two additional approaches to prototype selection that may be more appropriate in our case: the Modified CPS, which removes the outlier graphs with Hampel identifier; and MST informed selector, which selects levels of MST branches in a hierarchical manner.

Several study limitations are briefly discussed. First, our analyses are not based on source-localization, although manifold learning as we proposed here is capable of, at least in theory, uncovering the underlying intrinsic geometric properties of brain dynamics regardless of whether the connectivity was channel-based or source-localized. Second, it can be challenging to objectively measure emotion regulation, due to the known complexity and diversity of emotion regulation strategies (Gross and John, 2003) (to our knowledge currently available instruments to clinically evaluate ERT performance are all based on subjective ratings). Results with the negative affect ratings should be interpreted with caution due to the fact that ratings were collected during an fMRI ERT and not during the EEG ERT. Furthermore, in the graph dissimilarity embedding framework (Bunk and Riesen 2008), a matrix norm is used to quantify the difference between two connectome graphs. However, concerns in applying standard matrix norms to connectomes have been raised as matrix norm may be sensitive to extreme outliers and incapable of capturing higher order similarity (Chung et al., 2017). Additionally, although results from different prototype selectors were consistent, thus likely collectively recovering the true properties of the phase space, different selectors nevertheless resulted in various numbers of prototype connectomes. Last, the local neighborhood construction step is dependent on the choice of k when determining the k nearest neighbors of each connectome (Wang et al., 2005), although the overall trend of our findings is consistent across a range of k values (Fig. A4).

In conclusion, our connectome manifold learning approach provides a novel analytic and visualization framework for understanding EEG dynamics. When applied to EEG data obtained in participants with and without SAD during emotion processing and regulation, this novel framework revealed complex differences in brain dynamics between SAD and healthy control groups as well as across tasks. In the future, these novel phase-space features may be used to determine brain-based biomarkers for treatment selection and monitoring treatment response.

Abbreviations

2D

Two Dimensional

CPS

Center prototype selector

ERQ

Emotion Regulation Questionnaire

ERT

Emotion regulation Task

GDM

Geodesic Distance Matrix

HAM-A

Hamilton Anxiety Rating Scale

HC

Healthy Control

LSAS

Liebowitz Social Anxiety Scale

MST

Minimum Spanning Tree

SAD

Social Anxiety Disorder

SPS

Spanning Prototype Selector

WPLI

Weighted Phase Lag Index