Sliding window correlation analysis: Modulating window shape for dynamic brain connectivity in resting state

Abstract

The sliding window correlation (SWC) analysis is a straightforward and common approach for evaluating dynamic functional connectivity. Despite the fact that sliding window analyses have been long used, there are still considerable technical issues associated with the approach. A great effort has recently been dedicated to investigate the window setting effects on dynamic connectivity estimation. In this direction, tapered windows have been proposed to alleviate the effect of sudden changes associated with the edges of rectangular windows. Nevertheless, the majority of the windows exploited to estimate brain connectivity tend to suppress dynamic correlations, especially those with faster variations over time. Here, we introduced a window named modulated rectangular (mRect) to address the suppressing effect associated with the conventional windows. We provided a frequency domain analysis using simulated time series to investigate how sliding window analysis (using the regular window functions, e.g. rectangular and tapered windows) may lead to unwanted spectral modulations, and then we showed how this issue can be alleviated through the mRect window. Moreover, we created simulated dynamic network data with altering states over time using simulated fMRI time series, to examine the performance of different windows in tracking network states. We quantified the state identification rate of different window functions through the Jaccard index, and observed superior performance of the mRect window compared to the conventional window functions. Overall, the proposed window function provides an approach that improves SWC estimations, and thus the subsequent inferences and interpretations based on the connectivity network analyses.

1. Introduction

Functional brain network connectivity has been proven to be an informative method for studying brain function in different states (Allen et al., 2014; Richiardi et al., 2011; Shirer et al., 2012), and among different populations (Belmonte et al., 2004; Mokhtari et al., 2018b; Rashid et al., 2014). Brain imaging studies have long assumed that functional connectivity was stationary and could be quantified by measuring static temporal correlations of the functional magnetic resonance imaging (fMRI) time series between separate brain regions (Smith et al., 2011). However, this approach may be insufficient to estimate the full extent of the functional connectivity, as recent studies have shown that brain connectivity exhibits meaningful variations over time (Allen et al., 2014; Chang and Glover, 2010; Chang et al., 2013; Handwerker et al., 2012; Hutchison et al., 2013), see (Laumann et al., 2016) for alternative view. Not only does brain network organization differ between and during various task states (Bianciardi et al., 2009; Chang et al., 2011; Sun et al., 2006), there is convincing evidence of highly dynamic behavior of resting state fMRI (rsfMRI) connectivity (Allen et al., 2014; Chang and Glover, 2010; Handwerker et al., 2012). The mind wandering that occurs in participants during a resting state scanning session likely produces dynamic alterations of functional brain connectivity (Andrews-Hanna et al., 2010; Christoff et al., 2016; Kucyi and Davis, 2014). Additionally, the brain’s response to changing internal and external stimuli requires dynamic changes in connectivity networks organization over time (Chang and Glover, 2010; Chang et al., 2011).

Among the various statistical methodologies, including time‐frequency analyses (Allen et al., 2014; Chang and Glover, 2010; Thompson and Fransson, 2015) and data-driven modeling (Broumand et al., 2015; Broumand and Hu, 2015; Cribben et al., 2012; Lindquist et al., 2014), the sliding window correlation (SWC) analysis has remained the most popular approach to evaluate dynamic functional connectivity (Allen et al., 2014; Hutchison et al., 2013; Mokhtari et al., 2018a; Preti et al., 2016; Rashid et al., 2014; Sakoglu et al., 2010 ). Analogous to a moving average function, a sliding window analysis computes a succession of pairwise correlation matrices using the time series from a given parcellation of brain regions. Despite the growing success of this methodology, the sliding window technique suffers from substantial challenges (Hindriks et al., 2016; Hutchison et al., 2013; Leonardi and Van De Ville, 2015); e.g. there are multiple parameters such as window function, length and step size that must be set, but the appropriate settings remain unknown due to lack of ground truth in resting state fMRI data.

In this direction, a great effort has recently been dedicated to investigate the sensitivity of SWC to different parameters using both simulated and real fMRI data (Leonardi and Van De Ville, 2015; Shakil et al., 2018; Shakil et al., 2016; Wilson et al., 2015). To address the challenge of “no ground truth” (Shakil et al., 2016), created simulated networks with altering states using real fMRI time series and investigated the sensitivity of SWC measures to the state transitions within a wide range of varying parameters including window length, step size and window type (Shakil et al., 2016). Interestingly, rectangular window showed superior sensitivity to the state transitions compared to the tapered windows. Such an outcome might be due to the sharp alterations associated with the connectivity network transitions that could be tracked better by the rectangular window. Although a considerable amount of functional connectivity studies have exploited the common rectangular window (Leonardi and Van De Ville, 2015; Shakil et al., 2015), there is a major shortcoming associated with such an elementary window. In fact, all the points within this window are given the same weight, which increases the sensitivity of SWC to outliers. To limit this adverse effect (Allen et al., 2014; Handwerker et al., 2012; Rashid et al., 2014), recommended tapered windows to estimate the SWC connectivity.

Nevertheless, the sliding window function comes with another challenge, which to our knowledge has not previously been addressed in the neuroimaging literature. As explained above, the sliding window is simply a weighted moving average operation in time domain. However, the window operates as a non-uniform low-pass filter in the frequency domain (Leonardi and Van De Ville, 2015; Shakil et al., 2015). Ideally, the low-pass filter is supposed to cover a limited bandwidth, i.e.(−Ω_c; Ω_c) uniformly, where Ω_c is the filter cut-off. However, for the commonly-used windows, the frequency spectrum shows a tapered shape, thus as the frequency of the dynamic correlation goes up, it is assigned a smaller weight by the low-pass filter. This unwanted spectral variation can significantly affect the interpretation of dynamic functional connectivity through artificial suppression of the higher frequency contents within the bandwidth ð (Ω_c;Ω_c). This effect becomes even worse when a tapered window function, such as Hamming or Tukey, is exploited.

In order to address the issue of a non-uniform frequency spectrum, here, we proposed a window named modulated rectangular (mRect) with a flattened spectrum within the bandwidth. The mRect window was actually generated by the superposition of a regular rectangular window and a second rectangular window with larger length multiplied by a cosine function. To achieve a better insight into the low-pass filtering effect of the window, we started with simulated time series fluctuating with a few given frequencies. Comparison between the different windows demonstrated that the mRect window outperformed the common window functions in retrieving the dynamic correlations. In addition to the temporal analysis, we also provided a frequency domain analysis to address the above-mentioned issue. As exploited by the previous studies (Leonardi and Van De Ville, 2015; Shakil et al., 2018; Shakil et al., 2015; Shakil et al., 2016), the frequency-based perspective is particularly informative for SWC analysis of fMRI data, as fMRI time series possess broad spectra that may not be easily perceived using temporal analysis.

Moreover, we generated simulated networks with varying states over time, and compared different windows in network state identification. For each window, we ran a separate k-means clustering to identify the network states. Interestingly, we observed that the mRect window significantly outperformed the conventional windows in detecting state transitions, as estimated using Jaccard similarity index between the ground truth and the states detected by the k-means clustering. Thus, the proposed window function can improve the SWC estimations, yielding modified outcomes and interpretations based on the dynamic connectivity network analyses.

2. Methods

2.1. Window functions

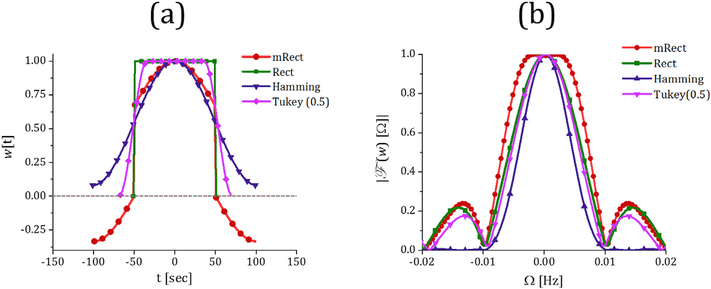
The rectangular and tapered, including Hamming and Tukey, windows have been widely used for dynamic functional connectivity analysis in neuroimaging studies (Allen et al., 2014; Leonardi et al., 2013; Leonardi and Van De Ville, 2015; Preti et al., 2016; Shakil et al., 2016). The temporal profile of these windows and the mRect window, w[t], in association with their amplitude spectral density $|\mathcal{F}(W)[\mathrm{\Omega }]|$ (referred to as frequency spectrum in the rest of the paper) are shown in Fig. 1.

Fig. 1.

Temporal profile (a) and frequency spectrum (b) of mRect (red), rectangular noted as rect (green), Hamming (dark purple), and Tukey with the cosinetapered length ratio 0.5 (magenta) windows. The length of the windows is adjusted to achieve the same cutoff frequency at Ω_c = 0.01. As it is apparent in (b), Hamming window suppresses high frequency ripples significantly with the cost of increasing window length and intensifying spectral variation within the frequency range of interest. On the other hand, the mRect window provides a flattened spectrum in the frequency domain with the cost of increasing window length, note that the side lobes are comparable to rectangular and Tukey windows. As shown in section 3.1, using step size greater than 1 time point, the unwanted frequency content captured by the side lobes can be suppressed significantly.

As demonstrated by the frequency spectrums, each window actually represents a low pass filter in the frequency domain, with a cut-off frequency, Ω_C = 0.01 Hz, located where the frequency spectrum first meets a predefined small threshold value (for example zero) (Leonardi and Van De Ville, 2015; Shakil et al., 2015). In this study, we were particularly interested in investigating the effects of windows frequency domain characteristics on dynamic correlation retrieval; thus, we determined the length of different windows to achieve the same cut-off frequency.

The fluctuations of rsfMRI time series of the cerebral cortex are predominantly characterized within a low frequency range [0.01–0.1] Hz (Cordes et al., 2001). This range in conjunction with the fMRI time series sampling rate (known as repetition time (TR)) are the basic parameters that should be taken into account when determining parameters of the sliding window (Leonardi and Van De Ville, 2015; Shakil et al., 2015). The cutoff frequency of the low-pass filter corresponding with a sliding window operator is actually determined based on the window duration, such that increasing a window length results in decreasing the cut-off frequency. Decreasing the cutoff frequency (longer windows) decreases the sensitivity for identifying fast changes, with very long windows eventually measuring static connectivity. On the other hand, increasing the cutoff frequency (shorter windows) can increase sensitivity for detecting short transition states but at the expense of increasing the spurious fluctuations in the dynamic connectivity (Leonardi and Van De Ville, 2015; Shakil et al., 2016). Thus, it is essential to determine a window length that allows reducing spurious fluctuations and at the same time capturing faster dynamic correlations. Based upon this idea, a length, L, higher than 1/(TR·f_min) for the rectangular window was suggested by (Leonardi and Van De Ville, 2015), where f_min is the lowest frequency present in fMRI time series, i.e.∼ 0.01 Hz. Thus, the rectangular window length, L, should be over 100/TR time points. It was demonstrated that such window length selection results in a good balance of sensitivity and specificity by identifying real transitions while limiting the spurious fluctuations (Leonardi and Van De Ville, 2015) (also see Supplementary Materials, Fig. S. 1 for clarification). For the rectangular window, this window length leads to cut-off frequency located at Ω_C = 1/(L·TR). Here, the length of the different windows was determined to achieve a same cut-off frequency at Ω_C = 1/(L·TR) ≅ 0.01 Hz (where TR = 2 sec and L = 51), that led to a length of 101, 75 and 101 time points for the mRect, Hamming and Tukey windows, respectively. In general, to achieve the same cutoff frequency with a rectangular window of L time points, mRect, Hamming and Tukey (with the cosine-tapered length ratio 0.5) windows require about 2L, 1.5L, and 2L time points, respectively. For further details regarding the length of the Hamming and Tukey windows, refer to (Oppenheim and Schafer, 2014). Additionally, the rationale behind determining the length of the mRect window has been explained in the Supplementary Materials, Fig. S. 2.

It is evident from Fig. 1 that the windows frequency spectrum is not uniform within the bandwidth (−Ωc;Ωc), implying that these windows tend to arti_ficially suppress the dynamic correlations, especially the higher frequency/faster correlations within the bandwidth. In other words, the SWC fluctuations could vary slower compared to the real dynamic relationships between the time series, which may eventually lead to higher risk of false negative/positive results in the statistical analysis of dynamic connectivity networks.

To address the issue of window spectral variation, we designed a window function with a flattened spectrum within the bandwidth of interest. We named this function modulated rectangular (mRect) window and defined it as follows

$$w[n]=rect[n/L]+\alpha \cdot rect[n/2L]\cos \left(\pi {\mathrm{\Omega }}_{c}n+\varphi \right),$$ (1)

where n = t/TR is the index of time point, t is the discrete time variable, and α (relative amplitude) and ϕ (phase) are design parameters that can be empirically tuned to maximally flatten the window spectrum over (– Ω_c; Ω_c) Here, this was achieved by setting α = 0.5, and ϕ = 5/12π. Basically, the mRect window consists of a conventional rectangular window function with the length L = 1/(TR·Ω_c) time points (noted by rect [n/L]), added to a second rectangular window with the length 2L (noted by rect[n/2L]) multiplied by a cosine function fluctuating at frequency Ω_c/2 to flatten the window spectrum over the bandwidth(–Ω_c). Fig. 1 contrasts the temporal profile and frequency spectrum of the mRect window with other conventional windows, for a given cutoff frequency of Ω_c = 0.01Hz. Clearly, the mRect spectrum is significantly flattened over the range of interest, at the cost of increased window length by a factor of 2 in comparison with the rectangular window. Although window length is increased, it is equal or comparable to the popular tapered windows such as Tukey or Hamming windows, as shown in Fig. 1.

Intuitively, one can consider mRect window as a combination of two distinct windows operating in parallel. The first window, which is a conventional rectangular window, represents a low-pass filter. The second window operates as a band-pass filter with central frequency and bandwidth of Ω_c/2. Having said that, by fine tuning the design parameters, α and ϕ, the resulting combined window can be tailored to achieve the flattened spectrum within the frequency range of interest (– Ωc;Ωc). In principle, to achieve a maximally flattened spectrum, this idea can be generalized, with the cost of a longer window length, by having K –1 band-pass filters with a central frequency and bandwidth of (k– 1)Ω_c/k, and Ωc/k, respectively, where k = 2;…, K. Equation (1) represents the fillter for K = 2.

2.2. Simulated time series

To achieve a simple yet informative insight into the window function effect on SWC estimation, we started from the simulated time series fluctuating at a few known frequencies with given amplitudes, as used in (Leonardi and Van De Ville, 2015; Shakil et al., 2015). The basic idea of such analysis is that any discrete time series (such as an fMRI time series) can be linearly decomposed into a series of oscillating signals with known frequency and amplitude. Having said that, one may examine the simulated time series oscillating at a specific frequency, and generalize the resulting conclusions and interpretations to fMRI time series consisting of fluctuations within a wide frequency range. Let us consider two simulated time series as

$$x[n]=\cos (2\pi fn)y[n]=\cos \left(2\pi \left(f+\delta f_1\right)n\right)+\cos \left(2\pi \left(f+\delta f_2\right)n\right)$$ (2)

where f = 0.02 Hz, δf₁ = 0.001 Hz and δf₂ = 0.006 Hz. The static correlation of these two time series is very small. However, they exhibit meaningful low frequency dynamic correlations due to going in and out of phase with one another. The low frequency dynamic correlations, that are captured by the sliding window filter, occur at frequencies δf₁ and δf₂ (Leonardi and Van De Ville, 2015). In other words, dynamic correlation is independent of f, but is dependent on the time series frequency differences (i.e. δf₁ = 0.001 Hz and δf₂ = 0.006 Hz in our example data).

The frequency f = 0.02 was selected in the frequency range [f_min; f_max] ≈ (0.01, 0.1) Hz to be consistent with the signals found in real resting-state fMRI data (Cordes et al., 2001). As explained earlier, the sliding window operator is a low pass filter in the frequency domain with cut-off frequency Ω_C, where Ω_C is set to f_min = 0.01 Hz to limit spurious fluctuations (Leonardi and Van De Ville, 2015). Thus, we chose the dynamic correlation frequency values (i.e. δf₁ = 0.001 Hz and δf₂ = 0.006 Hz) in the frequency range of (0,f_min) = (0, 0.01) to be consistent with fMRI correlation connectivities.

Also, we chose slower (δf₁ = 0.001 Hz) and faster (δf₁ = 0.006 Hz) dynamic correlations, because we were able to compare different window functions in retrieving both slower and faster dynamic correlations. Note that we used these two specific time series for demonstration purposes only. We also simulated realistic resting state fMRI time series including multiple fluctuation frequencies in the range of (i.e. (0.01, 0.1) Hz), and statistically compared the performance of different windows in retrieving the realistic dynamic correlations.

2.3. Sliding window correlation coefficient

For simplicity of the formulas below, we assumed that the window is rectangular. The static correlation, r_xy, between the time series x and y of length N is defined as follows

$$r_{xy}=\frac{{\sum }_{n=1}^N\left(x_n{y}_n\right)-{\sum }_{n=1}^N\left(x_n\right){\sum }_{n=1}^N\left(y_n\right)}{\sqrt{{\sum }_{n=1}^N{\left(x_n-{\sum }_{k=1}^N\left(x_k\right)\right)}^2}\sqrt{{\sum }_{n=1}^N{\left(y_n-{\sum }_{k=1}^N\left(y_k\right)\right)}^2}}$$ (3)

where x_n and y_n denote the time point n of the time series x and y. Thus, each sample of the sliding window correlation coefficient can be formalized as below

$$r_{xy}[m]=\frac{{\sum }_{n=m}^{m^{\prime }}{x}_n{y}_n-\left({\sum }_{n=m}^{m^{\prime }}{x}_n\right)\left({\sum }_{n=m}^{m^{\prime }}{y}_n\right)}{\sqrt{{{\sum }_{n=m}^{m^{\prime }}\left(x_n-\left({\sum }_{k=m}^{m^{\prime }}{x}_k\right)\right)}^2}\sqrt{{\sum }_{n=m}^{m^{\prime }}{\left(y_n-\left({\sum }_{k=m}^{m^{\prime }}{x}_k\right)\right)}^2}}$$ (4)

where m∈[0,N− L+1] is the start point of the windowed time series, L is the window length and m’ = m+ L‒ 1. In other words, the SWC analysis is performed by computing the sample correlation coefficient between the points from times series x and y that are within the window length The window is then shifted over the time series and a new correlation coefficient is computed for each shift. Overall, with the time series of length N and window of length L,N – L + 1 sample correlation coefficients are yielded. Thus, using the sliding window correlation co-N and window of length L, N L + 1 sample correlation coef efficient, a population of correlation coefficients is created, while static correlation only produces one sample correlation. For other window functions, the time series of Eq. (4) are weighted with the window shapes. In this study, the SWC was computed using different window functions with the window sizes mentioned in the previous section and step size P=, the1 time point.

In Eq.(4),first term in the numerator accounts for the pointwise multiplication of the windowed time series. The second term in the numerator and the denominator term account for the windowed time series mean and standard deviation values, respectfully. An essential assumption in sliding window analysis is that the mean and standard deviation of the time series are static across the time sample (i.e. the data is statistically stationary, at least in the wide sense) (Akhlaghi and Dogariu, 2016, 2017; McCauley, 2009, 2013). However, this may not be necessarily true for every window length (Chen et al., 2016; Deco et al., 2011; Lee et al., 2013; Leonardi and Van De Ville, 2015). Inaccurate estimation of time series statistics (i.e. mean and standard deviation) due to a small sample size can cause spurious fluctuations in the SWC measures (see Fig. S. 1 for clarification). The rectangular window length lower bound limit proposed by (Leonardi and Van De Ville, 2015) provides a practically stationary estimation of time series statistics; thus, it can significantly reduce the spurious fluctuations. To define a ground-truth independent of window parameters, we determined the point-wise multiplication of the two time series, x.y = [x₁.y₁, x₂.y₂; …, x_N.y_N], as recommended by (Leonardi and Van De Ville, 2015). The main idea is that point-wise multiplication represents the temporal relationships between the time series and it is not affected by the spurious fluctuations (Leonardi and Van De Ville, 2015). However, two considerations should be taken into account when using pointwise multiplication: 1) as we were particularly interested in frequency domain analysis in this study, and since the sliding window technique operates as a low pass filter with the bandwidth of (‒Ω_c, Ω_c), we limited our comparisons to the frequency spectrum of x.y below in the range of (‒Ω_c, Ω_c). Second, the point-wise multiplication does not provide a normalized connectivity measure, thus we can only compare the spectral profiles of the SWC and pointwise-multiplication series, but not their absolute amplitudes. Clearly, a non-normalized measure is not comparable between different node pairs, and cannot be used in network connectivity analyses. Thus, we normalized the spectrum of each SWC series to its maximum value.

2.4. Simulated network states

In order to examine how the performance of the proposed window may differ from the popular windows on fMRI time series that lie in a wide frequency range, we created simulated resting-state fMRI time series using SimTB toolbox, developed by (Erhardt et al., 2012). Additionally, in order to compare different window functions in fMRI connectivity network analysis, we took advantage of the SimTB framework to simulate 10 fMRI time series under the model of spatiotemporal separability (Erhardt et al., 2012). The fundamental assumption of this model is that fMRI time series can be expressed as the product of task events and spatial maps. Each spatial map represents a unique connectivity state.

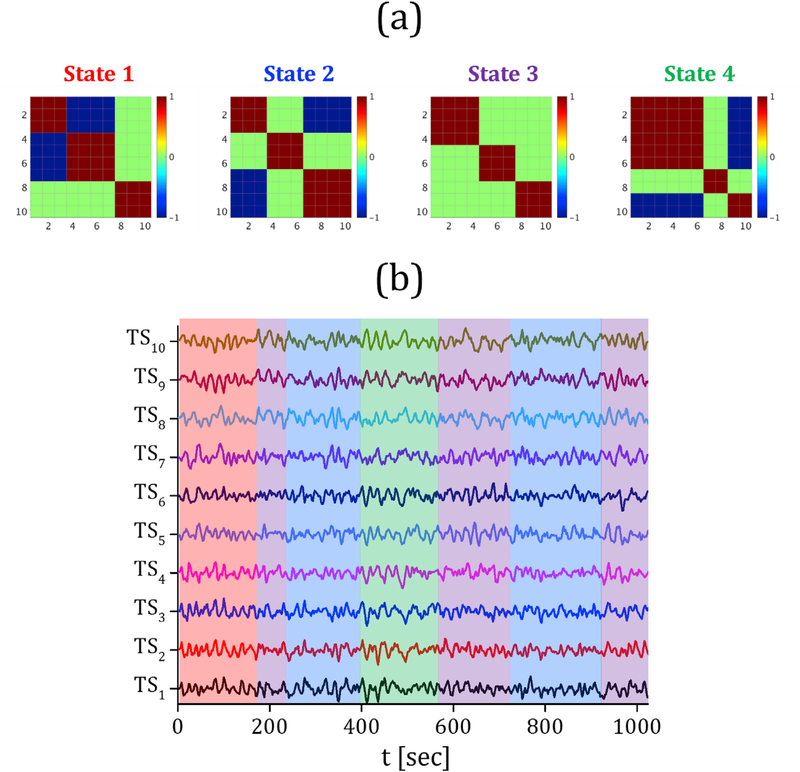
We defined the 4 states (i.e. spatial maps) shown in Fig. 2 (a). For a representative sample, the simulated fMRI time series are shown in Fig. 2 (b). We created 100 different samples (i.e. dynamic connectivity networks), for each of which the number of state transitions was in the range of ð6; 12+ and the states occurred at random orders. The resting-state networks showed long-term stability on the scale of minutes (Gonzalez-Castillo et al., 2014), thus tended to exhibit a same state for a long period (Allen et al., 2014; Shakil et al., 2016). The length of states was in the range of (30 TR, 90 TR) (where TR = 2 s) (Shakil et al., 2016), also (Allen et al., 2014) identified real fMRI connectivity states with comparable durations. Thus, here, a range of (30 TR, 90 TR) seconds was used for the state durations. Normal random noise $\mathcal{N}(0,0.1)$ was also added to each sample. The length of time series was set to 512 TR (TR = 2 s).

Fig. 2.

The spatial connectivity map corresponding with each state of the simulated network data (a); the SWC network at each time point was actually highly correlated with one of these 4 states; the 10 simulated time series forming a dynamic connectivity network with altering states over time for a representative sample (b); the period of each state is highlighted with a specific color on the time series, state 1, 2, 3 and 4 are indicated with red, blue, purple and green colors, respectively. The length of the state intervals, as shown in (b), is: 80 TR, 31 TR, 81 TR, 84 TR, 86 TR, 76 TR and 84 TR. Here, TS_i, 1 ≤ i ≤ 10 represents the time series of node i.

Following creating simulated fMRI time series, sliding window correlation matrices were generated by computing pairwise correlation coefficients between the windowed time series. Thus, in contrast to the spatial maps, correlations/anticorrelations are not necessarily perfect (i.e. they are different from +1 and‒1). Also, it is important to note that we assumed that state transitions were sharp.

2.5. Clustering network states

The SWC analysis was performed on the 100 simulated dynamic connectivity networks using each of the four different window functions. For each sample, the dynamic connectivity network, i.e. an array of size 10 ×10 ×(512 ‒l+ 1), was a series of connectivity matrices over time, i.e. an array of size 10 × 10, where l, the window length, was 101, 51, 101, and 75 time points for the mRect, rectangular, Hamming and Tukey windows. To achieve a fair paired-sample comparison between different windows, for each sample, we only used the first 412 connectivity matrices resulting from the different windows.

The k-means clustering algorithm has often been used to recognize ‘states’ in dynamic connectivity networks (Allen et al., 2014; Rashid et al., 2014; Shakil et al., 2016). Due to the symmetry of connectivity matrices at each time point and for each sample, the entries below the diagonal were embedded into a vector that resulted in an array of size 45 × 412 for each sample. Each connectivity vector (i.e. an array of size 45 × 1) at each time and for each sample was then considered as a data point in the clustering analysis. For each window, the k‒means algorithm involving 2 steps was used for clustering the data points. For the first step, random sub-sampling was performed to select 20 samples (equivalent to 20 times 412, i.e. 8240 data points) from the available 100 samples. The k-means++ approach was used to initialize the clustering algorithm (Arthur and Vassilvitskii, 2007). In contrast to random initialization that simply chooses the initial centroids randomly from among the data points, k‒means chooses one centroid randomly and then chooses the others so that they are as far apart from each other as possible. To estimate the distance between the data points, we used city block distance that has been suggested as a more effective distance measure compared to Euclidean distance for high-dimensional data (Aggarwal et al., 2001). We also repeated clustering in 10 iterations to avoid local minima solutions. The Silhouette index was computed to determine the number of clusters that best represented the data. The Silhouette index represents the similarity of points within the same cluster, in comparison to the points in other clusters. There are various metrics to determine the relevant number of clusters. These metrics can be categorized into direct and statistical testing methods. The direct methods consist of optimizing a criterion, such as the within-cluster sum of squares or the silhouette index. The testing methods, e.g. gap statistic method, compare the total intra-cluster variation for different values of k with their expected values under the null distribution (i.e. a distribution with no obvious clustering). In contrast to the within cluster sum of squares score that only measures the clusters cohesion, the silhouette index simultaneously measures how close a data point is to its own cluster (cohesion) compared to other clusters (separation). Additionally, it is easier to implement and interpret than the statistical testing methods which incorporate more sophisticated computations (Desgraupes, 2013).

The number of clusters, k, varied between 2 and 12. The number of clusters that resulted in the highest Silhouette index was chosen for further analyses. For each window, the value of k associated with the maximum Silhouette index and the resulting centroids were then used to initialize the second clustering step for the same window. The remaining 80 samples were partitioned to 4 subsets each including 20 samples. We randomly divided the samples to 4 subsets, because we needed to estimate the average and standard deviation of clustering accuracy for statistically comparing the performance of different windows. The k-means algorithm (initialized using the centroids of the first clustering step) was separately performed for each subset. Note that to achieve comparable results, the same 20 samples and the same partitioning of 80 samples were used in the first and second steps of clustering algorithm for all the window functions. The Jaccard index was computed to evaluate the clustering performance. The Jaccard index was defined as the ratio of number of data points with correct state identifications to the total number of data points used in each sample subset. The clustering performance measures can be categorized into two general types: 1) the external measures compare the clustering outcome with an external ground truth, 2) the internal measures estimate the average of inter and intra-clustering similarity (separation and cohesion respectively) (Desgraupes, 2013; Guerrini et al., 2007). In this study, as the true network states were available for simulated data, using an external ground truth measure was preferred. Additionally, a clustering measure was needed for discrete data that assumed no relationship between the clusters with nearby labels, e.g. there is not a higher similarity between clusters 1 and 2 compared to clusters 1 and 4. Given that the Jaccard index satisfies all of these requirements, it was used to evaluate the clustering models in this study. Finally, a repeated measures one-way analysis of variance (ANOVA) test was performed to statistically compare the clustering performance for different window functions.

3. Results

3.1. Simulated time series

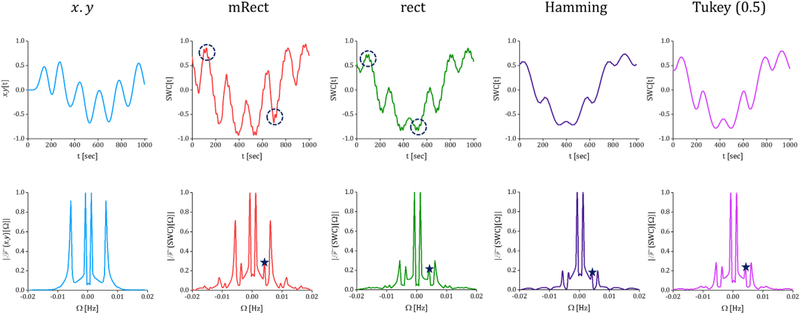
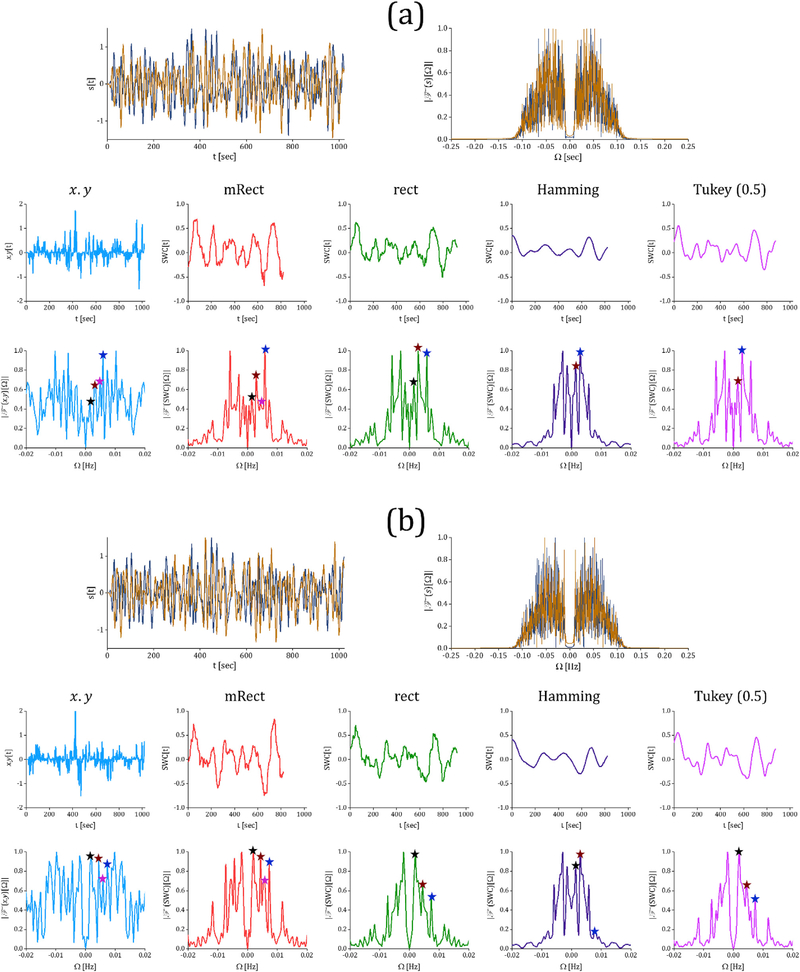
Fig. 3 represents pointwise multiplication of the two simulated time series and SWC computed using different windows together with their corresponding frequency spectrum. As shown by the figure, the pointwise multiplication fluctuates at 2 frequencies: the slow fluctuation with the frequency of 0.001 Hz, and the fast fluctuation with the frequency of 0.006 Hz. While different windows operate similarly in computing the slow dynamic correlation, the mRect window outperforms the regular windows in revealing the relative amplitude between the fast vs. slow dynamic correlations. Remember that only the temporal behaviors of SWC series and pointwise multiplication are directly comparable, only relative amplitudes can be assessed. Comparison of the frequency spectrums (the second row of the figure) similarly shows that the mRect window outperforms the regular windows in retrieving the faster fluctuation power, as compared to the pointwise multiplication frequency spectrum. Note that for comparing SWC frequency spectrum resulting from different window functions, each frequency spectrum was normalized to its maximum value. These outcomes actually illustrate how using rectangular and tapered windows may lead to suppression of the higher frequency correlations within the bandwidth of interest, as explained earlier. Note that the pointwise multiplication and SWC time series were all mean-centered. Thus, the static connectivity was removed from the SWC measures, as we were mainly interested in comparing the windows in capturing dynamic correlations.

Fig. 3.

Pointwise multiplication and SWC time series computed using the mRect window and the conventionally-used rectangular and tapered windows (the first row); frequency spectrum of the pointwise multiplication (only low frequency components) and the SWC computed using different windows (the second row). As shown by the pointwise multiplication (as the ground truth), the two time series should show dynamic correlations oscillating at δf₁ = 0.01 Hz and δf₂ = 0.006 Hz. Comparing the time series and frequency spectrum of the SWC measures and pointwise multiplication shows that the mRect window outperforms the rectangular and tapered windows in retrieving the relative amplitude/power of the fast dynamic correlation (occurring at δf₂ = 0.006 Hz). The spurious fluctuation that emerged at 0.004 is marked with a star on the SWC spectrums. Also, the sample of fast-weak ripples are marked with a circle on the SWC time series of rect and mRect windows.

Note that as shown by the frequency spectrums, the SWC measures show a weak component around 0.004 Hz (marked with a star), added by the fluctuations of the time series’ (x[n] and [y]n) standard deviations in the denominator of the correlation coefficient formula. We observed that increasing window length can decrease the spurious fluctuation that emerged at 0.004 Hz; for example using L = 61 instead of L = 51 decreased the spurious fluctuation by half; however, on the other hand, as expected, increasing window size suppressed real dynamic correlations (see Fig. S. 3). Basically, the presence of spurious fluctuations is the byproduct of error in estimation of mean value and standard deviation of the time series. Increasing window length increases the estimation accuracy for the standard deviation and mean values, which results in weaker spurious fluctuations. Overall, to weaken the spurious fluctuations further, the window length (over 1/f_min) can be increased or window side lobes can be reduced (e.g. Tukey or Hamming). However, analyses performed with these settings significantly underestimate the faster dynamic correlations. Thus, the window parameters should be set to achieve a reasonable balance between reducing spurious fluctuations and retrieving higher frequency dynamic correlations. Overall, the spurious fluctuations may be suppressed but they cannot be totally removed from sliding window correlation analyses.

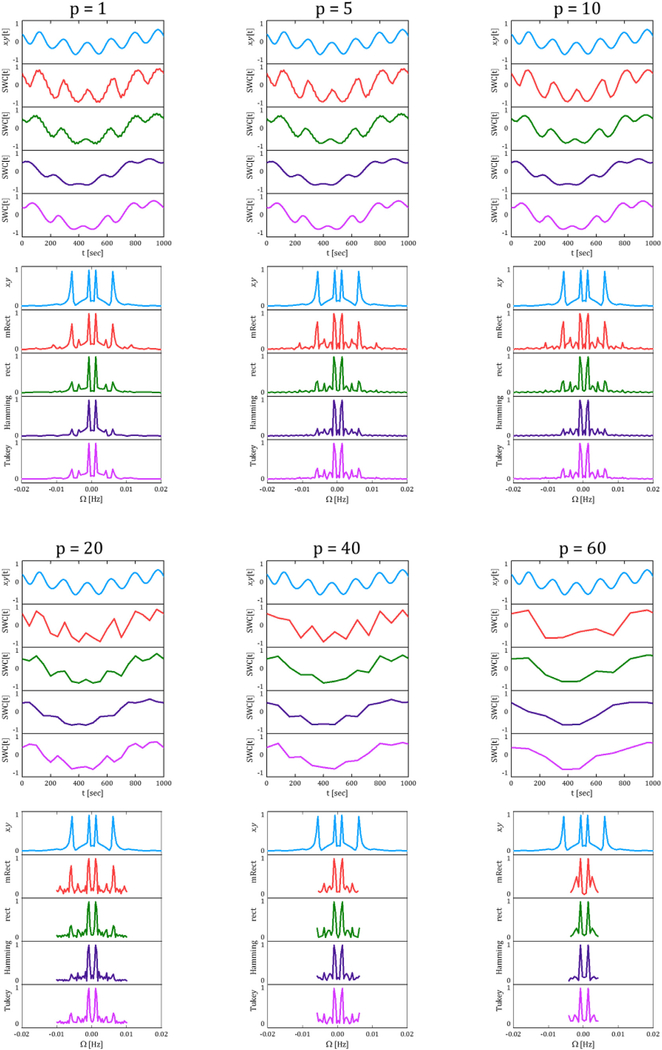
As shown in the figure, fast-weak ripples (marked with a circle) were present in the SWC time series of rectangular and mRect windows. The side lobes associated with these windows (represented by Fig. 1) and the SWC sampling rate (i.e. 1/TR.p)) explain the emergence of the fastweak ripples. This issue could be addressed by increasing the step size. Fig. 4 represents the SWC time series and frequency spectrums computed at different step sizes p 2 f1; 5; 10; 20; 40; 60g. The SWC time series illustrate that increasing step size gradually decreased the ripples, such that at step size of 10 time points, the ripples almost vanished. However, it was observed that for higher step sizes, the SWC time series became distorted such that for p ∈ {40; 60}, the fast dynamic correlation was no longer distinguishable. Note that with varying step size, mRect window still best represented the relative amplitude of the fast vs. slow dynamic correlations. Additionally, the frequency spectrums did not show a significant difference for p ∈ {1; 5; 10}. However, the frequency domain information loss was clearly visible for p ∈ f40; 60g. As an evident example, in the mRect frequency spectrum, the fast dynamic correlation occurring at 0.006 has been lost for p ∈ {40; 60}. This frequency domain information loss is only evident for the mRect window, because it was able to retrieve the fast dynamic correlation, while the regular windows all suppressed that correlation. Note that increasing the step size by a factor of p actually decreases the resulting SWC bandwidth by the same factor. This is evident by the frequency spectrum of SWC measures obtained with p 2 {20; 40; 60}. The bandwidth of the SWC computed with p = 1 was 1⁄ ((2 .TR)) = 0.25 Hz. Thus, for p = 5 and p = 10, the bandwidth should be 0.05 and 0.025 respectively. However, as we limited the frequency axis range to (−0.02, 0.02), the bandwidth decrease was not visible for these values of the step size.

Fig. 4.

The SWC time series and frequency spectrums obtained using different step sizes; increase in step size contributed to removal of the fast-weak ripples, while it did not significantly affect the fast dynamic correlation for p ∈ {5, 10}. However, as p further increased, the SWC measures underwent significant distortions due to evident by both temporal and frequency proinformation loss. For example, with p = {40, 60} the fast dynamic correlation (occurring at 0.006 Hz) was majorly distorted, and could barely be distinguished as evident by both temporal and frequency profiles.

In addition, the Fig. S. 4 in the Supplementary Materials illustrates that increasing the step size, in the range of ð1; 100+ with increments of 1, did not lead to significant distortions for p < 20 time points. However, as this limit was passed, high frequency information started becoming folded into the low frequency contents due to aliasing, resulting in distorted slow variations. Also, refer to the Discussion section for further explanations.

3.2. Simulated fMRI data examples

For the representative sample whose time series are shown in Fig. 2 (b), two connectivities between the nodes {1, 5} and the nodes {2, 6} are shown in Fig. 5. For each connectivity, the corresponding nodes’ time series, the pointwise multiplication and SWC time series and their frequency spectrum are presented. Note that the comparison between the pointwise multiplication and SWC measures are legitimate only within the bandwidth of interest given the low-pass filtering effect of the sliding window function on dynamic correlations. It is evident by the frequency spectrums of Fig. 5 that pointwise multiplication possessed several components beyond the cut-off frequency (i.e. 0.01 Hz), whereas they were significantly suppressed by the SWC operation. Due to lack of ground truth, at the current stage, we were not able to distinguish which high frequency correlation components (occurring beyond the cut-off) represent real dynamic correlations. However, one should be aware that SWC operation is intrinsically impercipient of such high frequency fluctuations.

Fig. 5.

(a) The time series of nodes 1 and 5 (the first row) following band-pass filtering in the range (0.01, 0.1) Hz, the pointwise multiplication and SWC time series (the second row) and the frequency spectrums (the third row) resulting from different window functions for the representative sample; (b) corresponding data for the connectivity between nodes 2 and 6. The stars in the frequency spectrum of point-wise multiplication marked the frequencies that we referred to in the main document (i.e. 0.0015, 0.003, 0.005 and 0.006 respectively). Again, the fast-weak ripples that were particularly evident in the SWC time series resulting from mRect and rectangular windows could be eliminated through using a step size over 1 time point (e.g. using p = 5 or p = 10 as examined earlier).

Interestingly, for the dynamic connectivity between the nodes {1, 5}, as evident by the frequency spectrums, the mRect window showed superior performance in retrieving the relative power of slower vs. faster dynamic correlations (e.g. the relative power of the components at 0.0015, 0.003, 0.005 and 0.006 Hz is best represented by the mRect window compared to the conventional windows). For instance, Hamming and Tukey windows both suppressed the dynamic correlations at 0.005 and 0.006 Hz vs. the dynamic correlations occurring at 0.0015 and 0.003. Also, the SWC computed using the rectangular window shows a comparable power at 0.003 and 0.006, while the component at 0.006 should be stronger than the component at 0.003, as shown by the pointwise multiplication power spectrum. For clarification, the frequencies that we referred to were marked with a star in the frequency spectrum of point-wise multiplication. The similar observation can also be seen for the second representative connectivity between the nodes {2, 6}. In summary, the conventionally-used windows all suppressed the power of the fluctuations occurring over 0.005 Hz, while the amplitude of the fluctuations occurring in this frequency range is better captured by the mRect window. The comparable example data for real fMRI time series are also shown in the Supplementary Materials (Fig. S. 5). These example data show how the different window functions may differ in retrieving the real dynamic correlations power. In the next section, we see how these differences in SWC estimation may affect connectivity analyses in the network scale.

3.3. Network states clustering

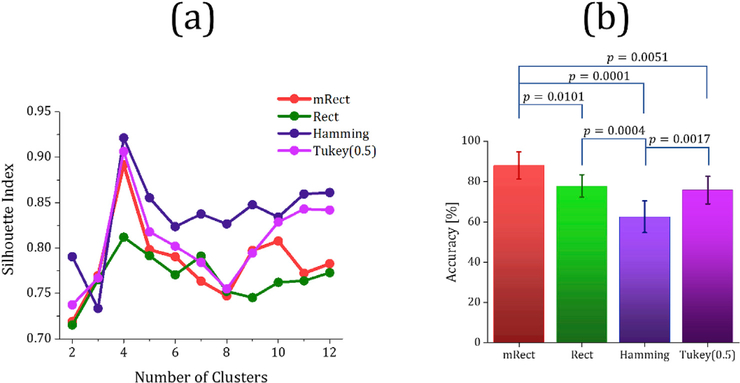
As expected for the simulated network data, for all the window functions, the Silhouette index was maximum with cluster number of k = 4. The Silhouette index measure (computed in the first step of clustering algorithm) versus cluster numbers is shown in Fig. 6 (a). The mean std. of the Jaccard index over the 4 subsampling repetitions is shown in Fig. 6 (b). The repeated measures one-way ANOVA test revealed significant differences (p < 0.0001) between the windows. Post-hoc paired sample ttests showed that mRect window outperformed the widely-used windows in network state identification as measured by the Jaccard index. The significantly different window pairs are shown in Fig. 6 (b).

Fig. 6.

Silhouette index resulting from different window functions in the first step of the clustering algorithm (a); the mean ± std. of Jaccard index over 4 subsampling repetitions in the second step of the clustering algorithm (b).

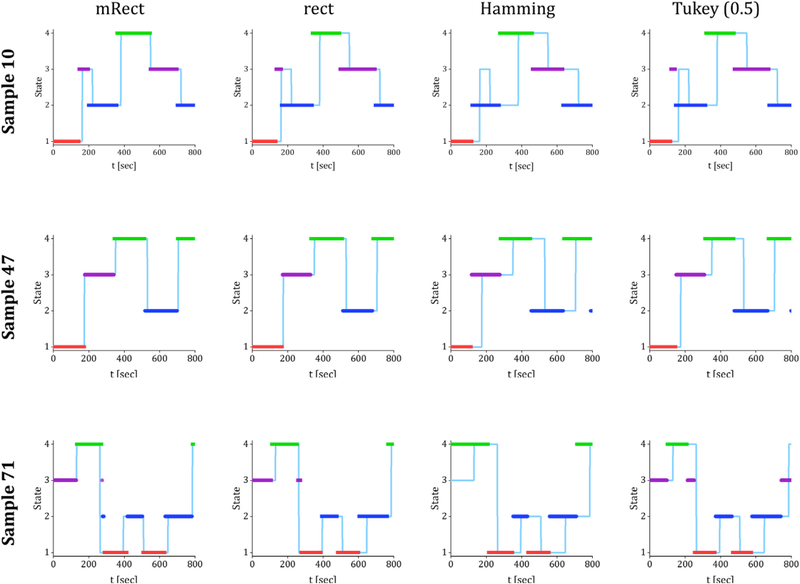
Fig. 7 represents the real network states and the identified network states for three representative samples, sample 10 is the one whose simulated time series was shown in Fig. 2. As evident by this figure, there is a better matching between the real state series and the identified state series for the mRect window. This outcome suggests that mRect window can more efficiently retrieve dynamic network connectivities, especially faster dynamic connectivities that are associated with the state transitions (Allen et al., 2014; Shakil et al., 2016).

Fig. 7.

The light blue time series in the background indicates the real states of the simulated networks. The thick colored lines indicate the identified network states through k-means clustering, the states 1, 2, 3, and 4 are shown with red, dark blue, purple and green colors, respectively.

4. Discussion

There exists a growing interest in quantifying dynamic brain connectivity. Among the different statistical methodologies, the sliding window technique has gained the most popularity in measuring dynamic functional connectivity in different populations and tasks, (Allen et al., 2014; Allen and Cohen, 2010; Hindriks et al., 2016; Rashid et al., 2014), likely due to simplicity and interpretability. As a consequence, a considerable amount of work has recently been directed at assessing sliding window technique performance in quantifying the dynamic functional connectivity (Hindriks et al., 2016; Leonardi and Van De Ville, 2015; Shakil et al., 2016). A major approach used by the previous studies has been to investigate the SWC sensitivity to different parameters, i.e. window function, length, and step size (Hindriks et al., 2016; Leonardi and Van De Ville, 2015; Shakil et al., 2016). A brief summary of these studies suggests that there is no so called “optimal settings” for sliding window parameters to achieve the optimum dynamic functional connectivity estimations. For example, while smaller window lengths can result in spurious fluctuations, long windows may lead to the suppression of fast transitions. Moreover, although tapered windows have been recommended to alleviate the issue of high noise sensitivity associated with the rectangular window, they showed lower sensitivity to network state transitions (Shakil et al., 2016).

While previous studies have investigated the effects of a broad range of the window settings on SWC measures, little attention has been dedicated to the effect that the various window functions have on the frequency characteristics of the dynamic connectivity. Recent studies have investigated the low-pass filtering effect of the sliding window technique in the frequency domain (Leonardi and Van De Ville, 2015; Shakil et al., 2015; Shakil et al., 2016); nevertheless, to our knowledge no previous study has addressed the non-uniform frequency spectrum of the widely-used window functions. The tapered and rectangular windows that are commonly used in dynamic brain connectivity studies are all characterized by a frequency spectrum that passes the lower frequency dynamic correlations with a higher rate compared to the higher frequency dynamic correlations. Here, we suggested a modulated rectangular window to address the issue associated with the varying frequency spectrum of the conventional window functions. The proposed window function was defined as a linear combination of a conventional rectangular window with a second rectangular window multiplied by a cosine function to achieve a flattened frequency spectrum. Thus, the resulting combined window weights the bandwidth of the SWC spectrum more evenly.

Using time series fluctuating at given frequencies, we showed that the frequency spectral variations of the conventional window functions lead to the suppressed high frequency contents. The mRect window outperformed the tapered and rectangular windows in retrieving the faster dynamic correlations. Moreover, we showed that the fast-weak ripples found in SWC series could be eliminated by increasing the step size, p, from 1 time point to 10 time points. Having a step size of 1 is equivalent to sampling SWC with the same rate as the original time series, i.e. Ω_s = 1/TR. As explained earlier, using a sliding window, one practically limits the frequency range of SWC to (−Ω_c, Ω_c). Thus, oversampling the SWC at the rate of Ω_s > 2Ω_c lead to unwanted high frequencies in the range of (Ω_c, Ω_s/2) that were captured by the side lobes. Having the SWC sampled at the rate Ω_s, where p = 1, the sampling rate of the SWC for p >1 decreases to Ω_s/p. Consequently, according to the Nyquist sampling rate, “theoretically,” one can down sample the signal without significant information loss if Ω_s/p ≥ 2Ω_c, or equivalently if p≤Ω_s/2Ω_c. This relation is valid irrespective of the window function. Nevertheless, for the rectangular window, this relation can be further simplified to p≤ L/2, as Ω_s = 1/TR and Ω_c = 1/(L.TR). Practically though, we recommend a stricter step size limit to avoid dynamic correlation distortion due to the small number of sampling points. For example, as it is apparent in Fig. S. 4, as p approaches its limit, SWC becomes distorted. Additionally, Fig. 4 illustrates the SWC distortion for p = 20 that is less than the upper bound limit (25 time points) for the simulated data. Thus, as a rule of thumb, we recommend limiting shift size to half of its theoretical limit, i.e. p ≤ Ω_s/ 4Ω_c for SWC analysis in real Fmri time series.

Also, we observed that mRect window led to higher network state identification rate, compared to the widely-used windows. It is important to reiterate that here we created simulated networks that remain in a single state for a long period (over 60 s), as the spatial maps (referred as ‘states’ in this study) of resting state brain connectivity networks have shown a long stability on the scale of minutes (Allen et al., 2014; Gonzalez-Castillo et al., 2014). We postulated that the fast variations associated with the state transitions contributed to the outperformance of mRect window compared to the regular rectangular and tapered windows. We observed that there is a significant lag between the real time of state transitions and the transition time identified by the tapered windows (see example data shown in Fig. 7). Using these windows, the time points are not weighted evenly, with the central point weighted the highest. Thus, their sensitivity to a sharp state transition is lower compared to the rectangular and mRect windows. Although the tapered shape of these windows can yield lower sensitivity to noisy observations, it can also decrease their sensitivity to the fast state transitions; similar outcomes have also been reported by (Shakil et al., 2016). Although the length of mRect window was higher throughout our analyses, we showed a statistically higher state identification performance for the mRect window compared to the rectangular window. Remember that larger window lengths can be associated with lower state identification rates (Shakil et al., 2016). Thus, this outcome emphasizes the importance of efficient fast dynamic correlations retrieval in state identification independent of the window length.

Of course, the current study has its own limitations. For instance, mRect requires a window function with larger number of time points in comparison with the conventional rectangular window. This could be a potential challenge especially in the studies with short Fmri time series. Furthermore, analyses using a longer window size may fail to detect short state transitions (Shakil et al., 2016). Note that although resting state networks tend to remain in the same state for a long period (Gonzalez-Castillo et al., 2014; Shakil et al., 2015), short transitions may also occur in resting state (Allen et al., 2014). A major challenge for studies evaluating SWC measures is the absence of ground truth. Here, we used pointwise multiplication of the two time series to validate the SWC series and compare them between different window functions. The pointwise multiplication is supposed to only represent the dynamic relations between the time series, and is not affected by the spurious fluctuations that correlation coefficient may represent. However, note that pointwise multiplication is not a perfect ground-truth for network connectivity analysis, as it does not provide a normalized connectivity measure. Finally, although we presented how the proposed window operated on simulated Fmri connectivity networks with sharp transitions over time and examples of real Fmri time series, future studies are required to reproduce and validate the findings of this paper using real Fmri connectivity networks. Future work should investigate how the performance of different windows may differ in retrieving the real Fmri connectivity data which show smooth transitions over time (Allen et al., 2014).

5. Conclusions

The SWC analysis consists of essential frequency-dependent properties that can significantly vary the dynamic functional connectivity measures quantified by this methodology. For instance, a sliding window operates as a low-pass filter on the dynamic correlations. Here, we demonstrated that there is a non-uniform frequency spectrum associated with sliding window functions. We showed that the conventionally-used sliding window functions tend to suppress the fast dynamic correlations. We then proposed the mRect window with a flattened spectrum to modify the suppressing effect on the fast dynamic correlations. The proposed window significantly outperformed the popular windows in network state identification suggesting that it should be a prominent window function candidate in sliding window correlation analysis of functional connectivity networks.