Divergent Aging of Isogenic Yeast Cells Revealed through Single-Cell Phenotypic Dynamics

Summary

Although genetic mutations that alter organism’s average lifespans have been identified in aging research, our understanding of the dynamic changes during aging remains limited. Here, we integrate single-cell imaging, microfluidics, and computational modeling to investigate phenotypic divergence and cellular heterogeneity during replicative aging of single S. cerevisiae cells. Specifically, we find that isogenic cells diverge early in life towards one of two aging paths, which are characterized by distinct age-associated phenotypes. We captured the dynamics of single cells along the paths with a stochastic discrete-state model which accurately predicts both the measured heterogeneity and the lifespan of cells on each path within a cell population. Our analysis suggests that genetic and environmental factors influence both a cell’s choice of paths and the kinetics of paths themselves. Given that these factors are highly conserved throughout eukaryotes, divergent aging might represent a general scheme in cellular aging of other organisms.

Introduction

Cellular aging is a complex, dynamic process, driven by a wide variety of molecular and cellular damage (Kennedy et al., 2014). As a result, even genetically identical cells can age with distinct phenotypic changes and at significantly different rates. Previous studies have focused on identifying genes and factors that influence the average lifespan of a cell population (Guarente and Kenyon, 2000). However, the temporal dynamics of cellular changes during aging and how these dynamics differ among individual cells remain largely unclear. Careful investigations of single-cell aging dynamics, which hold the promise of tremendously advancing the mechanistic understanding of cellular aging, have long been hindered by technological challenges. Recent developments in timelapse imaging technologies have provided powerful tools for analyzing single-cell dynamics (Harton and Batchelor, 2017; Levine et al., 2013; Purvis and Lahav, 2013). In this study, we integrated advances in these technologies with stochastic modeling to investigate cellular aging processes and unraveled how isogenic cells undergo distinct age-dependent phenotypic changes and progress through divergent aging trajectories.

We chose the replicative aging of yeast S. cerevisiae as a model system to study the dynamics of single-cell aging. For over 50 years since its first analysis, yeast replicative aging has served as a genetically tractable model for the aging of mitotic cell types such as stem cells and has led to the identification of many well-conserved genetic and environmental factors that influence longevity throughout eukaryotes (He et al., 2018; Steinkraus et al., 2008). Similar to stem cells (Inaba and Yamashita, 2012), budding yeast cells divide asymmetrically: the mother cell keeps more volume than daughter cells, and cellular components are also partitioned unequally between the mother and daughter cells. Due to this asymmetric segregation, aging-promoting factors, such as damaged proteins and aberrant genetic material, are believed to be primarily retained in the mother cell so that daughter cells can be rejuvenated and start a healthy life with full replicative potential (reviewed in Henderson and Gottschling, 2008; Yang et al., 2015).

Replicative lifespan (RLS) is defined as the number of cell divisions of a mother cell before its death (Mortimer and Johnston, 1959). The conventional method for studying replicative aging in yeast involves manual removal of daughter cells from mother cells after each division (Steffen et al., 2009), which is labor-intensive and low-throughput. Furthermore, it does not allow tracking of cellular changes during aging. Advances in microfluidic technology have enabled continuous live-cell measurements of aging mother cells and hence have made possible studying the dynamics of physiological changes during single-cell aging (Chen et al., 2016).

We have recently reported the development of a microfluidic device that enables tracking of mother cells and each of their new-born daughters during their entire lifespan, thereby capturing the complete aging process (Li et al., 2017). Here we combined this experimental platform with computational modeling to analyze the heterogeneous aging dynamics in single yeast cells and to examine how distinct genetic and environmental factors regulate these dynamics.

Results

Early-life divergence of isogenic cells towards two distinct aging paths

Using a recently-developed microfluidic device and time-lapse microscopy, we tracked the phenotypic changes of isogenic yeast cells during aging in a well-controlled and constant environment. A unique feature of our device is the long finger-shaped chamber that can trap the mother cell throughout its entire lifespan, which specifically allows monitoring daughter cells for at least one cell cycle (Li et al., 2017). This design provides important information about the sizes and morphologies of new-born daughter cells, which could reflect the physiological state of their mother cell at different ages. We observed heterogeneous phenotypic changes during the aging process of isogenic cells. Some cells, during aging, continuously produced daughter cells with a characteristic elongated morphology until death, whereas the other cells, during later stages of aging, produced small round daughters with sharply increased cell cycle length (Figure. 1A).

Figure 1. Single-Cell Phenotypic Analysis Reveal Two Divergent Aging Paths.

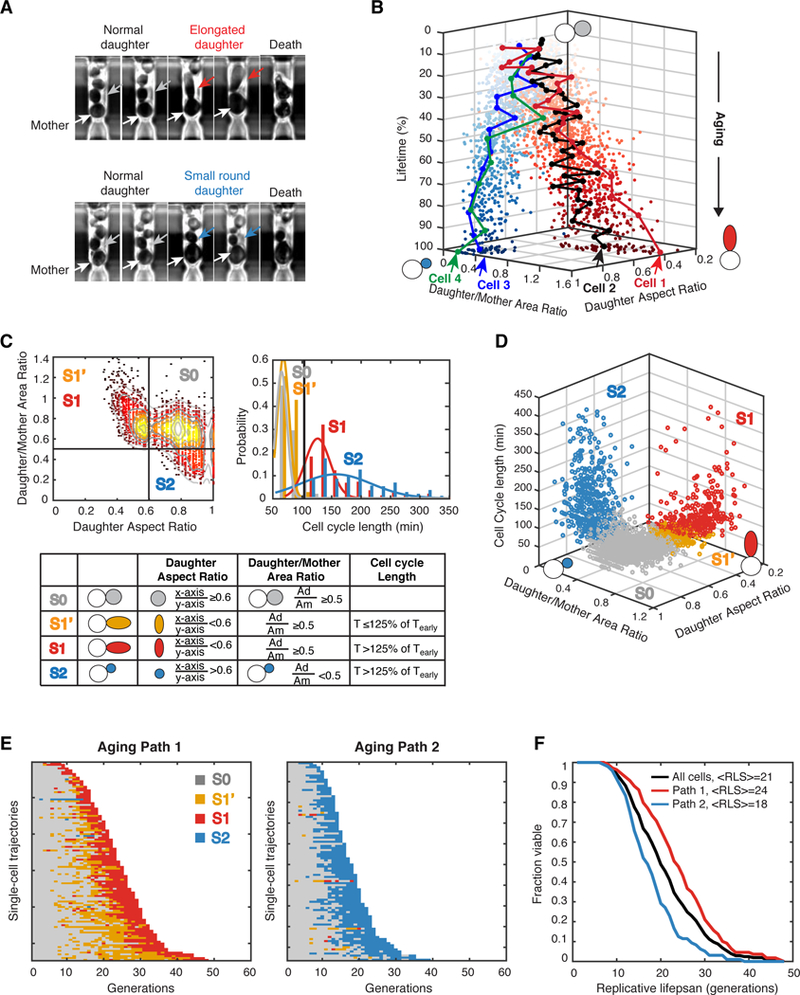
(A) Representative images of cells illustrating two distinct types of morphological changes during replicative aging. Top row: a mother cell producing elongated daughters during aging; bottom row: a mother cell producing small round daughters during aging. White arrows point to mother cells. Grey arrows point to early normal daughters. Red arrows point to elongated daughters. Blue arrows point to small round daughters. (B) Representative single-cell aging trajectories along two diverged paths toward cell death. Each dot represents the morphology state (Daughter/Mother Area Ratio; Daughter Aspect Ratio) of an aging mother cell at one cell division. Z axis shows the percentage of lifetime. Four representative single-cell trajectories are shown: Cell1 and Cell 2 are moving along the path with elongated daughters (red dots), while Cell 3 and Cell 4 are moving along the path with small round daughters (blue dots). The distance between two adjacent dots in one single-cell trajectory represents the length of this cell division. Arrows indicate the points of cell death. (C) Categorization of age-dependent phenotypic conditions into four states. Daughter/Mother Area Ratio, Daughter Aspect Ratio, and Cell Cycle Length have been measured for each aging mother cell at each cell division. Thresholds used to define states are indicated by black lines. Top left panel: the distribution of daughter aspect ratio vs daughter/mother area ratio. Top right panel: the distributions of cell cycle lengths. Bottom panel: the definitions of the four states (S0, S1’, S1 and S2) based on the three quantified phenotypic metrics. T_early-the mean cell cycle length of the first 25% of lifespan. See also Figure S8. (D) Distributions of the four states within the 3-D phenotypic metric space. (E) Single-cell state transition trajectories along two distinct aging paths. Each row represents the time trace of a single cell throughout its lifespan. Cells are sorted by their lifespans. Colors represent their cellular states: S0-grey, S1’-orange, S1-red, and S2-blue. Aging Path 1 (left): cells transitioned through S0, S1’ and S1 (n=109); Aging Path 2 (right): cells transitioned through S0 and S2 (n=96). (F) Replicative lifespans of two aging paths. Aging Path 1-red; Aging Path 2-blue; Combined-black.

To quantitatively analyze the dynamic changes during single-cell aging, we measured three phenotypic metrics for each mother cell at each of its divisions: the aspect ratio of width and height for elliptical fit of the daughter cell; the area ratio between daughter and mother cells; and the cell cycle length. We performed this quantification for a total of 205 wild-type mother cells throughout their entire lifespans. We tracked the age-dependent changes of these phenotypic metrics in individual mother cells and found two highly divergent aging paths: one path moving towards decreasing aspect ratios of daughters (elongated daughter morphology) until death, whereas the other path progresses towards lower daughter/mother area ratios (small round daughter). The majority of cells entered one of these two paths quite early in their life and proceed along the selected path toward their final death (see representative cell trajectories in Figure. 1B and Movies S1 and S2).

Based on the distributions of the three phenotypic metrics, we further categorized the age-dependent phenotypic conditions into four discrete states (Figures. 1C and 1D). State 0 (S0) is the initial state of young mother cells, characterized by producing round daughter cells with comparable sizes to that of the mother cell (aspect ratio ≥ 0.6; daughter/mother area ratio ≥ 0.5). State 1 (S1) is the state when a mother cell produces elongated daughters (aspect ratio < 0.6; daughter/mother area ratio > 0.5) and the cell cycle becomes significantly longer (> 125% of the mean cell cycle length of the first 25% of lifespan). Between State 1 and State 0, we also defined State 1’ (S1’), where a mother cell produces an elongated daughter cell, but the cell cycle length is similar to that of S0 state (≤ 125% of the mean cell cycle length of the first 25% of lifespan). State 2 (S2) is the state when a mother cell goes through significantly extended cell cycle (> 125% of the mean cell cycle length of the first 25% of lifespan) and gives birth to a small round daughter (aspect ratio ≥ 0.6; daughter/mother area ratio < 0.5). These thresholds for state distinction are chosen according to inherent features of the distributions of daughter aspect ratio, daughter/mother area ratio and cell cycle duration, as shown in Figure. 1C (see Quantification of Phenotypic Metrics in the Methods for more details).

We plotted the state transition traces for all aging mother cells in Figure. 1E. About 51% (104 out of total 205 cells) of cells first transition back and forth between S0 and S1’ during the early phase of aging and then proceed to a more frequent S1’ state and eventually a consecutive S1 phase until death (defined as “Aging Path 1”; Figure. 1E, left). In contrast, 41% (83 out of 205) of cells never transition to S1’ or S1 in the whole life; instead, these cells switch directly from S0 to a consecutive S2 state at the intermediate aging phase (defined as “Aging Path 2”; Figure. 1E, right). Intriguingly, the vast majority of cells make their fate decisions at early ages. The decision between two aging paths occurs as early as the first transition to S1’ or S2, within 5–10 divisions after birth. Once the decision has been made, most cells will proceed through this path until death, though a small fraction of cells did undergo cross-path transitions. About 6% (13 out of total 205 cells) of cells showed occasional transitions to S1’ or S1 before switching to the consecutive S2 state, while 2% (5 out of total 205 cells) of cells experienced S2 before committing to Aging Path 1 (Figure. 1E). These results indicate that fate switching is possible but rare. For simplicity, we categorized this small fraction of cross-path cells into Path 1 or 2 based on their terminal states.

The two aging paths result in different average lifespans. Aging Path 1 has a longer lifespan than Aging Path 2 (Figure. 1F, 24 vs 18). Hence, cells moving along Aging Path 1 are more likely to be longer-lived than Path 2 cells. In addition, lifespan is also influenced by the state transition kinetics during aging. We observed that, among Path 1 cells, longer-lived cells usually have a longer S0/S1’ (grey/orange in Figure. 1E) phase, while the later sustained S1 (red in Figure. 1E) phase remains relatively constant among cells. This observation suggested that the transition between S0 and S1’ delays a cell’s entry into the consecutive S1 phase and hence is highly correlated with the final lifespan (Figure. S1). For Path 2 cells, a longer lifespan is often associated with a later switching to S2. Therefore, the divergence of aging trajectories and the variance in state transition kinetics, together, contribute to the heterogeneity in lifespans of isogenic cells.

A stochastic discrete-state model for single-cell aging

To establish a quantitative framework for understanding heterogeneous aging processes, we developed a stochastic discrete-state model for single-cell aging (Figure. 2A). Based on the phenotypic measurements and quantifications described in Figure. 1, our model assumes that a cell can be in one of the four states, S0, S1’, S1 and S2, at each age. A new-born mother cell always starts from S0 and switches to other states during aging. Transition from state Si to Sj is stochastic and described by the transition probability p_ij that depends on the cell age. For example, p₀₁(N) indicates the probability to switch from S0 to S1 at the age N. Our experimental data suggest thatp_01,, p₀₁ and p₀₂ all increase with replicative age, whereas p₀₀ (the probability of remaining at S0) decreases with age. In addition, from the data, we did not observe any direct transitions between S1’ and S2 or between S1 and S2, so we set those transition probabilities at zero. Finally, based on the data, we assume that an extended S1 or S2 phase can lead to cell death, the probabilities of which depend on the number of consecutive divisions (M) in either state.

Figure 2. A Stochastic Model for Phenotypic State Transitions During Aging.

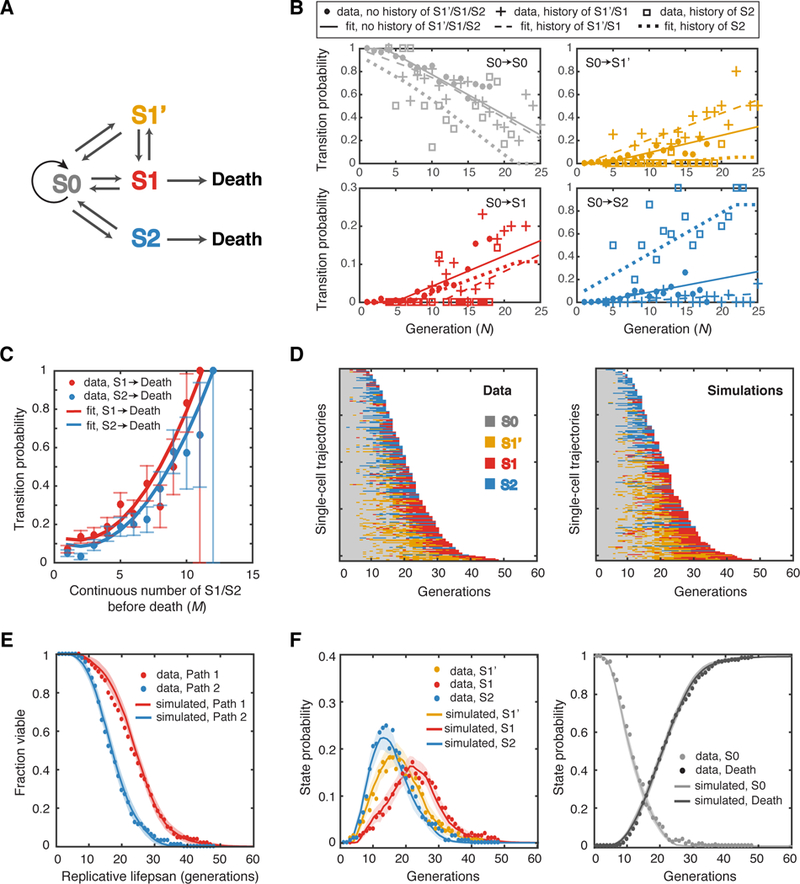
(A) Schematic diagram of the discrete-state model. The transitions between states are indicated by arrows. (B) Transition probabilities deduced from data fitting. The fractions of all cells at S0 of a given generation N that switch to S0, S1’, S1 or S2 at the next cell cycle (gray, yellow, red and blue solid circles, respectively) have been computed as a function of age (N). The transition probabilities for S0 cells with the experience of only S0 (no history), the most recent experience of S1’/S1 (history of S1’/S1) or S2 (history of S2) have been calculated separately. The best linear fits are shown by lines with the same color. See also Figures S2, S4 and S9 and Table S1. (C) The transition probabilities from S1 or S2 to death deduced from data fitting. Solid circles represent the fractions of cells that died exactly after M consecutive generations in S1 or S2 over the total number of cells that lived for at least M consecutive generations in S1 or S2 (red-S1, blue-S2). Red and blue curves are best fits of these data using polynomial functions of M. The error bars indicate the expected standard deviation, as described in Method, Computational Modeling. See also Figure S3 and S10. (D) Single-cell state transition trajectories from the data (205 cells) (left), and from stochastic simulations (right). Each row represents the time trace of a single cell throughout its lifespan. (E) The lifespans of two aging paths from simulations (red and blue curves) in comparison with experimental data (red and blue solid circles). Simulated lifespans were averaged from 50 simulations, each with 205 cells. Standard deviations of simulations are shown by shaded areas. (F) Age-dependent state distributions of S1’, S1, S2 (left panel) and S0 and Death (right panel). Solid circles represent the experimental data. Solid curves represent simulated results averaged from 50 simulations with shaded areas showing standard deviations of simulations.

To deduce the transition probabilities from the single-cell data, we computed the fraction of all the cells at Si (i=0, 1’, 1, 2) of a given age that switch to Sj (j=0, 1’, 1, 2) at the next cell cycle. As these data showed, the probability of staying at S0 decreases linearly with age, while the probabilities of transitioning from S0 to other states increases linearly with age (Figure. 2B). To accurately simulate the experimental data, we found it necessary to separately compute the transition probabilities from S0 to Sj (j=0,1’,1,2) depending on the previous history that cells in state S0 have experienced. In this context, we consider cells to have a “history of S1’/S1” if their most recent state excursion from the S0 state was to states S1’ or S1. Similarly, we define cells in state S0 as having a “history of S2” if their most recent excursion from S0 was to state S2. Cells that are in state S0 with a history of S1’/S1 have a higher transition probability to switch to S1’ or S1 than cells currently in S0 but with a different history (Figure. 2B, panels for S0-> S1’ and S0-> S1). Conversely, cells with a history of S2 are significantly more likely to transit from S0 back to S2 compared to cells with a history of S1’ or S1 (Figure. 2B, panel for S0-> S2). In our model, we found that it is sufficient to recapitulate the history effects on current S0 cells by only considering the most recently visited state other than S0 (S1’/S1 and S2), and without considering the time that has passed since. Using linear regression, we approximated three sets of p₀₀, p₀₁’, p₀₁, p₀₂, based on their histories, by linear functions of replicative age N (Figure. 2B-with only experience of S0, with the most recent experience of S1’/S1, or S2; Figure. S2). To keep assumptions minimal, we did not consider the history effects for other transition probabilities and hence computed only a single set of values for p₁’₀, p₁’₁’, p₁’₁, p₁₀, p₁₁’, p₁₁, p₂₀ and p₂₂ (Figure. S2 – all of the transition probabilities in WT). Furthermore, we calculated the fraction of cells that die after M consecutive divisions in S1 or S2. The fraction of cell death elevates dramatically as M increases. We approximated the probability of transition to death from S1 or S2 by a second-order polynomial function of M (Figure. 2C; Figure. S3A).

Using the transition probabilities from fitting, we performed stochastic simulations using our discrete-state model. The simulations generated single-cell state trajectories (Figure. 2D) that faithfully reproduce the single-cell data from experiments (Figure. 1E). The simulations also quantitatively captured the statistical properties of age-dependent state transitions within an aging population, including the average lifespans for Aging Path 1 and 2 (Figure. 2E) and the fractions of cells at each state during aging (Figure. 2F). The age-dependent state distributions (Figure. 2F) confirmed that the cells started to switch from S0 to either S1’ or S2 at about 5 to 10 divisions after birth. During this phase of life, through these transition events, cell fates are determined and diverge between two different aging paths towards death. Furthermore, from the model simulations, very few cells switch their paths in the middle of lifespan because of two reasons: First, the two paths appear largely irreversible due to rapidly decreasing probabilities of transitioning back to S0 during aging. Second, individual cells’ histories further bias cells to stay in the same path. It is important to note that, without the assumption of history-dependent transition probabilities from S0, the model produced switching frequencies between two paths significantly higher than those observed experimentally (Figure. S4A). Therefore, the history effect is critical for the early fate decision described above and thus for the divergence of the two aging paths.

In summary, our simple discrete-state model is sufficient to reproduce the observed heterogeneous dynamics of single-cell aging process. We next set out to use this model to investigate how genetic and environmental perturbations affect state transitions during aging and thereby influence lifespan.

Sir2 primarily regulates the state transition kinetics in Aging Path 1

We first examined the effect of sir2Δ mutants. SIR2 is the best-studied longevity gene to date, conserved from bacteria to humans. It encodes a lysine deacetylase that controls chromatin silencing and gene expression at various genomic sites (Gartenberg and Smith, 2016). We measured and quantified age-dependent phenotypic changes in sir2Δ cells. The sir2Δ cells showed all of the four states identified in aging WT cells, although the average lifespan is significantly shortened compared to that of WT (12 vs 21 divisions). As shown in Figure. 3A, the absence of SIR2 increased the fraction of cells that experience Aging Path 1 (142 cells in path 1, 46 cells in Path 2), reduced the appearance of S1’, and generally accelerated the transitions from S0 to other states.

Figure 3. Aging-Dependent State Transitions in the Short-Lived sir2Δ Mutant.

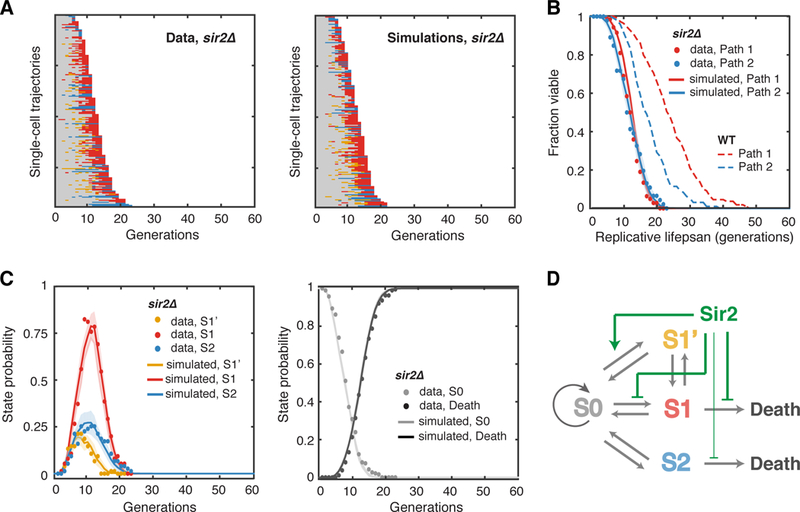
(A) Single-cell state transition trajectories of sir2Δ from the data (188 cells, 142 in Path 1, 46 in Path 2) (left), and from stochastic simulations (right). (B) The lifespans of two aging paths in sir2Δ from experimental data (red and blue solid circles) and from simulations (red and blue curves). Dashed curves are the WT lifespans from Figure. 1F for comparison. (C) Age-dependent state distributions of S1’, S1, S2 and S0 and Death in sir2Δ. Solid circles represent the experimental data. Solid curves represent simulated results averaged from 50 simulations with shaded areas indicating standard deviation. (D) Schematic diagram illustrates the effects of Sir2 at specific state transition steps. See also Table S1, Figures S4, S5 and S9.

We computed and fit the transition probabilities of the sir2Δ mutant at different cellular ages.Compared to that of WT, the transition probability from S0 to S1’ is significantly reduced, with or without a history of S1’/S1, whereas the transition probability from S0 to S1 becomes clearly elevated (Figure. S5 – all of the transition probabilities in sir2Δ). The probability of transition from continuous S1 to death is also increased (Figure. S3B). With these transition probabilities obtained from experimental data in sir2Δ, stochastic simulations reproduced the single-cell trajectories and the statistical properties of the aging population of sir2Δ cells (Figure. 3A–C).

Our modeling simulations revealed that sir2Δ can increase the fraction of cells going through Aging Path 1 due to a higher transition probability from S0 to S1, and at the same time, sir2Δ can reduce the appearance of S1’ cells by decreasing the transition probability from S0 to S1’. In WT, most cells transitioning through Aging Path 1 will first switch back and forth between S0 and S1’ for multiple cycles and then enter the consecutive S1 phase. In contrast, most sir2Δ cells will skip or shorten the intermittent S1’ phase and shortcut directly to the S1 phase (Figure. 3A and 3C). Therefore, Aging Path 1 in sir2Δ is accelerated towards death, resulting in a significantly shortened lifespan of Path 1 cells (Figure. 3B, comparing solid and dashed red curves). These results raise the possibility that the transition to S1’ might serve to signal as a damage rescue process, which is partially dependent on Sir2. Mother cells, at intermediate phases of aging, may occasionally segregate some cellular damage to daughters, coinciding with an abnormally elongated morphology of these daughter cells, and thereby temporarily alleviate damage accumulation in mother cells and slow their aging.

Taken together, these findings from our single-cell data and model simulations suggest that Sir2 primarily regulates the state transition kinetics in Aging Path 1. In particular, Sir2 slows aging by promoting the transition to S1’, a potential rescue state, and also functions by repressing the transitions to S1 and to death (Figure. 3D).

Sgf73 ensures the early-life divergence of the two aging paths

Having tested the effect of the short-lived sir2Δ mutant on state transitions during aging, we next considered sgf73Δ, a long-lived mutant with the most extended lifespan ever reported (McCormick et al., 2015). SGF73 is the yeast ortholog of human ataxin-7 (Mal, 2006), the gene that causes the neurodegenerative disease spinocerebellar ataxia type 7. SGF73 encodes a histone deubiquitinase module component of the SAGA/SLIK complexes that control the expression of numerous genes (Kohler et al., 2008; Lee et al., 2009). SGF73 has been found to regulate many aging-related processes, including rDNA recombination, subtelomeric silencing, and asymmetric segregation of rDNA circles (Denoth-Lippuner et al., 2014; Mason et al., 2017; McCormick et al., 2014).

We tracked the phenotypic changes of the sgf73Δ cells during aging and found that these cells, like wild-type, showed all four states. However, their times in S1’, S1 and S2 became much more intermittent, compared to those in aging WT cells. Interestingly, we observed that the two aging paths were less divergent and, the mutant cells would continue to switch between the two paths more frequently until late in their life (Figure. 4A, left, 93 cells in Path 1, 67 cells in Path 2). Compared with WT cells, a larger fraction (11% in sgf73Δ vs 6% in WT) of sgf73Δ cells transitioned to S1’ or S1 before switching to continuous S2 and death (17 out of total 160 sgf73Δ cells). Similarly, more cells (8% in sgf73Δ vs 2% in WT) showed transient transitions to S2 before entering the terminal S1 state (13 out of total 160 sgf73Δ cells). This cannot be simply explained by increased cell division numbers in sgf73Δ cells. Instead, the history dependence in transition rates from S0 to other states is the dominating factor for the high switching frequencies (Figure. S6; also see Figure. S4C).

Figure 4. Aging-Dependent State Transitions in the Long-Lived sgf73Δ Mutant.

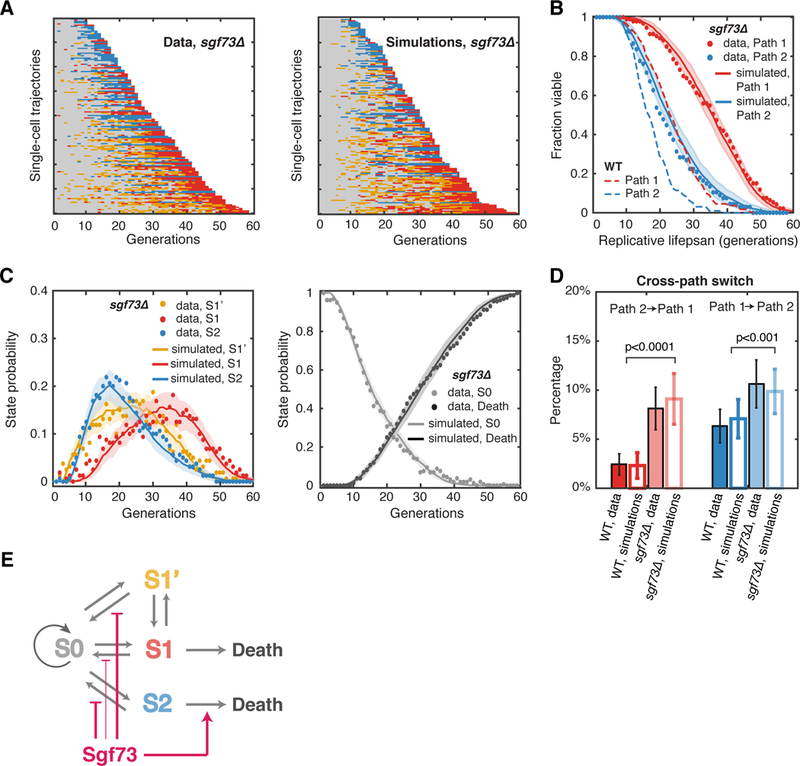
(A) Single-cell state transition trajectories of sgf73Δ from the data (16O cells, 93 in Path 1, 67 in Path 2) (left), and from stochastic simulations (right). (B) The lifespans of two aging paths in sgf73Δ from experimental data (red and blue solid circles) and from simulations (red and blue curves). Dashed curves are the WT lifespans from Figure. 1F for comparison. (C) Age-dependent state distributions of S1’, S1, S2 and S0 and Death in sgf73Δ. Solid circles represent the experimental data. Solid curves represent simulated results averaged from 50 simulations with the shaded areas showing the standard deviations of simulations. (D) Cross-path switching frequency in WT and sgf73Δ, calculated as a percentage of the total number of cells. Solid bars represent experimental data, with error bars indicating expected standard deviation (details see Method, Computational Modeling). Open bars represent simulations, with error bars indicating standard deviation of 50 simulations. p< 0.001 for both paths with two-sample t-test. See also Table S1, Figures S4, S6, S9 and S10. (E) Schematic diagram illustrates the effects of Sgf73 at specific state transition steps.

We computed and fit the transition probabilities of sgf73Δ and found that the transition probabilities from S1’, S1 and S2 back to S0 decreased much more slowly with age in the mutant compared to that of WT. In addition, the previous history had a weaker influence on the transition probabilities from S0 to S1’ or S1 (Figure. S6 – all of the transition probabilities in sgf73Δ). These two changes together contribute to more frequent reverse transitions and even switching between the aging paths. Furthermore, the transition probability from continuous S2 phase to death became dramatically reduced in the mutant (Figure. S3C). Consistently, our simulations showed that sgf73Δ did not postpone the onset of transitions to S1’, S1 or S2. Instead, due to more frequent reverse transitions and delayed cell death, the induction of cell fractions in these states lasted longer, resulting in an extended lifespan (Figures. 4B and 4C). The simulation showed higher possibilities of cross-path state transitions in sgf73Δ, consistent with the experimental observations (Figure. 4D).

These results from the sgf73Δ mutant revealed that Sgf73 promotes aging through at least two mechanisms (Figure. 4E). First, Sgf73 inhibits the reverse transition steps to S0 and thus represses cross-path transitions, which functions to ensure an early-life differentiation of individual cells with accelerated progression towards distinct aged states (S1 or S2). Second, once cells enter the S2 state, Sgf73 also expedites the progression to cell death.

Caloric restriction (CR) promotes the potential rescue state S1’

CR is the most robust intervention that extends lifespan in a wide range of organisms from yeast to mammals (Colman et al., 2009; Fontana et al., 2010; Lakowski and Hekimi, 1998; Partridge et al., 2005). However, the mechanisms underlying how CR, or environmental factors in general, influence aging-related processes remain obscure. Having examined the roles of genetic factors as described above, we now applied our approach to CR, to evaluate its effects on aging dynamics.

We found that, under CR (0.05% glucose), the majority of aging cells displayed an earlier and highly extended intermittent S1’ phase (Figure. 5A, left). As a result, a much larger fraction of cells went through Aging Path 1 than Path 2 (75% in Path 1, 192 cells vs 25% in Path 2, 65 cells), significantly different from aging under nutrient-rich conditions (Figure. 1E, left). In addition, the occurrence of the subsequent S1 phase and death in these cells was dramatically delayed, leading to a significantly extended lifespan of Path 1 cells. In contrast, the lifespan of Path 2 cells was not affected (Figure. 5B). We further computed transition probabilities and performed stochastic simulations. In agreement with the observations from single-cell data, the transition from S0 to S1’ occurred much earlier and more frequently under CR and lasted much longer, resulting in a delayed accumulation of cells in S1 (Figure. 5C; Figure. S7 – all of the transition probabilities under CR). The transition from S1 to death is also delayed under CR (Figure. S3D). At the same time, due to the competition from the early increased transition to S1’, the transition probability from S0 to S2 became much lower (Figure. 5C; Figure. S7A), and even among the cells with the terminal S2 state, ~58% of them experienced S1’ state early in their life (38 out of 65 cells ended in Path 2) (Figure. 5A, left). Therefore, CR regulates the aging dynamics primarily by promoting S1’, which biases cells toward a slowed Aging Path 1 (Figure. 5D).

Figure 5. Aging-Dependent State Transitions under CR.

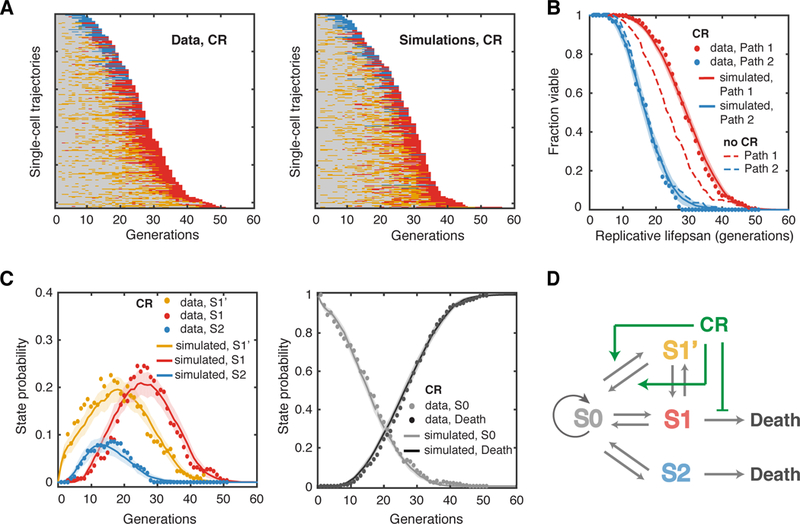
(A) Single-cell state transition trajectories under CR from the data (257 cells, 192 in Path 1, 65 in Path 2) (left), and from stochastic simulations (right). (B) The lifespans of two aging paths under CR from experimental data (red and blue solid circles) and from simulations (red and blue curves). Dashed curves are the WT lifespans under the glucose-rich conditions from Figure. 1F for comparison. (C) Age-dependent state distributions of S1’, S1, S2 and S0 and Death under CR. Solid circles represent the experimental data. Solid curves represent simulated results averaged from 50 simulations with shaded areas indicating standard deviation. See also Table S1, Figures S4, S7 and S9. (D) Schematic diagram illustrates the effects of CR at specific state transition steps.

These results are in support of our postulation that S1’ might serve as a potential rescue state that slows aging. Whereas the occurrence of S1’ is reduced in the short-lived sir2Δ mutant (Figure. 3), it becomes much more frequent in sgf73Δ and under CR (Figures. 4 and 5), both of which extend longevity. This correlation between S1’ and lifespan also holds true with measurements from single cells. Throughout isogenic populations tested in our study, individual cells with more frequent transitions to S1’ tend to have a longer lifespan (Figure. S1).

Model prediction and experimental validation

To further challenge our model, we wanted to see whether the model can capture all essential aspects of the aging dynamics in a condition it has not previously seen. In our model, the final lifespan of a cell largely depends on how late a cell enters the sustained S1 or S2 state; therefore, if the sustained S1 state is induced earlier in life, the lifespan would be shortened. We set out to test whether our model can predict (without fitting parameters) the state changing dynamics of an experiment during which we artificially introduce the S1 state in the middle of the average WT lifespan.

To chemically induce the S1 state, we used nicotinamide (NAM), an inhibitor of Sir2. We have previously showed that cells exposed to 5 mM NAM largely resembled the phenotypic changes and aging dynamics of the sir2Δ mutant (Li et al., 2017), featuring an early occurrence of the S1 state. To quantify the S1 induction effect of NAM, we did control experiments in which cells are treated with constant 5 mM NAM and obtained transition rates from the data. The state transition dynamics and lifespan with constant 5mM NAM treatment are similar to those of sir2Δ (Figure. 6A–D).

Figure 6. Model Prediction and Validation for a Dynamic Perturbation of Aging.

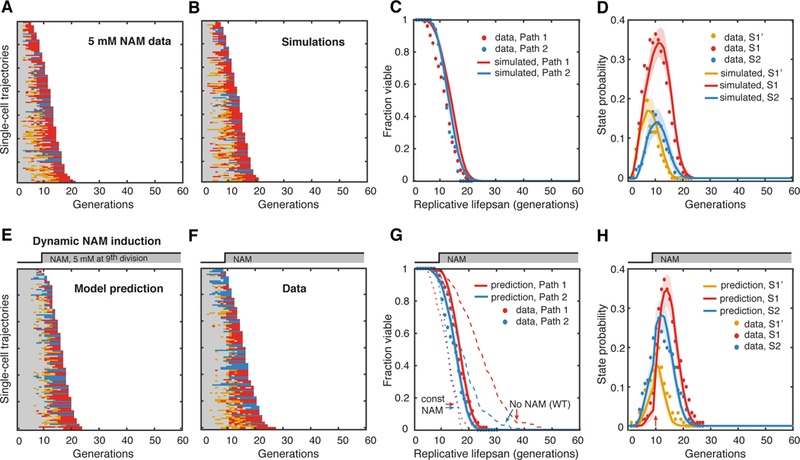
(A) Single-cell state transition trajectories under 5 mM constant NAM from the data (137 cells with 104 in Path 1, 33 in Path 2) and (B) from stochastic simulations. (C) The lifespans of two aging paths under 5 mM constant NAM from experimental data (red and blue solid circles) and from simulations (red and blue curves). (D) Age-dependent state distributions of S1’, S1, S2 under 5 mM NAM. Solid circles represent the experimental data. Solid curves represent simulated results averaged from 50 simulations with shaded areas indicating standard deviation. (E) Model-predicted single-cell state transition trajectories of WT cells in response to the step input of 5 mM NAM at 9^th generation. (F) Experimental state transition trajectories of WT cells with the step input of 5 mM NAM after 600 mins, when more than 70% of cells just enter their 9^th generation. (G) The lifespans of two aging paths in response to the dynamic perturbation. Predictions: red and blue curves; Experimental data: red and blue solid circles. Dashed curves are the lifespans for no NAM treatment and constant NAM treatment. (H) Model-predicted age-dependent state distributions of S1’, S1, S2. Note the sharp increase of S1 and S2 at 10^th division (pointed by the red arrow). Solid curves are predictions averaged from 50 simulations with shaded areas indicating standard deviation. Solid circles represent the experimental data. See also Table S1.

With this information on NAM-driven S1 induction, we then let our model to predict the aging dynamics when the S1 state is artificially induced in “middle-aged” WT cells. More specifically, the model generated predictions of state transitions and lifespan distributions for a scenario where WT cells first age normally and then NAM is added to induce the S1 state at the 9^th generation (Figure. 6E, and curves in G and H). The model predicted a sharp increase in the S1 state (also S2 state, though not as much as S1) (Figure. 6E and curves in H) and a shortened lifespan that falls between that of normal aging and that of NAM treated from age zero (Figure. 6G, curves).

To test the predictions, we performed corresponding experiment, in which 5 mM NAM was introduced to normally aging WT cells after 600 minutes, when about 71% cells just entered the 9^th generation, close to half of their normal RLS (21 generations). As shown in Figure. 6F, dots in G and H, the experimental data quantitatively matches the model predictions. This is significant in that, based only on the rates inferred from the normal aging condition and the constant NAM-treated condition, our model can accurately predict dynamic perturbations, without fitting parameters or any additional assumptions.

These results validated our model and convincingly demonstrated its predictive power. Furthermore, the analysis of dynamic perturbations, such as the one presented here, can be used to shed light on mechanisms that drive the aging process.

Discussion

Recent developments in microfluidics have enabled direct observations of phenotypic and molecular changes during aging at single-cell and molecular resolution, which will shed light on the mechanisms that drive single-cell aging (Chen et al., 2016). It nicely complements the traditional microdissection method, which measures lifespan as the primary readout, and provides important information about aging-related biological changes that result in the observed lifespan (Polymenis and Kennedy, 2012). Yet an emerging challenge is to interpret newly available single-cell dynamic data to advance our understanding of aging process. In this study, we developed a quantitative framework for analyzing the single-cell aging data. In particular, we defined distinct age-related cellular states from phenotypic changes and devised a stochastic model to describe heterogeneous state changes in individual aging cells with transition probabilities from single-cell data. We used this framework to investigate how and why isogenic cells age with different phenotypic changes and rates, a long-standing question in the biology of aging.

Cellular aging is associated with numerous molecular changes and damage accumulations (Crane and Kaeberlein, 2018). One scenario of the aging process is that, individual cells end up with different causes of aging and death, simply depending on which molecular changes or damages dominate near the end of lifespan. Therefore, stochasticity in the progression of and competition between different molecular changes or damage accumulation might underlie the heterogeneity in phenotypes and lifespans of genetically identical cells. Another possible scenario is that aging is a well-programmed process, with sequentially ordered molecular events leading to death. In this case, the heterogeneity might come from the variability in the kinetics between transition steps.

Our analysis revealed that the aging process is likely a combination of both scenarios: during the early phase of aging, at least two major molecular processes compete and result in two divergent aging paths. Once the decision has been made, a cell will proceed along the selected path, with characteristic phenotypic changes, toward cell death. The two paths are relatively irreversible as switching between the two paths rarely occurs. Hence, the two paths should be driven by distinct and sequentially programmed molecular processes leading to cell death. Previous studies suggested that one aging path characterized with elongated daughters (Path 1) might be associated with a loss of chromatin silencing at the rDNA region (Li et al., 2017), whereas the other path with small round daughters and sharply extended cell cycle lengths (Path 2) might be related to mitochondrial dysfunction (Xie et al., 2012). A future systematic analysis of aging-related molecular markers is needed to elucidate the molecular basis of these aging paths.

Previous modeling studies of aging have focused primarily on specific molecular networks that drive deterministic population-level aging processes (Auley et al., 2015; Janssens et al., 2015; Kriete et al., 2010; Lorenz et al., 2009; Rodriguez-Brenes and Peskin, 2010; Wieser et al., 2011). Due to the scarcity of aging-related data, very few of the studies were based on sufficient experimental data. Our model differs from previous studies in that it addresses the stochastic nature of cellular aging, focusing on the variability in single-cell aging dynamics, and it is supported by extensive single-cell data. The model is phenomenological and simple, considering only four discrete cellular states, but it effectively reproduces the observed dynamics and variability of phenotypic changes in isogenic cell populations. Moreover, it also provides crucial insights into the kinetics, history dependence and divergence of single-cell aging trajectories. For example, the model reveals two reasons that contribute to the divergence in aging paths. One is due to a rapidly increasing transition probability from S1’ and S1 to S1(p_1’1, p₁₁) and a decreasing transition probability from S2 to S0 (p₂₀) during aging. Once a cell has transitioned to S1’ or S2, it becomes unlikely to switch back to S0 and hence will stay in Aging Path 1 or 2. However, with only this mechanism at work, switching between the two paths would still be more frequent than that observed in experiments (Figure. S4). The second cause of divergence comes from the history effect on transitions away from S0 in the early or middle phase of lifespan-the histories of most recent visits to S1’/S1 or S2 strongly bias the transition from S0 to the previously visited state, locking the cell into the path that is chosen in the early phase of lifespan.

Taking one step forward, we used our experimental and modeling approaches to analyze the effects of relevant genetic and environmental factors and obtained new insights in how these factors regulate the aging processes. Sir2, a well-studied deacetylase that controls chromatin silencing, stands as a proof-of-concept example in our studies. Our analysis of the single-cell data showed that Sir2 specifically regulates the state transitions in one of the aging paths (Aging Path 1, characterized with elongated daughters), linking this path, as well as states S1’ and S1, to the changes in chromatin silencing process. This is in accordance with previous molecular-level observations that a loss of chromatin silencing leads to the aging phenotype featured by the elongated daughter morphology (Li et al., 2017). It suggests that Sir2, by enhancing the intermittent dynamics of chromatin silencing, enables cells to switch back and forth between S0 and S1’ states and hence impedes the progression of these cells along Aging Path 1 towards death, leading to an extended lifespan. We also pursued analysis of SGF73, the deletion of which drastically extends the lifespan through mechanisms significantly less well studied than SIR2. We found that, in contrast to Sir2, which regulates a specific aging path, Sgf73 controls multiple different transition steps in both aging paths, consistent with previous biochemical results showing the pleiotropic functions of Sgf73 on many molecular processes (Denoth-Lippuner et al., 2014; Mason et al., 2017; McCormick et al., 2014). Moreover, although the two aging paths are mostly divergent in WT cells, we observed a larger fraction of sgf73Δ cells switch between the two paths, which suggests that the divergence in aging paths might represent a precisely regulated differentiation process, governed by molecular factors, such as Sgf73 or its substrate(s). The molecular mechanisms and physiological roles of this aging-dependent differentiation deserve further investigation. Finally, when applying our approach to examine the effects of CR, we found that CR biases cells toward Aging Path 1 and at the same time, decelerates the cells’ progression through Aging Path 1 to death. Previous studies showed that CR extends longevity through conserved nutrient-mediated kinases, including PKA, TOR and Sch9 (Kaeberlein et al., 2005). Our analysis suggests that these kinases might regulate aging primarily through modulating molecular processes driving Aging Path 1, again setting the stage for the discovery of aging-critical phospho-proteins.

The analysis of the genetic and environmental perturbations we focused on uncovered a potential anti-aging role of a specific cellular state, S1’, which is characterized by elongated daughter morphology and normal cell cycle length. Whereas the short-lived sir2Δ mutant showed a reduced appearance of S1’, the long-lived sgf73Δ mutant and CR both promoted the occurrence of this state during aging. We speculate that this state in some ways weakens the damage segregation barrier between mother and daughter cells. This will result in daughter cells with an abnormal morphology and probably a shortened lifespan, but at the same time, will temporarily relieve the mother cell from damage accumulation, slowing its aging. Our previous study revealed a correlation between this phenotypic state with short-term losses of chromatin silencing or Sir2 activity (Li et al., 2017). For future studies, it would be interesting to test this damage relief hypothesis and examine how Sir2 or chromatin silencing contributes to the process by monitoring intracellular damage molecules and phenotypic changes in the same aging cells in response to perturbations of Sir2 activity.

In this study, we integrated single-cell dynamic measurements with computational modeling and revealed the divergence of genetically identical cells along two major aging paths. The selection of the aging paths is tightly regulated by genetic and environmental factors, suggesting that cellular aging might be an actively regulated differentiation process, rather than a passive damage accumulation process. Our quantification and modeling efforts generated testable predictions that can guide future mechanistic studies. Furthermore, the phenomenological model we developed in this study could serve as a basic model for yeast aging, upon which more detailed, continuous, and mechanistic models can be built in the future.

KEY RESOURCES TABLE

Experimental Models: Organisms/Strains

REAGENT or RESOURCE	SOURCE	IDENTIFIER
BY4741 MATa his3Δ1 leu2Δ0 met15Δ0 ura3Δ0	S288C-derived strain	NH0256
BY4741 MATa his3Δ1 leu2Δ0 met15Δ0 ura3Δ0, NHP6a- iRFP-kanMX	Li et al., 2017	NH0268
BY4741 MATa his3Δ1 leu2Δ0 met15Δ0 ura3Δ0, RDN1::NTS1-PTDH3-GFP, NHP6a-iRFP-kanMX	Li et al., 2017	NH0270
BY4741 MATa his3Δ1 leu2Δ0 met15Δ0 ura3Δ0, NHP6a- iRFP-kanMX, RDN1::NTS1-PTDH3-GFP-URA3, sir2::HIS3	Li et al., 2017	NH0277
BY4741 MATa his3Δ1 leu2Δ0 met15Δ0 ura3Δ0, NHP6a- iRFP-kanMX, RDN1::NTS1-PTDH3-GFP-URA3, sgf73::HIS3	Li et al., 2017	NH0465

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Nan Hao (nhao@ucsd.edu).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Strain Construction

Standard methods for the growth, maintenance, and transformation of yeast and bacteria and for manipulation of DNA were used throughout. The yeast strains used in this study were generated from the BY4741 (MAT a his3Δ1 leu2Δ0 met15Δ0 ura3Δ0) strain background.

METHOD DETAILS

Time-Lapse Microfluidic Experiments

Replicative aging experiments were performed using microfluidic devices following the design principles previously described and validated in Li et al., 2017. Relevant to the work described here, each single cell trap has a wider opening on the top (6 μm) and a slightly narrower (3 μm) opening at the bottom. The design of the trap allows the mother cell at the bottom to bud either upwards or downwards. If a daughter cell is budded from the top of its mother cell, it will be pushed out of the trap; if born at the bottom of a mother cell, the daughter cell will leave the trap from the bottom opening. This design feature allows daughter cells to be observed after they detach from their mothers and as long as a few cell cycles if they are born from the top. The limitation of this device is that we could not observe daughter cells long enough to determine their lifespan or final morphologies.

The microfluidic device was designed in AutoCAD (Autodesk Inc.). Modeling of fluid flow in the device using COMSOL Multiphysics aided in design (COMSOL Multiphysics® v.5.3. COMSOL AB, Stockholm, Sweden.). The cell trapping region of this device is 18 μm long, 6 μm wide and 4.3 μm high, with a 3 μm opening at the bottom. The media flow channel is 100 μm wide and 20 μm high. Each device contains 100 cell traps. Two chrome quartz glass masks (HTA Photomask), one for each layer of the device, were used to pattern SU-8 negative epoxy photoresist (MicroChem Corp.) onto clean silicon wafers (University Wafer Inc.). SU-8 2005 and SU-8 2015 (MicroChem Corp.) were used to build the cell trapping region and the media flow layer, respectively.

Yeast cells were inoculated into 2 ml of synthetic complete medium (SC, 2% dextrose) and cultured overnight at 30°C. 2 μl of saturated culture was diluted into 20 ml of fresh SC medium and grown at 30°C overnight until it reached OD600_nm ~ 1.0. For loading, cells were diluted by 10-fold and transferred into a 60 ml syringe (Luer-Lok Tip, BD) connected to plastic tubing (TYGON, ID 0.020 IN, OD 0.060 IN, wall 0.020 IN). For WT, sir2Δ, and sgf73Δ experiments, SC medium with 2% dextrose and 0.04% Tween 20 was used. For caloric restriction experiments, SC medium with 0.05% dextrose and 0.04% Tween 20 was used.

Since the experiments studied the aging dynamics from the beginning to the end of a cell’s lifespan, it is important to ensure that cells loaded in our device indeed start from the beginning of their lifespans. To make sure only new born mother cells are loaded into traps, we consistently use cell culture at exponentially growing phase (confirmed in Li et al., 2017). In exponentially growing cultures, 50% cells are just born, 25% just divided once, 12.5% divided twice, 6.25% divided three time, etc. Thus, 93.5% cells have only divided no more than three times.

Time lapse microfluidic experiments were conducted as described in Li et al., 2017. In brief, devices were vacuumed for 20 min before imaging, and primed with 0.075% Tween 20 (Sigma-Aldrich Co.) for 5 min after vacuuming. Media ports were connected to 60 ml syringes with fresh medium with 0.04% Tween-20 via plastic tubing (TYGON, ID 0.020 IN, OD 0.060 IN, wall 0.020 IN). The waste ports were connected to a 50ml Falcon tube. A 60-inch-height difference between medium and waste was set to allow a flow rate (measured by amount of waste medium collected during experiments) of about 2.5 ml/day for all experiments.

Quantification of Phenotypic Metrics

Phase contrast images from microfluidic experiments were used for quantification. Daughter cells were fit to ellipses with the elliptic selection tool in ImageJ (Rasband, W.S., ImageJ 1.49v, National Institutes of Health, Bethesda, Maryland, USA, https://imagej.nih.gov/ij/,1997–2018. ) and both the area and aspect ratio of corresponding elliptic fits were measured using ImageJ. For each daughter cell, these metrics were measured consistently at the time frame immediately after the daughter cell was completely separated from the mother. The area of mother cells was measured in the same way at the same time point. Each cell division was identified and counted at the time frame when a bud was first observed in the mother. The time between two adjacent cell divisions of the mother cell is defined “Cell Cycle Length”.

The threshold for aspect ratio (0.6) comes from the minimum between the two peaks in the aspect ratio – daughter/mother area ratio space (Figure. 1C-left panel) along the aspect ratio axis. The threshold for daughter/mother area ratio (0.5) is chosen such that all cells with daughter aspect ratio <0.6 will stay above this threshold, and that cells with high daughter/mother area ratios stay orthogonal to the S1/S1’ area (a.k.a. cells with small daughter aspect ratio). The thresholds for aspect ratio and daughter/mother area ratio are drawn as the black lines in Figure. 1C-left panel. The cell cycle threshold is chosen by the difference in the distributions of cell cycle duration for those in S0 area and those in S2 area and S1 area. The threshold of cell cycle is drawn as the black line in Figure. 1C-right panel.

We systematically performed sensitivity analysis for threshold values to confirm whether the quantitative effects of mutants (sir2Δ and sgf73Δ) and the growth condition (0.05% glucose) on various transition rates (Figures. 3D, 4E and 5D) still hold (Figure. S8). The thresholds were varied within a −15% to 15% range at 5% intervals from the current chosen values. We varied the aspect ratio threshold (0.6) in the range of [0.51 0.54 0.57 0.6 0.63 0.66 0.69], the daughter/mother area ratio threshold (0.5) in the range [0.425 0.45 0.475 0.5 0.525 0.55 0.575] and cell cycle threshold (125%) with [106% 112% 118% 125% 131% 137% 143%] increase from the mean T_early. For each threshold change, we calculated transition rates in all experiments, and compared specific transition rates of interest: p₀₁’, p₀₁ and p_1D between WT and sir2Δ cells, p₁’₀, p₂₀, p_2D between WT and sgf73Δ cells, and p₀₁,p₁’₀,p_1D between WT and CR treated cells (Figure. S8). Since the same transition rates are defined for different ranges of replicative age in different experiments, it is not immediately obvious how to compare them directly (such as Figure. S8A). For a fair comparison, we therefore calculated the “total transition probability $P_{ij}=\frac{{\sum }_{k=1}^{\infty }{n}_{S_i\to S_j}^k}{{\sum }_{k=1}^{\infty }{n}_{S_i}^k}$, k=i, …, last generation, which is independent of the typical lifespan. Compared with WT cells, P₀₁’ remained smaller, P₀₁ and P_1D are higher in sir2Δ cells for all 3 sets of thresholds we tested (Figure. S8B–D). sgf73Δ cells kept higher P₁’₀, P₂₀ but smaller P_2D compared with WT cells (Figure. S8E–G). CR consistently led to P₀₁ and P₁’₀ higher than those of WT cells, and lowered P_1D (Figure. S8H–J). Our conclusions about the effects of different mutants and growth conditions on state transition dynamics therefore hold within the range of tested thresholds.

Computational Modeling

Our state transition model makes several assumptions: (1) mother cells start from state S0 and can exist in any one of the four states; (2) cells transition from one state to another with transition probabilities per cell division that are functions of replicative age; (3) the most recent visits to states S1’/Sl and S2 affect the transition probability from S0 to S1’, S1 and S2; and (4) if mother cells are in state S1 or S2, they have a certain probability to die, and the transition probability from S1 or S2 to death are a function of the number of continuous cell divisions in either S1 or S2 state.

Transitions between states are purely stochastic and are characterized by transition probabilities p_ij (i,j=0,1’,1,2) that depend on the replicative age of mother cells. To estimate these transition probabilities from single-cell data, we computed the fraction of all the cells at the state i (i=0, 1’, 1, 2) of a given generation that switch to the state j (j=0, 1’, 1, 2) at the next cell division for all available generations. As experimental data shows, the transition probabilities change linearly with cell division number (replicative age), though these rates fluctuate strongly when the incidences of transitions are low (Figures. S2, S5–S7). Using linear regression of the data, we approximate the dependence of p_ij at replicative age N by linear functions. The transition probabilities are fit by weighted linear least squares with metropolis sampling, where the weight is the square root of the number of cells which underwent the corresponding state transitions at a given generation N (Figures. S2, S5–S7). Transition probabilities are grouped into 6 sets: 3 sets for p_0j(j=0,1’,1,2) with three history conditions (see below for details), 1 set for p₁’_j (j=0,1’,1), 1 set for p_1j-(j=0,1’,1), 1 set for p_2j (j=0,2). Since transition rates represent probabilities per generation, they are capped at 0 and 1. If a transition rate, p_ij, hits the cap at any generation N, then all rates describing transitions originating from the same state $P_{\text{ik}}(\text{k}\ne \text{j})$, are kept at their current values for all generations following generation N. The transition rates in each of the six sets are fit simultaneously with the constraint that the sum of them equals 1. The error bar of transition probability pij at generation m (m=1, 2, 3, …) is the expected standard deviation, since we only have one dataset for each condition (each dataset contains 2–3 experiments to include more than 150 cells). For transition Si->Sj at division m, the expected standard deviation is calculated as the square root of (pij(1-pij)/N), where pij is the transition probability and N is the total number of cells in state Si at division m. This corresponds to the expected variability of pij due to the limited number of cells in our experiments, assumingthat pij is the true transition probability. This variability is inherent to binomial sampling of cells in state Si, where success is defined as a transition to Sj. When pij = 1 or 0, we use the square root of (1/N) to be conservative. Similarly, the error bars of switching frequency between paths are calculated in the same manner, as the “expected standard deviation”, indicating the uncertainty due to the limited number of cells, inherent to the nature of the experiments.

For transitions from state S0 to S0, S1’, S1 and S2, we further distinguish them based on whether a mother cell currently in state S0 has experienced S1’, S1 or S2 states before. This history dependence is equivalent to introducing two additional hidden states of S0 into the model: one is an S0 state where a cell enters after most recently visiting S1’ or S1 state (other than S2 state), the other is an S0 state where a cell enters after most recently visiting S2 state (other than S1’ or S1 state). We took the history into consideration because simulations without this differentiation consistently over-estimate the amount of cells switching between aging path 1 and path 2. That is, more trajectories switch to S2 state before they finally commit in S1 state, and vice versa (Figure S4). For the effect of history, we calculated three sets of transition rates from S0: one for cells with no history in states S1’, S1 or S2 (i.e. which have never left state S0); one for cells whose most recent excursion from S0 was to states S1’ or S1; and one for cells whose most recent excursion from S0 was to state S2. The history between S1’ and S1 are not further distinguished, since it is not necessary to reproduce the experimental data.

Based on the observation that almost all cells died after consecutive cell divisions in state S1 or S2, we postulate that cellular damages accumulate continuously in these states, and that the probability to die increases with the number of consecutive generation in either state. To estimate probabilities to cell death, we calculated the probability to die from S1 or S2 by the fraction $f_{\text{Si}\to \text{D}}(\text{i}=1,2)$ of cells that died after M consecutive generations in S1 or S2 to total number of cells that lived through M consecutive generations of S1 or S2. Evidently, this fraction increases with M until it reaches 1; meanwhile it becomes much noisier since the number of cells satisfied these conditions decreases drastically. We fit this ratio for all experiments to the simplest polynomial functions possible (Table S1, Figure. S3). For WT and sgf73Δ cells, the best fits are second-order polynomials; for sir2Δ and caloric restriction cells, first-order polynomials fit well.

Thus, this phenomenological model depends on state transition rates and death rates. Time unit in simulations is one generation/cell division. We simulated this model stochastically and in each in silico experiment we generated the same number of mother cell trajectories as in the experiment with the corresponding cell type or condition. Averaging over 50 in silico experiments for all experiments, we computed the fraction of cells in each state as a function of their replicative age N and the faction of cells alive at replicative age N as a function of M. The shaded regions in Figures. 2E–F, 3B–C, 4B–C, and 5B–C indicate standard deviations of the corresponding metrics from multiple runs, showing that the simulations faithfully reproduce the experimental data. We also plotted a set of individual cell state trajectories from one run ordered by their replicative lifespan (Figures. 2D, 3A, 4A, and 5A).

To check whether linear approximation for transition probabilities between S0, S1’, S1 and S2 is necessary, we tested a model that assumes of constant transition rates. We found the best constant fits for transition probabilities between the four states, and then performed simulations with these best fits for all four experiments. The best simulations using constant transition rates deviated greatly from the state distributions and survival curves of the experimental data (Figure. S9, compared to Figures. 2–5), justifying the use of linear approximations for the transition probabilities. We also tested the linear approximations for the transition probabilities to death for WT and sgf73Δ cells (simpler than the second order polynomials approximations used in the main text). In both cases, the survival rates from simulations deviated more from the data compared with simulations using second order polynomial fits (Figure. S10, compared to Figure. 2E and Figure. 4B). We calculated the mean square distance (msd) between simulations and the data to compare the linear vs second-order polynomial assumptions of death probability. For WT, the msd for survival rates are 2-and 3-fold of those in Figure. 2E for Path 1 and Path 2, respectively. For sgf73Δ cells, the msd for survival rate is 3-fold of that in Figure. 4B for Path 2, and comparable to that in Figure. 4B for Path 1.

Simulations and plots were generated using MATLAB (MATLAB and Statistics Toolbox Release 2015a, The MathWorks, Inc., Natick, Massachusetts, United States). The code from this work is available at GitHub https://github.com/MengJ-bioDyn/agingmodelstatetrans.

Supplementary Material

Movie S1. Morphological changes of a representative mother cell in Aging Path 1.

Left: the phase contrast movie of a mother cell trapped at the bottom of a finger-shaped chamber. The time-lapse images were taken from the beginning of the experiment to the end of this mother cell’s replicative lifespan, every 15 min. Right: the quantification of phenotypical changes of this mother cell at all cell divisions in the 3D space of Daughter/Mother ratio, Daughter Aspect Ratio and lifetime percentage as Figure. 1B. Each dot represents one cell division, color of dots represents the mother cell's state in that cell division. Z axis, the percentage of time in each cell division in the whole lifespan, from top to bottom, indicates the progress of aging.

Movie S2. Morphological changes of a representative mother cell in Aging Path 2.

Left: the phase contrast movie of a mother cell trapped at the bottom of a finger shaped chamber. The time-lapse images were taken from the beginning of the experiment to the end of this mother cell's replicative lifespan, every 15 min. Note that this cell budded downwards. Right: the quantification of phenotypical changes of this mother cell at all cell divisions in the 3D space of Daughter/Mother ratio, Daughter Aspect Ratio a 846 nd lifetime percentage as Figure. 1B. Each dot represents one cell division, color of dots represents the mother cell's state in that cell division. Z axis, the percentage of time in each cell division in the whole lifespan, from top to bottom, indicates the progress of aging.