Muscle force, work and cost: a novel technique to revisit the Fenn effect

ABSTRACT

Muscle produces force by forming cross-bridges, using energy released from ATP. While the magnitude and duration of force production primarily determine the energy requirement, nearly a century ago Fenn observed that muscle shortening or lengthening influenced energetic cost of contraction. When work is done by the muscle, the energy cost is increased and when work is done on the muscle the energy cost is reduced. However, the magnitude of the ‘Fenn effect’ and its mirror (‘negative Fenn effect’) have not been quantitatively resolved. We describe a new technique coupling magnetic resonance spectroscopy with an in vivo force clamp that can directly quantify the Fenn effect [E=I+W, energy liberated (E) equals the energy cost of isometric force production (I) plus the work done (W)] and the negative Fenn effect (E=I−W) for one muscle, the first dorsal interosseous (FDI). ATP cost was measured during a series of contractions, each of which occurred at a constant force and for a constant duration, thus constant force–time integral (FTI). In all subjects, as the FTI increased with load, there was a proportional linear increase in energy cost. In addition, the cost of producing force greatly increased when the muscle shortened, and was slightly reduced during lengthening contraction. These results, though limited to a single muscle, contraction velocity and muscle length change, do quantitatively support the Fenn effect. We speculate that they also suggest that an elastic element within the FDI muscle functions to preserve the force generated within the cross-bridges.

Summary: A novel non-invasive technique allows measurement of muscle force production and ATP use simultaneously. Muscle shortening is most energy costly, and lengthening least costly, a test of the Fenn effect.

INTRODUCTION

All muscles produce force during contraction. The mechanisms, costs and consequences have been the fodder for studies for at least the past century. Prominent among these studies are the pioneering experiments of A. V. Hill and his remarkable students (for review, see Bassett, 2002). One of those students, Wallace Fenn, is credited with the observation that if a muscle does work (in a shortening contraction), the energy it requires is increased by an amount roughly equal to the work done (Fenn, 1923). In an outstanding paper, Rall (1982) summarized the ‘Fenn effect’ quantitatively with the simple equation E=I+W [energy liberated (E) equals the energy cost of isometric force production (I) plus the work done (W)] but cautioned that the Fenn effect has not been quantitatively demonstrated.

A second observation also emerged from the same early experiments of Fenn. Namely, if muscles are stretched when they actively ‘contract’, the energy cost of force production is reduced compared with an isometric contraction of the same magnitude and duration. Fenn's second and less familiar conclusion was that ‘lengthening during contraction decreases the energy liberated’. Specifically he stated, ‘When the work done by the muscle is negative, the excess energy is also negative’ (Fenn, 1924). This observation caused considerable intrigue and, in retrospect, a somewhat puzzling search led by none other than Fenn's mentor A. V. Hill. Hill led an effort to demonstrate that the identical chemical reactions that consume ATP in muscle during shortening could be reversed when muscles are subjected to mechanical stretch (‘negative work’) during lengthening (eccentric) contractions (Abbott and Aubert, 1952; Abbott et al., 1952; Hill, 1960; Hill and Howarth, 1959). In other words, the operational hypothesis was that during lengthening (eccentric) contractions, muscles synthesize ATP, minimizing the energy cost relative to an isometric contraction (E=I−W?). For an outstanding review of this topic and its history, see Loiselle et al. (2008).

Although the notion of a muscle behaving like a generator when used ‘in reverse’ has been rejected and forgotten, the reduced cost of muscle force production during a lengthening contraction remains a poorly explained reality. Lengthening contractions are common in all animal movements, and it is apparent that these occur at a reduced energetic cost for the equivalent amount (magnitude and duration) of force produced relative to a shortening contraction (Bigland-Ritchie and Woods, 1976). Despite the general acceptance of this idea, there is no clear consensus of the magnitude of energy savings, let alone its cause. For example, when lengthening contractions are compared with isometric contractions, Beltman et al. (2004), like Bigland-Ritchie and Woods (1976), reported a reduction in the cost of lengthening contractions while paradoxically Ryschon et al. (1997) found a slight increase in cost, although neither result was statistically significant. One study on isolated single fibers examined energetics via inorganic phosphate release in shortening and isometric contractions (Homsher et al., 1997). They confirmed that shortening was more energetically costly than the equivalent force produced isometrically. Interestingly, this same study also included four fibers that were stretched while activated. Energy costs in these fibers were among the lowest measured in their study but an inadequate sample size prevented a statistical analysis.

Thus, rather than ‘settling’ the debate initiated by Fenn, many questions linger after nearly a century of research. Significant gaps remain in our understanding, in particular of the in vivo relationship between force production, energy cost and the magnitude and nature of the muscle load. While both the mechanics and cost of cross-bridge formation are well understood, the substantial movement-dependent variation in the energy cost of the force–time integral (FTI – the product of force production and its duration) of skeletal muscle is not. What is the nature of the Fenn effect in vivo? Is there a ‘negative Fenn effect’ such that lengthening (eccentric) contractions occur at a reduced cost compared with isometric force production?

List of symbols and abbreviations

Δx

change in length of spring

ANCOVA

analysis of covariance

D

displacement

E

energy liberated

F

force

FDI

first dorsal interosseous

FLA

force–length apparatus

FTI

force–time integral

I

isometric cost

k

spring stiffness

k₁

conversion coefficient from mmol l⁻¹ to J mol⁻¹

MRS

magnetic resonance spectroscopy

MVC

maximum voluntary contraction (isometric)

PCr

phosphocreatine

W

work

ΔG_ATP

the free energy of ATP hydrolysis (J mol⁻¹)

ΔPCr

PCr breakdown

Rall (1982) ended his extensive review of the Fenn effect with a cautionary note suggesting that due largely to experimental inadequacies, ‘This relation [the Fenn effect] is not generally valid and is thus of limited utility’. He concludes, ‘The approach developed by Mommaerts [Mommaerts, 1969, 1970] to compare energy liberated in working contractions to isometric contractions generating an equivalent force is a useful and unifying concept’ (Rall, 1982). In other words, the validity of the Fenn effect must be tested by comparing contractions of identical duration and force by maintaining equivalence of the FTI (Beltman et al., 2004) – whether shortening, isometric or lengthening.

Our approach to this challenge was to use a unique in vivo experimental design. We coupled measurement of the flux of high energy phosphates with experiments that controlled and quantified muscle mechanics. This combination made it possible to investigate these questions quantitatively in vivo using non-invasive techniques that isolate the effect of mode of contraction (shortening, isometric, lengthening) on the energy cost of muscle force production. In order to isolate the effect of contraction mode, we used a novel technique that allowed the magnitude of force production, as well as the duration of force production, to be held constant. We then measured ATP cost under constant FTIs in the three modes of muscle contraction: shortening, isometric and lengthening. By controlling the FTI and the external muscle movement, we isolated the effects of shortening and lengthening on muscle contraction costs. We designed this study to take advantage of a novel muscle system, the first dorsal interosseous (FDI) of the human hand (Jubrias et al., 2008; Nelson et al., 2011), coupled with a new apparatus to control and isolate muscle force independent of the release of elastic energy contributing to muscle work. The FDI muscle is a simple biomechanical (muscle lever) system with low inertia, making it ideal for mechanical studies (Jubrias et al., 2008). Abduction of the second digit is performed exclusively by the FDI, which is a mixed fiber-type muscle with 57% type I fibers (Johnson et al., 1973). This muscle lever system fits in the bore of a magnet for simultaneous mechanical and energetic measurements during muscle contraction.

Within the imposed limitations of this initial study we asked: (1) how much additional energy is required if the muscle performs work at a given magnitude and duration of force production in vivo (a true test of the Fenn effect, E=I+W)?; and (2) is the energy required to produce force decreased if the muscle is lengthened while force is generated, and, if so, is the energy requirement equal to the cost of isometric contraction minus the work done on the muscle, i.e. the negative Fenn effect (E=I−W)? To test these possibilities, we subjected the FDI muscle to three series of contractions (shortening, isometric and lengthening) of varying force. This technique allowed us to isolate ATP utilization as a function of muscle movement, keeping force and duration constant.

RESULTS

Perhaps the most significant result of this study is a demonstration of the proof of concept: we were able to simultaneously measure muscle force production and ATP consumption. In applying this technique to the FDI muscle, we controlled the FTI at each of five loads up to 75% of each subject's maximum voluntary contraction (MVC). Thus, in shortening, isometric and lengthening contractions, each subject generated identical force (fixed by the apparatus) for an identical (subject target-match) duration, in serial contractions of the FDI. In each trial, phosphocreatine breakdown (ΔPCr) was used to calculate the depletion of ATP as a function of time. Using the change in ATP, the amount of metabolic energy (in J) consumed by the muscle was calculated for each trial (see Eqn 1, Materials and methods). In all contractions (shortening, isometric and lengthening), the energetic cost increased in direct relation to the magnitude of the FTI (Fig. 1). By dividing the energetic cost by the FTI, one derives a cost per unit of maintained force produced by the FDI. Because the increases in FTI and energetic cost were linear, the ratio of cost to FTI is nearly constant. When data from all subjects and all trials are analyzed, several patterns emerge. There were two key results of this study that apply to the FDI muscle measured at a single contraction velocity.

Fig. 1.

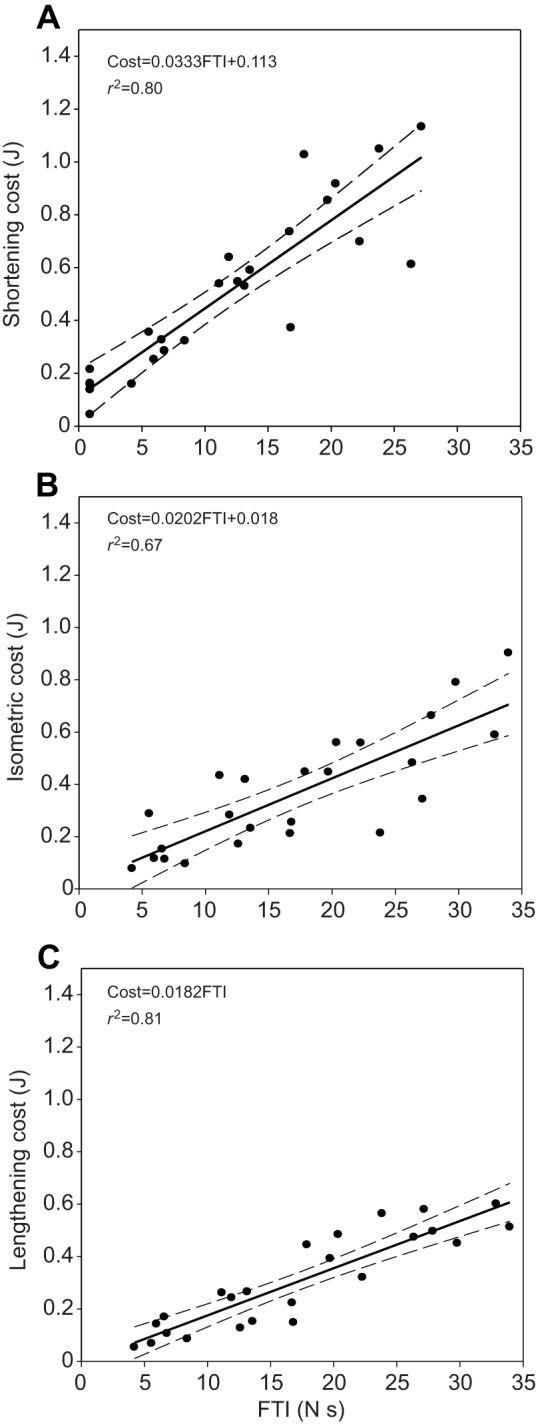
The energy cost of force generation as a function of the force–time integral (FTI) in the first dorsal interosseus (FDI) muscle. When data from all subjects and all trials are combined for shortening (A), isometric (B) and lengthening (C) contractions, the energy cost to produce force during each type of contraction increases linearly with the magnitude of the force produced (all contractions were 0.9 s in duration). Dashed lines represent the 95% confidence intervals of the regression equations shown. When external work is performed during shortening contraction (A) the cost is significantly higher than if no work is done (B) for the identical FTI. When energy is absorbed by the FDI muscle (i.e. ‘negative work’) during lengthening contraction (C), there is a slight but significant reduction in the cost of producing the equivalent amount of force relative to the isometric contraction (B).

The energetic cost of force production increases linearly with the FTI, in all contraction types

As the magnitude of force produced by the muscle increased so did the energetic cost required to produce that force. When energetic cost (in J) is plotted as a function of the FTI (in N s), for shortening, isometric or lengthening contractions (Fig. 1A–C), the result is a linear relationship in each condition. This figure represents all trials of all subjects for each type of contraction. While the y-intercept is near zero for both isometric and lengthening contractions, there is an apparent cost to shortening contractions as witnessed by an offset intercept, suggesting that shortening itself imposes an additional cost. The slopes of each of these relationships represent the energy cost of force production (J/N s) under each of the three conditions as the force produced increases. In other words, this cost of force production represents the cost of producing and maintaining each unit of force during shortening, isometric or lengthening contractions; as the FTI increases, so does the energy cost in all three conditions.

The energetic cost of force production is highest in shortening and lowest in lengthening contractions

In order to determine whether cost varies as a function of contraction type, the data were analyzed by analysis of covariance (ANCOVA). Both FTI (F-ratio=151, P<0.001) and contraction type (F-ratio=52, P<0.001) were statistically significant when regressed against the energy cost of force production. Contraction type had a large physiological effect (Fig. 1) such that the cost of generating force varies as: shortening>isometric>lengthening. The energy cost of force production for shortening contractions (0.0333FTI+0.113, R²=0.80) is nearly 50% greater than the cost of isometric contractions (0.0202FTI+0.018, R²=0.67). If the muscle is performing a lengthening contraction, the cost of force production (0.0182FTI+0, R²=0.81) is reduced by over 10% compared with isometric contraction. To examine the significance of these differences, the ANCOVA program performed a series of pairwise post hoc Student's t-tests (LSMeans differences Student's t, JMP Pro 9.0) to identify significant differences among the contraction types. The result of this analysis revealed that all three types of contraction are significantly unique (P<0.05). Thus, the cost of shortening contraction is greatest and significantly different from the cost of isometric contraction. Likewise, the energy cost of isometric contraction is significantly greater than the cost of lengthening contraction. In summary, both the magnitude of the FTI and the contraction type were found to be significant predictors of the energy cost of muscle contraction in the FDI.

DISCUSSION

The coupling of magnetic resonance spectroscopy (MRS) with an in vivo muscle force lever permitted us to control both the magnitude of force and its duration during contraction. When the muscle changed length during contraction, both the magnitude and velocity of the length change were also controlled. In this way, we were able to isolate, in vivo, cost as a function of mode of force production during shortening, isometric and lengthening muscle contractions. In all conditions, the energy cost increased as a linear function of the force produced (FTI). In addition, the cost was highest when the muscle shortened while contracting, in comparison to contracting isometrically. Further, when the muscle was lengthened while activated, the energy cost of force production was lowest. Because the muscle is performing work when shortening, one can also calculate the increment of additional cost to produce work (the Fenn effect). Likewise, it is possible to quantitatively calculate the energy savings when work is done on the muscle (negative Fenn effect) during an eccentric contraction.

Is there a Fenn effect?

The experiments allow us to directly test for a Fenn effect (E=I+W) and a negative Fenn effect (E=I−W) using the cost data from each shortening, isometric and lengthening trial in conjunction with the calculations of the work (positive or negative) in each treatment. That is, by adding the work (F×D for shortening or F×–D for lengthening, where F is force and D is displacement) to the isometric cost, it is possible to quantitatively test for the presence of a positive or negative Fenn effect.

For each subject and each trial, the isometric cost of each trial (15%, 30%, 45%, 60% and 75% of MVC) can be used as the ‘no work’ FTI reference. By adding or subtracting the work done by or on the muscle, respectively, it is possible to quantitatively test both the Fenn effect (I+W) and the negative Fenn effect (I−W). Thus, we started with the full set of isometric cost values (Fig. 2B) and added the energy equivalent of the work done during each shortening contraction (I+W) to construct a new variable, Fenn's theoretical cost of shortening (I+W, isometric cost plus work, Fig. 2A). Once constructed, Fenn's theoretical cost of shortening was directly compared with the actual cost of shortening contractions (Fig. 2B). Not only was there no statistical difference but also the two lines are virtually superimposed. These results are consistent with the concept of the Fenn effect as defined by Rall (1982). For the FDI muscle and under these conditions, the energy cost of shortening contractions equals the isometric cost plus the work done during the contraction (Cost=I+W).

Fig. 2.

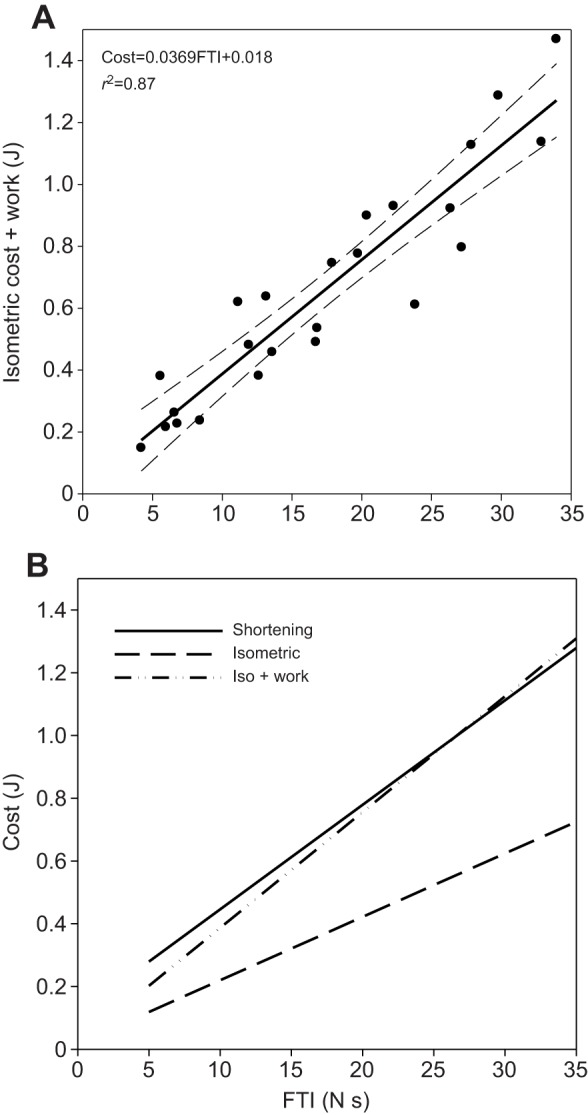
Test of the Fenn effect. (A) The measured energy cost of isometric contraction combined with the work done by the FDI muscle during a shortening contraction shown as a function of FTI (filled circles). Solid line represents least square regression equation (R²=0.87) and dashed lines represent the 95% confidence intervals of the regression equations. (B) When the external work (force×distance) done by the FDI muscle during shortening contraction is added to the cost of isometrically producing the same force, the result is a direct test of the Fenn effect. Here, we compare the calculated energy cost of external work performed during shortening contractions added to the isometric cost of force production (Iso + work) and the measured cost of shortening contraction and isometric contraction. In short, these results are consistent with the Fenn effect, Cost=W+I.

Fenn's second hypothesis that ‘negative work results in negative excess energy’ has received much less attention than the century old Fenn effect. Indeed, our results demonstrated that lengthening contractions had the lowest energy cost. However, these results also demonstrate that the cost of lengthening contractions, though low, was roughly equal to the negative work done on the muscle. Thus, when the negative work is subtracted from the isometric cost (I−W), the predicted cost is near zero (Fig. 3A). Thus, there is little support for a quantitative negative Fenn effect (Cost≠I−W). However, our results do demonstrate that the cost to generate force in the FDI muscle varies as a function of muscle shortening and lengthening.

Fig. 3.

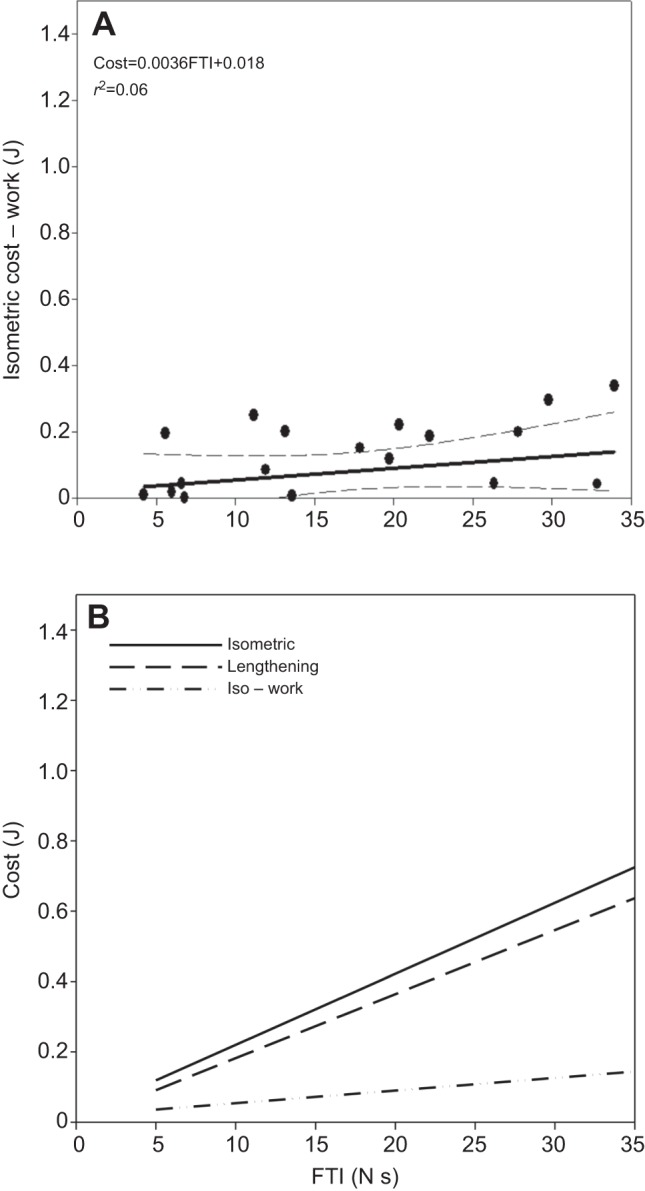
Test of the negative Fenn effect. (A) Theoretic cost of performing negative work during lengthening contraction as a function of FTI (filled circles). Solid line represents least square regression equation (R²=0.06) and dashed lines represent the 95% confidence intervals of the regression equations. When the external work (force×distance) done by the FDI muscle during lengthening contraction is subtracted from the cost of isometrically producing the same force, the result is a direct test of the negative Fenn effect. Because the cost of an isometric contraction is nearly equal to the energy absorbed by the FDI (i.e. ‘negative work’) during lengthening contraction, the predicted cost of lengthening contractions according to the negative Fenn effect was close to zero. (B) The calculated energy cost of external work performed during lengthening contractions subtracted from the isometric cost of force production (Iso – work) and the measured cost of lengthening contraction and isometric contraction. These results suggests that, at least under these experimental conditions in the FDI muscle, there could be no true negative Fenn effect unless there was no energy cost of lengthening contraction.

Thus, the key findings of this study are: (1) when the FDI muscle does work, the cost of force generation is equal to the isometric cost plus the work done (Cost=I+W); (2) when work is done on the muscle during a lengthening contraction, there is a reduction in cost relative to the isometric cost. However, the magnitude is not nearly the same as that of the ‘negative’ work itself. In other words, we failed to find a negative Fenn effect (Cost≠I−W).

Limitations and speculation

This study introduces a novel system to simultaneously and non-invasively measure both force production and ATP cost in real time. We chose a muscle and experimental design that were in part constrained by the magnet as well as by both human and magnet dimensions. In this ‘proof of concept’ study, we did not vary what could be critical variables, such as contraction velocity or the magnitude of muscle length change. Thus, the results presented here are necessarily limited by the muscle used and imposed constraints of experimental design. It would be beneficial in a future study to examine the effect of contraction velocity on the cost difference between shortening and lengthening contractions. However, despite these limitations, this novel technique resulted in insights that add to our general knowledge with regard to the coupling of muscle mechanics and energetics. The following discussion is intended to fit these results into a larger context and present some reasoned speculation based upon them.

These findings are consistent with some much older results. For example, force depression with shortening in a concentric contraction and force enhancement with lengthening in an eccentric contraction have been recognized for decades (Abbott and Aubert, 1952). When force is kept constant, more muscle effort (energy) is required in shortening and less in lengthening contractions. The causes of these muscle properties have remained elusive; the relationship between force and muscle shortening or lengthening has defied explanation using only the sliding filament theory (Herzog et al., 2008). Recent interest in this phenomenon has resulted in the conclusion that both force enhancement with muscle stretch and depression with shortening must be ‘affected by a common mechanism’ (Kosterina et al., 2009).

The sliding filament theory has provided numerous insights linking Hill muscle mechanics with energetics. Accordingly, as both the force produced and energy cost are accepted to be constant per cross-bridge, and because the cycling rate of each cross-bridge is a function of the myosin ATPase present, the ATP cost of muscle contraction should be a constant function of (1) the duration and (2) the magnitude of the force produced. However, as Fenn observed, the cost of generating force actually varies as a function of muscle movement. Among the explanations put forward to reconcile this observation are a discontinuity of cross-bridge binding rates (Smith and Sicilia, 1987), length changes in the actin filaments (Schutt and Lindberg, 1993) and differential binding of myosin heads resulting in ‘molecular synchrony’ (Duke, 1999). Each of these and many other proposed theories rely on the cross-bridges as the sole source of muscle force.

Importantly, when the sliding filament model was first proposed 60 years ago by the Huxleys (Huxley and Niedergerke, 1954; Huxley and Hanson, 1954), they had no knowledge of the largest known protein and third most abundant protein in muscle, titin. Thus, this protein was absent from the model. Titin is an elastic protein that parallels and partners with the cross-bridges. While only the cross-bridges can produce force, an elastic element within the muscle could store energy and preserve force, providing a mechanistic basis of the Fenn effect (Loiselle et al., 2010). What are the consequences when the elastic element, titin, is incorporated into the sliding filament model?

When muscle is stretched, elastic recoil energy is stored in titin. In fact, the elasticity of this molecule exactly coincides with the passive tension of muscle fibers (Linke et al., 1998; Tskhovrebova and Trinick, 2010). For that reason, in cardiac muscle, titin (which is much stiffer in cardiac than in skeletal muscle) has been proposed to play a key role in cardiac contractility, providing a mechanical explanation of the Frank–Starling law of the heart (Granzier et al., 1997). However, in skeletal muscle, titin has the unique characteristic of changing its stiffness with muscle activation to act as a molecular spring. When the muscle is relaxed, titin acts as a very compliant spring that would have to be stretched to non-physiological lengths to function as a molecular spring. Recent evidence suggests that in the presence of Ca²⁺, titin binds to actin (Kellermayer and Granzier, 1996) and most likely in the N2A region, functionally removing the compliant portion (the tandem Ig domains) and engaging, much like a clutch, the stiff (PEVK) region of the titin molecule (Monroy et al., 2012; Nishikawa et al., 2012). In other words, in the presence of Ca²⁺, binding of titin to actin results in an instantaneous increase in stiffness that can function to store and return elastic potential energy and thus preserve sufficient tension to greatly minimize the force required and energy consumed by cross-bridges during isometric and lengthening contractions (Nishikawa et al., 2012). It seems to us that the results of the present study may be most simply explained by the contribution of the elastic molecule titin to the active tension produced by the cross-bridges.

In conclusion, by coupling MRS and an in vivo constant force lever, we were able to quantify ATP use as a function of contraction type in the FDI muscle. While these initial measurements primarily demonstrate the feasibility of this novel experimental design, they do provide one direct test of the Fenn effect.

MATERIALS AND METHODS

Experimental design

The design of our study is based on the fact that when force is developed in a muscle, concentrically, isometrically or eccentrically, the only input of energy is the free energy available from ATP within the muscle and that this chemical energy is converted into mechanical energy to sustain force over time. The effect of mode (shortening, isometric or lengthening) on the energetic cost of muscle contraction can be calculated from the ratio of the input of chemical energy to the FTI during muscle activation. We studied five male volunteers, aged 34–61 years (mean±s.d.: 47±11 years). Subjects were healthy with no known musculoskeletal disease and were right handed. All subjects voluntarily gave informed, written consent. The study was undertaken in accordance with the Declaration of Helsinki and was approved by the University of Washington Human Subjects Review Committee.

Exercise

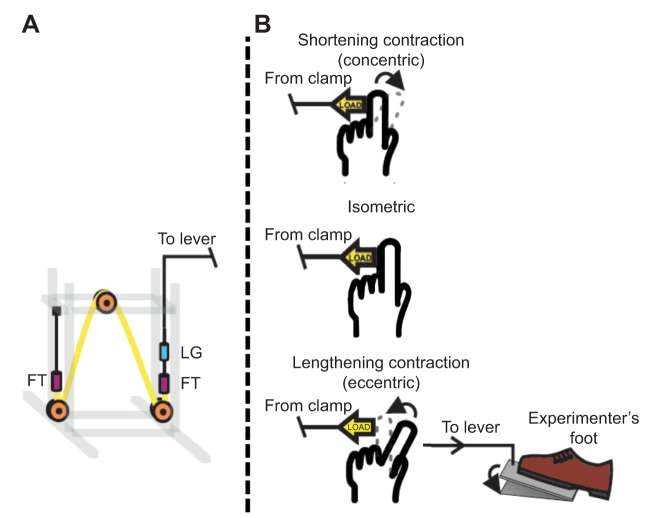
We determined the FTI and ATP cost over a 5-fold range of loads (15%, 30%, 45%, 60%, 75% MVC) and three modes of contraction (shortening, isometric and lengthening) performed by the FDI muscle of the right hand. Prior to collecting experimental trials, the MVC force for the FDI was identified in each subject as the highest value of three maximal finger abductions against a fixed load cell. All of the experimental submaximal contractions were maintained for a duration of 0.9 s, and both shortening and lengthening contractions were voluntary ramp contractions with a fixed distance of movement (15 mm). The tasks of the subject can be visualized in Fig. 4. The goal for shortening and lengthening contraction was to make the change of finger position as constant as possible, hence a continuous ramp of position change (Fig. 5). Subjects were trained to produce both shortening and lengthening contractions at a rate of 0.67 Hz and with 15 mm of finger movement against each of the five preset loads. They were also trained to relax the finger quickly at the end of each contraction to minimize resistance to the falling load, and to maintain relaxation as the finger rested until the next contraction. For shortening contractions, the finger was returned to the ‘rest’ position by the tension of the spring element of the apparatus (Fig. 4A). For lengthening contractions, an experimenter foot pedal–pulley system was used to passively return the subject's index finger to the ‘rest’ position and hold the load until the next contraction (Fig. 4B).

Fig. 4.

Illustrations demonstrating the force–length apparatus (FLA) and the simple FDI muscle lever system in the starting position for each contraction type. (A) The FLA acts as an in vivo force clamp composed of an electronic length gauge (LG, blue), two force transducers (FT, purple), and latex tubing (yellow) oriented around three low friction pulleys (orange). (B) The starting position (solid lines) and ending position (dashed lines) of the index finger are shown for shortening (top panel), isometric (middle panel) and lengthening (bottom panel) contractions of the FDI muscle. In all three conditions, the resistive force acts in the same direction, as indicated by the force vector arrow. For the shortening and isometric condition, contractions began with the finger in a neutral position (0 deg at center) whereas the starting position of the finger for the lengthening condition was 15 mm abducted from neutral. The illustration also shows how the foot pedal control system was used to set the finger position for a lengthening contraction.

Fig. 5.

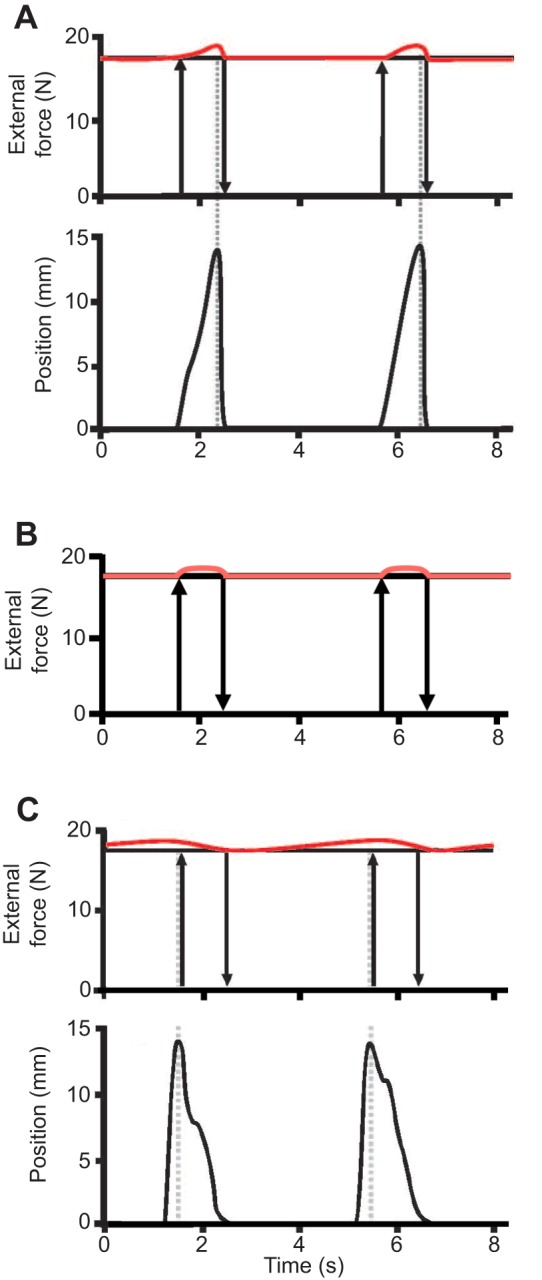
Index finger force and position as a function of time during contractions. (A) Shortening, (B) isometric and (C) lengthening contractions. For all three conditions, finger force (red line) was held nearly constant as the finger was concentrically abducted (shortening contraction) 15 mm, held in place (isometric contraction), or eccentrically adducted (lengthening contraction) 15 mm.

Mechanical and energetic data were recorded during each test bout, which lasted ∼11 min and consisted of 5 min of resting ischemia followed by a 36–108 s bout of exercise (7–28 ramp contractions) during ischemia, and then a minimum of 10 min of resting aerobic recovery was given between the ischemic portions of sequential test bouts. Ischemia was produced by a pressure cuff placed around the upper arm inflated to 55 Torr (where 1 Torr=1 mmHg) above the subject's systolic blood pressure. Subjects performed three randomly ordered bouts of contractions (shortening, isometric and lengthening) across the range of five randomly ordered external loads. The order of the contraction modes and external loads was randomized for each subject by Latin squares. Energetic cost and mechanics (FTI) were determined during the same experimental session.

We constructed a reusable cast for the right forearm and hand of each subject that immobilized the limb below the elbow with the exception of the second digit. This cast isolated the movement of the FDI muscle during measurement of the ATP flux and mechanical output during each exercise bout. The second digit was free to abduct and adduct along the surface of a platform. A magnetic resonance coil was placed over the FDI to measure ATP flux. A plastic cradle was used to position the limb and maintain the FDI at the magnet's isocenter. For each exercise bout, a constant afterload was applied to the FDI using a custom-designed force–length apparatus (see description below). The afterload was applied in series to a light-weight, high stiffness (0.07 mm N⁻¹) cord that connected to a brace placed around the proximal interphalangeal joint of the index finger (Jubrias et al., 2008).

Force and length measurement

A custom-designed magnetic resonance-compatible force and length measuring apparatus (FLA) was developed for the study (Fig. 4A). This apparatus permitted measurement of the magnitude and duration of contraction force during each bout of exercise. It also controlled the length of movement during the shortening and lengthening contractions. We constructed the FLA out of non-ferromagnetic components to be compatible with using magnetic resonance to measure the ATP flux.

This FLA allows all modes of contractions (shortening, isometric and lengthening) to be performed at identical force levels (both magnitude and duration) as suggested by Mommaerts and colleagues (1962). A servomotor is typically used to apply a force clamp and measure length change in vitro or in situ, but these motors are not compatible with the magnetic fields of a magnetic resonance imager (MRI). Instead, we adopted Hill's suggestion (Hill, 1965) to use a lever system with small inertia and a constant force (Jubrias et al., 2008). Resistive force was regulated by stretching different sized Hookean spring elements (low stiffness latex tubing, k=0.0053 N mm⁻¹), each of which was calibrated and found to provide a nearly constant magnitude of force to the finger brace. The force in a Hookean spring is equal to the product of the spring constant (k) and the change in length (Δx). The length of the tubing when stretched was 133-fold greater than the displacement of the finger. As a result of the spring's low stiffness and large stretch, the tensile force fluctuations caused by the abduction of the subject's index finger were small. Generation of a non-inertial load with minimal fluctuation was further achieved with a light-weight, high stiffness cord that connects the finger brace via pulleys to the FLA. Thus, force was regulated and held constant for each trial with a non-inertial force clamp. The consequence was a non-invasive measure of the ATP cost of force production in vivo during shortening, isometric and lengthening contractions with the precision of in vitro muscle mechanics experiments.

The FLA contains a length transducer (Novotechnik T 150, Southborough, MA, USA) for measuring length in series with two force transducers (Entran ELFS T3E-50L, Fairfield, NJ, USA) on either end of the latex tubing spring element. The apparatus is fixed to a rigid frame built from 2.5 cm square T-slotted aluminium beams (80/20 Inc., Columbia City, IN, USA) and was firmly held on the laboratory floor with lead anchors. This frame provided a rigid structure to affix the length transducer and force transducers. To measure the movement of the finger, the length transducer was positioned vertically in the apparatus between the hand and the first force transducer, which in turn was attached to the spring element. Length measurements from the FLA were also used to provide subjects with a real-time LED display of their finger movement, allowing them to accurately control the length and rate of movement during bouts of shortening and lengthening contraction, such that the movements for both contraction modes were equal and opposite as suggested by Hill (1965) (Fig. 5). Force and movement analog signals were digitized with an AD scan rate of 1 kHz and recorded continuously on a computer (Jubrias et al., 2008).

Accuracy of force and length measurements

The two force transducers, one on either side of the latex tubing, were used to verify that the same force was generated on both sides of the resistive force element. The error in the force measurement was simply the error in the strain gauges (±0.3 N), because the average force was the same in both transducers. In order to verify that the length transducer accurately measures finger movement, we compared the movement at the finger using a caliper with the displacement measured using the length transducer. The results of this comparison showed that the error in the length transducer measurements was ±0.12 mm (<1%).

FTI and mechanical work

In order to compare the cost of force generation between the different contraction modes (shortening, isometric and lengthening), we determined the total FTI for each exercise bout. We calculated the total FTI by integrating the contraction force with respect to time as measured by the FLA and then summing the contraction FTIs across each exercise bout.

To test the Fenn effect and ‘negative’ Fenn effect, we calculated the total external work output (in J) for shortening and lengthening contractions at each level of force using the force magnitude and displacement measurements from the FLA. The external work of each contraction was calculated as the product of the average force (in N) and the distance moved (in m) for that contraction. The total external work performed during each shortening or lengthening test bout was calculated as the sum of work for all contractions in the 42 s of exercise.

Metabolic cost (ATP flux)

The metabolic cost of each exercise bout was measured using phosphorus MRS (Bruker 4.7T, Karlsruhe, Germany). The breakdown of the storage form of high-energy phosphates in the muscle cell, phosphocreatine (PCr), provided a direct measure of ATP flux. This was achieved by making the muscle anoxic by ischemia. PCr breakdown (ΔPCr) reflects ATP turnover by the muscle (Blei et al., 1993) minus glycolytic ATP synthesis (<8% of total ATP supply). We have validated this approach by testing for an ATP balance using separate measures of ATP supply and demand, and against direct measurements of O₂ uptake and lactate (Kemper et al., 2001). This non-invasive in vivo method allows us to measure phosphorylation (ATP flux) and thereby determine the cost of contraction in the FDI muscle.

Conversion of chemical changes into thermodynamic energy is described as:

(1)

where Cost is the chemical energy (J), [ATP] is the muscle content (mmol l⁻¹), ΔG_ATP is the free energy of ATP hydrolysis (J mol⁻¹) and k₁ is the conversion coefficient from mmol l⁻¹ to J mol⁻¹.

The ATP cost of contraction was examined as a function of the FTI, contraction mode and subject. In order to determine whether cost varies as a function of contraction type, the data were analyzed by ANCOVA (JMP Pro 9.0). Cost was analyzed with FTI and contraction type as model effects and with subject as an additional random model effect. Statistical significance was determined at α=0.05.