Analyzing Dyadic Data Using Grid-Sequence Analysis: Interdyad Differences in Intradyad Dynamics

Abstract

Objectives

Spouses are proximal contexts for and influence each other’s behaviors, particularly in old age. In this article, we forward an integrated approach that merges state space grid methods adapted from the dynamic systems literature with sequence analysis methods adapted from molecular biology into a “grid-sequence” method for studying interdyad differences in intradyad dynamics.

Method

Using dyadic data from 108 older couples (M_Age = 75.18 years) with six within-day emotion and activity reports over 7 days, we illustrate how grid-sequence analysis can be used to identify a taxonomy of dyads with different emotion dynamics.

Results

Results provide a basis for measuring a set of dyad-level variables that capture dynamic equilibrium, daily routines, and interdyad differences. Specifically, we identified four groups of dyads who differed in how their moment-to-moment happiness was organized, with some evidence that these patterns were related to dyad-level differences in agreement on amount of time spent with partner and in subjective health.

Discussion

Methodologically, grid-sequence analysis extends the toolbox of techniques for analysis of dyadic experience sampling data. Substantively, we identify patterns of dyad-level microdynamics that may serve as new markers of risk/protective factors and potential points for intervention in older adults’ proximal context.

Dyadic relationships are influential throughout the entire life span. In childhood, for example, parents, peers, and siblings are all proximal influences on individual’s behavior and long-term development (Kuczynski, 2002; McHale, Updegraff, & Whiteman, 2012; Parker, Rubin, Erath, Wojslawowicz, & Buskirk, 2006). In adulthood, romantic partners and children influence individuals’ health and well-being (Baltes & Staudinger, 1996; Dixon, 1999; Homish & Leonard, 2008; Hoppmann & Gerstorf, 2014). Likewise, in old age, caregivers, adult children, and members of the social network affect individuals’ health and well-being (Silverstein & Giarrusso, 2010). Methods to analyze dyadic data continue to evolve (Gonzalez & Griffin, 2012; Kenny, Kashy, & Cook, 2006; Laurenceau & Bolger, 2005; Ram, Shiyko, Lunkenheimer, Doerksen, & Conroy, 2014). Generally, researchers seek to describe and understand patterns of behavior that occur within the context of dyadic relationships, whether within a romantic partnership or within a caregiver-/care-receiver relationship, and how those patterns contribute to developmental and aging processes. For example, researchers seek to identify how patterns in spousal dyads’ emotional experiences reflect differential quality of dyadic and individual functioning—with the long-term goal of being able to help couples optimize their health, well-being, and development. In this article, we develop and describe a new analytical approach that integrates state space grid methods adapted from the dynamic systems literature with sequence analysis methods adapted from molecular biology and sociology into a grid-sequence analysis method for the study of interdyad differences in intradyad processes.

Dyadic Time Series, Dyad-level Scores, and Interdyad Differences

Researchers have collected rich repeated measures data to understand how dyads function and how they differ. For example, working from video or audiotapes of conversations, researchers code the behaviors or verbalizations of the dyad members, second-by-second or speaking-turn-by-speaking-turn (e.g., Gottman, Coan, Carrere, & Swanson, 1998). Similarly, in longitudinal panel or experience sampling studies, members of a dyad complete questionnaires repeatedly, and often simultaneously (e.g., Choi, Yorgason, & Johnson, 2016; Gerstorf, Windsor, Hoppmann, & Butterworth, 2013; Skoyen, Blank, Corkery, & Butler, 2013). Both approaches produce dyadic repeated measures data to examine how dyad members change and/or interact over time (intradyad processes) and how dyads differ (interdyad differences).

A wide variety of procedures are used to analyze dyadic longitudinal data, most of which distinguish dyad members (e.g., husbands, wives) and quantify time-dependent relationships between them (see Kenny et al., 2006 for overview). For example, dyadic longitudinal panel data are often analyzed using a variant of the actor–partner-interdependence model (Kenny, 1996). Here, the outcome variable of interest for each dyad member, for example, level of happiness at Wave 2, is modeled as a function of his/her own level of happiness at Wave 1 (the “actor effects”), and the other person’s level of happiness at Wave 1 (the “partner effects”). The actor and partner effects, usually derived from the interdyad covariances, are often interpreted as a quantification of the prototypical intradyad process. With observational or experience sampling designs, dyadic longitudinal data are often placed in a multilevel/hierarchical framework that explicitly separates intradyad and interdyad associations. In Stage/Level 1, the dyads are each examined separately. Temporal dependencies between dyad members are quantified using a time-series approach where each dyad members’ happiness at each occasion, t (= 2 to T), are modeled as a function of his/her own level of happiness at the prior occasion, t − 1, and the other person’s level of happiness at the prior occasion, t − 1, to obtain dyad-specific quantifications of the intradyad actor and partner effects. In Stage/Level 2, these dyad-specific quantifications are treated as interdyad differences and examined in relation to other individual- or dyad-level variables. This general approach—to first quantify the intradyad relationships and then examine interdyad differences in the intradyad relationships—is the basis for most contemporary dyadic data analysis techniques, including sequential and state space grid analyses, coupled dynamic systems, and multilevel modeling (Bakeman & Gottman, 1997; Bakeman & Quera, 2011; Boker & Laurenceau, 2007; Gonzalez & Griffin, 2012; Gottman, Murray, Swanson, Tyson, & Swanson, 2002; Hollenstein, 2013; Laurenceau & Bolger, 2005; Ram & Pedersen, 2008).

Notably, most of these existing techniques start by summarizing each dyad’s bivariate longitudinal time series with some regression-type method to obtain new dyad-level variables. For instance, even in the most sophisticated models, Gottman and colleagues (2002) used complex differential equation models to summarize a dyad’s entire conversation as a single number. Consider a situation where 50 repeated measures are obtained for each member of a dyad. Formally, the bivariate time-series data obtained from each dyad would be configured as a 50-occasions × 2-person data matrix. In most dyadic analytic techniques, these bivariate time-series data are immediately reduced to a single dyad-level variable, a 1-occasion × 1-dyad matrix of data, by collapsing across both time and dyad members. The resulting dyad-level scores are then examined in relation to other dyad-level variables (e.g., relationship satisfaction). Additional understanding of a dyad can be gained by reducing the bivariate time-series data in a slightly different way. In this article, we develop an approach where each dyad’s bivariate time-series data (50-occasions × 2-person matrix of data) are first reduced to a univariate dyad-level time series (50-occasions × 1-dyad matrix of data), and in a separate step summarized and examined for relations to other variables. Constructing and analyzing the dyad-level time series allows researchers to identify intradyad dynamics that may be lost in the immediate reduction to single scores. Substantively, for example, reduction of the bivariate time-series into a single “lability” score (i.e., entropy; Shannon, 1948) informs us about the range of experiences the dyad had, but ignores the order in which the experiences occurred. Reduction to the dyad-level time series, however, provides opportunity to identify the patterns of behavior—the dynamic processes (order and timing of events) underlying that lability. We develop a new approach that explicitly obtains and examines interdyad differences in the dyad-level time series. In particular, following along with other initiatives to examine univariate sequences holistically (e.g., Hamming distance, Lichtwarck-Aschoff, Kunnen, & van Geert, 2009; T patterns, Magnusson, Burgoon, & Casarrubea, 2016), and in contrast to analytical approaches that examine specific types of occasion-to-occasion changes (sequential analysis, Bakeman & Quera, 2011; differential equations, Gottman et al., 2002), we promote an analytical procedure that may be applied to dyadic categorical, ordinal, or interval repeated measures to holistically identify and study a wide variety of nonlinear and/or repeating patterns that were not explicitly hypothesized a priori.

Grid Analyses

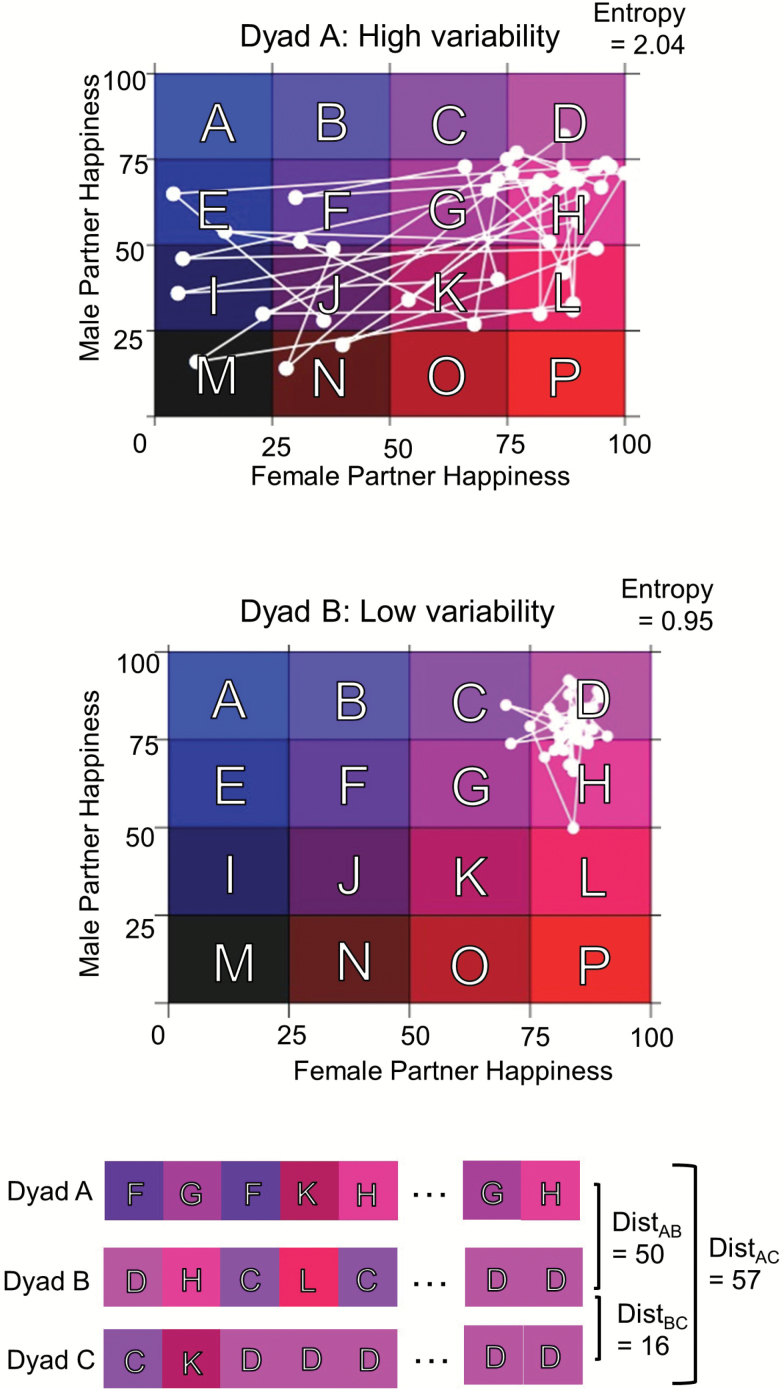
Grid analyses emerged in the study of human development to articulate propositions of dynamic systems theory (Lewis, Lamey, & Douglas, 1999; van Geert, 1998). For example, developmental psychologists use state space grid methods to study interpersonal dynamics of parent–child dyads to locate and examine “attractors”—behavior combinations to which a dyad often returns (e.g., Hollenstein, Granic, Stoolmiller, & Snyder, 2004; Hollenstein & Lewis, 2006; Zaidman-Zait, Marhsall, Young, & Hertzman, 2014). Similar to how latitude and longitude are used to represent specific locations in physical space, the cells within a state space grid represent specific locations in a psychological or behavioral space (see Hollenstein, 2013 for a comprehensive primer). In the empirical example to be presented later, a two-dimensional state space grid is used to depict and study how the emotional states of a dyad (e.g., members of a heterosexual couple) change over the course of a week. As shown in the upper portion of Figure 1, the time series of mood reports obtained from a dyad are depicted in a plane defined by the female partner’s mood ratings on the x-axis (ordinal categories: very unhappy, mildly unhappy, mildly happy, very happy) and the male partner’s mood ratings on the y-axis (very unhappy, mildly unhappy, mildly happy, very happy). The state space is constructed as a grid, in this case with 4 × 4 = 16 cells, where the cells along the diagonal indicate concordance of the female’s and the male’s mood, and the cells off the diagonal indicate discordance in mood. The dyad’s trajectory of psychological states or behaviors is mapped in the grid, allowing for easy empirical identification of the locations visited (e.g., where they spend the most time) and how they travel through the state space over time. Interdyad differences are evident visually and can be quantified in a wide variety of ways to articulate dynamic systems concepts and hypotheses (Hollenstein, 2013). For example, the two dyads shown in the upper portion of Figure 1 differ in variability, with Dyad A having entropy of 2.04 and Dyad B having entropy of 0.95. As noted earlier, entropy quantifies dyad-level differences in variability through immediate reduction to a single dyad-level score that omits information about the ordering and patterning of movement around the grid. However, the state space grid method provides a foundation to map and study interdyad differences in intradyad dynamics embedded in the ordered sequence of grid cells visited.

Figure 1.

(Top portion) Two dyads’ daily reports of happiness mapped in order of their occurrence onto state space grids. The x-axis represents female’s happiness, and the y-axis represents the male’s happiness. The upper state space grid (Dyad A) represents a couple that has unstable levels of happiness, whereas the lower state space grid (Dyad B) represents a couple in which both members are happy. (Bottom portion) Extracted sequences from Dyads A, B, and C (not pictured above). The distance metric used is the optimal-matched-based “cost” of transforming one sequence into the other, with greater distance indicating more dissimilarity between dyads.

Sequence Analysis

As might be inferred from the coloring and lettering of the grid cells in the upper portion of Figure 1, the path each dyad takes through the state space grid has been redepicted as a time-ordered sequence of colors/letters in the lower portion of Figure 1—a visual reminiscent of the nucleotide sequences (e.g., ACGT, CGAT) that make up our DNA. Indeed, a variety of methods have been developed in biology to identify DNA sequences through matching to known sequence structures, including sequence analysis (although similar in name, “sequence analysis,” Sankoff & Kruskal, 1983, is an analytic technique distinct from “sequential analysis,” Bakeman & Gottman, 1997). Sociologists (Abbott, 1995), seeing parallels between the plots of the DNA sequences and the plots of some of their categorical time series (e.g., employment sequences), began to use sequence analysis methods to study a variety of topics, including occupational trajectories (e.g., Halpin & Cban, 1998), dance rituals (MacIndoe & Abbott, 2004), and residential mobility (Stovel & Bolan, 2004). Here, we forward an application to data on dyad members’ psychological states.

In brief, sequence analysis uses optimization algorithms (e.g., Needleman & Wunsch, 1970) to calculate the “distance” between pairs of sequences. Formally, this distance is operationalized as the minimum work needed to transform one sequence (e.g., Dyad A in the lower portion of Figure 1) into another sequence (e.g., Dyad B) through iterative insertion, deletion, and substitution (to be described in more detail later). Then, sequences that are similar to one another (low transformation cost) are placed, using a cluster analytic approach, into one group and differentiated from dissimilar sequences (high transformation costs) that are placed into other groups. In Figure 1, we see the cumulative cost of transforming Dyad A into Dyad B is high (distance = 50), so these two sequences may be considered as having been produced by distinct types of dyads. In contrast, the cumulative cost of transformation between Dyad B and Dyad C is low (distance = 16), which may indicate these dyads are of similar type. Notably, unlike several other methods being used to identify patterns in dyadic data through examination of sequential dependencies that appear within a collection of small windows (e.g., sequential analysis, Bakeman & Gottman, 1997; T patterns, Magnusson, 2000), the sequence analysis method examines the entire sequence as a whole. The sequence is not broken into smaller subsections. As such, sequence analysis is a descriptive technique that can be used to systematically identify typologies of sequences. Furthermore, having been developed for study of strands of DNA with arbitrary beginnings and endings, the technique prioritizes identification of sequences with similar patterns relatively independently of where those patterns sit within the overall sequence of observations (e.g., at beginning or end of a week). As such, sequence analysis is particularly well suited for description of experience sampling data where strands of temporal sequences are plucked from a random week of dyads’ ongoing lives.

Grid-Sequence Analysis—The Present Study

In this article, we illustrate how state space grid methods and sequence analysis methods can be combined to facilitate the examination of interdyad differences in intradyad processes. Specifically, we formulate grid-sequence analysis as a multistep process wherein we (a) track each dyad’s movement through a two-dimensional state space grid that is labeled using a researcher-chosen “alphabet”; (b) convert each dyad’s movements into a (univariate) categorical sequence (or “sentence”) by extracting, in order, the letters of the visited cells; (c) use an optimal matching algorithm to establish and compute the distance between sequences; (d) cluster sequences/sentences that are similar; and (e) use the resulting cluster groups to examine meaningful interdyad differences.

Grid-sequence analysis, by explicitly creating and working with the dyad-level time series, may provide for identification of distinct patterns of dyadic function that are related to overall function. This method is unique in three key ways, (a) the state space grid provides a framework for re-representing bivariate time-series data as univariate time series, (b) the sequence analysis provides for identification of patterns or trends that account for order and relative timing of change, and (c) the cluster analysis (or grouping technique of choice) provides for identification of groups of dyads who exhibit patterns that are holistically similar. In particular, as a new method for the analysis of dyadic experience sampling data, we suggest that grid-sequence analysis will help identify new typologies of dyad-level microdynamics that indicate risk or protective factors that are useful for intervention efforts. In this initial demonstration, we apply grid-sequence analysis to dyadic experience sampling data obtained in a study of older couples’ daily lives. Specifically, we illustrate the potential value of this new approach by identifying a taxonomy of dyad-level subtypes that differ in how their emotions (i.e., multiple within-day ratings of happiness—chosen here as an exemplar variable with variance properties useful for methods development) vary through normal daily life, and examine how that taxonomy is related to a set of theoretically meaningful variables—subjective health, dyadic adjustment (agreement on amount of time spent with partner), and relationship satisfaction, all of which constitute important characteristics of older couples’ well-being (Hoppmann & Gerstorf, 2016). In doing so, we introduce grid-sequence analysis as a new approach to examine interdyad differences in intradyad dynamics using experience sampling data.

Method

Data for the current illustration come from the Berlin Couple Dynamics Study, an experience sampling study wherein older adult couples completed up to 42 reports (six times per day for 7 consecutive days) about their feelings, activities, and actions during a typical week. Additional information about the study design can be found in Hülür and colleagues (2016). Details relevant to the present illustration of grid-sequence analysis are given below.

Participants

Participants were 110 older couples who volunteered, after seeing announcements in local Berlin newspapers, for an experience sampling study of the daily lives of older couples. At initial telephone contact, participants were screened for qualification, so that both partners (a) were at least age 65 years, and at least one partner was at least age 70 years; (b) lived in the same household; (c) were fluent in German; (d) had corrected vision that was sufficient to read small newspaper titles (the assessments would be presented on an iPad); and (e) had corrected hearing that was sufficient to hear the door or phone bell (the assessments would be prompted by an audio signal). Participants were Germans between age 67 and 93 years (M = 75.18; SD = 3.86); were married, in a civil union, or in a cohabiting relationship for, on average, 44.8 years (SD = 13.07; range = 1–63); and had spent, on average, 14.24 years (SD = 2.97, range = 9–18) in school. Overall, participants completed 99.2% of happiness items, with the majority providing information at all 42 time points (M = 41.59; SD = 1.45; range = 24–42). Here, we make use of data from 108 distinguishable dyads. Data from two dyads were excluded because the partners could not be distinguished by gender (same-sex couple; a point we shall return to in the discussion) or because the data from one partner was not recorded due to a technical problem.

Procedure

After expressing interest in the study, receiving more details about the experience sampling protocol, and completing the screening, couples were scheduled for an introductory visit on what they considered a “typical week.” In case of unusual events (e.g., health or family emergencies), participants were rescheduled. Participants were visited at their homes (or at the university if preferred) by two research assistants who gave each participant an iPad and provided instruction on the study procedures. Over the next 7 days, participants interacted with an iPad-based application (iDialogPad; G. Mutz, Cologne, Germany) to complete six short questionnaires each day, each of which also prompted provision of a saliva sample (not used in the present analysis). Immediately upon waking, participants completed a “morning questionnaire” (and 30-minute follow-up items related to the assessment of cortisol awakening response). Throughout the remainder of the day, the iPad-based application prompted completion of five more questionnaires (10 a.m., 1 p.m., 4 p.m., 7 p.m., 9 p.m.; with exact times adjusted to accommodate participants’ schedules) with an insistent chime. The audio signal activated simultaneously for both members of the dyad, so that both partners completed reports at the same time. Participants were asked to carry on with the study at times when they were outside their home and instructed to respond to all items by themselves without discussing them with their partners or other individuals. On the second day of the study, a research assistant visited the couple to clarify procedures and deliver background questionnaires. As well, research assistants were on call throughout the study period to answer questions and solve technical issues. At the conclusion of the week, a research assistant again visited the couples’ homes, collected the devices, had each participant complete additional questionnaires, assessed cognitive ability, and debriefed the participants. The participants were thanked and received 100 euro and a small gift for integrating the assessment protocol into what was otherwise deemed a relatively typical week (M = 3.63, SD = 1.11, on a 1 = very untypical to 5 = very typical scale).

Measures

Our empirical example makes use of the repeated reports of happiness and (time-invariant) measures of participants’ subjective health, dyadic adjustment, and relationship satisfaction.

Happiness

Participants self-reported happiness at each occasion (six times per day) as slider-based response to the item “How happy are you at the moment?” For this methodology-oriented didactic example, we use happiness scores that were coded on an easily gridded and explained 4-point Likert scale. Notably, the analytic approach, and in this case the substantive findings, is similar when using other coding schemes (e.g., 5-point, 10-point, 100-point). We chose a simple four-category approach here solely for didactic purposes (i.e., easier to explain and interpret 4 × 4 matrices than 100 × 100 matrices) and encourage application with larger grids. Trajectories of two couples’ happiness are represented as movement within a two-dimensional plane, as shown in the upper portion of Figure 1. Across all 108 couples (= 216 persons), happiness tended to be in the “mildly happy” range with substantial occasion-to-occasion change. Data were fairly complete, with the ~0.8% missing reports labeled as “NA” and serving as a fifth category in the coding scheme (more details addressed in the Data analysis section).

In general, we do not recommend use of ordinal response categories in modern experience sampling studies. Rather, we encourage the use of continuous scales and data. However, as noted above, we use a “degraded” 4-point ordinal scale here for clarity in presentation of the method—which emerges from work that concentrated on and was designed around categorical and ordinal time series (e.g., Abbott, 1995). Extension to continuous (i.e., interval scale) variables is straightforward (see Hollenstein, 2013, pp. 105–108 for details on how continuous data can be placed in state space grids).

Interperson/dyad differences

Background and general information were obtained from each participant via questionnaire on the second day of the study. Gender, a factor that distinguished the members of the dyad, was a binary variable (female = 1, male = 0) and used to organize the repeated measures into the state space grids (x-axis = female, y-axis = male). Interdyad differences were examined in relation to three factors. Individuals’ subjective health was measured as a response to the item “How would you rate your current state of health?” on a 5-point scale (1 = very good to 5 = very poor; M = 2.36, SD = 0.71). Dyadic adjustment was measured using the Abbreviated Dyadic Adjustment Scale (Sharpley & Rogers, 1984; German translation, Köppe, 2001), and specifically quantified here as an individual’s rating of agreement with partner on the amount of time spent together on a 6-point scale (0 = always disagree to 5 = always agree; M = 3.99, SD = 0.79). Relationship satisfaction was measured as response to the item “All in all, how would you rate your current relationship?” on a 5-point scale (1 = very good to 5 = very bad; M = 1.47, SD = 0.57). Of note, we treat these variables as time invariant, while fully acknowledging that these constructs may in other situations be conceived and measured as time-varying characteristics (e.g., daily relationship satisfaction). Furthermore, rather than combine dyad members’ ratings of health, dyadic adjustment, and relationship satisfaction into dyad-level variables, we kept the gender specificity intact in order to examine gender-specific associations (e.g., health × gender).

Data Analysis

The first stage of analysis examines intradyad processes, placing the repeated measures of happiness into state space grids and extracting the sequence of grid cells visited by the dyad. In the second stage of the analysis, interdyad differences are identified through quantification and clustering of distances between dyad-level sequences. For clarity of presentation, the entire set of procedures (and choice points) is outlined in Table 1.

Table 1.

Suggested Procedures for Implementing Grid-Sequence Analysis

0. Problem definition

a. Define the research question

i. Do theoretically meaningful interpersonal dynamics change over time (i.e., minutes, hours, days)?

ii. Are there clusters of patterns of these interpersonal dynamics that are theoretically meaningful?

iii. Are particular patterns of interpersonal dynamics predictive of theoretically relevant variables?

b. Data preparation

1. Create state space grid for each dyad

a. Define the meaning of each axis and assign a member of the dyad to each axis (e.g., y-axis for male’s happiness and x-axis for female’s happiness)

b. Create meaningful intervals on each axis

i. Choose: Equally spaced divisions v. standardized divisions based on cell usage; choices made empirically or theoretically

c. Identify each point for the dyad in the state space grid sequentially

d. Connect points sequentially

2. Extract sequences

a. Letter each cell of the grid (Note: Analyses with nondistinguishable dyads should consider a symmetric lettering around a diagonal)

b. For each dyad, create a longitudinal sequence by extracting the letter of each cell visited along the trajectory

3. Establish cost matrix (number of cells + 1 × number of cells + 1) and sequence analysis

a. Establish the “costs” associated with transforming one sequence into another through insertion/deletion/substitution

i. Establish “indel” costs for insertion and deletion of cells into or from sequence (usually scaled at 1.0)

ii. Establish substitution cost of moving from each cell to every other cell (e.g., Euclidian distance, Manhattan distance, theoretical propositions)

iii. Establish cost of moving from measured state to missing data state (usually designated as half of the highest substitution cost)

b. Run sequence analysis on sequences created in Step 2 using cost matrix established in Step 3a to obtain distances among all pairs of sequences

i. Choose: Optimal matching techniques (e.g., Needleman–Wunsch algorithm) are most frequently used; however, other options are available

4. Cluster determination

a. Cluster analysis of resulting distance matrix to classify sequences into groups

i. Choose: Cluster algorithm (e.g., hierarchical clustering based on Ward’s method, latent mixture models)

5. Examine how cluster groups differ with respect to other intradyad and interdyad variables

a. Use cluster assignment as a predictor or outcome variable in examination of interdyad differences

i. Examples:

1. Clusters as outcome in logistic or multinomial regression (e.g., does marital satisfaction predict cluster membership?)

2. Clusters as predictor in ANOVA (e.g., do clusters differ in their average levels of subjective health?)

Note: ANOVA = analysis of variance.

Data Preparation

Data are organized in two tables, one holding the intradyad information and the other holding the interdyad information. For the empirical example, this meant the repeated measures variables were arranged in a long-format data table with multiple rows per dyad and with separate columns for each dyad member’s repeated ratings of happiness. For simplicity of illustration, time was operationalized as assessment number (1–42) with missing observations kept intact so that each dyad had exactly 42 rows of data. The interdyad variables were arranged in a separate wide-format data table with one row per dyad and with separate columns for each dyad member’s ratings of health, agreement on time spent with partner, and relationship satisfaction. As we proceed through the analysis steps, new variables are added to each table. Stage 1 is concentrated on the long-format data, and Stage 2 on the wide-format data (see Kenny et al., 2006, Table 1.3 for a visual depiction of the data formats).

Stage 1: Intradyad Analyses

In the first stage of the analysis, each dyad’s longitudinal data are examined separately, and summarized as a univariate dyad-level time series (in contrast to other approaches where the longitudinal data are summarized as a dyad-specific score).

Step 1 (gridding)

In Step 1, each dyad’s bivariate time-series data are transferred into a two-dimensional (state space) grid that is labeled using a researcher-chosen “alphabet.” As shown in the upper portion of Figure 1, a two-dimensional plane is constructed with one dyad member represented on the horizontal axis and the other dyad member represented on the vertical axis. Importantly, researchers should maintain consistency in who is placed on which axis through choice of a meaningful distinguishing feature. In the current example, we use gender. The bivariate time series is then plotted in the two-dimensional space. Once this picture is in place, the plane is overlaid with a grid that establishes a (usually nominal or ordinal) metric for each dimension. The number and location of the grid lines can be determined using theory, measurement, or statistical information. In many cases, theory-based knowledge about where to draw the grid lines will already be embedded in the coding of the variables (if originally coded on an ordinal scale; e.g., negative, neutral, positive affect). Other options include placement of grid lines at the quartiles or deciles of the empirical distributions (for each individual, dyad, or sample) or at equally spaced intervals on the response scale. Here, we used a 4-point ordinal coding (cut points at 25, 50, 75) of the original slider responses. As seen in Figure 1, this results in a picture of how a dyad moves within a 4 × 4 grid with 16 cells. For our empirical example, we obtained 108 such grids, one for each dyad. Code for organizing the data and preparing the often informative visualizations (inspired by the state space grid software; Hollenstein, 2013) makes use of the base package in R (R Core Team, 2015), the ggplot2 and reshape packages in R (Wickham, 2007, 2009), and is available on the Penn State Quantitative Developmental Systems Group website (https://quantdev.ssri.psu.edu/).

Step 2 (conversion from grids to sequences)

In Step 2, each dyad’s movement in the grid is converted into a (univariate) dyad-level categorical sequence. First, each cell in the grid is labeled with a researcher-determined “alphabet.” For simplicity of demonstration, we labeled the cells in order, starting with A in the top left corner, and proceeding left to right across all columns and from top to bottom across all rows, placing successive letters of the English alphabet (A, B, C,…, P) into each cell. More descriptive labeling may be useful to articulate theoretical conceptions where specific locations within the grid have special meaning. For example, with nondistinguishable dyads, it may be useful to consider a symmetric lettering that captures distance from the diagonal. Once the grid is labeled, one works through each bivariate time series and extracts which cell was visited at each occasion. Simply, a set of if-then statements is used to calculate a new variable in the long-format data table. For illustration, three of our 108 dyad-level (univariate) vectors are shown in the lower portion of Figure 1, each of which might now be thought of as dyad-specific “sentences” that are a verbal representation of the 42 reports of happiness obtained over 7 days of study. Where missingness appears (for one or both dyad members) the occasion is noted as “NA” and treated as an additional (17th) cell. In these data, only ~1.4% of occasions became missing in the dyad-level sequences because of one or the other member missing a report. Once constructed, the sequences are considered as holistic summaries of the intradyad dynamics and used in Stage 2 to examine interdyad differences.

Stage 2: Interdyad Analyses

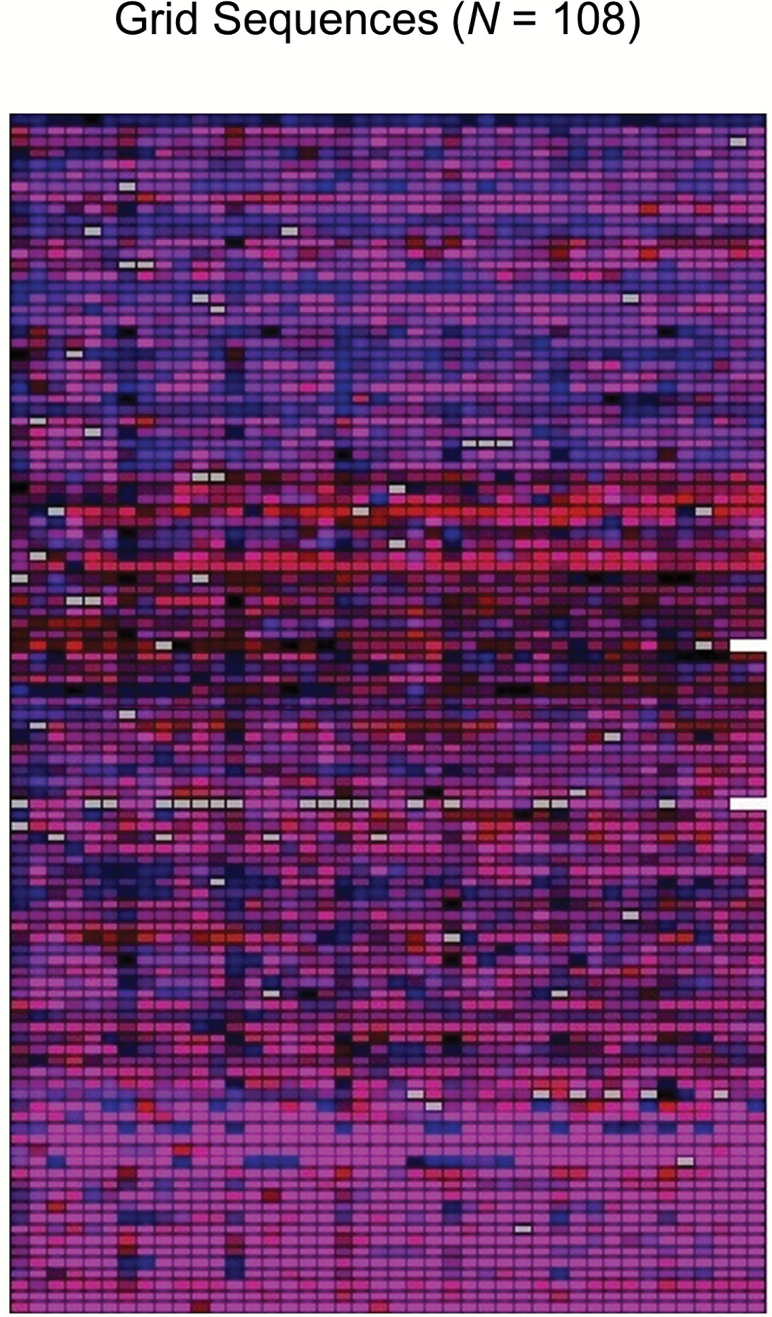
In the second stage of the analysis, the dyad-level time series are examined to identify a typology of couples and to test whether those types are related to the other interdyad differences. For illustration, all 108 dyad-level sequences from our empirical example are plotted in Figure 2, each row showing how a specific dyad moved through the grid space. Our task now is to quantify and analyze the differences apparent in the plot.

Figure 2.

Time series plots depicting the 108 dyad-level sequences extracted from the state space grid. Each colored row indicates how one dyad moved through the grid over time (time running left to right; color indicating location of cell as per Figure 1).

Step 3 (distances between sequences)

In Step 3, sequence analysis methods are used to establish and compute the distances between sequences. Following the precedents used in molecular biology, transformation of one sequence into another makes use of three actions, insertion, deletion, and substitution, each of which has an associated cost. Typically, insertion and deletion costs are both set = 1.0 (see MacIndoe & Abbott, 2004), and provide a scale for defining the cost of substituting one letter with another. Given that the grids were initially constructed to track how a dyad moved within a two-dimensional space, these costs can be conceived in terms of how much it costs to move from one location in the (psychological) space to another location in the space. How much effort is needed to move from cell A to cell A, from cell A to cell B, from cell A to cell D, from cell A to cell P, and so on? In practice, the researcher constructs a c × c substitution cost matrix (where c = the number of cells in the grid) and fills in the cost associated with each possible move. Conceived as distance between locations in space, these costs can be formalized based on other empirical data, theoretical proposition, or using standard metrics such as Euclidean or Manhattan distance (Gauthier, Widmer, Bucher, & Notredame, 2013). Using Manhattan (i.e., “city block”) distance in our example, the cost of moving from cell A to cell A = 0, from cell A to cell M = 3, and from cell A to cell P = 6. Of note, dyadic longitudinal data often have missingness, unknown locations in space, for which the cost of moving to or from other locations is indeterminate. To accommodate, missingness is conceived as an additional state and the cost matrix is expanded to size c + 1 × c + 1, and the substitution costs for missingness are set to be relatively expensive (e.g., to half the maximum substitution cost, which eliminates the possibility of using missingness as a “pass-through” state; MacIndoe & Abbott, 2004).

After establishing the transformation costs (which, to clarify, establish the cost of inserting, deleting, and moving among grid cells), the dyad-level sequences are evaluated using an algorithm that calculates the distances between sequences. Each sequence is conceived as a whole and compared to all other sequences. The optimal transformation of one sequence to another, through insertion, deletion, and substitution, is obtained using “optimal matching” algorithms that use dynamic programming to iteratively determine how any one sequence can be transformed into each of the other sequences using the fewest actions (e.g., Needleman & Wunsch, 1970). As seen in the bottom portion of Figure 1, the total costs of transforming Dyad Sequence A into Dyad Sequence B = 50, A to C = 57, and B to C = 16. In line with the differences intuitively garnered from the colored/lettered sequences, the optimal matching algorithm provided the quantitative material needed to support the inference that Dyads B and C are relatively similar to each other and are relatively dissimilar to Dyad A. It may be noted that the optimal matching algorithm does not completely rely on the sequences having the same sequence order at the same absolute time. Rather, the relatively low cost of insertion and deletion de-emphasizes differences in relative timing (e.g., the sequence ABCDEF can be transformed into AABCDE with a single insertion and single deletion = low cost = similar). That is, identical patterns that appear earlier in time for one dyad or later in time for another dyad (i.e., small shifts to the left or right) are considered similar. The allowance for (or prioritization of) shifts to the left or right emerges from the structure of the transformation costs (insertion, deletion, and substitution). The way we structured our substitution costs, as more costly than the insertion and deletion costs that accrue with the right/left shift, allows for similarity among sequences characterized by small shifts to the left or the right. Larger shifts, which may also require transformation in the other portions of the time series, may overwhelm identification of some temporally displaced identities. Researchers can select transformation cost structures that prioritize or downplay specific types of location, movement, and temporal shifts.

Using the optimal matching algorithm, the distances among all the dyad-level time series are quantified and collected together into an n × n dissimilarity matrix (where n = number of dyads). For our empirical example, we obtained the 108 × 108 symmetric dissimilarity matrix relatively easily using the TraMineR and TraMineRextras packages in R (Gabadinho, Ritschard, Müller, & Studer, 2011; Studer & Ritschard, 2015; scripts available on our website).

Step 4 (classification into types)

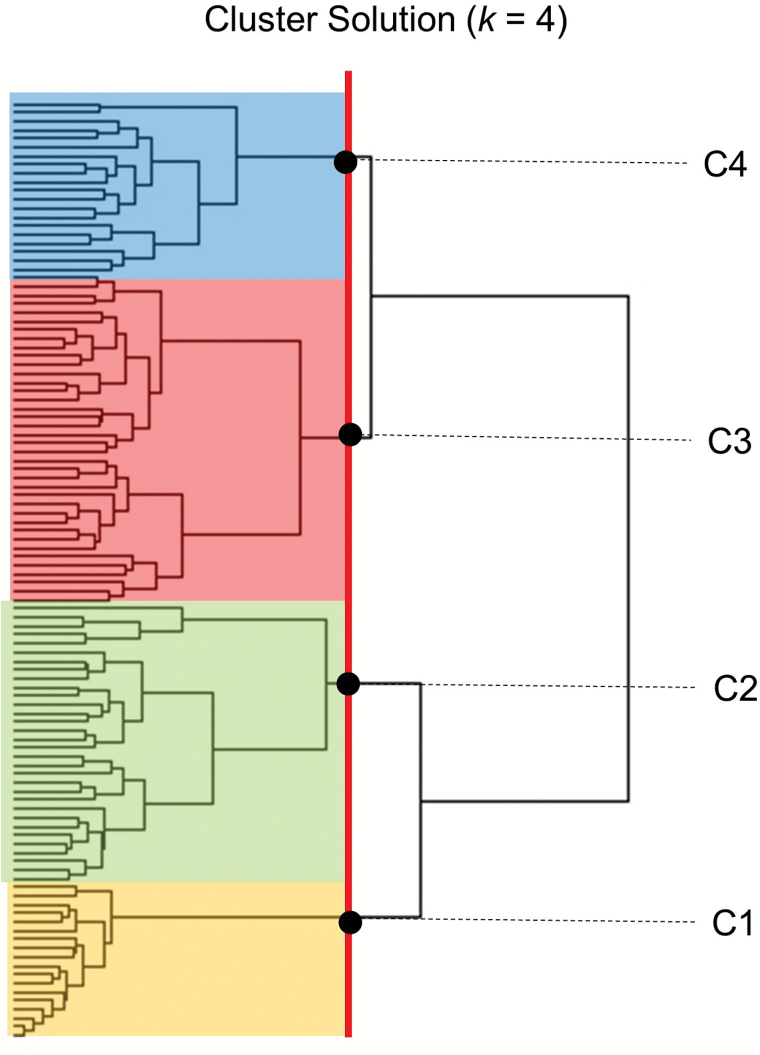
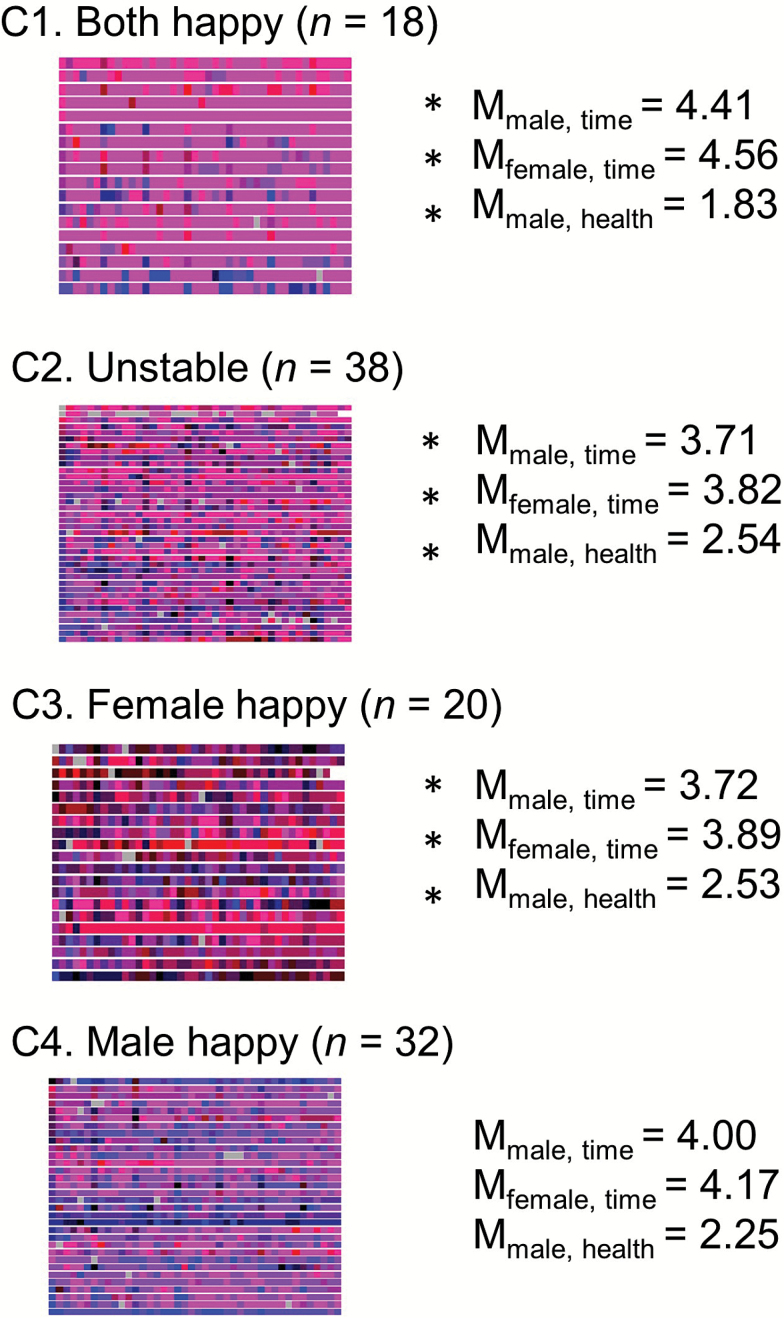
In Step 4, the dissimilarity matrix obtained in the previous step is used to identify a typology of sequences/sentences and classify each sequence into groups—dyad-level scores that formally capture the interdyad differences in intradyad dynamics. Once the dissimilarity matrix is obtained, the analyses proceed using multidimensional scaling, clustering, or mixture methods to organize sequences along one or more dimensions or into relatively homogeneous clusters (see also Ram, Benson, Brick, Conroy, & Pincus, in press). For example, we applied agglomerative hierarchical cluster analysis to the 108 × 108 dissimilarity matrix obtained in Step 3. As shown in Figure 3, we chose the number of clusters using a dendrogram based on Ward’s (1963) single linkage method—all facilitated by the cluster package in R (Maechler, Rousseeuw, Struyf, Hubert, & Hornik, 2016). In brief, with the left-to-right layout, the vertical lines in the dendrogram indicate agglomeration of sequences into clusters, and the lengths of the horizontal lines indicate how different the clusters are. For didactic purposes, we work one cluster solution forward, quantifying interdyad differences as a four-category multinomial variable that is added into the wide-format data table (in these data, cluster solutions derived with different cost matrices or response scales lead to qualitatively similar findings). The within-cluster homogeneity and between-cluster heterogeneity is readily apparent in the four-cluster solution depicted in Figure 4. The clusters are then named descriptively to facilitate interpretation—here, the four-cluster names meant to distinguish the groups based on the most prominent features of location and/or pattern of change: Cluster 1 (C1): Both happy, Cluster 2 (C2): Unstable, Cluster 3 (C3): Female happy, Cluster 4 (C4): Male happy.

Figure 3.

A dendrogram depicting results of a hierarchical cluster analysis for the “sentence” level analysis. The vertical red line indicates the cut point for a four-cluster solution.

Figure 4.

Cluster group profiles of happiness for a four-cluster solution. Visible are within-group similarity, and between-group differences in the intradyad dynamics. Significant group differences indicated by *.

Step 5 (differences among grid-sequence types)

In the final Step 5, the cluster groupings are used to examine meaningful interdyad differences. The grouping variable is treated just like any other dyad-level variable and can be used as an outcome, predictor, mediator, or moderator. Generally, the entire variety of analysis of variance (ANOVA) or regression-type methods can be used to examine how the dyad-level grouping variables obtained in Step 4 are related to other interdyad difference variables. In our empirical example, for instance, we were interested in how the typology of intradyad dynamics captured by the cluster membership variable was related to dyad members’ subjective health, agreement on time spent together, and relationship satisfaction. Articulating the general hypothesis that intradyad dynamics are related to multiple aspects of general function, we ran a series of ANOVAs to uncover group differences. Results are shown in Table 2.

Table 2.

Mean Differences Among Four Intradyad Happiness Pattern Types

				Cluster 1: Both happy (n = 18)	Cluster 2: Unstable (n = 38)	Cluster 3: Female happy (n = 20)	Cluster 4: Male happy (n = 32)
Interdyad difference variable	df	F	p Value	Mean (SD)	Mean (SD)	Mean (SD)	Mean (SD)
Subjective health (female)	3,98	1.62	.190	2.06 (0.66)	2.46 (0.70)	2.53 (0.84)	2.45 (0.68)
Subjective health (male)	3,102	5.62	.001	1.83 (0.62)2,3	2.54 (0.61)1	2.53 (0.77)1	2.25 (0.62)
Agreement on time spent with partner (female)	3,96	4.17	.008	4.56 (0.62)2,3	3.82 (0.85)1	3.89 (0.74)1	4.17 (0.75)
Agreement on time spent with partner (male)	3,98	3.73	.013	4.41 (0.71)2,3	3.71 (0.75)1	3.72 (0.75)1	4.00 (0.80)
Relationship satisfaction (female)	3,99	1.35	.264	1.33 (0.49)	1.60 (0.60)	1.67 (0.49)	1.47 (0.62)
Relationship satisfaction (male)	3,100	2.08	.107	1.22 (0.43)	1.50 (0.56)	1.56 (0.70)	1.28 (0.46)

Note: ANOVA = analysis of variance; df = degrees of freedom; HSD = honestly significant difference. N = 108, with df sometimes < 108 because of missing data in predictor variables. F and p values are from the overall ANOVA. Significant group contrasts with Tukey HSD correction are indicated by numerical subscripts indicating the groups that are significantly different than the current group. Prominent differences in group profiles shown in bold. Subjective health coded so that lower scores indicate better health. Cluster labels are purely descriptive.

The groupings in the typology of intradyad dynamics we obtained from the cluster analysis did not differ on the female partners’ subjective health, or either partner’s relationship satisfaction (Fs < 2.08, ps > .05). However, the typology groups did differ on the male partners’ subjective health (F(3,102) = 5.62, p < .05), and both partners’ perceptions of agreement on time spent together: F(3,98) = 3.73, p < .05 for men; F(3,96) = 4.17, p < .05 for women. Follow-up tests indicated the group whose intradyad dynamics were characterized as both happy differed significantly from the groups whose dynamics were characterized as unstable and female happy in that they had healthier men (M_C1 = 1.83 vs M_C2 = 2.54 vs M_C3 = 2.53, lower score = better health), and men and women both reported higher levels of agreement on amount of time spent together (M_C1 = 4.56 vs M_C2 = 3.82 vs M_C3 = 3.89 for women and M_C1 = 4.41 vs M_C2 = 3.71 vs M_C3 = 3.72 for men, on the 0–5 scale). In sum, the typology derived through the analysis of dyad-level grid-sequences captured a holistic representation of intradyad dynamics that holds valuable information related to overall function.

Discussion

In this article, we presented a grid-sequence analysis method to study interdyad differences in intradyad processes. Constructed through merging state space grid methods from dynamic systems literature with sequence analysis methods from molecular biology and sociology, the method serves as an example that emerges from the interstices between fields. Using empirical data from a study of 108 older couples, we outlined a five-step procedure for implementing grid-sequence analysis (summarized in Table 1). Our initial implementations suggest this method may be particularly useful to identify interdyad differences in dyadic experience sampling data. We are hopeful that, as we and others experiment with different types of data and research questions, the range of applications will expand.

Interdyad Differences in Intradyad Dynamics

Our empirical illustration was constructed to explore the emotional lives of older couples. Specifically, we used grid-sequence analysis to identify a typology of overall intradyad emotion dynamics using experience sampling data wherein dyad members simultaneously reported on their happiness, six times per day for 7 days. We acknowledge explicitly that our invocation of a general research question was not based in a theoretical framework. Rather, our implementation was driven by our need to, at the initial stages of methods development, work with variables that exhibited intraindividual and intradyad variability. Nonetheless, the empirical results and demonstration do provide some insight into dyadic function. Using grid-sequence analysis, we found that clusters with different intradyad dynamics also differ on both men’s and women’s dyadic adjustment (as indicated by perceptions of agreement on amount of time spent with partner) and on men’s subjective health. Both results align with prior findings. For example, the cluster characterized as both happy (C1) was the most adjusted, in line with the finding that higher dyadic adjustment is associated with higher levels of personal well-being (e.g., Proulx, Helms, & Buehler, 2007). The cluster characterized by unstable (C2) happiness included men who had worse health, partially replicating the finding that greater variability in happiness is associated with lower subjective health (e.g., Angner, Ray, Saag, & Allison, 2009). However, contrary to expectations, the typology of intradyad dynamics we identified was not associated with dyad members’ relationship satisfaction. Constructed without a priori knowledge about the types of intradyad dynamics that might be identified in 42-occasion data, the emergence of group differences suggests the method can capture different types of dynamics and help us further understand the specific features of everyday dyad-level function that indicate risk and/or resilience. In sum, grid-sequence analysis may offer a new approach for theory development.

New Research Questions

Grid-sequence analysis uses the intradyad dynamics captured in state space grids (Hollenstein, 2013) and the identification of typologies facilitated by sequence analysis (MacIndoe & Abbott, 2004) to describe dyad-level movement and to categorize dyads based on their dynamics. Similar to many other dyadic analysis methods (e.g., actor–partner interdependence, social relations models), intradyad characteristics are quantified in Stage 1 and then interdyad differences examined in Stage 2 (e.g., Gonzalez & Griffin, 2012; Kenny et al., 2006; Laurenceau & Bolger, 2005). However, a key difference in grid-sequence analysis is that we explicitly construct the (categorical) dyad-level time series and treat it as a holistic unit (similar to the functional data analysis approach for continuous time series; Ramsay & Silverman, 2005). As such, the method may be particularly suited to discover complex dyad-level dynamics.

Life-span theoretical perspectives all consider the dyad as something more than the sum of the parts, with mother/child, peer/peer, husband/wife, parent/adolescent, and caregiver/care-recipient relationships all making important contributions to both individuals’ short-term function and their long-term development. Grid-sequence analysis was constructed to integrate a holistic approach through prioritization of the dyad-level dynamics. We see potential application to a wide range of research questions centered on identification of systematic dyad-level patterns that manifest in many couples, as was done here, or that repeat over time within-dyad. For example, Butler (2011), Tuma and Hannan (1984), and Gottman and colleagues (2002) have outlined typologies based on dyad-level dynamics. In the context of aging, older couples’ dyad-level activity and emotion patterns (dynamics spanning across time spent together and apart) are likely to differ in relation to dyad-level health configurations. We look forward to using grid-sequence analysis to make use of intensive repeated measures data being obtained in recordings of dyad’s conversations and in experience sampling studies to explore how such associations manifest in real life.

Constraints and Affordances of Dyadic Longitudinal Data

This study developed the grid-sequence approach using 42-occasion experience sampling data obtained from 108 older dyads. We highlight some data features and issues that may arise in application of grid-sequence analysis. First, it is conceptually important when constructing the dyad-level grid and sequence that the two members of the dyad provide reports at the same time. The simultaneity of happiness assessments allowed us to locate, at each instance, where the dyad is situated in the two-dimensional dyadic space. Data where dyad members are not queried at the same moment would require another layer of assumptions and inference. Second, the length of the time series influences the length of the temporal patterns identified. For example, our empirical example treated the 42-occasion series as a whole so that the intradyad dynamics were defined by week-long “sentences.” Alternatively, we could treat each dyads’ data as seven separate day-long series and develop a typology of “words.” Given the possibilities, length of time series should be matched to specific hypotheses about how, and at what time-scale, the dynamics manifest. Third, the measurement scale and selection of grid size can influence results. We worked the empirical example through using the equivalent of a 4-point Likert-type ordinal scale. The relatively small number of categories provided a parsimonious set of (4 × 4 = 16) locations that many dyads would visit and an illustration that could easily be considered with respect to the categorical, ordinal, or interval measures that researchers may have. In the more general space, however, we suggest that grid-sequence analysis be applied to the most precise level of measurement available (see Hollenstein, 2013, pp. 105–108). Fourth, longitudinal data often have missingness. Here, missing data were accommodated by adding an additional “missing” state into the substitution cost matrix used in the optimal matching. This worked well here, in a situation with relatively complete data (~99% reported observations). In situations with near 50% missingness, noncompliers may emerge as a separate group in the typology. Fifth, the choice of transformation costs (insertion, deletion, substitution) influences how location, movement, and temporal shifts are weighted in the holistic determination of distance between sequences. Consistent with a study design where couples began providing reports on an arbitrary/convenient day, we prioritized similarity of small temporal shifts. Other applications should consider how to best match the transformation cost structure to both study design and substantive area.

It is also important to note that our construction of the dyad-level space was predicated on gender distinguishability. We were not able to include same-gender couples in the analysis and will explore ways to adapt the spatial structure to be inclusive. The study of indistinguishable dyads may be facilitated by a symmetric labeling scheme where, for example, the cells on opposites of the diagonal might be considered equivalent (e.g., if we altered the labeling in Figure 1, so the cells A and P were both labeled A, cells E and O both labeled E, etc.). Furthermore, we already see that the “grid” can be expanded from two-dimensional space to multidimensional space—through inclusion of dyad-level variables (e.g., third dimension = physical proximity) and/or additional individual-level variables (e.g., third and fourth dimensions = experience of particular stressor types and severity of stress). The potential to track how dyads move through high-dimensional spaces promises understanding of some of the complexity in dyads’ daily lives.

Synopsis

Theories of interpersonal interaction and social behavior emphasize the need to examine intradyad dynamics and the need for methods that operationalize new types of dynamics (Butler, 2011; Tuma & Hannan, 1984). We present grid-sequence analysis as a new approach for identifying and studying interdyad differences in intradyad dynamics. With technology affording more possibility for simultaneous experience sampling and automated coding of video/speech, we hope this novel combination of state space grid methods and sequence analysis methods may provide additional understanding of how dyads function and how we help them achieve their goals.

Funding

This work was supported by the National Institute on Health (R01 HD076994, R24 HD041025, and UL TR000127), the Penn State Social Science Research Institute, and the German Research Foundation (DFG: GE 1896/6-1).