Abstract
Background.
First-stage palliation of neonates with single-ventricle physiology is associated with poor outcomes and challenging clinical management. Prior computational modeling and in vitro experiments introduced the assisted bidirectional Glenn (ABG), which increased pulmonary flow and oxygenation over the bidirectional Glenn (BDG) and the systemic-to-pulmonary shunt in idealized models. In this study, we demonstrate that the ABG achieves similar performance in patient-specific models and assess the influence of varying shunt geometry.
Methods.
In a small cohort of single-ventricle prestage 2 patients, we constructed three-dimensional in silico models and tuned lumped parameter networks to match clinical measurements. Each model was modified to produce virtual BDG and ABG surgeries. We simulated the hemodynamics of the stage 1 procedure, BDG, and ABG by using multiscale computational modeling, coupling a finite-element flow solver to the lumped parameter network. Two levels of pulmonary vascular resistances (PVRs) were investigated: baseline (low) PVR of the patients and doubled (high) PVR. The shunt nozzle diameter, anastomosis location, and shape were also manipulated.
Results.
The ABG increased the pulmonary flow rate and pressure by 15% to 20%, which was accompanied by a rise in superior vena caval pressure (2 to 3 mm Hg) at both PVR values. Pulmonary flow rate and superior vena caval pressures were most sensitive to the shunt nozzle diameter.
Conclusions.
Patient-specific ABG performance was similar to prior idealized simulations and experiments, with good performance at lower PVR values in the range of measured clinical data. Larger shunt outlet diameters and lower PVR led to improved ABG performance.
Neonates born with single ventricle congenital heart defects typically undergo a three-staged palliative surgical repair. Stage 1 involves insertion of a systemic-to-pulmonary shunt (SPS) that provides a source of pulmonary blood flow. This physiology is usually sustainable until a more stable cavopulmonary connection, typically the bidirectional Glenn (BDG), can be implemented at 3 to 6 months. First-stage palliation has the highest mortality rate of the three stages, leading to high ventricular volume load, imbalance of systemic and pulmonary flow, and shunt thrombosis [1, 2]. Early efforts to implement the Glenn in neonates resulted in poor clinical outcomes [3, 4], attributed to low pulmonary flow, elevated neonatal pulmonary vascular resistance (PVR), and high superior vena caval (SVC) pressures, leading to SVC syndrome [4].
The assisted bidirectional Glenn (ABG) was introduced as an alternative to the SPS [5] and modified the conventional BDG with an additional shunt between the innominate artery and SVC to increase pulmonary flow. A related concept that anastomosed the shunt directly to the branch pulmonary arteries (PAs) was previously proposed but resulted in high SVC pressures [6]. In an acute pilot study, an SVC–PA pump assist to increase pulmonary flow in stage 1 Norwood patients lowered SVC pressures [7]. Here, the ABG shunt is anastomosed to the SVC, and the shunt outlet is constricted to act as an ejector pump, whereby the high-velocity jet from the shunt mixes with the low-energy SVC flow to ideally increase pulmonary flow and to maintain low SVC pressure upstream of the anastomosis. Potential advantages over a conventional SPS include ventricular load reduction, a stable source of pulmonary flow and hepatic flow, and a secondary source of pulmonary flow in the event of shunt thrombosis. An early implementation of the ABG would potentially eliminate the stage 1 SPS, reducing the number of surgical stages to two, because the ABG shunt could later be closed by catheterization.
Prior studies revealed the ABG as a promising approach for stage 1 single ventricle palliation. Multiscale modeling and in vitro experiments of an idealized three-dimensional (3D) ABG model demonstrated improved pulmonary flow and systemic oxygen saturation compared with the BDG at low and high PVR values [5, 8]. Idealized models were also used to optimize shunt geometry [9]. Here, we assess ABG performance in three patient-specific models, using multiscale modeling that combines 3D image-based computational fluid dynamics with lumped-parameter models of circulatory physiology. We aim to verify that prior idealized model results are replicated in patient-specific models and to examine patient variability in ABG performance, measured with clinically relevant parameters. We also manipulate ABG shunt geometry to identify parameters governing performance, because prior experiments found dependence on shunt geometry [8], and this knowledge will contribute to further shunt optimization [9].
Patients and Methods
Geometric Modeling
Magnetic resonance imaging and clinical data, including patient demographic characteristics, initial diagnosis, and cardiac catheterization data, were acquired before stage 2 surgery for patients A, B, and C (Supplemental Table 1). For each patient, we constructed 3D models of the pre-stage 2 vasculature by using the open-source SimVascular software (http://simvascular.org) [10]. Medical image data were imported; centerline paths were constructed along the vessels of interest, segmentations (cross-sections) of the vessels were generated along the paths and lofted to create a 3D solid model. To generate the virtual BDG model, an automated script removed the SPS and re-oriented and anastomosed the SVC to the right PA, in consultation with a pediatric cardiac surgeon.
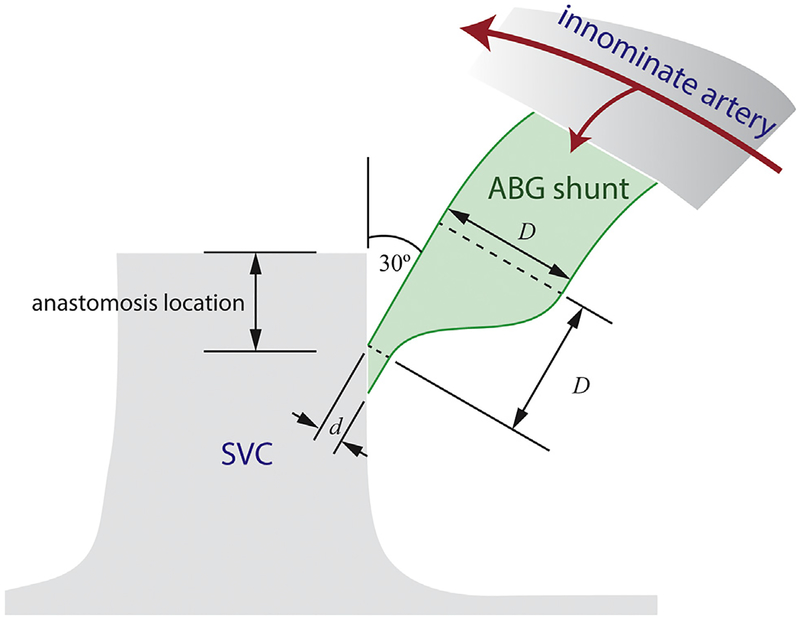
As originally proposed, the ABG shunt was constricted with a Ligaclip (Ethicon, Somerville, NJ) near the SVC anastomosis [5]. Although this method is easily adopted in the clinic, a prefabricated shunt nozzle would be more repeatable. Here, we prescribe the main shunt diameter D, luminal outlet diameter d, outlet eccentricity (elliptical versus circular), and SVC anastomosis location (Fig 1). The shunt was angled at 30° with respect to the SVC. A script automatically generated and unioned the shunt to the BDG model in SimVascular. To assess ABG performance compared with the SPS and BDG across different patients, a baseline shunt geometry was used with diameters D of 3.5 mm and d of 1.2 mm (Supplemental Fig 1). To evaluate the sensitivity of ABG performance to shunt parameters, the following variations were implemented for patient A: nozzle diameter: 3.5-mm diameter shunt with d of 0.6 mm or 1.8 mm; nozzle shape: elliptical nozzle (d = 1.2 mm, major axis 3.5 mm, minor axis 0.41 mm), whose circumference is 90% larger over a circular outlet; and location: shunt anastomosed to the SVC–pulmonary junction.
Fig 1.
Schematic of assisted bidirectional Glenn (ABG) shunt geometry, illustrating the shunt narrowing proximal to the superior vena cava (SVC). (D = main shunt diameter; d = luminal outlet diameter.)
Multiscale Simulations
We used a multiscale modeling framework to couple local hemodynamics in the 3D model to a 0D closed-loop lumped parameter network that represented circulatory physiology [11, 12]. The lumped parameter networks, comprised of circuit elements in organ blocks, were adapted from prior studies and were tuned to match patient-specific data [13, 14], including patient-specific pulmonary pressures, flow splits, and flow rates. For the BDG and ABG simulations, the lumped parameter network was modified to connect the upper body venous return to the SVC, leaving all parameter values unchanged. The total excess blood volume was also adjusted from the stage 1 surgery to the ABG or BDG to maintain constant systemic systolic blood pressure, which would be autoregulated.
At the time of data acquisition (2 to 6 months), patients A, B, and C had PVR values of 3, 3, and 6 WU-m2, respectively. The typical range of neonatal PVR values for patients with single-ventricle physiology remains largely unknown. Therefore, we performed a comprehensive retrospective single-institution chart review to determine PVR values in neonatal single-ventricle physiology. The Lucile Packard Children’s Hospital database was interrogated to identify all patients in the past 20 years who were younger than 1 month of age at the time of catheterization and were diagnosed with a single ventricle defect. PVR values for all patients (n = 7) identified are shown in Table 1. Prior studies also report similar PVR values after indexing to body surface area [15, 16]. Together, these data confirm that the baseline PVR values used in the computational modeling are in line with clinical measurements. It is commonly believed, however, that neonatal PVR is higher, so additional simulations were performed at twice the baseline PVR by doubling pulmonary resistances at each outlet. Increasing vascular resistance decreased oxygen saturation and delivery in Norwood circulation models [17].
Table 1.
PVR Values From a Single-Institution, Retrospective Chart Review of Patients With Single-Ventricle Physiology Younger Than 1 Month Old
| Case | Diagnoses | SPS | Age, days | PVR, WU-m2 |
|---|---|---|---|---|
| 1 | Heterotaxy, hypoplastic left ventricle, mitral valve, atrial valve, long-segment arch hypoplasia, parachute mitral valve, atrial and ventricular septal defects | Before | 7 | 3.24 |
| 2 | PA+IVS, right ventricle with sinusoidal communications to all coronary arteries; left coronary artery was anomalous, coming off rightward/anterior cusp | Before | 5 | 0.83 |
| 3 | HLHS, left ventricle coronary sinusoids, restrictive atrial septum | After | 27 | 1.35 |
| 4 | HLHS | Before | 2 | 1.32 |
| 5 | HLHS, aortic arch hypoplasia, aortic valvar stenosis | Before | 17 | 16.62 |
| 6 | PA+IVS, severe coronary abnormalities, multiple aortopulmonary collaterals | Before | 6 | 2.3 |
| 7 | PA+IVS | Before | 3 | 2.86 |
HLHS = hypoplastic left heart syndrome; PA+IVS = pulmonary atresia with intact ventricular septum; PVR = pulmonary vascular resistance; SPS = systemic-to-pulmonary shunt.
In the 3D domain, we solved the Navier-Stokes equations for an incompressible, Newtonian fluid (density = 1,060 kg/m3; dynamic viscosity = 0.004 Pa-s) and rigid walls with the SimVascular finite-element solver [18, 19]. The time step size was 1/1,000th of a cardiac cycle, determined by the patient’s heart rate. A coupled Dirichlet boundary condition was imposed at the ascending aorta [12, 20]. To prevent simulation divergence due to backflow, outlet stabilization was used [21]. Simulations were run for six cardiac cycles to ensure convergence; the last cycle was post-processed.
Mesh generation was done with MeshSim (Simmetrix, Inc, Troy, NY). We performed a mesh convergence study with one to four refinement adaptations based on the Hessian of the velocity field [22]; three adaptations were sufficient to obtain SVC pressures and pulmonary flows within 0.1% of the finest mesh. The final number of elements ranged from 2.5 to 3.9 million.
Results
Patient Comparison
Simulation results comparing the SPS, the BDG, and the baseline ABG are shown in Table 2. For patients A and B, the BDG at both PVR values substantially decreased the ventricular load (>30%) and increased oxygen delivery rates and saturations, as expected. Patient C had a low pulmonary-to-systemic flow (Qp/Qs) ratio (<0.5) with the central shunt, resulting in poor oxygen delivery and saturation. With the BDG, patient C’s Qp/Qs ratio increased, along with the anticipated ventricular offload and increase in oxygen delivery and saturation. For all patients, the BDG decreased the pulmonary pressure by a similar amount at both PVR values, relative to the stage 1 surgery. However, the SVC pressure with the SPS anatomy was stable and low at both PVR values, whereas the SVC pressure with the BDG increased by as much as 5 mm Hg between low and high PVR values (patient C).
Table 2.
Simulation Results of Surgical Options at Low and High PVR for All Patients
| Patient A | Patient B | Patient C | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| mBT | BDG | ABGa | mBT | BDG | ABGa | mBT | BDG | ABGa | mBT | BDG | ABGa | C | BDG | ABGa | C | BDG | ABGa | |
| Low PVR | High PVR | Low PVR | High PVR | Low PVR | High PVR | |||||||||||||
| PVR, WU-m2 | 3.13 | 3.32 | 3.23 | 5.83 | 6.22 | 6.05 | 3.39 | 3.07 | 3.02 | 6.43 | 5.73 | 5.63 | 6.03 | 6.03 | 6.06 | 11.4 | 12 | 12.1 |
| Pao, mm Hg | 50.4 | 58.4 | 56.4 | 48.5 | 54.3 | 52.3 | 50.7 | 55.3 | 50.7 | 47.5 | 51.3 | 48.8 | 40 | 44.5 | 43 | 40.6 | 43.7 | 42.3 |
| Psys, mm Hg | 79.3 | 79.6 | 79.1 | 75.5 | 73 | 72 | 75.9 | 72.3 | 68.6 | 70.6 | 66.4 | 65 | 69.8 | 69.3 | 68.6 | 70 | 66.4 | 65.7 |
| Ppulm, mm Hg | 17.1 | 11.6 | 13.7 | 21.8 | 15.1 | 17.7 | 11.3 | 6.72 | 7.94 | 15.1 | 8.93 | 11.1 | 12.4 | 11.5 | 13.4 | 18.1 | 17 | 19.5 |
| Psvc, mm Hg | 8.39 | 12.7 | 15.2 | 6.97 | 15.9 | 18.8 | 4.3 | 7.82 | 10.2 | 3.13 | 9.89 | 13.1 | 5.18 | 12.5 | 14.8 | 4.84 | 17.8 | 20.3 |
| CO, L/min | 1.63 | 1.08 | 1.17 | 1.5 | 0.92 | 1 | 1.23 | 0.78 | 0.84 | 1.11 | 0.68 | 0.76 | 1.39 | 1.04 | 1.11 | 1.37 | 0.93 | 0.98 |
| Qs, L/min | 0.83 | 1.08 | 0.97 | 0.79 | 0.92 | 0.81 | 0.61 | 0.78 | 0.66 | 0.55 | 0.68 | 0.59 | 0.94 | 1.04 | 0.94 | 0.97 | 0.93 | 0.84 |
| Qp, L/min | 0.81 | 0.61 | 0.75 | 0.71 | 0.52 | 0.64 | 0.63 | 0.43 | 0.54 | 0.56 | 0.38 | 049 | 0.46 | 0.57 | 0.66 | 0.4 | 0.45 | 0.52 |
| Qshunt, L/mint | … | … | 0.2 | … | … | 0.18 | … | … | 0.18 | … | … | 0.17 | … | … | 0.17 | … | … | 0.14 |
| Qp/Qs | 0.97 | 0.56 | 0.77 | 1.13 | 0.56 | 0.78 | 0.98 | 0.55 | 0.82 | 1.02 | 0.55 | 0.84 | 0.49 | 0.55 | 0.7 | 0.41 | 0.59 | 0.62 |
| HL, Nm/min | 14.8 | 10.1 | 10.9 | 12.9 | 7.92 | 8.37 | 10.4 | 6.81 | 6.93 | 8.56 | 5.44 | 5.84 | 11.5 | 8.6 | 9.09 | 11.3 | 7.35 | 7.68 |
| OD, mL/s | 2.14 | 3.17 | 2.99 | 1.93 | 2.61 | 2.43 | 1.39 | 2.06 | 1.9 | 1.13 | 1.7 | 1.63 | 1.64 | 3.03 | 2.83 | 1.42 | 2.53 | 2.37 |
| Satao, % | 69 | 78.7 | 82.4 | 64.9 | 75.4 | 79.6 | 60.6 | 70.5 | 76.5 | 56.3 | 66.9 | 74.3 | 46.7 | 77.5 | 80.3 | 39.1 | 72.2 | 75.6 |
The ABG shunt was 3.5 mm in diameter with a 1.2-mm diameter circular nozzle.
ABG = assisted bidirectional Glenn; BDG = bidirectional Glenn; C = central shunt; CO = mean cardiac output; HL = ventricular load; mBT = modified Blalock-Taussig shunt; OD = systemic oxygen delivery; Pao = aortic average pressure; Ppulm = mean pulmonary artery pressure; Psvc = superior vena caval average pressure; Psys = systolic average pressure; PVR = pulmonary vascular resistance; Qp = pulmonary flow rate; Qs = systemic flow rate; Qp/Qs = pulmonary to systemic flow ratio; Qshunt = flow rate through the ABG shunt; Satao = oxygen saturation in the aorta.
The ABG increased the pulmonary flow rate by 15% to 30% at both PVR values compared with the BDG. The ventricular load increase was negligible (<10%). However, the improvement in pulmonary flow was accompanied by a proportional increase in the SVC pressure of at least 2 mm Hg. SVC pressures of 2 patients remained less than 15 mm Hg with the ABG at low PVR, and 1 patient remained under this threshold at high PVR.
With the ABG, the cardiac output increased by an amount less than the added flow through the shunt; the shunt diverted some systemic circulation into the pulmonary circulation. Consequently, the systemic oxygen delivery decreased, although overall oxygen saturation increased for the ABG compared with the BDG. The increase in oxygen saturation with the ABG was as much as 6% to 7%.
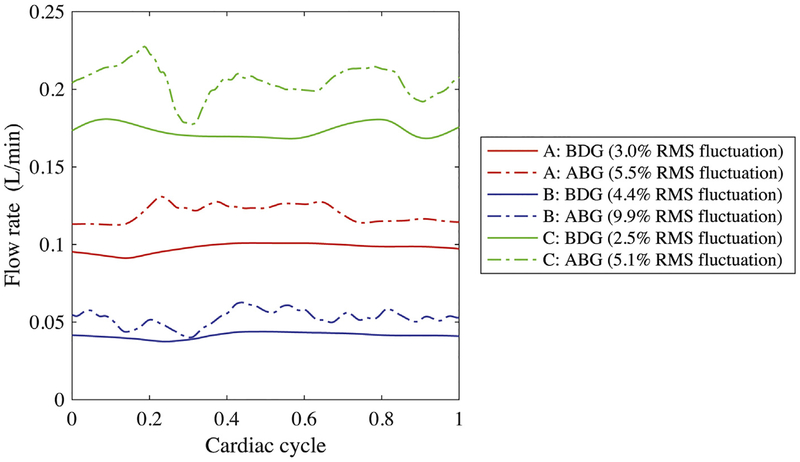
The ABG may also benefit pulmonary endothelial function by supplying pulsatile pulmonary flow. Figure 2 illustrates variations in pulsatility index at low PVR, defined as (peak systolic flow rate – minimum diastolic flow rate)/(mean flow rate). Modifications to the waveform can be long-wave (patient A) or short-wave (patients B and C). The change in pulsatility index was likely determined by branching of the ABG shunt flow; overall the ABG increased pulsatility by a factor of 1.5 to 3.3.
Fig 2.
Flow rate through the largest pulmonary artery for each patient, comparing bidirectional Glenn (BDG) and assisted bidirectional Glenn (ABG). (RMS = root mean square.)
Shunt Geometry
The effects of shunt geometry on patient A are summarized in Table 3. Variations considered include nozzle diameter, shunt outlet shape, and shunt location.
Table 3.
Simulation Results of BDG and ABG at Low and High PVR, With Varying Shunt Geometry
| Low PVR | High PVR | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ABGa | ABGa | |||||||||||
| Variable | BDG | i | ii | iii | iv | v | BDG | i | ii | iii | iv | v |
| PVR, WU-m2 | 3.32 | 3.29 | 3.23 | 3.16 | 3.22 | 3.23 | 6.22 | 6.18 | 6.05 | 5.91 | 6.03 | 6.06 |
| Pao, mm Hg | 58.5 | 59.1 | 56.4 | 52.6 | 56.3 | 57.2 | 54.3 | 54.9 | 52.3 | 48.6 | 52.1 | 53.0 |
| Psys, mm Hg | 79.6 | 81.2 | 79.1 | 76.0 | 78.9 | 79.8 | 73.0 | 74.3 | 72.0 | 68.6 | 71.8 | 72.6 |
| Ppulm, mm Hg | 11.6 | 12.7 | 13.7 | 15.2 | 13.7 | 13.4 | 15.1 | 16.4 | 17.7 | 19.6 | 17.8 | 17.3 |
| Psvc, mm Hg | 12.7 | 13.7 | 15.2 | 16.9 | 15.1 | 14.8 | 15.9 | 17.2 | 18.8 | 20.8 | 18.8 | 18.4 |
| CO, L/min | 1.08 | 1.13 | 1.17 | 1.24 | 1.18 | 1.16 | 0.924 | 0.968 | 0.995 | 1.03 | 0.996 | 0.987 |
| Qs, L/min | 1.08 | 1.06 | 0.970 | 0.837 | 0.965 | 0.996 | 0.924 | 0.911 | 0.813 | 0.682 | 0.809 | 0.841 |
| Qp, L/min | 0.606 | 0.644 | 0.750 | 0.878 | 0.758 | 0.728 | 0.517 | 0.566 | 0.635 | 0.731 | 0.640 | 0.616 |
| Qshunt, L/min | 0.063 | 0.202 | 0.400 | 0.211 | 0.163 | 0.057 | 0.181 | 0.350 | 0.188 | 0.146 | ||
| Qp/Qs | 0.563 | 0.625 | 0.774 | 1.05 | 0.786 | 0.730 | 0.560 | 0.621 | 0.781 | 1.07 | 0.791 | 0.732 |
| HL, Nm/min | 10.1 | 10.8 | 10.9 | 11.0 | 10.9 | 10.9 | 7.92 | 8.45 | 8.37 | 8.24 | 8.37 | 8.39 |
| OD, mL/s | 3.17 | 3.21 | 2.99 | 2.66 | 2.98 | 3.06 | 2.61 | 2.64 | 2.43 | 2.09 | 2.42 | 2.49 |
| Satao, % | 78.7 | 80.4 | 82.4 | 84.7 | 82.6 | 82.0 | 75.4 | 77.4 | 79.6 | 82.0 | 79.8 | 79.0 |
The ABG shunt was 3.5 mm in diameter with (i) 0.6-mm circular nozzle, (ii) 1.2-mm circular nozzle (baseline), (iii) 1.8-mm circular nozzle, (iv) 1.2-mm elliptical nozzle, and (v) 1.2-mm circular nozzle anastomosed to the superior vena cava–pulmonary junction.
ABG = assisted bidirectional Glenn; BDG = bidirectional Glenn; CO = mean cardiac output; HL = ventricular load; OD = systemic oxygen delivery; Pao = aortic average pressure; Ppulm = mean pulmonary artery pressure; Psvc = superior vena caval average pressure; Psys = systolic average pressure; PVR = pulmonary vascular resistance; Qp = pulmonary flow rate; Qs = systemic flow rate; Qp/Qs = pulmonary to systemic flow ratio; Qshunt = flow rate through the ABG shunt; Satao = oxygen saturation in the aorta.
nozzle diameter.
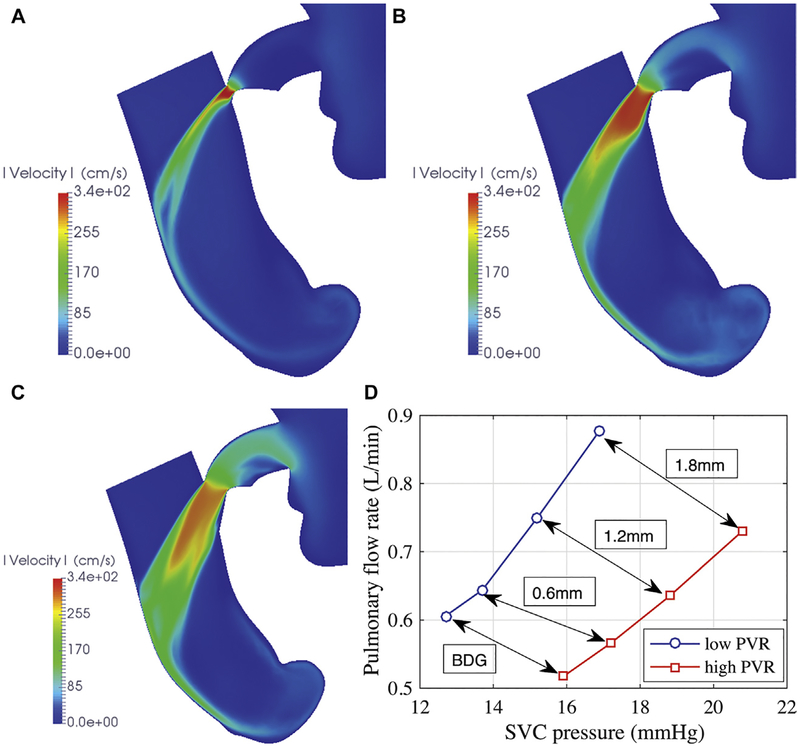
The highest speed in the ABG shunt (approximately 3 m/s) occurs at the narrowest point (Figs 3A–3C). The jet expands in the SVC and impinges the opposite wall before washing downstream. The shunt flow rate increased non-linearly with nozzle diameter; a regression fit showed that the shunt flow is proportional to d1.69 at low PVR and d1.65 at high PVR (Fig 4A). The similarity between the two relations showed that the shunt flow did not change with PVR.
Fig 3.
Simulated flow speed in a plane bisecting the assisted bidirectional Glenn (ABG) shunt and the superior vena cava (SVC). Shunt flow is right to left. Shunts have nozzle diameters of (A) 0.6 mm, (B) 1.2 mm, and (C) 1.8 mm. (D) Pulmonary flow versus SVC pressure in the ABG, varying nozzle diameters. Arrows compare the same anatomic models at different pulmonary vascular resistance (PVR). (BDG = bidirectional Glenn.)
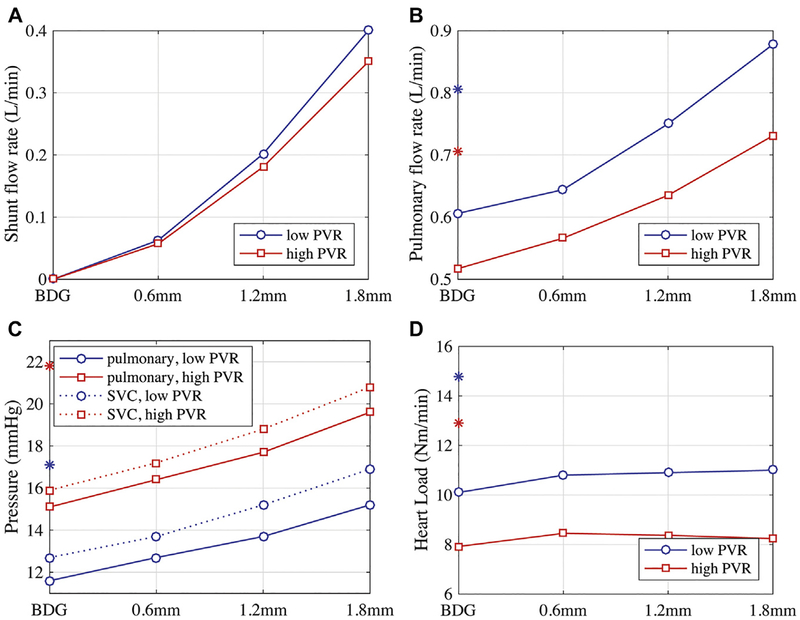
Fig 4.
Clinically relevant parameters of (A) shunt flow rate, (B) pulmonary flow rate, (C) pressure, and (D) heart load versus assisted bidirectional Glenn (ABG) nozzle diameters; the bidirectional Glenn (BDG) is shown as a zero-diameter variant of the ABG. *Modified Blalock-Taussig shunt values. (PVR = pulmonary vascular resistance; SVC = superior vena cava.)
The change in pulmonary flow rate was also nonlinear with nozzle diameter (Fig 4B). Compared with the BDG, the ABG augmented pulmonary flow by 6% to 45%, depending on the nozzle diameter at low PVR (8% to 41% at high PVR) (Table 3). The pulmonary pressure increased by as much as 4 mm Hg for the largest shunt and SVC pressure increased in tandem, exceeding 16 mm Hg at low PVR and 20 mm Hg at high PVR (Fig 4C). At low PVR, pulmonary flow increased with SVC pressure more steeply than at high PVR (Fig 3D). If the increase in the SVC pressure could be tolerated, the ABG did not substantially increase the heart load regardless of nozzle diameter (Fig 4D). The effect on oxygen delivery and saturation depended on the nozzle flow rate. Although the oxygen delivery rate decreased with diameter because of decreasing systemic flow, the overall systemic saturation increased by 6% for the largest nozzle (Table 3).
shunt outlet shape.
A nozzle with increased surface area could promote mixing and boost the ejector pump effect. We found that surface area had a negligible effect on performance. The jet from an elliptical nozzle was better aligned with the SVC and diffused more quickly, which would seem beneficial to performance (Fig 5A), but the decrease in SVC pressure was less than 1% at both PVR values (Table 3).
Fig 5.
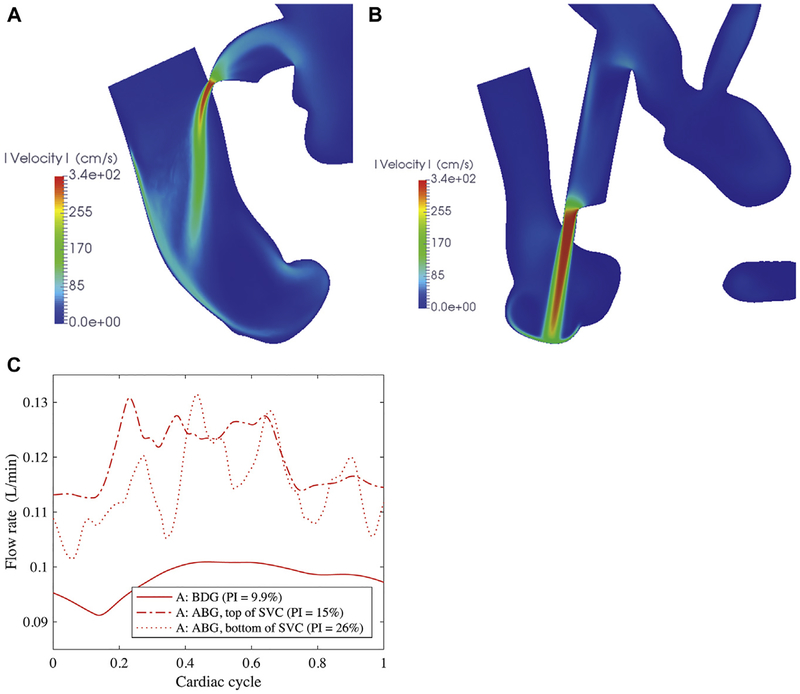
Simulated flow speed in a plane bisecting the assisted bidirectional Glenn (ABG) shunt and the superior vena cava (SVC) for (A) an elliptical nozzle and (B) an anastomosis near the SVC–pulmonary junction. (C) Flow rate through the largest pulmonary artery, comparing anastomosis location. (BDG = bidirectional Glenn; PI = pulsatility index.)
shunt location.
Anastomosing the ABG shunt to the SVC–pulmonary junction could deliver flow more directly to the pulmonary arteries. However, the jet caused recirculation in the junction (Fig 5B). When shunts were anastomosed to the top of the SVC (Fig 3B), the momentum of the SVC flow swept the jet downstream. In contrast, the flow in a T-junction must decelerate to bifurcate into the left and right PAs. This design had a lower flow rate through the shunt and PAs (Table 3, column v) and consequently did not perform as well as the shunt placed upstream. However, shunt placement could enhance pulsatility of the pulmonary flow. Higher amplitude perturbations were introduced by the shunt inserted at the SVC–pulmonary junction, with pulsatility index of 26% compared with 15% for the anastomosis at the top of the SVC (Fig 5C).
Comment
We reported ABG performance in a cohort of patient-specific models and explored effects of shunt geometry. ABG performance relative to the BDG was consistent across patients, despite the disparity in patients’ conditions prestage 2. The ABG possessed many of the benefits of the BDG compared with a SPS and enhanced pulmonary pressure and flow rate by approximately 20%, increasing the systemic saturation. Similar performance was noted in prior simulations and in vitro experiments in idealized models. The goal of reducing or maintaining the SVC pressure, however, was not realized with the ABG, which always increased the SVC pressure; at high PVR, the SVC pressures could increase beyond a reasonable value. Our measured PVR data, corroborated by prior studies, however, suggest that neonatal PVR may be modest, in which case the predicted SVC pressures could remain manageable. Patients for whom a low SVC pressure was predicted for the BDG may be appropriate candidates for the ABG.
The ABG induced pulmonary flow pulsatility compared with the BDG. A prior study suggested that pulsatile cavopulmonary flow may have benefits for exercise tolerance [23]. The ABG may also mitigate formation of pulmonary arteriovenous malformations. Diverting hepatic effluent from the pulmonary circulation may contribute to development of arteriovenous malformations with a BDG [24] and can potentially be avoided by introducing hepatic flow to the pulmonary bed with the ABG. Furthermore, introducing the supplemental flow through the SVC promotes an even distribution of hepatic flow to the right and left PAs.
The ABG flow rate was most affected by nozzle outlet diameter, in agreement with prior in vitro experiments [8]. Varying shunt anastomosis location and outlet shape led to marginal improvement, also in agreement with experiments [8]. The high velocity through the nozzle may counteract thrombosis; the timescale of occlusion can only be assessed with a biological model. In the event of occlusion, the ABG would revert to a BDG and provide a source of pulmonary flow.
The ABG ejector pump effect is relatively weak, because the jet maintains momentum as it enters the pulmonary trunk and does not substantially mix with the primary stream. Moreover, use of an elliptical nozzle to increase jet surface area was not enough to reduce SVC pressure to levels near BDG. A more steeply inclined shunt will increase coaxial momentum, but it will be somewhat counteracted by the larger cross-section in which the shunt is anastomosed to the SVC, which will increase the jet’s expansion on entering the SVC. Optimization studies show that pulmonary flow rates with the ABG increase modestly and SVC pressures are unchanged with decreased shunt angle [9]. However, the ABG may hold promise when combined with PVR-lowering drugs, because the ejector pump effect increases when PVR is reduced.
The patient-specific modeling performed here highlights the variability in patient response to virtual surgeries. Patient-specific surgical planning performed by using the proposed simulation framework could be used to select candidates for the ABG, and it illustrates the potential benefits of multiscale modeling for surgical planning [25]. The inability to reduce SVC pressure for patients with high PVR remains a concern for clinical translation, although our limited data indicate that neonatal PVR may be lower than previously thought. However, because of the challenging nature of invasive catheterization measurements in stage 1 neonates, additional clinical data from multicenter studies should be obtained to further characterize PVR levels in neonates with single ventricle physiology. Such data will be critical to identifying appropriate guidelines for the clinical use of ABG surgery.
Supplementary Material
Acknowledgments
This study was supported a Burroughs Wellcome Fund Career Award at the Science Interface; a Leducq Foundation Network of Excellence Grant, and a National Science Foundation CAREER Award No. OCI-1150184. This project used computational resources from the Extreme Science and Engineering Discovery Environment (XSEDE). J.K.S. was supported by the National Institutes of Health, National Heart, Lung, and Blood Institute Grant T32 HL098049.
Footnotes
The Supplemental Table and Figure can be viewed in the online version of this article [http://doi.org/10.1016/j.athoracsur.2018.10.024] on shttp://www.annalsthoracicsurgery.org.
References
- 1.Tamisier D, Vouhé PR, Vernant F, Leca F, Massot C, Neveux J-Y. Modified Blalock-Taussig shunts: results in infants less than 3 months of age. Ann Thorac Surg 1990;49:797–801. [DOI] [PubMed] [Google Scholar]
- 2.Bartram U, Grünenfelder J, Van Praagh R. Causes of death after the modified Norwood procedure: a study of 122 postmortem cases. Ann Thorac Surg 1997;64:1795–802. [DOI] [PubMed] [Google Scholar]
- 3.Glenn WW. Circulatory bypass of the right side of the heart, IV: shunt between superior vena cava and distal right pulmonary artery; report of clinical application. N Engl J Med 1958;259:117–20. [DOI] [PubMed] [Google Scholar]
- 4.Glenn WW, Browne M, Whittemore R. Circulatory bypass of the right side of the heart: cava-pulmonary artery shunt—indications and results (report of a collected series of 537 cases) In: The Heart and Circulation in the Newborn and Infant. New York, NY: Grune & Stratton; 1966:345. [Google Scholar]
- 5.Esmaily-Moghadam M, Hsia T-Y, Marsden AL. Modeling of Congenital Hearts Alliance (MOCHA) Investigators. The assisted bidirectional Glenn: a novel surgical approach for first-stage single-ventricle heart palliation. J Thorac Cardiovasc Surg 2015;149:699–705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Gervaso F, Kull S, Pennato G, Migliavacca F, Dubini G, Luisi VS. The effect of the position of an additional systemic-to-pulmonary shunt on the fluid dynamics of the bidirectional cavo-pulmonary anastomosis. Cardiol Young 2004;14(Suppl 3):38–43. [DOI] [PubMed] [Google Scholar]
- 7.Honjo O, Merklinger SL, Poe JB, et al. Mechanically assisted bidirectional cavopulmonary shunt in neonates and infants: an acute human pilot study. J Thorac Cardiovasc Surg 2017;153:441–7. [DOI] [PubMed] [Google Scholar]
- 8.Zhou J, Esmaily-Moghadam M, Conover TA, et al. In vitro assessment of the assisted bidirectional Glenn procedure for stage one single ventricle repair. Cardiovasc Eng Technol 2015;6:256–67. [DOI] [PubMed] [Google Scholar]
- 9.Verma A, Esmaily M, Shang J, et al. Optimization of the assisted bidirectional Glenn procedure for first stage single ventricle repair. World J Pediatr Congenit Heart Surg 2018;9:157–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Updegrove A, Wilson NM, Merkow J, Lan H, Marsden AL, Shadden SC. SimVascular: an open source pipeline for cardiovascular simulation. Ann Biomedcal Eng 2017;45:525–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bove EL, Migliavacca F, de Leval MR, et al. Use of mathematic modeling to compare and predict hemodynamic effects of the modified Blalock-Taussig and right ventricle-pulmonary artery shunts for hypoplastic left heart syndrome. J Thorac Cardiovasc Surg 2008;136:312–20. [DOI] [PubMed] [Google Scholar]
- 12.Moghadam ME, Vignon-Clementel IE, Figliola R, et al. A modular numerical method for implicit 0D/3D coupling in cardiovascular finite element simulations. J Comput Phys 2013;244:63–79. [Google Scholar]
- 13.Schiavazzi DE, Kung EO, Marsden EL, et al. Hemodynamic effects of left pulmonary artery stenosis after superior cavopulmonary connection: a patient-specific multiscale modeling study. J Thorac Cardiovasc Surg 2015;149:689–96. [DOI] [PubMed] [Google Scholar]
- 14.Arbia G, Corsini C, Baker C, Pennati G, Hsia T-Y, Vignon-Clementel IE. Pulmonary hemodynamics simulations before stage 2 single ventricle surgery: patient-specific parameter identification and clinical data assessment. Cardiovasc Eng Technol 2015;6:268–80. [DOI] [PubMed] [Google Scholar]
- 15.Hoffman GM, Tweddell JS, Ghanayem NS, et al. Alteration of the critical arteriovenous oxygen saturation relationship by sustained afterload reduction after the Norwood procedure. J Thorac Cardiovasc Surg 2004;127:738–45. [DOI] [PubMed] [Google Scholar]
- 16.Naito Y, Aoki M, Watanabe M, et al. Factors affecting systemic oxygen delivery after Norwood procedure with Sano modification. Ann Thorac Surg 2010;89:168–73. [DOI] [PubMed] [Google Scholar]
- 17.Migliavacca F, Pennati G, Dubini G, et al. Modeling of the Norwood circulation: effects of shunt size, vascular resistances, and heart rate. Am J Physiol Heart Circ Physiol 2001;280:H2076–86. [DOI] [PubMed] [Google Scholar]
- 18.Moghadam ME, Bazilevs Y, Marsden AL. A new pre-conditioning technique for implicitly coupled multidomain simulations with applications to hemodynamics. Comput Mech 2013;52:1141–52. [Google Scholar]
- 19.Moghadam ME, Bazilevs Y, Marsden AL. Impact of data distribution on the parallel performance of iterative linear solvers with emphasis on CFD of incompressible flows. Comput Mech 2015;55:93–103. [Google Scholar]
- 20.Marsden AL, Esmaily-Moghadam M. Multiscale modeling of cardiovascular flows for clinical decision support. Appl Mech Rev 2015;67:030804–1–11. [Google Scholar]
- 21.Moghadam ME, Balilevs Y, Hsia T-Y, et al. A comparison of outlet boundary treatments for prevention of backflow divergence with relevance to blood flow simulations. Comput Mech 2011;48:277–91. [Google Scholar]
- 22.Sahni O, Müller J, Jansen KE, Shephard MS, Taylor CA. Efficient anisotropic adaptive discretization of the cardiovascular system. Comput Methods Appl Mech Eng 2006;195:5634–55. [Google Scholar]
- 23.Hunt D, Edwards WS, Deverall PB, Bargeron LM Jr. Superior vena cava to right pulmonary artery anastomosis. Results in 46 infants and children. Thorax 1970;25:550–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Srivastava D, Preminger T, Lock JE, et al. Hepatic venous blood and the development of pulmonary arteriovenous malformations in congenital heart disease. Circulation 1995;92:1217–22. [DOI] [PubMed] [Google Scholar]
- 25.Sundareswaran KS, de Zélicourt D, Sharma S, et al. Correction of pulmonary arteriovenous malformation using image-based surgical planning. JACC Cardiovasc Imaging 2009;2:1024–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.