Expectation-induced modulation of metastable activity underlies faster coding of sensory stimuli

Abstract

Sensory stimuli can be recognized more rapidly when they are expected. This phenomenon depends on expectation affecting the cortical processing of sensory information. However, the mechanisms responsible for the effects of expectation on sensory circuits remain elusive. Here, we report a novel computational mechanism underlying the expectation-dependent acceleration of coding observed in the gustatory cortex of alert rats. We use a recurrent spiking network model with a clustered architecture capturing essential features of cortical activity, such as its intrinsically generated metastable dynamics. Relying on network theory and computer simulations, we propose that expectation exerts its function by modulating the intrinsically generated dynamics preceding taste delivery. Our model’s predictions were confirmed in the experimental data, demonstrating how the modulation of ongoing activity can shape sensory coding. Altogether, these results provide a biologically plausible theory of expectation and ascribe a new functional role to intrinsically generated, metastable activity.

Introduction

Expectation exerts a strong influence on sensory processing. It improves stimulus detection, enhances discrimination between multiple stimuli and biases perception towards an anticipated stimulus^1–3. These effects, demonstrated experimentally for various sensory modalities and in different species^2,4–6, can be attributed to changes in sensory processing occurring in primary sensory cortices. However, despite decades of investigations, little is known regarding how expectation shapes the cortical processing of sensory information.

While different forms of expectation likely rely on a variety of neural mechanisms, modulation of pre-stimulus activity is believed to be a common underlying feature^7–9. Here, we investigate the link between pre-stimulus activity and the phenomenon of general expectation in a recent set of experiments performed in the gustatory cortex (GC) of alert rats⁶. In those experiments, rats were trained to expect the intraoral delivery of one of four possible tastants following an anticipatory cue. The use of a single cue allowed the animal to predict the availability of gustatory stimuli, without forming expectations on which specific taste was being delivered. Cues predicting the general availability of taste modulated the firing rates of GC neurons. Tastants delivered after the cue were encoded more rapidly than uncued tastants, and this improvement was phenomenologically attributed to the activity evoked by the preparatory cue. However, the precise computational mechanism linking faster coding of taste and cue responses remains unknown.

Here we propose a mechanism whereby an anticipatory cue modulates the timescale of temporal dynamics in a recurrent population model of spiking neurons. In our model, neurons are organized in strongly connected clusters and produce sequences of metastable states similar to those observed during both pre-stimulus and evoked activity periods^10–15. A metastable state is a vector across simultaneously recorded neurons that can last for several hundred milliseconds before giving way to the next state in a sequence. The ubiquitous presence of state sequences in many cortical areas and behavioral contexts^16–22 has raised the issue of their role in sensory and cognitive processing. Here, we elucidate the central role played by pre-stimulus metastable states in processing forthcoming stimuli, and show how cue-induced modulations drive anticipatory coding. Specifically, we show that an anticipatory cue affects sensory coding by decreasing the duration of metastable states and accelerating the pace of state sequences. This phenomenon, which results from a reduction in the effective energy barriers separating the metastable states, accelerates the onset of specific states coding for the presented stimulus, thus mediating the effects of general expectation. The predictions of our model were confirmed in a new analysis of the experimental data, also reported here.

Altogether, our results provide a model for general expectation, based on the modulation of pre-stimulus ongoing cortical dynamics by anticipatory cues, leading to acceleration of sensory coding.

Results

Anticipatory cue accelerates stimulus coding in a clustered population of neurons

To uncover the computational mechanism linking cue-evoked activity with coding speed, we modeled the gustatory cortex (GC) as a population of recurrently connected excitatory and inhibitory spiking neurons. In this model, excitatory neurons are arranged in clusters^10,23 (Fig. 1a), reflecting the existence of assemblies of functionally correlated neurons in GC and other cortical areas^24,25. Recurrent synaptic weights between neurons in the same cluster are potentiated compared to neurons in different clusters, to account for metastability in GC^14,15 and in keeping with evidence from electrophysiological and imaging experiments^24–26. This spiking network also has bidirectional random and homogeneous (i.e., non-clustered) connections among inhibitory neurons and between inhibitory and excitatory neurons. Such connections stabilize network activity by preventing runaway excitation and play a role in inducing the observed metastability^10,13,14.

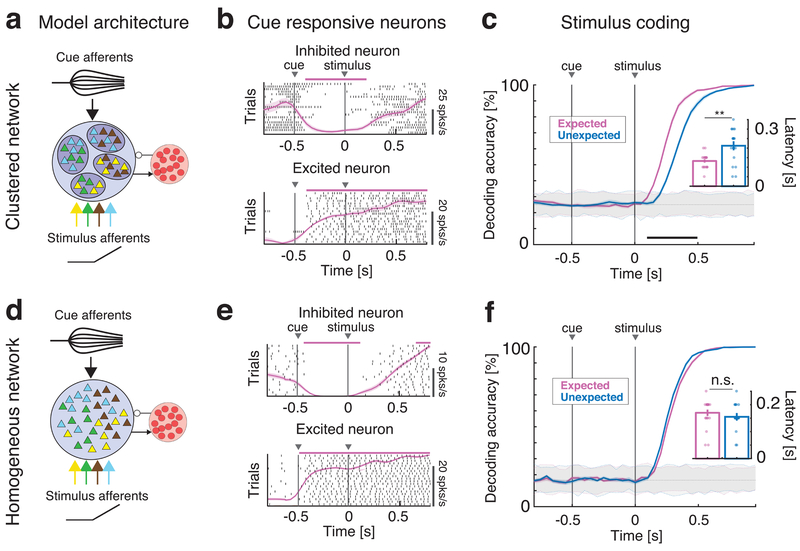
Fig. 1: Anticipatory activity requires a clustered network architecture.

Effects of anticipatory cue on stimulus coding in the clustered (a-c) and homogeneous (d-f) network. a: Schematics of the clustered network architecture and stimulation paradigm. A recurrent network of inhibitory (red circles) and excitatory neurons (triangles) arranged in clusters (ellipsoids) with stronger intra-cluster recurrent connectivity. The network receives bottom-up sensory stimuli targeting random, overlapping subsets of clusters (selectivity to 4 stimuli is color-coded), and one top-down anticipatory cue inducing a spatial variance in the cue afferent currents to excitatory neurons. b: Representative single neuron responses to cue and one stimulus in expected trials in the clustered network of a). Black tick marks represent spike times (rasters), with PSTH (mean±s.e.m.) overlaid in pink. Activity marked by horizontal bars was significantly different from baseline (pre-cue activity) and could either be excited (top panel) or inhibited (bottom) by the cue. c: Time course of cross-validated stimulus-decoding accuracy in the clustered network. Decoding accuracy increases faster during expected (pink) than unexpected (blue) trials in clustered networks (curves and color-shaded areas represent mean±s.e.m. across four tastes in n=20 simulated networks; color-dotted lines around gray shaded areas represent 95% C.I. from shuffled datasets). A separate classifier was used for each time bin, and decoding accuracy was assessed via a cross-validation procedure, yielding a confusion matrix whose diagonal represents the accuracy of classification for each of four tastes in that time bin (see text and Fig. S3 for details). Inset: aggregate analysis across n=20 simulated networks of the onset times of significant decoding (mean±s.e.m.) in expected (pink) vs. unexpected trials (blue) shows significantly faster onsets in the expected condition (two-sided t-test, p=0.0017). d: Schematics of the homogenous network architecture. Sensory stimuli modeled as in a). e: Representative single neuron responses to cue and one stimulus in expected trials in the homogeneous network of d), same conventions as in b). f: Cross-validated decoding accuracy in the homogeneous network (same analysis as in c). The latency of significant decoding in expected vs. unexpected trials is not significantly different. Inset: aggregate analysis of onset times of significant decoding (same as inset of c; two-sided t-test, p=0.31). Panels b, c, e, f: pink and black horizontal bars, p < 0.05, two-sided t-test with multiple-bin Bonferroni correction. Panel c: ** = p < 0.01, two-sided t-test. Panel f: n.s.: non-significant.

The model was probed by sensory inputs modeled as depolarizing currents injected into randomly selected neurons. We used four sets of simulated stimuli, wired to produce gustatory responses reminiscent of those observed in the experiments in the presence of sucrose, sodium chloride, citric acid, and quinine (see Methods). The specific connectivity pattern used was inferred by the presence of both broadly and narrowly tuned responses in GC^27,28, and the temporal dynamics of the inputs were varied to determine the robustness of the model (see below).

In addition to input gustatory stimuli, we included anticipatory inputs designed to produce cue-responses analogous to those seen experimentally in the case of general expectation. To simulate general expectation, we connected anticipatory inputs with random neuronal targets in the network. The peak value of the cue-induced current for each neuron was sampled from a normal distribution with zero mean and fixed variance, thus introducing a spatial variance in the afferent currents. This choice reflected the large heterogeneity of cue responses observed in the empirical data, where excited and inhibited neural responses occurred in similar proportions⁹ and overlapped partially with taste responses^6,9. Fig 1b shows two representative cue-responsive neurons in the model: one inhibited by the cue and one excited by the cue. Cue responses in the model were in quantitative agreement with the observed responses for a large range of cue-induced spatial variance (Fig. S1; see Fig. S2 for representative unresponsive neurons).

Given these conditions, we simulated the experimental paradigm adopted in awake-behaving rats to demonstrate the effects of general expectation^6,9. In the original experiment, rats were trained to self-administer into an intra-oral cannula one of four possible tastants following an anticipatory cue. At random trials and time during the inter-trial interval, tastants were unexpectedly delivered in the absence of a cue. To match this experiment, the simulated paradigm interleaves two conditions: in expected trials, a stimulus (out of 4) is delivered at t=0 after an anticipatory cue (the same for all stimuli) delivered at t=-0.5s (Fig. 1b); in unexpected trials the same stimuli are presented in the absence of the cue. Importantly, in the general expectation paradigm adopted here, the anticipatory cue is identical for all stimuli in the expected condition. Therefore, it does not convey any information regarding the identity of the stimulus being delivered.

We tested whether cue presentation affected stimulus coding. A multi-class classifier (see Methods and Fig. S3) was used to assess the information about the stimuli encoded in the neural activity, where the four class labels correspond to the four tastants. Stimulus identity was encoded well in both conditions, reaching perfect accuracy for all four tastants after a few hundred milliseconds (Fig. 1c). However, comparing the time course of the decoding accuracy between conditions, we found that the increase in decoding accuracy was significantly faster in expected than in unexpected trials (Fig. 1c, pink and blue curves represent expected and unexpected conditions, respectively). Indeed, the onset time of a significant decoding occurred earlier in the expected vs. the unexpected condition (decoding latency was 0.13 ± 0.01 s [mean±s.e.m.] for expected compared to 0.21 ± 0.02 s for unexpected, across 20 independent networks; p=0.002, two-sided t-test, d.o.f.=39; inset in Fig. 1c). These measures refer to the decoding accuracy averaged across all tastants; similar results were obtained for each individual tastant separately (Fig. S3b). Thus, in the model network, the interaction of cue response and activity evoked by the stimuli results in faster encoding of the stimuli themselves, mediating the expectation effect.

To clarify the role of neural clusters in mediating expectation, we simulated the same experiments in a homogeneous network (i.e., without clusters) operating in the balanced asynchronous regime^23,29 (Fig. 1d, intra- and inter-cluster weights were set equal; all other network parameters and inputs were the same as for the clustered network). Even though single neurons’ responses to the anticipatory cue were comparable to the ones observed in the clustered network (Fig. 1e and Fig. S1–S2), stimulus encoding was not affected by cue presentation (Fig. 1f). In particular, the onset of a significant decoding was similar in the two conditions (latency of significant decoding was 0.17 ± 0.01 s for expected and 0.16 ± 0.01 s for unexpected tastes averaged across 20 sessions; p=0.31, two-sided t-test, d.o.f.=39; inset in Fig. 1f).

A defining feature of our model is that it incorporates excited and inhibited cue responses in such a manner to affect only the spatial variance of the activity across neurons, while leaving the mean input to the network unaffected. As a result, the anticipatory cue leaves average firing rates unchanged in the clustered network (Fig. S4), and only modulates the network temporal dynamics. Our model thus provides a mechanism whereby increasing the spatial variance of top-down inputs has, paradoxically, a beneficial effect on sensory coding.

Robustness of anticipatory activity

To test the robustness of anticipatory activity in the clustered network, we systematically varied key parameters related to the sensory and anticipatory inputs, as well as network connectivity and architecture (Fig. 2 and S5). We first discuss variation in stimulus features. Increasing stimulus intensity led to a faster encoding of the stimulus in both conditions and maintained anticipatory activity (Fig. 2a; two-way ANOVA with factors “stimulus slope”, p < 10⁻¹⁸, F(4)=30.4, and “condition” – i.e., expected vs. unexpected –, p < 10⁻¹⁵, F(1)=79.8). Anticipatory activity induced by the cue depended on stimulus intensity only weakly (p(interaction)=0.05, F(4)=2.4), and was present even in the case of a step-like stimulus (Fig. S5a). Moreover, anticipatory activity was obtained in the presence of larger numbers of stimuli and did not depend appreciably on the total number of stimuli (Fig. S5b; two-way ANOVA with factors “number of stimuli” (p=0.57, F(3)=0.67) and “condition” (p < 10⁻⁷, F(1)=35.3; p(interaction)=0.66, F(3)=0.54). Finally, anticipatory activity was present also when the stimulus selectivity targeted both excitatory and inhibitory neurons, rather than excitatory neurons only (Fig. 2b).

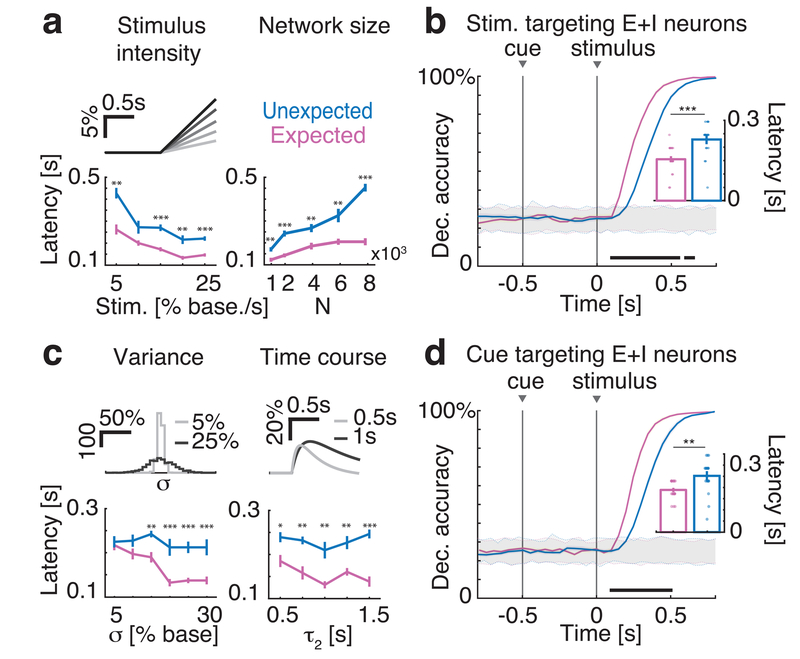
Fig. 2: Robustness of anticipatory activity to variations in stimulus (top row) and cue (bottom row) models.

a: Latency of significant decoding increased with stimulus intensity (left panel: top, stimulus peak expressed as percent of baseline, darker shades represent stronger stimuli; bottom, decoding latency, mean±s.e.m. across n=20 simulated networks for each value on the x-axis, see main text for panels a-c statistical tests) in both conditions, and it is faster in expected (pink) than unexpected trials (blue). Anticipatory activity was present for a large range of network sizes (right panel: J₊ =5, 10, 20, 30, 40 for N=1, 2, 4, 6, 8 x10³ neurons, respectively). Network synaptic weights scaled as reported in Table 1 and 2 of Methods. b: Anticipatory activity was present when stimuli targeted both excitatory (E) and inhibitory (I) neurons (notations as in Fig. 1c; 50% of both E and I neurons were targeted by the cue; inset: mean±s.e.m. across n=20 simulated networks, two-sided t-test, p=0.0011). c: Increasing the cue-induced spatial variance in the afferent currents σ² (top left: histogram of afferents’ peak values across neurons; x-axis, expressed as percent of baseline; y-axis, calibration bar: 100 neurons) leads to more pronounced anticipatory activity (bottom left, latency in unexpected (blue) and expected (pink) trials). Anticipatory activity was present for a large range of cue time courses (top right, double exponential cue profile with rise and decay times [τ₁, τ₂] = g × [0.1, 0.5]s, for g in the range from 1 to 3; bottom right, decoding latency during unexpected, blue, and unexpected, pink, trials). d: Anticipatory activity was also present when the cue targeted 50% of both E and I neurons (σ = 20% in baseline units; inset: mean±s.e.m. across n=20 simulated networks, two-sided t-test, p=0.0034). Panels a-d: *=p<0.05, **=p<0.01, ***=p<0.001, post-hoc multiple-comparison two-sided t-test with Bonferroni correction. Horizontal black bar, p<0.05, two-sided t-test with multiple-bin Bonferroni correction; Insets: **=p<0.01, ***=p<0.001, two-sided t-test. Panel c-d: notations as in Fig. 1c of the main text.

We then performed variations in network size and architecture. We estimated the decoding accuracy in ensembles of constant size (20 neurons) sampled from networks of increasing size (Fig. 2a), fixing both cluster size and the probability that each cluster was selective to a given stimulus (50%). Cue-induced anticipation was even more pronounced in larger networks (Fig. 2a, two-way ANOVA with factors “network size” (p < 10⁻²⁰, F(3)=49.5), “condition” (p < 10⁻¹⁶, F(1)=90; p(interaction)=p < 10⁻¹⁰, F(3)=20). In our main model the neural clusters were segregated in disjoint groups. We investigated an alternative scenario where neurons may belong to multiple clusters, resulting in an architecture with overlapping clusters³⁰. We found that anticipatory activity was present also in networks with overlapping clusters (Fig. S5d).

Next, we assessed robustness to variations in cue parameters – specifically: variations in the spatial variance σ² of the cue-induced afferent currents; variations in the kinetics of cue stimulation; and variations in the type of neurons targeted by the cue. We found that coding anticipation was present for all values of σ above 10% (Fig. 2c, two-way ANOVA with factors “cue variance” (p=0.09, F(7)=1.8) and “condition” (p < 10⁻⁷, F(1)=31); p(interaction)=0.07, F(7)=1.9). Anticipatory activity was also robust to variations in the time course of the cue-evoked currents (Fig. 2c, two-way ANOVA with factors “time course” (p=0.03, F(4)=2.8) and “condition” (p < 10⁻¹⁵, F(1)=72.7; p(interaction)=0.12, F(4)=1.8). We also considered a model with constant cue-evoked currents (step-like model), to further investigate a potential role (if any) of the cue’s variable time course on anticipatory activity, and found anticipatory coding also in this case (Fig. S5c).

Finally, we tested whether or not anticipation was present if inhibitory neurons, in addition to excitatory neurons, were targeted by the cue (while maintaining stimulus selectivity for excitatory neurons only), and found robust anticipatory activity also in that case (Fig. 2d). Given the solid robustness of the anticipatory activity in the clustered network, one may be tempted to conclude that any cue model might induce coding acceleration in this type of network. However, in a model where the cue recruited the recurrent inhibition (by increasing the input currents to the inhibitory population), stimulus coding was decelerated (Fig. S6), suggesting a potential mechanism mediating the effect of distractors.

Overall, these results demonstrate that a clustered network of spiking neurons can successfully reproduce the acceleration of sensory coding induced by expectation and that removing clustering impairs this function.

Anticipatory cue speeds up the network’s dynamics

Having established that a clustered architecture enables the effects of expectation on coding, we investigated the underlying mechanism.

Clustered networks spontaneously generate highly structured activity characterized by coordinated patterns of ensemble firing. This activity results from the network hopping between metastable states in which different combinations of clusters are simultaneously activated^11,13,14. To understand how anticipatory inputs affected network dynamics, we analyzed the effects of cue presentation for a prolonged period of 5 seconds in the absence of stimuli. Activating anticipatory inputs led to changes in network dynamics, with clusters turning on and off more frequently in the presence of the cue (Fig. 3a). We quantified this effect by showing that a cue-induced increase in input spatial variance (σ²) led to a shortened cluster activation lifetime (top panel in Fig. 3b; Kruskal-Wallis one-way ANOVA: p<10⁻¹⁷, χ²(5) =91.2), and a shorter cluster inter-activation interval (i.e., quiescent intervals between consecutive activations of the same cluster, bottom panel in Fig. 3b, Kruskal-Wallis one-way ANOVA: p<10⁻¹⁸, χ²(5) =98.6).

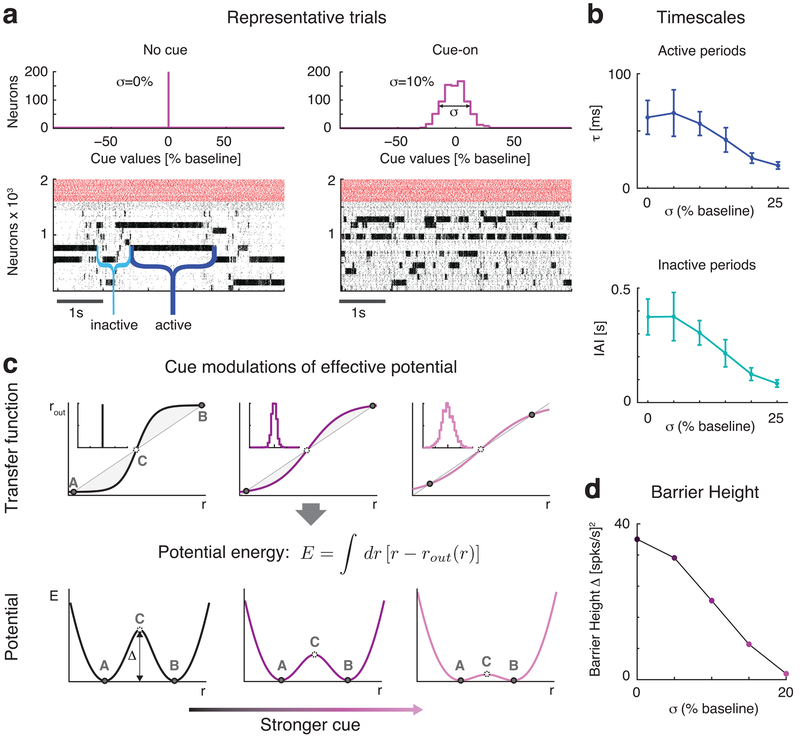
Fig. 3: Anticipatory cue speeds up network dynamics.

a: Raster plots of the clustered network activity in the absence (left) and in the presence of the anticipatory cue (right), with no stimulus presentation in either case. The dynamics of cluster activation and deactivation accelerated proportionally to the increase in afferent currents’ variance σ² induced by the cue. Top panels: distribution of cue peak values across excitatory neurons: left, no cue; right, distribution with S.D. σ = 10% in units of baseline current. Bottom panels: raster plots of representative trials in each condition (black: excitatory neurons, arranged according to cluster membership; red: inhibitory neurons). b: The average cluster activation lifetime (top) and inter-activation interval (bottom) significantly decrease when increasing σ (mean±s.e.m. across n=20 simulated networks). c: Schematics of the effect of the anticipatory cue on network dynamics. Top row: the increase in the spatial variance of cue afferent currents (insets: left: no cue; stronger cues towards the right) flattens the “effective f-I curve” (sigmoidal curve) around the diagonal representing the identity line (straight line). The case for a simplified two-cluster network is depicted (see text). States A and B correspond to stable configurations with only one cluster active; state C corresponds to an unstable configuration with 2 clusters active. Bottom row: shape of the effective potential energy corresponding to the f-I curves shown in the top row. The effective potential energy is defined as the area between the identity line and the effective f-I curve (shaded areas in top row; see formula). The f-I curve flattening due to the anticipatory cue shrinks the height Δ of the effective energy barrier, making cluster transitions more likely and hence more frequent. d: Effect of the anticipatory cue (in units of the baseline current) on the height of the effective energy barrier Δ, calculated via mean field theory in a reduced two-cluster network of LIF neurons (see Methods).

Previous work has demonstrated that metastable states of co-activated clusters result from attractor dynamics^11,13,14. Hence, the shortening of cluster activations and inter-activation intervals observed in the model could be due to modifications in the network’s attractor dynamics. To test this hypothesis, we performed a mean field theory analysis^30–33 of a simplified network with only two clusters, therefore producing a reduced repertoire of configurations. Those include two configurations in which either cluster is active and the other inactive (‘A’ and ‘B’ in Fig. 3c), and a configuration where both clusters are moderately active (‘C’). The dynamics of this network can be analyzed using a reduced, self-consistent theory of a single excitatory cluster, said to be in focus³¹ (see Methods for details), based on the effective transfer function relating the input and output firing rates of the cluster (r and r_out, Fig. 3c). The latter are equal in the A, B and C network configurations described above – also called ‘fixed points’ since these are the points where the transfer function intersects the identity line, r_out = Φ(r_in).

Configurations A and B would be stable in an infinitely large network, but they are only metastable in networks of finite size, due to intrinsically generated variability¹³. Transitions between metastable states can be modeled as a diffusion process and analyzed with Kramers’ theory³⁴, according to which the transition rates depend on the height Δ of an effective energy barrier separating them^13,34. In our theory, the effective energy barriers (Fig. 2c, bottom row) are obtained as the area of the region between the identity line and the transfer function (shaded areas in top row of Fig. 3c; see Methods for details). The effective energy is constructed so that its local minima correspond to stable fixed points (here, A and B) while local maxima correspond to unstable fixed points (C). Larger barriers correspond to less frequent transitions between stable configurations, whereas lower barriers increase the transition rates and therefore accelerate the network’s metastable dynamics.

This picture provides the substrate for understanding the role of the anticipatory cue in the expectation effect. Basically, the presentation of the cue modulates the shape of the effective transfer function, which results in the reduction of the effective energy barriers. More specifically, the cue-induced increase in the spatial variance, σ², of the afferent current flattens the transfer function along the identity line, reducing the area between the two curves (shaded regions in Fig. 3c). In turn, this reduces the effective energy barrier separating the two configurations (Fig. 3c, bottom row), resulting in faster dynamics. The larger the cue-induced spatial variance σ² in the afferent currents, the faster the dynamics (Fig. 3d; lighter shades represent larger σs).

In summary, this analysis shows that the anticipatory cue increases the spontaneous transition rates between the network’s metastable configurations by reducing the effective energy barrier necessary to hop among configurations. In the following we uncover an important consequence of this phenomenon for sensory processing.

Anticipatory cue induces faster onset of taste-coding states

The cue-induced modulation of attractor dynamics led us to formulate a hypothesis for the mechanism underlying the acceleration of coding: The activation of anticipatory inputs prior to sensory stimulation may allow the network to enter more easily stimulus-coding configurations while exiting more easily non-coding configurations. Fig. 4a shows simulated population rasters in response to the same stimulus presented in the absence of, or following, a cue. Spikes in red hue represent activity in taste-selective clusters and show a faster activation latency in response to the stimulus preceded by the cue compared to the uncued condition. A systematic analysis revealed that in the cued condition, the clusters activated by the subsequent stimulus had a significantly faster activation latency than in the uncued condition (Fig. 4b,0.22 ± 0.01 s (mean±s.e.m.) during cued compared to 0.32 ± 0.01 s for uncued stimuli; p<10⁻⁵, two-sided t-test, d.o.f.=39).

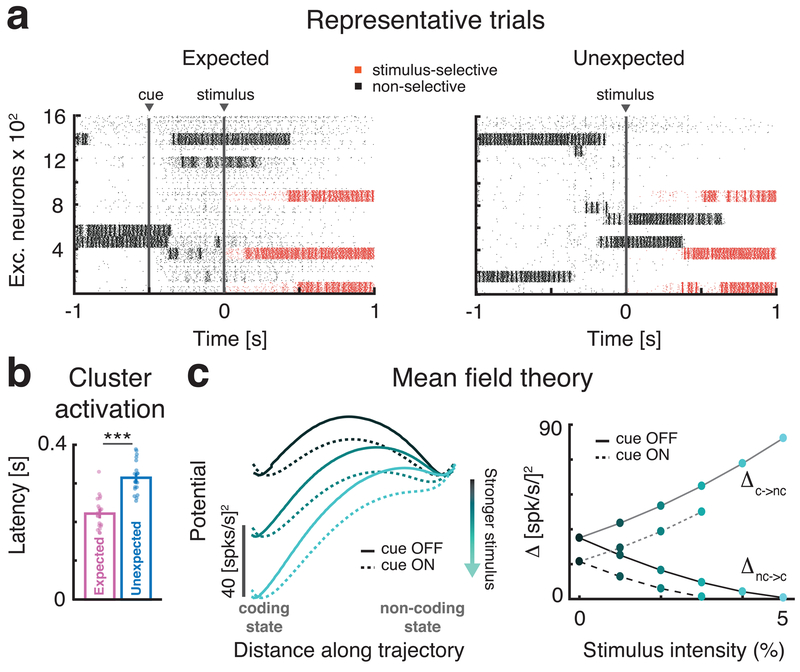
Fig. 4: Anticipatory cue induces faster onset of stimulus-coding states.

a: Raster plots of representative trials in the expected (left) and unexpected (right) conditions in response to the same stimulus at t=0. Stimulus-selective clusters (red tick marks, spikes) activate earlier than non-selective clusters (black tick marks, spikes) in response to the stimulus when the cue precedes the stimulus. b: Comparison of activation latency of selective clusters after stimulus presentation during expected (pink) and unexpected (blue) trials (mean±s.e.m. across 20 simulated networks, two-sided t-test, p=5.1x10^-7). Latency in expected trials is significantly reduced. c: The effective energy landscape and the modulation induced by stimulus and anticipatory cue on two-clustered networks, computed via mean field theory (see Methods). Left panel: after stimulus presentation the stimulus-coding state (left well in left panel) is more likely to occur than the non-coding state (right well). Right panel: barrier heights as a function of stimulus strength in expected (`cue ON’) and unexpected trials (`cue OFF’). Stronger stimuli (lighter shades of cyan) decrease the barrier height Δ separating the non-coding and the coding state. In expected trials (dashed lines), the barrier Δ is smaller than in unexpected ones (full lines), leading to a faster transition probability from non-coding to coding states compared to unexpected trials (for stimulus ≥ 4% the barrier vanishes leaving just the coding state). Panel b: *** = p < 0.001, two-sided t-test.

We elucidated this effect using mean field theory. In the simplified two-cluster network of Fig. 4c (the same network as in Fig. 3d), the configuration where the taste-selective cluster is active (“coding state”) or the nonselective cluster is active (“non-coding state”) have initially the same effective potential energy (local minima of the black line in Fig. 4c). The onset of the cue reduces the effective energy barrier separating these configurations (dashed vs. full line). After stimulus onset, the coding state sits in a deeper well (lighter lines) compared to non-coding state, due to the stimulation biasing the selective cluster. Stronger stimuli (lighter shades in Fig. 4c) progressively increase the difference between the wells’ depths breaking their initial symmetry, making a transition from the non-coding to the coding state more likely than a transition from the coding to the non-coding state³⁴. The anticipatory cue reduces further the existing barrier and thereby increases the transition rate towards coding configurations. This results into faster coding, on average, of the encoded stimuli.

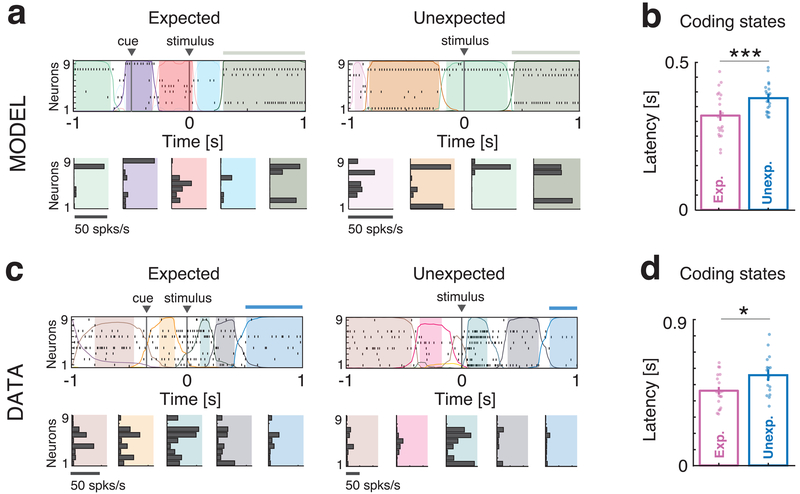
We tested this model prediction on the data from Samuelsen et al. (Fig. 5)⁶. To compare the data to the model simulations, we randomly sampled ensembles of model neurons so as to match the sizes of the empirical datasets. Since we only have access to a subset of neurons in the experiments, rather than the full network configuration, we segmented the ensemble activity in sequences of metastable states via a Hidden Markov Model (HMM) analysis (see Methods). Previous work has demonstrated that HMM states can be treated as proxies of metastable network configurations¹⁴. In particular, activation of taste-coding configurations for a particular stimulus results in HMM states containing information about that stimulus (i.e., taste-coding HMM states). If the hypothesis originating from the model is correct, transitions from non-coding to taste-coding HMM states should be faster in the presence of the cue. We indeed found faster transitions to HMM coding states in cued compared to uncued trials for both model and data (Fig. 5a and 5c, respectively; coding states indicated by horizontal bars), with shorter latency of coding states in both cases (Fig. 5b–d, mean latency of first coding state in the model was 0.32 ± 0.02 s for expected vs 0.38 ± 0.01 s for unexpected trials; two-sided t-test, d.o.f.=39, p=0.014; in the data, mean latency was 0.46 ± 0.02 s for expected vs 0.56 ± 0.03 s for unexpected trials; two-sided t-test, d.o.f.=37, p=0.026).

Fig. 5: Anticipation of coding states: model vs. data.

a: Representative trials from one ensemble of 9 simultaneously recorded neurons from clustered network simulations during expected (left) and unexpected (right) conditions. Top panels: spike rasters with latent states extracted via a HMM analysis (colored curves represent time course of state probabilities; colored areas indicate intervals where the probability of a state exceeds 80%; thick horizontal bars atop the rasters mark the presence of a stimulus-coding state). Bottom panels: Firing rate vectors for each latent state shown in the corresponding top panel. b: Latency of stimulus-coding states in expected (pink) vs. unexpected (blue) trials (mean±s.e.m. across n=20 simulated networks, two-sided t-test, p=0.014). Faster coding latency during expected trials is observed compared to unexpected trials. c-d: Same as a)-b) for the empirical datasets (mean±s.e.m. across n=17 recorded sessions, two-sided t-test, p=0.026). * = p < 0.05, ***= p < 0.001, two-sided t-test.

Altogether, these results demonstrate that anticipatory inputs speed up sensory coding by reducing the effective energy barriers from non-coding to coding metastable states.

Discussion

Expectations modulate perception and sensory processing. Typically, expected stimuli are recognized more accurately and rapidly than unexpected ones^1–3. In the gustatory cortex, expectation of tastants has been related to changes in firing activity evoked by anticipatory cues⁶. What causes these firing rate changes? Here, we propose that the effects of expectation follow from the modulation of the intrinsically generated cortical dynamics, ubiquitously observed in cortical circuits^{14,16–18,22,35–37}.

The proposed mechanism entails a recurrent spiking network where excitatory neurons are arranged in clusters^14,15. In such a model, network activity unfolds through state sequences, whose dynamics speed up in the presence of anticipatory cue. This anticipates the onset of ‘coding states’ (containing the most information about the delivered stimulus), and explains the faster decoding latency observed by Samuelsen et al⁶ (see Fig. 1c).

Notably, this anticipatory mechanism is unrelated to changes in network excitability, which would lead to unidirectional changes in firing rates. It relies instead on an increase in the spatial (i.e., across neurons) variance of the network’s activity caused by the anticipatory cue. This increase in the input’s variance is observed experimentally after training⁹, and is therefore the consequence of having learned the anticipatory meaning of the cue. The consequent acceleration of state sequences predicted by the model was also confirmed in the data from ensembles of simultaneously recorded neurons in awake-behaving rats.

These results provide a new functional interpretation of ongoing cortical activity and a precise explanatory link between the intrinsic dynamics of neural activity in a sensory circuit, and a specific cognitive process, that of general expectation.^6,38

Clustered connectivity and metastable states

A key feature of our model is the clustered architecture of the excitatory population. Theoretical work had previously shown that a clustered architecture can produce stable activity patterns¹⁰. Noise (either externally^11,39 or internally generated^13,14) may destabilize those patterns and ignite a progression through metastable states. These states are reminiscent of those observed in cortex during both task engagement^12,16,40,41 and inter-trial periods^14,36, including those found in rodent gustatory cortex during taste processing and decision making^14,39,42. Clustered spiking networks also account for various physiological observations such as stimulus-induced reduction of trial-to-trial variability^11,13,14,43, neural dimensionality¹⁵, and firing rate multistability¹⁴.

In this work, we showed that clustered spiking networks also have the ability to modulate coding latency and therefore explain the phenomenon of general expectation. The uncovered link between generic anticipatory cues, network metastability, and coding speed, is dependent on a clustered architecture, since removing the excitatory clusters (i.e., homogeneous connectivity) eliminates the anticipatory mechanism (Fig. 1d–f).

Functional role of heterogeneity in cue responses

As stated in the previous section, the presence of clusters is a necessary ingredient to obtain a faster latency of coding. Here we discuss the second necessary ingredient, i.e., the presence of heterogeneous neural responses to the anticipatory cue (Fig. 1b).

Responses to anticipatory cues have been extensively studied in cortical and subcortical areas in alert rodents^6,9,44,45. Cues evoke heterogeneous patterns of activity, either exciting or inhibiting single neurons. The proportion of cue responses and their heterogeneity develops with training,^9,45 suggesting a fundamental function of these patterns. In the generic expectation paradigm considered here, the anticipatory cue does not convey any information about the identity of the forthcoming tastant, rather it just signals the availability of a stimulus. Experimental evidence suggests that the cue may induce a state of arousal, which was previously described as “priming” the sensory cortex.^6,46 Here, we propose an underlying mechanism in which the cue is responsible for acceleration of coding by increasing the spatial variance of pre-stimulus activity. In turn, this modulates the shape of the neuronal current-to-rate transfer function and thus lowers the effective energy barriers between metastable configurations.

We note that the presence of both excited and inhibited cue responses poses a challenge to simple models of neuromodulation. The presence of cue-evoked suppression of firing⁹ suggests that cues do not improve coding by simply increasing the excitability of cortical areas. Additional mechanisms and complex patterns of connectivity may be required to explain the suppression effects induced by the cue. However, here we provide a parsimonious explanation of how heterogeneous responses can improve coding without postulating any specific pattern of connectivity other than i) random projections from thalamic and anticipatory cue afferents and ii) the clustered organization of the intra-cortical circuitry. Notice that the latter contains wide distributions of synaptic weights and can be understood as the consequence of Hebb-like re-organization of the circuitry during training^47,48.

Specificity of the anticipatory mechanism

Our model of anticipation relies on gain reduction in clustered excitatory neurons due to a larger spatial variance of the afferent currents. We have shown that this model is robust to variations in parameters and architecture (Fig. 2 and Fig. S5); what about the specificity of its mechanism? A priori, the expectation effect might be achieved through different means, such as: increasing the strength of feedforward couplings; decreasing the strength of recurrent couplings; or modulating background synaptic inputs⁴⁹. However, when scoring those models on the criteria of coding anticipation and heterogeneous cue responses, we found that they failed to simultaneously match both criteria, although for some range of parameters they could reproduce either one (see Fig. S7–S9 and Table S1 for a detailed analysis).

While our exploration of the alternative models’ parameter space did not produce an example that could match the data, we cannot in principle exclude that one of the alternative models could match the data in a yet unexplored parameter region. This may be particularly the case for the model of Fig. S7c, which can produce anticipation of coding but does not match the patterns of cue responses observed in the experiments. We are aware that, due to the typically large number of cellular and network parameters, it is hard to rule out these or other alternative models entirely. We could, however, demonstrate that the main mechanism proposed here (Fig. 1a) captures the plurality of experimental observations pertaining to anticipatory activity in a robust and biologically plausible way.

Cortical timescales, state transitions, and cognitive function

In populations of spiking neurons, a clustered architecture can generate reverberating activity and sequences of metastable states. Transitions from state to state can be typically caused by external inputs^13,14. For instance, in frontal cortices, sequences of states are related to specific epochs within a task, with transitions evoked by behavioral events^16,17,20. In sensory cortex, progressions through state sequences can be triggered by sensory stimuli and reflect the dynamics of sensory processing^21,40. Importantly, state sequences have been observed also in the absence of any external stimulation, promoted by intrinsic fluctuations in neural activity^14,37. However, the potential functional role, if any, of this type of ongoing activity has remained unexplored.

Recent work has started to uncover the link between ensemble dynamics and sensory and cognitive processes. State transitions in various cortical areas have been linked to decision making^39,50, choice representation²⁰, rule-switching behavior²², and the level of task difficulty²¹. However, no theoretical or mechanistic explanations have been given for these phenomena.

Here we provide a mechanistic link between state sequences and expectation in terms of specific modulations of intrinsic dynamics, i.e., the anticipatory cue triggers a change of the transition probabilities. The modulation of intrinsic activity can dial the duration of states, producing either shorter or longer timescales. A shorter timescale leads to faster state sequences and coding anticipation after stimulus presentation (Figs. 1 and 5). Other external perturbations may induce different effects: for example, recruiting the network’s inhibitory population slows down the timescale, leading to a slower coding (Fig. S6).

The interplay between intrinsic dynamics and anticipatory influences presented here is a novel mechanism for generating diverse timescales, and may have rich computational consequences. We demonstrated its function in increasing coding speed, but its role in mediating cognition is likely to be broader and calls for further explorations.

Methods

Behavioral training and electrophysiology.

The experimental data come from a previously published dataset Ref.⁶. Experimental procedures were approved by the Institutional Animal Care and Use Committee of Stony Brook University and complied with university, state, and federal regulations on the care and use of laboratory animals. Movable bundles of 16 microwires were implanted bilaterally in the gustatory cortex and intraoral cannulae (IOC) were inserted bilaterally. After postsurgical recovery, rats were trained to self-administer fluids through IOCs by pressing a lever under head-restraint within 3s presentation of an auditory cue (“expected trials”; a 75 dB pure tone at a frequency of 5 kHz). The inter-trial interval was progressively increased to 40 ± 3s. Early presses were discouraged by the addition of a 2s delay to the inter-trial interval. During training and electrophysiology sessions, additional tastants were automatically delivered through the IOC at random times near the middle of the inter-trial interval and in the absence of the anticipatory cue (“unexpected trials”). The following tastants were delivered: 100 mM NaCl, 100 mM sucrose, 100 mM citric acid, and 1 mM quinine HCl. Water (50 μl) was delivered to rinse the mouth clean through a second IOC, 5s after the delivery of each tastant. Multiple single-unit action potentials were amplified, bandpass filtered, and digitally recorded. Single units were isolated using a template algorithm, clustering techniques, and examination of inter-spike interval plots (Offline Sorter, Plexon). Starting from a pool of 299 single neurons in 37 sessions, neurons with peak firing rate lower than 1 spks/s (defined as silent) were excluded from further analysis, as well as neurons with a large peak around the 6–10 Hz in the spike power spectrum, which were classified as somatosensory^27,28. Only ensembles with 5 or more simultaneously recorded neurons were included in the rest of the analyses. Ongoing and evoked activity were defined as occurring in the 5s-long interval before or after taste delivery, respectively.

Cue responsiveness.

A neuron was deemed responsive to the cue if a sudden change in its firing rate was observed during the post-cue interval, detected via a “change-point” (CP) procedure described in Ref.²⁸. Briefly, we built the cumulative distribution function of the spike count (CumSC) across all trials in each session, in the interval starting 0.5s before, and ending 1 s after, cue delivery. We then ran the CP detection algorithm on the CumSC record with a given tolerance level p=0.05. If any CP was detected before cue presentation, the algorithm was repeated with lower tolerance (lower p-value) until no CP was present before the cue. If a legitimate CP was found anywhere within 1s after cue presentation, the neuron was deemed responsive. If no CP was found, the neuron was deemed not responsive. For neurons with excited (inhibited) cue responses, ΔPSTH was defined as the difference between positive (negative) peak responses post-cue and the mean baseline activity in the 0.5s preceding cue presentation.

Ensemble states detection.

A Hidden Markov Model (HMM) analysis was used to detect ensemble states in both the empirical data and model simulations. Here, we give a brief description of the method used and we refer the reader to Refs.^14,16,21,40 for more detailed information.

The HMM assumes that an ensemble of N simultaneously recorded neurons is in one of M hidden states at each given time bin. States are firing rate vectors r_i(m), where i = 1 is the neuron index and m = 1,…,M identifies the state. In each state, neurons were assumed to discharge as stationary Poisson processes (Poisson-HMM) conditional on the state’s firing rates. Trials were segmented in 2 ms bins, and the value of either 1 (spike) or 0 (no spike) was assigned to each bin for each given neuron (Bernoulli approximation for short time bins); if more than one neuron fired in a given bin (a rare event), a single spike was randomly assigned to one of the firing neurons. A single HMM was used to fit all trials in each recording session, resulting in the emission probabilities r_i(m) and in a set of transition probabilities between the states. Emission and transition probabilities were calculated with the Baum-Welch algorithm⁵¹ with a fixed number of hidden states M, yielding a maximum likelihood estimate of the parameters given the observed spike trains. Since the model log-likelihood LL increases with M, we repeated the HMM fits for increasing values of M until we hit a minimum of the Bayesian Information Criterion (BIC, see below and Ref.⁵¹). For each M, the LL used in the BIC was the sum over 10 independent HMM fits with random initial guesses for emission and transition probabilities. This step was needed since the Baum-Welch algorithm only guarantees reaching a local rather than global maximum of the likelihood. The model with the lowest BIC (having M* states) was selected as the winning model, where BIC = −2LL + [M(M – 1) + MN] ln T, T being the number of observations in each session (= number of trials × number of bins per trials). Finally, the winning HMM model was used to “decode” the states from the data according to their posterior probability given the data. During decoding, only those states with probability exceeding 80% in at least 25 consecutive 2ms-bins were retained (henceforth denoted simply as “states”)^15,40. This procedure eliminates states that appear only very transiently and with low probability, also reducing the chance of overfitting. A median of 6 states per ensemble was found, varying from 3 to 9 across ensembles.

Coding states.

In each condition (i.e., expected vs. unexpected), the frequencies of occurrence of a given state across taste stimuli were compared with a test of proportions (chi-square, p<0.001 with Bonferroni correction to account for multiple states). When a significant difference was found across stimuli, a post-hoc Marascuilo test was performed⁵². A state whose frequency of occurrence was significantly higher in the presence of one taste stimulus compared to all other tastes was deemed a ‘coding state’ for that stimulus (Fig. 5).

Spiking network model.

We modeled the local neural circuit as a recurrent network of N leaky-integrate-and-fire (LIF) neurons, with a fraction n_E = 80% of excitatory (E) and n_I = 20% of inhibitory (I) neurons.¹⁰ Connectivity was random with probability p_EE = 0.2 for E to E connections and p_EI = p_IE = p_II = 0.5 otherwise. Synaptic weights J_ij from pre-synaptic neuron j ∈ E, I to post-synaptic neuron i ∈ E, I scaled as $J_{ij}=j_{ij}/\sqrt{N}$, with J_ij drawn from normal distributions with mean J_αβ (for α, β = E, I) and 1% SD. Networks of different architectures were considered: i) networks with segregated clusters (referred to as “clustered network,” parameters as in Tables 1 and 2); ii) networks with overlapping clusters (see Suppl. Figure S5d and Table S2 for details), iii) homogeneous networks (parameters as in Table 1). In the clustered network, E neurons were arranged in Q clusters with N_c = 100 neurons per clusters on average (1% SD), the remaining fraction n_bg of E neurons belonging to an unstructured “background” population. In the clustered network, neurons belonging to the same cluster had intra-cluster synaptic weights potentiated by a factor J₊; synaptic weights between neurons belonging to different clusters were depressed by a factor J₋ = γf(J₊ − 1) < 1 with γ = 0.5; f = (1 − n_bg)/Q is the average number of neurons in each cluster.¹⁰ When changing the network size N, all synaptic weights J_ij were scaled by $\sqrt{N}$, the intra-cluster potentiation values were J₊=5, 10, 20, 30, 40 for N = 1, 2, 4, 6, 8 × 10³ neurons, respectively, and cluster size remained unchanged (see also Table 1); all other parameters were kept fixed. In the homogeneous network, there were no clusters (J₊ = J₋ = 1).

Table 1:

Parameters for the clustered and homogeneous networks with N LIF neurons. In the clustered network, the intra-cluster potentiation parameter values were J₊ = 5, 10, 20, 30, 40 for networks with N = 1, 2, 4, 6, 8 × 10³ neurons, respectively. In the homogeneous network, J₊=1.

Symbol	Description	Value
jEE	Mean E→E synaptic weight × $\sqrt{N}$	1.1 mV
jEI	Mean I→E synaptic weight × $\sqrt{N}$	5.0 mV
jIE	Mean E→I synaptic weight × $\sqrt{N}$	1.4 mV
jII	Mean I→I synaptic weight × $\sqrt{N}$	6.7 mV
jE0	Mean afferent synaptic weights to E neurons × $\sqrt{N}$	5.8 mV
jI0	Mean afferent synaptic weights to I neurons × $\sqrt{N}$	5.2 mV
J+	Potentiated intra-cluster E→E weights factor	see caption
$r_{ext}^E$	Average afferent rate to E neurons (baseline)	7 spks/s
$r_{ext}^I$	Average afferent rate to I neurons (baseline)	7 spks/s
$V_{thr}^E$	E neuron threshold potential	3.9 mV
$V_{thr}^I$	I neuron threshold potential	4.0 mV
Vreset	E and I neurons reset potential	0 mV
τm	E and I membrane time constant	20 ms
τref	Absolute refractory period	5 ms
τsyn	E and I synaptic time constant	4 ms
nbg	Background neurons fraction	10%
Nc	Average cluster size	100 neurons

Table 2:

Parameters for the simplified 2-cluster network with N=800 LIF neurons (the remaining parameters were as in Table 1).

Symbol	Description	Value
jEE	Mean E→E synaptic weight × $\sqrt{N}$	0.8 mV
jEI	Mean I→E synaptic weight × $\sqrt{N}$	10.6 mV
jIE	Mean E→I synaptic weight × $\sqrt{N}$	2.5 mV
jII	Mean I→I synaptic weight × $\sqrt{N}$	9.7 mV
jE0	Mean afferent synaptic weights to E neurons × $\sqrt{N}$	14.5 mV
jI0	Mean afferent synaptic weights to I neurons × $\sqrt{N}$	12.9 mV
J+	Potentiated intra-cluster E→E weights factor	9
$V_{thr}^E$	E neuron threshold potential	4.6 mV
$V_{thr}^I$	I neuron threshold potential	8.7 mV
nbg	Background neurons fraction	65%

Model neuron dynamics.

Below threshold the LIF neuron membrane potential evolved in time as

$$\frac{d}{dt}V=-\frac{V}{{\tau }_m}+I_{rec}+I_{ext},$$

where τ_m is the membrane time constant and the input currents I are a sum of a recurrent contribution I_rec coming from the other network neurons and an external current I_ext = I₀ + I_stim + I_cue (units of Volt/s). Here, I₀ is a constant term representing input from other brain areas; I_stim and I_cue represent the incoming stimuli and cue, respectively (see Stimulation protocols below). When V hits threshold V_thr, a spike is emitted and V is then clamped to the rest value V_reset for a refractory period τ_ref. Thresholds were chosen so that the homogeneous network neurons fired at rates r_E = 5 spks/s and r_I = 7 spks/s. The recurrent contribution to the postsynaptic current to the i-th neuron was a low-pass filter of the incoming spike trains

$${\tau }_{syn}\frac{d}{dt}{I}_{rec}=-I_{rec}+{\sum }_{j=1}^N{J}_{ij}{\sum }_k\delta \left(t-t_k^j\right),$$

where τ_syn is the synaptic time constant; J_ij is the recurrent synaptic weights from presynaptic neuron j to postsynaptic neuron i, and $t_k^j$ is the k-th spike time from the j-th presynaptic neuron. The constant external current was I₀ = N_extp_i0J_i0v_ext, with N_ext = n_EN, p_i0 = 0.2, $J_{i0}=j_{i0}/\sqrt{N}$ with j_E0 for excitatory and j_I0 for inhibitory neurons (see Table 1), and r_ext = 7 spks/s. For a detailed mean field theory analysis of the clustered network and a comparison between simulations and mean field theory during ongoing and stimulus-evoked periods we refer the reader to Refs^14,15.

Stimulation protocols.

Stimuli were modeled as time-varying stimulus afferent currents targeting 50% of neurons in stimulus-selective clusters I_stim(t) = I₀ r_stim(t), where r_stim(t) was expressed as a fraction of the baseline external current I₀. Each cluster had a 50% probability of being selective to a given stimulus, thus different stimuli targeted overlapping sets of clusters. The anticipatory cue, targeting a random 50% subset of E neurons, was modeled as a double exponential with rise and decay times of 0.2 s and 1 s, respectively, unless otherwise specified; its peak value for each selective neuron was sampled from a normal distribution with zero mean and standard deviation σ (expressed as fraction of the baseline current I₀; σ=20% unless otherwise specified). The cue did not change the mean afferent current but only its spatial (quenched) variance across neurons.

In both the unexpected and the expected conditions, stimulus onset at t = 0 was followed by a linear increase r_stim(t) in the stimulus afferent current to stimulus-selective neurons reaching a value r_max at t = 1 s (r_max = 20%, unless otherwise specified). In the expected condition, stimuli were preceded by the anticipatory cue r_cue(t) with onset at t = −0.5s before stimulus presentation.

Network simulations.

All data analyses, model simulations and mean field theory calculations were performed using custom software written in MATLAB (MathWorks), and C. Simulations comprised 20 realizations of each network (each one representing a different experimental session), with 20 trials per stimulus in each of the 2 conditions (unexpected and expected); or 40 trials per session in the condition with “cue-on” and no stimuli (Fig. 3); otherwise explicitly stated. Each network was initialized with random synaptic weights and simulated with random initial conditions. Stimulus and cue selectivities were assigned to randomly chosen sets of neurons in each network. Sample sizes were similar to those reported in previous publications^13,14,15. Across-neuron distributions of peak responses and across-network distributions of coding latencies were assumed to be normal but this was not formally tested. Dynamical equations for the LIF neurons were integrated with the Euler method with 0.1 ms step.

Mean field theory.

Mean field theory was used in a simplified network with 2 excitatory clusters (parameters as in Table 2) using the population density approach^53–55: the input to each neuron was completely characterized by the infinitesimal mean μ_α and variance ${\sigma }_{\alpha }^2$ of the post-synaptic current for Q+2 neural populations: the first Q populations representing the Q excitatory clusters; the (Q+1)-th population representing the ``background” unstructured excitatory population; and the (Q+2)-th population representing the inhibitory population (see Table 1 for parameter values):

$${\mu }_{\alpha }={\tau }_{m,E}\sqrt{N}[\frac{n_{E}f}{Q}\left(p_{EE}{J}_{+}{j}_{EE}{r}_{\alpha }+{\sum }_{\beta =1}^{Q-1}{p}_{EE}{J}_{-j_{EE}}{r}_{\beta }\right)+n_E\left(1-f\right)p_{EE}{J}_{-}{j}_{EE}{r}_E^{\left(bg\right)}-n_I{p}_{EI}{j}_{EI}{r}_I+n_E{p}_{E0}{j}_{E0}{r}_{ext}],$$

$${\sigma }_{\alpha }^2={\tau }_{m,E}[\frac{n_{E}f}{Q}\left(p_{EE}{\left(J_{+j_{EE}}\right)}^2\left(1+{\delta }^2\right)r_{\alpha }+{\sum }_{\beta =1}^{Q-1}{p}_{EE}{\left(J_{-j_{EE}}\right)}^2\left(1+{\delta }^2\right)r_{\beta }\right)+n_E\left(1-f\right)p_{EE}{\left(J_{-}{j}_{EE}\right)}^2\left(1+{\delta }^2\right)r_E^{\left(bg\right)}+n_I{p}_{EI}{j}_{EI}^2\left(1+{\delta }^2\right)r_I],$$

where r_α, r_β, with α, β = 1,…,Q, are the E-clusters firing rates; $r_E^{\left(bg\right)}$ is the background E-population firing rate; r_I is the I-population firing rate; n_E = 4/5, n_I = 1/5 are the fractions of E and I neurons, respectively, and δ = 1% is the SD of the synaptic weights distribution. The two sources contributing to the variance ${\sigma }_{\alpha }^2$ are thus the temporal variability in the input spike trains from the presynaptic neurons, and the quenched variability in the synaptic weights and connectivity. The afferent current to a background E population neuron reads:

$${\mu }_E^{\left(bg\right)}={\tau }_{m,E}\sqrt{N}[\frac{n_{E}f}{Q}{\sum }_{\beta =1}^Q{p}_{EE}{J}_{-}{j}_{EE}{r}_{\beta }+n_E\left(1-f\right)p_{EE}{j}_{EE}{r}_E^{\left(bg\right)}-n_I{p}_{EI}{j}_{EI}{r}_I+n_E{p}_{E0}{j}_{E0}{r}_{ext}],$$

$${\left({\sigma }_E^{\left(bg\right)}\right)}^2={\tau }_{m,E}[\frac{n_{E}f}{Q}{\sum }_{\beta =1}^Q{p}_{EE}{\left(J_{-}{j}_{EE}\right)}^2\left(1+{\delta }^2\right)r_{\beta }+n_E\left(1-f\right)p_{EE}{j}_{EE}^2\left(1+{\delta }^2\right)r_E^{\left(bg\right)}+n_I{p}_{EI}{j}_{EI}^2\left(1+{\delta }^2\right)r_I],$$

and, similarly, for an I neuron:

$${\mu }_I={\tau }_{m,I}\sqrt{N}\left[\frac{n_{E}f}{Q}{\sum }_{\beta =1}^Q{p}_{IE}{j}_{IE}{r}_{\beta }+n_E\left(1-f\right)p_{IE}{j}_{IE}{r}_E^{\left(bg\right)}-n_I{p}_{II}{j}_{II}{r}_I+n_E{p}_{I0}{j}_{I0}{r}_{ext}\right],$$

$${\sigma }_I^2={\tau }_{m,I}[\frac{n_{E}f}{Q}{\sum }_{\beta =1}^Q{p}_{IE}{j}_{IE}^2\left(1+{\delta }^2\right)r_{\beta }+n_E\left(1-f\right)p_{IE}{j}_{IE}^2\left(1+{\delta }^2\right)r_E^{\left(bg\right)}+n_I{p}_{II}{j}_{II}^2\left(1+{\delta }^2\right)r_I].$$

The network fixed points satisfied the Q + 2 self-consistent mean field equations¹⁰

$$r_{\alpha }=F_{\alpha }\left({\mu }_{\alpha }\left(\mathit{r}\right),{\sigma }_{\alpha }^2\left(\mathit{r}\right)\right),$$ (1)

where $\mathit{r}=\left[r_1,\dots ,r_Q,r_E^{bg},r_I\right]$ is the population firing rate vector (boldface represents vectors).Fα is the current-to-rate function for population α, which varied depending on the population and the condition. In the absence of the anticipatory cue, the LIF current-to-rate function $F_{\alpha }^0$ was used

$$F_{\alpha }^0\left({\mu }_{\alpha },{\sigma }_{\alpha }^2\right)={\left({\tau }_{ref}+{\tau }_{m,\alpha }\sqrt{\pi }{\int }_{H_{eff,\alpha }}^{{\Theta }_{eff,\alpha }}{e}^{u^2}\left[1+\text{erf}\left(u\right)\right]\right)}^{-1},$$

where ${\Theta }_{eff,\alpha }=\frac{V_{thr,\alpha }-{\mu }_{\alpha }}{\surd {\sigma }_{\alpha }^2}+a{k}_{\alpha },$ $H_{eff,\alpha }=\frac{V_{reset,\alpha }-{\mu }_{\alpha }}{\surd {\sigma }_{\alpha }^2}+a{k}_{\alpha }$. Here, $k_{\alpha }=\sqrt{{\tau }_{syn,\alpha }/{\tau }_{m,\alpha }}$, $a=\frac{\left|\zeta \left(1/2\right)\right|}{\sqrt{2}}~1.03$.^56,57 In the presence of the anticipatory cue, a modified current-to-rate function $F_{\alpha }^{cue}$ was used to capture the cue-induced Gaussian noise in the cue afferent currents to the cue-selective populations (α = 1,…,Q):

$$F_{\alpha }^{cue}\left({\mu }_{\alpha },{\sigma }_{\alpha }^2\right)=\int Dz{F}_{\alpha }^0\left({\mu }_{\alpha }+z\sigma {\mu }_{ext},{\sigma }_{\alpha }^2\right),$$

where $Dz=dz\mathrm{e}\mathrm{x}\mathrm{p}(-\frac{z^2}{2})/\sqrt{2\pi }$ is the Gaussian measure with zero mean and unit variance, μ_ext = I₀ is the baseline afferent current and σ is the anticipatory cue’s SD as fraction of μ_ext (Fig. 3d). For the plots in Fig. 3c we replaced the transfer function $F_E^0\left({\mu }_E,{\sigma }_E^2\right)$ of the LIF neuron with the simpler function $f_E^0=0.5(1+\tanh \left({\mu }_E\right))$. Note that the latter depends only on the mean input current, as the mean input is the only variable required to implement the effect of the anticipatory cue on the transfer function via $f_E^{cue}\left({\mu }_E\right)=\int Dz{f}_E^0\left({\mu }_E+z{\sigma \mu }_{ext}\right)$. Fixed points r* of equation (1) were found with Newton’s method; the fixed points were stable (attractors) when the stability matrix

$$S_{\alpha \beta }=\frac{1}{{\tau }_{syn,\alpha }}\left(\frac{\partial F_{\alpha }\left({\mu }_{\alpha }\left(\mathit{r}\right),{\sigma }_{\alpha }^2\left(\mathit{r}\right)\right)}{\partial r_{\beta }}-\frac{\partial F_{\alpha }\left({\mu }_{\alpha }\left(\mathit{r}\right),{\sigma }_{\alpha }^2\left(\mathit{r}\right)\right)}{\partial {\sigma }_{\alpha }^2}\frac{\partial {\sigma }_{\alpha }^2}{\partial r_{\beta }}-{\delta }_{\alpha \beta }\right),$$ (2)

evaluated at r* was negative definite. Stability was defined with respect to an approximate linearized dynamics of the mean m_α and SD s_α of the input currents⁵⁸

$${\tau }_{syn,\alpha }\frac{d{m}_{\alpha }}{dt}=-m_{\alpha }+{\mu }_{\alpha }\left(\mathit{r}\right),$$

$$\frac{{\tau }_{syn,\alpha }}{2}\frac{d{s}_{\alpha }^2}{dt}=-s_{\alpha }^2+{\sigma }_{\alpha }^2\left(\mathit{r}\right),$$ (3)

$${r_{\alpha }\left(t\right)=F}_{\alpha }\left(m_{\alpha }\left(\mathit{r}\right),s_{\alpha }^2\left(\mathit{r}\right)\right),$$

Where μ_α and ${\sigma }_{\alpha }^2$ are the stationary values given above^14,15.

Effective mean field theory for the reduced network.

The mean field equations (1) for the P=Q+2 populations may be reduced to a set of effective equations governing the dynamics of a smaller subset of q<P of populations, henceforth referred to as populations in focus.³¹ The reduction is achieved by integrating out the remaining P-q out-of-focus populations. This procedure was used to estimate the energy barrier separating the two network attractors in Fig. 3d and Fig. 4c. Given a fixed set of values $\tilde{\mathit{r}}=[{\tilde{r}}_1,\dots ,{\tilde{r}}_q]$ for the in-focus populations, one solves the mean field equations for P-q out-of-focus populations

$$r_{\beta }\left({\tilde{r}}_1,\dots ,{\tilde{r}}_q\right)=F_{\beta }\left[{\mu }_{\beta }\right({\tilde{r}}_1,\dots ,{\tilde{r}}_q,r_{q+1},\dots ,r_P),{\sigma }_{\beta }^2({\tilde{r}}_1,\dots ,{\tilde{r}}_q,r_{q+1},\dots ,r_P\left)\right],$$

for β = q + 1,…,P to obtain the stable fixed point ${\mathit{r}}^{\prime }\left(\tilde{\mathit{r}}\right)\doteq [r_{q+1}\left(\tilde{\mathit{r}}\right),\dots {,r}_P\left(\tilde{\mathit{r}}\right)]$ of the out-of-focus populations as functions of the in-focus firing rates $\tilde{\mathit{r}}$. Stability of the solution ${\mathit{r}}^{\prime }\left(\tilde{\mathit{r}}\right)$ is computed with respect to the stability matrix (2) of the reduced system of P-q out-of-focus populations. Substituting the values ${\mathit{r}}^{\prime }\left(\tilde{\mathit{r}}\right)$ into the fixed-point equations for the q populations in focus yields a new set of equations relating input rates $\tilde{\mathit{r}}$ to “output” rates r^out:

$$r_{\alpha }^{out}\left(\tilde{\mathit{r}}\right)=F_{\alpha }\left[{\mu }_{\alpha }\right(\tilde{\mathit{r}},{\mathit{r}}^{\mathrm{\prime }}\left(\tilde{\mathit{r}}\right)),{\sigma }_{\alpha }^2(\tilde{\mathit{r}},{\mathit{r}}^{\mathrm{\prime }}\left(\tilde{\mathit{r}}\right)\left)\right],$$

for α = 1,…,q. The input $\tilde{\mathit{r}}$ and output r^out firing rates of the in-focus populations will be different, except at a fixed point of the full system where they coincide. The correspondence between input and output rates of in-focus populations defines the effective current-to-rate transfer functions

$$r_{\alpha }^{out}(\tilde{\mathit{r}})=F_{\alpha }^{eff}[{\mu }_{\alpha }(\tilde{\mathit{r}}),{\sigma }_{\alpha }^2(\tilde{\mathit{r}})],$$ (4)

for α = 1,…,q in-focus populations at the point $\tilde{\mathit{r}}$. The fixed points $r_{\alpha }^{out}\left({\tilde{\mathit{r}}}^{*}\right)={\tilde{r}}_{\alpha }^{*}$ of the in-focus equations (4) are fixed points of the entire system. It may occur, in general, that the out-of-focus populations attain multiple attractors for a given value of $\tilde{\mathit{r}}$, in which case the set of effective transfer functions $F_{\alpha }^{eff}$ is labeled by the chosen attractor; in our analysis of the two-clustered network, only one attractor was present for a given value of $\tilde{\mathit{r}}$.

Energy potential.

In a network with Q=2 clusters, one can integrate out all populations (out-of-focus) except one (in-focus) to obtain the effective transfer functions for the in-focus population representing a single cluster, with firing rate $\tilde{r}$ (equation (4) for q=1). Network dynamics can be visualized on a one-dimensional curve, where it is well approximated by the first-order dynamics (see ref.³¹ for details):

$${\tau }_{syn,\alpha }\frac{d\tilde{r}}{dt}=-\tilde{r}+r^{out}\left(\tilde{r}\right).$$

These dynamics can be expressed in terms of an effective energy function $E\left(\tilde{r}\right)$ as

$${\tau }_{syn,\alpha }\frac{d\tilde{r}}{dt}=-\frac{\partial E\left(\tilde{r}\right)}{\partial \tilde{r}},$$

so that the dynamics can be understood as a motion in an effective potential energy landscape, as if driven by an effective force $-\frac{\partial E\left(\tilde{r}\right)}{\partial \tilde{r}}=-(\tilde{r}-r^{out}\left(\tilde{r}\right))$. The minima of the energy with respect to $\tilde{r}$ are the stable fixed points of the effective 1-dimensional dynamics, while its maxima represent the effective energy barriers between two minima, as illustrated in Fig. 3c. The one-cluster network has 3 fixed points, two stable attractors (‘A’ and ‘B’ in Fig. 3c) and a saddle point (‘C’). We estimated the height Δ of the potential energy barrier on the trajectory from A to B through C as minus the integral of the force from the first attractor A to C:

$$\text{Δ}={\int }_A^C(\tilde{r}-r^{out}\left(\tilde{r}\right))d\tilde{r},$$

which represents the area between the identity line ($y=\tilde{r})$ and the effective transfer function $(y=r^{out}(\tilde{r})$) (see Fig. 3c). In the finite network, where the dynamics comprise stochastic transitions among the states, switching between A and B would occur with a frequency that depends on the effective energy barrier Δ, as explained in the main text.

Population decoding.

The amount of stimulus-related information carried by spike trains was assessed through a decoding analysis⁵⁹ (see Fig. S3 for illustration). A multiclass classifier was constructed from Q neurons sampled from the population (one neuron from each of the Q clusters for clustered networks, or Q random excitatory neurons for homogeneous networks). Spike counts from all trials of n_stim taste stimuli in each condition (expected vs. unexpected) were split into training and test sets for cross-validation. A “template” was created for the population PSTH for each stimulus, condition and time bin (200 ms, sliding over in 50 ms steps) in the training set. The PSTH contained the trial-averaged spike counts of each neuron in each bin (the same number of trials across stimuli and conditions were used). Population spike counts for each test trial were classified according to the smallest Euclidean distance from the templates across 10 training sets (‘bagging’ or bootstrap aggregating procedure⁶⁰). Specifically, from each training set L, we created bootstrapped training sets L_b, for b = 1,..,B=10, by sampling with replacement from L. In each bin, each test trial was then classified B times using the B classifiers, obtaining B different “votes”, and the most frequent vote was chosen as the bagged classification of the test trial. Cross-validated decoding accuracy in a given bin was defined as the fraction of correctly classified test trials in that bin.

Significance of decoding accuracy was established via a permutation test: 1000 shuffled datasets were created by randomly permuting stimulus labels among trials, and a ‘shuffled distribution’ of 1000 decoding accuracies was obtained. In each bin, decoding accuracy of the original dataset was deemed significant if it exceeded the upper bound, α_0.05, of the 95% confidence interval of the shuffled accuracy distribution in that bin (this included a Bonferroni correction for multiple bins, so that α_0.05 = 1 – 0.05/N_b, with N_b the number of bins). Decoding latency (insets in Figs. 1c and 1f) was estimated as the earliest bin with significant decoding accuracy.

Cluster dynamics.

To analyze the dynamics of neural clusters (lifetime, inter-activation interval, and latency; see Figs. 3 and 4), cluster spike count vectors r_i (for i = 1,…,Q) in 5 ms bins were obtained by averaging spike counts of neurons belonging to a given cluster. A cluster was deemed active if its firing rate exceeded 10 spks/s. This threshold was chosen so as to lie between the inactive and active clusters’ firing rates, which were obtained from a mean field solution of the network¹⁴.

Reporting Summary.

Further information on research design is available in the Life Sciences Reporting Summary linked to this article.