Nonequivalence of Second Sphere “Noncatalytic” Residues in Pentaerythritol Tetranitrate Reductase in Relation to Local Dynamics Linked to H-Transfer in Reactions with NADH and NADPH Coenzymes

Abstract

Many enzymes that catalyze hydride transfer reactions work via a mechanism dominated by quantum mechanical tunneling. The involvement of fast vibrational modes of the reactive complex is often inferred in these reactions, as in the case of the NAD(P)H-dependent pentaerythritol tetranitrate reductase (PETNR). Herein, we interrogated the H-transfer mechanism in PETNR by designing conservative (L25I and I107L) and side chain shortening (L25A and I107A) PETNR variants and using a combination of experimental approaches (stopped-flow rapid kinetics, X-ray crystallography, isotope/temperature dependence studies of H-transfer and NMR spectroscopy). X-ray data show subtle changes in the local environment of the targeted side chains but no major structural perturbation caused by mutagenesis of these two second sphere active site residues. However, temperature dependence studies of H-transfer revealed a coenzyme-specific and complex thermodynamic equilibrium between different reactive configurations in PETNR–coenzyme complexes. We find that mutagenesis of these second sphere “noncatalytic” residues affects differently the reactivity of PETNR with NADPH and NADH coenzymes. We attribute this to subtle, dynamic structural changes in the PETNR active site, the effects of which impact differently in the nonequivalent reactive geometries of PETNR−NADH and PETNR−NADPH complexes. This inference is confirmed through changes observed in the NMR chemical shift data for PETNR complexes with unreactive 1,4,5,6-tetrahydro-NAD(P) analogues. We show that H-transfer rates can (to some extent) be buffered through entropy–enthalpy compensation, but that use of integrated experimental tools reveals hidden complexities that implicate a role for dynamics in this relatively simple H-transfer reaction. Similar approaches are likely to be informative in other enzymes to understand the relative importance of (distal) hydrophobic side chains and dynamics in controlling the rates of enzymatic H-transfer.

Introduction

Understanding the physical basis of enzyme catalysis is important from a fundamental point of view and also to drive applications in contemporary areas of research, such as biotechnology and synthetic biology. The development of sustainable and clean chemical manufacturing practices requires deep appreciation of the physical basis of enzyme catalysis that enables us to mimic and improve Nature’s catalysts. Enzymes catalyze many chemical reactions with extraordinary selectivity and specificity and, in some cases, extreme efficiency.¹⁻³ While it is difficult to pinpoint the exact origin of the catalytic effect for even one particular enzyme, the importance of electrostatic contributions,⁴ i.e., stabilization of the transition state and hydrogen bonding,⁵ has long been recognized. Diverse experimental and theoretical methods have been used to probe chemical steps and have contributed to debates relating to physical models of catalysis, in some cases moving beyond traditional semiclassical frameworks for enzyme catalysis.⁶⁻⁹ A fast-growing number of experimental studies indicate that protein dynamics might play a role in catalysis, across a hierarchy of time scales.¹⁰⁻¹⁴ Beyond experimental approaches, the involvement of dynamics has been supported also by computation.¹⁵⁻¹⁹ Slower (microsecond to millisecond) dynamics attributed to large-scale protein domain motions have been identified using NMR methodologies. Direct coupling of fast (femtosecond to nanosecond) dynamics to chemistry is mostly inferred from kinetic isotope effect (KIE) studies and supported by computational analysis such as transition path sampling.²⁰⁻²² The temperature dependence of KIEs is regarded as a “gold standard” for probing quantum mechanical tunneling (QMT) for H-transfer reactions and some interpretations have inferred a role for distance sampling dynamical contributions in facilitating the tunneling reaction²³⁻²⁷ (although others have questioned these models²⁸⁻³⁰). Studies with variant enzymes have led to models in which the temperature dependence of the KIE has been attributed to modulation of donor–acceptor distance (DAD) distributions and perturbation of high-frequency motions³¹ or disruption of dynamic networks³² that extend to remote residues within the enzyme. Mutagenesis has been used to perturb active site structure and probe effects on H-transfer and inferred dynamical contributions using a number of enzyme systems (e.g., dihydrofolate reductase,³³ soybean lipoxygenase-1,³⁴ thymidylate synthase,³⁵ ene-reductases³⁶). Experimental KIE measurements have also been extended to include the use of high pressure^37,38 and “heavy enzymes” (²H, ¹³C, and/or ¹⁵N stable isotope-labeled)³⁹⁻⁴⁴ to probe these effects further and supported using computational simulations. Much of our current understanding of enzymatic catalysis has come from probing the effects of mutagenesis on catalytic rates and from computational simulations. For H-transfer reactions, this has opened up debates on the relative importance of dynamics in these reactions and challenged the community to develop integrated experimental⁴⁵ and theoretical²² approaches to address this problem.

Old Yellow Enzymes (OYEs) are an intensively investigated class of ene-reductases, which catalyze the asymmetric reduction of a wide variety of activated α,β-unsaturated compounds, with high specificity for substrates bearing nitro or keto groups.⁴⁶ While their physiological role and natural substrates are often not known,⁴⁷ OYEs are particularly attractive to study from a mechanistic perspective and for their biocatalytic potential. Pentaerythritol tetranitrate reductase (PETNR) is one such enzyme. PETNR has dual-specificity and is reduced by both NADH and NADPH, but with a preference toward the latter coenzyme.⁴⁸ The basis of this dual-specificity is not well understood. The catalytic cycle of PETNR follows a single-site ping-pong mechanism. The first step (the reductive half-reaction) involves hydride transfer from the C4 pro-R hydrogen atom of the NAD(P)H coenzyme to the N5 atom of the noncovalently bound flavin mononucleotide (FMN) cofactor.⁴⁹ QMT contributes to this catalytic step,⁴³ and several experimental studies have suggested an involvement of fast (picosecond to nanosecond) dynamics in the H-transfer reaction.^23,50,51 Here, we interrogated the H-transfer mechanism in PETNR by designing four variants of two second sphere residues (L25 and I107) positioned along the FMN-NAD(P)H N5–C4 axis (Figure 1), as inferred from the structure of PETNR in complex with the unreactive NADH analogue 1,4,5,6-tetrahydro-NAD.⁴³ L25 is located below the FMN, with the side chain in van der Waals contact with the isoalloxazine ring of the FMN cofactor, while the side chain of I107 is positioned above the nicotinamide ring of the coenzyme. These residues are “noncatalytic” and are assumed not to contribute to major active site electrostatic effects. We have altered these residues by making conservative (L25I and I107L) and side chain length shortening (L25A and I107A) variants of PETNR, with the objective of understanding how second sphere residues influence catalysis, H-tunneling and any vibrational modes linked to H-transfer. We used X-ray crystallography to assess the impact of mutagenesis on overall structural properties and stopped-flow spectroscopy to analyze the kinetics of hydride transfer through a combination of concentration and temperature dependence studies with both coenzymes (NADPH and NADH). Building on the recent NMR work in which a full sequential backbone assignment of PETNR holoenzyme was undertaken,⁵² we also used the coenzyme analogues 1,4,5,6-tetrahydro-NAD(P) (NAD(P)H₄) to investigate coenzyme binding modes in the ground-state PETNR−NADPH₄ and PETNR−NADH₄ complexes. Our overall aim was to understand how localized dynamics can impact H-transfer in each of these complexes and to investigate how perturbation of second sphere residues through mutagenesis impacts QMT and active site dynamics associated with this reaction with both NADPH and NADH.

Figure 1.

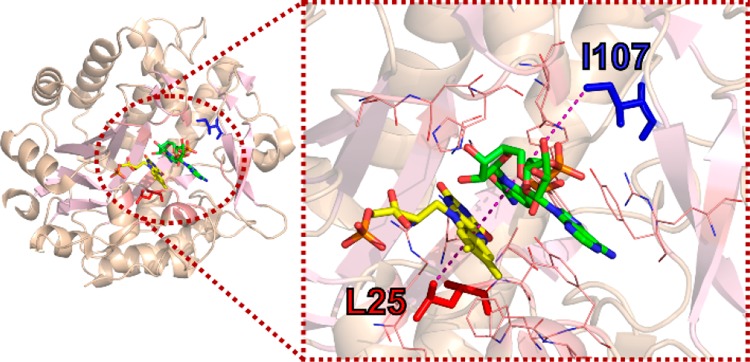
Crystal structure of the PETNR−NADH₄ complex (PDB: 3KFT),⁴³ showing the location of residues L25 (red) and I107 (blue), which have been targeted for mutagenesis. Residues located 5 Å away from the NADH₄ C4-H are represented as wireframes in the right panel of the figure. Residue L25 is located ∼ 4 Å away from the FMN cofactor (yellow), with the side chain pointing directly below the H-transfer coordinate, while I107 is located ∼8 Å above the coenzyme site (green) and is positioned above two bulky side chains (Y68 and Y186) that form one side of the active site hydrophobic cavity.

Results and Discussion

First, to ensure that mutagenesis of PETNR had not influenced the coordination of the noncovalently bound FMN cofactor, we recorded UV–vis absorption spectra of the PETNR variants. All variants displayed the same spectroscopic features as wild-type PETNR (WT PETNR), with full FMN occupancy in the active site, and maintaining the characteristic PETNR-bound FMN spectral signature, with maxima at 380 and 465 nm (Figure S1 and Table S1). To assess any impact of mutagenesis on the general structure of the enzyme, we determined X-ray crystallographic structures for all variant forms isolated (Figures S2–S3 and Table S2). When compared to WT PETNR (PDB: 3P62), the RMSD values based on Cα positions corresponding to each variant were in the range 0.3–0.4 Å, indicating a high degree of similarity. No major reorientations occurred in the loops bearing the side chain mutations, and superpositioning of all the structures indicates the tertiary TIM-barrel fold and external secondary features were largely unaffected by mutagenesis. Despite the overall structures of each of the four variants remaining largely unperturbed by mutagenesis, some subtle shifts in side chains are observed. One key shift in the I107A variant has led to a reorientation of the side chain of Q241 (highlighted in Figure S2). Removal of the I107 side chain bulk allows the side chain of Q241 to rotate toward the vacated space, leading to a slight increase in the coenzyme binding pocket in this region. Altogether, the spectroscopic and structural evidence supports the hypothesis that the targeted residues are not directly involved in FMN binding and that the mutations do not affect the overall architecture of the enzyme. Secondary impacts of these mutations resulting in subtle alterations within the active site are investigated below.

One of the benefits in using PETNR to study enzymatic hydride transfer mechanisms is that individual catalytic steps can be accessed by stopped-flow measurements that track changes in FMN absorbance during the reductive half-reaction of the enzyme catalytic cycle. The loss of FMN absorbance during reduction of PETNR by NAD(P)H reports directly on the hydride transfer step, which is essentially irreversible. The observed limiting rate constant (k_red) at saturating coenzyme concentration is therefore the rate of hydride transfer from which the intrinsic KIE values can also be obtained when using deuterated coenzyme. Note that previously we have not observed evidence for other processes affecting the kinetics of H-transfer in OYEs, e.g., isomerization of the enzyme–substrate complex, and we propose that the measured KIE is therefore an intrinsic value, but we accept that the absence of evidence cannot be taken as proof.⁵³ To further support this proposition, we have measured the effect of pH on the rate of FMN reduction with NADPH and (R)-[4-²H]-NADPH. Neither reaction is significantly pH-dependent (Figure S4 and Table S3), suggesting kinetic complexity is minimal and observed rate constants report directly on hydride transfer kinetics.

For the PETNR variant enzymes, the coenzyme concentration dependencies of hydride transfer rates were recorded (Figure S5). H-transfer was monitored by following the quenching of PETNR-bound FMN absorbance at 465 nm when mixing the enzyme with NAD(P)H (for representative kinetic traces, see Figure 2), as described previously.^50,51 Limiting rate constants (k_red) and apparent saturation constants (K_S) at 25 °C for PETNR-catalyzed hydride transfer are shown in Table 1. Although a plethora of data is available for WT PETNR from previous investigations, we re-examined all the kinetics of the WT enzyme for the purpose of this study to eliminate any possible disparities arising from slightly different conditions, coenzyme purity, or experimental setup. We were able to confirm that there is no difference between the k_red and K_S values obtained in this study and those previously published for WT PETNR.⁴⁸

Figure 2.

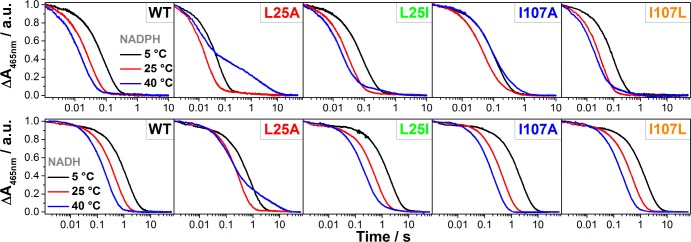
Stopped-flow kinetic traces showing FMN reduction for the PETNR variants with NADPH (top panel) and NADH (bottom panel) at selected representative temperatures (5, 25, and 40 °C). All absorbance values were normalized for a better comparison. Conditions: 50 mM potassium phosphate buffer (pH 7.0), 20 μM enzyme, 10 mM NADPH or 25 mM NADH (final concentrations).

Table 1. Observed Rates of FMN Reduction at 25 °C for PETNR Variants with NADPH and NADH^a.

	kred (s–1)	KS (μM)	kred/KS (s–1 μM)
NADPH
WT	33.43 ± 0.22	103 ± 4	(3.25 ± 0.13)×10–1
L25A	55.75 ± 0.35	199 ± 6	(2.80 ± 0.09)×10–1
L25I	29.49 ± 0.49	130 ± 8	(2.27 ± 0.14)×10–1
I107A	21.22 ± 0.25	130 ± 9	(1.63 ± 0.11)×10–1
I107L	28.37 ± 0.20	107 ± 5	(2.65 ± 0.12)×10–1
NADH
WT	2.03 ± 0.01	1067 ± 13	(1.90 ± 0.03)×10–3
L25A	3.62 ± 0.04	2294 ± 91	(1.58 ± 0.06)×10–3
L25I	1.74 ± 0.04	306 ± 40	(5.69 ± 0.94)×10–3
I107A	2.05 ± 0.04	329 ± 37	(6.23 ± 0.71)×10–3
I107L	1.94 ± 0.02	889 ± 36	(2.18 ± 0.09)×10–3

^aCalculated from fitting data presented in Figure S5 to k_obs1 = k_red[NAD(P)H]/(K_S + [NAD(P)H]). Reaction conditions: 50 mM potassium phosphate buffer (pH 7.0), 20 μM enzyme concentration, [NAD(P)H] ranging 0.1–50 mM, 25 °C.

The kinetic traces measured at 25 °C were adequately fit using a single exponential function for WT PETNR and for some variants. However, the behavior of a number of variants was found to be more complex (vide infra for a more detailed analysis), with the majority of the reaction transients fitting to a double-exponential function, comprising a fast rate (k_obs1) and a slow rate (k_obs2 < 5 s^–1). The values presented in Table 1 reflect only the fast rate of the reaction, as extracted from the fits of the concentration dependence studies (Figure S5). By determining the saturation constant (K_S) for each variant, we noticed that there is no major difference in the apparent affinity for NADPH, with the I107L variant having the same affinity (107 ± 5 μM) as WT PETNR (103 ± 4 μM), while the other variants have slightly higher values for K_S, with the most prominent change for L25A PETNR, which exhibits a 2-fold increase (K_S = 199 ± 6 μM).

Analyzing the limiting rate of reduction, we observed correlations between the size of the side chain and the H-transfer rates: while the conservative (L25I and I107L) mutations have only a minor effect on the rate of FMN reduction, the alanine substitutions impose a markedly modified reaction rate. The rate of H-transfer is 60% faster for the L25A variant than for WT PETNR, while a 40% reduction in rate is observed for the I107A variant (Table 1). This suggests that an increase in the mobility of the FMN binding site, caused by shortening the L25 side chain, is enhancing catalytic rates, while a larger void above the NADPH substrate, induced by truncation of I107 side chain, is decreasing catalytic rates. While the L25A and L25I variants exhibit a very similar change in rate for the reaction with NADH (when compared to NADPH), the mutations introduced at the I107 site do not affect the limiting rate constant and, moreover, afford better binding of NADH. When comparing k_red/K_S (which reports, in this case, on the efficiency of each variant to perform the reductive half-reaction), we conclude that the increase in rate for L25A variants comes with a cost of lower binding affinity, leading to a slightly less efficient enzyme. We have noticed similar compensatory behavior in the reaction of other OYEs with nicotinamide coenzyme biomimetics, where elevated catalytic rates are associated with inverse changes in binding affinity.⁵⁴ The I107A variant is more efficient in the reaction with NADH and is noticeably less efficient for performing H-transfer from NADPH. Further, we performed temperature dependence studies of the rate of FMN reduction with both NADPH and NADH coenzymes, along with their corresponding deuterated forms, in the range of 5–40 °C. The unusual behavior of the variants is first noticed through the shape of the transients observed, with all variants manifesting multiple kinetic phases at elevated temperatures (Figure 2). In general, the kinetic traces could be fitted to a single exponential function for low temperatures (<20 °C), while at higher temperatures the FMN reduction takes place with multiple resolvable kinetic phases.

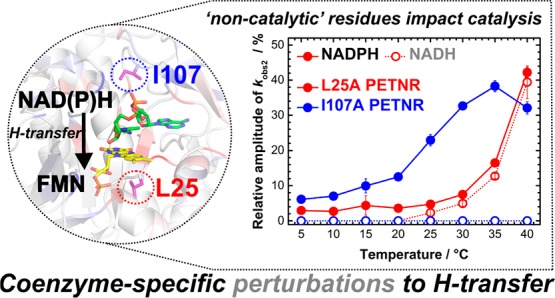
It was observed that the amplitude of the slow kinetic components increases with increasing temperature (Figure 3), with the effect being more pronounced for the L25A and I107A variants in the case of PETNR reduction by NADPH (∼40% of the total absorbance change attributed to k_obs2 at 40 °C). The reduction with deuterated substrates follows closely that observed for NADPH (Figure S6 and Tables S4–S13). This suggests that the reaction chemistry (H vs D transfer) is not kinetically controlled, and the differences observed are solely attributed to perturbations in the enzyme–coenzyme complex arising from mutagenesis of PETNR. FMN reduction follows the same trend with NADH for L25A and L25I variants, with multiple reactive configurations (MRCs) at elevated temperature and similar changes of amplitude contributions for each kinetic component. However, the mutagenesis of the I107 site does not induce the formation of MRCs in reactions with NADH (the kinetic traces fit to a single exponential function across the studied temperature range, Figure 3 and Figure S7), a contrasting behavior when compared to reduction by NADPH. This indicates that truncation of the I107 site has no detrimental effect on H-transfer from NADH coenzyme, while the NADPH reaction is noticeably affected. This suggests truncation of the I107 side chain induces propagated effects (which extend beyond the tilting of the Q241 side chain observed from X-ray data) on the structure (and dynamics) of the enzyme.

Figure 3.

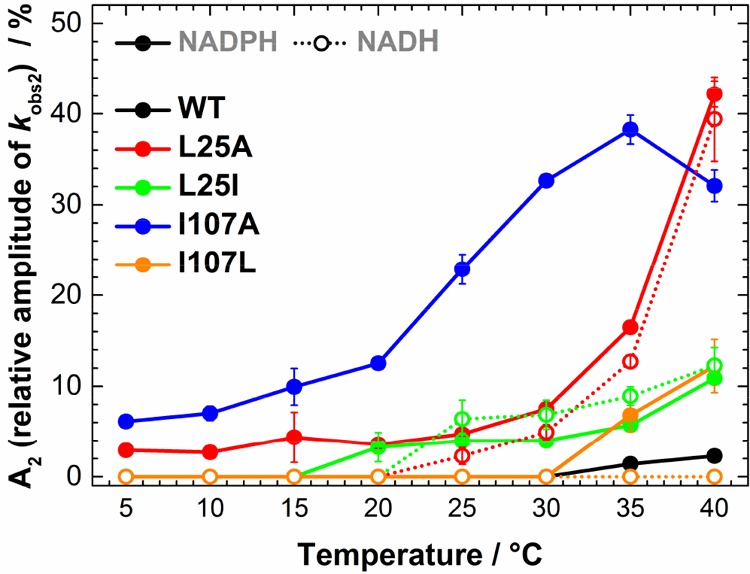
Manifestation of multiple reactive configurations as a function of temperature for investigated PETNR variants. For variants manifesting MRCs, the relative amplitude of the slow kinetic phase (k_obs2) during FMN reduction of PETNR variants by NADPH and NADH increases with temperature. The relative amplitude is reporting on the change in amplitude corresponding to the slow kinetic phase out of the total change in amplitude measured during FMN reduction. For L25A variant, the amplitude value at 40 °C represents the sum of two slow kinetic phases (k_obs2 and k_ob3, see Tables S5 and S10).

We have previously detected MRCs in the N189A variant of morphinone reductase (MR), another enzyme belonging to the OYE family, in which four detectable MRCs could be kinetically resolved.³⁶ Likewise, the data for the reduction of PETNR variants suggests that NADPH and NADH are able to bind in multiple conformations in the active site of PETNR variants, which leads to different competent states of the enzyme–coenzyme complex that are able to perform H-transfer, observed as multiple kinetic phases bearing KIEs (Figures S8 and S9). While the k_red value is highest for L25A, this fast reactive conformation is very slowly interconverting (<1 s^–1) with another slow reactive conformation. In our previous work involving MR,³⁶ we were able to corroborate that the resolved kinetic phases represent different configurations of the enzyme–coenzyme complex using computational methods. Herein, we propose that our observations with PETNR are consistent with those we have reported previously with MR. However, we cannot exclude other explanations at this stage, e.g., a mechanism involving multiple free enzyme species that have different reactivities. For example, an isotopically insensitive isomerization from an inactive configuration into an active configuration would be expected to diminish the observed KIE. Regardless of the origin of multiple kinetic phases observed in the variants presented here, these data demonstrate that second sphere mutations in the PETNR active site have differing effects on the reaction with NADH and NADPH.

Given the KIE values at 25 °C are only slightly affected by mutagenesis, with small differences between the studied variants (Figure S8), we consider that a better way to interpret the data (as we have recently described elsewhere⁵¹) is by comparing the activation parameters (presented in Table 2). We analyzed the thermodynamic parameters of the H-transfer reaction by fitting the Arrhenius plots of k_obs1 (Figure 4) to the nonlinear Eyring-based function

1

where ΔH_T0^⧧ and ΔS_T0^⧧ are the apparent activation enthalpy and entropy, respectively, at a reference temperature (T₀, 298 K in this study), ΔC_p^⧧ is the difference in heat capacity between the reactant and transition states, and k_B, h, and R are the Boltzmann, Planck, and ideal gas constants, respectively.^55,56 This model has recently been used for interpreting curvatures observed in Eyring plots for a number of enzymes,^57,58 and recent computational work suggests changes in ΔC_p^⧧ are related to dynamical changes during catalysis and these changes are attributed from contributions of not only active site regions but also distal domains of the enzyme (dynamical changes that are dispersed throughout the entire structure).⁵⁹

Table 2. Extracted Parameters from Kinetic and Thermodynamic Studies^a.

	ΔHT0⧧ (kJ mol–1)	ΔST0⧧ (J mol–1 K–1)	ΔCp⧧(kJ mol–1 K–1)	ΔHT0⧧ (kJ mol–1)	ΔST0⧧ (J mol–1 K–1)	ΔCp⧧(kJ mol–1 K–1)
	NADPH			NADH
WT	30.4 ± 0.3	–113.9 ± 0.9	–0.50 ± 0.05	35.4 ± 0.1	–120.5 ± 0.5	0.39 ± 0.03
L25A	23.3 ± 1.2	–133.7 ± 4.1	–0.92 ± 0.12	33.6 ± 0.5	–122.1 ± 1.7	0.28 ± 0.05
L25I	30.4 ± 0.6	–114.9 ± 2.0	–0.43 ± 0.07	42.7 ± 1.7	–97.7 ± 6.0	0.32 ± 0.18
I107A	17.8 ± 2.3	–160.2 ± 7.7	–1.08 ± 0.23	46.4 ± 1.1	–83.8 ± 3.6	–0.47 ± 0.22
I107L	31.5 ± 0.7	–111.6 ± 2.4	–0.44 ± 0.08	38.7 ± 0.2	–110.0 ± 0.8	0.23 ± 0.04
	(R)-[4-2H]-NADPH			(R)-[4-2H]-NADH
WT	36.8 ± 0.3	–108.0 ± 0.1	–0.32 ± 0.04	40.3 ± 0.1	–120.4 ± 0.5	0.46 ± 0.02
L25A	31.9 ± 1.1	–120.5 ± 3.7	–0.78 ± 0.15	40.3 ± 1.1	–115.7 ± 3.8	0.42 ± 0.14
L25I	36.7 ± 0.5	–109.5 ± 1.6	–0.53 ± 0.09	44.9 ± 0.2	–106.8 ± 0.8	0.30 ± 0.07
I107A	19.0 ± 0.2	–172.6 ± 0.7	–1.43 ± 0.02	53.5 ± 1.7	–77.0 ± 5.6	0.17 ± 0.22
I107L	35.7 ± 0.4	–112.9 ± 1.4	–0.65 ± 0.07	45.4 ± 0.3	–103.9 ± 0.9	0.43 ± 0.07
	Isotope Effect: (R)-[4-2H]-NADPH–NADPH			Isotope Effect: (R)-[4-2H]-NADH–NADH
WT	6.4 ± 0.4	5.8 ± 1.5	0.18 ± 0.06	4.9 ± 0.2	0.1 ± 0.7	0.07 ± 0.04
L25A	8.6 ± 1.27	13.3 ± 5.6	0.14 ± 0.19	6.6 ± 1.2	6.4 ± 4.2	0.13 ± 0.15
L25I	6.3 ± 0.7	5.4 ± 2.5	–0.11 ± 0.11	2.3 ± 1.8	–9.2 ± 6.0	–0.03 ± 0.19
I107A	1.2 ± 2.3	–12.3 ± 7.7	–0.35 ± 0.23	7.1 ± 2.0	6.8 ± 6.7	0.64 ± 0.31
I107L	4.2 ± 0.8	–1.3 ± 2.8	–0.22 ± 0.11	6.7 ± 0.4	6.1 ± 1.2	0.19 ± 0.08

^aApparent activation parameters were obtained by fitting the data in Figure 4 to eq 1 with T₀ = 298 K. The isotope effects are the differences in activation parameters (e.g., ΔH_T0^⧧,D – ΔH_T0^⧧,H).

Figure 4.

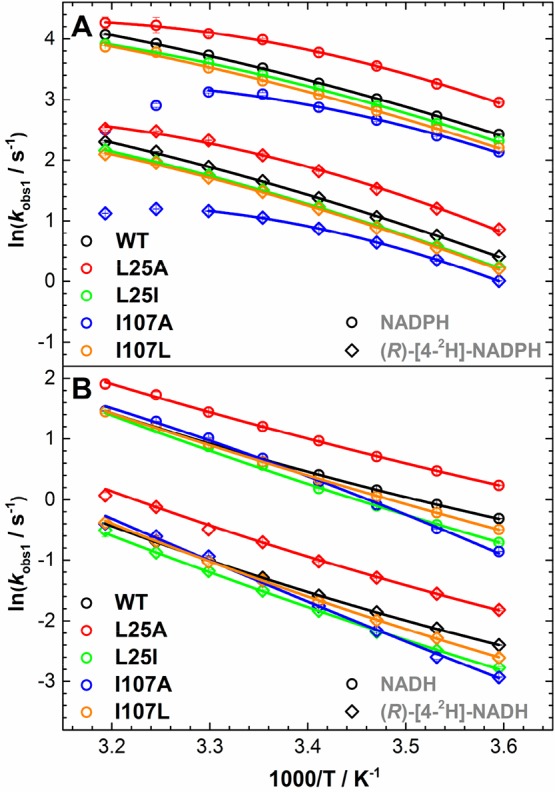
Arrhenius plots of the observed rate of hydride transfer from (A) NADPH and (R)-[4-²H]-NADPH and (B) NADH and (R)-[4-²H]-NADH to FMN in studied PETNR variants; plots of k_obs1, data from Tables S4–S13. See Table 2 for extracted parameters. Note: The decrease in k_obs1 values for I107A PETNR reaction with NADPH and (R)-[4-²H]-NADPH at 35–40 °C suggests a different mechanism at elevated temperatures; hence, the data were omitted during the fitting.

For the reactions with NADPH and (R)-[4-²H]-NADPH, the apparent activation enthalpy values for WT PETNR are identical with those previously reported, with a coenzyme isotope effect of 6.4 ± 0.4 kJ mol^–1, which we previously inferred to be an evidence of a “soft” promoting motion (a promoting vibration with a relatively small force constant) contributing to catalysis.⁴³ The kinetic isotope effect on the FMN reduction with NADH and (R)-[4-²H]-NADH in WT PETNR manifests less temperature independence (ΔΔH_T0^⧧ = 4.9 ± 0.2 kJ mol^–1) when compared with the KIE on the NADPH reaction (note that early work indicated a measurable temperature-independent KIE, which we now consider to be underestimated⁴³). Overall, when comparing the apparent activation enthalpies and entropies for the PETNR variants, we observed a strong compensatory behavior (Figure S10). This linear enthalpy–entropy compensation was recently observed in a study involving “heavy” PETNR isotopologues.⁵¹ This compensation effect is closely observed for ΔΔH_T0^⧧ and ΔΔS_T0^⧧: changes in ΔΔH_T0^⧧ values are reflected by similar changes in ΔΔS_T0^⧧ (Figure 5A). Moreover, for the NADPH reaction, there is a strong correlation between the rate of the reaction and the coenzyme KIEs (differences in the apparent activation enthalpy, (R)-[4-²H]-NADPH–NADPH), but there is no correlation for the NADH reaction (Figure 5B).

Figure 5.

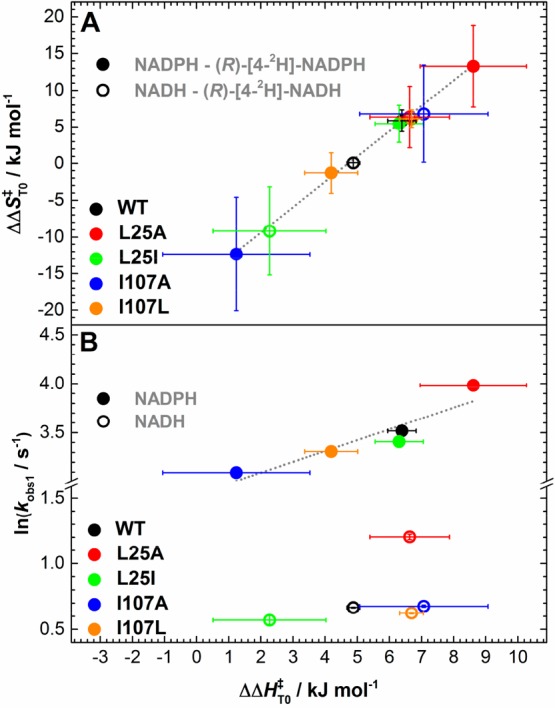
Relationship between the differences (coenzyme KIE) in apparent activation enthalpy (ΔΔH_T0^⧧) and entropy (A) and correlations between ΔΔH_T0^⧧ and observed rate constant (B) during H-transfer for the PETNR variants.

The more prominent changes in ΔC_p^⧧ are observed for the variants with side chain truncations (L25A and I107A), which manifest a more negative ΔC_p^⧧ when compared to WT PETNR. A recent study of ketosteroid isomerase and α-glucosidase MalL showed that the decrease in ΔC_p^⧧ can be explained through significant dynamical contributions of regions remote from the active site.⁵⁹ In the case of PETNR, the effect of side chain truncation on catalytic rates, enthalpy values, coupled with the nonequivalence in reactivity toward the two coenzyme and changes in ΔC_p^⧧, could inform on vibrational coupling (previously observed in “heavy enzyme” studies^19,50) that is extended beyond the mutagenesis site(s). While it is assumed that ΔC_p^⧧ values are negative for enzyme systems in which the chemical reaction is rate limiting (as the heat capacity for enzyme–substrate complex is larger than for the enzyme–transition state complex),⁵⁹ most of the data for PETNR reduction by NADH show positive values for ΔC_p^⧧.

The kinetic and thermodynamic analysis of the reduction of FMN in the PETNR variants reveals coenzyme-specific perturbations to the H-transfer chemistry and thermal equilibrium of reactant states. The current knowledge we have at hand to rationalize these findings comes mainly from crystallographic studies (presented herein) and previously performed molecular dynamics (MD) simulations. The MD data suggest a similar binding mode for both NADPH and NADH coenzymes in the active site of PETNR,⁴³ which makes it difficult to rationalize the differences in H-transfer chemistry and thermal conformation equilibrium presented above. Although the crystal structure of the PETNR−NADH₄ complex (PDB: 3KFT(43)) provides valuable insight into the structural proximity of reacting groups in the active site, π–π stacking between the symmetry-related adenosine moieties of NADH₄ in the two PETNR−NADH₄ monomers present in the asymmetric unit of the crystal lattice results in the pyrophosphate and adenosine groups of NADH₄ being poorly coordinated by PETNR. The absence of such interactions limits predictions and analyses that can be made regarding the conformational preferences of NADPH₄ binding to PETNR. Despite numerous attempts, we have been unable to crystallize the PETNR−NADPH₄ complex, which limits further structural and computational investigations. Consequently, we pursued NMR studies of WT PETNR and recently reported the ¹H, ¹⁵N, and ¹³C sequential backbone resonance assignments of the holoenzyme.⁵² Building on this recent work, we have now performed near-complete backbone resonance assignments of the ground-state PETNR−NADH₄ and PETNR−NADPH₄ complexes at saturating concentrations of either NADH₄ or NADPH₄, which we further used to inspect differences in the binding modes between the coenzymes.

Given the large size of PETNR (40 kDa), TROSY-based 3D heteronuclear experiments were acquired and analyzed, which enabled a highly successful degree of assignment (97%) of the ¹H–¹⁵N TROSY spectrum for each complex. Compared to the extent of assignment achieved for PETNR (333 residues), in the case of the PETNR−NADH₄ complex, 334 residues were successfully assigned, as H184 could be identified as a sharp and intense peak after ligand addition. Further assignment of one more residue of the flexible loop (D274) was also achieved; however, residue R164 could not be assigned, most probably due to peak overlap. The PETNR−NADPH₄ complex was assigned to the greatest extent (335 residues), with all residues identified as in the PETNR−NADH₄ complex, as well as the additional assignment of residue R164.

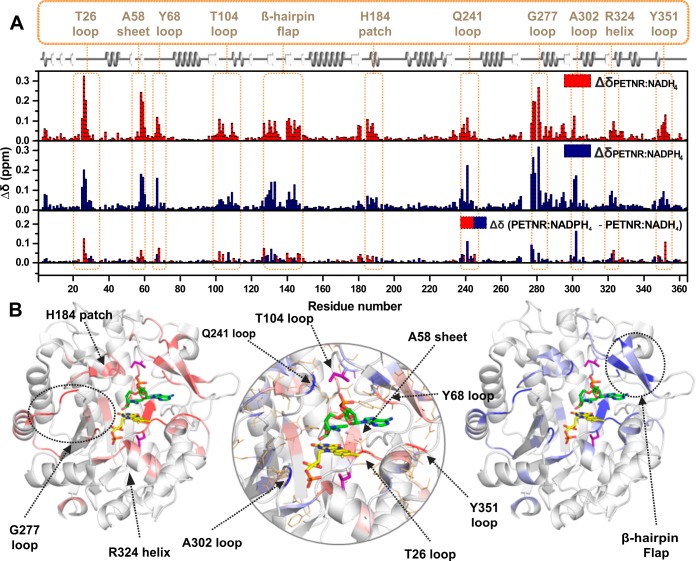
In order to assess the impact of the NAD(P)H₄ coenzyme analogue binding on the PETNR structure, we comparatively analyzed the ¹H–¹⁵N TROSY spectrum of PETNR with ¹H–¹⁵N TROSY spectra of the PETNR−NADH₄ and PETNR−NADPH₄ complexes. Overall, the changes in chemical shift for ¹H_N and ¹⁵N are limited to similar residue segments for all complex comparisons (Figure S11). The differences in combined chemical shift between each complex and PETNR, and a visual mapping of these changes onto the crystal structure of the PETNR−NADH₄ complex (PDB: 3KFT(43)) is illustrated in Figure 6. It can be observed that, while the majority of the peaks are essentially not sensitive to coenzyme analogue binding, localized areas of PETNR are noticeably affected by the addition of either NADPH₄ or NADH₄ (see Figure S12 for a structural overview of notably affected regions). Most of the changes that occur in PETNR upon binding of the coenzyme analogues are localized approximately 5 Å away from either NADH₄ or the FMN cofactor, with similarly affected sites for both the NADPH₄ and NADH₄ analogues. The regions that are affected significantly by binding of NAD(P)H₄ are depicted in Figure 6B. These encompass several loop regions (with maximum chemical shift differences recorded at residues T26, Y68, T104, Q241, G277, A302, Y351), a histidine “patch” that is known from crystallographic data to coordinate the NADH₄ coenzyme analogue⁶⁰ (denoted the H184 patch) and an α-helix found in close contact with the FMN cofactor (denoted the R324 helix). Coenzyme analogue binding is also observed to cause significant chemical shift changes in the β-hairpin flap (a region encompassing N126-T147), suggesting a major role of this structural motif in binding the NAD(P)H coenzyme in the active site. The significant differences in chemical shift between PETNR and the PETNR−NAD(P)H₄ complexes observed in the β-sheet containing A58 and the loop involving Y351 (which are known to coordinate the FMN cofactor⁶⁰), along with differences located at the top of the β-barrel that is in close proximity to FMN, suggest that NAD(P)H₄ binding induces FMN repositioning within the active site for efficient H-transfer. This is supported by the formation of a charge-transfer complex between NAD(P)H₄ and FMN, resulting in changes to the electrostatic distribution within the system, which contributes to the observed differences in chemical shift. For T26, the large difference in chemical shift can be explained by the formation of a hydrogen bond between the side chain hydroxyl group of T26 and the NH₂ group of the carboxamide function of the nicotinamide ring in NAD(P)H₄ and by perturbations in the hydrogen bond between the backbone amide proton of T26 and the N5 atom of FMN. For the resonances assigned in the G277 loop, the NMR data suggest that coenzyme analogue binding induces a dramatic reorganization of the loop. This effect is propagated into the α-helix from which the G277 loop emerges, which is also moderately affected by NAD(P)H₄ binding, even though it is positioned far away from the active site.

Figure 6.

Observed changes in chemical shift for PETNR upon binding the NADH₄ or the NADPH₄ coenzyme analogues. (A) Histograms of the residue-specific chemical shift changes for the backbone amide groups in PETNR upon binding NADH₄ (red) or NADPH₄ (blue). The absolute chemical shift changes were calculated using the following equation: Δδ_X = [(δ_HNPETNR – δ_HNX)² + (C(δ_NPETNR – δ_NX))²]^1/2, where δ_HN is the backbone amide proton chemical shift, δ_N is the backbone amide nitrogen chemical shift, C value is 0.12 (for rescaling of δ_N values), and X is either the PETNR−NADH₄ complex or the PETNR−NADPH₄ complex. The lower histogram shows the residue-specific chemical shift differences between the PETNR−NADH₄ complex and the PETNR−NADPH₄ complex, with red and blue bars indicating larger changes in PETNR upon binding NADH₄ or NADPH₄, respectively. The absolute chemical shift differences between the PETNR−NAD(P)H₄ complexes were calculated as Δδ = [(Δδ_{PETNR−NADPH4} – Δδ_{PETNR−NADH4})²]^1/2. The secondary structure of PETNR is shown at the top of the figure with gray helices denoting α-helices and white arrows indicating β-strands. Regions with significant Δδ values are highlighted with segment labels. (B) Distributions of Δδ values plotted onto the structure of the PETNR−NADH₄ complex (PDB: 3KFT). Residues with significant Δδ values are colored red (Δδ_{PETNR−NADH4}, left panel) and blue (Δδ_{PETNR−NADPH4}, right panel). The FMN cofactor is shown as yellow sticks, the NADH₄ coenzyme analogue is shown as green sticks, and the mutation sites (L25 and I107) are depicted as purple sticks. The central panel encompasses a zoomed-in view of the active site and highlights the Δδ values between the two complexes (red, larger Δδ upon PETNR−NADH₄ complex formation; blue, larger Δδ upon PETNR−NAPDH₄ complex formation) and is a structural visualization of the data in the lower histogram. Side chains are shown as gold wireframes and regions with significant ΔΔδ values are highlighted with segment labels. Proline residues, unassigned residues, and residues with Δδ < 0.04 ppm (the standard deviation) are left blank in the representation, while residues with Δδ ≥ 0.04 ppm are colored as described above, with a stronger intensity of color representing a higher Δδ value. In the central panel, no cutoff was applied for Δδ.

Overall, similar residue segments show differences in backbone amide ¹⁵N chemical shifts between the PETNR−NADH₄ and PETNR−NADPH₄ complexes (Figure 7). Analysis of amide ¹⁵N chemical shift changes (Δδ_N) can provide valuable information on the location of conformational differences between the complexes, as they report mainly on changes in backbone torsion angles. The only structural difference between the coenzyme analogues is the presence of a 2′-phosphate group on the ribose ring of the adenosine moiety in NADPH₄. Therefore, Δδ_N values reported between these analogues reflect how PETNR specifically modifies its conformational and dynamic preferences to accommodate NADPH₄ binding in the active site.

Figure 7.

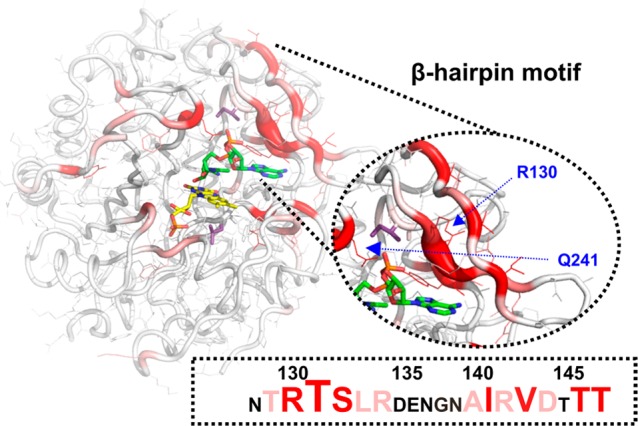
Structural mapping of absolute chemical shift differences for backbone amide ¹⁵N atoms calculated as Δδ_N = [(δ_NPETNR−NADPH₄ – δ_NPETNR−NADH₄)²]^1/2 plotted onto the structure of the PETNR−NADH₄ complex (PDB: 3KFT) (Figure S11). Residues with significant Δδ_N values are colored red, with a stronger intensity of color representing a higher Δδ_N value, with a cutoff of 0.1 ppm applied. The side chains are shown as wireframes in the putty representation of the protein, the FMN cofactor is shown as yellow sticks, the NADH₄ coenzyme analogue is shown as green sticks, and the mutation sites (L25 and I107) are depicted as purple sticks. The zoomed-in view of the β-hairpin flap highlights the Δδ_N values between the two complexes and identifies the location of R130 and Q241, which are residues with significant differences between the two complexes.

The residue with the largest Δδ_N value involves T131, present in a cluster of contiguous residues (T129–R134 and A140–T147 of the β-hairpin flap), which have significant ¹⁵N chemical shift differences (Figure 7 and Figure S11). Although the R130 side chain and the putative location of the 2′-phosphate group are not within the hydrogen-bonding distance in the crystal structure of the PETNR−NADH₄ complex, it is likely that bond rotation would allow productive coordination of these groups in solution. Structural perturbations within the β-hairpin flap are propagated to Y68 and also to Q241 via a network of side chain hydrogen bonds involving Y186, which are positioned directly over the face of the nicotinamide ring of NADH₄ in close proximity to I107. Conformational differences within the β-hairpin flap are also propagated through side chain hydrogen bonding with R134 to the L25–I31 and E348–G352 regions. For the D274–G277 loop with missing structural density in the crystal, chemical shift differences in the G278–E283 region indicate that the loop likely coordinates the coenzyme. Remarkably, chemical shift perturbations are also noted for G301–A302 and F322–G323, which are residues that coordinate the phosphate group present in FMN, indicating that conformational and dynamic preferences for NADH₄ and NADPH₄ coordination by PETNR are propagated through the charge-transfer complex formed with FMN.

Based on the differences in chemical shift observed between PETNR and the PETNR−NAD(P)H₄ complexes, we can now rationalize, in part, the kinetic behavior of the investigated variants. Residue L25 presents large differences in chemical shift for both PETNR−NADH₄ and PETNR−NADPH₄ complexes, and these observations are most readily explained by its close proximity to T26, which is a residue directly involved in FMN cofactor binding.⁶⁰ In the crystal structure, residue I107 is positioned ∼8 Å away from the face of the NADH₄ nicotinamide ring and is sandwiched between Y68, Y186, and Q241, which make direct contact with the coenzyme analogue and a segment of the β-hairpin flap. I107 is slightly affected by NADPH₄ binding, but not by NADH₄ binding, suggesting that the presence of phosphate in the coenzyme analogue contributes to a more pronounced reorientation of the loop containing I107. Overall, the structural features in the vicinity of the FMN cofactor (and residue L25) are highly affected by both coenzymes, with higher chemical shift changes occurring upon NADH₄ addition, while the regions affected more by NADPH₄ binding are situated in the vicinity of residue I107 (Figure 6B). The fact that residue I107 is not affected by NADH₄ binding, and H-transfer kinetics are also not majorly affected for the reduction with NADH (i.e., FMN reduction occurs in a single phase), as in contrast with NADPH₄, informs clearly about differences in the binding modes of the two coenzymes, which have consequences on the H-transfer mechanism. Along with the observed reorientation of Q241 side chain in I107A variant, the NMR and thermodynamic data suggests extended vibrational coupling is present during H-transfer from NADPH to PETNR.

To further the analysis of the binding modes of the two coenzymes, we performed an analysis of the ¹H line width of peaks in the ¹H–¹⁵N TROSY spectra (Figure S13), which enables detection of residues that have a significant exchange contribution to the transverse relaxation rate (R₂). Broadening of the line width suggests conformational exchange between two or more species on the microsecond to millisecond NMR time scale.⁶¹ It can be observed that PETNR exhibits a high degree of conformational exchange on this time scale, with most of the regions affected being located around the active site (Figure S14). A reduction in the exchange contribution to R₂ can be observed for some residues following addition of NADH₄, such as those situated in the G277 loop. The minimization of this dynamic behavior is even more pronounced in the case of the PETNR−NADPH₄ complex, for which most of these slow conformational exchange processes are removed. The data indicate that the NADPH₄ coenzyme mimic is interacting more tightly with PETNR than its nonphosphorylated counterpart, which explains the higher affinity of PETNR for NADPH than for NADH (Table 1). The mutations chosen for kinetic studies are located on the edge of these regions that exhibit microsecond to millisecond conformational exchange in PETNR. Residue I107 is not a dynamic center, but it is located in a region with moderate dynamic behavior in PETNR, while line widths for residues in the vicinity of L25 are considerably broadened. Both regions around the targeted residues show a restriction in conformational exchange on addition of coenzyme, suggesting an important role of binding in controlling enzyme motions on the microsecond to millisecond time scale.

This study was undertaken to investigate how second sphere “noncatalytic” residues influence vibrational modes linked to H-transfer and H-tunneling in PETNR. The use of a combination of experimental tools (e.g., stopped-flow rapid kinetics, isotope/temperature dependence studies of H-transfer and NMR spectroscopy) allowed us to underpin a complex, coenzyme-specific kinetic and thermodynamic equilibrium during H-transfer in the investigated variants. The side chain modifications (L25I, L25A, I107A, and I107L PETNR) were designed on the basis of their location within the active site (situated along the FMN-NAD(P)H N5–C4 axis in the PETNR−NAD(P)H complexes). The hypothesis that the targeted side chains are not involved in major electrostatic interactions within the active site was confirmed through stationary UV–vis spectroscopy and crystallographic data. The side chain modifications are subtle, but they prompt changes to the conformational landscape of the enzyme that can be observed during the reductive half-reaction using stopped-flow techniques. The rate of H-transfer at room temperature is broadly maintained through enthalpy–entropy compensation. However, temperature dependence studies of H-transfer revealed a coenzyme-specific and complex thermodynamic equilibrium between different reactive configurations in PETNR–coenzyme complexes. We find that mutagenesis of these second sphere “noncatalytic” residues (L25 and I107) has differing effects on the reactivity (activation entropy and enthalpy) of PETNR with NADPH and NADH coenzymes. We attribute these differences in coenzyme reactivity to subtle, dynamic structural changes in the PETNR active site. This interpretation is aided by NMR chemical shift data measured for PETNR−NADH₄ and PETNR−NADPH₄, which show structural differences between the two complexes.

Concluding Remarks

Enzymes have evolved to catalyze chemical reactions with extraordinary selectivity and specificity, and it is often assumed that predominantly one configuration of the enzyme–substrate complex will be the catalytically active one. This hypothesis has a strong physical basis for the reaction of WT enzymes with their natural substrates. However, when dealing with enzyme variants, the perturbation of the finely tuned enzyme structure by mutagenesis can change the conformational flexibility and geometries in the enzyme to the extent that multiple reactive conformations are populated. To date, kinetic studies of OYEs have allowed us to demonstrate that variants of two enzymes in this family (N189A variant of MR³⁶ and this study) exhibit shifted distributions of reactive conformational states when compared to the corresponding WT enzymes. While the N189A variant of MR could be considered a disruptive mutation (N189 is intimately involved in coenzyme binding through H-bonding), it is not the case for the variants in the current study. Herein, the synergistic use of complementary spectroscopic techniques has allowed us to unravel the nonequivalence of second sphere “noncatalytic” residues in PETNR. The complex kinetic behavior observed upon truncation of L25 and I107 side chains indicates long-range cooperativity throughout the active site. We suggest that formation of MRCs could be a common feature when investigating variant enzymes, and other authors have pointed toward the existence of parallel reaction pathways during catalysis.⁶²⁻⁶⁵ Moreover, kinetic complexities on H-transfer caused by (distal) mutagenesis have been observed in dihydrofolate reductase catalysis,³¹ and these effects have been correlated with protein dynamics contributions.^{26,33,66−68} While we are aware of the experimental challenges that would allow us to visualize MRCs in a wider range of H-transfer enzymes, we propose that synergistic experimental approaches should aid interpretation of kinetic data. This study is an illustration of how the use of integrated structural and kinetic experimental tools can uncover details often masked in more traditional studies of H-transfer (e.g., those reliant only on the use of steady-state turnover studies with isotopically labeled substrates). These approaches are needed to identify these hidden complexities even for relatively simple reactions such as H-transfer. Similar approaches are therefore likely to be informative with other enzymes to understand the relative importance of small-scale dynamics in controlling enzymatic rates of reaction.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acscatal.8b02810.

• Experimental details including overexpression of PETNR variants and ²H,¹³C,¹⁵N-labeled PETNR, synthesis of deuterated and reduced coenzymes, conditions used (and data analysis details) for stopped-flow experiments, crystallography and NMR spectroscopy; additional data including static UV–vis spectroscopy, crystallography, tabulated rate constants, and additional figures for kinetic and NMR data (Figures S1–S14, Tables S1–S13) (PDF)

The authors declare no competing financial interest.