Generalized Born Based Continuous Constant pH Molecular Dynamics in Amber: Implementation, Benchmarking, and Analysis

Abstract

Solution pH plays an important role in structure and dynamics of biomolecular systems; however, pH effects cannot be accurately accounted for in conventional molecular dynamics simulations based on fixed protonation states. Continuous constant pH molecular dynamics (CpHMD) based on the λ-dynamics framework calculates protonation states on the fly during dynamical simulation at a specified pH condition. Here we report the CPU-based implementation of the CpHMD method based on the GBNeck2 generalized Born (GB) implicit-solvent model in the pmemd engine of the Amber molecular dynamics package. The performance of the method was tested using pH replica-exchange titration simulations of Asp, Glu and His sidechains in 4 miniproteins and 7 enzymes with experimentally known pK_a’s, some of which are significantly shifted from the model values. The added computational cost due to CpHMD titration ranges from 11 to 33% for the data set and scales roughly linearly as the ratio between the titrable sites and number of solute atoms. Comparison of the experimental and calculated pK_a’s using 2 ns per replica sampling yielded a mean unsigned error of 0.65, a root-mean-squared error of 0.90, and a linear correlation coefficient of 0.78. While this level of accuracy is similar to the GBSW-based CpHMD in CHARMM, in contrast to the latter, the current implementation was able to reproduce the experimental orders of the pK_a’s of the coupled carboxylic dyads. We quantified the sampling errors, which revealed that prolonged simulation is needed to converge pK_a’s of several titratable groups involved in salt-bridge-like interactions or deeply buried in the protein interior. Our benchmark data demonstrate that GBNeck2-CpHMD is an attractive tool for protein pK_a predictions.

Graphical Abstract

INTRODUCTION

Solution pH is an important environmental factor that modulates the energetics and conformational dynamics of biomolecular systems. Many biological processes, such as protein folding,¹ enzyme catalysis² and ion/substrate transport³ are controlled by pH. However, pH effects are largely overlooked in the molecular dynamics (MD) community, and MD simulations are performed with titratable sites fixed in the protonated or the deprotonated state based on the solution or model pK_a values. Over the past decade, two types of techniques have been developed to control solution pH in MD simulations. In the discrete constant pH molecular dynamics (CpHMD) technique, which is also known as the stochastic titration method,⁴ molecular dynamics is periodically interrupted by Monte-Carlo sampling of protonation states. This technique, using implicit-, explicit- or mixed-solvent schemes, has been implemented in widely used MD packages, such as Amber,^5,6 CHARMM^7,8 and Gromacs.⁴ In the continuous CpHMD technique, which has roots in the λ-dynamics method for free energy calculations,⁹ a set of fictitious λ coordinates, whose end points represent the protonated and deprotonated states, are propagated at the same time as the spatial coordinates.¹⁰ The continuous CpHMD technique, with the aforementioned three solvent schemes, has been implemented in CHARMM^10–15 and recently in Gromacs.¹⁶ The development and application of both discrete and continuous CpHMD techniques have been recently reviewed.¹⁷ Here we focus on continuous CpHMD and for convenience, we will drop the word continuous in the remainder of the paper.

The original CpHMD method, which was implemented in CHARMM, utilizes the generalized Born (GB) implicit-solvent model, Generalized Born using molecular volume (GBMV)¹⁸ or Generalized Born with simple switching (GBSW),¹⁹ to sample conformational and protonation states.^10,11 Making use of the temperature replica-exchange protocol to enhance sampling and ensure convergence,²⁰ the GBSW-based CpHMD method was applied to understand protein folding mechanisms^1,21,22 and blind prediction of protein pK_a values.²³ The latter study, which used 500 ps per replica sampling at a single pH condition to blindly predict the abnormally shifted pK_a’s of 87 titratable sites, showed that GBSW-CpHMD was one of the most accurate and robust pK_a calculation tools.²⁴ Nevertheless, in the post-prediction analysis²³ and other studies^12,25 two issues that affect the accuracy of pK_a calculations were identified. First, the effective Born radii of buried atoms given by the GBSW model¹⁹ are relatively insensitive to the degree of burial, which resulted in a systematic underestimation of the desolvation energies and consequently absolute pK_a shifts for deeply buried sites.²³ Second, small errors in describing the conformational environment and dynamics by the GBSW model, for example, partial loss of native structure,¹² overcompaction²² and reduced mobility of hydrophobic cluster,^12,25 and inability to represent solvent-mediated ion-pair interactions due to the lack of solvent granularity,¹² can lead to pK_a shifts in either directions.¹² These GBSW-related errors are sometimes compounded by the force field bias, for example, overstabilization of α helix in the folded state.^21,22 Thus, it appears that the accuracy of GB-based CpHMD methods may significantly benefit from the improved GB models and force fields. Further development of GB-based CpHMD is particularly desirable for pK_a predictions, as it has an unmatched convergence speed among all constant pH methods.¹²

Over the past decade, the GB models in Amber molecular dynamics package²⁶ have undergone considerable development. In the GBNeck model by Mongan et al., a so-called neck correction was introduced to account for the finite size of water molecules.²⁷ In the most recent GBNeck2 model by Nguyen et al., the parameter set of GBNeck was significantly improved to better reproduce Poisson-Boltzmann solvation free energies and more importantly, the experimental structure, stability, and salt-bridge profiles of model peptides.²⁸ Excitingly, the GBNeck2 model, when used with the newest ff14SB force field (sidechain only version)²⁹ folded 16 proteins of various sizes and topologies to the native structures.³⁰ These GB simulations also took advantage of GPU acceleration,³¹ which provided trajectories of 1 μs per day per GPU.

Motivated by the above developments and the desire to offer the community an accurate and fast pK_a prediction tool, we implemented the GBNeck2-based CpHMD method in Amber (abbreviated as GBNeck2-CpHMD henceforth). To accelerate the convergence of pK_a estimates,¹² the existing pH replica-exchange (pH-REX) method in Amber³² was adapted. Following a brief description of methods and implementation details, we report pK_a calculations for 4 mini-proteins and 7 enzymes that exhibit large pK_a shifts and have been previously used to benchmark the CHARMM CpHMD methods.^12,20 The method scales with the number of CPUs and has low computational cost. The accuracy of the calculated pK_a’s will be compared to the GBSW-CpHMD in CHARMM.^12,20 A detailed analysis of the deviations between calculated and experimental pK_a’s will be presented, with a special emphasis on residues deeply buried in the protein interior and those involved in salt-bridge-like interactions, as they are the most challenging sites for accurate pK_a predictions and showed the largest errors in the CHARMM CpHMD methods.^12,20 We will also quantify sampling errors and compare results obtained with different force fields and solvent models before drawing conclusions.

METHODS AND IMPLEMENTATION

Continuous constant pH molecular dynamics

Based on the λ dynamics method for free energy calculations,⁹ the continuous CpHMD method makes use of an extended Hamiltonian to simultaneously propagate the atomic positions and the coordinates of the fictitious λ particles representing protonation/deprotonation of titratable sites.¹⁰ Expressing λ as sin²θ, the λ coordinate is continuous and bound between 0 and 1. Thus, the discretized version of λ can be used to represent the protonation state.

$$\tilde{\lambda }=\{\begin{array}{ll}1(\text{deprotonated}),\hfill & \text{if}\lambda >{\text{cut}}_1\hfill \\ 0(\text{protonated}),\hfill & \text{if}\lambda <{\text{cut}}_0\hfill \end{array}$$ (1)

where cut₁ and cut₀ are the two cutoffs chosen to be 0.8 and 0.2, respectively. The total Hamiltionian that accounts for a set of deprotonation equilibria of ionizable sidechains in proteins, ${\text{HA}}_{\text{j}}\rightleftharpoons {\text{A}}_{\text{j}}^{-}$, becomes

$$\begin{array}{l}H\left(\left\{r_a\right\},\left\{{\lambda }_j\right\}\right)=\sum _a^{N_{\text{atom}}}\frac{1}{2}{m}_a{\dot{r}}_a^2+U^{\text{bond}}\left(\left\{r_a\right\}\right)+\\ U^{\text{nbond}}\left(\left\{r_a\right\},\left\{{\lambda }_j\right\}\right)+\sum _j^{N_{\text{titr}}}\frac{1}{2}{m}_j{\dot{\lambda }}_j^2+U^{*}\left(\left\{{\lambda }_j\right\}\right).\end{array}$$ (2)

In the above equation, the first and forth terms express the kinetic energies of the real atoms and fictitious λ particles, respectively. The second term represents the λ-independent bonded energies. The third term represents the λ-dependent electrostatic and van der Waals energies. For electrostatics, the atomic partial charges on a titratable site are linearly interpolated between the protonated (λ=0) and deprotonated (λ=1) states,

$$q_{a,j}={\lambda }_j{q}_{a,j}^{\text{deprot}}+\left(1-{\lambda }_j\right)q_{a,j}^{\text{prot}}$$ (3)

which enables the λ-dependent modulation of electrostatic energies, including the Coulomb energy as well as the GB solvation free energy,

$$U^{\text{GB}}=-\frac{1}{2}\sum _{a,b}(\frac{1}{{ϵ}_{\text{p}}}-\frac{e^{-\kappa r_{ab}}}{{ϵ}_{\text{w}}})\frac{q_a{q}_b}{\sqrt{r_{ab}^2+{\alpha }_a{\alpha }_b{e}^{-r_{ab}^2/4{\alpha }_a{\alpha }_b}}}.$$ (4)

Here r_ab is the distance between atom a and atom b, q_a, q_b are the respective partial charges, α_a, α_b are the respective effective Born radii, ϵ_p (1), ϵ_w (80) are the dielectric constants for the protein and water, respectively. κ is the inverse Debye length, κ² = 8πq²I/ek_BT, where I is the ionic strength, q is the charge of the salt ion, e is the elementary charge unit, and k_B is the Boltzmann constant. Similarly, the van der Waals interactions involving titratable hydrogens are linearly scaled by λ.

The final term in Eq. 2 contains three biasing potential energies dependent on λ only,

$$U^{*}\left(\left\{{\lambda }_j\right\}\right)=\sum _j^{N_{\text{titr}}}\left[-U^{\mathrm{mod}}\left({\lambda }_j\right)+U^{\text{pH}}\left({\lambda }_j\right)+U^{\text{barr}}\left({\lambda }_j\right)\right].$$ (5)

Here U^mod is a potential of mean force (PMF) function for titrating a model compound in solution, typically a blocked single amino acid. Subtraction of U^mod from the total Hamiltonian allows the calculation of the relative deprotonation free energy of a titratable site in the protein environment (ΔG^protein) with respect to solution (ΔG^mod). U^mod is a quadratic function of λ

$$U_j^{\text{mod}}=A_j{\left({\lambda }_j-B_j\right)}^2,$$ (6)

where A_j and B_j are the two parameters which can be determined using a fitting procedure (see Simulation Protocol).

The next biasing potential U^pH allows the calculation of the deprotonation free energy change due to a change in solution pH,

$$U^{\text{pH}}({\lambda }_j)=\ln (10)k_{B}T(\text{p}{K}_a^{\text{mod}}-\text{pH}){\lambda }_j,$$ (7)

where k_B is Boltzmann constant, T is temperature, and pK_a^mod is the model pK_a, which can be taken from experiment. U^pH(λ_j) is zero in the CpHMD simulation of a model compound at a solution pH identical to the model pK_a, i.e., the protonated and deprotonated states are sampled with equal probability.

The last biasing potential U^barr is a harmonic potential designed to decrease the probability of λ in the unphysical intermediate state.

$$U_j^{\text{barr}}=4\beta {\left({\lambda }_j-0.5\right)}^2,$$ (8)

where β is the height of the energy barrier. Finally, we note that the equations presented are used for single-site titration, e.g., Lys or Cys. The formalism for double-site titration, e.g., carboxyl and histidine residues can be found in ref.¹¹

Implementation details

A new module (phmd) that implements the GB-based continuous CpHMD method^10,11 was added in the pmemd molecular dynamics engine in Amber.²⁶ Currently, the GBNeck2 model is used for the propagation of both spatial and titration coordinates, but other GB models can be readily adopted. The pH replica-exchange method implemented for the Monte Carlo based discrete constant pH method³² was adapted to work with CpHMD.

To mimic protonation/deprotonation events, CpHMD methods adopt a single topology approach, i.e., dummy hydrogens attached to the titration sites lose their partial charges and van der Waals interactions upon deprotonation. Additionally, a protonation state change is represented by the switch between two sets of sidechain atomic charges. With the CHARMM force fields, the implementation is straightforward, as only the sidechain charges are affected by the change in protonation state. However, with the Amber force fields, the backbone charges are dependent on the sidechain protonation state, which coupled with the fact that the backbone atoms can interact with sidechain atoms of neighboring residues due to 1–4 electrostatic interactions, presents a problem for CpHMD methods (both discrete and continuous) that rely on a single reference state.⁵ To circumvent this problem, a pragmatic approach similar to that used by Mongan et al.⁵ was adopted: the partial charges on the backbone are fixed to the values of a single protonation state (charged Asp/Glu and neutral His), and the residual charge (ranging from 0.10 to 0.14 e for Asp, Glu, and His) is absorbed onto the C-β atom. In order to avoid introducing potential artifacts to conformational dynamics, such a scheme is only deployed for titration dynamics. For conformational dynamics, the partial charges are unmodified and the charge interpolation between the protonated and deprotonated states is made to both backbone and sidechain atoms.

The dummy hydrogens on Asp and Glu require special attention. The dummy hydrogen can be on the same (syn) or opposite (anti) sides of the second carboxyl oxygen. Previous work showed that once an uncharged dummy hydrogen rotates to the latter position, it can no longer gain charge, i.e., titrate.^5,10 Thus, following the CHARMM implementation,¹¹ the dummy hydrogens were placed in the syn position at the beginning of the simulation, and the rotation barrier around the C-O bond was raised to 6 kcal/mol, to prevent the transition to the anti position. Although fixing the dummy hydrogens to the syn position is justified by its stability over the anti position based on the NMR experiment and quantum calculations of carboxylic acids,¹¹ it is a topic that deserves further examination in the future.

In contrast to the CHARMM GB models (e.g., GBSW), hydrogen atoms have nonzero intrinsic Born radii in the Amber GB models. In contrast to the CHARMM GB models (e.g., GBSW), hydrogen atoms have nonzero intrinsic Born radii in the Amber GB models. As such, the intrinsic Born radius of the titratable hydrogen on a carboxylic group contributes to the solvation free energy of the protonated state. Consequently, the derivative of U_GB (Eq. 4) with respect to λ should contain a term to account for the change in the effective Born radii due to protonation. The contribution of such a term is expected to be much smaller than that due to the λ-dependent charge perturbation. Additionally, the implementation would be computationally inefficient, given the complexity of how the implicit Born radii enter into the GB solvation free energy. Thus, we made the following approximation. The contributions of the titratable hydrogens of carboxylic residues (e.g., Asp and Glu) to the Born radii were excluded from the calculation in both the spatial and titration dynamics, and the intrinsic Born radii of the carboxyl oxygens were set to 1.4 Å regardless of the protonation state. For histidines, the intrinsic Born radius of the imidazole hydrogens was set to 1.17 Å regardless of the protonation state. Note, the default radius for the imidazole hydrogens is 1.3 Å. We reduced it to compensate for the overstabilized salt-bridge-like interactions, following the radius reduction of the guanodinium hydrogens on arginines by Nguyen, Roe, and Simmerling.²⁸ Further details on the implementation and usage are available in Amber18 Reference Manual (http://ambermd.org/).

SIMULATION PROTOCOL

Structure preparation.

Blocked Asp, Glu and His (ACE-X-NH₂) were built using the LEaP facility in Amber.²⁶ The crystal structures or NMR models of the following proteins were retrieved from Protein Data Bank: the 36-residue villin headpiece subdomain (HP36, pdbid 1VII),³³ 45-residue binding domain of 2-oxoglutarate dehydrogenase multienzyme complex (BBL, pdbid 1W4H),³⁴ 56-residue N-terminal domain of ribosomal protein L9 (NTL9, pdbid 1CQU),³⁵ 56-residue turkey ovomucoid third domain (OMTKY, pdbid 1OMU),³⁶ 105-residue reduced form of human thioredoxin (pdbid 1ERT),³⁷ 129-residue hen egg-white lysozyme (HEWL, pdbid 2LZT),³⁸ 143-residue hyperstable Δ+PHS variant of staphylococcal nuclease (SNase, pdbid 3BDC),³⁹ 124-residue ribonuclease A (RNase A, pdbid 7RSA),⁴⁰ 155-residue E. coli ribonuclease H (RNase HI, pdbid 2RN2),⁴¹ 185-residue oxidized form of Bacillus circulans xylanase (xylanase, pdbid 1BCX),⁴² and 389-residue unbound β-secretase 1 catalytic domain (BACE1, pdbid 1SGZ). If applicable, the first chain in the crystal structure or the first entry in the NMR models was used; the hydrogen atoms as well as crystal waters were removed.

The following steps were performed with CHARMM (version c42a1).⁴³ The PDB structures were acetylated at N terminus and amidated at C terminus. Disulfide bonds were added as needed. Missing hydrogens were added with protonated His/Lys/Arg/Cys/Tyr and deprotonated Asp/Glu sidechains. The hydrogen positions were relaxed using 50 steps of steepest descent energy minimization in GBSW implicit solvent¹⁹ (default setting, see CHARMM documentation) where a harmonic force constant of 50 kcal/mol/Ų was placed on the heavy atoms. Next, dummy hydrogens in syn orientation were added to Asp/Glu sidechains, followed by 10 steps of steepest descent and 10 steps of adopted basis Newton Raphson minimization in GB solvent. The resulting pdb files were converted into Amber parameter and coordinate files in LEaP.

Derivation of model parameters.

Following previous work,¹¹ the average forces ⟨∂U/∂θ⟩ at fixed θ_x and ⟨∂U/∂θ_x⟩ at fixed θ were obtained for blocked model compounds, Ace-X-NH₂, where X=Asp, Glu and His, using GB simulations of 5 ns per window. The ionic strength was 0.1 M in accordance with the experimental model pK_a determination.⁴⁴ For Asp/Glu, θ/θ_x values of 0.2, 0.4, 0.7854, 1.0, 1.2 and 1.4 were used, corresponding to λ/x values of 0.04, 0.15, 0.5, 0.71, 0.87 and 0.97, respectively. ⟨∂U/∂θ⟩ and ⟨dU/dθ_x⟩ values were fit to the model potential of mean force (PMF) function, U^model(λ, x) = (a₁λ²+a₂λ+a₃)(x+a₄)²+a₅λ²+a₆λ, where a₁, ...a₆ are the fitting parameters. For His, fewer data points were needed.¹¹ ⟨∂U/∂θ⟩ was determined with θ_x fixed at 0 and 1.57 (x = 0 or 1), and ⟨∂U/∂θ_x⟩ was determined with θ fixed at 1.57 (λ = 1). The force values were then fit to the following PMF function with five parameters: U^model(λ, x) = λ²(a₁ײ + a₂x + a₃) + λ(a₄x + a₅).

Molecular dynamics protocol.

Molecular dynamics was performed using the modified version of the pmemd molecular dynamics engine in Amber.²⁶ Proteins were represented by the ff14SB Amber force field.²⁹ Solvent was represented by the GBNeck2 implicit-solvent model (igb=8) with mbondi3 intrinsic Born radii.²⁸ A 2-fs time step was used with bonds involving hydrogen atoms constrained with the SHAKE algorithm.⁴⁵ In the GB calculations, a 0.15 M ionic strength was used.

pH replica-exchange CpHMD titration of blocked amino acids and pentapeptides

Five sets of titration simulations were run for each model compound and pentapeptide. Each REX simulation contained six pH replicas, placed in the pH range encompassing 1.5 pH unit below and 1 pH unit above the model pK_a, with 0.5-pH unit interval. Exchanges were attempted every 1000 MD steps (2 ps), and each replica was run for 1 ns. The model pK_a’s from Thurlkill et al. were used (Table 1).

Table 1:

Calculated pK_a’s of blocked model compounds and alanine pentapeptides in solution

Residue	Compounda	Peptidea	Thurlkillb	Nozakic	Castanẽdad
Asp	3.7±0.07	3.8±0.05	3.67±0.04	4.0	3.90±0.01
Glu	4.2±0.11	4.1±0.05	4.25±0.05	4.4	4.36±0.01
His	6.4±0.03	6.4±0.03	6.54±0.04	6.3	n/d
HID	7.0±0.04	7.0±0.05	n/d	6.92e	n/d
HIE	6.5±0.05	6.5 0.02	n/d	6.53e	n/d

^aError bars of the calculated pK_a’s are the standard deviations based on five independent sets of REX titration runs, each lasting 1 ns per replica. Blocked model compound refers to Ac- X-NH₂, while pentapeptide refers to Ac-Ala-Ala-X-Ala-Ala-NH₂, where X is the titratable residue Asp, Glu or His.

^bpK_a’s of pentapeptides in 0.1 M salt solution determined by Thurlkill et al. using NMR.⁴⁴ These pK_a’s were used as the model pK_a’s in our simulations.

^cpK_a’s of blocked amino acids given by Nozaki and Tanford⁴⁶ using potentiometric titration. Ionic strength is unclear.

^dpK_a’s of tripeptides Ac-Ala-X-Ala-NH₂ in 0.1 M salt solution determined by Castañeda et al. using NMR.³⁹

^eHID refers to the titration HID ⇌ HIP. HIE refers to the titration HIP ⇌ HIE.

^epK_a’s of model compounds measured by Tanokura using NMR titration.⁴⁷

pH replica-exchange CpHMD titration of proteins.

One set of pH REX simulation was run for each protein. For proteins containing only acidic residues (HP36 and NTL9), the replicas were placed in the pH range 0–7.5 with 0.5-pH unit intervals. For other proteins, the replicas were placed in the pH range 0–9.5, with the same pH interval. Exchanges were attempted every 250 steps (0.5 ps), and each replica was run for 2 ns (unless otherwise stated).

pK_a calculations and error analysis

We first calculated the unprotonated fractions (S) using the following definition: λ < 0.2 for the protonated, and λ > 0.8 for the deprotonated state. The residue-specific pK_a’s were calculated by fitting S at the simulation pH conditions to the Hill equation,

$$S=\frac{1}{1+{10}^{n\left(\text{p}{K}_a-\text{pH}\right)}},$$ (9)

where n is the Hill coefficient. Note, the pK_a’s are insensitive to the cutoffs used to defined the protonation states. Tests using λ < 0.1 for the protonated and λ > 0.9 for the deprotonated state resulted in the same pK_a’s.

There are a number of ways to estimate the errors in the calculated pK_a’s. Here we present the one based on error propagation from the errors in the unprotonated fractions at different pH, δS_i.

$$\delta \text{p}{K}_a^2=\sum _i{\left(\delta S_i\frac{\partial \text{p}{K}_a}{\partial S_i}\right)}^2$$ (10)

where index i refers to a pH condition. The derivation for ∂pK_a/∂S_i is presented in SI. δS_i can be calculated using the block standard error formula

$$\delta S_i=\frac{{\sigma }_n}{\sqrt{N/n}},$$ (11)

where σ_n is the standard deviation of S_i, N is the total number of data points in the time series of λ, and n is the number of data points in each block. We chose the minimum block length to be the correlation time τ, which can be estimated using the autocorrelation function (ACF),

$$c(\Delta t)=\frac{\langle [\tilde{\lambda }(t)-S_i][\tilde{\lambda }(t+\Delta t)-S_i]\rangle }{{\sigma }^2}$$ (12)

where ⟨. . . ⟩ indicates an average over all Δt intervals considered, Δt is the lag time, $\tilde{\lambda }$ is the discretized version of λ for representing the protonation state (Eq. 1). The ACF tends toward zero, as Δt increases and $\tilde{\lambda }\left(t^{\prime }\right)$ looses memory. τ was estimated as the value of t for which the ACF first crosses zero. We note, this definition worked well for most residues, but not so for residues that have S values that are not converged (see later discussion).

RESULTS AND DISCUSSION

Titration of model compounds and alanine pentapeptides

To verify the accuracy of the model PMF parameters, titration simulations were performed on two sets of model systems, the blocked amino acids (model compounds), Ac-X-NH₂, and alanine pentapeptides, Ac-Ala-Ala-X-Ala-Ala-NH₂, in solution. If the model PMF parameters were accurate, the input model pK_a’s would be reproduced exactly. We also expect identical pK_a’s for the blocked amino acid and pentapeptide containing the same titratable group, as it is completely exposed to solvent. Table 1 lists the calculated pK_a’s of Asp, Glu, and His in the two model systems and the experimental values reported by Thurlkill et al. (pentapeptides⁴⁴), which were used as the input model values in the current work. Table 1 also gives the old reference set reported by Nozaki and Tanford,⁴⁶ which were used in the CpHMD implementations in CHARMM,^12,15,20 and the pK_a’s measured by Castañeda et al. for Asp and Glu in alanine tripeptides Ac-Ala-X-Ala-NH₂.³⁹ The calculated pK_a’s, based on five independent sets of pH-REX CpHMD titration simulations (1 ns per replica), show a standard deviation of about 0.05. The deviation between the pK_a’s in the model compound and pentapeptide is below 0.1 pH units. Thus, in addition to the convergence of the unprotonated fractions and individual pK_a’s (Fig. S1–S3), these data offer assurance that the sampling for the model systems is complete. The calculated pK_a’s are within 0.1 pH units from the intended model values (from Thurlkill et al.⁴⁴), indicating that the model PMF functions are accurate. We note that the deviations are smaller than the differences (up to 0.2–0.3 pH units) among the experimental values by Nozaki, Thurlkill, and Castañeda.

Overall convergence and CPU scaling for protein titration

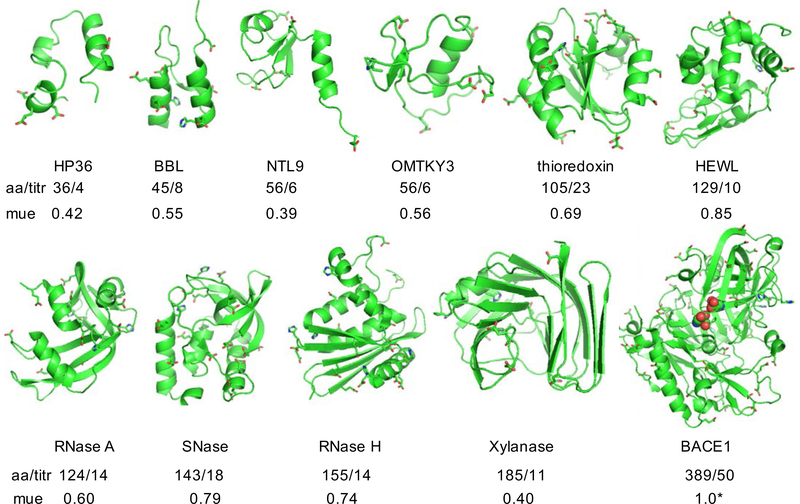
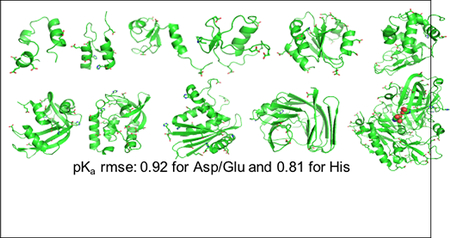
To benchmark the performance of the current implementation, we carried out titration simulations on 4 small proteins and 7 enzymes which show large pK_a’s shifts relative to the model values (Fig. 1), making them ideal test systems for evaluating the accuracy of pK_a calculations.⁴⁸ Except for BACE1, these proteins have been previously used to benchmark the GBSW-CpHMD method in CHARMM.^12,20 We titrated BACE1, which is a much larger enzyme and contains a hydrogen-bonded catalytic aspartic dyad, for which the pK_a’s are experimentally known but very challenging to predict.^2,49

Figure 1: Proteins used in the current benchmark set.

aa/titr refers to the number of amino acids/number of titratable groups. Titratable groups include Asp, Glu and His sidechains shown in the stick model. mue refers to the mean unsigned error with respect to the experimental pK_a’s. For BACE1, mue calculation includes only the pK_a’s of the catalytic dyad (highlighted in the van der Waals representation), as they were the only ones with experimental data.

We first examine the convergence behavior. Insufficient sampling and poor convergence of pK_a’s could lead to poor fitting (of fraction of deprotonation vs. pH) to the generalized Henderson-Hasselbalch (or Hill) equation.^5,20,32,50 No obviously bad fitting could be spotted in the titration plots (Fig. S4–S13). We then compared the pK_a’s from the 2-ns and 1-ns simulation times (Table 3). The differences are all within 0.1 pH units, except for five residues showing pK_a changes around 0.3 units (see later discussion). We also examined the time trace of the fraction of deprotonation S at all pH conditions. Except for the aforementioned five residues showing continued drift in the S values, all S curves converge within 1 ns (Fig. S14–S24). These data demonstrate that, for most residues, the pK_a’s converge with 1 ns sampling per replica, which is on par with the GBSW-based CpHMD in CHARMM (note, the early data were obtained using the temperature-based replica exchange).^12,20 We will come back to the pK_a’s that are not converged.

Table 3:

Calculated and experimental pK_a’s for 4 small proteins and 7 enzymes

Residue	Expt	Calc	Residue	Expt	Calc	Residue	Expt	Calc	Residue	Expt	Calc
BBL			HP36			OMTKY			HEWL
Asp129	3.9	2.8 (2.8)	Asp44	3.1	2.1 (2.1)	Asp8	2.7	2.5 (2.3)	Glu7	2.6	3.5 (3.5)
Glu141	4.5	4.1 (4.1)	Glu45	4.0	3.7 (3.7)	Glu11	4.1	3.9 (3.9)	His15	5.5	6.5 (6.6)
His142	6.5	6.9 (7.0)	Asp46	3.5	3.6 (3.5)	Glu20	3.2	3.7 (3.7)	Asp18	2.8	1.1 (1.1)
Asp145	3.7	2.6*(2.2)	Glu72	4.4	4.1 (4.2)	Asp28	2.3	3.6 (3.6)	Glu35	6.1	4.6 (4.7)
Glu161	3.7	3.3 (3.3)				Glu44	4.8	4.6 (4.6)	Asp48	1.4	1.8 (1.6)
Asp162	3.2	3.2 (3.2)	RNase A			His53	7.5	6.6 (6.7)	Asp52	3.6	3.3 (3.2)
Glu164	4.5	4.0 (4.1)	Glu2	2.8	3.2 (3.2)				Asp66	1.2	2.1 (2.2)
His166	5.4	6.0 (6.0)	Glu9	4.0	3.4 (3.3)	RNase H			Asp87	2.2	1.8*(1.4)
			His12	6.2	6.4*(6.8)	Glu6	4.5	4.3*(4.1)	Asp101	4.5	4.8 (4.9)
NTL9			Asp14	2.0	2.4 (2.3)	Asp10	6.1	3.4 (3.4)	Asp119	3.5	2.4 (2.2)
Asp8	3.0	2.1 (2.1)	Asp38	3.5	2.8 (2.9)	Glu32	3.6	3.2 (3.2)
Glu17	3.6	3.4 (3.5)	His48	6.0	7.2 (7.1)	Glu48	4.4	2.5 (2.5)	SNase
Asp23	3.1	2.9 (3.0)	Glu49	4.7	2.6 (2.4)	Glu57	3.2	4.1 (4.0)	His8	6.5	6.5 (6.5)
Glu38	4.0	3.6 (3.5)	Asp53	3.9	4.3 (4.2)	Glu61	3.9	2.8 (2.8)	Glu10	2.8	3.7 (3.7)
Glu48	4.2	3.8 (3.8)	Asp83	3.5	2.9 (2.9)	His62	7.0	6.9 (6.9)	Asp19	2.2	2.3 (2.0)
Glu54	4.2	3.8 (3.8)	Glu86	4.1	3.5 (3.4)	Glu64	4.4	3.1 (2.9)	Asp21	6.5	3.7 (4.0)
			His105	6.7	6.3 (6.3)	Asp70	2.6	4.1 (4.1)	Asp40	3.9	2.8 (2.8)
Thioredoxin			Glu111	3.5	3.5 (3.5)	His83	5.5	6.2 (6.0)	Glu43	4.3	3.7 (3.9)
Glu6	4.8	3.9 (4.0)	His119	6.1	6.1 (6.0)	Asp94	3.2	3.2 (3.1)	Glu52	3.9	3.9 (3.9)
Glu13	4.4	4.4 (4.4)	Asp121	3.1	3.5 (3.5)	Asp102	<2.0	3.4 (3.2)	Glu57	3.5	3.4 (3.4)
Asp16	4.0	4.0 (4.0)				Asp108	3.2	3.1 (3.0)	Glu67	3.8	4.5 (4.6)
Asp20	3.8	2.9 (2.9)	Xylanase			His114	<5.0	7.0 (6.9)	Glu63	3.3	3.9 (3.9)
Asp26	9.9	6.2 (6.3)	Asp5	3.0	3.3 (3.1)	Glu119	4.1	3.9 (3.8)	Glu75	3.3	2.6 (2.5)
His43	n/d	6.1 (6.1)	Asp12	2.5	2.5 (2.4)	His124	7.1	6.2 (6.2)	Asp77	<2.2	1.9 (1.6)
Glu47	4.1	4.3 (4.5)	Glu79	4.6	5.1*(5.4)	His127	7.9	6.6 (6.8)	Asp83	<2.2	2.1*(1.8)
Glu56	3.3	4.5 (4.6)	Asp84	<2.0	3.4 (3.3)	Glu129	3.6	4.6 (4.6)	Asp95	2.2	4.3 (4.3)
Asp58	5.3	3.8 (3.6)	Asp102	<2.0	3.3 (3.4)	Glu131	4.3	4.3 (4.4)	Glu101	3.8	3.5 (3.8)
Asp60	2.8	3.6 (3.6)	Asp107	2.7	3.1 (3.2)	Asp134	4.1	4.3 (4.2)	His121	5.2	6.8 (6.9)
Asp61	4.2	4.6 (4.5)	Asp120	3.2	4.0 (4.0)	Glu135	4.3	4.2 (4.3)	Glu122	3.9	3.0 (2.9)
Asp64	3.2	3.1 (3.3)	Asp122	3.6	3.4 (3.6)	Glu147	4.2	3.9 (3.8)	Glu129	3.8	4.5 (4.5)
Glu68	4.9	4.3 (4.3)	His150	<2.3	4.8 (4.8)	Asp148	<2.0	2.4 (2.1)	Glu135	3.8	4.2 (4.1)
Glu70	4.6	5.0 (5.0)	His157	6.5	7.3 (7.3)	Glu154	4.4	3.8 (3.8)
Glu88	3.7	3.8 (3.8)	Glu173	6.7	7.0 (6.8)
Glu95	4.1	3.5 (3.5)				BACE1			max	3.7
Glu98	3.9	3.9 (3.8)				Asp32	5.2	3.9 (3.9)	mue	0.65
Glu103	4.4	4.7 (4.6)				Asp228	3.5	2.7 (2.8)	rmse	0.90

In parentheses are the pK_a’s calculated from the first half of the simulations (1 ns per replica). pK_a’s with large uncertainties are indicated by an asterisk. Experimental data were obtained from the NMR titration of HP36,⁵² BBL,^53,54 NTL9,⁵⁵ OMTKY,^56,57 thioredoxin,⁵⁸ HEWL,⁵⁹ SNase^39,60 RNase A,⁶¹ RNase H,^62,63 xylanase,^64,65 and BACE1.⁶⁶ The maximum unsigned error (max), mean unsigned error (mue), and root-mean-square error (rmse) are listed. BACE1 pK_a’s are excluded to facilitate comparison with CHARMM (see Fig. 3 and Table 2).

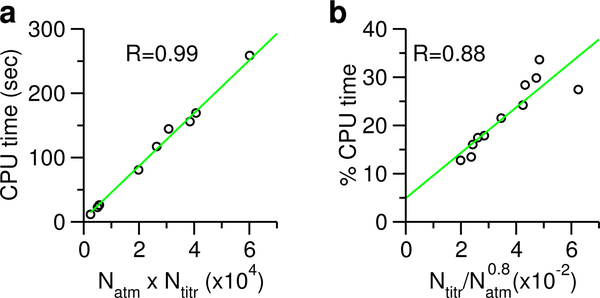
For CpHMD to become a practical tool, it must scale well with number of processors and not have high computational overhead. Since the major CPU time for CpHMD titration is spent on evaluating the forces on λ particles, which involves calculations of the interactions between the real atoms and λ particles, it should increase with the number of atoms multiplied by the number of titratable sites, N_atm × N_titr. This is indeed the case for the 11 proteins that were titrated here, which span a range of 35–389 residues with 4–50 titration sites (Fig. 2a). Thus, CpHMD titration scales linearly with the system size, with a prefactor which is the number of titration sites.

Figure 2: Timing statistics of the current GBNeck2-CpHMD implementation.

a) CPU time for CpHMD titration scales linearly as the product of number of atoms (N_atm) and number of titratable sites (N_titr). The regression line is shown in green. For clarity, the data point for BACE1 is hidden. b) Percentage CPU time for the CpHMD titration relative to the GB calculation scales approximately linearly as the ratio between N_titr and $N_{\text{atm}}^{0.8}$. Timing was based on the 5-ps single pH CpHMD runs using 2 cores on a workstation.

Now we come to the added CPU cost due to CpHMD titration. Given the above scaling behavior and the fact that the current GB calculation scales approximately as $N_{\text{atm}}^{1.8}$ (slightly better than the expected quadratic scaling), we reasoned that the percentage CPU time used by CpHMD titration relative to the GB calculations should increase linearly as the ratio between N_titr and $N_{\text{atm}}^{0.8}$. Regression of the actual CPU usage data returned a correlation coefficient of 0.88, thus confirming this conjecture (Fig. 2b). Thus, the percentage CPU usage for CpHMD titration scales approximately linearly as the fraction of titratable atoms. For the current data set, the CPU cost is 11– 33% of the GB calculations.

Overall accuracy of the protein pK_a calculations

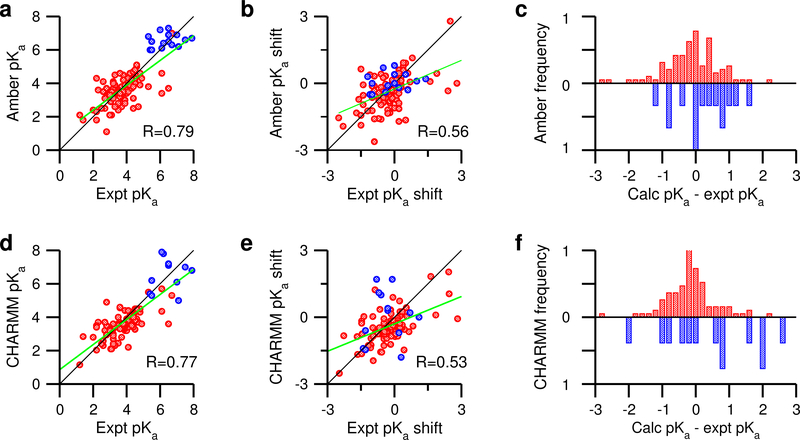
To assess the accuracy of the pK_a calculations, we compare the calculated and experimental pK_a’s as well as their pK_a shifts with respect to Thurlkill’s model values. The pK_a comparison returns a mean unsigned error (mue) of 0.70, a root-mean-square error (rmse) of 0.91, and a linear correlation coefficient R of 0.78 (Fig. 3a). Comparing the calculated and experimental pK_a shifts yields an R of 0.56 (Fig. 3b). The worse correlation for the latter confirms that predicting pK_a shifts is a more stringent test of pK_a prediction techniques, as pointed out by Warshel and coworkers two decades ago.⁴⁸

Figure 3: Comparison of the pK_a calculations using the current GBNeck2-CpHMD in Amber and GBSW-CpHMD in CHARMM.

Left panel. Correlation between the experimental and calculated pK_a’s from the Amber (a) and previously published CHARMM (d) CpHMD simulations. Middle panel. Correlation between the experimental and calculated pK_a shifts from the Amber (b) and CHARMM (e) CpHMD simulations. Model pK_a’s obtained by Thulkill et al. were used for the Amber CpHMD and those reported by Nozaki and Tanford were used for the CHARMM CpHMD simulations (Table 1). Data for Asp/Glu are shown in red while those for His are shown in blue. For clarity, the data points for Asp99 in thioredoxin are hidden in a, b, d, and e. The linear correlation coefficients R for the entire data set are given. The best fit lines are shown in green. The black lines indicate y = x. Right panel. (c) and (f): Histograms for the deviations between the calculated and experimental pK_a’s for Asp/Glu (red) and His (blue). Bin size is 0.2 pH units. The histograms for His are inverted for better viewing. The CHARMM data were generated using the c22 force field⁵¹ and 1 ns per replica. For the CHARMM data, pH replica-exchange was used for HP36, BBL, NLT9, HEWL and SNase,¹² and temperature replica-exchange was used for OMTKY, RNase A, RNase H, xylanase and thioredoxin.²⁰

Examining the calculation errors for carboxylic groups and histidines separately is instructive. For the carboxylic groups, the mue, rmse, and R are 0.65, 0.92, and 0.62 respectively, while for His, they are 0.67, 0.81, and 0.16, respectively (Table 2). Although the rmse for histidines is only slightly lower than that for the carboxylic groups, the correlation is much worse, which may be related to the smaller range of the pK_a values (about 3 for His vs. over 7 for carboxylic groups). We plotted the histograms of the pK_a errors (Fig. 3c). For carboxylic groups, the highest peak is at zero, and the histogram is slightly skewed to the right, indicating a slight systematic overestimation of Asp/Glu pK_a’s. For histidines, the peak is at zero; the error has a slightly broader range but no obvious skewness; however, no reliable conclusion can be drawn here due to the very limited data set.

Table 2:

Comparison of the pK_a calculations for carboxylic groups and histidines with GBNeck2-CpHMD in Amber and GBSW-CpHMD in CHARMM^a

		Amber			CHARMM
residue	N	mue	rmse	R	mue	rmse	R
Asp/Glu	98	0.65	0.92	0.62	0.59	0.86	0.68
His	15	0.67	0.81	0.16	1.1	1.3	0.00

^aListed are the total number of residues (N), the mean unsigned error (mue), root-mean- square error (rmse), and linear correlation coefficient (R) from comparing the calculated and experimental pK_a’s.

The overall rmse and correlation with respect to the experimental pK_a’s and pK_a shifts of the current implementation are similar to that of the GBSW-based CpHMD in CHARMM (Fig. 3b and e). For carboxylic groups, GBSW-CpHMD gives a slightly better correlation (R of 0.68 vs. 0.62) and slightly smaller error (rmse of 0.86 vs. 0.92, see Table 2). The histograms of the pK_a errors for carboxylic groups are clearly left skewed (Fig. 3c and f). For histidines, GBSW-CpHMD gives much larger errors (rmse of 1.3 vs. 0.81, Table 2), and there is no correlation between calculation and experiment (R of 0.0 vs. 0.16, Table 2), although the latter conclusion may not be reliable due to the small number of histidine pK_a’s.

A useful application of a pK_a calculation tool is to predict the acid and nucleophile components in catalytic dyads.⁴⁹ For this purpose, the pK_a order is the quantity of interest. The current GBNeck2-CpHMD correctly predicted the pK_a order for Glu35/Asp52 in HEWL, Asp19/Asp21 in SNase, and Asp32/Asp228 in BACE1, although the pK_a splitting is consistently smaller than experiment. In contrast, the GBSW-CpHMD in CHARMM cannot distinguish the pK_a’s of coupled dyads.¹² The latter was attributed to the distortion of the conformational environment of the buried dyad residues.¹² Our previous work showed that the hybrid-solvent CpHMD in CHARMM, which uses explicit solvent for conformational sampling, can accurately predict the pK_a splitting of the dyad residues because it more faithfully captures the protein conformational dynamics.¹² Specifically, these simulations demonstrated that the nucleophile forms more hydrogen bonds than the proton donor (acid), while having similar or slightly higher solvent exposure.⁴⁹ Remarkably, these local conformational features are reproduced in the GBNeck2-CpHMD simulations (Fig. S26), allowing better predictions than the GBSW-CpHMD in CHARMM.

Correlating the pK_a errors with the degree of solvent exposure

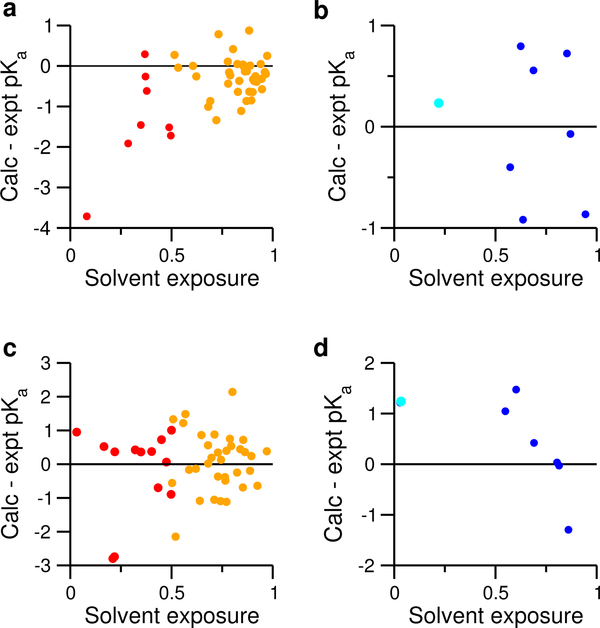
The pK_a’s of buried residues are the most challenging to predict.²⁴ Previous work showed that pK_a shifts due to desolvation penalty are insufficiently reproduced in the GBSW-based CpHMD.^11,20,23 As a result, the pK_a’s of buried carboxylic groups and histidines are systematically under- and overestimated, respectively.²³ To determine whether desolvation is also underestimated in GBNeck2 and if so, whether it is a major source of pK_a errors in GBNeck2-CpHMD titration, we plotted the pK_a errors against fSASA, the ratio between the solvent accessible surface area of the titratable site in the protein and in solution. To isolate the error in estimating the desolvation penalty, we excluded the residues that have the carboxylic oxygen or histidine nitrogen within a 5 Å distance from the carboxylic oxygen in Asp/Glu or nitrogen in His/Lys/Arg in the crystal structure; the pK_a’s of these residues may be subject to another source of error, namely, inaccurate representation of strong electrostatic interactions.^12,23

Fig. 4a shows that the pK_a errors of carboxylic groups not involved in strong electrostatic interactions are mostly negative. As fSASA decreases, there is a tendency for the error to become larger in magnitude (linear correlation coefficient of 0.54). The two largest errors (−3.7 for Asp26 of thioredoxin and −1.9 for Glu48 of RNase H) are associated with fSASA of 8% and 28%, respectively. These data suggest that the desolvation penalties of buried, and particularly deeply buried carboxylic groups are underestimated in the GBNeck2 model, consistent with the fact that the effective Born radii for these buried sites are too small as compared to the Poisson-Boltzmann radii.²⁷ Performing the same analysis for histidines, we found no clear correlation between fSASA and pK_a error, although the data set may be too small to draw a reliable conclusion (Fig. 4b).

Figure 4: Correlating the pK_a errors with the degree of solvent exposure.

Upper panel. pK_a errors vs. fSASA for carboxylic groups (a) and histidines (b) not involved in strong electrostatic interactions. fSASA refers to the ratio between the solvent accessible surface area (SASA) of the sidechain in protein and in the model. The average fSASA over all pH conditions are used. To guide the eye, a green regression line is drawn for the data in a). The correlation coefficient R is given. For Asp/Glu, SASA includes the carboxylic group (COO) and dummy hydrogens. For His, SASA includes all imidazole ring atoms. Lower panel. pK_a errors vs. fSASA for carboxylic groups (c) and histidines (d) involved in strong electrostatic interactions. In all plots, data for carboxylic groups are colored red, and those for histidines are colored blue.

Residues involved in strong attractive electrostatic interactions

Overstabilization of salt-bridge interactions, a known limitation of the GB models,⁶⁷ was a major source of error for GBSW-CpHMD in CHARMM.^11,12,20 Thus, we examined the pK_a errors of residues involved in strong electrostatic interactions, which, for simplicity, were defined as those with a distance below 5 Å between a carboxylic oxygen and nitrogen in His/Lys/Arg in the crystal structure. We divide the residues into two groups based on their fSASA values. For those with fSASA≥50%, the pK_a errors are more or less symmetrically distributed around zero (Fig. 4c), suggesting no systematic error. Since the desolvation effect is small for these groups, it indicates that solvent-exposed salt bridges involving carboxylic groups are not overly strong, which is not surprising, as in GBNeck2, the intrinsic Born radii for Asp/Glu and Lys/Arg were optimized to closely match the explicit-solvent salt-bridge profiles.²⁸

We next examine the carboxylic groups with fSASA less than 50%, for which the pK_a’s are subject to both desolvation and salt-bridge-like interactions. Both factors, desolvation, which shifts the pK_a up, and salt-bridge-like interactions, which shift the pK_a down, may be underestimated, leading to error compensation, although the extent of the compensation is unclear. We note the latter, underestimation of salt-bridge interactions (“too wet”), which was observed in the GBSW-based CpHMD simulations,^12,49 may be reduced here, as the Neck model approximately accounts for the interstitial water.²⁷ Indeed, Fig. 4c shows that most of the pK_a errors are small, except for Asp21 of SNase and Asp10 of RNase H, for which the pK_a’s are underestimated by about 2.7 units (Table 3). Both residues are deeply buried (about 20% solvent exposure) and hydrogen bonded to another Asp in the enzyme active site.^39,62 Considering our previous discussion regarding desolvation errors (Fig. 4a), we suggest that the underestimation of desolvation is much larger than the underestimation of attractive electrostatic interactions, leading to the negative pK_a errors.

We turn to the histidines involved in strong electrostatic interactions. Due to the small number of data points, a general trend is hard to deduce. Therefore, we focus our attention on two extreme cases: the fully exposed His127 of RNase H, which has a calculated pK_a of 6.6 (1.3 units lower than experiment), and the fully buried His48 of RNase A, which has a calculated pK_a of 7.2 (1.1 units higher than experiment). In RNase H, the crystal structure shows a salt bridge between His127 and Glu119, which justifies the large experimental pK_a shift of His127 (1.4 units). However, the salt bridge contradicts the small experimental pK_a shift of Glu119 (−0.2 units). In the simulation, the salt bridge is formed for a small fraction of time (11 % at pH 5, see SI), consistent with the small pK_a shifts for both His127 (0.1 units) and Glu119 (−0.4 units). Interestingly, the current results are consistent with the previous GBSW-CpHMD simulation.²⁰ Thus, we could not find an explanation for the discrepancy between the calculated and experimental pK_a of His127 in RNase H. We will defer further discussion to future studies using titration in explicit solvent.

His48 of RNase A is nearly completely buried (3% solvent exposure) and forms a salt bridge with Asp14. Thus, we believe the positive pK_a error of 1.1 can be understood similarly as for Asp21 of SNase and Asp10 of RNase H. That is, the underestimation of desolvation (which shifts the histidine pK_a down) overwhelms the underestimation of buried salt-bridge interaction (which shifts the histidine pK_a up), leading to a positive pK_a error for His48.

Analysis of sampling errors and convergence

To quantify sampling noise, we performed error analysis for the calculated pK_a’s based on error propagation from the block standard error of the fraction of deprotonation (S) at different pH (see Methods). Most of the pK_a’s have “sampling” errors below 0.1; however, six of them have errors in the range 0.2–0.3, as indicated by asterisks in Table 3 (actual data not shown). Not surprisingly, the large errors correspond to the aforementioned titratable groups with significant drift in the time trace of S values and 0.3–0.4 units changes in the pK_a’s based on the first and second ns of the simulations. Thus, while the sampling noise is small for converged pK_a’s, large errors are flags for incomplete protonation state sampling.

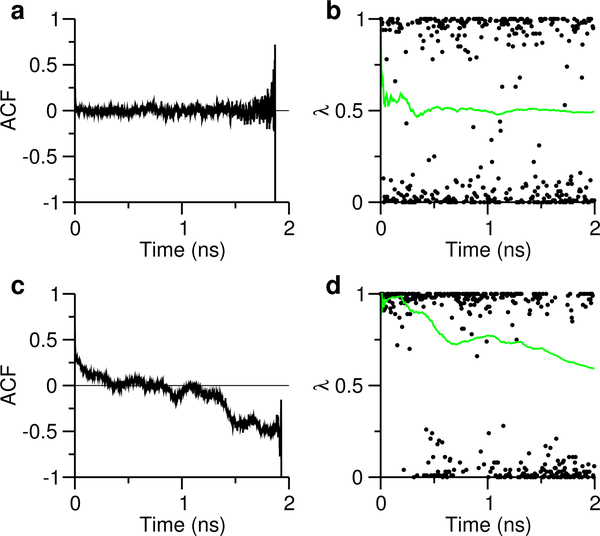
We examine the correlation time to better understand the convergence behavior. Fig. 5a shows that for Glu7, the autocorrelation function (ACF) of $\tilde{\lambda }$ (Eq. 1) decays to zero after about 15 ps and oscillates around zero for the remainder of the simulation. This behavior is typical for pK_a’s with small sampling errors, and can be attributed to fast convergence of the S value (Fig. 5b). In contrast, for Asp87 of HEWL, the ACF does not reach zero until about 350 ps and keeps decreasing for the remainder of the simulation (Fig. 5c). This behavior is typical for pK_a’s with large sampling errors, and can be attributed to the incomplete convergence of the S value, which shows a decreasing trend toward the end of the simulation (Fig. 5d), indicating that the pK_a would be higher and closer to the experimental value (Table 3) if the simulation was to continue. A closer look at the trajectory showed that the Asp87 forms a persistent salt-bridge-like interaction with His15 in the first half of the simulation, while in the second half of the simulation, the interaction is largely disrupted (data not shown). Persistent attractive interaction leads to prolonged correlation time, and is also the underlying reason for the large sampling errors in the pK_a’s of Asp145 in BBL and Glu6 in RNaseH. The other two pK_a’s with large sampling errors are from buried residues, His12 in RNase A and Glu79 in Xylanase. Consistently, the time trace of S shows a trend that decreases the deviation from the experimental pK_a. The above analysis shows that the large “sampling” errors are due to insufficient convergence of the protonation-state sampling. Indeed, extending the simulations to 4 ns per replica improved the convergence of the unprotonated fractions S (Fig. S25) and reduced the errors for all pK_a’s (Table 4), although Asp87 of HEWL and Glu79 of HEWL require even more sampling, as the errors are around 0.2, and the unprotonated fractions have not fully plateaued (Fig. S25). Encouragingly, however, with the prolonged sampling the changes of the pK_a’s are mostly in the direction of the experimental values (Table 4).

Figure 5: Analysis of correlation time and protonation state sampling.

(a) and (c): Autocorrelation functions of $\tilde{\lambda }$ (defined in Eq. 1) for Glu7 and Asp87 in HEWL, respectively. (b) and (d): λ (black) and S (green) values as functions of simulation time. The pH 3.5 replica for Glu7 and pH 2 replica for Asp87 were used.

Table 4:

Prolonged simulations improve slowly converging pK_a’s.

Protein	Residue	Expt	2 ns	4 ns
BBL	Asp145	3.7	2.6 (0.3)	2.8 (0.1)
HEWL	Asp87	2.2	1.8 (0.2)	1.9 (0.2)
RNase A	His12	6.2	6.4 (0.3)	6.4 (0.1)
SNase	Asp83	<2.2	2.1 (0.3)	1.8 (0.1)
RNase H	Glu6	4.5	4.3 (0.2)	4.3 (0.1)
Xylanase	Glu79	4.6	5.1 (0.3)	4.4 (0.2)

In parentheses are the sampling errors calculated using error propagation (Eq. 10).

Dependence on the force field and solvent model

To test the dependence on the force field, we performed an additional titration simulation for HEWL using GBNeck2 and the CHARMM c22 force field in Amber (Table 5). Since GBNeck2 is optimized for the Amber and not CHARMM force field, we avoid comparing to experimental values and instead focus on the pK_a differences. The largest pK_a differences are for the catalytic residues Glu35 and Asp52. With the ff14sb force field, the experimental pK_a order is reproduced; however, with the c22 force field, the two pK_a’s are nearly identical and higher than the ff14sb results by 1.6 and 3 units, respectively. Considering the desolvation penalty may be similar given the same Neck2 model, we suggest the large difference may come from the vacuum hydrogen bond strength in the two force fields.

Table 5:

Calculated pK_a’s of HEWL using different force fields and solvent models

Residue	Expta	Neck2-ff14sb	Neck2-c22c	SW-c22d
Glu7	2.6	3.5	3.5	2.6
His15	5.5	6.5	7.6	5.3
Asp18	2.8	1.1	3.2	2.9
Glu35	6.1	4.6	6.2	4.4
Asp48	1.4	1.8	1.3	2.8
Asp52	3.6	3.3	6.3	4.6
Asp66	1.2	2.1	2.3	1.2
Asp87	2.2	1.8	2.2	2.0
Asp101	4.5	4.8	3.9	3.3
Asp119	3.5	2.4	2.6	2.5

^aExperimental data taken from Webb et al.⁵⁹

^bNeck2-ff14sb denotes the GBNeck2-CpHMD simulation with the Amber ff14sb force field.

^cNeck2-c22 denotes the GBNeck2-CpHMD simulation with the CHARMM c22 force field⁵¹ in Amber.

^dSW-c22 denotes the previously published GBSW-CpHMD simulation with the GBSW model and CHARMM c22 force field.⁶⁸

Next, we considered results with the c22 force field and the published GBSW-CpHMD data. The largest pK_a differences are again Glu35 and Asp52 in addition to His15. The two pK_a’s are nearly identical but lower than the Neck2-c22 results by 1.8 and 1.7 units, respectively. The lowered pK_a values demonstrates that the desolvation induced pK_a upshift is much smaller with the GBSW model, consistent with the previous observation that the GBSW model significantly underestimates the pK_a’s of buried carboxylic groups.^11,20,23

CONCLUDING REMARKS

We presented the implementation of the generalized Born (GB) implicit-solvent based continuous constant pH MD (CpHMD) method in Amber. The implementation was tested using pH replica-exchange titration of 2 ns per replica on 11 proteins, ranging from the 36-residue mini-protein HP36 to the 389-residue BACE1 enzyme. The simulations utilized the most recent GBNeck2 model²⁸ and ff14sb force field.²⁹ The CPU cost relative to the fixed-protonation-state GB calculations scales linearly as the ratio of titratable and total number of residues. For the present test set, where all carboxylic groups and histidines were allowed to titrate, the added computational cost was 11–33 %. Comparison of the calculated and experimental pK_a’s of 96 carboxylic groups and 15 histidines gave a mean unsigned error of 0.65, a root-mean-squared error of 0.90, and a linear correlation coefficient of 0.78. Comparison of the calculated and experimental pK_a’s shifts relative to the model values gave a linear correlation coefficient of 0.56. This level of accuracy is similar to the GBSW-based¹⁹ CpHMD implementation^11,20 with the c22 force field⁵¹ in CHARMM.⁴³ We found that the accuracy is slightly worse for carboxylic groups (a total of 97) but much better for histidines compared to the GBSW-CpHMD in CHARMM, although the number of histidines (15) is rather small. However, surprisingly, the current implementation correctly predicted the experimental orders of the pK_a’s of the buried carboxylic dyads in hen egg white lysozyme, staphylococcal nuclease, and β-secretase 1, while GBSW-CpHMD could not distinguish them. Our analysis showed that the GBNeck2 simulations preserved the local hydrogen bonding environment and solvent exposure of the titratable sidechain, which are the molecular determinants for the pK_a order. A systematic error in the GBNeck2-CpHMD titration is the underestimation of pK_a shifts for deeply buried carboxylic groups, which can be largely attributed to the underestimation of the desolvation penalties, as was observed for the GBSW model. As to the pK_a calculations for histidines, no definitive conclusions could be drawn due to the small range of pK_a values and too few data points. We note that buried residues can become kinetically trapped in a conformational substate more readily than solvent-exposed residues. Thus, lack of conformational sampling is likely another contributor to the pK_a errors. In principle, one can probe the extent of such errors by extensive conformational sampling to uncover all substates, as demonstrated in the CHARMM hybridsolvent CpHMD titration of a deeply buried lysine, for which both closed (crystal structure) and open states needed to be sampled to reproduce the experimental macroscopic pK_a.⁶⁹ This type of study was not pursued here, because prolonged conformational sampling in GB solvent likely leads to larger deviations from the native state and consequently larger pK_a errors.⁶

We also conducted analysis of random sampling errors in the calculated pK_a’s. With the simulation time of 2 ns per replica, the errors are below 0.1 pH units for all but 6 pK_a’s which were not converged due to incomplete sampling of salt-bridge-like interactions and/or hydrophobic burial. Prolonging the simulations to 4 ns per replica demonstrated significant improvement in convergence and agreement with experimental data. Finally, we tested the dependence on the force field and solvent model using HEWL. The pK_a’s of the catalytic dyad are most sensitive, which could be attributed to the differences in the hydrogen bond strength between the ff14sb and c22 force fields and the more severe underestimation of desolvation penalty by the GBSW model.

The current work points toward several directions of future improvement. The GB models in the Amber package are under active development,⁷⁰ and improved GB models could be easily incorporated in CpHMD to potentially improve accuracy. The present method uses GB solvent for the propagation of both conformational and protonation degrees of freedom; however, the hybrid-solvent and all-atom CpHMD in CHARMM have demonstrated significantly improved accuracy relative to the GB-based version. Currently, extensions to use a hybrid-solvent scheme¹² or fully explicit solvent¹² are underway. To accelerate the computational speed, a GPU implementation will be pursued in the near future.