Automated segmentation of changes in FLAIR-hyperintense white matter lesions in multiple sclerosis on serial magnetic resonance imaging

Abstract

Longitudinal analysis of white matter lesion changes on serial MRI has become an important parameter to study diseases with white-matter lesions. Here, we build on earlier work on cross-sectional lesion segmentation; we present a fully automatic pipeline for serial analysis of FLAIR-hyperintense white matter lesions. Our algorithm requires three-dimensional gradient echo T1- and FLAIR- weighted images at 3 Tesla as well as available cross-sectional lesion segmentations of both time points. Preprocessing steps include lesion filling and intrasubject registration. For segmentation of lesion changes, initial lesion maps of different time points are fused; herein changes in intensity are analyzed at the voxel level. Significance of lesion change is estimated by comparison with the difference distribution of FLAIR intensities within normal appearing white matter. The method is validated on MRI data of two time points from 40 subjects with multiple sclerosis derived from two different scanners (20 subjects per scanner). Manual segmentation of lesion increases served as gold standard. Across all lesion increases, voxel-wise Dice coefficient (0.7) as well as lesion-wise detection rate (0.8) and false-discovery rate (0.2) indicate good overall performance. Analysis of scans from a repositioning experiment in a single patient with multiple sclerosis did not yield a single false positive lesion. We also introduce the lesion change plot as a descriptive tool for the lesion change of individual patients with regard to both number and volume. An open source implementation of the algorithm is available at http://www.statistical-modeling.de/lst.html.

Highlights

• •Quantification of white matter lesion changes is important in multiple sclerosis.
• •We developed and validated an algorithm for automated detection of lesion changes.
• •Our algorithm requires T1-weighted and FLAIR images derived at 3 T as well as available cross-sectional lesion segmentations.
• •With data from 2 different scanners, the tool showed good agreement with manual tracing.
• •An open-source application is available.

1. Introduction

Longitudinal analysis of white matter (WM) lesion changes on serial magnetic resonance imaging (MRI) has become an important parameter to study diseases with WM lesions (WMLs) such as multiple sclerosis (MS). The pathological hallmark of MS is WMLs in brain and spinal cord. WMLs appear T2-hyperintense on MRI. WML load has become the most important paraclinical tool to monitor disease activity and response to immunomodulatory treatment (Sormani and Bruzzi, 2013; Wattjes et al., 2015). This is of clinical relevance, as the disease course of MS is very heterogeneous – from benign to disastrous, while various immunomodulatory drugs with different modes of action are available, and while early treatment is most effective (Kappos et al., 2015; Sormani et al., 2014). Therefore, serial brain MRI is indispensable for clinical routine, clinical trials, and research (Sormani and Bruzzi, 2013; Wattjes et al., 2015). WML load is commonly described by either number or total volume. Although both measures relate to each other, they can diverge considerably; for example, the same lesion volume can result from few large lesions or many small lesions. However, we are not aware of a commonly accepted descriptive tool for individual lesion development accounting for number, volume and their interrelation. More importantly, quantification of WML load is challenging. Manual WML segmentation is time-consuming and bears the risk of a considerable inter- and intra- rater bias. Several algorithms have been suggested for automated cross-sectional segmentation of WMLs (Danelakis et al., 2018; Garcia-Lorenzo et al., 2013; Valverde et al., 2015). Longitudinal WML segmentation is even more challenging and particularly prone to misinterpretations. Varying WML contrast and different positioning of the patient in serial scans may hamper detection of WML changes, particularly when they are more subtle. Accordingly, agreement among experienced observers was poor for counting enlarging lesions (Rovaris et al., 1999). Nevertheless tools for automatic segmentation of WML changes over time have been regarded desirable (Vrenken et al., 2013). We believe that such a pipeline should ideally cover both absolute WML load (i.e. WML load per time point) and changes of WMLs over time in a single frame work with the possibility to analyze more than two time points and to saliently illustrate individual lesion change. Besides reliable performance, it should be freely available, easy to use and easy to implement. To the best of our knowledge, the majority of the suggested tools focus on the analysis of difference images derived from coregistered T2- or FLAIR-weighted images; most of these tools use subtraction images (Battaglini et al., 2014; Eichinger et al., 2017; Elliott et al., 2010; Ganiler et al., 2014; Sweeney et al., 2013), whilst others use deformation fields with (Salem et al., 2018) or without (Cabezas et al., 2016) the necessity to apply a training dataset beforehand. Finally, an algorithm (https://icometrix.com/ products/icobrain-ms) was compared to a ß-version of the algorithm proposed here (Jain et al., 2016). This study built on earlier work on cross-sectional WML segmentation (Jain et al., 2015). Table 1 summarizes studies on the segmentation of WML changes.

Table 1.

Studies on segmentation of white matter lesion changes.

Study	n	MRI parameters, voxel size (mm)	Description/comments	Lesion-wise performance parameters (range)a
				TPR	FDR/FPR
(Elliott et al., 2010)	23	1.5 T; T1w, PD/T2w: 1 × 1 × 3	Bayesian classification framework on subtraction images (T2w), training dataset (n = 66); specificity not quantitatively evaluated	0.84 (n.i.)	n.d.
(Sweeney et al., 2013)	5	1.5 T; 2D FLAIR, PD, T2w, 3D T1w: 1 × 1 × 1 (extrapolated)	Logistic regression model using multiple sequences and subtraction images, ROC curve analysis	0.95 (voxel-wise)	0.01 (voxel-wise)
(Battaglini et al., 2014)	19	PD, T2w, T1w, FLAIR: 3 × 1 × 1	Based on subtraction images (PD); multicenter trial (Miller et al., 2012)	0.91 (n.i.)	0.21 (n.i.)
(Ganiler et al., 2014)	20	1.5 T; PD, T2w, T1w: 3 × 1 × 1	Based on subtraction images (PD)	0.77 (n.i.)	0.18 (n.i.)
(Cabezas et al., 2016)	36	3 T; PD/T2w: 0.8 × 0.8 × 3; FLAIR: 0.5 × 0.5 × 3 T1w: 1 × 1 × 1.2	Multichannel pipeline based on deformation fields	0.81 (n.i.)	0.18 (n.i.)
(Jain et al., 2016)	12	3 T; T1w, FLAIR: 1 × 1 × 1	Expectation-maximization framework	0.62 (0.53–0.69)	0.16 (0.00–0.51)
(Eichinger et al., 2017)	106	3 T; FLAIR: 1 × 1 × 1.5; T1w: 1 × 1× 1	Based on subtraction images (FLAIR); relating to a consensus reference, main focus on DIR subtraction images	0.79 (n.i.)	0.05(n.i.)
				(patient-wise)	(patient-wise)
(Salem et al., 2018)	60	3 T; PD/T2w: 0.8 × 0.8 × 3; FLAIR: 0.5 × 0.5 × 3; T1w: 1× 1× 1.2	Multichannel pipeline, use of intensities, subtraction images, and deformation fields; 36 MS patients, 24 controls	0.74 (+/− 0.29)	0.12 (±0.18)

^aPerformance parameters (with ranges as given in the original publications) refer to lesions unless indicated by italic letters; FLAIR, fluid attenuated inversion recovery; FDR/FPR, false discovery/positive rate; MS, multiple sclerosis; MRI, magnetic resonance imaging; n.d., not determined; n.i., not indicated; PD, proton density; ROC, response operator characteristics; T, Tesla; TPR, true positive rate, i.e. detection rate or sensitivity; w, weighted.

In this work, we aimed at the introduction and validation of an automated algorithm for segmentation of WML changes by extending earlier work on cross-sectional WML segmentation (Schmidt et al., 2012) as implemented in the lesion segmentation tool LST, which is freely available (www.statistical-modelling.de/ lst.html). Although our approach enables analysis of multiple time points in principle, we here focus on segmentation of WML changes between two time points assuming available cross-sectional WML segmentation of both time points.

2. Methods

2.1. Subjects

This study was performed in accordance with the Code of Ethics of the World Medical Association (Declaration of Helsinki) for experiments involving humans and was approved by the local ethics committee of all participating centers. Patients were recruited from the national cohort study of the German Competence Network Multiple Sclerosis (http://www.kompetenznetz-multiplesklerose.de/en). For internal validation, we selected serial data sets of 5 patients from each of three sites: Ruhr University of Bochum, Johannes Gutenberg University Mainz, and Technical University of Munich (TUM). All these patients had an increase in WML load according to the reports of the evaluating radiologists. For external validation, we analyzed serial data sets of another 40 patients from two centers (20 per center), namely the Max Planck Institute of Psychiatry (MPIP) Munich and TUM. These patients represented a broader spectrum of WML evolution with 5 stable patients per site and the remaining patients with activity ranging from mild to severe. Baseline demographic data of patients are summarized in Table 2.

Table 2.

Baseline and follow-up demographic data.

	Male/female	Age (yrs) mean (SD)		Disease duration (mths), mean (SD)		Disease type CIS/RRMS		WML count mean (SD)		WML volume (ml) mean (SD)		EDSS	Median (range)
		t	t + 1	t	t + 1	t	t + 1	t	t + 1	t	t + 1	t	t + 1
Internal validation
Bochum	0/5	38.8 (13.3)	41.2 (13.2)	10.5 (3.4)	38.56 (7.7)	3/2	0/5	22 (13)	21 (13)	2.2 (1.7)	1.9 (1.7)	1.5 (1.0–1.5)	2.0 (1.0–2.5)
Mainz	1/4	29.8 (8.9)	31.0 (9.3)	7.8 (5.9)	21.9 (6.7)	2/3	2/3	8 (12)	15 (12)	0.5 (0.6)	1.6 (1.6)	2.0 (0–3.0)	1.0 (0–2.0)
Munich TUM	2/3	31.6 (5.3)	32.8 (6.0)	13.8 (19.1)	29.5 (15.4)	2/3	1/4	24 (14)	26 (16)	4.4 (2.9)	4.8 (2.8)	2.0 (1.5–3.0)	1.0 (0–2.0)
Total	5/15	31.5 (9.3)	33.2 (9.5)	10.1 (10.0)	30.7 (10.9)	8/12	3/17	16 (13)	18 (13)	2.1 (2.2)	2.4 (2.3)	1.5 (0–3.0)	1.0 (0–2.5)
External validation
Munich MPIP	8/12	32.1 (9.2)	34.2 (9.1)	8.9 (7.7)	33.5 (14.0)	7/13	3/17	30 (20)	28 (18)	4.2 (3.2)	3.3 (2.1)	1 (0–3)	1 (0–3)
Munich TUM	7/13	36.8 (6.9)	39.2 (6.6)	8.7 (9.7)	37.8 (19.8)	9/11	4/16	41 (29)	34 (25)	6.1 (5.8)	5.5 (5.9)	1.5 (0–2.5)	1.3 (0–6)
Total	15/25	34.4 (8.5)	36.7 (8.3)	8.8 (8.8)	35.7 (17.3)	16/24	7/33	36 (17)	31 (14)	5.2 (3.1)	4.4 (3.0)	1.3 (0–3)	1.0 (0–6)

CIS, clinically isolated syndrome; EDSS, expanded disability status scale; MPIP, Max Planck Institute Psychiatry; mths, months; RRMS, relapsing-remitting multiple sclerosis; SD, standard deviation; t, time point 1; t + 1, time point 2; TUM, Technical University of Munich; WML, white matter lesion; yrs., years.

2.2. Magnetic resonance imaging

MR scans were acquired in the context of regular follow-up visits in the national cohort study of the German Competence Network Multiple Sclerosis. Data storage and quality control was performed centrally (Bochum). We exclusively used scans, which had passed all quality checks. Those included controls for completeness, and scanning protocol (as agreed upon by the respective center before recruitment start) and thorough visual inspection. Details on the MRI protocols of the different sites are given in Table 3.

Table 3.

Scanning protocols.

		Bochum	Mainz	Munich MPIP	Munich TUM
	Scanner	3 T Achieva, Philips, Netherlands	3 T Trio, Siemens, Germany	3 T Signa MR750, GE, United States	3 T Achieva, Philips, Netherlands
3D GRE T1	Orientation	180 contiguous sagittal slices	192 contiguous sagittal slices	160 contiguous sagittal slices	170 contiguous sagittal slices
	Slice thickness (mm)	1	1	1	1
	Field of view (mm)	240 × 240	256 × 256	256 × 256	240 × 240
	Voxel size (mm)	1.0 × 1.0 × 1.0	1.0 × 1.0 × 1.0	1.0 × 1.0 × 1.0	1.0 × 1.0 × 1.0
	TR (ms)	10	1900*	8.2	9
	TE (ms)	4.6	2.52	3.2	4
3D FLAIR	Orientation	170 contiguous sagittal slices	192 contiguous sagittal slices	160 contiguous sagittal slices	144 contiguous axial slices
	Slice thickness (mm)	1	1	1	1.5
	Field of view (mm)	240 × 240	256 × 256	256 × 256	230 × 185
	Voxel size (mm)	1.0 × 1.0 × 1.0	1.0 × 1.0 × 1.0	1.0 × 1.0 × 1.0	1.0 × 1.0 × 1.5
	TR (ms)	4800	5000	7500	10,000
	TE (ms)	291	389	118	140
	TI (ms)	1650	1800	2173	2750

3D, three-dimensional; 3 T, 3 Tesla; FLAIR, fluid-attenuated inversion recovery; GE, General electrics; MPIP, Max Planck Institute of Psychiatry Munich; TE, echo time; TI, inversion time; TR, repetition time; TUM, Technical University of Munich *Siemens here actually indicates the duration of the shot interval.

3. Preprocessing

3.1. Initial cross-sectional WML segmentation per time point

Cross-sectional WML segmentation was used to aid intrasubject image coregistration of T1w (T1-weighted) images through lesion filling, and to aid manual segmentation for internal validation (see next sections). WMLs were segmented for each time point independently by the lesion growth algorithm (Schmidt et al., 2012) as implemented in the lesion segmentation tool LST (www.statistical-modelling.de/lst.html) for SPM12. The algorithm first segments the T1w images into the three main tissue classes (cerebrospinal fluid, grey matter, WM). This information is then combined with the coregistered FLAIR intensities in order to calculate lesion belief maps. By thresholding these maps with a pre-chosen initial threshold (κ), an initial binary lesion map is obtained which is subsequently grown along voxels that appear hyperintense in the FLAIR image. The result of this procedure is a lesion probability map. We used the same initial threshold (κ = 0.3) for all images. This value has been proven to be useful in previous studies (Mühlau et al., 2013; Rissanen et al., 2014) and was confirmed by visual inspection.

3.2. Lesion filling

Lesion filling was used to aid intrasubject image coregistration of T1w images, as it has been shown that the presence of WMLs can have a negative impact on registration results (Chard et al., 2010; Sdika and Pelletier, 2009). Therefore, lesions are first filled in all T1w images with intensities of normal-appearing white matter (NAWM). This task is accomplished by the lesion filling routine implemented in LST.

3.3. Intrasubject registration

Images of both time points have to be in alignment with each other to compare the segmented WML maps. For intrasubject registration, we used the filled T1w images as they show more contrast between tissue classes than FLAIR images. It has been recognized that non-symmetric registration protocols, i.e. methods that align each scan to a baseline, increase the risk of inducing false positive differences (Ashburner and Ridgway, 2012). Addressing this problem, different symmetric strategies have been developed including the affine transformation of all scans into a ‘halfway’ space (Smith et al., 2001). Here, images of two time points are aligned to a point that lies in between the scans of different time points by using the square root of the transformation matrix. Here, we used such an algorithm (longitudinal rigid registration) as currently implemented in the SPM12 toolbox CAT12 (http://dbm.neuro.uni-jena.de/cat/). It combines rigid-body registration with initial bias-field correction and uses sinc interpolation. Coregistration matrices were also applied to corresponding FLAIR images after bias field correction (SPM12) and initial co-registration to the corresponding T1w image (same subject, same time point, LST).

4. Segmentation of WML changes between two time points

4.1. Overview on the segmentations of WML changes between two time points

Once all images are in alignment, the core of our longitudinal pipeline can be applied (Fig. 1). A joint lesion map is rendered from cross-sectional WML segmentations of both time points by logical disjunction (i.e. fusion) in order to divide WM into lesion voxels (part of any lesion at any time point) and non-lesion voxels, i.e. NAWM. The distribution of FLAIR intensity differences is estimated within the voxels of NAWM to enable statistical quantification of intensity changes within the joint lesion map. Significant changes are interpreted as increase (new or enlarged lesion) or decrease (disappeared or shrunken lesion). Non-significant changes but different cross-sectional lesion segmentation results is interpreted as lesion at both time points. Here we followed our experience that false positive lesion segmentations are less likely than false negative lesion segmentations (see discussion).

Fig. 1.

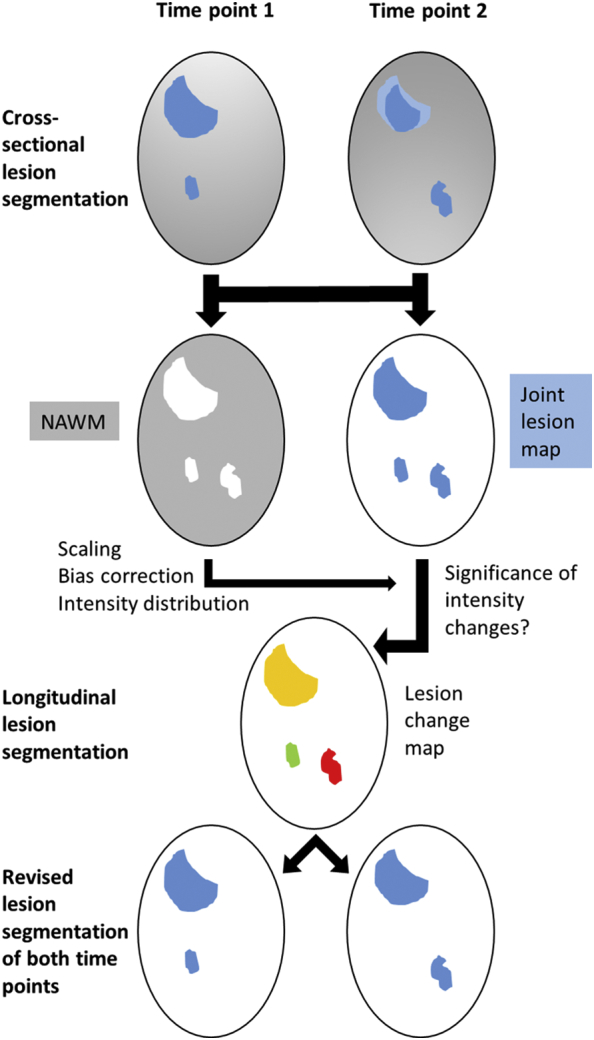
Overview on image processing for the segmentation of WML changes.

After coregistration of individual T1-weighted and FLAIR images and cross-sectional lesion segmentation, a joint lesion map is rendered. Normal appearing white matter (NAWM) is derived from the remainder (WM segmentation without WM lesions); after correction for the bias field, intensity scaling according to grey matter, the distribution of FLAIR intensity differences is estimated from NAWM differences to enable statistical testing for intensity changes within the joint lesion map. Significant changes are classified as increase (new lesion in red) or decrease (disappeared lesion in green). Non-significant changes but different cross-sectional lesion segmentation results are interpreted as lesion at both time points (yellow). For example, the large lesion fades out at its outer sections over time (light blue area at time point 2); since the intensity difference is not significant, no lesion change is indicated. For details, see text. NAWM, normal-appearing white matter.

4.2. Assessment of WML change

Once lesion maps, bias corrected FLAIR images and information about tissue classes of all time points are in alignment with each other, the core of the longitudinal pipeline can be applied. FLAIR intensities of consecutive time points are compared by the procedure explained below. As a result of this process, the initial lesion maps are updated. The final result of this algorithm is that each voxel of each time point is either classified as lesion or not by an update of lesion maps of all time points; further, a lesion change label (LCL) for comparison of both time points is rendered. Six combinations can occur from the initial cross-sectional results (Table 4). If the initial state of a voxel does not differ, the corresponding label in the LCL is either ‘no lesion at both time points’ or ‘lesion at both time points’, depending on the initial segmentation. If the initial voxel states differ, two choices remain. If the difference in FLAIR intensity (δ, see below) is significant, the LCL of the voxel is marked as ‘lesion appeared’ or ‘lesion disappeared’. Otherwise, the LCL of the voxel is labeled as ‘lesion at both time points.’ For consistency between LCLs and lesion maps of both time points, the lesion map ‘no lesion’ is updated to ‘lesion’. We have chosen this strategy as, in our experience, both the lesion growth algorithm as implemented in LST for cross-sectional lesion segmentation and the manual segmentation pipelines (see below) tend to produce false negatives rather than false positives (see discussion).

Table 4.

Lesion change labels and updates of cross-sectional lesion maps.

Initial voxel state (lesion yes/no)		Significant difference in FLAIR intensities (δ) (+/−)	Updated voxel state (lesion yes/no)		Lesion change label
t	t + 1		t	t + 1
No	No	Ignore	No	No	No lesion at both time points
Yes	Yes	Ignore	Yes	Yes	Lesion at both time points
No	Yes	−	Yes	Yes	Lesion at both time Points
No	Yes	+	No	Yes	Lesion appeared
Yes	No	−	Yes	Yes	Lesion at both time points
Yes	No	+	Yes	No	Lesion disappeared

t, time point 1; t + 1, time point 2.

4.3. Comparison of FLAIR intensities

Here we explain how a change in FLAIR intensities between time points t and t + 1 is classified as significant or not.

First, FLAIR intensities of both time points are normalized (scaled) by dividing all voxel values by the mean of segmented grey matter (of the respective time point) as implemented in LST. In addition, a joint lesion map is created. This is a binary mask that indicates whether a voxel was segmented as WML in at least one time point. Next, relative differences in FLAIR intensities are computed for each voxel by the following formula:

$$\mathrm{\delta i},\mathrm{t}=\frac{y\mathrm{i},\mathrm{t}+1-y\mathrm{i},\mathrm{t}}{\left(y\mathrm{i},\mathrm{t}+y\mathrm{i},\mathrm{t}+1\right)/2},i=1,\dots .,n.$$

Here, y_i,t is the FLAIR intensity of voxel i at time point t obtained from the scaled coregistered bias corrected FLAIR image. Due to noise of various sources, we expect δ_i,t ≠ 0 even if the corresponding tissue has not changed. Hence, we have to apply a rule in order to distinguish a significant change. We derive this rule by analyzing δ_i,t within the class of NAWM, i.e. voxels that were segmented as WM but not as WML at both time points. We approximate the distribution of these values by a Gaussian distribution with mean μ_WM and standard deviation σ_WM which are estimated by the empirical mean and empirical standard deviation, respectively. Here, we introduce alpha; it controls the amount of differences identified as significant changes, where high alpha values lead to more changes. The optimal alpha is determined by an internal validation study (see below). These thresholds for distinguishing normal variation from significant changes are obtained by calculating the α and 1- α, 0 < α < 1, quantiles from this distribution, yielding lower and upper thresholds θ_L(α) and θ_U(α), respectively. These thresholds are then applied to voxels within the joint lesion map, that is, to voxels that were segmented as lesions at least at one time point. Significant change in FLAIR intensity is detected if either δi, t < θL(α) or δi, t > θU(α).

4.4. Lesion change plot

When inspecting the results of longitudinal lesion segmentation, it can be hard to gain a comprehensive overview on all changes. To this end, we developed the lesion change plot. This plot depicts the change of each lesion between two time points by plotting the lesion volume of time point t (x-axis) against the lesion volume of time point t + 1 (y-axis). Lesions are represented by squares, whose size is proportional to the joint lesion volume. The area of the squares is divided into colored blocks that encode volumes that disappeared (green), remained constant (yellow), and appeared new (red). Further, a column on the right encodes the volume changes as a whole with the same colors as in the diagram. The descriptive tool is further complemented by a maximum intensity projection (Wallis et al., 1989) for the LCL along the sagittal, coronal and transverse plane to allow localization of the lesion evolution in the brain.

5. Validation

5.1. General validation strategy and validation outcome parameters

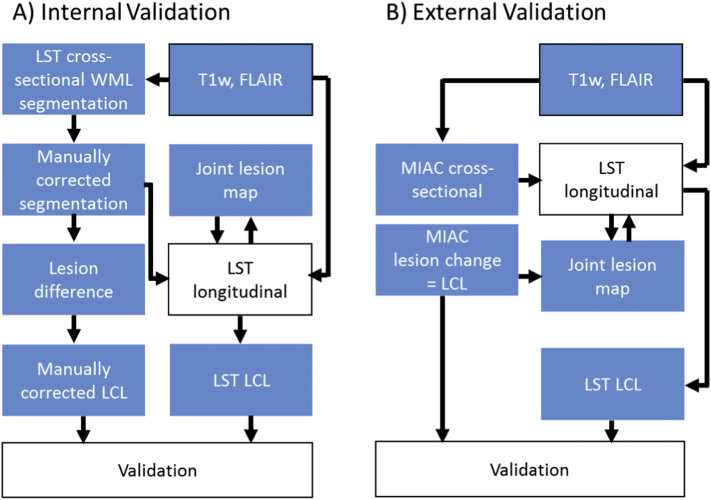
We chose a two-step approach, comprising an internal and an external validation step (Fig. 2). Both were based on manual segmentation as gold standard – yet with technical differences. 1) Internal validation: This served to stabilize the diverse steps of our pipeline, exclusion of a systematic bias towards WML decrease or increase, and identification of an optimal value for α. This part of the validation was carried out by in-house software, standard fast preprocessing steps and manual segmentation by one co-author (PS) not blinded to time points. 2) External validation: This served to eventually assess the performance of the entire tool on the basis of the LCL maps without elements of circularity and without co-authors being directly involved. This strict procedure in combination with new independent samples of MS patients was chosen to approach generalizability of our results. Comparison of LCL maps were restricted to changes of at least 15 μl in contiguous volume corresponding to a diameter of about 3 mm as stipulated by the current criteria to diagnose MS (Thompson et al., 2018).

Fig. 2.

Overview of image processing for the validation analysis.

A) For the internal validation, we used the lesion segmentation tool (LST) for cross-sectional lesion segmentation separately for each time point. These lesion segmentations were manually corrected. Lesion changes were created by difference images which were also manually corrected (manually corrected lesion change label, LCL). Manually corrected cross-sectional lesion segmentations served as starting point for the segmentation of white matter lesion changes by LST (including the joint lesion map). For validation analysis, manually corrected LCLs were compared to LCLs derived from LST.

B) For the external validation, MIAC AG (Medical Image Analysis Center Basel, Switzerland) delivered coregistered cross-sectional lesion segmentations of both time points and segmentations of white matter lesion changes (LCL). MIAC cross-sectional lesion segmentation served as starting point for the longitudinal lesion segmentation by LST including the joint lesion map. The latter was complemented by MIAC LCLs. For validation analysis, MIAC LCLs were compared to LCLs derived from LST.

5.2. Internal validation: details on manual segmentation and optimization of alpha

Here (Fig. 2A), WMLs were manually segmented by one observer (PS) with over 6 years of experience in segmenting WMLs in MS. First, WMLs were cross-sectionally segmented by LST and manually corrected by means of the drawing tools of MRIcron, version 1.4 (Rorden and Brett, 2000) according to previous work (Caligiuri et al., 2015; Droby et al., 2015; Gamboa et al., 2014; Zimmermann et al., 2015) in chronological order. Axial slices served as primary orientation; sagittal or coronal slices of the same time point as well as slices of the other time point were used on demand. These binary manually corrected cross-sectional segmentations were saved and LCLs calculated through subtraction of both time points; these LCLs were again manually corrected. For each LCL, the Dice coefficient (DC) was calculated.

α critically influences the quality of the longitudinal segmentation (see above section on comparison of FLAIR intensities). Smaller values will yield more conservative LCLs while larger values are able to recognize smaller changes in FLAIR intensities, yet increasing the risk of false positive lesion change voxels. We performed a sensitivity analysis across α values ranging from 0.01 to 0.40. First, we applied our pipeline to the images of 5 subjects from TUM since LST (Schmidt et al., 2012) had been developed based on these same sequences. Then, we compared this to the performance on two other platforms (5 patients per scanner). LCLs obtained from our pipeline were compared to reference LCLs derived from manual segmentation using the voxel-wise Dice coefficient (Dice, 1945):

$$\mathit{DC}=\frac{2\times \mathit{TP}}{2\times \mathit{TP}+\mathit{FN}+\mathit{FP}}$$

TP, FP, and FN refer to the number of true positives, false positives, and false negatives, respectively. Voxels that were not segmented as WML at any time point with either of the two methods were excluded from validation analysis. Voxels are counted as TP if ‘change’ or ‘no change’ has been estimated correctly. In contrast, the number of misclassified voxels, i.e. F = FN + FP, is composed of voxels with different lesion labels. Dice coefficients derived from the voxel-wise comparison were analyzed across α values using local polynomial regression LOESS (Cleveland and Devlin, 1988).

5.3. External validation: details on segmentation procedure and performance parameters

The external validation (Fig. 2B) was performed by Medical Image Analysis Center AG (MIAC) Basel, Switzerland (http://miac.swiss/en/), a certified imaging clinical research organization providing high precision WML segmentations, e. g. for international phase III pharmaceutical trials (Kappos et al., 2010). The full technical details are undisclosed. It is manual but aided by a semi-automated contour-detection algorithm to be applied slice-by-slice and based on independent lesion segmentation by two professional readers with an intrarater variability of ≤5% (Kappos et al., 2010). Interrater variability is kept low by lesion segmentation through two independent readers and consensus decisions led by a neuroradiologist. To use the MIAC pipeline for validation of our algorithm, some adaptations were necessary: First, the MIAC pipeline yields coregistered FLAIR images and WML segmentations of both time points as well as the LCLs in DICOM (Digital Imaging and Communications in Medicine) format. After conversion to NIFTI (Neuroimaging Informatics Technology Initiative) format, MIAC images were coregistered to the images derived from our intrasubject registration by subjecting FLAIR images of the first time point to a standard coregistration routine as implemented in SPM12 and applying the same transformation to all other images. The LCLs coregistered in this way were used for eventual quantification steps. Second, as the applied MIAC pipeline is manual, LCLs do not necessarily fully overlap with at least one of the two cross-sectional WML maps. Therefore, we calculated a joint lesion map from the coregistered MIAC WML maps of both time points and the coregistered MIAC LCLs. Of note, this step does not change the MIAC based segmentation results, but is needed to have a comparable analysis space.

For the external validation, we aimed at lower dependence from absolute volumes and also calculated additional similarity measures (beyond the voxel-wise DC). Since for MS monitoring, the number of new WMLs is more established than the overall volume of new WMLs, lesion-wise measures were determined. As proposed more recently (Ganiler et al., 2014), we considered segmentation of a new WML TP in case of at least 1 voxel intersecting with a WML according to manual segmentation; in contrast, we considered segmentation of a WML FP in case of no voxel intersecting with a WML according to manual segmentation. This way, we determined sensitivity, which can be referred to as detection or true positive rate (TPR) in our case,

$$\mathit{Sensitivity}=\mathit{Detection\; rate}=\mathit{TPR}=\frac{\mathit{TP}}{\mathit{TP}+\mathit{FN}}$$

and the false discovery rate (FDR), which can be referred to as false positive rate (FPR)

$$\mathit{FDR}=\mathit{FPR}=\frac{\mathit{FP}}{\mathit{FP}+\mathit{TP}}$$

in a lesion-wise manner in addition to the voxel-wise DC. We also calculated these parameters across different WML size ranges. Finally, we performed simple correlation analyses to identify effects of age, disease duration or severity (EDSS) on performance parameters. Subject-wise mean values of both time points (age, disease duration, EDSS) were entered into analyses.

6. Repositioning experiment

To investigate test-retest reliability, we re-analyzed data of a re-positioning experiment performed in the context of another study at the scanner of Munich MPIP (Biberacher et al., 2016). Four scans were acquired in sequence; between scans, the patient (with MS) stood up, rotated once, and was repositioned. We compared the results of the cross-sectional pipeline of LST with its longitudinal pipeline, which builds upon WML segmentations derived from the cross-sectional pipeline. Then, it segments WML changes and updates segmentations of cross-sectional WML per time point, as suggested in this study, to achieve coherence between lesion segmentation per time point and lesion changes between time points. Of note, the data set is challenging as the patient has over twenty lesions many of them fading out at the borders and with a lesion sizes near the commonly proposed minimal WML size of at least 15 μl in contiguous volume corresponding to a diameter of about 3 mm (Thompson et al., 2018).

7. Implementation

We will implement this tool in the next version of our open source software package LST. The user can choose between different thresholds (α) for the relative difference in FLAIR intensities. As a default, the optimal threshold derived from the validation (α = 0.1) is used. The tool finally returns corrected lesion probability maps of all time points, lesion change labels of all pairs of consecutive scans, as well as coregistered T1w and FLAIR images. In addition, an HTML report with segmentation overlays, lesion change plots and maximum intensity projections is generated. For each subject, lesion number and volume (total, decreased, increased and unchanged) of all time points are summarized in a table (CSV format).

8. Results

8.1. Internal validation

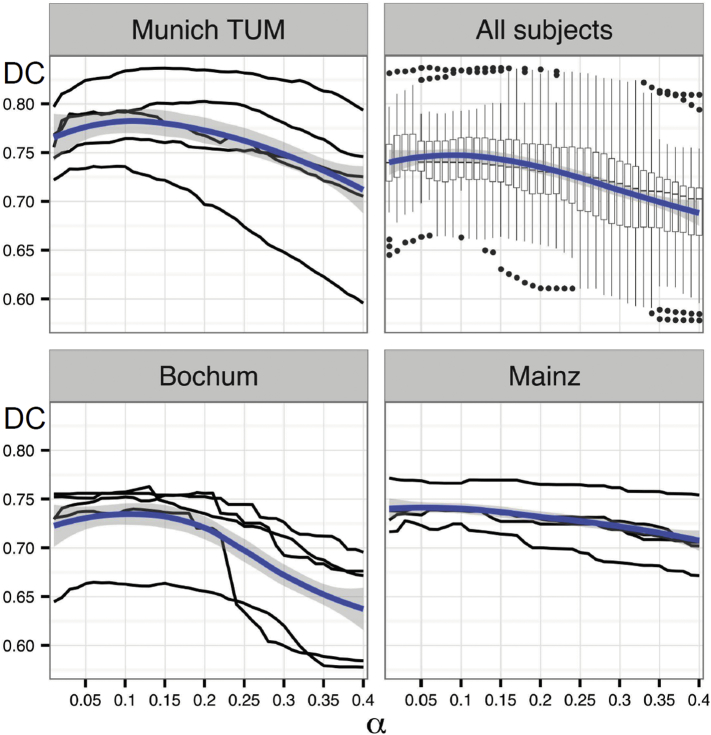
Similarity of automated WML change segmentation with the manual segmentation was estimated by the voxel-wise DC. In the upper panel of Fig. 3, the DCs along different α values are depicted (upper left, TUM; upper right, common analysis of all 3 centers; lower left, Bochum; lower right, Mainz). With increasing α, the agreement between manual and automatic segmentations first increases, then reaches a plateau and finally decreases. We found the optimal threshold to be near 0.1, which is indicated by the maximum of the blue line representing the fit of LOESS. The shape of LOESS is similar for all centers with a maximum near α = 0.1, confirming that α = 0.1 is a suitable choice for the data of all centers. The DCs obtained with α = 0.1 ranged from 0.67 to 0.81 and differed only slightly between centers (mean and range): Bochum, 0.73 (0.66–0.76), Mainz, 0.73 (0.72–0.74), and TUM 0.77 (0.74–0.81).

Fig. 3.

Effect of α on reliability of segmentations.

Evolution of Dice coefficients (DC, y-axis) over different α values for the TUM data (left upper panel). Black lines display relationships between Dice coefficient and different α values for each subject. Fit of local polynomial regressions (LOESS) are indicated by blue lines; corresponding confidence regions are highlighted in grey. Analogous plots are displayed for a common analysis of all centers (right upper panel) and for the sites of Bochum (left lower panel) and Mainz (right lower panel).

Univariate linear regression analyses of WML volumes from automated longitudinal lesion segmentation with WML volumes from manual segmentation across subjects provided no evidence of systematic shifts or differences. Analyzing disappeared/decreased, new/increased, and unchanged WML volumes separately, all 95% confidence intervals for the intercepts contained 0 [−0.01, 0.27], [−0.19, 0.27], [−0.11, 0.59]) and all intervals for the slopes contained 1 ([0.88, 1.13], [0.79, 1.12], [0.91, 1.1]). Coefficients of determination (R²) were 0.94, 0.89, 0.97, respectively. Hence, we set α to 0.1 for the external validation analyses.

8.2. External validation

Overall performance was good. Volumes of new/increased WMLs derived from both methods showed high correlations (MPIP: R² = 0.53; TUM: R² = 0.44) although there was a systematic bias towards higher volumes derived from the manual segmentation with a 95% confidence of the slope below one (common analysis: [0.47; 0.96]; MPIP: [0.48, 1.32]; TUM: [0.3, 1.03] whilst the interval of the intercept contained zero (common analysis: [−1.32; 0.21]; MPIP: [−0.08, 0.1]; TUM: [−0.02, 0.42]). Across all WMLs, voxel-wise DC was 0.7, lesion-wise detection rate (sensitivity) 0.8 and lesion-wise false-discovery rate 0.2. Performance tended to decrease with decreasing WML volume (Table 5). Simple correlation analyses did not indicate an effect of age, disease duration or severity (EDSS) on performance parameters.

Table 5.

Results of external validation.

Lesion size (range in ml)	Number of WMLs	DC voxel-wise	Sensitivity voxel-wise	FDR voxel-wise	Sensitivity lesion-wise	FDR lesion-wise
All	496	0.72 [0;1]	0.74 [0;1]	0.08 [0;0.96]	0.81 [0;1]	0.22 [0;1]
(0.015,0.02]	66	0.52 [0;1]	0.52 [0;1]	0.01 [0;0.22]	0.53 [0;1]	0.33 [0;1]
(0.02,0.025]	51	0.55 [0;1]	0.57 [0;1]	0.04 [0;0.71]	0.59 [0;1]	0.32 [0;1]
(0.025,0.03]	52	0.76 [0;1]	0.76 [0;1]	0.02 [0;0.5]	0.79 [0;1]	0.27 [0;1]
(0.03,0.04]	70	0.67 [0;1]	0.70 [0;1]	0.09 [0;0.95]	0.76 [0;1]	0.27 [0;1]
(0.04,0.05]	40	0.73 [0;1]	0.74 [0;1]	0.08 [0;0.95]	0.83 [0;1]	0.25 [0;1]
(0.05,0.075]	86	0.82 [0;1]	0.85 [0;1]	0.11 [0;0.96]	0.94 [0;1]	0.14 [0;1]
(0.075,0.1]	30	0.80 [0;1]	0.85 [0;1]	0.14 [0;0.79]	0.93 [0;1]	0.19 [0;1]
(0.1,0.15]	38	0.85 [0.22;1]	0.88 [0.43;1]	0.14 [0;0.87]	1 [1;1]	0.14 [0;1]
(0.15,0.2]	27	0.82 [0.11;0.98]	0.86 [0.42;1]	0.18 [0.01;0.94]	1 [1;1]	0.17 [0;1]
(0.2,0.3]	14	0.85 [0.57;0.98]	0.83 [0.48;1]	0.10 [0;0.41]	1 [1;1]	0.21 [0;1]
(0.3,0.5]	14	0.88 [0.68;0.98]	0.92 [0.68;1]	0.13 [0.02;0.44]	1 [1;1]	0.07 [0;1]
(0.5,1]	5	0.82 [0.72;0.96]	0.88 [0.66;1]	0.21 [0.09;0.42]	1 [1;1]	0.14 [0;1]
(1,3]	3	0.94 [0.93;0.96]	0.94 [0.88;0.97]	0.05 [0;0.10]	1 [1;1]	0 [0;0]

DC, Dice coefficient, FDR, false discovery rate; ml, milliliters; WMLs, white matter lesions.

9. Repositioning experiment

The longitudinal pipeline of LST did not find a single (false positive) new or disappeared lesion whilst the cross-sectional pipeline of our lesion segmentation algorithm yielded varying lesion numbers. Changes in volumes of WML were also drastically reduced by the longitudinal pipeline of LST but not zero. The results of the repositioning experiment are summarized in Table 6.

Table 6.

Results of repositioning experiment.

Scan	WML
	Total volume (ml)		Numbers
	CS	LT	CS	LT
1	7.33	8.94	26	35
2	7.17	8.95	30	35
3	6.75	8.93	29	35
4	7.25	8.90	24	35
Mean difference	0.36	0.02	3.3	0

Total volume and numbers of white matter lesions per scan are given as derived by the cross-sectional (CS) or longitudinal (LT) pipeline of LST. Mean differences were derived by averaging absolute values of differences (n = 3) between consecutive scans.

9.1. Lesion change plot

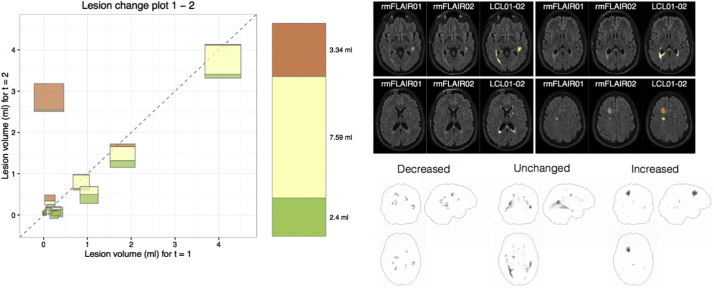
Moreover, lesion change plots helped to exemplify the main information from individual segmentation of WML changes at first glance. Each WML is plotted in the diagram by considering its volume at time point 1 (t = 1) at the x-axis and its volume at time point 2 (t = 2) at the y-axis resulting in new or enlarging lesions displayed left to the diagonal, vanishing or shrinking lesions displayed right to the diagonal, and stable lesions displayed on the diagonal. An example of a patient, randomly chosen from patients with an increase in WML load according to the reports of the evaluating radiologists, is given in Fig. 4 and allows for a fast intuitive interpretation. Between time point 1 and 2, MS was active as indicated by one new larger WML (left frontal) and one smaller enlarged WML (posterior callosum), whilst the other WMLs shrank or remained stable.

Fig. 4.

Example of a lesion change plot of the lesion segmentation tool (LST) derived from two scans of 1 MS patient who was randomly chosen from patients with an increase in WML load according to the reports of the evaluating radiologists. Lesion numbers (>0.015 ml) were 35, and 37. Each lesion is plotted in the diagram by considering its volume at time point 1 (t = 1) at the x-axis and its volume at time point 2 (t = 2) at the y-axis. The area of the square is proportional to the volume of the lesion and divided in three categories (red, new; yellow, unchanged; green, disappeared). The bar right to the diagram illustrates the overall lesion volume the same way. On the upper right, axial slices of FLAIR images are shown (left, time point 1; middle, time point 2; right, lesion changes with the same color coding projected on time point 2). On the lower right, maximum intensity projections of lesion changes labels are displayed. FLAIR, fluid-attenuated inversion recovery; LCL, lesion change label.

10. Discussion

We introduced and validated a pipeline on segmentation of FLAIR hyperintense WML changes between two time points. This pipeline shares a common framework with a previously developed method for cross-sectional WML segmentation but can also be combined with other methods for cross-sectional WML segmentation.

Although it is critical to compare values of performance measures across studies and, hence, across different study populations and MRI sequences, performance of our algorithm seems to be in the range of those of other algorithms for the detection of WML changes (Table 1). Lacking a commonly accepted gold standard and given the broad overlap of ranges of different algorithms, it seems very difficult to demonstrate superiority of one algorithm over another. This is well in line with experiences from a previous challenge on longitudinal WML segmentation (Carass et al., 2017). The type of longitudinal WML segmentation, investigated in this study, must be distinguished from segmentation of WML changes, since WML segmentations per time point but not WML changes were evaluated. Of note, the performance of 15 algorithms on this less challenging task were compared but ranges of values of performance parameters overlapped largely so that the best algorithm could not be identified. However, we believe that our algorithm primarily constitutes a conceptual advantage, since it can be integrated in a common frame work with cross-sectional WML segmentation, it can potentially analyze more than two time points, and its current version will be made freely available as part of the LST toolbox of the SPM12 software package.

Several methods for longitudinal segmentation of WMLs in MS have been proposed. These methods were roughly categorized into lesion detection and change detection methods (Llado et al., 2012a; Llado et al., 2012b). In the context of lesion detection methods, WMLs are segmented at each time point and the change in segmented lesions is measured. These simple approaches seem to be insufficiently precise, since they do not make use of the full information of available data. At the beginning of our project, we inspected many longitudinal datasets with the naked eye. Sometimes, it was very challenging to distinguish a real change in lesions from technically driven variation in visibility due to variation in positioning, magnetic field inhomogeneity, or intensity scaling. Intriguingly, some lesions could only be identified in one FLAIR image with the knowledge of the FLAIR image acquired at another time point – bearing the risk to erroneously conclude a lesion change by segmenting a persistent lesion at only one time point. In contrast to lesion detection methods, change detection methods address the issue of these classification errors by focusing on intensity changes over time in the raw data (Battaglini et al., 2014; Eichinger et al., 2017; Elliott et al., 2010; Ganiler et al., 2014; Salem et al., 2018; Sweeney et al., 2013). However, many studies also require absolute cross-sectional measures of WML load. This necessitates the compatibility with tools for cross-sectional WML segmentation and prompts the challenge not only to enable application of both pipelines one after the other but also to gain consistent results from both cross-sectional lesion segmentation and segmentation of lesion changes. Otherwise, incoherent results are likely to occur. For example, according to the cross-sectional segmentation, a voxel may be classified as ‘no lesion’ at time point 1 and ‘lesion’ at time point 2, whilst the segmentation of WML changes does not identify a significant change. To prevent such inconsistencies, we decided to update the results of the cross-sectional segmentation according to the results of the segmentation of WML changes. Given that intensities are not fully stable over time, a significant change in intensities to conclude a lesion change seems inevitable. Assuming consistency, classification of the voxel as WML must be regarded either false positive at one time point or false negative at the other time point. We chose the latter as, in our experience on both automated segmentation by LST and manual segmentation, false positives occur less often than false negatives. Yet our experience may not be shared by others. It may also depend on the sequences analyzed. Of note, our choice on the update strategy on the cross-sectional data does not influence the result on the segmentation of WML changes between two time points. Strictly speaking, our update strategy on the cross-sectional WML segmentation was only encouraged by preliminary tests through visual inspection but deserves validation in another project.

The task of longitudinal lesion segmentation can be further complicated by data on more than two time points. Here discrepancy between cross-sectional and longitudinal lesion segmentation would hamper effective analysis even more. In case of 3 time points, results from the analysis of all 3 time points would not allow to simply add up the lesion change labels ‘time point 1 to time point 2’ and ‘time point 2 to time point 3’ to calculate the lesion change label ‘time point 1 to time point 3’. To avoid these problems, we aimed at a framework for longitudinal WML segmentation that is capable of consistently attributing the label of being a lesion or not to each voxel at each time point, rather than a framework for mere lesion detection or mere lesion change.

Accepting the necessity of a significant intensity change to identify changes in WMLs, we introduced the cut-off parameter α. Initially, we applied different α values to the TUM data, since LST was developed with these sequences. Segmentation with α = 0.1 showed plausible results according to visual inspection and greatest similarity with manual segmentation. The choice of α = 0.1 was encouraged by data of another two centers.

To investigate test-retest reliability, we analyzed scans of a repositioning experiment of a single patient with MS. We analyzed all four scans with the cross-sectional pipeline of LST and with the longitudinal pipeline of LST, which uses the segmentations of the cross-sectional pipeline as initial estimates. Then it segments significant changes and updates cross-sectional WML segmentation per time point as suggested in this study. This way, we tested for false positive WML changes and evaluated whether the update of cross-sectional WML segmentations leads to more coherent results. This was clearly the case with regard to the overall number and volume of WML load. At the same time, more lesions were segmented per time point, which resulted from the update strategy. The joint lesion map comprises all WML with the minimum requirement for a single WML of having been segmented as a WML by the cross-sectional pipeline of LST at least at one time point. Of note, this includes the minimum size of at least 15 μl in contiguous volume corresponding to a diameter of about 3 mm. Within this joint lesion map, smaller significant changes were identified but none of them with a contiguous volume of at least 15 μl. In consequence, higher WML load per time point were segmented with regard to both volume and number. The maximum difference in number of 11 WML is surprisingly high at first glance but understandable given that the data set was challenging as the patient had over twenty WML, many of them fading out at the borders and with a WML sizes near the commonly proposed minimal WML size of 3 mm in diameter. In these WML with sizes near the threshold of 3 mm in diameter, only slight differences in segmentation in the outer layers decided whether the cross-sectional pipeline detected a WML or not. In conclusion, analysis of this challenging data set did not indicate a tendency towards false positive WML changes. Although the number WML per time point increased, the update strategy led to more coherent results.

We acknowledge limitations of our work. Although successfully applied to data of four scanners in total, the choice of α = 0.1 cannot be regarded valid in general at this stage. Adaptation of α to process other data, perhaps even data based on other sequences, may be necessary. We caution that our algorithm was validated through high-quality, high-resolution MRI data acquired at 3 Tesla in patients primarily in early stages of MS. Hence, it may not work as well in other situations. We are unable to comment on the effect of lower image quality as we studied data of high image quality collected by the German Competence Network MS, which goes along with the disadvantage of limited generalizability to data as acquired in routine clinical practice, since blurred images may not allow for a precise estimation of difference distribution through NAWM. Our subjects were mainly in early stages of MS. Hence, performance parameters as estimated here may not apply to patients in later stages with high volumes of confluent lesions, more severe demyelination in lesions, or pronounced brain atrophy. Further, it is inherent to our approach that new lesions can only be correctly classified if detected by the preceding cross-sectional segmentation at least at one time point so that the performance of our algorithm critically depends on the precision of the preceding cross-sectional lesion segmentation. Moreover, the precision of our algorithm is not sufficient to make readings of professional observers dispensable. Small or low intensity lesions can still be missed and in single cases lead to misclassification of patients as also indicated by individual zero values of performance parameters.

Another problem is the lack of a commonly accepted gold standard. We chose a certified imaging clinical research organization (MIAC AG) as provider. Yet conventional reading could be aided and potentially improved by subtraction of follow-up images.

In addition to longitudinal lesions segmentation, we introduced the idea of a merely descriptive tool for individual lesion changes between two time points. The main goal was to combine the two common measures of lesion load, number and volume of lesions, in a salient way, also accounting for the fact that during the same interval some lesions may shrink or even disappear whilst others may occur or grow. For the handling of TUM in-house data with hundreds of follow-up data, we have already appreciated this tool.

Finally, by providing an open source implementation of this pipeline, which is freely available to the scientific community (http://www.statistical-modeling.de/lst.html). We hope that our algorithm will be further refined and eventually contribute to the analysis of MR images in both clinical routine and research.