Quantifying Complex Micro‐Topography of Degenerated Articular Cartilage Surface by Contrast‐Enhanced Micro‐Computed Tomography and Parametric Analyses

ABSTRACT

One of the earliest changes in osteoarthritis (OA) is a surface discontinuity of the articular cartilage (AC), and these surface changes become gradually more complex with OA progression. We recently developed a contrast enhanced micro‐computed tomography (μCT) method for visualizing AC surface in detail. The present study aims to introduce a μCT analysis technique to parameterize these complex AC surface features and to demonstrate the feasibility of using these parameters to quantify degenerated AC surface. Osteochondral plugs (n = 35) extracted from 19 patients undergoing joint surgery were stained with phosphotungstic acid and imaged using μCT. The surface micro‐topography of AC was analyzed with developed method. Standard root mean square roughness (R_q) was calculated as a reference, and the Area Under Curve (AUC) for receiver operating characteristic analysis was used to compare the acquired quantitative parameters with semi‐quantitative visual grading of μCT image stacks. The parameters quantifying the complex micro‐topography of AC surface exhibited good sensitivity and specificity in identifying surface continuity (AUC: 0.93, [0.80 0.99]), fissures (AUC: 0.94, [0.83 0.99]) and fibrillation (AUC: 0.98, [0.88 1.0]). Standard R_q was significantly smaller compared with the complex roughness (CR_q) already with mild surface changes with all surface reference parameters − continuity, fibrillation, and fissure sum. Furthermore, only CR_q showed a significant difference when comparing the intact surface with lowest fissure sum score. These results indicate that the presented method for evaluating complex AC surfaces exhibit potential to identify early OA changes in superficial AC and is dynamic throughout OA progression. © 2019 The Authors. Journal of Orthopaedic Research® Published by Wiley Periodicals, Inc. on behalf of the Orthopaedic Research Society. Society. 9999:1–12, 2019.

Osteoarthritis (OA) in the knee is a common and significant cause of disability in the aging population. OA exhibits morphological and topographical changes in articular cartilage (AC).1 These changes, particularly those in the superficial AC surface, are one of the earliest signs of AC degeneration.2 Therefore, AC surface features are commonly used to evaluate the pathological state of OA.3, 4, 5 AC surface features, such as surface irregularity, fibrillation(s), and fissures(s), are important in current histopathological grading systems, such as Mankin and OARSI gradings.3, 4 Although the AC surface may be still structurally intact, irregularity of the AC surface is one of the early OA signs suggesting an ongoing tissue reaction. Fibrillation, that is, “micro‐roughness,” of the AC surface is due to disruption and disorganization of the superficial AC is mainly attributed to the change in the collagen fiber alignment. This feature is considered a characteristic of slightly more progressed OA.4 Fissures are characteristics of even further progressed OA and appear as “cracks” extending from the AC surface typically towards the deep AC. Currently, these signs associated with early and moderate OA are evaluated visually, which is subjective. Furthermore, histology is applied to thin 2D sections, which only provides a glimpse of cartilage surface and true tissue architecture. Moreover, sectioning and staining are prone to sample processing artifacts.

Several studies have investigated AC surface topography directly or indirectly on a qualitative, semi‐quantitative, and quantitative basis. Early attempts to quantify AC surface topography include stylus profilometry of acrylic replicas of AC surface6 and conventional7, 8, 9 or stereotactic scanning electron microscope (SEM)10 images of dehydrated and coated AC samples. Ultrasound backscattering, which is associated with AC surface degeneration,11, 12, 13 provides an indirect assessment of AC surface roughness. Hacker et al.14 and Trudel et al.15 demonstrated a histology‐based approach to compare AC surface topography against reference points on the AC surface. Furthermore, evaluation of AC surface roughness has been determined from image information obtained by ultrasound microscopy,16, 17, 18 intravascular ultrasound,19, 20 and optical coherence tomography (OCT).21, 22 The most common clinically used imaging modality to quantify topography of degeneration is magnetic resonance imaging (MRI).5, 23, 24 However, all these approaches have limitations. Atomic force microscope, stylus profilometry, ultrasound, and OCT typically assess single or multiple scan lines by implicitly assuming a simple surface topography (one z value per xy‐coordinate), whereas real AC topography with fibrillation and fissures can be complex (one or more z values per xy‐coordinate). On the other hand, SEM approaches are qualitative or semi‐quantitative and are typically also limited to simple surface topography. ISO roughness standards, for example, 287, 4288, 11562, 12085, and 13565,22 do not, by definition, address complex topography. Histology‐based approaches are destructive and are subject to sectioning artifacts. MRI cannot quantify the micro‐topography of the AC surface due to insufficient resolution. To the authors' knowledge, the existing scientific literature does not quantitatively address the complex nature of the volumetric topography of the AC surface in a minimally destructive manner. Approaches that would meet these criteria would find use beyond AC applications given that surfaces of many natural (e.g., hydrophobic leaves and shark scales) and engineered materials (e.g., paper, wood, and composites) are complex.

As mentioned above, studies quantifying the micro‐topography of the AC surface24 have attempted to characterize the apparent simple surface of AC. Thus, in an orthogonal coordinate system, on the AC surface for every lateral coordinate (x, y), there is only one z‐value, where (x, y, z) represents a coordinate on AC surface (Fig. 1). However, a degenerated AC surface with fibrillation and fissures is typically complex in nature, i.e., for every lateral coordinate (x, y), there can be more than one z‐values. Assuming a simple surface prevents one from quantifying sub‐surface features, such as fibrillation and complex fissures in AC (Fig. 1). This limitation makes it more difficult to establish clinically relevant quantitative associations between parameters describing AC surface micro‐topography and the AC pathology.

Figure 1.

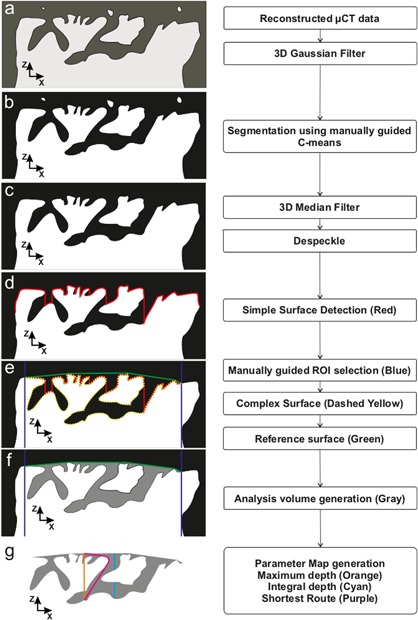
Flowchart and 2D slice example of data analysis procedure: a) Raw reconstructed μCT volume. b) Segmented (binarized) volume. c) Binarized volume after post‐segmentation filtering and despeckle. d) Simple surface generated (red) first sample voxel when scanning from positive z‐direction. e) ROI limits (blue) and reference surface elevated to highest sample points (green). f) Surface defining void (SDV) (a gray area) limited by reference surface (green) and segmented sample volume (white). g) Examples of different parameters calculated for each reference surface voxel.

Several computed tomography (CT) studies have addressed the visualization of micro‐structure of AC matrix using various contrast agents (CA4+, CA2+, Tantalum Oxide nanoparticles, Hexabrix®, Magnevist®).25, 26, 27, 28, 29, 30, 31, 32 Phase‐contrast synchrotron CT is also able to reveal the micro‐structure of the AC matrix.33 However, none of these studies have addressed a direct assessment of the collagen architecture in a large tissue volume. Recently, we developed a contrast‐enhanced μCT (CEμCT) method to visualize AC with a resolution (∼3 μm voxel side length) comparable with that of conventional histology slice thickness (3–5 μm).34 This approach exploits staining of the collagen matrix of AC using phosphotungstic acid (PTA),34, 35 providing excellent contrast for imaging the superficial AC, which subsequently enables reliable segmentation of AC from the background. One of the main advantages of this CEμCT method is the capability to visualize AC surface fibrillation and fissures with high resolution in 3D, which could be exploited to analyze complex AC surface micro‐topography potentially automatically and user‐independently.

The aims of the present study are (1) to develop CEμCT analysis method for quantifying complex micro‐topography of AC surface with early to moderate degeneration and (2) to demonstrate its sensitivity and specificity to identify early to moderate AC degeneration from intact AC using semi‐quantitative CEμCT grading as a reference.

METHODS

Samples

Human osteochondral (OC) tissues were obtained from 19 patients (14 females; age 71 ± 12 years and five males; age 69 ± 8) undergoing total knee arthroplasty surgery. Patients with clinically verified rheumatoid arthritis (RA) or any other joint disease except primary arthrosis diagnosis were not included in the study. RA was diagnosed by serum cyclic citrullinated peptide antibodies and rheumatoid factor. The sample handling was conducted in accordance with the institutional guidelines and regulations (Institutional ethics approval PPSHP 78/2013, The Northern Ostrobothnia Hospital District). Informed consent was obtained from all patients. Retrieved joint surfaces were visually evaluated for cartilage damage. Based on this visual evaluation we collected OC plugs with different stages of degradation. One plug from both the tibia plateau (n = 18) and femoral condyle (n = 17) from each patient was collected. To extract plugs a 4 mm trephine drill (Hu‐Friedy TRE040M, Ortomat Herpola, Turku, Finland) was attached to a water‐cooled high‐speed dental turbine handpiece operated at mid‐power with a portable dental unit (BD‐406, Plandent, Helsinki, Finland). Each OC plug was divided into two half samples. CEμCT half was trimmed to fit in the field of view (Fig. 2a). The adjacent tissue was subjected to histology.

Figure 2.

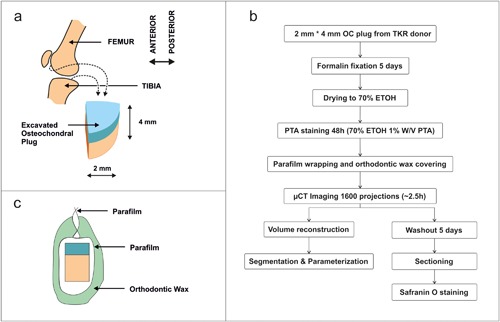
a) Schematics of sample locations of the osteochondral plug. b) Flowchart of OC plug preparation procedure. c) Schematic of sample packaging for μCT imaging.

μCT Imaging

Sample processing for μCT is presented in Figure 2b. The samples were fixed in 10% formalin for 5 days and stained for 48 h in 1% w/v PTA in 70% ethanol solution.34 Following PTA staining, the samples were wrapped in Parafilm (Parafilm M, Bemis Company Inc, Neenah, WI) and orthodontic wax (Orthodontic Wax, Ortomat Herpola, Turku, Finland) to prevent sample drying during imaging (Fig. 2c). Samples were imaged in two batches with μCT (Nanotom 180NF, Phoenix X‐ray Systems/GE; 80 kV, 150 μA, 1600 projections, 750 ms/frame, 5 frames/projection, isotropic 3.0 µm voxel size, ∼2 h imaging time, n = 22) (Skyscan 1272; Bruker microCT, Kontich, Belgium; 45 kV, 222 μA, 3.2 μm voxel side length, 3050 ms, 2 frames/projection, 1200 projections, and with 0.25 mm aluminum filter n = 14). Projections were reconstructed using proprietary software from the respective manufacturers (datos|x version 1.3.2.11, GE Measurement & Control Solutions/Phoenix X‐ray, Fairfield, CT) (NRecon version 1.6.10.4; Bruker microCT, Kontich, Belgium).

3D‐histopathological Grading

3D‐histopathological grading was performed on the reconstructed μCT data using a 3D grading scale.36 Relevant surface dependent sub‐scores (Surface Continuity 0‐2; Fibrillation 0‐2; Fissures 0–5) were defined from the randomized data. These reference parameters were defined as Surface Continuity (Smooth and continuous = 0; Slightly discontinuous =1; Moderately discontinuous = 2; Severely discontinuous = 3), Fibrillation (Absent = 0; Few =1; Many = 2) and Fissure (Zone 1 absent = 0; Zone 1 present = 2; Zone 2 top half present = 2; Zone 2 lower half present = 3; Zone 3 top half present = 4; Zone 3 lower half present = 5).

Surface Micro‐Topography Analyses

We developed a semi‐automatic analysis software pipeline using C++ (Visual Studio 2015, Microsoft Corp, Redmond, WA) and Matlab (R2014b, MathWorks Inc., Natick, MA) to characterize the AC surface from the reconstructed CEμCT data (Fig. 1). The analysis consisted of three major parts, 1. Segmentation, 2. Surface defining void (SDV) generation and 3. Parameterization, which are described below.

Segmentation was performed by first pre‐filtering the data with 3D Gaussian smoothing (5 voxel width 3D kernel, SD 1.2 voxels) to remove noise followed by fuzzy C‐Means clustering37 of image intensity to obtain the probability of the voxel to be included in sample segment. To obtain binarized data, that is, to judge which voxels belong to the foreground (AC) and which belong to the background (complement of AC), a threshold sample probability (0.25–0.9) was selected manually by visual inspection for each sample as there was no optimal global threshold for all samples. A 3‐voxel wide median filter (3D kernel) was then applied to the binarized volume to remove further noise caused by imaging and reconstruction; this process excluded voxels that erroneously belonged to foreground or background. Larger speckles and sample preparation artifacts were eliminated with an ad hoc small volume flip algorithm, where small isolated volumes (smaller than 270,000 μm³: 80 000–90 000 connected voxels of erroneous segmentation) were automatically searched and added to the right segment (AC or background) to correct the segmentation.

SDV was formed by first generating a simple surface (SS) by locating the first sample group voxel from the direction of the AC surface (Fig. 1d red contour). The ROI (900 × 900 μm²) was selected visually so that no edge artifacts from sample preparation appeared inside the selected ROI (Fig. 1e). A reference surface (RS) was elevated on top of SS by iterative Delaunay triangulation38 and surface extrema detection (Fig. 1e green contour). The SDV was defined as all of the non‐sample voxels that were limited by the reference surface and sample volume (Fig. 1f gray area).

Parameterized maps of the AC surface were generated using the SDV by calculating several parameter values for each (x, y) coordinate inside the ROI: Maximum Void Depth (MVD): the distance between RS and the deepest SDV voxel at the corresponding (x, y) (Fig. 1g orange line); Integral Void Depth (IVD): the distance between RS and the deepest SDV voxel at the corresponding (x, y), disregarding voxels that are not part of SDV (Fig. 1g cyan line); Shortest Route to Surface (ShRS): the distance between RS and the deepest SDV voxel at the corresponding (x, y) traveling along the SDV (Fig. 1g purple line); and Tortuosity‐like parameter (Tort): ShRS/MVD. For each parameter map, Maximum, Mean and Standard deviation (SD) were calculated within the ROI. Additionally, for each sample, we calculated the following parameters: Relative volume (RelV): Volume of SDV divided by Volume between RS and SS; R_q according to ISO 25178 (from SS):

$$R_q(x,y)=\sqrt{\frac{1}{n}\sum _{i=1}^n{(\overline{z}-z_i(x,y))}^2}$$ (1)

and Complex R_q (CR_q), which takes into account also the underlying sample interfaces:

$${CR}_q(x,y,z)=\sqrt{\frac{1}{m}\sum _{i=1}^m{(\overline{z}-z_{\mathrm{i}}(x,y,k(x,y)))}^2}$$ (2)

where k is the number of surfaces at coordinates (x, y) and m is the total number of complex surface points.

PTA Washout and Histology

Following μCT imaging, the samples were immersed in an ion‐exchanged water‐based washout solution (0.1 M/l Na₂HPO₄, 137 mM/l NaCl, 2.7 mM/l KCL, 0.55 mM/l NaOH) for 5 days to remove the PTA stain. The pH of the solution was set to 10 to reverse the charge of collagen to negative39 and thus to repulse the negatively charged PTA out of the tissue. After PTA washout, the samples were kept in phosphate‐buffered saline (pH 7.4) between 8 and 12 h. Both adjacent and PTA washout samples were subjected to decalcification, paraffin embedded and cut with a microtome to 3 µm sections for Safranin O staining.40 Washout samples were used to visually verify similar structural features between standard histology and CEµCT images. Histopathological OARSI grading4 was performed by two experienced readers microscopically.

Statistical Evaluation and ROC Analysis

Based on visual examination of scatter plots, the relationship between surface parameters and OARSI grade was evaluated by performing a regression analysis for the exponential curve fit. In addition, surface roughness behavior with varying levels of cartilage surface degeneration described by sub scores from the 3D histopathological analysis was evaluated with linear mixed models. Patient number, location and either of the R_q or CR_q were set as subject, repeated and a dependent variable, respectively. Then different models were used for R_q and CR_q by using one of the reference parameters as a fixed variable. Furthermore, R_q or CR_q were compared at different sub‐scores for all reference parameters by using the Wilcoxon test. A p‐value smaller than 0.05 was considered statistically significant. Regression and linear mixed model analyses were performed with SPSS software (Version 24, IBM Corp, Armonk, North Castle, NY).

For each reference parameter (Fissures, Fibrillation and Surface continuity), samples were divided into two categories according to the reference parameter: Normal: 0; Degenerated: >0. Simple marker parameters (Maximum, Mean and SD) were calculated for each of the constructed 2D‐parameter maps. Single‐valued parameters, such as R_q, were used as is. Subsequently, ROC analysis was conducted for each parameter calculated from SDV. AUC was calculated with estimated confidence intervals using 1500 sample bootstrapping (Matlab 2014b).

RESULTS

We developed a novel CEμCT analysis method to quantify a complex 3D micro‐topography of AC within a confined volume (Fig. 3). The ad hoc spatial parameters were established and calculated to describe the features associated with AC surface continuity, fibrillation, and fissures, which were evaluated as a reference using the semi‐quantitative μCT grading.36

Figure 3.

Representative CEμCT slice and corresponding histology from osteochondral plugs with different OA degeneration stages a) Smooth and continuous AC surface with no distinguishable features in parameter maps or 3D surface. b) Discontinuities in AC surface with a cavern‐like structure in the tortuosity map and discernable patterns in a Maximum Void Depth (MVD) map and 3D surface. c) Fibrillation with distinct changes in both MVD and Tortuosity; more areas with surface complexity can be seen on the 3D surface. d) Severe degeneration can be seen in the MVD and tortuosity maps as well as on the 3D surface with very complex defects penetrating to deep AC.

Comparison between conventional histology and μCT images was achieved by selecting a single plane from image stack with a most similar appearance to histology. Typically, degeneration of the AC surface was found to be similar in corresponding μCT slices and conventional histology (Fig. 3). However, when evaluating parameter maps, complex fissures are not always captured in conventional histology (e.g., in Fig. 3b in the case of maximum depth and tortuosity), suggesting that such maps could be useful visual tools for identifying AC surface irregularities. Established parameters were calculated as a function of (x, y) to produce a 2D‐parameter map of an AC surface (Fig. 3). To describe the predominant features in each AC sample, spatial maxima, mean and standard deviation (SD) were calculated for each map:

1. maximum void depth (MVD), a descriptor of the deepest point of the void (“empty” space between AC top surface and reference surface) (Fig. 1g, orange line), was sensitive and specific when used to discriminate intact samples from those with surface discontinuity (AUC: 0.89–0.93) and fissures (AUC: 0.90–0.94), especially those with fibrillation (AUC: 0.94–0.98) (Table 1);

2. integral void depth (IVD), a descriptor of “empty” space distance between AC top surface and a reference surface (Fig. 1g, cyan line), provided high sensitivity and specificity when used to identify surface discontinuity (AUC: 0.88–0.94), fissures (AUC: 0.88–0.94), and fibrillation (AUC: 0.94–0.97) (Table 1);

3. shortest route surface (ShRS) (Fig. 1g, purple line), the shortest route from the reference surface to the deepest point on AC surface, was sensitive and specific when used to identify fibrillation (AUC: 0.91–0.92) (Table 1);

4. parameters describing tortuosity (SHRS divided by MVD) of the voids were inferior markers when used to identify surface discontinuity (AUC 0.71–0.73), fibrillation (AUC 0.86–0.87) and fissures (0.78–0.82) (Table 1).

Table 1.

Area Under the Curve Values for Calculated Global Parameters and Detected Reference Surface Features >0.90 (Gray) and <0.80 (Black)

	Surface Continuity (0: n = 7, ≥1: n = 29)			Fibrillation (0: n = 12, ≥ 1: n = 24)			Fissures (0: n = 18, ≥1: n = 18)
	AUC	LCL	UCL	AUC	LCL	UCL	AUC	LCL	UCL	R 2 for Curve Fit
MVD max	0.92	0.79	0.99	0.97	0.87	1	0.94	0.83	0.99	0.5
MVD mean	0.89	0.62	0.98	0.94	0.78	1	0.9	0.76	0.97	0.44
MVD SD	0.93	0.79	0.99	0.98	0.88	1	0.94	0.81	0.98	0.48
IVD max	0.93	0.8	0.99	0.97	0.82	1	0.94	0.8	0.98	0.5
IVD mean	0.88	0.59	0.98	0.94	0.74	0.99	0.88	0.68	0.96	0.43
IVD SD	0.94	0.78	0.99	0.97	0.85	1	0.93	0.8	0.98	0.48
SHRS max	0.8	0.43	0.96	0.91	0.69	0.99	0.87	0.71	0.95	0.37
SHRS mean	0.84	0.61	0.96	0.92	0.77	0.98	0.89	0.73	0.97	0.43
SHRS SD	0.84	0.49	0.97	0.92	0.72	1	0.89	0.72	0.96	0.42
Tort max	0.71	0.3	0.91	0.86	0.53	0.97	0.78	0.57	0.9	0.15
Tort mean	0.73	0.27	0.91	0.86	0.59	0.97	0.83	0.65	0.94	0.19
Tort SD	0.72	0.32	0.92	0.87	0.58	0.98	0.82	0.62	0.93	0.25
δVoidV	0.81	0.62	0.93	0.91	0.78	0.98	0.87	0.69	0.95	0.26
Rq	0.91	0.78	0.98	0.95	0.79	0.99	0.94	0.81	0.98	0.46
CRq	0.91	0.75	0.98	0.95	0.8	1	0.94	0.82	0.98	0.48
δRq	0.75	0.56	0.89	0.89	0.72	0.96	0.87	0.7	0.96	0.24

Confidence limits (95%) (lower: LCL, upper: UCL) estimated by bootstrapping. The result suggests that normal surface structure (Surface Continuity score = 0), lack of fibrillation (Fibrillation score = 0) and lack of fissures (Fissure score = 0) can be sensitively and specifically (AUC>0.90) delineated from tissue with degeneration (Surface Continuity, Fibrillation or Fissure scores ≥ 1) by most of the experimental parameters, except for tortuosity and relative R_q. In the right most column R ² values for exponential curve fit when comparing surface features and OARSI grade. AUC are shown for maximum (max), mean and standard deviation of Maximum Void Depth (MVD), Integral Void Depth (IVD), Shortest Route to Surface (ShRS), Tortuosity‐like parameter (Tort), simple (ISO 25178) roughness (R_q), roughness complex (CR_q) as well as ratios between simple and complex roughness (δRq) and volume (δVoidV).

In histology, increasingly complex surface structures can be systematically observed at later degenerative stages (Fig. 3c–d Complex Surface). Increasing complexity most likely leads to exponential increase in the parameters describing surface roughness (Fig. 4a–f) with high complexity after OARSI becomes equal or higher than 2.0 (Fig. 4g and h). Exemplary receiver operating characteristic (ROC) curves for each of the AC features (surface continuity, fibrillation, and fissures) are presented in Figure 5, which presents the ROC curves for the best classifier (Highest AUC value) and R_q for each reference parameter (Surface continuity, Fibrillation, and Fissures).

Figure 4.

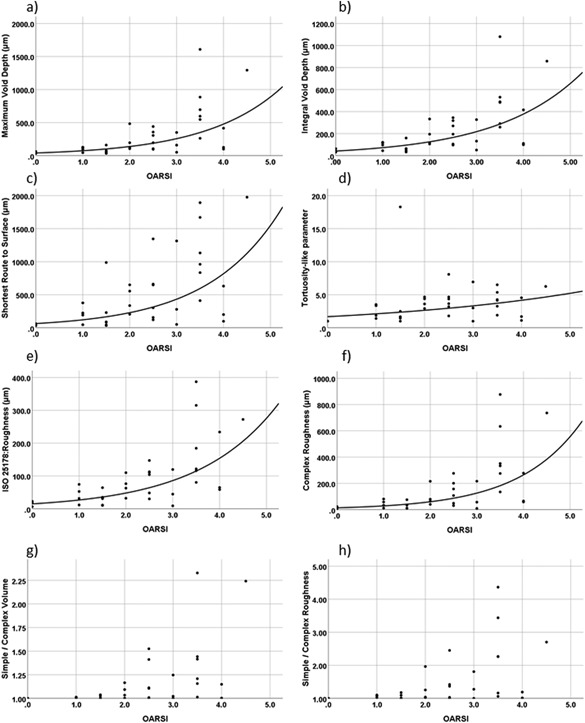
Relationships between histopathological OARSI grade and maximum values of novel parameters describing cartilage damage (a–d) as well as both standard (e) and complex (f) roughness. Except for Tortuosity‐like parameter, most of these parameters show an exponential increase with cartilage damage, especially after grade 3, where fissures become complex/branched. However, when evaluating ratios between complex and simple volumes (g) and roughness (h), it can be appreciated that complex features are present from very early osteoarthritis (OARSI ≥ 2.0).

Figure 5.

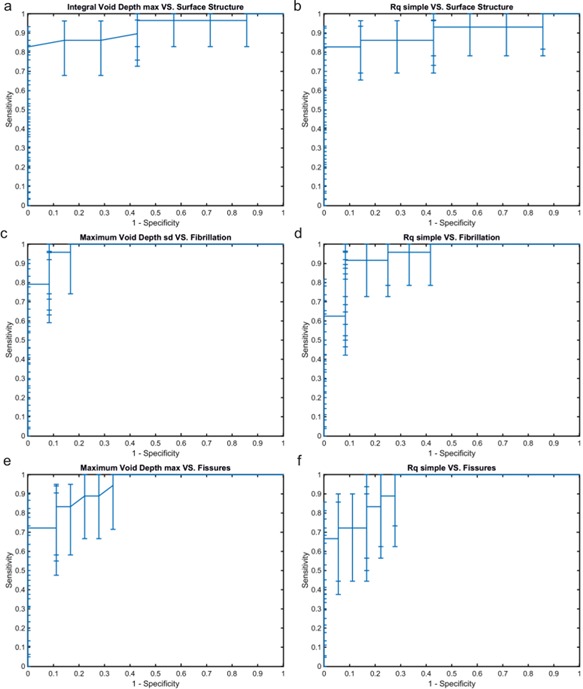
To compare sensitivity and specificity of simple roughness and novel parameters describing surface topology to detect surface structure, fibrillation and fissures ROC analyses were performed. The ROC curves of the best classifier for each reference parameter selected by AUC and estimated lower confidence limit and the corresponding ROC curve are shown. We can see that integral void depth a) has better sensitivity for identifying surface structure compared with simple roughness b). Similarly, maximum void depth has higher sensitivity for detecting fibrillation compared to simple roughness. Sensitivity and specificity for detecting fissures were similar between simple roughness f) and maximum void depth f).

The conventional surface roughness parameter R_q (ISO 25178), which assumes a simple AC surface, identified the presence of surface discontinuities (AUC 0.91 [0.78 0.98]), fibrillation (AUC: 0.95 [0.79 0.99]) and fissures (AUC: 0.94 [0.81 0.98]). The complex surface roughness parameter CR_q performed identical to R_q when used to identify surface discontinuity but marginally better when R_q was used to detect fibrillation (AUC: 0.95 [0.80 1.00]) and fissures (AUC: 0.94 [0.82 0.98]). The ratio of CR_q and R_q identified fibrillation (AUC: 0.89 [0.72 0.96]) and fissures (AUC: 0.87 [0.70 0.96]). The mean values of R_q were significantly smaller than the corresponding CR_q values especially with low and moderate reference sub‐scores (Fig. 6). The ratio of void volumes assuming either a simple AC surface or a complex AC surface was also sensitive and specific when used to detect fibrillation (AUC: 0.91 [0.78 0.99]). Both CR_q and R_q showed a significant increase from mild to moderate surface fibrillation and continuity. Furthermore, only CR_q showed a significant difference between intact and lowest fissure sub‐score and was able to show significant changes for highest fissure sub‐scores.

Figure 6.

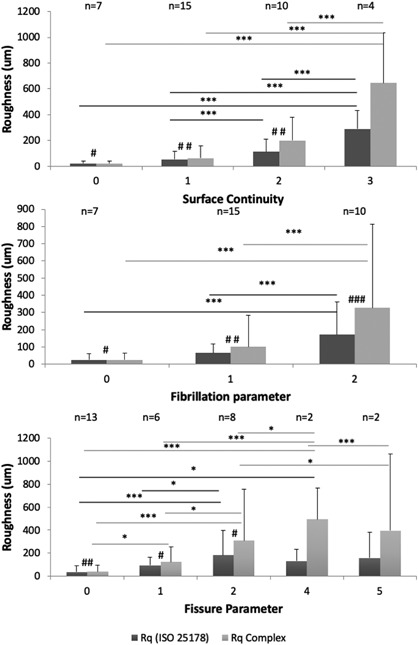
Complex Roughness (CR_q) and ISO 25178 Roughness (R_q) plotted as functions of reference parameters, which are defined as following: Surface Continuity (Smooth and continuous = 0; Slightly discontinuous = 1; Moderately discontinuous = 2; Severely discontinuous = 3), Fibrillation (Absent = 0; Few = 1; Many = 2) and Fissure (Zone 1 absent = 0; Zone 1 present = 1; Zone 2 top half present = 2; Zone 2 lower half present = 3; Zone 3 top half present = 4; Zone 3 lower half present = 5). Dark gray presents standard R_q and light gray actual complex surface roughness described by CR_q. For linear main effects in mixed models *p < 0.05; **p < 0.005 and ***p < 0.001 and for pairwise Wilcoxon test #p < 0.05; ##p < 0.005 and ###p < 0.001. These results show that realistic CR_q roughness values are significantly larger than R_q that underestimates the actual complex surface roughness. Furthermore, CR_q significant difference between intact and slightly fissured cartilage surface.

DISCUSSION

In this study, we developed a novel CEμCT analysis method to semi‐automatically segment, parameterize and quantify micro‐topographical features of a complex AC surface with increasing OA severity. Several parameters, especially MVD‐ and IVD‐based parameters, exhibited sensitivity and specificity when used to detect early micro‐topographical changes in AC, that is, fibrillation, as revealed by ROC analyses. Consequently, these parameters are potential markers for detecting early superficial AC degeneration (fibrillation) in 3D from AC samples (Table 1 and Fig. 5).

In addition to MVD and IVD, the shortest route from a reference surface to the deepest point (ShRS) of AC top surface exhibited the ability to identify fibrillation. Similar performance was observed with the relative volume parameter. MVD, IVD, and ShRS are candidates for identifying fissures, which could be used to identify these features in computational 3D‐histopathological grading of AC tissue on an automatic or semi‐automatic basis. Obtaining these parameters requires little user input from segmented sample data; the user only needs to select the AC surface region for analysis appropriately. Parameter maps provide simple color map visualization of the complex AC surface features and allow visual validation of the analysis region.

With regard to quantitative surface roughness parameters, R_q and CR_q were observed as potential identifiers for fibrillation and fissures. The R_q values in this study ranged from 20.5 ± 20.3 μm (mean ± 95%CI) for an intact surface (n = 7) to 289.6 ± 143.8 μm in samples with severe surface discontinuity (n = 4). The respective values for CR_q were 21.3 ± 21.8 μm in AC with intact surface (n = 7) and 644.9 ± 390.7 μm for a severely discontinuous surface (n = 4). In the previous literature, AC has been evaluated as follows:

1. Using stylus profilometry on acrylic replicas of AC from the human femoral head and acetabular AC, Walker et al. demonstrated a roughness of 48–320 μm in healthy and osteoarthritic human subjects (8‐month‐old fetus: Adults, age range = 26–67 years).6 Similarly, Sayles et al. demonstrated with profilometry an RMS roughness of 3.3–6.5 μm in normal human femoral condyle AC41;

2. Clarke et al. used SEM to detect 1‐ to 6‐μm deep depressions with an estimated diameter of 15–30 μm in the human femoral head and acetabular AC (age = 32–64 years) with no obvious signs of degeneration.8 Bloebaum et al. used stereographic SEM in human talus to detect AC irregularities with a height of 0.57–21.23 μm (age: 15–40)10;

3. Brill et al. used OCT in 105 samples and 20 TKR subjects (age range = 48–83 years) from femoral condyle and tibial plateau to demonstrate a roughness of R_q 0.2–4, 0.4–15, 4–11 μm for degenerative joint disease score (a surface‐focused Mankin score)3 grades 0, 3 and 6, respectively.22 Saarakkala et al. reported an OCT‐based R_q of 8.5 μm for intact bovine patella and R_q of 39.8 μm for enzymatically degraded patella.21

4. Saarakkala et al. reported ultrasonically determined R_q roughness values in the range of 6.8–12.3 μm before mechanical or chemical degradation and 12.4–34.8 μm after degradation.16 In their subsequent study, the average R_q in bovine patella was reported to be 7.4 μm for intact (Mankin score = 0) and 24.2 μm for spontaneously degenerated AC (Mankin score 1–11).17 Kaleva et al. reported an average ultrasound‐based R_q of 6.4 μm in intact bovine patella, 21.7 μm in enzymatically degenerated bovine patellar AC and 87.7 μm for spontaneously fibrillated human tibial plateau AC.18

5. Kaleva et al. reported a histology‐based average R_q of 4.8 μm in intact bovine patella, 26.9 μm with enzymatically degenerated bovine patella and 44.2 μm for fibrillated human tibial plateau.18 Adler et al. demonstrated histology‐based roughness of human femoral head with values of 7.9, 29.1, and 49.1 μm for smooth, intermediate and rough AC surfaces. US backscattering roughness measurement11 was further explored by Chiang et al. They reported a computed roughness (associated with R_q) of 5, 20, 37, and 100 μm for smooth, normal intermediate and rough human femoral condyles, respectively.13

By comparing the result of this study regarding AC surface roughness with earlier literature, it seems that the R_q values fall into the same value range as the values reported in earlier literature. However, the absolute values of CR_q in disrupted AC were considerably greater than the R_q values reported in this or earlier studies. On the other hand, in non‐degenerated AC, the CR_q values converge to those of R_q (Fig. 5). By definition, CR_q (Eq.  2) should converge to R_q (Eq.  1) when the surface complexity converges towards a simple surface. This feature explains the underestimation of detected roughness using R_q, especially in degenerated AC. In practice, when the roughness of AC is complex, the micro‐topography cannot be adequately described by assuming a simple surface, especially with OARSI grades equal or higher than 2.0. This reinforces the notion of quantifying the complex AC surface rather than assessing the AC using the simple surface approximation. Furthermore, the presented surface characterization method could be extended to the assessment of other materials, with complex surface features at different length scales. Consequently, the proposed roughness analyses are complementary to pre‐existing roughness analyses.

We used CEμCT to generate the volumetric image data for the AC surface micro‐topography analyses. The presented methodology can be applied to other modalities, such as light sheet microscopy and second‐harmonic imaging microscopy. The complex surface roughness, CR_q, could also be simplified to quantify 2D roughness, for example, for analysis of histological sections. The presented analysis method is suitable to the surface micro‐topography information gained by conventional surface roughness measurement techniques, such as profilometry, but provides little additional information given the assumption of a simple AC surface. Although clinical applications of the presented methodology may only be useful for characterizing OA far in the future given the current low resolution of these modalities, we foresee that the proposed method could potentially be used to evaluate AC degeneration or repair/regeneration in research and pharmacological studies as part of 3D histological grading.

There are also some limitations in this study. Reliable AC segmentation is essential for the analysis to produce relevant data. In this study, we used CEμCT protocol that provides excellent contrast but is not suitable for in‐vivo use. Currently, a user must manually check and correct the segmentation for each sample. Thus, a more robust segmentation method is needed in the future to automate the analysis process further. Moreover, the route calculation algorithm that extracts the ShRS and Tort parameters is computationally expensive (several hours to days by a modern multiprocessor computer), which reduces the cost‐benefit ratio of these parameters especially in time‐critical applications.

To summarize, this study introduced a novel semi‐automatic analysis method to quantify micro‐topographical features of complex degenerated AC surfaces in 3D volumes using CEμCT. This study also extends the concept of surface roughness assessment from simple to complex surfaces. The ordinary surface roughness parameter R_q assuming a simple surface was inadequate to characterize the complex surface morphology of AC quantitatively. However, roughness parameters, including R_q, CR_q, IVD, MVD, and ShRS, identified OA‐related surface features, such as fissures and fibrillation, with high specificity and sensitivity.

The developed analysis method could be used to more reliably and objectively characterize AC surface micro‐topography for determination of AC degeneration. It could also be used for verifying regeneration or repair resulting from therapy. Our method may find use in research as a reference methodology and operator‐independent in vitro diagnostics in the field of OA. Moreover, this approach could also find use outside the scope of OA or the field of medicine in applications where topological properties are crucial for modulating friction and flow.

AUTHORS' CONTRIBUTIONS

T.Y., H.K.G, S.S.K, M.F, H.S, E.H, K.P.H.P, S.S, and H.J.N contributed to the conception and design of the study. T.Y., H.K.G, S.S.K, M.F, H.S, E.H, K.P.H.P, S.S, and H.J.N participated in acquisition and analysis of the data. All authors contributed to interpreting the data, drafting or revising the manuscript and approved the submitted version of the manuscript.

ROLE OF THE FUNDING SOURCES

The Academy of Finland and the European Research Council are not associated with the scientific content of the study.

COMPETING INTEREST

Prof. Edward Hæggström, Assoc. Prof. Simo Saarakkala, Dr. Heikki J. Nieminen, Mr Tuomo Ylitalo are inventors in a patent application related to μCT imaging of articular cartilage. Dr. Harpal K. Gahunia, Mr Sakari S. Karhula, Dr. Mikko Finnilä, Dr. Heikki Suhonen, Dr. Maarit Valkealahti, Prof. Petri Lehenkari and Prof. Kenneth P.H. Pritzker declare no potential conflicts of interest.