Evaluating corrections for Eddy‐currents and other EPI distortions in diffusion MRI: methodology and a dataset for benchmarking

Abstract

Purpose

To propose a methodology for assessment of algorithms that correct distortions due to motion, eddy‐currents, and echo planar imaging in diffusion weighted images (DWIs).

Methods

The proposed method evaluates correction performance by measuring variability across datasets of the same object acquired with images having distortions in different directions, thereby overcoming the unavailability of ground‐truth, undistorted DWIs. A comprehensive diffusion MRI dataset, collected using a suitable experimental design, is made available to the scientific community, consisting of three DWI shells (Bmax = 5000 s/mm²), 30 gradient directions, a replicate set of antipodal gradient directions, four phase‐encoding directions, and three different head orientations. The proposed methodology was tested using the TORTOISE diffusion MRI processing pipeline.

Results

The median variability of the original distorted data was 123% higher for DWIs, 100–168% higher for tensor‐derived metrics and 28–111% higher for MAPMRI metrics, than in the corrected versions. EPI distortions induced substantial variability, nearly comparable to the contribution of eddy‐current distortions.

Conclusions

The dataset and the evaluation strategy proposed herein enable quantitative comparison of different methods for correction of distortions due to motion, eddy‐currents, and other EPI distortions, and can be useful in benchmarking newly developed algorithms.

1. INTRODUCTION

In the past couple of decades, Diffusion Tensor Imaging (DTI) ¹ and high angular resolution diffusion imaging (HARDI) ² , ³ , ⁴ , ⁵ , ⁶ , ⁷ have been extensively used to investigate the architectural, microstructural and compositional features of the human brain. ⁸ It is well known that obtaining reproducible and accurate diffusion MRI results is challenging given that diffusion weighted images (DWIs) are susceptible to artifacts, including image misregistration due to motion, that need to be corrected in preprocessing (See ⁹ for a review). DWIs are typically acquired with echo‐planar imaging (EPI) and suffer from geometric distortions along the phase‐encoding direction caused by the low bandwidth‐per‐pixel. ¹⁰ The most thoroughly analyzed EPI distortions in the field of diffusion MRI are those induced by eddy‐currents and cause misalignments among different DWI volumes. ¹¹ Eddy‐current‐induced distortions, which occur due to the rapid switching of diffusion gradients, are functions of the magnitude and direction of the applied diffusion gradients and mostly affect the DWIs, but not significantly the so‐called b = 0 s/mm² images. It is widely accepted that, in addition to accounting for subject motion, these distortions must be corrected to perform a reliable analysis, and numerous methodologies have been proposed to remedy these distortions. It is now recognized that eddy‐current‐distortion correction using affine transformations ¹¹ , ¹² is inadequate, ¹³ , ¹⁴ but methods that employ higher order deformation models ¹⁴ , ¹⁵ are capable of achieving near‐excellent correction performance.

Other EPI‐related distortions include those originating from static B ₀ field inhomogeneities due to magnetic susceptibility variations within the object, imperfect shimming, ¹⁰ and concomitant fields. ¹⁶ These distortions differ from eddy‐currents‐induced distortions, as they affect all DWIs, including the b = 0 s/mm² images in the same manner in the absence of motion. Such distortions, which we will collectively refer to as “EPI distortions,” have been shown to have a significant impact on the accuracy and reproducibility of tensor‐derived scalar maps ¹⁷ and fiber tractography. ¹⁸ Correction of EPI distortions generally requires acquisition of additional data, and several methodologies to correct for these distortions, including field‐mapping, ²² elastic registration ¹⁷ , ¹⁹ , ²⁰ and reversed phase‐encoding (or blip‐up blip‐down phase‐encoding), ²¹ , ²² , ²³ , ²⁴ have been proposed.

Optimization of diffusion MRI processing pipelines is still an active area of research, with novel strategies for artifact removal, denoising, and distortion correction still being proposed. Evaluating the performances of these correction strategies is a challenging task for eddy‐currents and EPI distortions. One approach for validation is to use simulated data with known ground‐truth generated with MRI simulators such as POSSUM from the FSL package. ²⁵ However, with real acquisitions, ground truth images are rarely available. Therefore, a typical approach is to compare corrected EPI images to an undistorted structural image, such as a T ₁‐weighted or T ₂‐weighted image, with different quality measures such as outlines, similarity metrics, or segmentation overlaps. Even though several of these measures are quantitative, large variations in validation procedures complicate a direct and meaningful comparison of these techniques. Moreover, evaluations are often performed on images that are not available to other researchers. Data repositories containing sets of images suitable for these tasks would also be very valuable, but few exist. The repository most relevant to this work is the recently published MASSIVE database, ²⁶ which is intended to facilitate diffusion MRI signal modeling. Most other image repositories, such as the Human Connectome Project (HCP), ²⁷ are not designed to perform quality control or reproducibility analysis.

In this work, we propose an analysis method for quantitative validation of eddy‐currents and EPI distortion correction strategies and provide a new dMRI dataset that is specifically designed for the proposed methodology. The design of the dataset enables quantitative validation of distortion correction performance without the need for ground truth images.

In Table 1, we summarize important features of this comprehensive dataset and compare and contrast it to MASSIVE: These two datasets serve two different purposes. While MASSIVE has features ideal for signal modeling, such as dense q‐space sampling or Cartesian grid‐based sampling, the proposed dataset offers other features, such as the acquisition of data with four phase‐encoding directions, which enables the assessment of EPI distortion correction quality. Additionally, it contains data with large differences in head position and orientation, which are absent in the MASSIVE data, to enable investigation of motion correction strategies and the secondary effects of motion on susceptibility.

Table 1.

Features a comprehensive dMRI dataset should have and a comparison between the proposed and the MASSIVE datasets

Features	Proposed Dataset	MASSIVE
High SNR	✓	✓
High Resolution
Multiple spherical shells	✓	✓
Dense q‐space distribution		✓
Cartesian q‐space sampling		✓
North & south hemisphere q‐space sampling	✓	✓
Two phase‐encoding direction acquisition	✓	✓
Four phase‐encoding direction acquisition	✓
Multiple head orientations	✓
Axial, sagittal coronal acquisitions
High quality T 1 W and T 2 W images	✓	✓
Fat‐suppressed T 1 W or T 2 W images	✓

2. METHODS

2.1. Distortion correction quality assessment

Obtaining undistorted ground truth DWIs for assessing the performances of distortion correction algorithms would require acquiring multi‐shot non‐EPI spin‐echo images, which would be very time consuming and the resulting images would likely suffer from ghosting. The main motivation that led to the development of the proposed distortion correction assessment methodology was that ground‐truth images are rarely available for dMRI. Therefore, one needs to rely on the DWI data itself to derive measures of correction quality. The philosophy behind the proposed framework is that if two datasets are acquired in a noise‐free environment with identical diffusion experimental designs, but with different acquisition parameters that only affect distortions, the acquired images would have identical contrast but differ only in distortions. Therefore, if a perfect distortion correction method existed, its application to these two datasets would produce identical images. An imperfect correction method, however, would not produce identical images and the difference between the two corrected images would be attributable to residual distortions. Therefore, variability metrics detecting remaining differences between corrected images can be used for a quantitative evaluation of correction quality.

2.1.1. Eddy‐currents distortions

In the absence of motion, and if diffusion effects of imaging gradients are negligible, displacement fields due to eddy‐current distortions would be similar in magnitude but in opposite direction when the diffusion gradients are played out with the same orientation but different polarities. To formalize, let i be the volume index, g _i be the i ^th diffusion gradient, I _i be the corresponding distorted (raw) DWI, $I_i^{\prime }$ be the corresponding distortion‐free image, ϕ_i be the displacement field and $\mathcal{J}$ be the determinant of the Jacobian operator to account for signal compression and expansion due to these distortions. Then,

$$I_i^{\prime }\left(\mathbf{x}\right)=I_i\left(\mathbf{x}+{\mathrm{\varphi }}_i(\mathbf{x})\right)\mathcal{J}\left({\mathrm{\varphi }}_i(\mathbf{x})\right)\text{for}{g}_i$$ (1)

For the opposite gradient direction, −g _i, disregarding the effects of imaging gradients, the diffusion contrast would be identical to g _i but the displacements would be different as described in. ¹⁵ In the remainder of this manuscript, I ^N (N standing for north) will refer to images acquired with diffusion gradients with positive z components and I ^S (S for south) will refer to images corresponding to the antipodal direction with negative z components. In the absence of other artifacts, for the same phase‐encoding direction, I ^N and I ^S will have the same diffusion contrast but different distortions. Therefore, with a perfect eddy‐currents distortion correction method, the corrected images $I_i^{\prime N}$ and $I_i^{\prime S}$ would be identical.

For diffusion MRI acquisitions, it is uncommon to acquire images with diffusion gradients spanning the full diffusion sphere, especially with exact hemisphere replicates, as this design does not provide any additional q‐space sampling. However, if such a dataset existed, it would be possible to quantitatively assess the quality of the correction by computing a voxelwise map of the differences of the corresponding corrected images from the two hemispheres using, for example, a Mean‐Squared‐Error (MSE) metric:

$${\text{MSE}}_{\text{eddy}}=\left(\frac{1}{n}\sum _{i=1}^n\left(\Vert I_i^{\prime N}-I_i^{\prime S}{\Vert }^2\right)\right)$$ (2)

2.1.2. Other EPI distortions

The displacements due to EPI distortions occur along the phase‐encoding direction: a dataset acquired with Anterior‐Posterior (AP) phase‐encoding theoretically has distortions opposite to those acquired with Posterior‐Anterior (PA) direction. Similarly, data acquired with Right‐Left (RL) and Left‐Right (LR) phase‐encoding have opposite distortions, which occur along the x‐axis for axial acquisitions. This concept gave rise to a relatively new family of EPI distortion correction methods, referred in this manuscript as blip‐up blip‐down correction. ²¹ , ²² , ²⁴ , ²⁸

For EPI distortion correction quality assessment, we build on principles we started developing in our previous works. ¹⁷ , ²⁴ Let AP_corr, PA_corr, RL_corr and LR_corr be the images acquired with different phase‐encoding and corrected for EPI distortions with traditional techniques, such as field‐mapping or elastic image registration. A perfect distortion correction algorithm, with both geometric distortion correction and proper signal redistribution, would be able to produce morphologically identical corrected images. Therefore, a measure of voxelwise variance computed from these four corrected datasets would be informative of the correction performance of an algorithm. These variance maps can be computed from the b = 0 s/mm² images, DWIs, or tensor/HARDI‐derived scalar maps, such as the trace (TR), fractional anisotropy (FA), propagator anisotropy (PA), or non‐gaussianity (NG). Blip‐up blip‐down correction algorithms might combine data with the same phase‐encoding orientation, producing APPA_corr or RLLR_corr images. Therefore, to benchmark the quality of a blip‐up blip‐down correction, one needs to have data acquired with all four phase‐encoding directions, and compute MSE maps between APPA_corr and RLLR_corr images.

For algorithms performing simultaneous correction of distortions due to motion, eddy‐currents, and other EPI distortions or for a complete distortion correction check, the two proposed correction‐quality assessment approaches can be combined and performed on the final corrected data.

2.2. Dataset

The experimental design of the accompanying dataset was tailored toward enabling the assessments described in the previous section. DWIs were collected from a single healthy volunteer on a 3T Siemens Prisma scanner with a single‐shot spin‐echo EPI sequence (resolution = 2.5 mm isotropic, matrix size = 96 × 96, 64 slices, TR/TE = 9300/89 ms). Twice‐refocusing was disabled and a GRAPPA factor of two was used. A single acquisition session consisted of three volumes with b = 0 s/mm² and 30 diffusion weighted volumes with gradients sampled uniformly from the northern hemisphere (33 volumes). This acquisition was repeated for three b‐values: b = 1000, b = 2500, b = 5000 s/mm², with identical diffusion gradients to generate the north dataset (99 volumes). The b = 1000 s/mm² and b = 5000 s/mm² shells were reacquired with identical diffusion gradient orientations, but with opposite diffusion gradient polarity (south dataset, 165 volumes). This set was subsequently repeated for four different phase‐encodings: AP, PA, RL, and LR (660 volumes). Finally, to be able to test the effect of motion on EPI distortions and data reproducibility, this acquisition scheme was repeated twice more on different days with different head orientations (once with 25^∘ rotation along the z‐axis and once with 8^∘ along the x, 19^∘ along the z‐axes), yielding a total of 1980 volumes. These positions will be referred to as Pos ₁, Pos ₂ and Pos ₃ in the remainder of the manuscript. Additionally, T ₁‐weighted and fat‐suppressed T ₂‐weighted fast spin‐echo structural images were acquired for prospective users to test their nonlinear registration algorithms to generate field‐maps. The entire acquisition was performed in three sessions and took nearly 7 total hours of scan time. Informed consent was obtained from the subject with a research protocol approved by the Institutional Review Board. The raw distorted images, the images that underwent correction with the TORTOISE dMRI processing pipeline, ²⁹ the structural images, and the brain masks used in the analysis are available to researchers upon request.

2.3. Pre‐processing

For all tests, the DIFFPREP component of the TORTOISE was used to correct both motion and eddy‐currents distortions, and the DR‐BUDDI ²⁴ component was used for blip‐up blip‐down EPI distortion correction. DWIs were initially corrected for Gibbs‐ringing artifacts ³⁰ and motion and eddy‐currents distortions were corrected simultaneously as described in. ¹⁴ After distortion correction, the DWIs were rigidly aligned to the ACPC oriented T ₂‐weighted structural image, as typically done by the TORTOISE pipeline (www.tortoisedti.org). The final DWIs were output with this orientation at 1.5 mm isotropic resolution and the diffusion tensors were estimated using non‐linear fitting and the MAPMRI parameters were estimated using constrained quadratic‐programming.

2.4. Distortion correction tests

Four distortion correction tests were performed and for each test, variability maps for various target quantities were computed as described in the Appendix in order to asses the performance of the correction. The first test addressed the effect of correcting for small motion, eddy‐currents, and EPI distortions. It used only the Pos ₁ subset. For each phase‐encoding direction, and for the north and south data, the datasets were initially corrected for motion and eddy‐currents distortions and subsequently for EPI distortions. For this blip‐up blip‐down correction, the north and south datasets were corrected separately, producing the four corrected sets: ${\text{APPA}}_{\text{corr}}^{\text{north}},$ ${\text{APPA}}_{\text{corr}}^{\text{south}},$ ${\text{RLLR}}_{\text{corr}}^{\text{north}}$ and ${\text{RLLR}}_{\text{corr}}^{\text{south}}$. The modalities that we evaluated were: average DWI variability maps calculated separately for each diffusion shell; FA, TR and primary eigenvector variability maps from the DTI model; and PA, NG and return‐to‐origin‐probability (RTOP) variability maps computed from the MAPMRI model. ³¹ The primary eigenvector variability maps were computed voxelwise using the dispersion measure described in. ³² For the DTI model, DWIs with b‐values larger than 1000 s/mm² were excluded from the fitting process. To compare the variability maps of the corrected and distorted data, the b = 0 s/mm² image for each of the four subsets was rigidly registered to the T ₂‐weighted structural image and this transformation was applied to all of the DWIs, including the resampling step.

The second test was identical to the first one; however, it was performed on the entire dataset, including the three Pos components to evaluate the performance of the correction pipeline with respect to large motion. This was the most comprehensive test, because all possible distortion and misregistration effects were assessed simultaneously.

The third and fourth tests also used the entire dataset, but were aimed at assessing the specific effects of correcting EPI distortions. For these experiments, variability of FA and TR were tested.

The third test aimed to emulate the case where data can differ for both subject positioning and phase‐encoding direction of the acquisition. This mimics the case in which historic data from different centers are pooled for analysis, similarly to what is performed by the ENIGMA initiative. ³³ In this situation different sites may even have different phase‐encoding directions in their acquisitions. For this test, the 12 datasets from four phase‐encoding directions and three head orientations were stacked together for variability computations.

The fourth test aimed to simulate a longitudinal scan by computing the variability over the head position subsets assuming the the phase encode direction would not change. Differences in head positions and shimming could cause non‐negligible differences in EPI distortions, ¹⁰ , ³⁴ even with acquisitions of the same subject on the same scanner. In this case, the maps were computed separately for each phase‐encoding direction, once for fully‐corrected datasets and once for the versions corrected for only motion and eddy‐currents distortions. The goal of this test was to uncover how much variability is introduced to the data due to EPI distortions.

An additional test was performed and provided in the Supporting Figures S1–S3 to demonstrate the use of the variability concept from a series of repeated scans on the same subject in order to determine non‐distortion related sources of variability such as physiological noise and cardiac pulsation. This additional dataset was collected on a Philips Achieva 3T system with 10 repetitions of AP, PA, LR and RL phase‐encoded data, each with a single b = 0 and eight b = 1100 s/mm² images.

3. RESULTS

Figure 1 illustrates features of the provided dataset: the diffusion weighting levels, different head orientations, and the magnitude of eddy‐currents and EPI distortions are displayed in different rows of the figure. As can be seen from Figure 1A, the shell with the largest diffusion weighting, ie, b = 5000 s/mm², still has sufficient signal for distortion correction quality assessment. Additionally, both the eddy‐current distortions and EPI distortions are detectable at visual inspection (Figure 1C and D). The dataset also contains significant motion in the form of different head orientations (Figure 1B).

Figure 1.

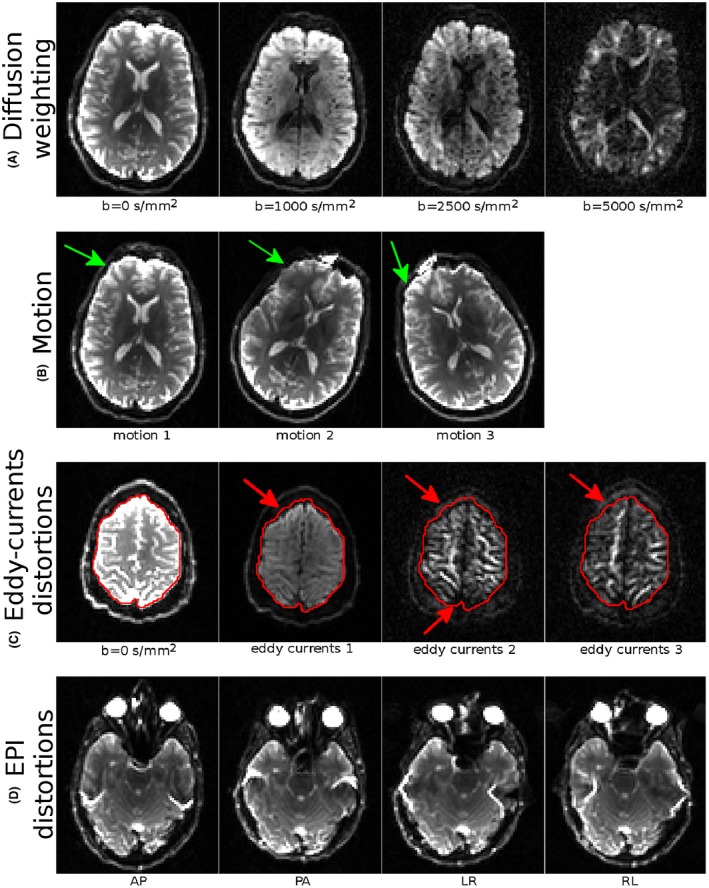
Salient features of the provided dataset. (A) Different diffusion weighting (window level set separately for each image). (B) Different head orientations. The green arrows point to regions with different signal intensities due to coil sensitivity. (C) Illustration of the level of eddy‐currents distortions. Red arrows indicate regions with significant mismatch between a DWI and the b = 0 s/mm² image. (D) Magnitude of EPI distortions for each phase encoding directions

3.1. Assessment motion, Eddy‐currents, and EPI distortion corrections

3.1.1. Single head orientation

Figure 2 displays the variability maps for the dataset with the first head orientation at two different slice levels. The first column of the figure displays the standard deviations (computed according to Equation (A1) in the Appendix) of all b = 0 s/mm² images in the four subsets. The variability in the distorted data can be attributed to positional differences among images and EPI distortions. The second column displays the DWI variability (Equation (A2)), for the b = 5000 s/mm² shell, which also includes the effects of the eddy‐currents distortions. The other three columns display the variability of tensor‐derived quantities, FA and TR (Equation (A3)), and the primary eigenvector of the diffusion tensor (Equation (A6)).

Figure 2.

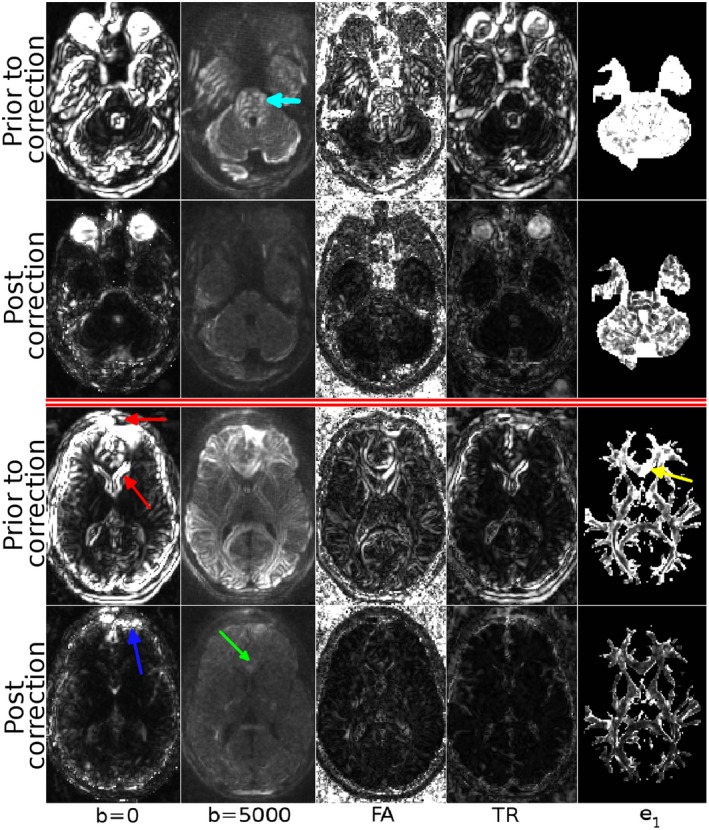
Variability maps before and after eddy‐current and EPI distortion correction. The maps were computed from the raw, distorted dataset and fully corrected datasets to illustrate the quality assessment pipeline. The maps are visualized at two difference slice levels. The first two columns display the standard deviations of two shells of the diffusion weighted images, and the next three columns represent the tensor‐derived quantities, FA and TR, and primary eigenvectors respectively. W/L are identical column‐wise

It is evident from the figure that motion and distortion correction significantly reduces the overall variability, as indicated by the larger (brighter) values in the maps for the uncorrected data. The misalignments among the b = 0 images of the uncorrected data cause large variations near the periphery of the brain and around the ventricle regions (red arrows). Correction significantly reduces this variability, however, residual misalignments due to EPI distortions can still be observed near the frontal edges of the brain (blue arrow). For the b = 5000 s/mm² shell of the uncorrected data, there is significant variation within the brain stem/pons regions (light blue arrow). Additionally, in the second slice, misalignment of gyri/sulci is evident from the standard deviation map. Distortion correction successfully reduced this variability. The misalignments that could be observed in the uncorrected b = 5000 s/mm² shell were reflected into the fractional anisotropy variability map, which showed a similar pattern in structures within the pons, high variability at the boundaries between white matter and CSF, and in white and gray matter. Similar to b = 0, the Trace variability was the largest near the periphery of the brain and around the ventricles, but was low inside the brain. The primary eigenvector variability map indicated large deviations even in directionally homogeneous regions, such as the genu of the corpus callosum (yellow arrow). After distortion correction, the variability of all the tensor‐derived quantities was substantially reduced.

Table 2 summarizes the median variability metric values for both the uncorrected and corrected data, for the same modalities. For all of the examined modalities, distortion correction significantly decreased the variability compared to the distorted version, hence increasing the agreement among DWIs and AP and RL encoded data.

Table 2.

Median variability values for the modalities displayed in Figure 2 and 4. These values were computed from the whole brain, except for e ₁ that was computed only in regions with FA higher than 0.2

Median σ	b = 0	b = 5000	FA	TR	e 1	PA	RTOP	NG
Distorted	14.45	4.25	0.045	129.61	0.132	0.074	0.032	0.047
Corrected	5.25	2.24	0.019	65.10	0.036	0.035	0.025	0.028
% increase in distorted	175%	90%	137%	99%	267%	111%	28%	68%

The proposed quality assessment technique can also be used to assess the effect of correction on higher order diffusion models. To illustrate this concept, the MAPMRI model ³¹ was fit to the same datasets, and several scalar maps were computed. Figure 3 displays these scalar maps. The variability from these maps, displayed in Figure 4, was computed with Appendix Equation (A3), and the median values can be found in Table 2. MAPMRI‐derived variability maps exhibit a similar behavior to their DTI counterparts. However, one interesting aspect is the sensitivity of the RTOP measures to EPI distortions. This map contains very large values both near the orbito‐frontal cortex (red arrow) and around the ventricles (blue arrow). The pattern near the orbito‐frontal cortex was not evident with other MAPMRI‐derived or tensor‐derived measures. Similarly to DTI, distortion correction was able to reduce the variability and remove most structured patterns from the maps, although for NG and PA, high variability, remains in regions of partial volume between tissue and CSF, where even subvoxel misregistration can have a large impact on these metrics.

Figure 3.

Scalar maps derived from the MAPMRI model. PA: Propagator anisotropy, describing the difference of the propagator from an isotropic one. RTOP: Return to origin probability, describing the probability that a water particle will return to its starting position, which is inversely proportional to pore size. NG: Non‐gaussianity

Figure 4.

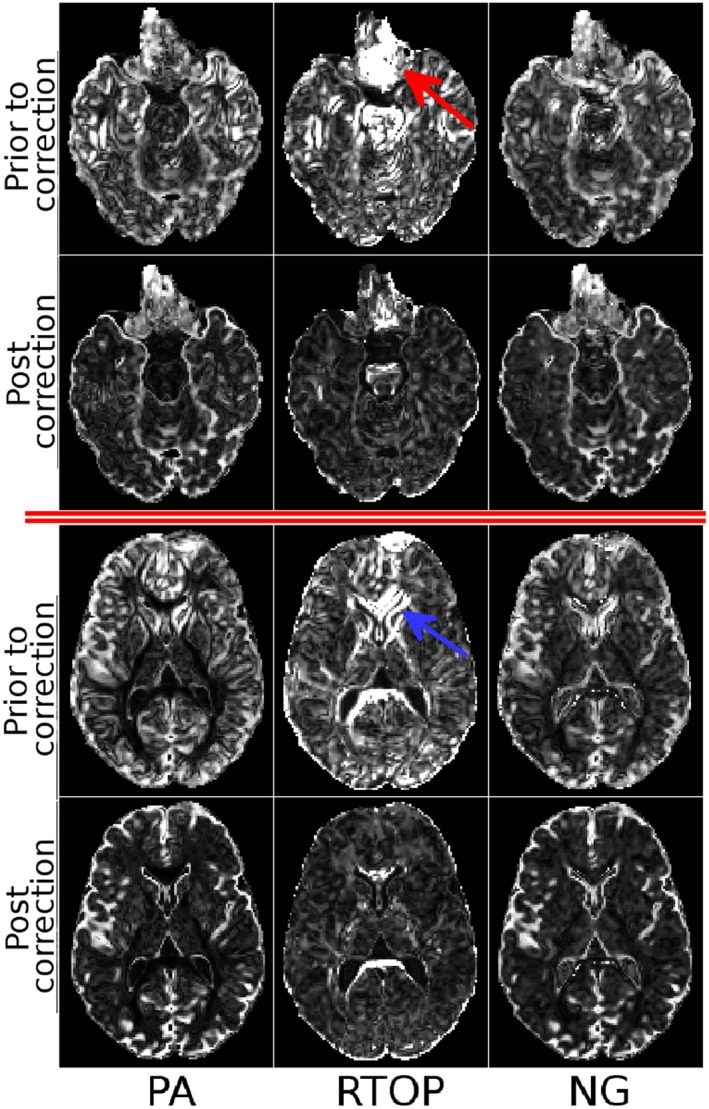
Variability maps using the MAPMRI diffusion model computed from the raw, distorted dataset and fully corrected datasets. Variability maps are visualized at two different slice levels. The columns visualize the variability of PA, RTOP and NG. Window and leveling are identical column‐wise

3.1.2. Multiple head orientations

The previous test used only a single head orientation from the entire dataset. Table 3 reports the variability values for the DTI and MAPRI‐derived quantities computed using all head orientation subsets. The TORTOISE pipeline was able to correct for the large orientational differences in the dataset, and the quantitative measures show similar behavior, with the values being significantly reduced for both the DTI and MAPMRI‐derived maps after correction. The figure corresponding to this data subset is omitted as the images appear very similar to those in Figure 2.

Table 3.

Median variability values for the tensor and MAPMRI‐derived modalities. The values were computed only from the brain tissue region using a brain mask for both the distorted and distortion corrected data

Median σ	FA	TR	PA	RTOP	NG
Distorted	0.034	106.46	0.060	3.0E−05	0.040
Corrected	0.016	62.85	0.031	2.1E−05	0.029
% increase in distorted	113%	69%	94%	43%	38%

3.2. Reproducibility

Figure 5 displays the variability maps for the third test computed with Equation (A7). We remind the reader that for this and the last tests, the "uncorrected" data were indeed corrected for eddy‐current distortions and motion, therefore the observed variability pertains only to other EPI distortions. The uncorrected datasets have very large variability due to different EPI distortion directions. Correction significantly reduced variability.

Figure 5.

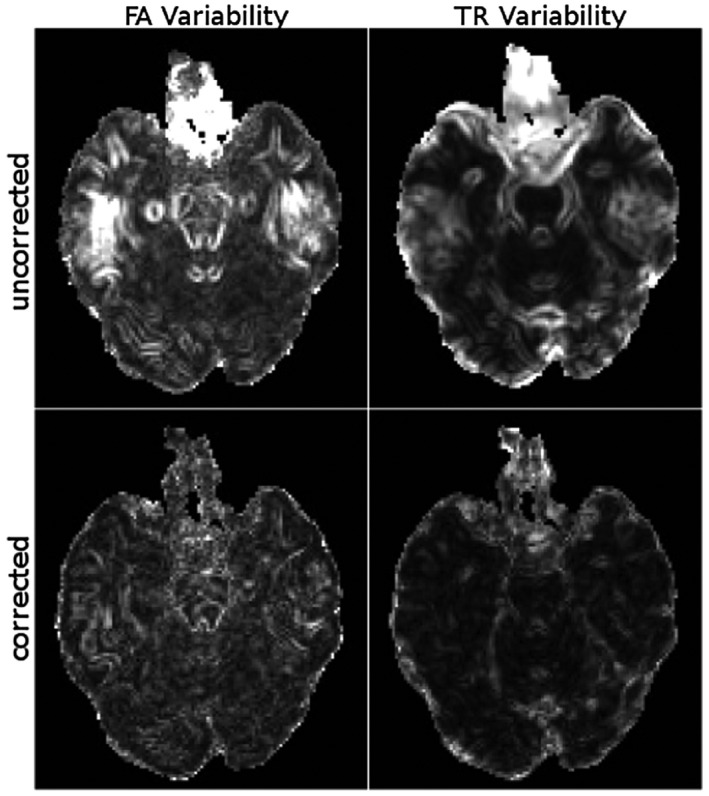
The variabilities were computed over all the images with different phase‐encoding directions and head orientations. The uncorrected datasets result in very large variances due to the differences in distortion directions. However, distortion correction reduces these variances to the levels comparable to those displayed in Figure 6 . All images are displayed with identical window/levels

The goal of the last test was to emulate a longitudinal scan and determine the variability introduced by EPI distortions due to different head orientations. Figure 6 displays the FA variability maps computed for each phase‐encoding direction using data from the three distinct head orientations. For all phase‐encoding directions, the variability of the derived tensor quantities, computed with Equation (A8), shows regional increases, likely resulting from inconsistent distortions across the data. The variability maps from the corrected datasets, which are displayed in the bottom row, have these variances significantly reduced. These findings suggest that EPI distortion correction should be performed in longitudinal studies to improve result reproducibility. Table 4 displays the median values over the brain region. Distortion correction reduced the variability and increased reproducibility in every case.

Figure 6.

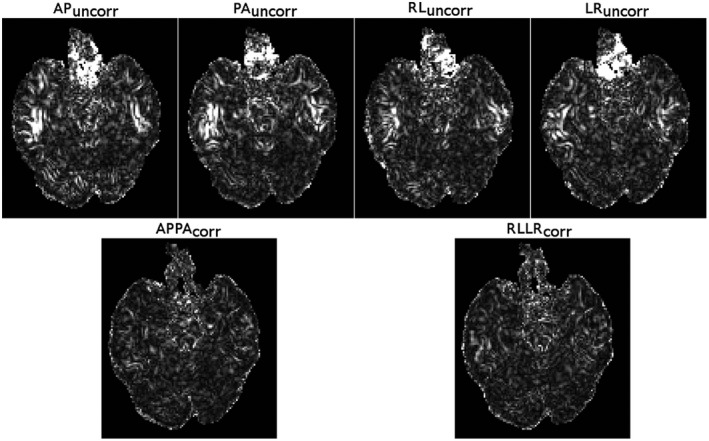
The variability of FA was computed for each phase‐encoding direction using the three different head orientations. The images in the top row are from datasets not corrected for EPI distortions and the bottom row was corrected for EPI distortions. For all phase‐encoding directions, the head orientation differences among the acquisitions cause significant changes in the underlying susceptibility fields, which reduces the reproducibility of the scans, as indicated by the large variances. EPI distortion correction virtually eliminated the increase of variance in regions affected by susceptibility differences. All images are displayed with identical window/levels

Table 4.

Median standard deviation values were computed over the three positions before and after motion and eddy‐currents distortion correction for TR, FA and the Principal eigenvector orientation dispersion (PEOD)

Uncorrected	AP	PA	RL	LR	Corrected	APPA	RLLR
TR	123.79	112.31	109.7	110.51	TR	83.93	89.63
FA	0.03	0.0275	0.028	0.0275	FA	0.02368	0.0255
PEOD	0.127	0.1178	0.117	0.115	PEOD	0.0865	0.0914

EPI distortion correction reduces these variances in all cases, indicating increased reproducibility. The variability in the distorted data was 31% higher for Trace, 15% higher for FA and 34% higher for PEOD on average, compared to the corrected data.

4. DISCUSSION

The goal of assessing the performances of different distortion correction techniques for diffusion MRI applications has remained elusive. In light of the recent emphasis on the importance of correcting EPI distortions to improve accuracy of diffusion MRI ¹⁷ , ¹⁸ and the available choice of EPI distortion correction techniques, ¹⁰ , ²² , ²³ , ²⁴ , ²⁸ , ³⁴ , ³⁵ , ³⁶ , ³⁷ , ³⁸ the goal of this work was the creation of a reliable, quantitative, unbiased methodology to assess the performance of EPI correction methods in addition to eddy‐currents and motion related corrections for diffusion MRI applications. In addition to proposing the methodology we acquired a specially‐designed dataset that can be used for this purpose and show as an example how this can be used with an available distortion correction pipeline. ²⁹

We observed significantly higher variability in the uncorrected datasets than in their corrected counterparts with all image modalities. Within the brain parenchyma, the median value of the variability metric in the distorted b = 0 images was 175% higher, and in the heavily diffusion‐weighted images 90% higher than in their corrected versions. This difference in DWI variability propagated into tensor‐derived maps with 137%, 99% and 267% increases in FA, TR, and primary eigenvector variability in the distorted data, respectively. The large reduction in the the primary eigenvector variability after distortion correction is especially interesting for fiber tractography and ___connectivity___ analysis applications. ¹⁸

Another set of experiments was designed to analyze the effect of DWI processing on the reproducibility of diffusion MRI, with implications for cross‐sectional and longitudinal studies. In multi‐center studies, the phase‐encoding direction of diffusion MRI data acquisition may be inconsistent across sites. Although it is unlikely that the data would be acquired with AP and RL phase‐encoding in the same study, the polarity of the blips of the typically‐used AP acquisitions might vary across scanners leading to high variability of the derived diffusion metrics in regions of high susceptibility gradients. ³⁹ The results of our study showed that this undesirable effect can be counteracted by using an effective method to perform EPI distortion correction. Therefore, the acquisition of blip‐up and down data should be considered an important feature in the protocol design of prospective diffusion MRI studies. For studies in which blip‐up blip‐down data is not available, it is important to be weary of the effect of EPI distortions on reproducibility and across‐center variability. A particularly interesting finding was from test four, which mimicked a longitudinal scan of the same subject. With this data subset, differences in head orientations and positions caused significantly different EPI distortions among scans. ³⁴ , ³⁹ This resulted in a high variance in the computed DTI metrics, even after motion and eddy‐current distortion correction. In longitudinal studies, the goal is often to detect very small changes in diffusion metrics that may be indicative of subtle biological changes due to disease progression or therapeutic intervention. However, these small changes can go undetected if variability caused by uncorrected misregistration is present. In our experiments, we observed that data corrected only for motion and eddy‐current distortion, but not for EPI distortions, as typically done in major studies, have a median variability higher by 32% for Trace, 15% for FA, and 34% for the primary eigenvector, compared to the EPI corrected data. These findings underscore the importance of including EPI distortion correction to increase the power of diffusion MRI studies, in particular when seeking subtle biological changes, for example those due to mild traumatic brain injury. ⁴⁰ , ⁴¹

4.1. Non‐distortion related sources of variability

The core idea behind the proposed method is to acquire replicates of the same data with the same diffusion contrast, but different distortions. This is achieved by reversing the diffusion gradient polarity for eddy‐current distortions, and by changing the phase‐encoding (PE) direction for EPI distortions. However, changing the phase‐encoding direction can cause other non‐distortion‐related differences in the acquired images. For instance, ghosts, which appear along the PE direction, can cause regional differences in the images acquired with different PE directions. In our acquisition protocol, we tried to minimize the impact of several of these other factors: The acquisition parameters for the proposed dataset were chosen in such a way that ghosts never overlapped with the brain region. In addition to ghosting, non‐square fields of view (FoV) can also create differences, due to changes in phase‐encoding bandwidth that alter distortions and echo‐time, and hence SNR, and can prevent direct comparisons of datasets. For this reason, our acquisitions employed a square FoV. The third confound indirectly affected by phase‐encoding are the Gibbs ringing artifacts. Even though Gibbs ringing is not related to PE, the differences in the location and orientation of large signal pile‐ups caused by EPI distortions also change the manifestation of the ringing artifacts. The dataset of this work used the Gibbs ringing removal strategy proposed by Kellner et al. ³⁰

While we took precautions to prevent the non‐distortion‐related artifacts described above, they are not eliminated. The proposed acquisition scheme (four replicates of the same image acquired with different phase‐encoding directions) can be used for detecting and removing such artifacts, because one of the two phase encode directions will be locally artifact‐free while the other will be corrupted. Once detected, these artifacts can be cleaned by combining the datasets with locally‐varying weights, with smaller weights assigned to images/regions, during the diffusion model estimation process. An interesting example of non‐distortion‐related artifacts that our methodology could help identify can be seen by inspecting the b = 5000 s/mm² shell after overall distortion correction in Figure 2. In this shell, distortion correction performed very well, as can be inferred from the significantly reduced variability and the absence of any structured patterns in the variance map, compared to the distorted case. However, at the second slice level (bottom two rows), the variability map of this shell contained localized clusters of high variance (green arrows) that are consistent with effects of cardiac pulsation artifacts. ⁹

4.2. Caveats and limitations

An aspect to take into account when applying our methodology to DWIs is the contribution of spatial signal variations due to coil sensitivity differences. This phenomenon can be observed in the Supporting Video S1, an animation displaying the same slice from all b = 0 volumes including the different subject positions. The large variations in signal intensity were preponderant over distortion effects in affecting variability; therefore, computing variances from a stacked set of b = 0 images was not ideal for assessing correction quality. Given that the presented data are not corrected for coil sensitivity variations, computing variance measures over either the b = 0 s/mm² images or DWIs should be done only within each positional set.

Another point to be considered is that the quality measures proposed in this work were solely based on the similarity of two or more corrected images. With these measures, a distortion correction algorithm that produces very similar but anatomically inaccurate images, such as blank images, would still get a good, albeit incorrect score. Another issue with our methodology involves the degree of smoothing of the corrected images. An algorithm that performs successive multiple interpolations or an algorithm that over‐smooths the data for denoising purposes would have an unfair advantage in the computed measures with respect to algorithms that preserve details. Prospective users of the dataset should consider these aspects when using the measures provided in this manuscript. The TORTOISE processing pipeline used in this work combines the transformations generated by each distortion type and generates the final data through a single interpolation step, therefore producing sharp corrected images.

There are other sources of misregistration in diffusion MRI that this dataset does not address, such as the severe slice‐by‐slice misregistration within an acquired volume that can occur with very uncooperative patients or in fetal MRI scanning. If one needs to analyze intra‐volume motion, the dataset can be used along with MRI simulators ²⁵ to corrupt the dataset with such motion effects.

4.3. Applicability to high angular resolution diffusion imaging

In this work, assessments of correction quality were performed using the DWIs themselves, the tensor‐derived metrics and the mean apparent propagator (MAPMRI) derived quantities. MAPMRI was chosen to illustrate the use of the technique with a HARDI model, however, prospective users of the dataset are not constrained to this model, as the technique and the dataset can be used with any model such as constrained spherical deconvolution, ⁴² Q‐ball, ⁵ NODDI ⁴³ or other HARDI methods. It is also not restricted to scalar or vector images and can be used with propagators, orientation distribution functions or fiber orientation distributions. The proposed dataset can also be used to better understand the susceptibility of these higher‐order models and fiber tractography methods to distortions.

Supporting information

VIDEO S1 The supporting video displays the same slice for all b = 0 s/mm² images acquired with AP phase‐encoding direction after motion correction. The large differences in signal are due to the coil sensitivity differences in the native space of the images

FIGURE S1 Sample distorted and distortion‐corrected images for the AP and LR encoded images for the additional test

FIGURE S2 Variability maps computed from the additional test and dataset

FIGURE S3 Variance of AP and LR data from repeated scans of the additional test

APPENDIX 1. A

The Appendix describes the details of each test. For all the equations, image I refers to the image in consideration, such as b = 0 s/mm², FA, TR images. APPA and LRRL refer to combined data corrected with blip‐up blip‐down EPI correction. AP, LR refer to uncorrected raw data. The superscripts N and S refer to North and South diffusion gradients.

A1. Test1

• Purpose: To assess the quality of correction for small motion, eddy‐currents distortions, and EPI distortions.

• Datasubset: Pos ₁

• b = 0imagevariability: 9 b = 0 images per acquisition × four image types: {APPA^N, APPA^S, LRRL^N, LRRL^S} for corrected and {AP^N, AP^S, LR^N, LR^S} for uncorrected data.

  $${\xi }_{b=0}^1=\sqrt{\frac{1}{35}\sum _{i=1}^{36}{\left(I_i-\overline{I}\right)}^2}$$ (3)
• b = 1000, b = 5000 image variability: i for four image types: {APPA^N, APPA^S, LRRL^N, LRRL^S} for corrected and {AP^N, AP^S, LR^N, LR^S} for uncorrected data.

  $${\xi }_{b=1000}^1=\sqrt{\frac{1}{30}\sum _{j=1}^{30}\left(\frac{1}{3}\sum _{i=1}^4{\left(I_{\mathit{ij}}-\frac{1}{4}\sum _{i=1}^4{I}_{\mathit{ij}}\right)}^2\right)}$$ (4)
• FA, TR, NGandPA, RTOPvariability: i for four image types: {APPA^N, APPA^S, LRRL^N, LRRL^S} for corrected and {AP^N, AP^S, LR^N, LR^S} for uncorrected data.

  $${\xi }_{\mathit{FA}}^1=\sqrt{\frac{1}{3}\sum _{i=1}^4{\left(I_i-\frac{1}{4}\sum _{i=1}^4{I}_i\right)}^2}$$ (5)

• PEOD: i for four image types: {APPA^N, APPA^S, LRRL^N, LRRL^S} for corrected and {AP^N, AP^S, LR^N, LR^S} for uncorrected data.

Let $e_1^i$ be the principal eigenvalues of the diffusion tensor corresponding to image I _i.

$$\mathbf{M}=\frac{1}{4}\sum _{i=1}^4(e_1^i).{(e_1^i)}^T$$ (6)

Let β ₁, β ₂, β ₃ be the eigenvalues of M. Then

$${\xi }_{\mathit{PEOD}}^1=\sqrt{\frac{{\beta }_2+{\beta }_3}{2{\beta }_1}}$$ (7)

A2. Test2

• Purpose: To assess the quality of correction with large motion.

• Data subset: Pos ₁, Pos ₂, Pos ₃

• FA, TR, NG and PA, RTOP variability: i for four image types: {APPA^N, APPA^S, LRRL^N, LRRL^S} for corrected and {AP^N, AP^S, LR^N, LR^S}, j for the 3 positions Pos ₁, Pos ₂ and Pos ₃.

  $${\xi }_{\mathit{FA}}^2=\sqrt{\frac{1}{3}\sum _{j=1}^3\left(\frac{1}{3}\sum _{i=1}^4{\left(I_{\mathit{ij}}-\frac{1}{4}\sum _{i=1}^4{I}_{\mathit{ij}}\right)}^2\right)}$$ (8)

A3. Test3

• Purpose: To assess the possibility of pooling historic data with head position or phase‐encoding direction differences.

• Data subset: Pos ₁, Pos ₂, Pos ₃

• FA, TR variability: i for 12 image types: ({APPA^N, APPA^S, LRRL^N, LRRL^S} or {AP^N, AP^S, LR^N, LR^S}) × (Pos ₁, Pos ₂ and Pos ₃).

  $${\xi }_{\mathit{FA}}^3=\sqrt{\frac{1}{11}\sum _{i=1}^{12}{\left(I_i-\frac{1}{12}\sum _{i=1}^{12}{I}_i\right)}^2}$$ (9)

A4. Test4

• Purpose: To emulate a longitudinal study with differences in head positioning.

• Data subset: Pos ₁, Pos ₂, Pos ₃ independently using the North datasets.

• FA, TR variability: $i\in \{Po{s}_1,Po{s}_2$ and Pos ₃}. The analysis was repeated separately for each phase‐encoding direction: AP^N, PA^N, LR^N, RL^N (for uncorrected) and APPA^N, LRRL^N (for corrected).

  $${\xi }_{\mathit{FA}}^4=\sqrt{\frac{1}{2}\sum _{i=1}^3{\left(I_i-\frac{1}{3}\sum _{i=1}^3{I}_i\right)}^2}$$ (10)

Okan Irfanoglu M, Sarlls J, Nayak A, Pierpaoli C. Evaluating corrections for Eddy‐currents and other EPI distortions in diffusion MRI: methodology and a dataset for benchmarking. Magn Reson Med. 2019;81:2774–2787. 10.1002/mrm.27577