Patterns of seasonal influenza activity in U.S. core-based statistical areas, described using prescriptions of oseltamivir in Medicare claims data

Abstract

Using Medicare claims data on prescriptions of oseltamivir dispensed to people 65 years old and older, we present a descriptive analysis of patterns of influenza activity in the United States for 579 core-based statistical areas (CBSAs) from the 2010–2011 through the 2015–2016 influenza seasons. During this time, 1,010,819 beneficiaries received a prescription of oseltamivir, ranging from 45,888 in 2011–2012 to 380,745 in 2014–2015. For each season, the peak weekly number of prescriptions correlated with the total number of prescriptions (Pearson’s r ≥ 0.88). The variance in peak timing decreased with increasing severity (p < 0.0001). Among these 579 CBSAs, neither peak timing, nor relative timing, nor severity of influenza seasons showed evidence of spatial autocorrelation (0.02 ≤ Moran’s I ≤ 0.23). After aggregating data to the state level, agreement between the seasonal severity at the CBSA level and the state level was fair (median Cohen’s weighted κ = 0.32, interquartile range = 0.26–0.39). Based on seasonal severity, relative timing, and geographic place, we used hierarchical agglomerative clustering to join CBSAs into influenza zones for each season. Seasonal maps of influenza zones showed no obvious patterns that might assist in predicting influenza zones for future seasons. Because of the large number of prescriptions, these data may be especially useful for characterizing influenza activity and geographic distribution during low severity seasons, when other data sources measuring influenza activity are likely to be sparse.

1. Introduction

National statistics describing aggregate trends in influenza activity may mask contrary trends occurring at state or local levels (Charu et al., 2017; Viboud et al., 2014). For example, influenza activity at the national level was moderately severe during the 2015–2016 season; however, Arizona experienced unusually severe and synchronous influenza activity (Arizona Department of Health Services, 2016; Biggerstaff et al., 2017; Davlin et al., 2016; Tamerius et al., 2017). Estimates of how frequently small geographic areas experience unusually high influenza activity during otherwise low severity seasons may qualitatively change interpretations of influenza activity patterns, whether they are aggregated at state, multi-state, or national levels. Also, aggregating data for small geographic areas to larger areas may obfuscate information about asynchrony within the larger area, especially when the spatial autocorrelation of the data is negative (Gotway and Young, 2002). Understanding the likely distribution of influenza activity at the local level given a national statistic may refine public health decision making and messaging.

Statistics from national surveillance may be qualitatively different from analogous statistics at the state or local level. For example, Lee and colleagues use diagnosis claims in a large medical billing dataset to demonstrate that severity of influenza at the state level does not always reflect severity at the county level (Lee et al., 2018). Viboud and colleagues compared their measure of influenza-like illness from diagnoses coded in medical claims data against national surveillance for influenza and demonstrated strong correlations between their measure of influenza activity at a local level for New York State and national surveillance (Viboud et al., 2014). Yang and colleagues, however, found greater spatial heterogeneity of influenza activity in New York City by neighborhood relative to borough. Therefore, aggregating data may mask patterns of influenza activity, even within a large city (Yang et al., 2016)

Previously, we developed two measures of influenza activity using billing codes for the influenza antiviral oseltamivir in Medicare administrative data (Izurieta et al., 2015). In a recent paper, we compared influenza activity patterns with existing national influenza surveillance data (Dahlgren et al., 2018). We found strong correlations between our measures of influenza activity and national surveillance at a regional (multi-state) level. Here, we present results from analyses of medical claims data for therapeutic prescriptions of oseltamivir to describe influenza activity on finer geographic scales. We sought to measure agreement between state-level and local-level influenza activity and to characterize season-specific zones where influenza activity was similar.

2. Methods

2.1. Core-based statistical areas

The U.S. Census Bureau and the Office of Management and Budget defined core-based statistical areas (CBSAs) as groups of counties with a common urban core with at least 10,000 residents (Office of Management and Budget, 2015). The definitions also included adjacent counties with strong economic or social ties into these CBASs. As of July 15, 2015, there were 945 CBSAs. About 96% of the U.S. population lived in a CBSA during 2010–2016.

2.2. Medicare data

U.S. residents 65 years old and older are a large population at risk for serious complications of influenza infection (Reed et al., 2015). About 34 million people 65 years old and older are beneficiaries of Medicare Part D, which pays for prescription drugs filled in the community-outpatient setting. To analyze patterns of seasonal influenza across CBSAs among this population at risk, we used Medicare claims data for oseltamivir, an antiviral used for treatment and prophylaxis of influenza infections. We defined an influenza case as a beneficiary of Medicare Part D aged ≥ 65 years who was dispensed a prescription of 75 mg oseltamivir for 5 days twice per day from October 9, 2010 through October 7, 2016. We tabulated weekly case counts for CBSAs by influenza seasons from 2010–2011 through 2015–2016. Seasons began on the fortieth week and ended the following year on the thirty-ninth week. To have sufficient data for further analysis, we included data for CBSAs in which each of the 6 seasons had at least 5 weeks with at least one case. We only included these CBSAs because our methods for categorizing seasonal severity are not applicable when data are this sparse.

2.3. Mapping

To map our results, we used the political boundaries of North America from a joint venture between United States, Canada, and Mexico (Geological Survey, 2006). We also used county boundaries and county population estimates published by the U.S. Census Bureau (U. S. Census Bureau, 2010; U.S. Census Bureau and Population Division, 2016). We assigned point coordinates using the geometric centroid of CBSAs, assigned point size using the mean CBSA population size from 2010 to 2015, and assigned point color using results from our analyses on cases within a CBSA. For CBSAs that spanned state boundaries, we assigned these CBSAs to the state containing the geometric centroid. We used the haversine formula to compute great circle distances between CBSAs, which assumes the Earth is a perfect sphere (de Mendoza and Rios, 1797). We used analogous methods in this subsection for computing the point coordinates of states and distances between states.

2.4. Seasonal severity

We expected the weekly number of dispensed prescriptions of oseltamivir to vary widely among CBSAs. Therefore, we wanted to normalize oseltamivir time series data before assessing seasonal severity. We implemented the moving epidemic method (MEM) to categorize the severity of each season because MEM has been shown to normalize surveillance data from different jurisdictions, allowing for comparisons of different data on a common scale (Vega et al., 2013). Specifically, we computed the geometric mean of 30 weekly case counts for each CBSA: the largest 5 weekly values of the epidemic period from each of the 6 seasons. We computed one-sided (1-α) × 100% confidence intervals for the geometric mean at α = 0.50, 0.10, and 0.02 assuming a log-normal distribution. We used the exclusion criteria for CBSAs in the Medicare Data subsection 2.2 because the variance of a geometric mean equal to zero is undefined. We denoted the upper limit of these confidence intervals as intensity thresholds (ITs): IT₅₀, IT₉₀, and IT₉₈. Within each CBSA, seasons were categorized as

1. low severity seasons when the maximum weekly case count was less than IT₅₀,

2. moderate severity seasons when the maximum weekly case count was between IT₅₀ and IT₉₀,

3. high severity seasons when the maximum weekly case count was between IT₉₀ and IT₉₈, and

4. very high severity seasons when the maximum weekly case count was greater than IT₉₈.

For analysis of seasonal severity as an interval variable, we used 1–4 to represent increasing seasonal severity. Additionally, we compared this measure to a measure of seasonal severity within each CBSA based on the total number of cases in a season. We measured seasonal severity for each state similarly after aggregating data for CBSAs within each state. We also aggregated all the included CBSAs to measure national severity.

2.5. Seasonal timing

For each season, we measured peak timing with the average week weighted by the number of weekly cases. For example, a season with season weeks 1, 2, …, 52 and weekly number of cases w₁, w₂, …, w_S2, the average week weighted by the number of weekly cases was

$$\frac{1w_1+2w_2+\cdots +52w_{52}}{w_1+w_2+\cdots +w_{52}}$$

Then, we converted the average in season weeks to the average in calendar weeks before presenting results. The average week provided a measure of centrality of the influenza season while allowing for a second wave or right tail, often attributable to influenza B. The interpretation of this measure is the week of highest activity on average, or more rigorously, the expectation of the week of a prescription of oseltamivir within a CBSA for a given season. However, the average week did not always provide the best measure of relative timing of influenza activity among CBSAs within a season. For example, seasons with a large, late wave of influenza B have an average week between two waves, when influenza activity was low.

To investigate relative timing of influenza activity for each CBSA, we used methods for analyzing time series. Our goal was to assign a time lag in weeks to each CBSA for each season. In other words, by how many weeks did influenza activity in this CBSA precede or follow influenza activity in the other CBSAs?

We constructed a multivariate time series of the weekly counts among the CBSAs with an annual period of 52.25 weeks. Time series for influenza activity in the United States are not stationary because we expect low activity in summer and high activity in the winter. Reliable estimation of the variance for lagged time series is straightforward only when the series is stationary (Cryer and Chan, 2010). To obtain a stationary time series for further analyses, we used the remainder from a seasonal-trend decomposition obtained using LOESS (Cleveland et al., 1990). To determine a season-specific time lag for each CBSA, we modified a method from analysis of collective phenomena (Podobnik et al., 2010). Briefly, Podobnik et al. apply the singular value (SV) decomposition of cross correlation matrices for predicting various data. Instead of prediction, we are interested in quantifying the collective behavior of our time series with a single number. Then, we shift the time series for a specific CBSA backwards and forwards through time to find the time shift when collective behavior is strongest for that CBSA. Further details are in the supplemental methods.

2.6. Influenza zones

For each season, we sought to group together CBSAs with similar trends in influenza activity. Here, we refer to these groups of CBSAs as “influenza zones”. We defined influenza zones for each season with agglomerative hierarchical clustering of CBSAs using our results from the MEM analysis of seasonal severity, SV analysis of relative timing, and geographic place. Agglomerative hierarchical clustering is a class of deterministic clustering algorithms, and we chose this class because of the wealth of algorithms and methods available for determining the optimal number of influenza zones for each season (Charrad et al., 2014).

First, we defined a distance function on pairs of CBSAs for use in the clustering algorithm. We normalized the great circle distance between CBSAs with a divisor of 9623 km (the largest distance, between Kapaa, HI and Guayama, PR), normalized the absolute difference in seasonal severity between CBSAs with a divisor of 3, and normalized the absolute difference in seasonal time lag between CBSAs with a divisor of 10 weeks. We defined the seasonal distance between CBSAs as the root sum square of these 3 normalized distances.

To cluster the CBSAs for each season, we used Ward’s method, an agglomerative hierarchical clustering algorithm which minimizes intracluster variance at each step (Ward, 1963). Charrad and others reviewed the agglomerative hierarchical clustering literature and implemented 30 methods for determining the best number of clusters (Charrad et al., 2014). For each season, we chose the number of influenza zones using their majority rule across these 30 indices: the level in the hierarchy chosen by the largest number of indices. Because computing these indices required raw data instead of simply a distance matrix, we could not use the great circle distance when computing these indices. Therefore, we approximated the great circle distance by using a Euclidean distance when computing these indices, ignoring the curvature of the Earth. To reduce computation time, we limited this analysis to k clusters for 1 ≤ k ≤ 30. After applying the majority rule for each season, we defined CBSAs within the same cluster as an influenza zone. Using the shortest distance between counties, we assigned counties outside a CBSA to the geographically closest influenza zone, breaking ties with the largest population size. In this way, we assigned every county to an influenza zone for each season.

We regressed the number of influenza zones for each season on the proportion of influenza specimens that represented the dominant influenza A subtype for that season using Poisson regression. From the end of season surveillance summaries, the 2010–2011 season was 62% H3; 2011–2012 was 74% H3; 2012–2013 was 96% H3; 2013–2014 was 90% H1; 2014–2015 was 99.6% H3; and 2015–2016 was 81% H1 (Appiah et al., 2015; Brammer et al., 2013; Davlin et al., 2016; Epperson et al., 2014; Ganatra et al., 2012; Kniss et al., 2011). Similarly, we regressed the number of regions on the study season. Because of the small sample size, 6 seasons, we limited regression to models with a single covariate.

2.7. Statistical analysis

We used the Kruskal-Wallis H statistic to test whether factors were distributed the same across seasons: weekly cases, seasonal severity, the average week weighted by number of cases, and the lag time (Kruskal and Wallis, 1952). We also used the Kruskal-Wallis H statistic to test whether the average week was distributed the same across categories of seasonal severity. We used Levene’s W statistic to test the equality of variance of the average week across categories of seasonal severity (Levene et al., 1960). We used Pearson’s χ² to test the association between the previous year’s severity and the current year’s severity.

We used Pearson’s correlation coefficient r to test the association between the population size and the total number of cases within a season; the logarithm of the total number of cases within a season and the logarithm of the maximum number of cases within a season; the mean severity of the CBSAs from the MEM analysis for each season and the SV from the corresponding seasonal correlation matrix (without any lag); the average week at the CBSA level within each season and the average week at the state level within each season; and, the lag week at the CBSA level within each seasons and the lag week at the state level within each season. We considered values of ∣r∣ < 0.3 as negligible and values of ∣r∣ > 0.7 as evidence of strong correlation.

We used Cohen’s weighted κ to measure agreement between the MEM seasonal severity at CBSA level and state level and between the seasonal lag week at CBSA level and state level (Cohen, 1968). We interpreted Cohen’s weighted κ using the Landis-Koch criteria (Landis and Koch, 1977).

We used Moran’s Index I weighted by the inverse distance to measure spatial autocorrelation at both the CBSA and state level for the MEM seasonal severity, the seasonal average week, and the seasonal lag week (Gittleman and Kot, 1990). We considered values of ∣I∣ < 0.3 as negligible and values of ∣I∣ > 0.7 as evidence of strong autocorrelation.

2.8. Software

For all analyses, we used “R: A Language and Environment for Statistical Computing” (version 3.3.1, 2016, R Foundation for Statistical Computing, Vienna, Austria). We used the following R packages: mem: Moving Epidemic Method R Package v1.4 (2014, Jose E Lozano Alonsa), rgeos: Interface to Geometry Engine – Open Source (2016, Roger Bivand and Colin Rundel), grdal: Bindings for the Geospatial Data Abstraction Library (2016, Roger Bivand, Tim Keitt, and Barry Rowlingson), maptools: Tools for Reading and Handling Spatial Objects (2016, Roger Bivand and Nicholas Lewin-Koh), geosphere: Spherical Trigonometry (2016, Robert J Hijmans), car: An R Companion to Applied Regression (2011, John Fox and Sanford Weisberg), pysch: Procedures for Personality and Psychological Research (2017, William Revelle), fmsb: Functions for Medical Statistics Book with some Demographic Data (2015, Minato Nakazawa), and NbClust: An R Package for Determining the Relevant Number of Clusters in a Data Set (2014 Malika Charrad, Nadia Ghazzali, Veronique Boiteau, and Azam Niknafs).

3. Results

From October 9, 2010 (Week 40 2010) through October 7, 2016 (Week 39 2016), a total of 1,066,213 Medicare beneficiaries who resided in one of 945 CBSAs received a therapeutic prescription of oseltamivir. We did not include data on 366 CBSAs because they had less than 5 non-zero weekly case counts for at least 1 season. Our data for analysis included 1,010,819 (95%) prescriptions dispensed to residents of the 579 CBSAs with at least 5 non-zero weekly counts for each season (Fig. S1). The number of cases in each season ranged from a minimum of 45,888 in 2011–2012 to a maximum of 380,745 in 2014–2015 (Table 1).

Table 1.

The number of therapeutic prescriptions of oseltamivir, severity from the Moving Epidemic Method, and a measure of collective correlation by season.

Season	Oseltamivir Prescriptions	Median Weekly Cases	Interquartile Range of Weekly Cases	National Severitya	Severitya of core-based statistical areas (%)				SVb of Correlation Matrix
					Low	Moderate	High	Very High
2010–2011	77,921	8	4–17	Low	275 (47)	277 (48)	23 (4)	4 (0.7)	332.9
2011–2012	45,888	3	2–8	Low	472 (74)	86 (15)	18 (3)	3 (0.5)	321.0
2012–2013	227,983	21	11–51.5	High	5 (0.9)	349 (60)	210 (36)	15 (2)	380.3
2013–2014	137,469	10	5–22	Moderate	122 (21)	431 (74)	24 (4)	2 (0.3)	357.1
2014–2015	380,745	39	22–33	High	0	51 (9)	395 (68)	133 (23)	408.7
2015–2016	140,813	8	5–19	Moderate	201 (35)	347 (6)	27 (5)	4 (0.7)	328.9

^aAs categorized using the Moving Epidemic Method. See Severity subsection 2.4 of Methods for details.

^bThe first (largest) singular value of the correlation matrix is a measure of collective correlation of oseltamivir prescribing among core-based statistical areas for each season. See Seasonal Timing subsection 2.5 of the Methods for details.

The median weekly number of cases varied substantially by season (Table 1, p < 0.0001). The total number of cases within each CBSA for each season correlated with population size (Fig. S2, r > 0.83, p < 0.0001). On a logarithmic scale, the total number of influenza cases within each CBSA for each season correlated with the maximum weekly number of cases (Fig. S3, r > 0.88, p < 0.0001).

3.1. Seasonal severity

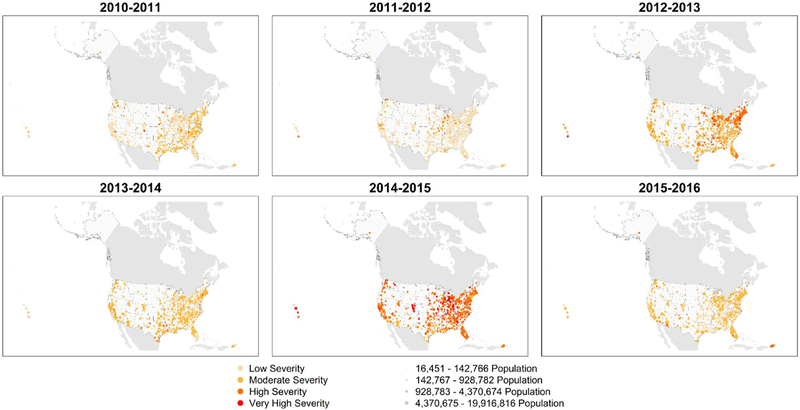
In the MEM analysis, the distribution of seasonal severity across the CBSAs varied for each season (Fig. 1, p < 0.0001). Spatial autocorrelation of seasonal severity among CBSAs was negligible (Table 2). Within CBSAs, the severity of the current season was associated with the severity of the previous year (Fig. S4, p < 0.0001), when high severity and very high severity severe seasons generally followed a moderate severity or low severity season.

Fig. 1.

Seasonal maps of severity as measured by the moving epidemic method.

Table 2.

Spatial autocorrelation of seasonal severity from the moving epidemic method, the seasonal average week weighted by cases, and the seasonal lag week at both the core-based statistical area (CBSA) level and the state level.

Indicator	Moran’s I
Season	CBSA	State
Severity
2010–2011	0.04**	−0.03
2011–2012	0.04**	0.004
2012–2013	0.06**	0.17**
2013–2014	0.06**	0.09**
2014–2015	0.06**	−0.03
2015–2106	0.09**	0.02
Average Week
2010–2011	0.15**	0.12**
2011–2012	0.05**	0.06*
2012–2013	0.23**	0.03*
2013–2014	0.20**	0.17**
2014–2015	0.16**	0.17**
2015–2106	0.05**	0.10**
Lag Week
2010–2011	0.12**	0.07*
2011–2012	0.02**	0.06*
2012–2013	0.19**	0.10**
2013–2014	0.15**	0.16**
2014–2015	0.17**	0.14**
2015–2106	0.11**	−0.004

^*Significant at p < 0.05.

^**Significant at p < 0.0001.

Agreement was fair between the seasonal severity of a CBSA with severity of the state (median κ = 0.32, IQR = 0.26–0.39). For the 2010–2011 and 2011–2012 seasons, 3 states contained at least 1 CBSA with low severity and at least 1 CBSA with very high severity. For the 2013–2014 season, CBSAs within 1 state experienced the full range of severity. No state contained CBSAs with the full range of severity during the other 3 seasons. Spatial autocorrelation of severity was qualitatively similar at the CBSA and state level (Table 2).

3.2. Seasonal timing

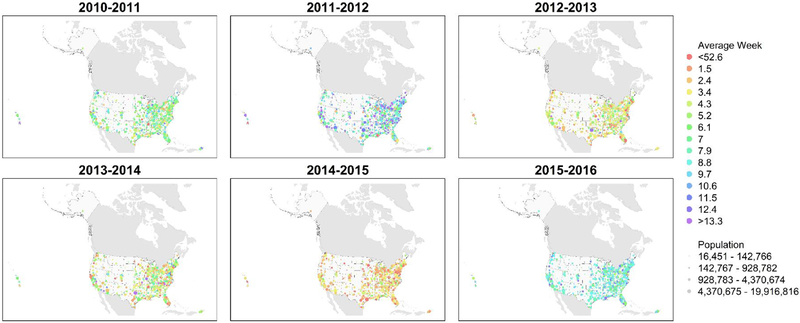
The distribution of the average week across CBSAs varied by season (Fig. 2, p < 0.0001). Spatial autocorrelation of the average week was negligible (Table 2). Among CBSAs, the average week tended to be earlier for more severe seasons (p < 0.0001) and more narrowly distributed for more severe seasons (p < 0.0001, Fig. 3). Within each season, the average week of CBSAs correlated with the average week at the state level (median r = 0.70, IQR = 0.57–0.73). Spatial autocorrelation of the average week was qualitatively similar at CBSA and state levels (Table 2). The average week moderately correlated with the lag time for seasons other than 2011–2012, when the correlation was weak (Fig. S5, p < 0.02), as a positive time lag generally means a later average week.

Fig. 2.

Seasonal maps of peak timing as measured by the average week weighted by the number of therapeutic prescriptions of oseltamivir. Red points represent early influenza activity, before the 1st week of the New Year (within an influenza season, week 1 comes after week 52). Violet points represent late influenza activity, after winter ends. The spectral colors between represent intermediate times.

Fig. 3.

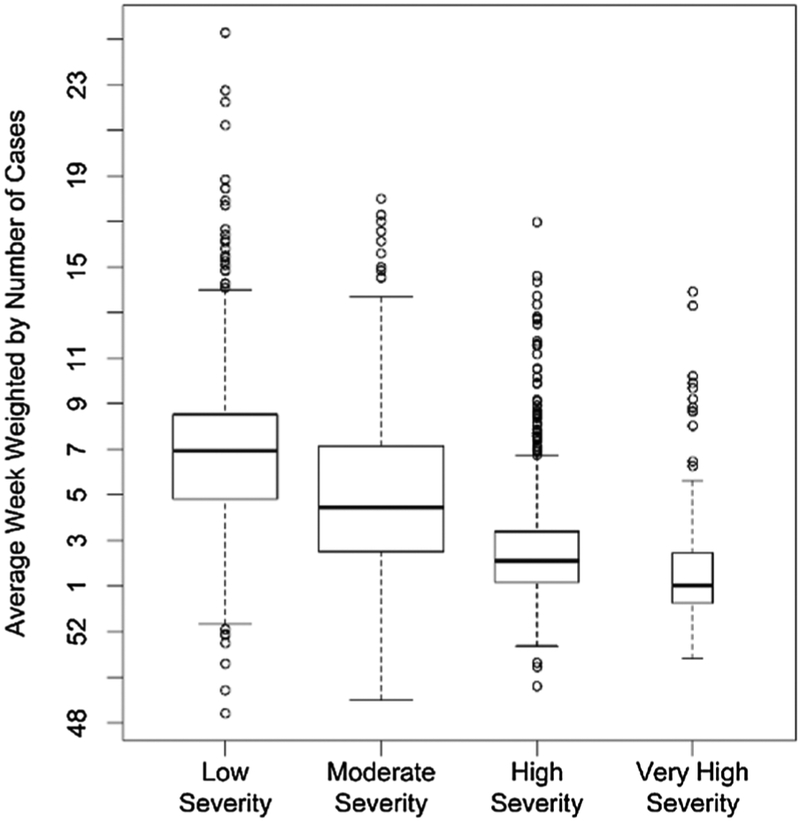
Distribution of average week weighted by the number of therapeutic prescriptions of oseltamivir stratified by seasonal severity for core-based statistical areas.

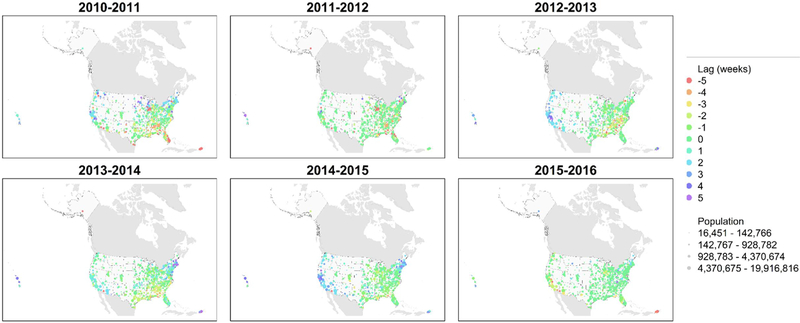
Several peaks remained after the seasonal-trend decomposition of the time series (Fig S6). The distribution of the lag times varied substantially by season (Fig 4, p < 0.0001). Spatial autocorrelation of the seasonal lag week was negligible (Table 2). The mean severity by CBSA for each season highly correlated with the SV of the correlation matrix for that season (r = 0.97, p = 0.001), where the SV was larger when the time series were more correlated. The seasonal lag time by CBSA correlated with the lag time at the state level (median r = 0.54, IQR = 0.40–0.60), and the seasonal agreement between the two was moderate (median κ = 0.50, IQR = 0.34–0.58). For the 2011–2012 season, 12 states contained CBSAs where the interquartile distance of the average week was at least 4 weeks. For the remaining seasons, the interquartile distance of the average week was less than 4 weeks for every state. Spatial autocorrelation of the lag time was qualitatively similar at the CBSA and state level (Table 2).

Fig. 4.

Seasonal maps of relative timing as measured by the time lag corresponding to the largest first singular value of the correlation matrices. Red points represent early influenza activity relative to the other core-base statistical areas (CBSAs). Violet points represent late influenza activity relative to other CBSAs. The spectral colors between represent intermediate times.

3.3. Influenza zones

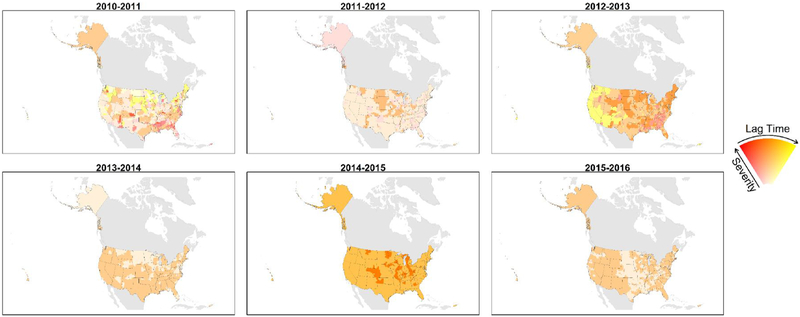
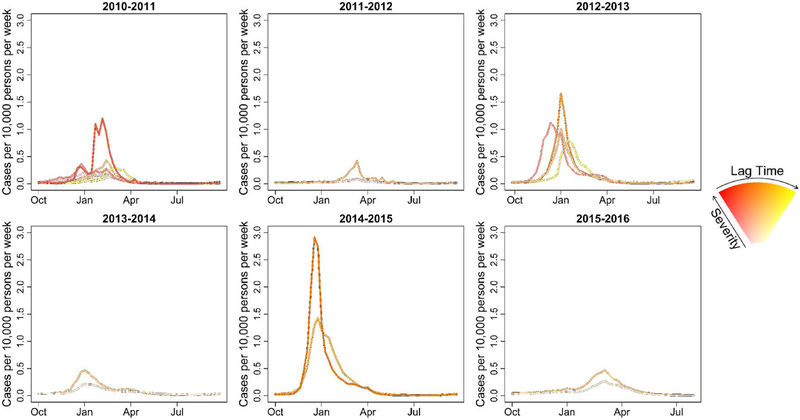
Using agglomerative clustering, the number of influenza zones decreased from 9 in the 2010–2011 season to 2 for the 2013–2014 and later seasons (Fig. 5). The two influenza zones in the later seasons generally were one zone with more severe, earlier influenza activity and another with less severe, later influenza activity (Table 3). Peak timing and severity by influenza zone was more complex for the 2010–2011 and 2012–2013 seasons (Fig 6). Using Poisson regression, the expected number of influenza zones increased as the proportion of influenza activity representing a dominant influenza A subtype decreased (p = 0.03). Similarly, the expected number of influenza zones decreased with time (p = 0.02).

Fig. 5.

Seasonal maps of influenza zones from hierarchical clustering. Red colors represent earlier relative timing, and yellow colors represent later relative timing. Intense colors represent very high severity severe seasons, and dull colors represent low severity seasons.

Table 3.

Descriptive statistics about influenza zones for each season.

Season	Land Area (106 km2)	Number of Core-Based Statistical Areas in Influenza Zone					Mean Lag (σ)
Influenza Zone		Low Severitya	Moderate Severitya	High Severitya	Very High Severitya	Total
2010–2011
1	0.93	104	0	0	0	104	−0.43 (0.94)
2	1.88	55	0	0	0	55	−0.38 (0.99)
3	0.41	50	0	0	0	50	−3.82 (0.90)
4	3.51	0	175	0	0	175	−0.23 (0.95)
5	0.59	41	0	0	0	41	2.80 (1.12)
6	0.33	25	1	0	0	26	2.23 (0.81)
7	0.99	0	46	8	2	56	2.96 (1.11)
8	0.38	0	55	0	0	55	−3.94 (0.85)
9	0.12	0	0	15	2	17	−2.65 (2.00)
2011–2012
1	5.37	352	17	1	0	369	0.14 (0.78)
2	2.37	120	0	0	0	120	−3.22 (1.29)
3	1.41	0	69	17	3	89	−0.45 (1.78)
2012–2013
1	2.35	0	0	191	13	204	−0.57 (1.38)
2	1.54	1	62	19	2	84	2.70 (1.17)
3	4.66	4	208	0	0	212	−0.01 (0.74)
4	0.60	0	79	0	0	79	−2.91 (1.06)
2013–2014
1	5.79	3	431	24	2	460	−0.16 (1.82)
2	3.36	119	0	0	0	119	0.21 (1.82)
2014–2015
1	8.12	0	51	395	21	467	−0.52 (1.72)
2	1.03	0	0	0	112	112	−0.62 (0.85)
2015–2016
1	6.58	0	347	27	4	378	−0.18 (1.51)
2	2.58	201	0	0	0	201	0.03 (1.08)

^aSeasonal severity categorized using the Moving Epidemic Method (Vega et al., 2013).

Fig. 6.

Seasonal time series of the weekly number of therapeutic prescriptions of oseltamivir (cases) per 10,000 population. Seasonal time series were aggregated by influenza zones from agglomerative hierarchical clustering. Population estimates obtained from the U.S. Census Bureau (2016).

4. Discussion

We describe the spatial and temporal trends in our indicator of influenza activity defined by therapeutic doses of oseltamivir dispensed to Medicare beneficiaries using claims data for the 2010–2011 through 2015–2016 influenza seasons. Generally, we found associations between increasing seasonal severity with earlier influenza activity and with smaller variance in the peak timing of influenza activity (Fig. 3). During influenza seasons classified as low severity at the national level, it was not unusual to find individual CBSAs experiencing high or very high severity (Table 1). In contrast, during seasons classified as high severity on a national level, few CBSAs experienced a season classified as low severity (Table 1). We found substantial variation in severity (Fig. 1), peak timing (Fig. 2), and relative timing (Fig 1), of influenza activity among CBSAs both within seasons and across seasons. We found no evidence of meaningful spatial autocorrelation in seasonal severity, in peak timing, or in relative timing (Table 2). These findings highlight the complexity of summarizing seasonal influenza trends on a national level in the United States

The original goal of this analysis was to construct influenza zones, areas of the United States where influenza activity was similar, in hopes of identifying useful patterns for decision making and tailored public health messaging. However, seasonal maps of influenza zones showed no obvious patterns that might assist predicting influenza zones for future seasons (Fig. 5). Seasons when either A(H1N1) or A(H3N2) virus subtypes were strongly predominant generally had fewer influenza zones. This finding suggests that each influenza season could be better described as a sum of multiple epidemics representing A(H1N1), A(H3N2), and B virus activity. Integrating data on circulating viruses into a more sophisticated analysis may elucidate more meaningful patterns.

Different measures of influenza activity may lead to qualitatively different conclusions about the severity of an influenza epidemic (Glezen et al., 1980). Viboud and others described a correlation between increased rates of influenza mortality and synchrony among states (Viboud et al., 2006). They hypothesized that this finding was consistent with “enhanced disease transmission facilitates spatial spread.” Our results at the CBSA level generally agree with this idea, with the caveat that we do not have data on severe outcomes at the CBSA level for comparison. Particularly during low severity seasons, our measure of influenza activity may not align with estimates of serious influenza-related outcomes, including mortality. For example, results from cohort studies demonstrate mortality attributable to influenza may not agree with other measures, such as hospitalizations attributable to influenza (Glezen, 1982; Glezen et al., 1980). Because we used a large data set that represents 70% of Medicare beneficiaries, our measures of influenza activity may be especially useful in understanding low and moderate severity seasons, when other national level data sources, such as mortality, may be sparse.

In our data, synchrony appears to be a feature of more severe seasons. For the 2014–2015 season, the SV of the correlation matrix of the weekly cases was higher than other seasons because the influenza activity among the CBSAs was more uniform. During this high severity season, influenza activity at the national level better reflected activity at the local level. Although the SV of the correlation matrix is in theory a summary measure of how correlated the data are, it is also a good summary measure of seasonal severity in these data, because more severe seasons also had larger SVs (Table 1). As our results rely on 6 seasons, this finding may be incidental.

Our results are subject to important limitations. First, our results are not generalizable to younger populations. Second, our data do not capture the true incidence of influenza. Rather, the data include treatment of both suspected and laboratory-confirmed influenza in a community medical treatment setting. Other measures of influenza seasonal severity — outpatient influenza-like illness, laboratory confirmed influenza hospitalizations, or mortality attributable to influenza — provide broader context for the external validity of our results (Biggerstaff et al., 2017). Third, our inclusion criterion for CBSAs biased our results towards higher severity, because we did not include CBSAs where the data were sparse. In a previous analysis, which was not limited to these 579 CBSAs, we classified national seasonal severity to the same or lower levels compared to our results here (Table 1) (Dahlgren et al., 2018). The developers of the MEM recommend that a minimum of 5 seasons of data be used with their method (Bangert et al., 2017). As data on additional seasons become available, our methods may result in a less biased, more complete understanding of trends in seasonal influenza at a metropolitan level. Fourth, our analyses are limited to only 6 influenza seasons. We caution against inferring future patterns of seasonal influenza from this small sample. For example, the decreasing number of influenza zones could be unrelated to the diversity of circulating influenza A viruses. Instead, this decrease may be attributed to a long-term trend in a factor unrelated to circulating viruses. Despite these limitations, we believe the trends we present here represent underlying trends in incidence of influenza among people 65 years old and older in the United States.

In conclusion, our results may assist in the interpretation of national, multi-state, and state level statistics for influenza activity. Importantly, they place limits on interpolating measures of influenza activity, as during a low severity season, one would still expect to see some localities experiencing higher severity. This cross-scale difference in severity patterns, where severity is more variable at small geographic scales, is most pronounced during low severity seasons. Additionally, our results may assist extrapolating results from small geographic areas to larger areas, especially during a high severity influenza season. If Medicare oseltamivir data were available in near real-time, analysis could reveal evolving dynamics of seasonal influenza likely not observable with data aggregated at the national, multi-state, or state level. Future directions may include analysis of recent data including the 2017–2018 season, a high severity season for all ages (Garten et al., 2018)

Abbreviations:

CBSA

core-based statistical area

MEM

moving epidemic method

SV

singular value

IQR

interquartile range