Nanoscale Chemical Imaging of Zeolites Using Atom Probe Tomography

Abstract

Understanding structure–composition–property relationships in zeolite‐based materials is critical to engineering improved solid catalysts. However, this can be difficult to realize as even single zeolite crystals can exhibit heterogeneities spanning several orders of magnitude, with consequences for, for example, reactivity, diffusion as well as stability. Great progress has been made in characterizing these porous solids using tomographic techniques, though each method has an ultimate spatial resolution limitation. Atom probe tomography (APT) is the only technique so far capable of producing 3D compositional reconstructions with sub‐nanometer‐scale resolution, and has only recently been applied to zeolite‐based catalysts. Herein, we discuss the use of APT to study zeolites, including the critical aspects of sample preparation, data collection, assignment of mass spectral peaks including the predominant CO peak, the limitations of spatial resolution for the recovery of crystallographic information, and proper data analysis. All sections are illustrated with examples from recent literature, as well as previously unpublished data and analyses to demonstrate practical strategies to overcome potential pitfalls in applying APT to zeolites, thereby highlighting new insights gained from the APT method.

1. Introduction

The realization of fully developed structure–composition–property relationships in zeolite‐based catalysts requires characterizing sub‐nanometer length scales of the atomic bond all the way to tens of meter length scales present in large industrial chemical reactors used for our current and future fuels, chemicals and materials.1, 2, 3 This effort is made to engineer superior solid catalysts, while working within the constraints of manufacturing, material limitations and ultimately economic drivers. Innumerable studies have produced many insights into structure–composition–property relationships in zeolite‐based catalyst materials across many length scales, and these are covered in a number of excellent review articles.1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23 A wealth of fundamental knowledge has been gained, but still with a significant gap in achieving 3D chemical reconstructions at sub‐nanometer‐scale resolution. Techniques that offer sub‐nanometer length scale information, for example, X‐ray diffraction (XRD) and nuclear magnetic resonance (NMR), mainly offer only bulk averages of a specific sample under study. While a number of powerful tomographic techniques have been developed to give 3D reconstructions, none currently offer sub‐nanometer spatial resolution, and they also have difficulty in differentiating the primary zeolite elements (i.e., Al, P and Si) due to their close and light atomic masses. Further challenges in studying zeolite catalysts arise as they commonly have small crystal sizes (<1 μm), the crystals may be complex intergrowths and they are susceptible to beam damage.1, 2, 3 Atom probe tomography (APT) is able to provide such unique information as it is the only technique today capable of creating 3D elemental reconstructions of materials with sub‐nanometer‐scale resolution.10, 24

The invention of the field ion microscope (FIM) was a precursor to the APT field, which led to the first observation of individual atoms in 1956.25 It was from this initial development that the modern local electrode atom probe (LEAP) instrument was developed, which led to a “second revolution in the development of the atom probe,” as this instrument is optimally able to collect millions of atoms per minute with a 200 nm wide field of view and high mass resolution as a result of its local electrode geometry.26 This “second revolution” was enabled by four key developments: 1) local electrode geometry, 2) focused ion beam (FIB) sample preparation, 3) improved computer performance and storage, and 4) quality thermal pulsing with lasers enabled by new laser technologies.26 All these developments came together in a timely manner, allowing APT to transition from studying primarily highly conductive metals that could be prepared by electropolishing to semiconductors and even nonconductive materials that required FIB preparation and laser pulsing to run successfully.

Some of the groundbreaking studies include reconstructing a transistor including the source, drain channel and gate oxide,27 studying the interface of a titanium implant and human bone tissue,28 an integrated high‐temperature cell for APT studies of gas–surface reactions,29 studying deuterium‐charged steel samples including the use of integrated cryogenic transfer to prevent deuterium diffusion,30 the analysis of a frozen water–ethanol solution,31 studying interfaces in ceramics and oxide materials,32 reconstructing metallic nanostructures including permanent magnets and grain boundaries,33 metal nanoparticles embedded in oxide materials,34 extensive studies of electronic materials,35, 36 quantitative analysis of zinc oxide nanostructures,37 correlated APT and transmission electron microscopy (TEM) to study oxide materials,38 studying lithium‐ion battery cathodes and battery degradation mechanisms,39, 40 reconstructing CdTe‐based solar cells,41 studying carbon‐supported metal nanoparticle catalysts,42 characterizing dopants in silicon nanowires,43 reconstructing the tooth of a marine mollusc,44 and the isotopic reconstruction of lab‐grown diamond.45 All of these studies, as well as others not mentioned, illustrate how APT is truly at the forefront of materials characterization, and innovations in the technique are leading to additional insights into a diverse range of materials.

In this Minireview we will start with a brief overview of the APT methodology followed by more specific information for applying APT to zeolite‐based materials, including proper sample preparation and data collection as well as rigorous data interpretation and analysis, with showcase examples from recent literature. We also will discuss the unique challenges encountered in applying the APT technique to zeolites, and successful strategies to mitigate these, as well as insights gained from applying APT to zeolite‐based catalysts. These insights may be equally valuable for the study of other functional nanomaterials and may spur our understanding of such solids using this single‐atom microscopy method.

2. Atom Probe Tomography

APT is able to create 3D reconstructions by deconstructing a sample in an ion‐by‐ion fashion, using the field evaporation of a hemispherically shaped specimen, with a 2D detector and time‐of‐flight (ToF) mass spectrometry (MS) to build a 3D compositional reconstruction with sub‐nanometer resolution. A schematic of the APT technique, including relevant length scales, is shown in Figure 1. The sample is prepared for the APT experiment by fashioning the material into a needle‐shaped specimen using FIB milling in a scanning electron microscope (SEM) or by electropolishing. The sample is then loaded into the instrument through a load lock and transferred to a cryogenic stage in ultrahigh vacuum (UHV) to position the needle within 40 μm from a local electrode aperture. An electric field on the order of tens of V nm⁻¹ is applied between the sample and local electrode, causing the atoms to be field evaporated as ions from the sample. ToF MS is achieved using fast laser or voltage pulses, which triggers the field evaporation of one or several ions, with the ToF starting at the pulse event and ending with a detection event, as is shown in Figure 1 b. As APT relies on ToF to determine chemical identity, it does not suffer from the same contrast issues that can plague other high‐resolution techniques in differentiating zeolite elements, for example, Al, Si, P, such as scanning transmission electron microscopy high‐angle annular dark‐field imaging (STEM‐HAADF).46 The ions are accelerated by the electric field, and their position is determined using a 2D detector. The <100 nm diameter needle is projected on a detector with a 4 cm diameter, equating to an approximate magnification of 10⁶. The mass‐to‐charge ratio of each ion is determined by ToF, using conservation of energy, as the potential energy is converted into kinetic energy during field evaporation: $M\left(\mathrm{D}\mathrm{a}\right)=\frac{m}{n}=2\mathrm{e}\mathrm{V}{\left(\frac{t_{\mathrm{f}\mathrm{l}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}}-t_0}{L_{\mathrm{f}\mathrm{l}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}}}\right)}^2$ , as is highlighted in Figure 1 b. The instrument outputs 2D detector data, order of detection events, and ToF associated with each detection event. The 3rd dimension (z) of the reconstruction can be determined using the known volume of the needle (determined by the voltage curve or imagining the needle before and after the APT experiment) and filling it in an atom‐by‐atom fashion by reverse projecting the detected position of the ions onto the surface of a virtual specimen.47

Figure 1.

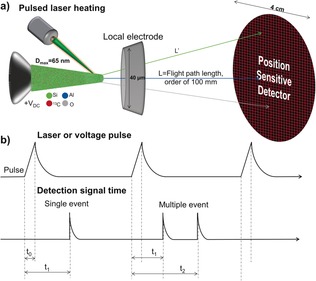
a) Schematic of an atom probe tomography (APT) instrument, including representative sizes of the various components. b) Overview of the APT pulse sequence using either applied electric field through voltage pulsing or pulsed laser heating to drive ion evaporation along with the recorded detector events with both single and multiple events illustrated.

With this information, the 3D location and chemical identity of each ion can be simultaneous determined with sub‐nanometer scale spatial resolution. Until the recent commercialization of the laser pulsed LEAP, most APT instruments used voltage pulses, requiring materials with high electrical conductivities to allow for the surface to be screened from the bulk, effectively limiting the use of APT to metals. Laser pulsing using picosecond lasers has only recently been technically possible, but now allows APT to be applied to nonconductive materials, such as zeolites, as the short laser pulses can induce evaporation by thermal heating. More detailed overviews of the APT technique are available in a number of authoritative references.10, 47, 48, 49, 50, 51, 52, 53, 54

3. Sample Preparation and Data Collection

3.1. Sample Preparation

Zeolite samples cannot be prepared by electropolishing due to the size and composition of these materials, so FIB‐based specimen preparation, in what is termed a site selective lift‐out technique, is used instead.50, 55, 56, 57, 58, 59, 60, 61 The traditional lift‐out and needle sharpening technique used most commonly for APT specimen preparation was first published by Thompson et al.55 For zeolites, this technique has been used for large crystals (ca. 100 μm) as well as mid‐size (ca. 15 μm) and smaller, about 4 μm crystals, and details on this well‐established technique can be found in Refs. 62, 63, 64.

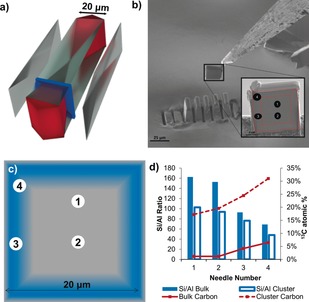
While the site‐selective lift‐out technique works well for large zeolite crystals, problems were encountered in attempting to prepare samples from industrial‐like zeolite crystals for APT measurements due to their small size. When studying industrially produced zeolite ZSM‐5 from, for example, Zeolyst (i.e. CBV2314), it was no longer possible to use a lift out as the crystals of the material are less than 1 μm (Figure 2 a,b). Instead, polycrystalline aggregates were transferred to Si microtips using electrostatic attractive force (Figure 2 c) and then attached to the Si microposts using FIB deposited Pt (Figure 2 e) and finally milled into needles for the APT measurement (Figure 2 f). Although this method is extremely time consuming, we were able to successfully prepare needles from small zeolite crystals for APT measurements. We did experience a higher proportion of sample failure from needles prepared using this manner compared to the large zeolite crystals we have initially been studying with APT, and we believe this was due to intercrystallite void spaces, but nevertheless this method did yield successful runs, and a similar approach has been reported for small crystals of Fe‐exchanged SSZ‐13 by another group.65

Figure 2.

Overview of the preparation of small, industrial‐type zeolite ZSM‐5 crystals (Zeolyst, CBV2314). SEM images of: a,b) Bare zeolite powder. c) Aggregate of ZSM‐5 crystals attached to manipulator using electrostatic force. d) ZSM‐5 crystals on a Si microtip. e) ZSM‐5 crystals on Si microtip after partial focused ion beam (FIB) milling with the protective Pt/C cap indicated. f) Final sample needle prior to APT measurement.

Beam damage is a well‐known phenomenon when studying zeolites.66 While preparing zeolites for APT using FIB milling (e.g. with a Ga ion source) we used several strategies to reduce this: 1) Minimize e‐beam imaging time. 2) The use of protective Pt layers, such as that shown in Figure 2 e. 3) The use of Ga as a marker for potentially damaged areas of the material during data analysis. During data analysis, regions of the needle that contained Ga, normally near the sample surface and especially the needle tip, would be excluded from the analysis volume to prevent any influence of Ga ions. This was normally limited to only a few nanometers of penetration.

3.2. Data Collection

Regular ion collection rates are easily realized with ideal APT samples, such as metals and semiconductors, but this is much more difficult with non‐conductive and heterogeneous materials. Local magnification effects, which are caused by density variations in the APT reconstruction using the assumption of a hemispherical shape, as is used within the most current CAMECA IVAS software, or evaporation field differences, can cause significant errors in sample reconstruction, and are further exacerbated with composite materials, leading to significant distortions in spatial resolution.67, 68 Local densities can be influenced by microstructural features, such as local voids, different phases, grain boundaries, interstitial segregations to dislocations, as well as artefacts caused by local magnification due to different evaporation fields of different phases and crystallographic variations.69 With zeolites, coke‐containing samples proved particularly difficult to run as they consist of a non‐conductive inorganic framework, with trapped carbonaceous species, and it was common to find “microbursts” of ions, believed to be trapped hydrocarbon species.70 We were forced to discard some data sets due to this issue, though using low data collection rates normally allowed us to achieve reliable data collection, found by examining the detector event histogram, and mass spectral quality. This cautions over‐interpretation of APT data, especially with regard to ion density differences, in the absence of any correlative technique(s); i.e. TEM or FIM.69 Another challenge in quantitative data collection is the possibility of multiple ionic evaporations during one pulse event, resulting in multiple simultaneous detector hits, which is a well‐known problem with oxide materials, and a factor in running zeolite materials.52, 68, 70, 71 It occurs when certain elements have a higher probability of simultaneous evaporation during a pulse event, resulting in this element becoming less detectable than other elements in the system as simultaneous detector hits in position and time are registered as a single event, resulting in inaccurate compositions.

There is also evidence that molecular ions can dissociate after field evaporation, such that one ion becomes deionized and does not hit the detector within the appropriate ToF window and is registered as background.52, 70, 71 We systematically found that that the Al contents in the APT data are below what is expected and measured in these samples by other techniques. Therefore, we have concluded that APT has difficulty in quantifying the Al content in zeolite materials perhaps due to Al being evaporated as multiple field evaporation events as both oxide molecular ions and/or elemental ions.52, 70 Additionally, we found that the quantification of Al was further exacerbated when coke carbonaceous species were present, potentially due to overlapping peaks in the mass spectra.70

3.3. Mass Spectrum Analysis and the Challenges of Hydrocarbons in Silica Frameworks

The molecular mass (reported in Daltons, Da) of all ions that hit the detector is determined using ToF, which should enable easy identification of all elements, but in practice this is complicated by several factors. 1) Unlike conventional mass spectrometry, “fingerprint” fragmentation patterns are not found in APT. 2) In zeolite samples, many elements could be present including: Al, C, H, N, O, P and Si, leading to many possible ions, especially when isotopes are accounted for. 3) It is well known in APT that non‐metallic elements, such as C and N, can evaporate in complex molecular forms, and this is further exacerbated in organic/inorganic hybrid materials, which is the case with coke or template containing zeolites.44, 72 4) Carbonaceous materials can produce complex fragmentation patterns with molecular ions of the general formula [C_nH_2n±m]⁺ where n=1–6 and m is variable.72, 73 5) Multiple ionization events are a well‐documented problem, especially with oxides.52 6) SEM imaging can easily cause C contamination.60 To avoid this, we have used ¹³C‐labelled reactants so that carbon atoms from coke could be unambiguously assigned.70 7) Overlapping species which are too close in atomic mass to be resolved by APT. Some examples are: ¹⁴  n ⁺ and ²⁸Si²⁺, ¹⁶O₂ ²⁺ and ¹⁶O⁺, AlH⁺ and AlH²⁺ with ²⁸Si and ²⁹Si, respectively, as well as numerous hydrocarbon fragments, and in our studies especially CO and Si. 8) There is evidence that molecular ions can dissociate after field evaporation, such that one ion becomes deionized and does not hit the detector within the appropriate ToF window and is registered as background.74

We encountered difficulties in the analysis of zeolite mass spectral data with the large crystals of zeolite ZSM‐5 used in the methanol‐to‐hydrocarbons (MTH) reaction, related to overlapping peaks, and want to highlight potential challenges with hydrocarbons in zeolites to other researchers.70 Accurate interpretation of the data required us to examine three distinct samples, the calcined, coke‐free crystals, crystals reacted with regular methanol (¹²CH₃OH) and crystals reacted with ¹³C isotopically labelled methanol (¹³CH₃OH), and mass spectra from the three samples are shown in Figure 3, and regions of interest are also expanded in the Figure.

Figure 3.

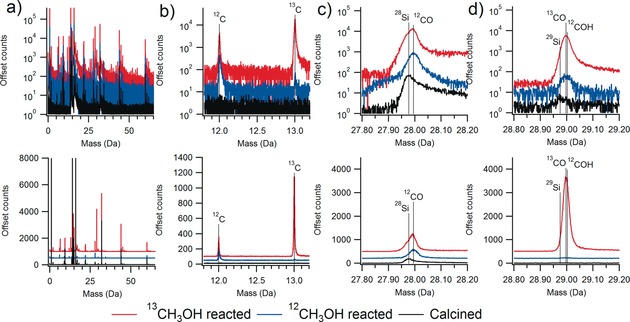
Example mass spectra for calcined zeolite ZSM‐5 and ZSM‐5 after the methanol‐to‐hydrocarbons (MTH) reaction using both normal methanol (¹²CH₃OH) and ¹³C isotopically labelled methanol (¹³CH₃OH), with the top traces in log sale and the bottom in linear scale for counts. a) Full relevant mass scale showing the abundance of peaks observed. b) Region showing the presence of ¹²C and ¹³C in both reacted samples, with an abundance of ¹³C from the labelled reaction. c) The peak near 28 Da contains contributions from ²⁸Si and then after the MTH reaction a clear shift due to ¹²CO is observed. d) The peak near 29 Da is from ²⁹Si and then after reaction predominately ¹³CO as well as a contribution from ¹²COH. Note the CO peak was determined to contain 80 % of all carbon making its quantification vital. Samples are from Refs. 64, 70.

We were able to accurately interpret the spectra by using known isotopic abundances of both Si (²⁸Si, ²⁹Si and ³⁰Si) and O (¹⁶O, ¹⁷O and ¹⁸O) and isotopically labelled methanol, as well as studying control samples that did not contain any template or coke molecules.52, 63, 70, 75, 76 Figure 3 a gives the full mass spectra for the materials, and Figure 3 b shows that the reacted materials contain carbon in the expected isotopic abundance based on the source of methanol. Figure 3 c shows the peak near 28 Da is from ²⁸Si, but then after reaction a distinct shift and change in peak shape is observed due to ¹²CO. The peak near 29 Da in Figure 3 d is from ²⁹Si, ¹³CO and potentially ¹²COH. Properly identifying these peaks allowed us to deconvolute them, this was very important as the CO peak was determined to contain 80 % of the carbon, highlighting the importance of careful consideration of the mass spectral data for zeolites, and especially those containing hydrocarbons.70

3.4. Spatial Resolution and Detector Efficiency Limitations

While APT has the highest spatial resolution of any 3D tomographic technique, it is important to understand its limitations, especially with regards to detector efficiency and spatial resolution, so that the data can be accurately interpreted.47 Non‐ideal detector efficiency and spatial resolution serve to blur the atomic positions in the APT dataset. The spatial resolution of APT has been measured to be better than 0.04 nm in depth and 0.20 nm laterally, and although this is extremely high, it is still larger than most interatomic spacings in the lateral dimension, resulting in a loss of information.47 It is also important to realize that this often‐quoted resolution is for single‐crystal metals and was developed as the lattice planes could be visualized, and it is known that the absolute value of resolution is sample specific.77, 78, 79 We were never able to visualize any lattice planes or pores in zeolite samples, so we do not believe we were able to achieve sub‐nanometer resolution for these functional porous materials.

In order to gain an estimate of the spatial resolution needed to visualize pores in zeolites using APT, we ran simulations using the structures of both CHA and MFI zeolites. Spatial resolution was simulated as a delocalization in 3D space, defined by a Gaussian distribution, with σ being the standard deviation. Each atom was distributed randomly from its lattice position based on a weighted random number generator with a 3D Gaussian distribution probability density function. In other words, each coordinate of an atom is displaced randomly in 3D based on a Gaussian distribution probability density function centered at its original position. The values of σ that we simulated were 0, 0.05, 0.1, 0.25, 0.5 and 1 nm. Views of the CHA and MFI frameworks down the a and b crystallographic axes, respectively, are shown in Figure 4. As this Figure illustrates, when σ=0 nm the crystal structure can be resolved. However, even with small values of σ the structure is quickly blurred and pores are lost by σ=0.25 nm. This simulation gives an estimate of the spatial resolution that would be necessary to recover crystallographic information for zeolites, and it is clearly below the expected resolution for these materials.

Figure 4.

Simulating the influence of spatial resolution on the ability to recover crystallographic information for zeolites with the framework structures CHA and MFI. A 2D projection down the a and b axes for CHA (top) and MFI (bottom) are shown, respectively, with all tetrahedral (blue) and oxygen (red) atoms shown. The simulation offset each atom in 3D by σ=0, 0.05, 0.1, 0.25, 0.5 and 1 nm. As is shown the pore system is quickly lost with the offset, showing that a very high spatial resolution would be needed to recover the pore system of zeolites.

The limited detector efficiency also impacts the analysis of atom probe data, as it will shift the median of the nearest neighbor distribution (NND) to higher values as less atoms are collected to fill a fixed volume. It also makes it difficult to identify very small clusters, especially those less than 10 atoms, though the use of randomly generated comparison data sets can help to ensure that identified clusters are statistically relevant.47 Overall, instrument spatial resolution and detection efficiency limit crystallographic reconstruction quality of even ideal samples for APT, that is, single‐crystal metals, and will certainly be even more restricting for zeolites as they are heterogeneous, non‐conductive oxide materials and organic/inorganic hybrid materials. A benefit though is that these should make the data appear more random than it actually is, avoiding incorrect conclusions.47

4. Data Analysis

The data collected from each specimen leads to data sets that contain the chemical identity and 3D position of typically >10⁶ ions, leading to many possibilities to analyze the data. The first level of analysis comes from examining the bulk composition of specimen needles, and this is especially useful if several specimens from distinct regions of a sample are studied as differences between needle compositions will indicate compositional heterogeneities that span length scales greater than 100 s of nanometers, which may motivate investigations by other characterization techniques capable of probing larger sample volumes, though with reduced resolution. Large crystals of zeolite ZSM‐5 have been characterized by numerous techniques, and it is known that the Si/Al ratio varies across the cross section, as is schematically shown in Figure 5, and the four needles studied, labeled as 1–4, were purposefully selected to represent distinct regions of the catalyst. The trend of lower Si/Al ratios near the edge of the cross section and high Si/Al ratios near the center agrees well with the known Al zoning in this material, and reinforces our confidence in the data.

Figure 5.

a) Expanded view 3D schematic of a large zeolite ZSM‐5 crystal showing the internal architecture of the material, which is composed of several distinct subunits, as well as the location of the removed cross‐section (blue panel) prepared by Focused Ion Beam (FIB) milling. b) The cross‐section that was removed for APT needle preparation. The red dashed lines show the locations of the subunits and the black numbered circles indicate the needle locations. c) Schematic representation of Al zoning in the zeolite ZSM‐5 cross‐section; blue represents regions with higher Al content and approximate needle positions are numbered 1 to 4. d) Bulk and cluster Si/Al ratio and ¹³C atomic % plotted for APT needles 1 to 4. Clusters are defined as groups of closely spaced ¹³C atoms and the cluster Si/Al ratio is inside the volume occupied by the clusters, averaged over all clusters in each needle. Adapted from Ref. 70.

In order to define isoconcentration surfaces the data must be binned into voxels so that local composition can be determined. The voxel size must be selected with the trade‐off that smaller voxels lead to better spatial resolution with an increase in the statistical error as a smaller voxel will contain a smaller number of ions. We generally used a 3×3×3 nm delocalization and 1 nm voxel size. However, there were instances in which the voxel size was reduced to create a higher polygon density to increase the signal to noise ratio because the edge polygons are not included in the proximity histogram analysis. The delocalization remained the same, so the shape of the interfaces was not significantly altered with the reduced voxel size.

4.1. Searching for Chemical Heterogeneities

The initial search for chemical heterogeneities in the data is normally first conducted “by eye” to look for obvious phase segregations and precipitates, and these can be quantitatively isolated using isoconcentration surface analysis. A more vigorous and quantitative approach is to use statistical tests and examine deviations from randomized data sets to be certain of all findings, and this is accomplished using the NND and frequency distribution analysis (FDA). The NND plots the number of counts as a function of the atom pair distance, and for a homogeneous sample this will give a normal distribution.47, 80 If a non‐random distribution is present, then the solute NNDs will be shifted to a smaller atom pair distance. The NND can then normally be described by at least two Gaussians, one centered at a smaller atom pair distance, representing the clustered atoms, and a second centered at an atom pair distance close to the normal distribution of the randomized data (though this may not be present depending on the extent of segregation). Analysis of a higher order nearest neighbor (kNN) distribution may be used and can help to remove statistical fluctuations in the data, and is also useful with higher concentrations of an element, and the selection of k is analogous to choosing a voxel size. Our recent study on Cu‐exchanged zeolites presents an example of a higher‐order kNN distribution, and this is shown in Figure 6, where a 4NN distribution allowed easier identification of a non‐random Cu distribution.64, 81

Figure 6.

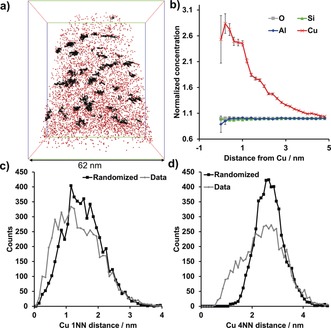
APT analysis of a fresh (calcined) zeolite Cu‐SSZ‐13. a) 3D map of all Cu ions in the needle, with Cu clusters shown in black. Bounding box dimensions of 70×62×62 nm³. b) Cu radial distribution function (RDF) showing a clear Cu–Cu affinity, but no significant affinity for any other species. c,d) Cu nearest neighbor distributions (NNDs) for the first (c) and fourth (d) nearest Cu neighbor in fresh Cu‐SSZ‐13 demonstrating that using a higher order NND can decrease noise in the analysis. Adapted from Ref. 64.

The FDA is a more rigorous statistical method of examining the distribution of ions in a sample, using ${\chi }^2$ ‐statistics to determine the reduced ${\chi }^2$ , p‐value and Pearson coefficient (μ), which can be easily calculated using the built in tools in Cameca's IVAS software.47, 49, 80, 82, 83 Compositions within bins with a set number of ions (typically 100) are calculated and compared to a binomial distribution. The ${\chi }^2$ value is calculated from comparison of the calculated composition distribution (observed) to that of a binomial distribution (expected) according to: ${\chi }^2=\sum \frac{{\left[\mathrm{o}\mathrm{b}\mathrm{s}\mathrm{e}\mathrm{r}\mathrm{v}\mathrm{e}\mathrm{d}-\mathrm{e}\mathrm{x}\mathrm{p}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{e}\mathrm{d}\right]}^2}{\mathrm{e}\mathrm{x}\mathrm{p}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{e}\mathrm{d}}$ . The degrees of freedom for this analysis are the observed compositions with more than five observations minus 1. Once the ${\chi }^2$ value is known it can then be compared to tabulate values to either confirm or refute a deviation from randomness. The p‐value is used in conjunction with a significance level, normally chosen as 0.010 for APT experiments, and if the value from the p‐test is less than this significance level, it signifies a departure from the random distribution.

The Pearson coefficient (μ) is a method used to remove the sample size dependence from the ${\chi }^2$ value, as with a simple ${\chi }^2$ value a larger sample size is more likely to lead to the finding of a non‐random distribution. The Pearson coefficient is calculated according to $\mu =\sqrt{{\chi }^2/(N+{\chi }^2)}$ , where N is the total number of 100 ion bins in the dataset (the total number of observations). The value of μ will be between 0 and 1, where 0 signifies a random distribution and 1 is a completely non‐random distribution. The real power of this statistic is that it can be used to compare between drastically different sample sizes, which are often encountered in atom probe data.84

4.2. Analysis Across the Dimensions

The data reconstruction produces a complete set of ion positions in 3D, allowing for a wide range of analyses. A 1D concentration profile, which can be done across any length of the sample, can be especially useful in identifying features such as grain boundaries or compositional gradients that span entire needles. A 1D concentration profile can also be used to verify the location of the sample surface by detecting a specific coating element that is present from deposition prior to sample preparation, such as Pt. 2D contour plots can be created to visualize the distribution of ions across a plane of interest, in which bins are defined with both an X and Y position, simplifying the visual detection of heterogeneities in the distribution of a species of interest. With 2D contour plots and 1D line profiles, care should be exercised in examining density variations due to the possibility of artefacts.

What truly sets APT apart is that 3D distributions of ion positions are produced with sub‐nanometer scale resolution, while other element‐sensitive techniques, such as STEM energy‐dispersive X‐ray spectroscopy (EDX), are typically limited to 2 dimensions for most applications (3D reconstructions can be created starting with quasi‐2D sections and then building these into a 3D model). After a heterogeneous distribution is indicated either by visual examination or by a statistical test, a simple method to visualize heterogeneities in the data is with an isoconcentration surface, which segregates regions by a user selected concentration boundary. Generally, the boundary of the isoconcentration surface is chosen at the concentration approximately midway between that of the element(s) of interest between the two phases.49 A proximity histogram (proxigram) calculates a 1D concentration profile with the ions binned with respect to proximity from the isoconcentration surface. In other words, the closest proximity of all ions to the isoconcentration surface within the dataset is calculated, and a concentration profile is calculated by counting all ions within discrete distance bins from the surface, which allows for analyzing the change in composition with respect to the curvature of the surface.

Isoconcentration surface analysis has been applied frequently in APT studies of zeolite‐based catalysts. With severe steaming, the Al atoms migrate into Al‐rich regions, and this migration of Al is in line with the known results of steaming, that Al is removed from framework positions.62 However, it offers important insight into the final state of Al after steaming, that not only is it removed from framework positions, but in fact migrates into Al rich regions, with the potential to block the pores in the material, thereby limiting diffusion of reactants and products. In the MTH reacted zeolite ZSM‐5 crystal, carbon‐poor regions were also identified using isoconcentration surface analysis, and one example is given in Figure 7.70 The proxigram across this isoconcentration surface (Figure 7 c) reveals that there is no significant change in the Si/Al ratio across the isoconcentration surface, leading to the conclusion that the coke poor region must be due to some structural feature that cannot be resolved using APT, such as pore blockage. Figure 7 also gives a side‐by‐side comparison of the 2D and 3D analysis of the material, with a comparison of the 2D composition map of the ¹³C concentration and the 3D view with the isoconcentration surface added. The isoconcentration surface is easily seen in the 2D view, which allows for easy visualization in the absence of a video or software to manipulate the 3D distribution of ions, though it could have been missed if the incorrect projection direction was chosen.

Figure 7.

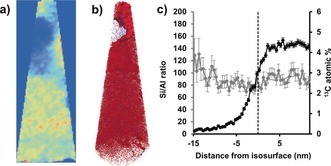
a) 2D compositional map of the ¹³C content in needle 3 of a zeolite ZSM‐5 crystal after contacting it with ¹³C‐labeled methanol at 623 K for 90 minutes (see Figure 5 for details on the needle choice. b) 3 % ¹³C isoconcentration surface over all ¹³C (red) and Al (blue) ions. Needle max dimensions of 187×69×68 nm³. c) Compositional histogram across the ¹³C isoconcentration surface in b. Adapted from Ref. 70.

Isoconcentration surface analysis was also applied to aged zeolite Cu‐ZSM‐5, shown in Figure 8, and with the proximity histograms a copper aluminate spinel phase, CuAl₂O₄, could be quantitatively identified.44 This is a known deactivating species, but previously was only found from bulk analyses, but with APT could be quantified as isolated features in 3D. Furthermore, the percentage of Cu and Al atoms within the region with Cu/Al=2 stoichiometry (in the 8 % Al isoconcentration surface) were quantified with isoconcentration surface analysis to give an estimate of the portion of Cu and Al atoms forming the phase that resembles CuAl₂O₄, determined to be 20 % of all Cu ions and 35 % of all Al ions present in the needle.

Figure 8.

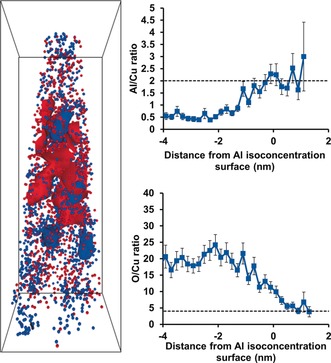
Reconstructed needle of an aged zeolite Cu‐ZSM‐5 with 5 % Cu (red) and 8 % Al (blue) isoconcentration surfaces shown, bounding box dimensions are 15×15×43 nm³. The Al/Cu and O/Cu ratios across the 8 % Al isoconcentration surface are in good agreement with the stoichiometry of Cu aluminate spinel, CuAl₂O₄, which is indicated on each graph by the dotted line. Adapted from Ref. 64.

4.3. Radial Distribution Function

The radial distribution function (RDF) is a powerful tool to examine affinity between species and test homogeneity. The method is extensively discussed in Refs. 85 and 86. The RDF can be conducted by normalizing the local concentration of a selected ion by the bulk concentration, which is done radially outward from the center of each atom of interest and averaged across the sample. In this way, the RDF offers another method of examining segregation of a species, especially at short distances. Error analyses are conducted using counting statistics, and the error bars are high for the first few data points because few ions will be counted near the center of the clusters.87 As the RDF is typically shown as a bulk normalized concentration, values between pairs of atoms will not be equal since they are defined over different volumes. Using the RDF, we were able to demonstrate that a nanoscopic relationship exists between deposited coke and Al atoms (Figure 9) in a coked zeolite ZSM‐5 crystal, which was exposed for 90 minutes at 623 K with ¹³C‐labeled methanol. While this is not surprising as Al atoms are Brønsted acid sites where coke deposits may form, finding a correlation highlights the resolution we are able to achieve using APT, and reinforces confidence in the data.

Figure 9.

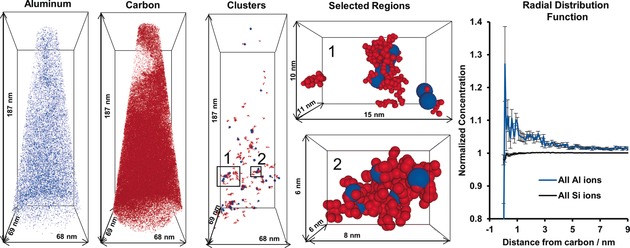
Overview of the analysis applied to a coked zeolite ZSM‐5 crystal after contacting it with ¹³C‐labeled methanol at 623 K for 90 minutes. The distributions of all Al (blue) and ¹³C (red) atoms in the needle are shown next to the carbon clusters. Two selected regions are expanded to show the association between coke and Al atoms (note Al atom sizes have been exaggerated for clarity). The radial distribution function shows an elevated Al content near coke carbon. Adapted from Ref. 70.

4.4. Cluster Analysis

When a non‐random distribution is indicated using the aforementioned statistical tests, a friends‐of‐friends cluster analysis can be performed to isolate solute clusters within a matrix (further stated as cluster analysis, detailed in Ref. 52). The purpose of a cluster analysis is to identify regions where the spacing between solute atoms in APT data is smaller than that in the bulk, effectively finding regions that are locally enriched in a specified element. This technique can identify clusters of less than five atoms, which would be difficult to do using an isoconcentration surface analysis due to gridding and delocalization. This cluster analysis method is conducted by iterating between the parameters of N _min, which is the minimum number of solute atoms that can form a cluster, and d _max, the maximum radius in which another solute atom must be found to form a cluster (one additional solute atom must be found for order=1, higher orders are also possible with more than one solute atom required to fall within d _max, similar to a kNN distribution). The key element of cluster analysis is how the parameters are determined and statistically significant clustering is identified. The CAMECA IVAS package, often used by APT users, contains a cluster count distribution algorithm that compares the number of clusters in the dataset of interest versus a position‐randomized dataset with respect to d _max and a fixed N _min. The resulting plot shows the number of clusters versus d _max. The cluster parameters are determined using an iterative process where N _min is first set, and then the cluster count is plotted as a function of d _max. If the solute data are found to be significantly separated from the randomized data (normally chosen as a point where greater than 95 % of the number of clusters that exist in the collected data do not exist in the randomized data), then d _max can be fixed. A fixed d _max can then be used to plot cluster count versus cluster size to set an optimal N _min. By iterating through these parameters, the optimal cluster d _max and N _min can be determined, where significant clusters can be found relative to the randomized data. Additional methods, besides the friends‐of‐friends method, are available for cluster analysis, and they are described in Ref. 47.

Cluster analysis has proven to be invaluable to identify features in the data from zeolite catalysts. In the fresh and steamed large zeolite ZSM‐5 crystals, cluster analysis was used to show that steaming caused the Al to migrate and aggregate into clusters that contained Al with a density twenty times greater than the bulk aluminum density in the fresh material, which did not contain Al clusters.62 In the ¹³C methanol MTH‐reacted zeolite ZSM‐5 crystals, cluster analysis of the coke in the material demonstrated that small, coke‐rich regions existed in the needles, and were found to correlate with regions nanoscopically enriched in Al using both the Si/Al ratio of the clusters compared to the bulk (Figure 5) as well as the RDF for ¹³C (Figure 9).70 A view of all ¹³C and Al ions next to the identified ¹³C clusters is shown in Figure 9. From a zeolite perspective, this finding might sound unsurprising as it is well‐established that the reactions to form coke molecules (or hydrocarbon pool molecules in the case of the MTH process) require a Brønsted acid site, which is linked to a framework Al atom. However, from an APT perspective this is an exciting result as it shows that even in a compositionally heterogeneous material the spatial resolution is still high enough to detect molecule‐sized clusters of carbon atoms as well as a spatial correlation between the carbon and the active site that forms the molecules.

In the APT study of Cu‐exchanged zeolite catalysts, Cu‐rich regions were easily identified in fresh and aged Cu‐ZSM‐5 as well as in aged Cu‐SSZ‐13 zeolites. However, it was only using cluster analysis that significant Cu‐rich regions could be identified in fresh Cu‐SSZ‐13. As Figure 6 illustrates, a non‐random Cu distribution is indicated in fresh Cu‐SSZ‐13 using the 1NN and 4NN distributions. Using a 4NN cluster analysis, the Cu clusters could be easily isolated in 3D, as is shown in Figure 6 a. The RDF for Cu indicates a Cu–Cu affinity, but does not show an affinity of Cu for any other elements. Interestingly, the UV/Vis diffuse reflectance spectra of this material showed that it contained only isolated, exchanged Cu²⁺ ions, so even in the Cu clusters all the material must be exchanged onto paired Al sites. A possible reason for the Cu clusters is preferential material accessibility that causes the Cu to aggregate in discrete regions of the material, which cannot be determined using APT. This finding is even more interesting in the context of a recent report on the importance of site proximity in NO_X reduction catalysis, and will be the subject of future investigations.88

4.5. Assessing the Significance of Findings

In studying zeolite‐based materials with APT, one of the most important evaluations of the data is its statistical significance and evaluation in the context of other characterization studies of the (same or the same type of) materials. The large size of the data sets generated by APT is one of the greatest assets of the technique as well as one of the potential pitfalls. The importance of using randomized data sets in cluster analysis was already discussed, and allows for confidence in cluster detection. Other statistical tests can also assist in evaluating the significance of heterogeneities in the data, particularly the FDA.

A second perspective to have on the data is its context in terms of other investigations in order to provide a framework for the findings and conclusions of APT results. This was especially important to support the application of the technique to zeolites, as they are a new class of materials to examine with APT. The first comparison to make is the composition of the collected APT needles with the known bulk composition of the material, to give an idea of the quantitative accuracy of the APT measurement. This has the potential drawback that the infinitesimally small size of an APT needle relative to a bulk sample means it may not be representative of the bulk, though of course this can be improved by running multiple needles from discrete locations within a sample.52 In the context of zeolites, a second major pitfall is the limited ability to detect oxygen and oxide molecules, and we have found that the aluminum detection in APT is lower relative to other elements present in the materials. We believe that we encountered this problem with large zeolite ZSM‐5 crystals as the bulk Si/Al ratio of the materials is known to be 17, but of the four needles we successfully tested the lowest Si/Al ratio was 69. This was further exacerbated by the presence of coke molecules in this material that will exhibit complex fragmentation patterns, and likely overlap with key peaks for determining the Si/Al ratio, as is shown in Figure 3 with the CO/Si overlap highlighted. In the Cu‐exchanged zeolites the Si/Al ratios detected were closer to the expected bulk value as the lack of coke in these materials makes quantification easier as there are less potential species to identify in the mass spectra, easily seen in Figure 3.64 Additional elements, which are present in zeolites and known to be difficult to reliably quantitate in APT are O and H, so we did not emphasize those elements in our analyses.47, 52, 70, 71, 72, 73

5. Conclusions and Future Perspectives

The information presented in this Minireview highlights the realized and future potential of the APT technique as a single‐atom microscopy method to study zeolite‐based catalysts as well as related porous materials. As APT is uniquely positioned to create 3D compositional reconstructions with possible sub‐nanometer resolution, we are of the opinion that it should be applied with much greater frequency to provide structure–composition–property relationships in these types of materials. Although various types of challenges have been encountered when applying APT to these non‐conductive heterogeneous materials, we have outlined practical strategies used to surmount these hurdles to obtain results consistent with other characterization techniques. As researchers continue to apply this technique to zeolites, and to solid catalysts in general, we believe there are several currently unmet challenges, which APT may be uniquely positioned to answer. These challenges are: 1) Differences between carefully prepared zeolite crystals in the laboratory versus industrially prepared zeolite crystals. This is important as there is often a disconnect between academic laboratories that (mostly) prepare their own catalysts under ideal conditions and industrially prepared zeolites that are subject to the economic requirements of large‐scale production plants.89, 90, 91, 92 From a characterization perspective, one of the key challenges of working with industrial crystals is that they often have very small crystal sizes and can crystallize as irregular intergrowths of crystallites due to the conditions applied to achieve rapid crystallization. APT has a strong potential to be applied to these materials and offers a way to compare industrially and laboratory prepared zeolites, as our recent APT study of a zeolite ZSM‐5, manufactured by Zeolyst, has demonstrated.64 2) Crystallographic reconstructions of zeolites to show the T‐site specific location of heteroatoms. Resolving the location of heteroatoms, such as Al, with respect to specific T‐sites in zeolites, remains one of the grand challenges of zeolite science and technology. Currently, the spatial resolution of APT applied to zeolites does not appear to be high enough to do this as our simulations in Figure 4 show, but perhaps advances in APT instrumentation and related measurement protocols will negate the issues in the near future, though we recognize this remains a serious hurdle to take. 3) Looking at other solid catalyst systems, such as supported metals, mixed metals and supported zeolites, which already has some precedent,42, 93, 94 though certainly this can be expanded further, thereby linking the APT methodology with other chemical imaging methods, such as X‐ray microspectroscopy.

There are future potential developments in APT that could provide solutions to these problems, and many of these are contained in the atom scale tomography (AST) 2020 vision.95 These goals include 100 % collection efficiency of large data sets of at least 10⁸ atoms with high enough resolution to reconstruct the atomic structure. To realize this goal, new detectors will need to be invented, and correlated studies will need to become routine, especially STEM/APT, with all the normal STEM functions intact including STEM‐HAADF, electron diffraction, electron energy loss spectroscopy (EELS) and EDX. The entire experiment will also need to be performed in ultra‐high vacuum and at cryogenic temperatures. Another possible combination is electron ptychography and APT, which would avoid the high accelerating voltages of STEM. These technical advances will by a necessity need to be accompanied by advances in simulations. Another technical improvement would be in the construction materials of atom probe chambers as the steel they are currently made of continuously outgasses hydrogen, making it impossible to quantify hydrogen, and perhaps a new material of construction could be found that does not have this problem. While these goals may seem far‐off, there is no reason to expect that they will not be realized in the future in order to give true, atom‐by‐atom chemical reconstructions of materials.

In summary, we have discussed the possibilities, potential pitfalls and some practical strategies to successfully apply APT to zeolite‐based catalyst materials. Through the use of rigorous controls and careful examination of the experimental data in the context of known material properties, we have developed and outlined strategies to successfully create atom‐by‐atom, 3D compositional reconstructions of these highly used functional materials, and presented insights into valuable structure–property relationships. Many future challenges remain in the application of APT to zeolite‐based materials, but the unique insights to be gained from this technique will continue to push researchers to apply it to functional porous materials, including, but not limited to, zeolites.

Conflict of interest

The authors declare no conflict of interest.

Biographical Information

Joel E. Schmidt obtained his BS and MS degrees in Chemical Engineering at The University of Dayton (Dayton, OH, USA), and at this time did research in the Thermal Sciences and Materials Branch of the US Air Force Research Labs. He received his Ph.D. in Chemical Engineering from California Institute of Technology (Pasadena, CA, USA) in the group of Mark E. Davis. In 2015 he began working as a postdoctoral researcher at Utrecht University in the group of Bert M. Weckhuysen.

Biographical Information

Linqing Peng is pursuing her undergraduate degree in physics and chemistry at Grinnell College (Grinnell, IA, USA), and worked with Dr. Jonathan D. Poplawsky at Oak Ridge National Laboratory through the ORSS internship program. She is interested in integrating computations and theoretical modeling with microscopic and spectroscopic tools to study physics, chemistry and materials science problems.

Biographical Information

Jonathan D. Poplawsky received his BS from The University of Scranton (Scranton, PA, USA) before receiving his MS and Ph.D. in Physics at Lehigh University (Bethlehem, PA, USA) in 2012 in the group of Volkmar Dierolf. He worked with Stephen J. Pennycook at ORNL for his post‐doctoral studies, and is currently in charge of the atom probe tomography laboratory within ORNL′s CNMS. His main research interests are focused on understanding and improving energy materials using microscopy techniques.

Biographical Information

Bert M. Weckhuysen obtained his MS and Ph.D. degree from KULeuven (Leuven, Belgium) and continued his research as a postdoctoral fellow at Lehigh University (Bethlehem, PA, USA) and Texas A&M University (College Station, TX, USA). He is since 2000 Professor of Inorganic Chemistry and Catalysis at Utrecht University (Utrecht, The Netherlands). Together with his research group, he works to deepen the fundamental understanding of how catalyst materials work and deactivate.

J. E. Schmidt, L. Peng, J. D. Poplawsky, B. M. Weckhuysen, Angew. Chem. Int. Ed. 2018, 57, 10422.