High‐permittivity pad design tool for 7T neuroimaging and 3T body imaging

Abstract

Purpose

High‐permittivity materials in the form of flexible “dielectric pads” have proved very useful for addressing RF inhomogeneities in high field MRI systems. Finding the optimal design of such pads is, however, a tedious task, reducing the impact of this technique. We present an easy‐to‐use software tool which allows researchers and clinicians to design dielectric pads efficiently on standard computer systems, for 7T neuroimaging and 3T body imaging applications.

Methods

The tool incorporates advanced computational methods based on field decomposition and model order reduction as a framework to efficiently evaluate the B ₁ ⁺ fields resulting from dielectric pads. The tool further incorporates optimization routines which can either optimize the position of a given dielectric pad, or perform a full parametric design. The optimization procedure can target either a single target field, or perform a sweep to explore the trade‐off between homogeneity and efficiency of the B ₁ ⁺ field in a specific region of interest. The 3T version further allows for shifting of the imaging landmark to enable different imaging targets to be centered in the body coil.

Results

Example design results are shown for imaging the inner ear at 7T and for cardiac imaging at 3T. Computation times for all cases are approximately a minute per target field.

Conclusion

The developed tool can be easily used to design dielectric pads for any 7T neuroimaging and 3T body imaging application within minutes. This bridges the gap between the advanced design methods and the practical application by the MR community.

1. INTRODUCTION

Obtaining MR images with spatially‐invariant tissue contrast becomes more challenging at higher static magnetic field strengths. The fundamental reason for this is the increase in Larmor frequency, which leads to a shortened wavelength of the RF field in tissue. For static fields strengths of 3T and higher, this wavelength becomes comparable to the dimensions of the body, or shorter. As a consequence, wave‐interference effects that reduce the homogeneity and strength of the transmit RF magnetic field, referred to as the B ₁ ⁺ field1, 2 become apparent. The homogeneity of this field is of crucial importance in obtaining a uniform contrast in MRI.

Over the past decade, many RF shimming studies have been devoted to improving the B ₁ ⁺ field distribution and efficiency. Active shimming techniques use multiple separate transmit coils: the amplitudes and phases are configured for each element individually, such that the B ₁ ⁺ field is tailored in a certain region of interest (ROI).3, 4, 5, 6 Alternatively, dielectric materials can be used to tailor the B ₁ ⁺ field, as a passive shimming approach. These materials typically have a high relative permittivity on the order of 80‐300, and they induce a strong secondary magnetic field in their vicinity.7, 8, 9, 10, 11, 12, 13, 14, 15 These materials can be produced easily by means of aqueous suspensions of calcium titanate and/or barium titanate to obtain the appropriate permittivity.16, 17, 18 Subsequently, the mixture is sealed in a polypropylene bag with appropriate dimensions to form flexible pads. Typically, these dielectric pads are placed in close vicinity to the imaging ROI tangent to the body.

Despite the ease of constructing such dielectric pads, their design is not trivial as it depends on many aspects; the optimal design varies with ROI, application requirements (e.g., transmit efficiency or homogeneity), and MR configuration (e.g., static field strength and transmit antenna). Therefore, the pad’s dimensions, location, and constitution need be optimized in an application‐specific manner. One common approach is to perform a parametric optimization using general‐purpose electromagnetic field solvers, based on a systematic trial‐and‐error approach and guided by user intuition, and then to choose the best pad‐properties afterward. As each of these simulations involve a large computational domain with an RF coil and heterogeneous body model, such procedures typically take multiple days for a single application.8, 19, 20, 21 Some applications also benefit from having more than 1 dielectric pad, which further complicates the design procedure. This limits the exploitation of this practical shimming approach.

In previous work,22 we have developed advanced reduced order modelling techniques to accelerate pad evaluations by characterizing stationary components such as the RF coil and body model in an offline‐stage, and compressing the resulting model. This yielded up to 4 orders of magnitude of acceleration when compared with using commercial software and enabled the automated design of a single dielectric pad in under a minute. Although these methods have been demonstrated, the offline procedures can present a challenging task for any MR user planning to use dielectric pads due to either lack of software, resources, or expertise in this specific field. The approach up to now did not allow for designing 2 dielectric pads at once, which can be beneficial in many applications.

In this work, we aim to extend our modeling approach to include 3T body imaging as well as 7T neuroimaging and bridge the gap between these advanced design methods and practical application by the MR community. We address this gap by integrating the automated design procedure into a stand‐alone software tool, which is available for download. This tool can be run on a standard PC, is fast, and can be used to design multiple dielectric pads to optimize either the homogeneity or the efficiency of the B ₁ ⁺ field, or a combination of both, in any arbitrary ROI in the head at 7T or the body at 3T. Furthermore, for 3T, the imaging landmark can be shifted throughout the torso to enable different imaging targets to be centered in the body coil.

2. METHODS

2.1. Configuration

The 7T neuroimaging configuration was simulated using a shielded and tuned high‐pass birdcage head coil with a radius of 15 cm operating at 298 MHz (7T). The body model “Duke” from the Virtual Family dataset was used,23 and the computational domain was discretized on a uniform and isotropic grid with a spatial resolution of 5 mm. The pad‐design domain was taken as a 1‐cm‐thick layer around the head model, which is constrained in practice by the tight‐fitting receive arrays used in neuroimaging.

The 3T body‐imaging configuration was simulated using a generic wide‐bore high‐pass birdcage body coil with a radius of 35 cm operating at 128 MHz, in which the “Duke” body model is situated. The computational domain was discretized on a uniform and isotropic grid with a spatial resolution of 7.5 mm and the pad‐design domain was defined as a 1.5‐cm‐thick layer around the torso extending from just below the top of the shoulders down to the hips. Whereas the position of the head with respect to the head coil is fixed in the 7T neuroimaging setting, this is not the case for 3T body imaging. Therefore, additional field simulations were performed for a 1.5‐cm‐spaced range of imaging landmarks within the torso to enable shifting of the body coil for different body imaging applications.

All field quantities were normalized to 1 W input power.

2.1.1. Modeling dielectrics

The backbone of the design tool is a modeling approach that stems from the work established in Van Gemert et al and Brink et al,24, 25 where an efficient forward model was presented for evaluating the effect of a dielectric pad. The basic idea is to split the computational domain into 2 parts as illustrated in Figure 1A,B for 7T neuroimaging and 3T body‐imaging, respectively. The first domain is stationary and consists of the heterogeneous body model and RF transmit coil. These components remain unaffected throughout the pad‐simulations and can, therefore, be characterized in advance. The second domain is dynamic and confines the pad‐design domain where any desired dielectric pad can be positioned during the design process, i.e., with arbitrary geometry, location, and material properties. This formulation allows us to compute a pad‐independent background field and field response library in an offline‐stage, such that only the pad‐specific secondary field needs to be computed in the online‐stage. As this latter domain is much smaller than the original full computational domain, computations are accelerated without compromising accuracy.

Figure 1.

Splitting of computational domains and the parameterization of the dielectric pad. A, The 7T neuroimaging configuration is divided into a static part, consisting of a heterogeneous body model, RF coils, and an RF shield, and a dynamic part to which the dielectric is confined. B, The 3T body‐imaging configuration is shown, here the wide‐bore birdcage is omitted for visualization purposes of the pad design domain. C, As only the pads that can be easily fabricated are of interest, the model is parameterized in the pad’s characteristics

The complexity of the calculations can be reduced further through the application of reduced order modeling techniques as has been shown in van Gemert et al.22 In this procedure, the practical degrees‐of‐freedom of the pad design problem (i.e., many fewer than allowed by the computational grid) are exploited to further compress the model. To this end, the pad design is parametrized in terms of its width, height, location, and constitution, through the parameter vector p = [ε; z_T; z_B; ϕ_L; ϕ_R] as illustrated in Figure 1C. Subsequently, the model is compressed by projecting onto a reduced order basis obtained from randomized pad simulations, to further accelerate B ₁ ⁺ field computations to under 1 s of computation time for any arbitrary dielectric pad.

In the 3T configuration, each landmark position of the body coil requires specific background fields to be generated in advance. Due to the close vicinity of the pad‐design domain to the body model, however, we argue that the field response library can be re‐used as coupling is dominated by the body model and is not significantly influenced by the body coil.

2.1.2. Optimization methods

The pad optimization procedure can be used in 2 different approaches. The first approach allows the user to find the optimal position for an existing pad, i.e., the user can define the dimensions and the material properties of the pad (which they may already have prepared), and the routine optimizes the placement of this pad. The second approach forms a full parametric design that optimizes the pad’s dimensions, material properties, and position simultaneously by iteratively minimizing a cost functional. In both cases, we measure the characteristics of the resulting B ₁ ⁺ field within the ROI in terms of its average magnitude as a measure of transmit efficiency, and its coefficient of variation C_v as measure of homogeneity. The latter is defined as the ratio of standard deviation to mean value.

The first approach uses a parameter sweep over all possible positions within the pad design domain for a given pad geometry and constitution. This sweep can be carried out quite rapidly, as the simulations are fast and the number of possible solutions is rather small, in contrast to the full parametric design. Subsequently, the optimum pad positioning is found by selecting the maximum of the following objective function:

$$O\left(\mathbf{p}\right)=\gamma {\mathrm{G}}_{\mathrm{e}\mathrm{f}\mathrm{f}\mathrm{i}\mathrm{c}\mathrm{i}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{y}}\left(\mathbf{p}\right)+\left(1-\gamma \right)[1-{\mathrm{C}}_{\mathrm{v}}\left(\mathbf{p}\right)],$$ (1)

where the first term on the right hand side is the gain in average transmit efficiency (${\mathrm{G}}_{\mathrm{e}\mathrm{f}\mathrm{f}\mathrm{i}\mathrm{c}\mathrm{i}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{y}})$ due to the dielectric pad and the second term is a measure of field homogeneity. The weight $\gamma$ is used to give a preference to either efficiency or homogeneity.

In the second approach, the pad optimization problem is formulated using a target field approach in which we aim to achieve a certain desired B ₁ ⁺ field magnitude in a defined ROI. This is achieved by minimizing a cost functional C as a function of the pad‐parameter vector p. This functional is defined as

$$C\left(\mathbf{p}\right)=\frac{1}{2}\frac{{||B_1^{+}\left(\mathbf{p}\right)-B_1^{+;\mathrm{d}\mathrm{e}\mathrm{s}\mathrm{i}\mathrm{r}\mathrm{e}\mathrm{d}}||}_{2;\mathrm{R}\mathrm{O}\mathrm{I}}^2}{{||B_1^{+;\mathrm{d}\mathrm{e}\mathrm{s}\mathrm{i}\mathrm{r}\mathrm{e}\mathrm{d}}||}_{2;\mathrm{R}\mathrm{O}\mathrm{I}}^2}$$ (2)

where B ₁ ^+;desired is the desired B ₁ ⁺ magnitude in the ROI, B ₁ ⁺(p) is the field due to a pad with model parameters p, and ${||·||}_{2;\mathrm{R}\mathrm{O}\mathrm{I}}$ denotes the L ² norm over the ROI. The cost function in Equation (2) aims to minimize the discrepancy between the prescribed B ₁ ⁺ field and the B ₁ ⁺ field generated by the model, integrated over the ROI.

To minimize this nonlinear function, we use a gradient descent method combined with a line search to determine the step‐size, as the gradient of the function can be computed analytically.24 ^,26 Other methods can also be used, but we found that this is the most efficient and stable method in the context of this application. To ensure smooth convergence, we adopted the following rules for the update steps:

1. For iteration j compute gradient as ${\mathbf{g}}^j={\mathrm{\nabla }}_{\mathbf{p}}C$

2. Set update direction as

${\mathbf{u}}^j\left(1\right)=-\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left\{{\mathbf{g}}^j\left(1\right)\right\}\ast 20$ % ε update

${\mathbf{u}}^j\left(2\right)=-\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left\{{\mathbf{g}}^j\left(2\right)\right\}\ast w_1\ast 0.75\mathrm{c}\mathrm{m}$ % z_T update

${\mathbf{u}}^j\left(3\right)=-\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left\{{\mathbf{g}}^j\left(3\right)\right\}\ast \frac{1}{w_1}\ast 0.75\mathrm{c}\mathrm{m}$ % z_B update

${\mathbf{u}}^j\left(4\right)=-\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left\{{\mathbf{g}}^j\left(4\right)\right\}\ast w_2\ast \frac{\pi }{8}\mathrm{c}\mathrm{m}$ % ϕ_L update

${\mathbf{u}}^j\left(5\right)=-\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left\{{\mathbf{g}}^j\left(5\right)\right\}\ast \frac{1}{w_2}\ast \frac{\pi }{8}\mathrm{c}\mathrm{m}$ % ϕ_R update

With the weights defined as

$w_1=\frac{\left|{\mathbf{g}}^j(2)\right|}{\left|{\mathbf{g}}^j(3)\right|}$ and $w_2=\frac{\left|{\mathbf{g}}^j(4)\right|}{\left|{\mathbf{g}}^j(5)\right|}$

and restricted to

$$\frac{1}{1.5}{\le w}_1\le 1.5\text{and}\frac{1}{1.5}{\le w}_2\le 1.5$$

• 3. Update pad parameters $\mathbf{p}$ as

${\mathbf{p}}^{j+1}={\mathbf{p}}^j+\alpha \mathbf{u}$ with an optimum step‐size $0\le \alpha \le 1$ found by line search.

The weights $w_1$ and $w_2$ control the weight between related variables and serve to include gradient sensitive information in the update steps.

2.1.3. Design tool

The tool is implemented in MATLAB (R2015a, The MathWorks, Inc., Natick, MA). It allows for computations on a GPU when available to speed up computations and requires approximately 3 GB of working memory for 7T neuroimaging and 7 GB for 3T body imaging. When the GPU is being used, it requires approximately 0.8 GB and 2.5 GB video memory on the GPU for 7T neuroimaging and 3T body imaging, respectively. The tool is available for download as an executable file at https://paddesigntool.sourceforge.io.

The graphical user interface of the design tool is shown in Figure 2. The top row depicts the tissue map of the head for the transverse, coronal, and sagittal slice, as well as a 3D view of the slices. If desired, the B ₁ ⁺ fields without dielectrics can be displayed here instead. The bottom row shows the B ₁ ⁺ field with pads, as well as a 3D view of the current pad design, which is updated throughout the optimization process. The contrast and brightness of all displays can be manually adjusted. The imaging landmark of the 3T body coil can be shifted manually as is illustrated in Figure 3.

Figure 2.

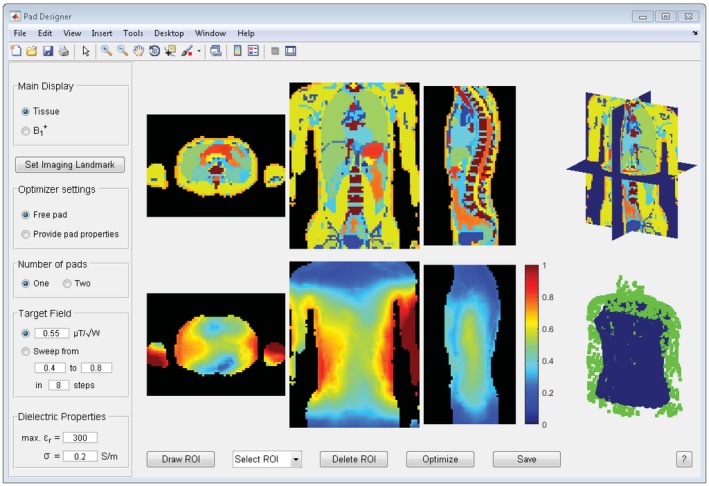
Graphical user interface of the pad design tool. Tissue profiles are shown in the top row, whereas B ₁ ⁺ fields are depicted in the bottom row. After a ROI is drawn, the user can start the optimization with the selected options

Figure 3.

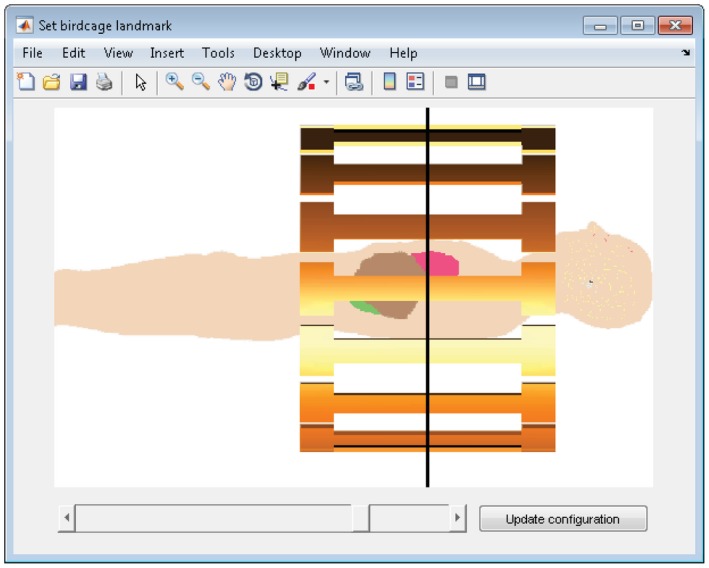
The landmark of the birdcage can be selected, after which the corresponding electromagnetic fields are updated

The tool allows optimization of the B ₁ ⁺ field using either 1 or 2 dielectric pads. In view of the implementation of the resulting pad design, we can limit the maximum allowed relative permittivity ε_r and incorporate a realistic conductivity throughout the iterations. Furthermore, the desired B ₁ ⁺ field efficiency for the ROI can be entered, or alternatively a sweep can be executed over a discrete set of predefined target fields to enable a trade‐off analysis between transmit efficiency and homogeneity.

The user can specify a custom ROI by drawing a 2D ellipsoid in each of the 3 isometric views. The 3D ROI is then generated by their cross‐section. Alternatively, for example purposes, a predefined ROI can be selected from a list. Subsequently, the optimization can be carried out, during which the design of the dielectric pad is continuously updated and illustrated in the bottom‐right corner.

After the optimization is complete, the obtained results are summarized in a separate window. The results display the dimensions (width, height, and thickness) and the dielectric properties of the optimized dielectric pad. Furthermore, the resulting average transmit efficiency and coefficient of variation are listed for the scenarios with and without dielectric pad. All results can be stored for later reference.

3. RESULTS

For demonstration purposes, we show 2 application examples in which the B ₁ ⁺ field is optimized in terms of transmit efficiency and homogeneity: first in cardiac imaging at 3T using a single dielectric pad, and then in imaging the inner ear at 7T using 2 dielectric pads.21 All computations have been executed on an Intel Xeon CPU X5660 @ 2.80 GHz (dual core) equipped with a NVIDIA Tesla K40c GPU.

For the 3T example the body coil was first shifted to be centered at the heart, which was then assigned as the ROI. A sweep over a set of 8 target fields was carried out using the sweep‐option, which took 2 min to compute on the GPU or under 8 min on the CPU. The maximum relative permittivity was set to 300 and the electrical conductivity of the pad was fixed at 0.2 S/m. The results for this sweep are shown in Figure 4A and the lookup table for the individual simulations is given in Supporting Information Table S1, which is available online. From the trade‐off analysis we chose iteration number 5 to be the optimum, yielding a dielectric pad with dimensions 22.5 × 35 × 1.5 cm³ and a relative permittivity of 206. This design corresponded to a target field equal to 0.5271 μT/√W, and improved the transmit efficiency by 28% and reduced the C_v from 13.3% to 6.0%. The optimization results are illustrated in Figure 4B and the results correspond with findings from Brink and Webb.19 Higher efficiencies can be obtained as well, e.g., iteration number 7, but as the dimensions of the dielectric pad become larger, its implementation becomes less practical.

Figure 4.

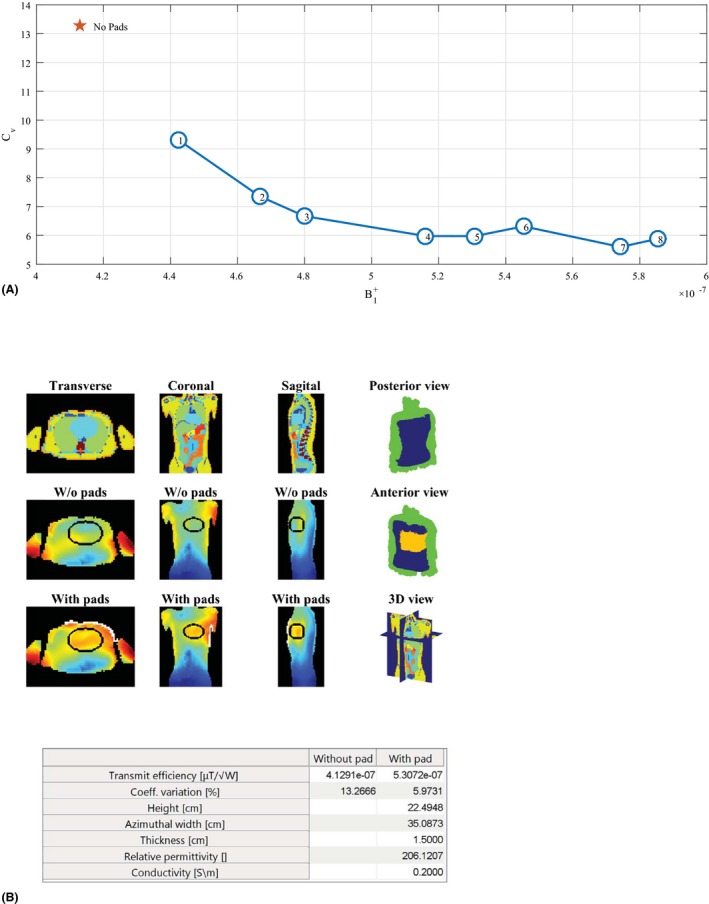
Design procedure for imaging the heart at 3T. A, The result is shown for a parameter sweep over a predefined set of target fields, after which a desired design can be selected based on the efficiency‐homogeneity plot. For the selected design (here, number 5), a single optimization is performed to obtain the results as shown in (B) for later reference. Design number 7 is not chosen here, as the dimensions of the dielectric pad are not practical. The lookup table for the individual simulations can be found in Supporting Information Table S1

For the 7T inner ear example an ROI was drawn that covered both inner ears, and the B ₁ ⁺ field was optimized with 2 dielectric pads. The optimal pad design was found using the sweep‐option in under 3 min on the GPU or in approximately 10 min on the CPU, which increased the transmit efficiency by 46% and reduced the C_v from 38% to 13%. The corresponding B ₁ ⁺ field and design summary are shown in Figure 5 and Supporting Information Figure S1, respectively, which suggested 1 pad with dimensions 11 × 16 × 1 cm³ and a relative permittivity of 269, and a second one with dimensions 22 × 12 × 1 cm³ and a relative permittivity of 300, which agrees with previous findings.21

Figure 5.

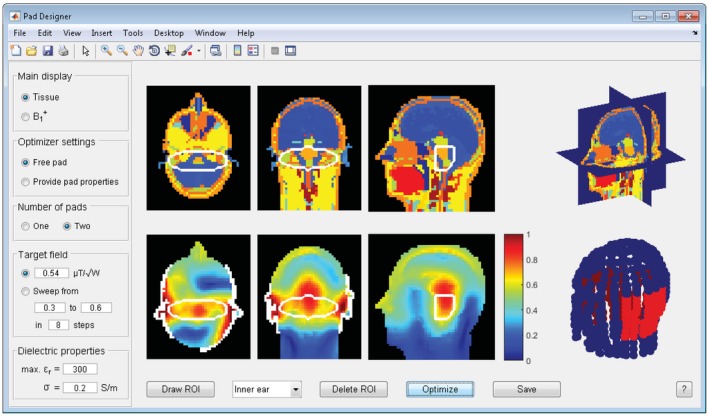
Pad design results for the inner ear using 2 dielectric pads. The improved field and the location and dimension of the 2 dielectric pads are shown. The details on the improvement and the pad’s parameters can be found in Supporting Information Figure S1

4. DISCUSSION AND CONCLUSIONS

In this work, we have presented a software tool that allows for designing dielectric pads for any arbitrary ROI in 3T body imaging and 7T neuroimaging applications. Computations are fast due to the underlying reduced order model, which enables MR operators to identify the optimal design and/or position in a matter of minutes. Aided by an optimization scheme, optimal design parameters can be determined which improve either the B ₁ ⁺ field magnitude or homogeneity within the ROI, or a combination of both.

The optimization method used in the tool has been chosen in view of its stability. Other methods may be considered as well, such as Gauss‐Newton methods which incorporate an approximant of the Hessian in the gradient direction. In our case, the Hessian is rank deficient and hence would need to be regularized in an application‐specific manner, so this approach was not pursued here. In addition, we truncated the update steps to ensure smooth convergence. Without these limitations, the algorithm had the tendency to converge to very large dielectrics with a low permittivity, which is not very practical to use. Using the truncated update steps, we avoided this undesired behavior. Alternatively, penalty terms can also be considered to discourage pad designs with large volumes or cross‐sectional areas.

The reduced order model that was used for 3T body imaging was created using snapshot datasets obtained in 1 single birdcage landmark, centered at the liver. We showed that the same field response library can be used in other landmarks as well, without the need to compute this time‐intensive part again. This exploits the fact that the electromagnetic interactions within the pad domain are dominated by the body, and, therefore, allows us to decouple the transmit coil from this response. We found that the errors that are introduced by this approximation are minimal and do not affect the solution quality. This suggests that a single library may be efficiently re‐used for other applications as well, e.g., in case of using a local transmit coil or transmit array. We do note that such translation still requires generating the corresponding background fields, i.e., corresponding with the body model and grid used in the reduced order model, to ensure compatibility.

In conclusion, an easy‐to‐use software tool has been made available to design dielectric pads in a matter of minutes for 3T body imaging and 7T neuroimaging applications. We anticipate this will help to bridge the gap between the advanced numerical design methods and the practical application by the MR community.

Supporting information

FIGURE S1 A summary of the pad design results for the inner ear using 2 dielectric pads. The improvement of the dielectric pad on the transmit efficiency and the coefficient of variation is shown. The dimensions and constitution of the 2 optimized dielectric pads are listed as well.

TABLE S1 Lookup table for the individual optimizations of the design procedure for imaging the heart at 3T. The result is shown for a parameter sweep over a predefined set of target fields, after which a desired design can be selected based on the efficiency‐homogeneity plot from Figure 4a and the table shown here.

van Gemert J, Brink W, Webb A, Remis R. High‐permittivity pad design tool for 7T neuroimaging and 3T body imaging. Magn Reson Med. 2019;81:3370–3378. 10.1002/mrm.27629