Abstract
Purpose
To explore the feasibility of MR Fingerprinting (MRF) to rapidly quantify relaxation times in the human eye at 7T, and to provide a data acquisition and processing framework for future tissue characterization in eye tumor patients.
Methods
In this single‐element receive coil MRF approach with Cartesian sampling, undersampling is used to shorten scan time and, therefore, to reduce the degree of motion artifacts. For reconstruction, approaches based on compressed sensing (CS) and matrix completion (MC) were used, while their effects on the quality of the MRF parameter maps were studied in simulations and experiments. Average relaxation times in the eye were measured in 6 healthy volunteers. One uveal melanoma patient was included to show the feasibility of MRF in a clinical context.
Results
Simulation results showed that an MC‐based reconstruction enables large undersampling factors and also results in more accurate parameter maps compared with using CS. Experiments in 6 healthy volunteers used a reduction in scan time from 7:02 to 1:16 min, producing images without visible loss of detail in the parameter maps when using the MC‐based reconstruction. Relaxation times from 6 healthy volunteers are in agreement with values obtained from fully sampled scans and values in literature, and parameter maps in a uveal melanoma patient show clear difference in relaxation times between tumor and healthy tissue.
Conclusion
Cartesian‐based MRF is feasible in the eye at 7T. High undersampling factors can be achieved by means of MC, significantly shortening scan time and increasing patient comfort, while also mitigating the risk of motion artifacts.
Keywords: compressed sensing, high field, magnetic resonance fingerprinting, matrix completion, ocular imaging
1. INTRODUCTION
Ophthalmologic disease diagnosis conventionally relies mainly on ultrasound and optical imaging techniques such as fundus photography and fluorescent angiography (FAG), MRI is increasingly being used in the radiological community.1, 2, 3 One of the main advantages of MRI is its capability to assess nontransparent tissues such as ocular tumors or structures behind the globe such as the eye muscles. Currently, however, these applications are mainly based on qualitative MRI methods using the large number of tissue contrasts addressable by MR. As an example, in Graves’ ophthalmopathy fat‐suppressed T2‐weighted MRI is the standard to detect inflammation in the eye muscles,4, 5 whereas in the diagnosis of retinoblastoma, a rare intraocular cancer in children, standard T1‐ and T2‐weighted MRI is often performed to confirm the presence of the tumor and to screen for potential optic nerve involvement.2 In more recent ophthalmologic applications of MRI, such as uveal melanoma (the most common primary intraocular tumor), quantitative MRI techniques including DWI6 and DCE imaging7 have been shown, but currently diagnosis is still based on qualitative methods.3
To personalize treatment plans quantitative parameters of the tissues involved, as can be acquired invasively for example by performing biopsies,8 are highly desirable. However, quantitative parameter mapping by means of MRI requires long examination times, which would result in significant eye‐motion artifacts, as well as patient discomfort.9 MR fingerprinting (MRF) is a recently introduced method for rapid quantitation of tissue relaxation times and other MR‐related parameters.10 It uses a flip angle sweep to induce a unique signal evolution for each tissue type. Incoherent undersampling can be applied during sampling of the MRF train, enabling acceleration of the MRF scans.10 Together with its ability to measure simultaneously T1 and T2, MRF offers a solution to the problem of obtaining quantitative measures in an efficient manner and in relatively short scanning times.
One of the main challenges in ocular imaging is in‐plane and through‐plane eye motion, often associated with eye blinking.11, 12, 13 The motion results in corrupted k‐space data that introduces artifacts and blurring throughout the entire image. Shortening the scans would reduce motion‐related artifacts, but standard acceleration techniques are not optimal for the current eye application due to the following 3 reasons. First, a cued‐blinking protocol is typically used to control and reduce the eye motion.3, 11 This requires an instruction screen placed at the end of the MR tunnel to be visible to the patient which complicates the use of small phased array receive coils in front of the eye, blocking the view. Instead, a custom‐built single‐element eye loop coil is used, which provides a high local SNR3 and screen visibility, but which clearly excludes the possibility of scan acceleration by means of parallel imaging.14 Second, the gel‐like vitreous body has an extremely long T1, particularly at high field.15 Its value of 3 to 5 s requires a long duration of the MRF sequence to encode the MR parameters (T1,T2) sufficiently. Thus, using a flip angle train with a small number of RF pulses is not feasible, hindering scan time reduction. Finally, a time‐efficient spiral sampling scheme, usually applied in MRF,10, 16, 17, 18, 19 introduces off‐resonance effects in each of the individual MRF images.20 This occurs even when combined with unbalanced sequences such as fast imaging with steady state precession,16 which are in themselves robust to off‐resonance effects.21 The off‐resonance effects present in spiral sampling schemes are much stronger at high field, where they result in blurring,22 caused by strong main field inhomogeneities (particularly in the eye region due to many air‐tissue‐bone interfaces), as well as the presence of significant amounts of off‐resonant orbital fat around the eye.
In this work, a Cartesian sampling scheme is used, which is more robust than spiral sampling to off‐resonance effects, but which is significantly less time‐efficient.23 With such a Cartesian sampling scheme, undersampling artifacts have a more structured nature compared with spiral sampling, which increases the temporal coherence of the artifacts in the MRF image series.10, 20 In this case, direct matching of the measured MRF signal reconstructed by plain Fourier transformations, to the simulated dictionary elements is not sufficiently accurate for high undersampling factors.24, 25 Therefore, the quality of the reconstructed MRF data has to be improved before the matching process.
Compressed sensing (CS) has been introduced as a technique to reconstruct images from randomly undersampled data by enforcing signal sparsity (in the spatial dimension only or both in spatial and temporal dimensions),26, 27 allowing a scan time reduction in many applications.28, 29, 30 The flexibility of MRF toward different sampling schemes and undersampling factors makes it possible to reconstruct the source images by means of CS.27, 31, 32 Higher acceleration factors might be feasible if the correlation in the temporal dimension is better used.33 Examples of such reconstructions specifically tailored to MRF are given in Davies et al, Pierre et al, and Zhao et al34, 35, 36 which take into account the simulated dictionary atoms in the image reconstruction process.
Recent work has shown that the temporal correlation in the MRF data can be exploited even further by incorporating the low rank structure of the data into the cost function,37 a technique which was introduced into MR in Liang38 and in MRF in Zhao39 and used by many others40, 41, 42: these techniques can also be combined with sparsity constraints.43, 44 Most of the aforementioned techniques involve Fourier transformations in each iteration, making the reconstruction process time‐consuming. In this application, the single‐element receive coil allows us to perform the reconstruction process entirely in k‐space when exploiting the low rank structure of the MRF data as is performed in matrix completion (MC)‐based reconstructions.42, 45
In this work, undersampled Cartesian ocular MRF is investigated using CS and MC‐based reconstructions. Simulations and experiments performed in 6 healthy volunteers for confirmation are compared with fully sampled MRF in terms of the quality of the parameter maps, and mean relaxation times were derived for different ocular structures at 7T. Finally, parameter maps after an MC‐based reconstruction are included for a uveal melanoma patient, showing the feasibility of ocular MRF in eye tumor patients.
2. METHODS
2.1. Fingerprinting definition
The MRF encoding principle is based on a variable flip angle train with relatively short TRs, so that the magnetization after each RF pulse is influenced by the spin history. Following closely the implementation of the sinusoidal MRF pattern described in Jiang et al,16 a flip angle pattern of 240 RF excitation pulses ranging from 0° to 60° (see Figure 1A) was defined by the function
Figure 1.
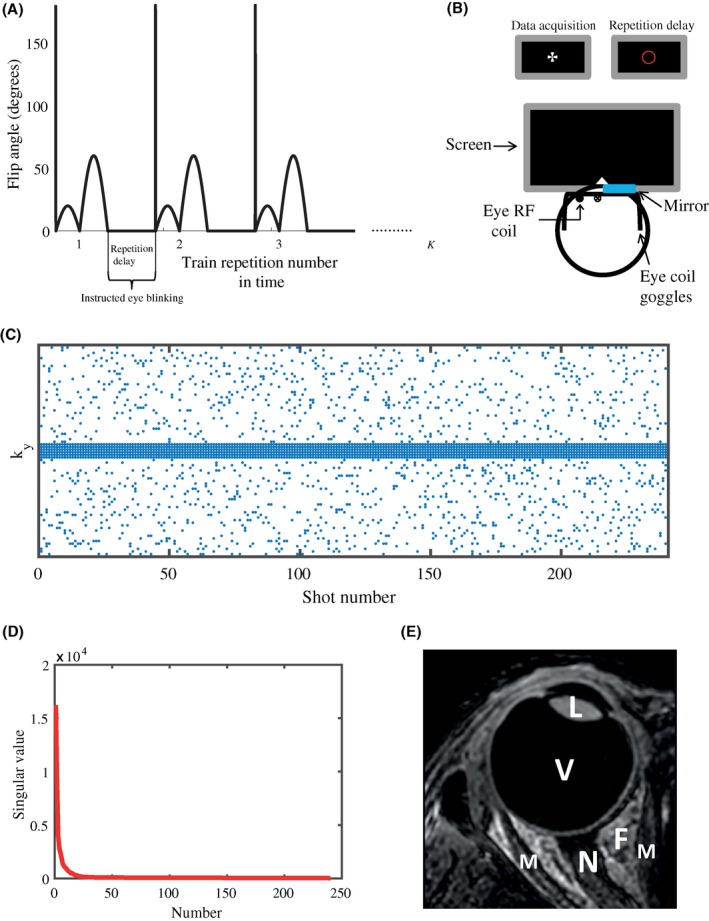
The MRF sequence, instructed blinking set‐up, sampling pattern, and temporal correlation used in all experiments. A, Each flip angle train is preceded by an adiabatic 180° inversion pulse. The flip angle pattern consists of 240 RF pulses ranging from 0° to 60°. The total number of repetitions K of the MRF train is determined by the undersampling factor. The 2.5 s repetition delay between trains allows for instructed eye blinking when the scanner is not acquiring data. B, During data acquisition, a cross is shown on a screen placed at the end of the MR tunnel, which can be seen through 1 eye by means of a small mirror attached to the eye coil. During the repetition delay, the cross changes into a red circle, indicating that blinking is allowed before data acquisition starts again. The single loop eye coil setup is illustrated as well. C, Each time point (shot number) in the flip angle train is sampled differently. A simple variable density scheme is used. The outer region of k‐space is randomly sampled, whereas the central part of k‐space is fully sampled for each time point. The incoherent variable density sampling allows a CS reconstruction, while the fully sampled center can be used as calibration data for the MC‐based reconstruction. D, The singular values of the central k‐space/calibration matrix decay very quickly, which shows the low rank property of the eye MRF data, and forms the basis of the MC‐based reconstruction. Plots were generated for an undersampling factor of R = 12.3 in the outer region of k‐space, which results in a total undersampling factor of 6.7. E, Anatomical T1‐weighted 3D MR image of the eye, showing different ocular structures. L, lens nucleus; V, vitreous body; F, orbital fat; M, extraocular muscle; N, optic nerve
preceded by an inversion pulse (16). A fast imaging with steady state precession sequence was used,16, 19 in which the TE was chosen as 3.5 ms and 4.0 ms for low resolution scans and high resolution scans, respectively. The selected excitation RF pulse had a time‐bandwidth product of 10, resulting in a reasonably sharp slice profile. The RF pulse phase was fixed to 0°. To simplify dictionary calculations, because of the simplification of the magnetization coherence pathways,46 the TR was set to a constant value of 11 ms.
A 3D dictionary was calculated following the extended phase graph formalism,21, 46 based on the Bloch equations,47, 48 incorporating 27,885 signal evolutions.46 T1 values ranged from 10 to 1000 ms in steps of 10 ms, and from 1000 to 5000 ms in steps of 100 ms. T2 values ranged from 10 to 100 ms in steps of 10 ms and from 100 to 300 ms in steps of 20 ms. A B1 + fraction ranging from 0.5 to 1.0 in steps of 0.05 was incorporated into the dictionary calculation. To shorten the scan time, we used a short waiting time between repetitions of the MRF train (called the repetition delay) of 2.5 s. Therefore, each MRF scan was preceded by 3 dummy trains to establish steady state magnetization,19 which was considered in the dictionary calculation. The longitudinal magnetization after the 3 dummy trains, required for correction of the M0 maps, was calculated for each T1/T2 combination. The repetition delay of 2.5 s was efficiently used as the blink time.3, 11
2.2. Experimental setup
All experiments were approved by the local medical ethics committee, and all volunteers and patients signed an appropriate informed consent form. The experiments in this study were performed on 6 healthy volunteers and 1 uveal melanoma patient using a 7T MR system (Philips Healthcare) equipped with a quadrature head volume coil (Nova Medical) for transmission and a custom‐built single‐element eye coil for reception, with a diameter of approximately 4 cm.3, 49 A cued‐blinking protocol was followed, which means that all subjects were instructed to focus on a fixation target shown on a screen during data acquisition and to blink in the 2.5 s repetition delay. This was performed using a small mirror integrated into the eye coil, allowing visualization of a screen placed outside the magnet through 1 eye, while the eye to be imaged was closed and covered by a wet gauze to reduce susceptibility artifacts in the eye lid.50 This setup is shown schematically in Figure 1B.
2.3. MR data acquisition
Because of the presence of significant orbital fat around the eye, and the sensitivity of the spiral to off‐resonance resulting in blurring,22 a Cartesian sampling scheme was used to acquire all data. The fingerprinting scans were acquired as a single slice at 2 different spatial resolutions: 1.0 × 1.0 × 5.0 mm3 and 0.5 × 0.5 × 5.0 mm3. The lower resolution scan was performed twice, the first fully sampled to serve as a reference, and the second one undersampled. The scan time of the fully sampled scan was 7:02 min, while the scan time of the undersampled scan, in which 15% of the data was acquired, was 1:16 min. The high resolution scan was only acquired as an undersampled data set, in which 12.5% of the data was acquired, resulting in a scan time of 1:57 min. In the undersampled scans a simple variable density k‐space sampling was applied, schematically shown in Figure 1C, supporting both CS and MC‐based reconstructions.
A fully sampled center of k‐space was acquired for each time point consisting of 6/8 k‐space lines for the low resolution/high resolution scans, respectively. For all scans, the FOV was set to 80 × 80 mm2, resulting in an acquisition matrix of 80 × 80 and 160 × 160 for the low and the high resolution scans, respectively. The phase encoding direction was set from left‐to‐right to minimize contamination by any residual motion artifacts in the eye lens, and the read out direction was set to the anterior‐posterior direction.
B1 + maps were acquired using the dual refocusing echo acquisition mode method51 with the following scan parameters: FOV = 80 × 80 mm2, in‐plane resolution 1 mm2, slice thickness 5 mm, 1 slice, TE1/TE2 = 2.38/1.54 ms, TR = 3.7 ms, FA = α:60°/ß:10°: the scan time for a single slice was less than 1 s.
2.4. Reconstruction
For each time point, the corresponding images were reconstructed from the available data, using custom software written in MATLAB (Mathworks, Inc) and run on a Windows 64‐bit machine with an Intel i3‐4160 CPI @ 3.6 GHz and 16 GB internal memory. Different reconstructions were performed: (i) a fast Fourier transform (FFT) of the fully sampled data and of the zero‐filled undersampled data; (ii) a CS reconstruction with total variation regularization in the spatial dimension (2D CS), and with total variation in both spatial and temporal dimensions (3D CS) of the undersampled data; (iii) an MC‐based reconstruction of the undersampled data.
2.4.1. CS reconstruction
In this reconstruction, the complete image series is reconstructed by iteratively solving the nonlinear problem
through the unconstrained version
| (1) |
In this formulation, is a block diagonal matrix with the 2D Fourier transform matrix in each diagonal block, is a diagonal matrix incorporating the sampling locations, is the undersampled k‐t space data, is an estimate of the true image series and is a total variation operator which is used to enforce sparsity in the reconstruction.52, 53 Here, is the number of k‐space locations per image frame and is the number of measured time points (or flip angles in the MRF train). The regularization parameters and in Equation [Link] were determined empirically and set to Two basic versions of the total variation operator,
| (2) |
| (3) |
were implemented to investigate the effect of promoting sparsity either only in the spatial dimension (2D CS) or in both the spatial and temporal dimensions (3D CS). In these expressions, and are the first derivative operators acting on the spatial and dimensions and the time dimension, respectively. Solving the problem given in Equation [Link] is done in this work using Split Bregman. For details on this algorithm the reader is referred to Goldstein and Osher.54
2.4.2. MC reconstruction
Similar to CS with the TV operator acting in 3 dimensions (see Equation (1)), MC uses the information from the temporal dimension.45, 55 A main difference between CS and MC, however, is that sparsity of singular values, which is a priori information in the MC reconstruction, can be observed both in image space and in k‐space. This allows one to complete the entire reconstruction in k‐space, which is computationally efficient, especially if only a single receiver coil is used.42 The MC‐based reconstruction iteratively solves
| (4) |
with being the nuclear norm, the sampling operator selecting the measured k‐t space locations, the undersampled k‐t space data and an estimate of the true k‐t space. The nuclear norm of M sums the singular values of M, and can thus be written as , where transforms into a vector containing the singular values of . The central k‐t space is used as calibration data, of which the rank can be used as a priori information in the reconstruction of undersampled data. In this process, a projection matrix projects in each iteration the undersampled data matrix onto a low‐rank subspace spanned by the columns of , such that
with
Here, contains the most significant left singular vectors of the calibration matrix and is constructed from the full singular value decomposition , , , , which is performed once at the beginning of the algorithm. In the second step of each iteration, the data are updated according to
The value was determined empirically from the singular value plots (shown in Figure 1D for 1 volunteer) and set to 4 for all MC‐based reconstructions. Further details of the adopted algorithm to solve Equation (2), and its implementation can be found in Doneva et al.42
To ensure convergence of the iterative CS and MC‐based reconstructions, 40 Split Bregman iterations (1 inner loop) were used for the CS reconstructions and 100 iterations were used for all MC‐based reconstructions.
To judge the performance of the reconstruction methods, relative error measures are defined throughout the manuscript as
| (5) |
where is the fully sampled image series and both and are vectorized.
2.5. Dictionary matching process
For each subject, the measured B1 + map was used to calculate an average B1 + value in the eye. Based on this value, a 2D subdictionary was chosen that matches the drop in B1 + for each volunteer. Each voxel signal in the reconstructed MRF image series was then matched to an element of the subdictionary.
In this process, the best match between the measured signal and the dictionary elements was found for each voxel by solving
| (6) |
where is the ith normalized dictionary element and is the normalized measured signal. The index that maximizes the inner product describes the dictionary element (with corresponding T1 and T2 values) that gives the best match with the measured signal. Finally, the scalar proton density per voxel was determined from the model
| (7) |
where is the nonnormalized signal per voxel and the nonnormalized dictionary element corresponding to the best match , such that
| (8) |
r is a value between 0 and 1, describing the fraction of the initial longitudinal magnetization that is left after the dummy trains, also depending on T1 and T2, which takes into account the short repetition delay in between the MRF trains. M0 maps are all shown on a log‐scale due to the high dynamic range of the respective proton densities, with that of the vitreous body being more than an order of magnitude larger than other structures. The processed T1, T2, and M0 maps were compared for different reconstruction methods (FFT, 2D CS, 3D CS, and MC) and for different acquisitions (low spatial resolution, high spatial resolution).
T1 and T2 values were averaged in different regions of interest, annotated in Figure 1E for each volunteer. These values were used to determine mean ± SD values over all volunteers for the different reconstructions.
3. RESULTS
3.1. Simulation results
Figure 2 shows the parameter maps (T1, T2, and M0) obtained for different reconstruction methods, after subsampling the fully sampled k‐space data of 1 healthy volunteer. Even though an incoherent sampling scheme was used, a zero‐filled FFT reconstruction does not lead to accurate parameter maps. The CS reconstruction with total variation regularization in the spatial domain leads to only minor improvement for the high undersampling factor that was chosen. The results show that including the sparsity constraint in the temporal dimension on top of the spatial dimension improves the CS reconstruction, with the largest improvement in the optic nerve and the lens nucleus, indicated by the white arrows. The total undersampling factor of 6.7, however, in combination with the low resolution reconstruction matrix and the single channel signal, results in loss of detail in the CS approach.
Figure 2.
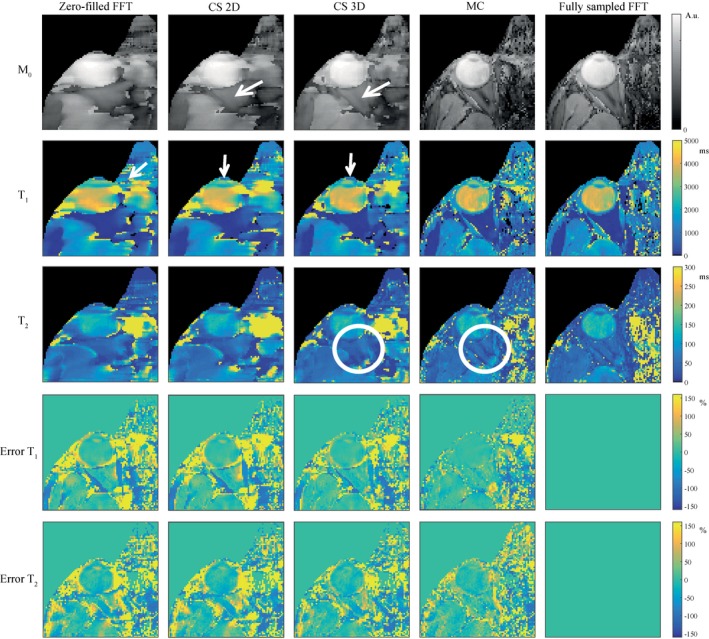
Simulated effect of different reconstruction methods on the parameter maps. Columns 1 to 4 show parameter maps after reconstruction of subsampled source images using a zero‐filled FFT, CS with spatial regularization (2D), CS with spatial and temporal regularization (3D), and MC. Column 5 shows parameter maps after an FFT of the fully sampled data. Adding the temporal regularization in the 3D CS reconstruction improves the quality of the parameter maps (M0, T1, T2) compared with the zero‐filled FFT and the 2D CS reconstruction (see white arrows). The parameter maps resulting from an MC‐based reconstruction show more detail (see white circles), much smaller errors, and the errors have a more noise‐like structure. Note that all M0 maps are shown on a log‐scale due to the high dynamic range of the tissue proton densities
This is not the case for the MC‐based reconstructions. The parameter maps resulting from the MC‐based approach are very close to the parameter maps obtained from the fully sampled scan, enabling visualization of the extraocular muscles and the orbital fat, indicated by the white circles. The error maps in Figure 2, defined as the relative difference with the parameter maps from the fully sampled scan, given in percentages, confirm these findings. The error has a more noise‐like behavior for the MC‐based reconstruction compared with the CS reconstruction, and is much lower in the sensitive region of the eye coil. The error maps for T1 show larger percentage improvements compared with T2. These general trends were also true for different undersampling factors (see Supporting Information Figure S1, which is available online).
3.2. Experimental results
Parameter maps obtained in an undersampled experiment are shown in Figure 3 for low spatial resolution images. The experimental results confirm the findings from the simulation study. The parameter maps obtained from the undersampled MRF scan with a 3D CS reconstruction show loss of detail compared with the parameter maps obtained with an MC‐based reconstruction. This is especially visible in the M0 maps. For the MC‐based reconstruction, the parameter maps are similar quality to those obtained from the fully sampled scans, showing the feasibility of accelerating MRF in the eye using a Cartesian sampling scheme. It should be noted that the full k‐space data and the undersampled k‐space data originate from different scans, which is why residual motion artifacts are different between the resulting parameter maps. The parameter maps at high resolution in Figure 4 show more detail compared with the parameter maps at low resolution in Figure 3, indicated by the white circle. For the high resolution case, however, the 3D CS reconstruction gives larger improvements compared with the low resolution case.
Figure 3.
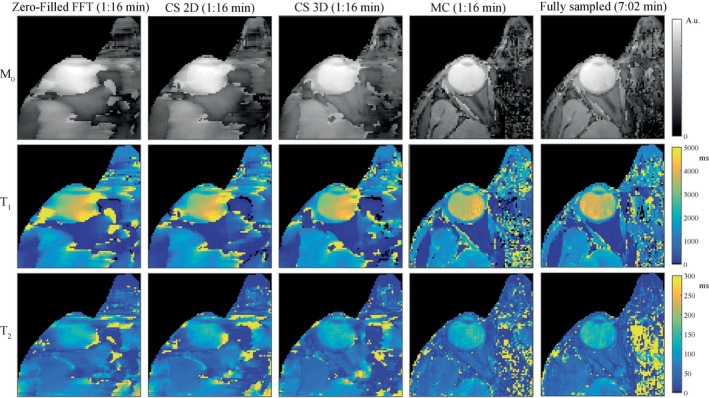
The effect of different reconstruction methods on the parameter maps of experimental data at low resolution. Parameter maps obtained at low (1.0 × 1.0 × 5.0 mm3) resolution confirm the findings from the simulation (c.f., Figure 2). The parameter maps obtained from a CS reconstruction show loss of detail. The quality of the maps obtained from the undersampled scan after an MC‐based reconstruction is comparable to the quality of the maps from a fully sampled scan. Inhomogeneities are visible in the vitreous body, which is very hard to accurately encode due to the low sensitivity of the MRF train for very long T1 values
Figure 4.
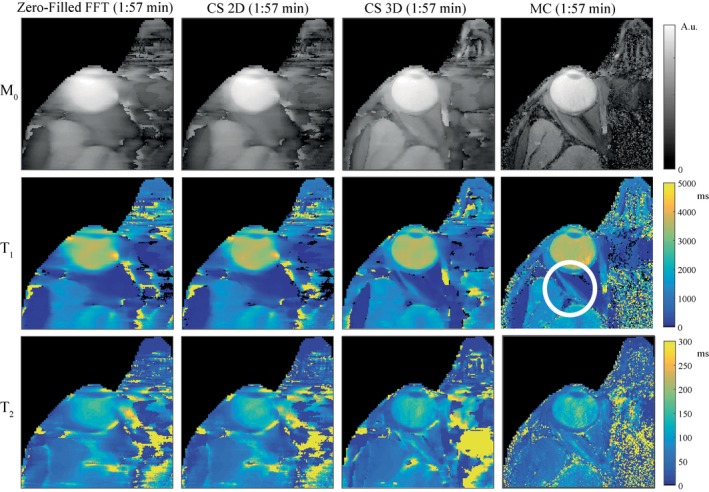
The effect of different reconstruction methods on the parameter maps of experimental data at high resolution. Parameter maps obtained at high (0.5 × 0.5 × 5.0 mm3) resolution for the same subject as in Figure 3 show more structural detail, indicated by the white circle. Note that Figure 3 and Figure 4 were different scans, in which motion artifacts are also different. Fully sampled data sets were not acquired for the high resolution case due to the prohibitively long scanning times required
Parameter maps obtained in the 6 different volunteers for the low resolution scans are shown in Figure 5. In all volunteers, some inhomogeneities are visible in the vitreous body, which is a region that is very sensitive to any type of motion or system imperfections because of the low sensitivity of the MRF sequence for very long T1 compared with short T1. This effect is illustrated in Figure 6, where differences in short T1 values (500‐1000 ms) result in more distinguishable dictionary elements compared with the same absolute differences in long T1 values, (3500‐4000 ms) especially in the first half of the MRF train. These inhomogeneities differ slightly between successive scans in the same volunteer, and are more visible in the scans of volunteer 3 (Figure 5C) and volunteer 5 (Figure 5E). Overall, the shortened scan time reduces the risk of motion artifacts, which is clearly visible in volunteers 5 and 6 (Figure 5E,F). The high resolution parameter maps for the same volunteers are shown in Supporting Information Figure S2A‐F, with several regions of improved structural detail indicated by the white circles.
Figure 5.
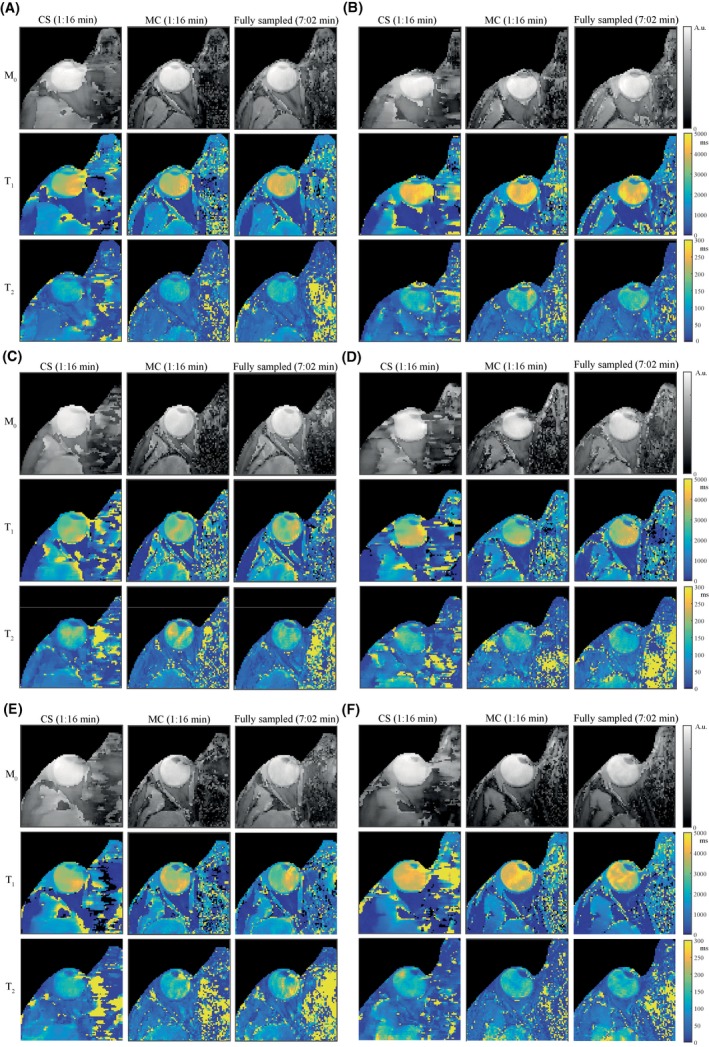
The parameter maps in all healthy volunteers. Parameter maps, resulting from low resolution scans, obtained in 6 healthy volunteers are shown in (A‐F), respectively. In all volunteers, the parameter maps obtained from a CS reconstruction (3D CS) show loss of detail compared with the maps obtained from the undersampled scan after an MC‐based reconstruction, for which the quality is comparable to that of the fully sampled scan: values are given in Table 1. In some volunteers the inhomogeneities in the vitreous body appear stronger than in others, which probably correspond with cases of more motion. This can also be seen in (E,F), where the quality of the maps is better for the shorter scans (MC) compared with the fully sampled ones
Figure 6.
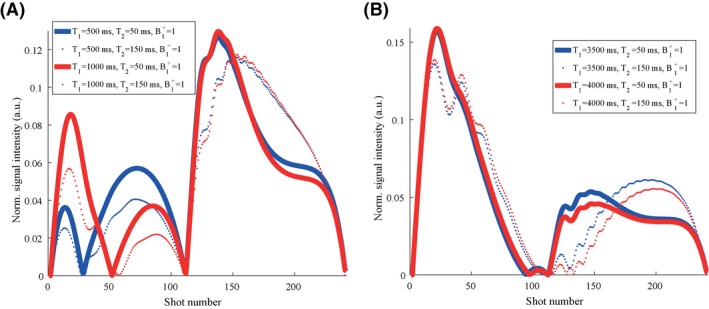
Simulated dictionary elements for different relaxation times. A, The simulated normalized absolute signal intensities for tissues with a T1 of 500 ms (blue) is plotted together with the signal evolution for tissues with a T1 of 1000 ms (red). Solid lines show simulation results for T2 values of 50 ms, while dotted lines show results for T2 values of 150 ms. Comparison of the red and blue graphs shows that the difference in T1 is encoded mostly in the first half of the MRF sequence, whereas T2 is encoded over the entire train. Comparison of the solid and dotted graphs shows that the second half helps to further encode differences in T2. B, The same results are plotted for a T1 of 3500 ms (blue) and 4000 ms (red), showing much smaller differences between the 2 simulated signal evolutions for the same absolute difference in relaxation times. This indicates that a certain difference in T1 is easier detected for lower T1 values with the current MRF train. Optimization of the MRF train might increase the encoding capability for large T1 values. For all simulations the B1 + fraction was set to 1
Average T1 and T2 values in the lens nucleus, the vitreous body, the orbital fat, and the extraocular muscles are reported in Table 1 for the different low resolution scans and reconstruction methods. The relaxation times obtained with a CS reconstruction are relatively close to those of the MC‐based reconstruction, but differences are observed in small anatomical structures such as the extraocular muscles and the eye lens. Differences between the relaxation times from the MC‐based reconstructions and the FFT of the fully sampled data can in part be explained by the fact that motion artifacts differ from scan to scan. Average relaxation times obtained from high resolution scans (not reported) follow the results for the low resolution scans. Reference T1 values at 7T reported in Richdale et al15 are included in Table 1; it should be noted that these reported values show large differences in relaxation times between different measurement techniques.
Table 1.
T1 and T2 values for different ocular structures (annotated in Figure 1C), averaged within the structure and over 6 volunteersa
| CS 3D | MC | Full | 7T Richdale et al. | |
|---|---|---|---|---|
| T1 (ms) | ||||
| Lens nucleus | 1403±178 | 1037±220 | 996±248 | 1520/1020 |
| Vitreous body | 3632±375 | 3614±444 | 3599±334 | 5000/4250 |
| Orbital fat | 93±23 | 100±29 | 95±26 | – |
| Extraocular muscle | 731±342 | 1736±346 | 1545±191 | – |
| T2 (ms) | ||||
| Lens nucleus | 29±9 | 29±12 | 21±10 | – |
| Vitreous body | 139±14 | 147±20 | 145±12 | – |
| Orbital fat | 55±12 | 51±16 | 51±19 | – |
| Extraocular muscle | 67±26 | 50±12 | 55±25 | – |
Values, given in milliseconds, were averaged in different regions of interest (lens nucleus, vitreous body, orbital fat, and extraocular muscle) from the different scans at low resolution, using different reconstruction methods, for each of the 6 healthy volunteers. The resulting values were used to determine mean ± SD values over all volunteers. The CS reconstruction produced different relaxation times in small anatomical regions such as the lens nucleus and the extraocular muscles. The TRs for the MC‐based reconstructions are close to the values for the fully sampled scans. Remaining differences can be explained by motion artifacts that differ from scan to scan. Reference values at 7T (variable flip angle gradient echo/inversion recovery) from previous literature were reported in the last 2 columns, showing large differences in T1 values between different techniques.
Parameter maps in a uveal melanoma patient are shown in Figure 7, together with a T2‐weighted, fat‐suppressed, TSE image for anatomical reference. The tumor and the detached retina are characterized in the MRF maps by much lower T1, T2, and M0 values compared with the vitreous body, which allows for clear discrimination between tumor and healthy tissue. Dictionary matches and measured signals (both normalized) in the detached retina, the lens nucleus, the eye tumor, and the fat are also shown. The average values in regions of interest are reported in Table 2.
Figure 7.
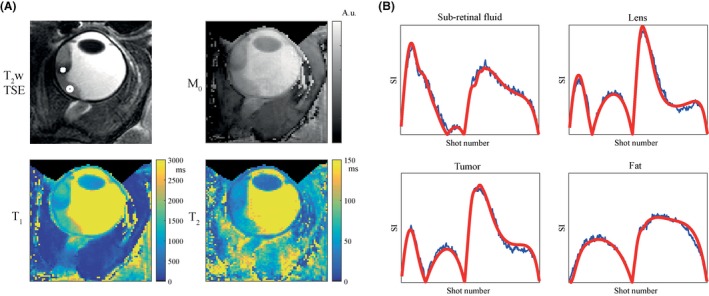
Parameter maps and matches in a uveal melanoma patient. A, T2‐weighted turbo spin‐echo (TSE) images with fat suppression (SPIR) were obtained and shown (zoomed‐in) for reference, with scan parameters: FOV = 40 × 60 mm2; in‐plane resolution 0.5 mm2; 2 mm slice thickness; 10 slices; TE/TR/TSE factor = 62 ms/3000 ms/12; FA = 110°; refocusing angle = 105°; WFS = 4.1 pixels; and scan time = 1:18 min. The eye tumor, indicated by the white cross, is visible as well as retinal detachment, pointed out by the white circle in the subretinal fluid. The high resolution parameter maps show much lower T1, T2, and M0 values in the tumor compared with the vitreous body, while the subretinal fluid can also be distinguished from the tumor by slightly higher T1, T2, and M0 values. B, Signal evolutions are shown in blue together with the matched dictionary element in red, for the retina (white circle), the lens nucleus, the eye tumor (white cross) and the fat
Table 2.
T1 and T2 values for different ocular structures in a uveal melanoma patienta
| T1 (ms) | T2 (ms) | |
|---|---|---|
| Lens nucleus | 916 | 24 |
| Vitreous body | 4218 | 209 |
| Orbital fat | 112 | 84 |
| Extraocular muscle | 1282 | 56 |
| Eye tumor | 883 | 36 |
| Liquid behind detached retina | 1814 | 64 |
T1 and T2 values in milliseconds were averaged over drawn regions of interest. The eye tumor shows different relaxation times (both T1 and T2) compared with the vitreous body and with the liquid behind the detached retina, which allows for discrimination between tumor and healthy tissue.
Reconstruction times for the different reconstruction methods were averaged over 6 healthy volunteers and reported in Table 3. The iterative nature of CS and MC increases the reconstruction times compared with the direct FFT reconstruction, but the MC‐based reconstruction is much more time‐efficient because it is performed entirely in k‐space, and uses only fast matrix vector multiplications.42
Table 3.
Reconstruction timesa
| Computation time (s) | ||
|---|---|---|
| Low resolution (1.0×1.0 mm2) | High resolution (0.5×0.5 mm2) | |
| CS 3D (40 SB iterations) | 584 | 2734 |
| MC (100 iterations) | 12 | 44 |
| FFT | 0.1 | 0.5 |
Mean values of reconstruction times in seconds calculated over 6 healthy volunteers for CS 3D, MC, and the direct FFT. The reconstruction times for both CS and MC take longer compared to the direct FFT due to the iterative process, but the MC‐based reconstruction is much more time‐efficient than the CS reconstruction because it is performed entirely in k‐space.
4. DISCUSSION
The results in the simulation study clearly show the benefit of using the temporal dimension in the reconstruction of MRF data, as is performed using MC. The low rank property of the signal evolutions allows higher undersampling factors than in a CS reconstruction, in which the TV operator was used to enforce sparsity in the temporal as well as in the spatial dimensions. The experimental results confirmed these findings, and showed the feasibility of reducing the MRF scan time with the proposed MC‐based reconstruction from 7:02 min to 1:16 min. Using MC, high resolution parameter maps can be obtained, which was out of practical reach for full sampling due to the long scan time. The technique was also demonstrated in a uveal melanoma patient, in which relaxation times showed a clear difference between tumor and healthy tissue.
The CS reconstruction resulted in smoothed parameter maps, which averages out motion artifacts, but also reduces the amount of visible detail. One reason why the CS reconstruction did not perform as well as the MC‐based reconstruction might be that the TV operator is not the optimal sparsifying transform for transforming the measured data along the temporal domain. Other sparsifying transforms, such as the Wavelet transform or even learned transforms or dictionaries,56, 57 might result in improvements of the parameter maps after a CS reconstruction. For the high resolution data, however, the 3D CS reconstruction seemed to perform better compared with the low resolution case, while the MC‐based reconstruction performed well in both the low and the high resolution cases. This suggests that the CS reconstruction is more dependent on the resolution of the acquired data than MC, which might be explained by the fact that MC, as implemented here, does not incorporate any spatial correlation into the reconstruction process. Furthermore, reducing the resolution might reduce the sparsity of the images in appropriate transform domains, while this is one of the key ingredients for CS to work.
Images from undersampled scans were reconstructed with MC, in which the chosen rank of the projection matrix influences the error. Here, the number of incorporated singular values was determined empirically in a simulation study: 4 singular values resulted in the smallest error after 100 iterations of the algorithm. Other sampling patterns, flip angle trains or anatomies will likely require new optimization of the projection matrix. In the current acquisition, 15% or 12.5% of the data was acquired with 6 or 8 fully sampled central k‐space lines for each image frame. Further tuning of the sampling pattern might improve the accuracy of the reconstructions or allow even shorter scan times. One should keep in mind, however, that the sampled k‐t lines are used to reconstruct the missing k‐t lines. Because higher undersampling factors result in shorter scan times, this reduces the risk of motion‐corrupted k‐space lines, but if there is still significant motion, this affects a larger percent of the acquired data. Therefore, care should be taken to find a balance between the scan time and the robustness of the reconstruction algorithm to motion.
In this work, the projection matrix was constructed from the central k‐t lines of the measurement data. In Doneva et al,42 it was shown that this type of projection matrix results in a more accurate reconstruction compared with a projection matrix constructed from randomly selected k‐t lines due to the lower SNR in the latter case. Other works have used the simulated MRF dictionary as calibration data, which would eliminate the need to fully sample the centers of k‐space.41 Such an approach will probably show a steeper decay in normalized singular values due to the absence of noise and motion in the simulations (see Supporting Information Figure S3). The central k‐space based projection matrix, however, results in a smaller reconstruction error, indicating that the central k‐space approximates the rank of the measurement data better. Further work should investigate whether this approach could be advantageous in terms of mitigating motion artifacts. As an alternative approach to the method used in our work, in which a low‐rank constraint is added as a penalty term to the cost function, the low‐rank property of the unknown image series can be incorporated directly in the data fidelity term, transforming the minimization problem into a linear one, which may be beneficial in terms of computational costs.41 It would be interesting to compare the accuracy of the 2 methods in future work.
Although this study has shown the feasibility of using MR fingerprinting to characterize the relaxation times of different anatomical structures in the eye, eye motion can still be a limiting factor. The parameter maps presented in the results section show inhomogeneities in the vitreous body, which can be a result of different types of motion in the eye (see Supporting Information Figure S4). The presence of motion in combination with the long T1 of the vitreous body and the low sensitivity of the MRF train to these long values, make it challenging to accurately map the relaxation times in the vitreous body itself, as was shown in Figure 6. Adopting a longer MRF train, as well as pattern optimization of the MRF train, might help to increase the encoding capability, but a longer time between the cued‐blinks will strongly increase the chance of blink‐induced artifacts.
However, one should recognize from a clinical point‐of‐view that for almost all ocular conditions the vitreous body is not affected and, therefore, an accurate quantification of its T1 is clinically not relevant. Outer volume suppression pulses, applied immediately before the inversion pulse or during 0 flip angle phases in the MRF train, might offer a way to reduce the flow of fresh magnetization (caused by motion) coming from slices above and below the imaging slice or from the left and the right of the imaging field of view, during repetitions of the flip angle train. However, such an approach and its effect on the quality of the parameter maps has to be investigated further.
The parameter maps corresponding to patient data showed a very large difference between tumor tissue and healthy vitreous body, suggesting that fully homogeneous regions of T1 in the vitreous body are not necessary for disease quantification and classification. Future work should investigate the extension of the current single slice approach to a 3D approach, such that the entire eye can be efficiently quantified from 1 scan.
The measured relaxation times are different between volunteers, potentially explained by anatomical or other volunteer‐specific differences. Small differences in relaxation times were observed for different scans in the same volunteer, caused by motion artifacts that change from scan to scan, but overall they are consistent within each volunteer, which is important for the use of this technique in practice. Considering the large deviations in measured relaxation times between different studies, it will be interesting to compare the MRF technique to standard T1 and T2 mapping techniques on a patient‐specific basis, and in this way investigate the origin of deviations from mean values as well as compare the robustness to motion for the different techniques.
It should be noted, however, that in Ma et al,58 it was already observed that MRF values do not always agree perfectly with reference values from other techniques, and potential reasons for this need to be investigated. Parameter maps in the current study were not corrected for slice profile effects, but all experiments were performed using an RF pulse with a very high time‐bandwidth product, minimizing the effects as demonstrated in Ma et al.58 The flip angle map, which is used as an input in the matching process, was produced with DREAM, in which the B1 + encoding slice thickness was set to be double the acquisition slice thickness to eliminate the slice profile effect.51
Values for the optic nerve were not reported in this study because the optic nerve was not visible in all scans due to small differences in planning and anatomy, and the slice thickness of 5 mm makes the measured values in the optic nerve very sensitive to partial volume effects. These partial volume effects also complicate quantification of heterogeneous tumors. In particular, tumor relaxation values could become inaccurate due to averaging with the strong signal coming from the surrounding vitreous body. Planning the imaging slice through the tumor as well as through the center of the vitreous body, such that the imaging plane is perpendicular to the tangent along the retina, would help to reduce these effects.
One limitation of the current study is the rather high slice thickness used (which is limited by the gradient strengths). With small changes in the sequence such as using a slightly longer echo time, acquisition and reconstruction of a 2‐mm‐thick slice is feasible (see Supporting Information Figure S5). The in‐plane resolution of 0.5 mm is satisfactory for tumor quantification and classification, as well as visualizing small structures such as the sclera and the ciliary body.
The results in this study show the potential to perform ocular MRF in tumor patients. To adopt ocular MRF in clinics, the technique could be further tailored to quantify specifically the relevant T1 and T2 values of tumors. Extensions to multislice or 3D acquisitions could be developed such that the whole tumor volume can be covered and quantified. Further studies should investigate which clinical applications will benefit from ocular MRF and in that way explore the clinical relevance of the technique.
In conclusion, the high undersampling factors used for this Cartesian, nonparallel imaging‐based approach shorten scan time and in this way reduce the risk of motion artifacts, which is most relevant for elderly patients, who typically experience difficulties focusing on a fixation target.
Supporting information
FIGURE S1 The effect of the undersampling factor on the performance of different reconstruction methods. Undersampled data sets were obtained by subsampling a fully sampled data set, while fixing the number of central k‐space lines to six for all undersampling factors. For larger undersampling factors, MC outperforms 2D and 3D CS. For undersampling factors smaller than three, MC has a slightly higher error compared to 3D CS. Overall, the error appears to be less affected by the undersampling factor for MC compared to the other reconstruction methods. Error measures are defined according to Equation 5
FIGURE S2 The parameter maps in all healthy volunteers for high resolution scans. Parameter maps obtained in six healthy volunteers are shown in (a)‐(f), respectively. The CS 3D reconstruction performs better for the high resolution scans than for the low resolution scans, but the parameter maps still show loss of detail compared to the maps obtained from the undersampled scan after an MC‐based reconstruction, with examples indicated by the white circles. Fully sampled reference scans were not obtained due to the long scan time required. A zoomed‐in version of the MC result in volunteer 1 is shown in (g), and repeated in (h) with a different color scale
FIGURE S3 Comparison of 2 different projection matrices. (a) The normalized singular value vector of the simulated MRF dictionary shows a steeper decay compared to the normalized singular vector of the central k‐space data. (b) The reconstruction error (defined as in Equation 5) as a function of the n most significant left singular values, is smaller when using the central k‐space as calibration data. A rank 3‐4 projection matrix results in the smallest reconstruction error when using the central k‐space data
FIGURE S4 The effect of motion on the parameter maps. (a) Motion was simulated by randomly replacing 1 of the 12 acquired k‐space lines in each MRF frame by (type 1) its phase‐modulated version with a random phase shift between 0 and 2π, mimicking in‐plane rigid body motion and (type 2) white gaussian noise (matching the maximum intensity of the replaced k‐space line), representing the worst case scenario of a completely corrupted signal. For motion type 1 larger differences are visible in the vitreous body. Motion type 2 results in noise break‐through in the parameter maps. For both types of motion, less than 6% change in T1 was observed in the vitreous body, while the T2 of the eye lens was changed by more than 20%, underlining the nonlinear effect of motion on the parameter maps. (b) The singular values of the calibration data show a less steep decay when k‐space lines are corrupted by motion
FIGURE S5 Parameter maps obtained from a thinner slice. By increasing the echo time from 3.5 ms to 4.6 ms, a slice of 2 mm can be acquired, spatial resolution 1×1×2 mm3. With this slice thickness the resulting parameter maps are less susceptible to partial volume effects, but slightly more noise is present in the maps due to the reduced SNR in the MRF images
ACKNOWLEDGMENTS
The authors thank Mariya Doneva for helpful discussions on reconstruction, and Thomas O’Reilly and Luc van Vught for useful insights during data acquisition.
Koolstra K, Beenakker J‐WM, Koken P, Webb A, Börnert P. Cartesian MR fingerprinting in the eye at 7T using compressed sensing and matrix completion‐based reconstructions. Magn Reson Med. 2019;81:2551–2565. 10.1002/mrm.27594
Funding information
This project was partially funded by the European Research Council Advanced Grant 670629 NOMA MRI.
REFERENCES
- 1. Townsend KA, Wollstein G, Schuman JS. Clinical application of MRI in ophthalmology. NMR Biomed. 2008;21:997–1002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. De Graaf P, Göricke S, Rodjan F, et al. Guidelines for imaging retinoblastoma: imaging principles and MRI standardization. Pediatr Radiol. 2012;42:2–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Beenakker JWM, Ferreira TA, Soemarwoto KP, et al. Clinical evaluation of ultra‐high‐field MRI for three‐dimensional visualisation of tumour size in uveal melanoma patients, with direct relevance to treatment planning. MAGMA. 2016;29:571–577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Bahn R, Heufelder A. Pathogenesis of Graves’ ophthalmopathy. N Engl J Med. 1993;329:1468–1474. [DOI] [PubMed] [Google Scholar]
- 5. Ohnishi T, Noguchi S, Murakami N, et al. Extraocular muscles in Graves ophthalmopathy: usefulness of T2 relaxation time measurements. Radiology. 1994;190:857–862. [DOI] [PubMed] [Google Scholar]
- 6. Foti PV, Longo A, Reibaldi M, et al. Uveal melanoma: quantitative evaluation of diffusion‐weighted MR imaging in the response assessment after proton‐beam therapy, long‐term follow‐up. Radiol Med. 2017;122:131–139. [DOI] [PubMed] [Google Scholar]
- 7. Kamrava M, Sepahdari AR, Leu K, et al. Quantitative multiparametric MRI in uveal melanoma: increased tumor permeability may predict monosomy 3. Neuroradiology. 2015;57:833–840. [DOI] [PubMed] [Google Scholar]
- 8. Sellam A, Desjardins L, Barnhill R, et al. Fine needle aspiration biopsy in uveal melanoma: technique, complications, and outcomes. Am J Ophthalmol. 2016;162:28–34. [DOI] [PubMed] [Google Scholar]
- 9. Tofts PS. Quantitative MRI of the Brain: Measuring Changes Caused by Disease. New York: John Wiley & Sons, Ltd; 2004. 633 p. [Google Scholar]
- 10. Ma D, Gulani V, Seiberlich N, et al. Magnetic resonance fingerprinting. Nature. 2013;495:187–192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Berkowitz BA, McDonald C, Ito Y, Tofts PS, Latif Z, Gross J. Measuring the human retinal oxygenation response to a hyperoxic challenge using MRI: eliminating blinking artifacts and demonstrating proof of concept. Magn Reson Med. 2001;46:412–416. [DOI] [PubMed] [Google Scholar]
- 12. Wezel J, Garpebring A, Webb AG, van Osch M, Beenakker JM. Automated eye blink detection and correction method for clinical MR eye Imaging. Magn Reson Med. 2016;78:165–171. [DOI] [PubMed] [Google Scholar]
- 13. Paul K, Huelnhagen T, Oberacker E, et al. Multiband diffusion‐weighted MRI of the eye and orbit free of geometric distortions using a RARE‐EPI hybrid. NMR Biomed. 2018;31:1–18. [DOI] [PubMed] [Google Scholar]
- 14. Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magn Reson Med. 1999;42:952–962. [PubMed] [Google Scholar]
- 15. Richdale K, Wassenaar P, Teal Bluestein K, et al. 7T MR imaging of the human eye in vivo. J Magn Reson Imaging. 2010;30:924–932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Jiang Y, Ma D, Seiberlich N, Gulani V, Griswold MA. MR Fingerprinting using Fast Imaging with Steady State Precession (FISP) with spiral readout. Magn Reson Med. 2015;74:1621–1631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Coppo S, Mehta BB, Mcgivney D, et al. Overview of magnetic resonance fingerprinting. Magnetom Flash. 2016;1:12–21. [Google Scholar]
- 18. Sommer K, Amthor T, Doneva M, et al. Towards predicting the encoding capability of MR fingerprinting sequences. Magn Reson Imaging. 2017;41:7–14. [DOI] [PubMed] [Google Scholar]
- 19. Amthor T, Doneva M, Koken P, Sommer K, Meineke J, Börnert P. Magnetic resonance fingerprinting with short relaxation intervals. Magn Reson Imaging. 2017;41:22–28. [DOI] [PubMed] [Google Scholar]
- 20. Bipin Mehta B, Coppo S, Francis McGivney D, et al. Magnetic resonance fingerprinting: a technical review. Magn Reson Med. 2018:10.1002/mrm.27403. [DOI] [PubMed] [Google Scholar]
- 21. Weigel M. Extended phase graphs: dephasing, RF pulses, and echoes ‐ pure and simple. J Magn Reson Imaging. 2015;41:266–295. [DOI] [PubMed] [Google Scholar]
- 22. Börnert P, Schomberg H, Aldefeld B, Groen J. Improvements in spiral MR imaging. MAGMA. 1999;9:29–41. [DOI] [PubMed] [Google Scholar]
- 23. Gao Y, Chen Y, Ma D, et al. Preclinical MR fingerprinting (MRF) at 7 T: Effective quantitative imaging for rodent disease models. NMR Biomed. 2015;28:384–394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Wang Z, Li H, Zhang Q, Yuan J, Wang X. Magnetic resonance fingerprinting with compressed sensing and distance metric learning. Neurocomputing. 2016;174:560–570. [Google Scholar]
- 25. Arberet S, Chen X, Mailhe B, et al. CS‐MRF: sparse and low‐rank iterative reconstruction for magnetic resonance fingerprinting. In: Proceedings of ISMRM Workshop on Magnetic Resonance Fingerprinting, Cleveland, OH, 2017. Abstract 3.
- 26. Candes EJ, Wakin MB. An introduction to compressive sampling. IEEE Signal Process Mag. 2008;25:21–30. [Google Scholar]
- 27. Donoho DL. Compressed sensing. IEEE Trans Inf Theory. 2012;52:1289–1306. [Google Scholar]
- 28. Otazo R, Kim D, Axel L, Sodickson DK. Combination of compressed sensing and parallel imaging for highly accelerated first‐pass cardiac perfusion MRI. Magn Reson Med. 2010;64:767–776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Liang D, Liu B, Wang J, Ying L. Accelerating SENSE using compressed sensing. Magn Reson Med. 2009;62:1574–1584. [DOI] [PubMed] [Google Scholar]
- 30. Chandarana H, Feng L, Block TK, et al. Free‐breathing contrast‐enhanced multiphase MRI of the liver using a combination of compressed sensing, parallel imaging, and golden‐angle radial sampling. Invest. Radiol. 2013;48:1–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Lustig M, Donoho D, Pauly JM. Sparse MRI: the application of compressed sensing for rapid MR imaging. Magn Reson Med. 2007;58:1182–1195. [DOI] [PubMed] [Google Scholar]
- 32. Boyer C, Chauffert N, Ciuciu P, Kahn J, Weiss P. On the generation of sampling schemes for magnetic resonance imaging. SIAM J Imaging Sci. 2016;9:2039–2072. [Google Scholar]
- 33. Tsao J, Boesiger P, Pruessmann KP. k‐t BLAST and k‐t SENSE: dynamic MRI with high frame rate exploiting spatiotemporal correlations. Magn Reson Med. 2003;50:1031–1042. [DOI] [PubMed] [Google Scholar]
- 34. Davies M, Puy G, Vandergheynst P, Wiaux Y. A compressed sensing framework for magnetic resonance fingerprinting. SIAM J Imaging Sci. 2013;7:2623–2656. [Google Scholar]
- 35. Pierre EY, Ma D, Chen Y, Badve C, Griswold MA. Multiscale reconstruction for magnetic resonance fingerprinting. Magn Reson Med. 2016;75:2481–2492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Zhao B, Setsompop K, Ye H, Cauley SF, Wald LL. Maximum likelihood reconstruction for magnetic resonance fingerprinting. IEEE Trans Med Imaging. 2017;35:39–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Mazor G, Weizman L, Tal A, Eldar YC. Low rank magnetic resonance fingerprinting. In: Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Orlando, FL, 2016. p. 439–442. [DOI] [PubMed]
- 38. Liang Z. Spatiotemporal imaging with partially separable functions. In: 4th IEEE International Symposium on Biomedical Imaging: From Nano to Macro, Arlington, VA. 2007. p. 988–991.
- 39. Zhao B. Model‐based iterative reconstruction for magnetic resonance fingerprinting. In: IEEE International Conference on Image Processing. 2015. p. 3392–3396.
- 40. Assländer J, Cloos MA, Knoll F, Sodickson DK, Hennig J, Lattanzi R. Low rank alternating direction method of multipliers reconstruction for MR fingerprinting. Magn Reson Med. 2018;79:83–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Zhao B, Setsompop K, Adalsteinsson E, et al. Improved magnetic resonance fingerprinting reconstruction with low‐rank and subspace modeling. Magn Reson Med. 2018;79:933–942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Doneva M, Amthor T, Koken P, Sommer K, Börnert P. Matrix completion‐based reconstruction for undersampled magnetic resonance fingerprinting data. Magn Reson Imaging. 2016;41:41–52. [DOI] [PubMed] [Google Scholar]
- 43. Zhao B, Haldar JP, Christodoulou AG, Liang ZP. Image reconstruction from highly undersampled (k, t)‐space data with joint partial separability and sparsity constraints. IEEE Trans Med Imaging. 2012;31:1809–1820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Zhao B, Lu W, Hitchens TK, Lam F, Ho C, Liang ZP. Accelerated MR parameter mapping with low‐rank and sparsity constraints. Magn Reson Med. 2015;74:489–498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Cai J‐F, Candes EJ, Shen Z. A singular value thresholding algorithm for matrix completion. SIAM J Optim. 2010;20:1956–1982. [Google Scholar]
- 46. Scheffler K. A pictorial description of steady‐states in rapid magnetic resonance imaging. Concepts Magn Reson. 1999;11:291–304. [Google Scholar]
- 47. Woessner DE. Effects of diffusion in nuclear magnetic resonance spin‐echo experiments. J Chem Phys. 1961;34:2057–2061. [Google Scholar]
- 48. Bloch F. Nuclear induction. Phys Rev. 1946;70:460–474. [Google Scholar]
- 49. Beenakker JWM, van Rijn GA, Luyten GPM, Webb AG. High‐resolution MRI of uveal melanoma using a microcoil phased array at 7 T. NMR Biomed. 2013;26:1864–1869. [DOI] [PubMed] [Google Scholar]
- 50. Bert RJ, Patz S, Ossiani M, et al. High‐resolution MR imaging of the human eye 2005. Acad Radiol. 2006;13:368–378. [DOI] [PubMed] [Google Scholar]
- 51. Nehrke K, Börnert P. DREAM ‐ a novel approach for robust, ultrafast, multislice B1 mapping. Magn Reson Med. 2012;68:1517–1526. [DOI] [PubMed] [Google Scholar]
- 52. Osher S, Burger M, Goldfarb D, et al. An iterative regularization method for total variation‐based image restoration. Multiscale Model Simul. 2005;4:460–489. [Google Scholar]
- 53. Block KT, Uecker M, Frahm J. Undersampled radial MRI with multiple coils. Iterative image reconstruction using a total variation constraint. Magn Reson Med. 2007;57:1086–1098. [DOI] [PubMed] [Google Scholar]
- 54. Goldstein T, Osher S. The Split Bregman method for L1‐regularized problems. SIAM J Imaging Sci. 2009;2:323–343. [Google Scholar]
- 55. Candès EJ, Recht B. Exact matrix completion via convex optimization. Found Comput Math. 2009;9:717–772. [Google Scholar]
- 56. Ravishankar S, Bresler Y. MR image reconstruction from highly undersampled k‐space data by dictionary learning. IEEE Trans Med Imaging. 2011;30:1028–1041. [DOI] [PubMed] [Google Scholar]
- 57. Zhan Z, Cai JF, Guo D, Liu Y, Chen Z, Qu X. Fast multiclass dictionaries learning with geometrical directions in MRI reconstruction. IEEE Trans Biomed Eng. 2016;63:1850–1861. [DOI] [PubMed] [Google Scholar]
- 58. Ma D, Coppo S, Chen Y, et al. Slice profile and B1 corrections in 2D magnetic resonance fingerprinting. Magn Reson Med. 2017;78:1781–1789. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
FIGURE S1 The effect of the undersampling factor on the performance of different reconstruction methods. Undersampled data sets were obtained by subsampling a fully sampled data set, while fixing the number of central k‐space lines to six for all undersampling factors. For larger undersampling factors, MC outperforms 2D and 3D CS. For undersampling factors smaller than three, MC has a slightly higher error compared to 3D CS. Overall, the error appears to be less affected by the undersampling factor for MC compared to the other reconstruction methods. Error measures are defined according to Equation 5
FIGURE S2 The parameter maps in all healthy volunteers for high resolution scans. Parameter maps obtained in six healthy volunteers are shown in (a)‐(f), respectively. The CS 3D reconstruction performs better for the high resolution scans than for the low resolution scans, but the parameter maps still show loss of detail compared to the maps obtained from the undersampled scan after an MC‐based reconstruction, with examples indicated by the white circles. Fully sampled reference scans were not obtained due to the long scan time required. A zoomed‐in version of the MC result in volunteer 1 is shown in (g), and repeated in (h) with a different color scale
FIGURE S3 Comparison of 2 different projection matrices. (a) The normalized singular value vector of the simulated MRF dictionary shows a steeper decay compared to the normalized singular vector of the central k‐space data. (b) The reconstruction error (defined as in Equation 5) as a function of the n most significant left singular values, is smaller when using the central k‐space as calibration data. A rank 3‐4 projection matrix results in the smallest reconstruction error when using the central k‐space data
FIGURE S4 The effect of motion on the parameter maps. (a) Motion was simulated by randomly replacing 1 of the 12 acquired k‐space lines in each MRF frame by (type 1) its phase‐modulated version with a random phase shift between 0 and 2π, mimicking in‐plane rigid body motion and (type 2) white gaussian noise (matching the maximum intensity of the replaced k‐space line), representing the worst case scenario of a completely corrupted signal. For motion type 1 larger differences are visible in the vitreous body. Motion type 2 results in noise break‐through in the parameter maps. For both types of motion, less than 6% change in T1 was observed in the vitreous body, while the T2 of the eye lens was changed by more than 20%, underlining the nonlinear effect of motion on the parameter maps. (b) The singular values of the calibration data show a less steep decay when k‐space lines are corrupted by motion
FIGURE S5 Parameter maps obtained from a thinner slice. By increasing the echo time from 3.5 ms to 4.6 ms, a slice of 2 mm can be acquired, spatial resolution 1×1×2 mm3. With this slice thickness the resulting parameter maps are less susceptible to partial volume effects, but slightly more noise is present in the maps due to the reduced SNR in the MRF images


