Spectroscopic and Computational Evidence of Intramolecular Au^I⋅⋅⋅H⁺−N Hydrogen Bonding

Abstract

Despite substantial evidence of short Au⋅⋅⋅H−X contacts derived from a number of X‐ray structures of Au^I compounds, the nature of Au^I⋅⋅⋅H bonding in these systems has not been clearly understood. Herein, we present the first spectroscopic evidence for an intramolecular Au^I⋅⋅⋅H⁺−N hydrogen bond in a [Cl−Au−L]⁺ complex, where L is a protonated N‐heterocyclic carbene. The complex was isolated in the gas phase and characterized with helium‐tagging infrared photodissociation (IRPD) spectra, in which H⁺−N‐mode‐derived bands evidence the intramolecular Au^I⋅⋅⋅H⁺−N bond. Quantum chemical calculations reproduce the experimental IRPD spectra and allow to characterize the intramolecular Au⋅⋅⋅H⁺−N bonding with a short r _Au⋅⋅⋅H distance of 2.17 Å and an interaction energy of approximately −10 kcal mol⁻¹. Various theoretical descriptors of chemical bonding calculated for the Au⋅⋅⋅H⁺−N interaction provide strong evidence for a hydrogen bond of moderate strength.

In the last two decades, gold complexes have been used in a wide range of applications in catalysis,1 materials science,2 and medicine.3 These applications fueled, among other things, theoretical and spectroscopic research on their electronic structure, including intra‐ and intermolecular interactions. We recently contributed to the development of this field by showing that aurophilic (Au⋅⋅⋅Au) interactions in Au^I dimers account for 6–7 kcal mol⁻¹ of the overall interaction energy.4

Further intra‐ or intermolecular stabilization of Au^I complexes may also occur through hydrogen bonding to Au^I. As described in a review by Schmidbaur et al.,5 this phenomenon is still a matter of debate, in contrast to the reasonably well‐understood “classical” hydrogen bonding involving Au^−I (auride) as a hydrogen bond acceptor as well as experimentally characterized agostic Au^III⋅⋅⋅H interactions (for example, via decreased ¹ J _C−H coupling of the corresponding C−H bond involved in the agostic Au^III⋅⋅⋅H−C interaction).6 Although a number of X‐ray structures of Au^I compounds were reported in which short Au⋅⋅⋅H−X contacts were observed, no solid spectroscopic evidence of Au^I⋅⋅⋅H bonding has been reported to date. It has been argued that the short contacts could be incidental, possibly driven by other interactions in corresponding molecules and were characterized as rather weak interactions. Accordingly, they are expected to have only little or no effect on the structure and dynamics of the Au^I complexes studied.5

Investigating Au^I⋅⋅⋅H bonding has been a subject of recent theoretical studies.7 Groenewald et al. calculated the interaction of L₁−Au^I−L₂ systems with a water molecule and found weak to moderate binding (ΔE _int=5–10 kcal mol⁻¹), classified as hydrogen bonding by various chemical bonding descriptors.7b Notably, relativistic effects were found to be crucially important for the correct description of Au^I⋅⋅⋅H bonding.7b Similarly, dimethylaurate was predicted to be a good H‐bond acceptor for various neutral H‐bond donors, such as HF, NH₃, or HCN.7c Berger et al. suggested, based on computational studies, that [(2‐(pyridinium‐2‐yl)phenyl)Au(SPh)]⁺ might be a suitable candidate for a Au^I system with an intramolecular Au^I⋅⋅⋅H⁺−N bond (r _Au−H≈2.06 Å; ΔE _int=−7.8 kcal mol⁻¹), arguing that formally, an Au^I atom can possess partial negative charge when proper ligands are employed.7d

Experimentally, Bakar et al. reported8 a system in which an Au₆ cluster is coordinated to large phosphine ligands, featuring relatively short Au⋅⋅⋅H−C contact distances (r _Au−H≈2.6 Å). Assuming a formal [Au₆]²⁺ oxidation state while observing corresponding ¹H and ¹³C NMR resonances deshielded with respect to a precursor molecule, the authors concluded “a kind of Au⋅⋅⋅H−C hydrogen bonding”8 present in their system. Our computational analysis of their system revealed, however, that the Au⋅⋅⋅H−C contacts are rather weak (ΔE _int≈1 kcal mol⁻¹) auride⋅⋅⋅hydrogen‐like bonds, partly dictated by other interactions in the system.9 A careful analysis of NMR chemical shifts showed that the observed deshielding at the respective nuclei is not sufficient evidence for Au⋅⋅⋅H−C hydrogen bonding.9

In this study, we provide experimental and theoretical evidence of a Au⋅⋅⋅H⁺−N hydrogen bond of moderate strength (ca. 10 kcal mol⁻¹) in complex 1 (Figure 1). This bond is qualitatively different from the previously discussed Au^I⋅⋅⋅H−N interactions,5 as the N−H⁺ moiety bears positive charge, but similar to the one in the theoretically predicted [(2‐(pyridinium‐2‐yl)phenyl)Au(SPh)]⁺ zwitterion system by Berger et al. discussed above.7d We characterized complex 1 in the gas phase by helium‐tagging infrared photodissociation (IRPD) spectroscopy. Furthermore, we also attempted to carry out similar experiments in the liquid and solid phase. However, the gold(I)–carbene complexes decomposed in the presence of an acid and therefore it was impossible to isolate and/or characterize the protonated complex in the bulk. We were able to isolate 1 by electrospray ionization mass spectrometry, a technique known to detect species from solution with high sensitivity, incomparable to standard methods such as NMR.

Figure 1.

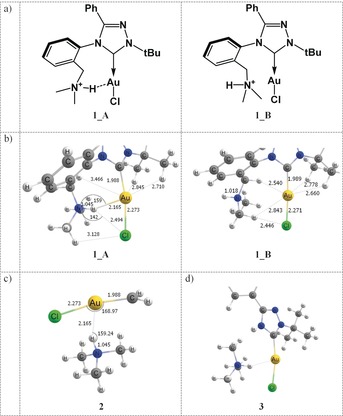
a) Molecule 1 in conformation A with a Au⋅⋅⋅H⁺−N contact, and conformation B with the N−H⁺ group pointing away from the Au^I ion (further denoted 1_A, 1_B). b) Equilibrium geometries of 1_A and 1_B calculated at PBE0‐D3/def2‐TZVPP. c) Model system 2 and d) model system 3, used to evaluate the magnitude of the Au⋅⋅⋅H⁺−N interaction.

The IRPD spectrum of 1 shows a substantial progression of vibrational bands below 3000 cm⁻¹ (Figure 2 a). Simultaneously, we detected no band above 3200 cm⁻¹ attributable to a free N−H vibration. Replacing hydrogen with deuterium in 1 results in the disappearance of the vibrational progression below 3000 cm⁻¹, and the corresponding bands shift to the region at 2000–2200 cm⁻¹. The data show that the N−H bond is involved in a strong intramolecular bonding associated with a red‐shift of about 500 cm⁻¹ in the N−H stretching mode with respect to its usual frequency range. The remarkable shift of the N−H mode observed experimentally prompted us to perform quantum chemical calculations and to predict anharmonic vibrational spectra of 1. For this purpose, equilibrium geometries of two possible conformers of 1_A and 1_B were calculated using various computational methods (see Computational details for more information). Figure 1 b and Table S1 (Supporting Information) show that the 1_A minimum is characterized by a rather short Au⋅⋅⋅H⁺−N contact with r _Au⋅⋅⋅H=2.14–2.17 Å, r _Au⋅⋅⋅N=3.13–3.19 Å, r _N−H=1.03–1.05 Å, and a Au−H−N angle of 159–165°, depending on the method used (Supporting Information, Table S1). The computed r _Au⋅⋅⋅H value is about 0.7 Å shorter than the sum of the van der Waals (vdW) radii of gold and hydrogen (2.86 Å). A short r _Au⋅⋅⋅H, an elongated r _N−H, and a nearly linear Au−H−N arrangement in 1_A fulfil the structural requirements for Au⋅⋅⋅H⁺−N hydrogen bonding very well.10 The geometrical parameters of the Au⋅⋅⋅H⁺−N bond in 1_A are comparable with those in [(2‐(pyridinium‐2‐yl)phenyl)Au(SPh)]⁺ predicted by Berger et al. (r _N−H=1.043 Å, r _H⋅⋅⋅Au=2.060 Å, and α(N−H−Au)=142°).7d

Figure 2.

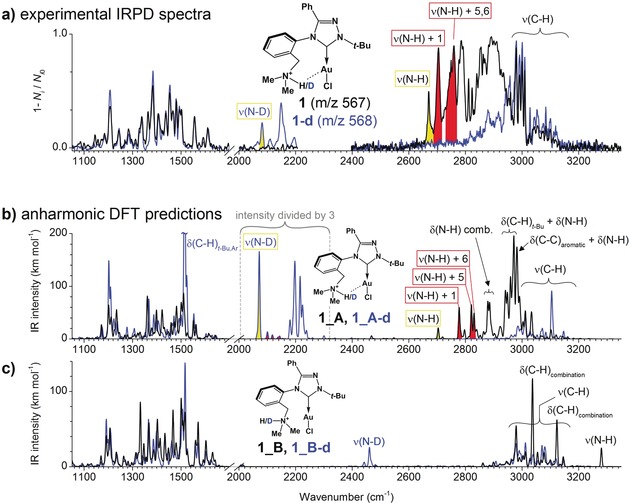
a) Experimental helium‐tagging IRPD spectra of the mass‐selected protonated complex 1 and its deuterated analog 1‐d. b),c) Calculated (B3LYP‐D3/6‐31G*/Au:def2‐SVP) anharmonic vibrational spectra of b) 1_A and c) 1_B and their deuterated analogues (1_A‐d, 1_B‐d). The displacement vectors of selected bands are shown in Figure 3.

The N−H bond in 1_A is slightly tilted towards the Cl atom, r _Cl⋅⋅⋅H=2.48–2.63 Å is about 0.4 Å shorter than the sum of the vdW radii of H and Cl (2.95 Å), and the Cl−H−N angle is 136–142° (Figure 1 b and Supporting Information, Table S1). Therefore, the N−H bond may feature some interaction with chlorine, which is discussed in more detail below. The gold atom is also in the vicinity of C−H bonds of the tert‐butyl group in 1_A with r _Au⋅⋅⋅H=2.71–2.84 Å (the sum of van der Waals radii is 2.86 Å). These interactions are rather weak, see below.

To assess the effect of the Au⋅⋅⋅H⁺−N interaction on the stability, we optimized another conformer of 1, named 1_B (Figure 1 b). The amine group is rotated by about 180° around the C−N bond in this conformer, thus resulting in the loss of the Au⋅⋅⋅H⁺−N interaction. Various methods predict that the 1_B isomer is about 10–12 kcal mol⁻¹ less stable than 1_A (Supporting Information, Table S2). The estimated barrier for the interconversion from 1_A to 1_B calculated at PBE0‐D3/def2‐TZVPP is about 12 kcal mol⁻¹. Notably, the N−H bond in 1_B is about 0.03 Å shorter than in 1_A (Figure 1 b), presumably due to the loss of the Au⋅⋅⋅H⁺−N interaction. Several short Au⋅⋅⋅H−C contacts are predicted in the conformer 1_B: one involving the bridging methylene (r _Au⋅⋅⋅H=2.54 Å) and two between Au and the tert‐butyl group (r _Au⋅⋅⋅H=2.66/2.78 Å).

The vibrational spectra of 1_A simulated at B3LYP‐D3/6‐31G*/Au:def2‐SVP reproduce all the main features of the experimental IRPD spectra as well as the effect of deuterium labeling very well (Figure 2 b). The small overall blue‐shift of the simulated spectra may be due to limitations of the small basis set enforced by the huge computational cost of the anharmonic calculations. The calculated spectra of conformer 1_B (Figure 2 c) show features inconsistent with the experimental IRPD spectra. In particular, the experimentally observed band between 2700 and 3100 cm⁻¹ is missing and the predicted N−H resonance at 3280 cm⁻¹ is not present in the experimental spectrum. Despite the limitations of these calculations, it is evident that the studied compound is present as conformer 1_A in the gas phase.

Further analysis of the calculated IR spectra of 1_A reveals strong anharmonic effects. In particular, the fundamental N−H mode normally expected to be above 3300 cm⁻¹ is strongly red‐shifted from the fundamental harmonic mode calculated at ν _N−H=3061 cm⁻¹ (unscaled, see Supporting Information, Figure S1) to ν _N−H=2704 cm⁻¹ in the anharmonic calculation (yellow peak in Figure 2 b). Its intensity is greatly diminished because of several anharmonic couplings with low‐frequency molecular modes. A strong red‐shift of ν _N−H due to intramolecular Au⋅⋅⋅H−N bonding was also predicted for [(2‐(pyridinium‐2‐yl)phenyl)Au(SPh)]⁺.7d

Although most couplings of the fundamental N−H mode have rather small intensities in the 2700–3100 cm⁻¹ region, the true fingerprint of the Au⋅⋅⋅H⁺−N interaction appears near 2800 cm⁻¹ (Figure 2 b, red peaks) which in fact comprises three combination resonances (calculated to be at 2778, 2821, and 2830 cm⁻¹) of the N−H mode with various low‐frequency modes of the molecular framework (Figure 3). Corresponding bands in the experimental IRPD spectrum are highlighted in red in Figure 2 a. In all these resonances, the N−H bond changes its position with respect to the Au−Cl bond (mutual bending or sliding of the Au−Cl/N−H moieties) as shown in Figure 3 for selected displacement vectors. These couplings provide clear spectroscopic evidence of Au⋅⋅⋅H⁺−N interactions. The coupling of the N−H vibration with the “translation” of the hydrogen atom between two attractors (gold and chlorine) resembles, to a certain extent, the effect observed by Craig et al. for the hydroxonium ion complexed within 18‐crown‐6 ether.11

Figure 3.

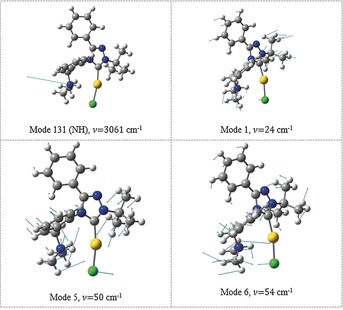
The N−H fundamental vibration and examples of the three modes responsible for coupling bands at 2780–2830 cm⁻¹ (unscaled frequencies).

Although the rather complicated structure of the wide band between 2850 and 3000 cm⁻¹ rules out a more detailed interpretation, some of these features are also attributable to the Au⋅⋅⋅H⁺−N interaction, primarily to the anharmonic modes in which combinations of the harmonic modes including N−H and tertiary amine bending in various directions couple with the modes corresponding to phenyl‐ring and methyl bending (Figure 2) on the opposing side of the molecule.

The deuterated system 1_A‐d features a simpler N−D vibration pattern as compared to 1_A (Figure 2 b). In particular, the N−D mode, calculated to be at 2071 cm⁻¹, has a strong intensity (yellow region in the blue spectrum in Figure 2 b) and the coupling with the sliding modes along the Au−Cl bond is weaker (red peaks in Figure 2 b). This is consistent with the results of Craig et al., who observed a diminished coupling between the O−D vibrational mode and the translation mode between two atractors.11 The coupling of the N−D stretching mode with the low‐frequency C−C and C−H modes is shifted towards about 2200 cm⁻¹.

To further confirm the presence of Au⋅⋅⋅H⁺−N bonding, we constructed model system 2 (Figure 1 c), which retains only the carbene→Au−Cl and tertiary ammonium units from the original system 1_A while keeping all atoms frozen in the equilibrium geometry of 1_A. We calculated the counterpoise‐corrected interaction energy between the two fragments in 2 to be ΔE _int=−7.0 (SCS‐MP2/def2‐TZVPP) and −10.8 kcal mol⁻¹ (PBE0‐D3/def2‐TZVPP, see also Computational Methods), thus providing an evidence for bonding. A similar system with a carbene CN₂ moiety instead of CH₂ yielded an interaction energy of −11.4 kcal mol⁻¹, whereas in model system 3 (Figure 1 d), the interaction between the dissected (CH₃)₃NH⁺ moiety and the rest of 1 was calculated to be ΔE _int=−23.1 kcal mol⁻¹ (SCS‐MP2). The former two values (ca. −10 kcal mol⁻¹) should represent a more rigorously “pure” Au⋅⋅⋅H⁺−N interaction. Notably, the interaction energy for 2 matches the energy difference between 1_A and 1_B. Switching off the dispersion correction using PBE0/def2‐TZVPP in calculations gives ΔE _int=−6.2 kcal mol⁻¹ for 2, the dispersion contribution (−4.6 kcal mol⁻¹) thus accounts for about 40 % of ΔE _int.

Despite our findings presented above, the question arises whether the reported Au^I⋅⋅⋅H⁺−N interaction is truly attractive or a forced contact. The results suggest that the N−H bond feels two attractors, Au and Cl. Undoubtedly, chloride is a stronger hydrogen‐bond acceptor than gold(I). As expected, in a model system with the R₃NH⁺ ligand dissected from the parent complex, the R₃NH⁺ moiety migrates and forms an ionic interaction with Cl⁻. The resulting isomer with a Cl⋅⋅⋅H⁺−N interaction is 8–10 kcal mol⁻¹ more stable than 1_A (depending on the model and method used; SCS‐MP2 or PBE0‐D3). Hence, the geometry of our complex prevents the formation of this stronger hydrogen bond. Instead, the weaker Au⋅⋅⋅H⁺−N interaction becomes crucial for the stabilization of the 1_A molecular framework with respect to 1_B. Attempts to find a minimum with a stronger Cl⋅⋅⋅H⁺−N interaction in 1_A failed. We have tested whether such an isomer could be formed by substituting gold(I) with silver(I) in 1_A. The silver analogue features a Cl⋅⋅⋅H⁺−N bond instead of a possible “forced contact” Ag⋅⋅⋅H⁺−N (r _Ag⋅⋅⋅H=2.47 Å, r _Cl⋅⋅⋅H=2.07 Å, r _N−H=1.05 Å, see Supporting Information, Figure S4; please note that both bond lengths in the C→Ag−Cl fragment are longer than those in the C→Au−Cl fragment).

To understand the nature of Au⋅⋅⋅H⁺−N bonding, we performed various chemical bonding analyses. Quantum theory of atoms in molecules (QTAIM) analysis calculations show a bond critical point (BCP) between Au and H in 1_A characterized by an electron density of ρ=0.033 e bohr⁻³ and a positive Laplacian of 0.08 e bohr⁻⁵ (Figure 4 a), indicating a moderate Au⋅⋅⋅H hydrogen bond.12 The calculated delocalization index (DI=0.13)12a between the Au and H atoms in 1_A indicates electron sharing between Au and H consistent with a hydrogen bond.12 The Au⋅⋅⋅H−C and Cl⋅⋅⋅H−C contacts in both 1_A and 1_B (Figure 1), for which BCPs were found (Figure 4), are less important, but present (Supporting Information, Table S3). The difference between 1_A and 1_B is nicely illustrated by the Laplacian of electron density in Figure 4 b, which clearly shows Au⋅⋅⋅H⁺−N bonding in 1_A and no significant interactions in 1_B.

Figure 4.

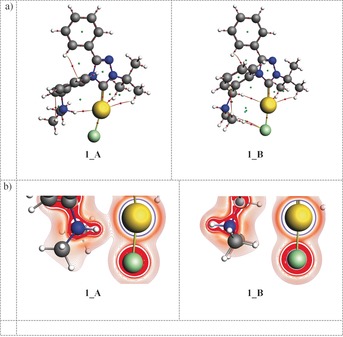
a) QTAIM analysis of 1_A and 1_B at ZORA–PBE0/TZP. Bond critical points (BCPs) shown in red, ring critical points (RCPs) in green. b) Laplacian of the electron density in systems 1_A and 1_B at ZORA–PBE0/TZP.

Extended‐transition‐state natural orbitals for chemical valence (ETS–NOCV) analysis reveals the Au⋅⋅⋅H interaction channel in 1_A and model system 2 with interaction energies of −11.5 and −9.6 kcal mol⁻¹, respectively. Notably, in 2 we also found an ETS–NOCV contribution corresponding to a Cl⋅⋅⋅H−N interaction (E _int=−2.2 kcal mol⁻¹), which was not observed in the full molecular system 1_A.

Energy decomposition analysis (EDA) of E _int in 2 using ZORA–PBE0/TZP (dispersion correction omitted) shows that the electrostatic term is approximately half as stabilizing as orbital (covalent) interaction (ΔE _orb=−15.4, ΔE _elstat=−8.8, ΔE _Pauli=18.0; ΔE _sum=−6.2 kcal mol⁻¹). Considering ΔE _disp=−4.6 kcal mol⁻¹ (see above), the overall Au⋅⋅⋅H⁺−N interaction thus arises circa 40 % from dispersion forces and 60 % from orbital and electrostatic interactions.

Natural bond orbital (NBO) analysis allows for characterization of hydrogen bonding via a perturbative analysis of the donor–acceptor (occupied‐vacant) interactions between the NBO orbitals.13 The NBO analysis of 1_A at PBE0‐D3/def2‐TZVPP found a strong coupling between the orbital corresponding to a lone‐pair (LP) on Au and an antibonding σ*(N−H) orbital with an estimated E(2) energy of −13 kcal mol⁻¹. A smaller coupling was also found between a LP(Cl) and a σ*(N−H) with E(2)=−2.4 kcal mol⁻¹, indicating a weak Cl⋅⋅⋅H⁺−N interaction. The discrepancy between the different analyses which either show or do not show a Cl⋅⋅⋅H⁺−N interaction (see above) means that it may be present but is much weaker than the Au⋅⋅⋅H⁺−N interaction.

Hydrogen bonding can be reflected by a deshielding NMR signal of the corresponding hydrogen atom, though the deshielding can be large even for rather weak bonds.8 The ¹H NMR chemical shift of the N−H⁺ hydrogen in 1_A is predicted to be 10.6 ppm, deshielded by 5.8 ppm in comparison to conformer 1_B. Notably, the spin–orbit‐induced relativistic contribution to the ¹⁵N NMR chemical shift in N−H⁺ is calculated as −5.8 ppm, causing additional shielding at the N nucleus. Such a large relativistic effect can only arise from a heavy atom, Au in this case, and this can only happen via propagation of the relativistic effect via Au^I⋅⋅⋅H⁺−N interactions.

In summary, the experimental IRPD spectra of the studied gold(I)–carbene system revealed an intramolecular Au^I⋅⋅⋅H⁺−N bond. Theoretical interpretation of the experimental spectra by anharmonic normal mode analysis provides a strong evidence of the Au⋅⋅⋅H⁺−N hydrogen bond, manifested as a large anharmonic shift of the N−H fundamental mode and its strong coupling with a number of low‐frequency modes, particularly those related to the bending of the carbene→Au−Cl moiety. The predicted Au⋅⋅⋅H contact at about 2.17 Å is one of the shortest ever reported. The predicted interaction energy at about −10 kcal mol⁻¹ originates partly from orbital and electrostatic interactions (40 % and 20 %, respectively) and partly from dispersion forces (40 %). Various chemical bonding analyses of the Au^I⋅⋅⋅H⁺−N interaction provide descriptors characteristic for a moderate Au⋅⋅⋅H−N hydrogen bond.30

Experimental Section

Helium‐tagging IRPD spectra 14 were acquired with the ISORI instrument,15 which allows us to record the IR spectra of ions at cryogenic temperatures using an electrospray ion source from TSQ 7000 (Finnigan). The ions 1 (m/z 567) and deuterated 1D (m/z 568) were prepared by ESI ionization of a <1 mm solution of the [(L)AuCl] complex16 (L=1‐(tert‐butyl)‐3‐phenyl‐4‐(2‐((dimethylamino)methyl)phenyl)‐1,2,4‐triazol‐5‐ylidene) in MeOH (1) or in MeOD (1D), acidified with 1 equivalent of HCl. The ions were mass‐selected and guided into the 3‐Kelvin wire quadrupole trap, where they were trapped by helium pulses. Under these conditions, ions formed weakly bound complexes with helium atoms. The trapped ions were irradiated by a tunable IR laser (OPO/OPA system from LaserVision, equipped a WS‐600 wavelength meter from HighFinesse GmbH; power output is shown in the Supporting Information, Figure S2). After irradiation, the ions were ejected from the trap and mass analyzed. Absorption of photons lead to vibrational excitation of the helium complexes, thereby causing the dissociation of helium atoms. The IRPD spectrum was thus obtained by monitoring of the number of helium complexes as a function of the IR wavelength. The spectrum was plotted as the dissociation yield 1−N_i/N _i0, where N_i is the number of surviving complexes after laser irradiation (wavelength function) and N _i0 is a reference complex count recorded by blocking the entrance of the IR light into the cold trap. The pulse sequence is shown in Figure S3 (Supporting Information). The spectra were recorded at the saturation regime. This mode allows us to detect weak bands. At the same time, almost all helium complexes are depleted at the strong absorption bands. The intensity of these bands is therefore relatively diminished.

Computational details: Structures were optimized using several methods by combination of the PBE018 and B3LYP19 density functionals with def2‐SVP,20 def2‐TZVPP,20 and 6‐31G* basis sets, as implemented in the Gaussian 16 program.17 The def2‐SVP20 and def2‐TZVPP20 basis sets used for Au utilized a relativistic effective core potential (ECP)21. Dispersion correction (D3) was used in most DFT calculations.22 The PBE0‐D3/def2‐TZVPP method is known to provide excellent structures of transition metal complexes.23 The SCS‐MP2/def2‐TZVPP20, 24 method was chosen as an accurate and affordable level for calculating interaction energies.4 All energy calculations were corrected for the basis‐set superposition error.25 Anharmonic vibrational spectra were calculated using second‐order vibrational perturbation theory and the B3LYP functional19 with Grimme's semiempirical dispersion correction26 implemented in Gaussian 16 (Reference 17). The 6‐31G* basis set was used for light atoms, def2‐SVP for the Au atom.20, 21 This method is denoted as B3LYP‐D3/6‐31G*/Au:def2‐SVP. QTAIM27 and ETS–NOCV28 analyses were performed using the ADF 201729 program, the PBE0 functional18 and the TZP basis set.28 Natural bond orbital analysis13 was done at PBE0/def2‐TZVPP using the NBO 3.0 program as implemented in Gaussian 16.17

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

M. Straka, E. Andris, J. Vícha, A. Růžička, J. Roithová, L. Rulíšek, Angew. Chem. Int. Ed. 2019, 58, 2011.