New metrics for meta‐analyses of heterogeneous effects

Abstract

We provide two simple metrics that could be reported routinely in random‐effects meta‐analyses to convey evidence strength for scientifically meaningful effects under effect heterogeneity (ie, a nonzero estimated variance of the true effect distribution). First, given a chosen threshold of meaningful effect size, meta‐analyses could report the estimated proportion of true effect sizes above this threshold. Second, meta‐analyses could estimate the proportion of effect sizes below a second, possibly symmetric, threshold in the opposite direction from the estimated mean. These metrics could help identify if (1) there are few effects of scientifically meaningful size despite a “statistically significant” pooled point estimate, (2) there are some large effects despite an apparently null point estimate, or (3) strong effects in the direction opposite the pooled estimate also regularly occur (and thus, potential effect modifiers should be examined). These metrics should be presented with confidence intervals, which can be obtained analytically or, under weaker assumptions, using bias‐corrected and accelerated bootstrapping. Additionally, these metrics inform relative comparison of evidence strength across related meta‐analyses. We illustrate with applied examples and provide an R function to compute the metrics and confidence intervals.

1. INTRODUCTION

Random‐effects meta‐analyses aggregate evidence across studies measuring heterogeneous effects. Reporting usually focuses on the estimated mean of the distribution of true effects. However, under heterogeneity, others caution against exclusive focus on the estimated mean and recommend also reporting the estimated variance of true effects, not only the proportion of variance attributable to heterogeneity.1, 2 Summarizing evidence strength by comparing only the estimated mean to a threshold of scientific importance is needlessly dichotomous and has, in the past, led authors to conflicting conclusions in meta‐analyses reporting nearly identical point estimates (see the works of Kirsch et al3 and Turner et al4 with additional commentary on dichotomization by Turner and Rosenthal5). Others have proposed informative summary metrics that consider heterogeneity by characterizing the range of effects in the distribution or providing a prediction interval for a new effect in the population or in a subgroup.1, 2, 6, 7, 8

Extending these previous recommendations regarding heterogeneity in meta‐analyses, we recommend also considering questions such as “How common are effects of a size that is scientifically meaningful?” along with the traditional question “What is the average effect size?” We therefore propose simple metrics that, unlike traditional metrics, directly address the former question. These metrics make inference to the population of true effect sizes while accounting for differences in precision across studies. As discussed below, this is distinct from simply “vote counting” the significant p values or the observed effect sizes (ie, those measured with statistical error in the meta‐analyzed studies) stronger than a threshold because the vote‐counting approach, unlike our metrics, does not account for differences in precision and sample size across studies.

Reporting these new metrics along with traditional metrics may better identify situations in which (1) a “statistically significant” point estimate obscures the fact that the population of effect sizes contains few of scientifically meaningful size or, conversely, (2) a null point estimate disguises the fact that, due to heterogeneity, there are large effect sizes in some settings. Additionally, these metrics help identify whether the treatment or exposure of interest may have scientifically meaningful effects in the opposite direction in some populations, pointing to the need to further examine potential effect modifiers. Lastly, they can inform comparison of relative evidence strength across related meta‐analyses.

2. METHODS

We make two recommendations to better characterize heterogeneous effect sizes represented by a given literature. First, in meta‐analyses with heterogeneity (ie, a nonzero estimate of τ, the standard deviation of the true effects), the investigator could select a threshold above which an effect size might be considered of scientifically meaningful size and could report the estimated proportion of true effect sizes exceeding this threshold, along with a confidence interval. There is a large, interdisciplinary literature considering how to choose such thresholds, which we briefly summarize in the Online Supplement. For example, if the effect sizes are relative risks, then depending on the scientific context and informed by considerations such as those described in the Online Supplement, we might consider only those above 1.1 to be scientifically meaningful. Again, depending on context, if fewer than (for example) 10% of true effect sizes surpass this threshold, we might consider evidence strength for scientifically meaningful effect sizes to be fairly weak.

Second, given a chosen threshold of scientific importance, we recommend that meta‐analyses report the proportion of effect sizes stronger than a second (possibly symmetric) threshold on the opposite side of the null hypothesis (eg, 1/1.1≈0.9). That is, we might estimate a pooled relative risk (R R) of 1.2, indicating that the mean effect is positive. Yet with enough heterogeneity, the population of effects may also contain a nonneglible proportion of strong inverse associations (for example, 18% below a symmetric R R of 1/1.1≈0.9). In practice, for both metrics, it may be informative to report results at more than one threshold of scientific importance as well as to report the meta‐analytic estimates (particularly inference on the heterogeneity estimate) required to allow a reader to compute our proposed metrics for an arbitrary threshold.

These two proportions with their confidence intervals can be computed using only the estimated mean, heterogeneity, and their standard errors from a random‐effects meta‐analysis fit with any estimation approach that yields unbiased estimates of the mean and variance of the effect distribution. Specifically, under standard assumptions of parametric random‐effects meta‐analysis,9 studies have true effect sizes θ _i that are independently normal with a grand mean μ and variance τ ². Suppose we estimate μ with a point estimate denoted $\widehat{\mu }$ and estimate τ ² using one of several heterogeneity estimators,10 denoted ${\widehat{\tau }}^2$. If $\widehat{\mu }$ is above the null value (eg, an estimated log‐O R of $\log (1.3)$), then the first proposed metric, namely, the estimated proportion of studies in the population with effect size greater than q (eg, $q=\log (1.1)$), is simply

$$\widehat{P}\left(\theta >q\right)=1-\mathrm{\Phi }\left(\frac{q-\widehat{\mu }}{\sqrt{{\widehat{\tau }}^2}}\right),{\widehat{\tau }}^2>0,$$ (1)

where Φ denotes the standard normal cumulative distribution function. For the second metric, we can estimate the proportion below a second threshold q ^∗ as

$$\widehat{P}\left(\theta <q^{\ast }\right)=\mathrm{\Phi }\left(\frac{q^{\ast }-\widehat{\mu }}{\sqrt{{\widehat{\tau }}^2}}\right),{\widehat{\tau }}^2>0.$$ (2)

In either case, asymptotic 95% confidence interval limits are

$$\begin{array}{ll}& \widehat{P}\pm 1.96\sqrt{\frac{\widehat{\mathrm{Var}}\left(\widehat{\mu }\right)}{{\widehat{\tau }}^2}+\frac{\widehat{\mathrm{Var}}\left({\widehat{\tau }}^2\right){\left(\widehat{\mu }-q\right)}^2}{4{\left({\widehat{\tau }}^2\right)}^3}}·\varphi \left(\frac{q-\widehat{\mu }}{\sqrt{{\widehat{\tau }}^2}}\right),\end{array}$$ (3)

where ϕ denotes the standard normal density function. $\widehat{P}$ in this expression can be computed from either Equation (1) or Equation (2), and q is replaced by q ^∗ when considering the second metric. Simulation results (Online Supplement) indicate that when the number of studies is less than 10, $\widehat{P}<0.15$, or $\widehat{P}>0.85$, it is preferable to estimate the confidence interval via bias‐corrected, accelerated bootstrapping.11, 12 Applied examples in this paper for which $\widehat{P}<0.15$ or $\widehat{P}>0.85$ use bootstrapped confidence intervals, for which code is available online (https://osf.io/pr2s9/).

If $\widehat{\mu }$ is below rather than above the null value (for example, we estimate a mean log‐O R of $\log (0.85)$), then we would simply switch the two equations, using Equation (2) to estimate the proportion of effects below a threshold (eg, a log‐O R of $\log (0.90)$) and Equation (1) to estimate the proportion of effects above a second threshold. (As usual, we use the log scale when considering odds ratios for approximate normality.) In practice, these proportions are easy to compute manually or using the R function prop_stronger, available in an open‐source public repository (https://osf.io/pr2s9/). We now illustrate how they can facilitate interpretation through three examples.

3. EXAMPLE 1: A “SIGNIFICANT” MEAN DESPITE LITTLE EVIDENCE FOR STRONG EFFECTS

Meta‐analyses often achieve large pooled sample sizes and high power, and thus, it can happen that a very small estimated mean attains “statistical significance” at a given significance threshold. The proposed metrics may then illustrate that, despite a “significant” p value, few effects are in fact strong enough to warrant scientific interest. For example, a recent meta‐analysis13 estimated a mean correlation of r= −0.06 (p = 0.01) between increased psychological stress and shorter telomeres, and subsequent literature largely interpreted this finding as supportive of an association. However, using the proposed methods, we can estimate that only 6% (95% CI: 0%, 71%) of true correlations between stress and telomere length are stronger than the modest threshold of r = −0.10 and that almost none (0%, 95% CI: 0%, 46%) is stronger than r = −0.20. It is important to note that the upper confidence interval limits for both choices of threshold represent nonnegligible proportions, so these results should not be interpreted as evidence against the occurrence of correlations stronger than these thresholds. The 95% prediction interval is (−0.13, 0.02); this additionally suggests that, with high probability, a new effect drawn from the population will be near the null.6, 7 These metrics perhaps better qualify the scientific relevance of the meta‐analyzed studies. Note that comparing the point estimate alone to the threshold would not adequately convey evidence strength. This meta‐analysis estimated little heterogeneity (τ= 0.03), and hence, the small point estimate suggests a small proportion of strong true effects; however, if the heterogeneity estimate had been larger (for example, three‐fold larger on the τ scale), then the estimated percent of true correlations stronger than r = −0.10 would increase from a negligible 6% to 30% (95% CI: 13%, 46%).

4. EXAMPLE 2: META‐ANALYSES WITH DIFFERENT CONCLUSIONS DESPITE SIMILAR EVIDENCE STRENGTH

These metrics can also inform comparison across meta‐analyses, which is of interest when a meta‐analysis is updated to reflect new literature, when applying different inclusion criteria or analysis methods to the same literature, or when meta‐analyses assess different, but related, outcomes. A common, but unsatisfactory, approach is to compare only estimated means and “statistical significance.” However, around the p value cut‐off (eg, 0.05), “statistical significance” can be highly sensitive to the inclusion of even one additional small study. Moreover, these metrics are not robust to the influence of large or outlying studies; they may therefore suggest a spuriously large discrepancy between meta‐analyses. Yet even when estimated means differ, the more stable proposed metrics may be similar and have substantially overlapping confidence intervals, suggesting less dramatic discrepancies. Alternatively, despite comparable point estimates, differences in heterogeneity across meta‐analyses can lead to different proportions of strong effect sizes.

We illustrate using two meta‐analyses investigating the effect of omega‐3 fatty acid supplementation on depression in randomized trials; the first meta‐analysis14 suggested a “significant” beneficial effect (standardized mean difference (S M D) = 0.26, 95% CI: 0.12, 0.39), whereas the second15 did not (S M D = 0.25, 95% CI: −0.07, 0.56). Using S M D = 0.50 as a threshold of scientific importance (based, for instance, on a minimum subjectively perceptible difference; see Online Supplement), our first metric estimates that 22% (95% CI: 6%, 38%) of S M Ds in the former meta‐analysis14 surpass this threshold, comparable to 30% (95% CI: 4%, 56%) in the latter15 (Figure 1). Using our second metric, neither meta‐analysis suggests a high proportion of strong detrimental effects (1% below S M D = −0.50 with 95% CI: 0%, 3% in the former and 6% with 95% CI: 0%, 22% in the latter). Thus, evidence strength in these two meta‐analyses is perhaps more concordant than their disagreement on “statistical significance” alone suggests. (A supplementary example regarding comparison between meta‐analyses with differing point estimates appears in the Online Supplement.)

Figure 1.

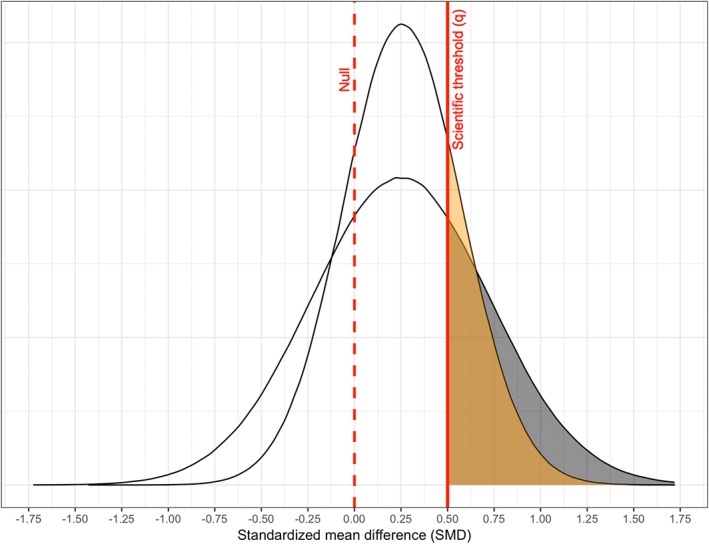
Estimated proportion of standardized mean differences (shaded) stronger than the threshold of scientific importance at S M D = 0.50 (solid red line) in two meta‐analyses with differing “statistical significance.” (Dashed red line) reference null value (S M D = 0). [Colour figure can be viewed at wileyonlinelibrary.com]

5. EXAMPLE 3: A WIDE PREDICTION INTERVAL DESPITE EVIDENCE FOR MANY STRONG EFFECTS

Others recommend reporting a prediction interval representing a plausible range for a new effect drawn from the distribution underlying the meta‐analyzed studies.2, 6, 7 We agree, while also noting that our metrics convey additional information. For example, a meta‐analysis16 of 19 trials on the effect of intravenous magnesium on mortality following acute myocardial infarction estimated an odds ratio of 0.72 (95% CI: 0.58, 0.90), corresponding to a 95% prediction interval of (0.42, 1.25). This interval is fairly wide and substantially overlaps the null, indicating considerable uncertainty about the size and direction of an effect in a new study. Nevertheless, if we consider inverse associations below O R = 0.8 to be scientifically meaningful, our proposed metrics suggest that a high proportion of true effects (66% with 95% CI: 28%, 100%) are more protective than this threshold and that few are comparably strong in the opposite direction (2% above O R = 1.2, 95% CI: 0%, 7%). These metrics suggest that there is strong evidence that a substantial proportion of studies have reasonably large protective effects, even though the prediction interval for any single true effect includes the null value of O R = 1. We provide this example for illustrative purposes only, noting that others have raised methodological concerns about this literature, including, for example, publication bias and possible data quality issues in some included studies.17

The findings of the prediction interval and of our metrics are not contradictory, but complementary: The prediction interval infers plausible values for a single effect by considering the middle 95% of the area of the effect distribution, whereas our metrics estimate the area of the lower and upper tails. Intuitively, as the effect distribution becomes more heterogeneous, the middle 95% widens, yielding a wider prediction interval. Simultaneously, the tails thicken, increasing the proportion of strong effects in both the same and the opposite direction as the estimated mean. Thus, with enough heterogeneity, an estimated mean near the null can belie the existence of meaningful effect sizes in some settings. In such cases, the first and second proposed metrics would likely indicate a substantial proportion of strong effect sizes both in the same and in the opposite direction from the estimated mean; this pattern of results would invite exploration of reasons for heterogeneity, for example, through individual patient data meta‐analysis with covariates or meta‐regression.

6. TECHNICAL POINTS

The proposed metrics are distinct from antiquated “vote‐counting” procedures based on the proportion of studies with significant p values. Such methods fail to differentiate small from large effect sizes (counting only those that are “statistically significant”) and fail to account for differences in precision and sample size across studies.1 A modified procedure could consider the proportion of observed effect sizes (rather than p values) above a threshold of scientific interest, but this would still limit attention to the observed effect sizes despite that these are measured with sampling error. In contrast, the proposed metrics make appropriately weighted inferences regarding the distribution of true effect sizes in the population (rather than of the observed estimates). In the telomere length example, a basic vote count finds that 14% of studies (3 of 21) had p < 0.05. A count of observed effect sizes stronger than a threshold, but ignoring sample sizes and sampling variability, finds that 24% (5 of 21) are below r = −0.20. In contrast, our approach concerns the true effect sizes and estimates that <0.1% of these are stronger than r = −0.20.

These metrics are model based; they assume that the true effect sizes are normally distributed. In practice, this implies the sometimes testable assumption that the observed point estimates are normal. Because this distributional assumption may be inexact, our proposed metrics are perhaps most usefully treated as summary metrics of evidence strength for effects of scientifically meaningful size rather than as precise proportions. Additionally, these metrics and inference require the meta‐analytic model to be statistically valid, but estimating the heterogeneity without bias, in particular, can be challenging.10 It is thus important to choose a heterogeneity estimator with good statistical properties for the chosen outcome type10 to enable good performance of our metrics and of traditional metrics. Lastly, publication bias can compromise our metrics in the same way that it compromises standard analyses. Therefore, when publication bias is suspected, we recommend conducting sensitivity analyses that estimate $\widehat{\mu }$ and ${\widehat{\tau }}^2$ in a manner that corrects for publication bias (eg, the work of Vevea and Hedges18). These bias‐corrected estimates can then be used to unbiasedly estimate our proposed metrics.

7. CONCLUSION

To better characterize heterogeneous effects in meta‐analysis, we recommend supplementing standard reporting with two simple metrics regarding the proportion of effects above a threshold of scientific importance and below a second threshold on the opposite side of the null. These metrics account for effect size, heterogeneity, and statistical error, and they are easy to compute manually or using the R function prop_stronger.

Supporting information

SIM_8057‐Supp‐0001‐SIM_2 MAM Supplement.pdf

SIM_8057‐Supp‐0002‐supplement.zip

Mathur MB, VanderWeele TJ. New metrics for meta‐analyses of heterogeneous effects. Statistics in Medicine. 2019;38:1336–1342. 10.1002/sim.8057