A mechanistic model of photosynthetic protein turnover explains leaf acclimation to light and nitrogen availabilities and suggests that suboptimal photosynthetic nitrogen partitioning is due to daily light fluctuations.
Keywords: Functional partitioning, light, mechanistic model, nitrogen reallocation, nitrogen supply, optimal, photosynthetic acclimation
Abstract
Plants continually adjust the photosynthetic functions in their leaves to fluctuating light, thereby optimizing the use of photosynthetic nitrogen (Nph) at the canopy level. To investigate the complex interplay between external signals during the acclimation processes, a mechanistic model based on the concept of protein turnover (synthesis and degradation) was proposed and parameterized using cucumber grown under nine combinations of nitrogen and light in growth chambers. Integrating this dynamic model into a multi-layer canopy model provided accurate predictions of photosynthetic acclimation of greenhouse cucumber canopies grown under high and low nitrogen supply in combination with day-to-day fluctuations in light at two different levels. This allowed us to quantify the degree of optimality in canopy nitrogen use for maximizing canopy carbon assimilation, which was influenced by Nph distribution along canopy depth or Nph partitioning between functional pools. Our analyses suggest that Nph distribution is close to optimum and Nph reallocation is more important under low nitrogen. Nph partitioning is only optimal under a light level similar to the average light intensity during acclimation, meaning that day-to-day light fluctuations inevitably result in suboptimal Nph partitioning. Our results provide insights into photoacclimation and can be applied to crop model improvement.
Introduction
Acclimation of leaf traits to fluctuating environments is a key mechanism to maximize fitness (Walters, 2005; Athanasiou et al., 2010). To maximize canopy carbon gain, dynamic modifications of photosynthetic traits to track heterogeneous light distribution within the canopy are crucial (Retkute et al., 2015), especially for herbaceous species with a continuously leaf-forming nature (Niinemets et al., 2015). One of the most important strategies in photoacclimation is to maintain efficient utilization of limited resources in the photosynthetic apparatus, e.g. nitrogen, by continuous modifications of (i) between-leaf distribution along the canopy depth and (ii) within-leaf partitioning between photosynthetic functions according to local light availability (Evans, 1989).
Vertical nitrogen distribution in response to light has been intensively studied (Hirose and Werger, 1987; Werger and Hirose, 1991; Anten et al., 1995; Dreccer et al., 2000; Moreau et al., 2012; Hikosaka et al., 2016). Nitrogen distribution was reported to closely follow the light gradient and thus approach its optimum in wheat stands (Dreccer et al., 2000). However, this relationship has not been found in other studies (Moreau et al., 2012; Hikosaka et al., 2016). In fact, many studies demonstrated that nitrogen distribution failed to track the within-canopy light gradient optimally due to a delay in nitrogen reallocation in the lower canopy layer and an underinvestment in the upper layer (Field, 1983; Evans, 1993; Hollinger, 1996; Hirose et al., 1997; Meir et al., 2002; Wright et al., 2006; Hikosaka, 2016). This discrepancy between optimum and reality could be explained by physiological limitations and the cost of nitrogen reallocation (Hikosaka, 2016; Kitao et al., 2018) or might result from incorrect predictions. In some cases (e.g. Hikosaka, 2014; Kitao et al., 2018), the optimal nitrogen distribution that followed the within-canopy light gradient estimated by the Beer–Lambert law was predicted to be extremely high in the upper canopy, which might not be biologically reachable. This could result from the oversimplification of models in three aspects: (i) neglecting the effects of variations in the structural characteristics, e.g. leaf elevation angle (Falster and Westoby, 2003), on light interception of the leaves; (ii) neglecting age-dependent modifications and limitations during leaf development and ageing (Niinemets et al., 2015; Niinemets, 2016); and (iii) assuming a linear relationship between photosynthetic capacity and photosynthetic nitrogen per unit leaf area instead of considering photoacclimation in functional nitrogen partitioning.
Optimizing functional partitioning within the leaf is of great importance because it improves carbon gain by enhancing photosynthetic nitrogen use efficiency (PNUE; Zhu et al., 2010). Photosynthetic rate is determined by the limited rate of ribulose 1,5-bisphosphate (RuBP) carboxylation and RuBP regeneration in the photosynthetic machinery (Farquhar et al., 1980). Besides driving photosynthesis, light also triggers fine adjustments in nitrogen investment between (i) RuBP carboxylation (Rubisco), (ii) RuBP regeneration (electron transport), and (iii) light harvesting functions (Yamori et al., 2010; Trouwborst et al., 2011; Vialet-Chabrand et al., 2017). The capability and significance of photoacclimation in functional nitrogen partitioning were empirically addressed in both light-demanding and shade-tolerant species (Evans, 1993; Hikosaka and Terashima, 1996; Pons and Anten, 2004; Hikosaka, 2005; Trouwborst et al., 2011). Recently, with a modelling approach, it was predicted that a decreasing investment in the light harvesting function can increase canopy PNUE (Song et al., 2017). However, genetic and physiological controls of photoacclimatory processes by environmental triggers are still not described mechanistically.
The degree of acclimation under a given environment is limited by the previous environmental conditions (Walters, 2005; Niinemets et al., 2006) along with continuous age-dependent modifications in physiological traits (Niinemets, 2016). This emphasizes that static models, which do not consider the dynamics of plant growth and environmental fluctuations, may not be sufficiently precise in predicting acclimation behavior. Prieto et al. (2012) proposed an empirical model describing the combined effects of leaf age and light on leaf nitrogen economics for a grapevine canopy and demonstrated that the mean daily light integral over the previous 10 d explained 73% of the variation in nitrogen per unit leaf area. Since environmental acclimation and developmental (genetic control of leaf ageing) acclimation are regulated distinctively (Athanasiou et al., 2010), it is possible to integrate internal (age) and external (environment) triggers into a mechanistic model for better understanding of the developmental and environmental effects on photosynthetic acclimation.
Acclimation processes in leaf functioning are regulated by constant updates of protein content as a result of protein turnover, driven by the concurrent actions of degradation and synthesis (Li et al., 2017). In growing leaves, photosynthetic proteins account for the highest cost in protein turnover (Li et al., 2017). At the expense of energy, protein turnover is necessary for adjusting protein levels in line with external triggers. It was experimentally shown that leaf Rubisco content increased with light (Yamori et al., 2010) and nitrogen supply level (Yamori et al., 2011a) and exhibited an evolution with leaf age that could be interpreted by Rubisco turnover (Suzuki et al., 2001; Ishimaru et al., 2001; Irving and Robinson, 2006). Based on the concept of protein turnover, Thornley (1998) proposed a mechanistic model predicting reasonable dynamics of photosynthetic acclimation at the leaf level. We refined this model to describe the dynamics of different photosynthetic nitrogen pools and to quantify the developmental and environmental effects of light and nitrogen availabilities on leaf acclimation. The optimality of nitrogen distribution and partitioning at the canopy scale was evaluated by integrating this model into a multi-layer model considering the structural characteristics of a cucumber canopy. This aims (i) to test whether the protein turnover can be a mechanistic explanation of the photosynthetic acclimation under dynamic environmental conditions; and (ii) to understand the regulatory mechanism of environmental triggers on the degree of optimality at the canopy level in terms of maximizing PNUE and canopy carbon assimilation, which can be considered as an indicator of the general fitness of the plants.
Materials and methods
Modelling the dynamics of photosynthetic protein turnover
Photosynthetic nitrogen (Nph, mmol N m−2) is defined as biologically active nitrogen in the proteins involved in photosynthetic functions, i.e. carboxylation, electron transport and light harvesting. Leaf Nph is calculated as the sum of nitrogen in the carboxylation pool (NV), electron transport pool (NJ) and light harvesting pool (NC, Trouwborst et al., 2011):
| (1) |
where NV includes only Rubisco and represents the nitrogen investment in carboxylation capacity, NJ includes the electron transport chain, photosystem II core and Calvin cycle enzymes other than Rubisco, and NC includes the photosystem I core and light harvesting complexes I and II. Functional pools NV, NJ, and NC are estimated from the maximum carboxylation rate (Vcmax, μmol CO2 m−2 s−1), maximum electron transport (Jmax, μmol e− m−2 s−1) and leaf chlorophyll (Chl, mmol Chl m−2), respectively (Buckley et al., 2013):
| (2a) |
| (2b) |
| (2c) |
where χV (μmol CO2 mmol−1 N s−1) is the carboxylation capacity per unit Rubisco nitrogen, and χJ (μmol e− mmol−1 N s−1) is the electron transport capacity per unit electron transport nitrogen. χCJ (mmol Chl mmol−1 N) and χC (mmol Chl mmol−1 N) are the conversion coefficients for chlorophyll per electron transport nitrogen and per light harvesting component nitrogen, respectively. Photosynthetic nitrogen partitioning fraction of a pool X (pX) is determined as the ratio of nitrogen in the pool X (NX, mmol N m−2) to Nph:
| (3) |
The rate of change of NX is determined by the instantaneous protein synthesis rate [SX(t), mmol N m−2 °Cd−1] and degradation rate [DX(t), mmol N m−2 °Cd−1] of the corresponding enzymes and protein complexes at a given leaf age (t, °Cd):
| (4) |
Protein synthesis as an age-dependent and zero-order process (Li et al., 2017) is described by a logistic function and independent of the current NX state:
| (5) |
where Smax,X (mmol N m−2 °Cd−1) is the maximum protein synthesis rate of NX that occurs at the early stage of leaf development (Supplementary Fig. S1 at JXB online). The constant td,X (°Cd−1) describes the relative decreasing rate of the protein synthesis over time (see Table 1 for the coefficients used in the protein turnover model). At age of 1/td,X, SX reduces to 53.8% of Smax,X.
Table 1.
List of coefficients used in the protein turnover model for photosynthetic nitrogen pools, carboxylation pool NV, electron transport pool NJ, and light harvesting pool NC
| Description | Coefficient | Unit | Pool NV | Pool NJ | Pool NC |
|---|---|---|---|---|---|
| Degradation constant [Eq. (6)] | D r | °Cd−1 | 0.0195 | 0.0195 | 0.0091 |
| Increase rate constant of Smax with ILd [Eq. (7)] | k I | mmol N m2 ground d m−2 LA °Cd−1 mol−1 photon | 0.173 | 0.130 | 0.234 |
| Michaelis–Menten constant relating NS to Smax [Eq. (8)] | k N | mM | 0.536 | 0.420 | 0.316 |
| Potential maximum synthesis rate [Eq. (7)] | S mm | mmol N m−2 °Cd−1 | 1.122 | 0.852 | 0.248 |
| Decreasing constant of synthesis rate [Eq. (5)] | t d | °Cd−1 | 0.001 | 0.002 | 0.001 |
The degradation rate DX is governed by first-order kinetics (Verkroost and Wassen, 2005; Li et al., 2017) with a degradation constant Dr,X (°Cd−1):
| (6) |
The variable Smax,X in Eq. (5) is a function of daily light interception (ILd, mol photons m−2 d−1):
| (7) |
where Smm,X (mmol N m−2 °Cd−1) is the potential maximum protein synthesis rate and kI,X is the rate constant describing the increase of Smax,X with ILd. The factor rN,X increases with nitrogen level in the nutrient solution (NS, mM) by a Michaelis–Menten constant, kN,X (mM):
| (8) |
Modelling leaf photosynthesis
Photosynthetic parameters Vcmax, Jmax, and Chl were estimated from functional nitrogen pools NV, NJ, and NC, using Eq. (2a–c). The net photosynthetic rate (A, μmol CO2 m−2 s−1) is defined as the minimum of RuBP carboxylation-limited (Ac, mmol CO2 m−2 s−1) and RuBP regeneration-limited (Aj, mmol CO2 m−2 s−1) net photosynthetic rate (Farquhar et al., 1980):
| (9a) |
| (9b) |
| (9c) |
where Cc (μmol CO2 mol−1) is the chloroplastic CO2 concentration, Γ* (μmol CO2 mol−1) is the CO2 compensation point in the absence of dark respiration, Kc (μmol CO2 mol−1) and Ko (mmol O2 mol−1) are Michaelis–Menten constants of Rubisco for CO2 and O2, respectively, O (mmol O2 mol−1) is the O2 concentration at the site of carboxylation, Vc (μmol CO2 m−2 s−1) is carboxylation rate, and J (μmol e− m−2 s−1) is electron transport rate. Daytime respiration rate Rd (μmol CO2 m−2 s−1) is assumed to vary with t and the mean ILd during the previous 4 d (ILd4d):
| (10) |
where Rmax (μmol CO2 d mol−1 photons s−1) relates ILd4d to the maximum Rd, Rg (m2 d °Cd−1 mol−1 photons) influences the decrease in the growth respiration, and Rm (μmol CO2 d °Cd−1 mol−1 photons s−1) affects the increase in the maintenance respiration with t.
V c and J are calculated from Vcmax and Jmax, respectively, depending on the photosynthetic photon flux density (PPFD) incident on the leaf (ILc, µmol photons m–2 s–1) according to Qian et al. (2012) and Ögren and Evans (1993), respectively:
| (11) |
| (12) |
where ϕ (µmol e– µmol photons−1) is the conversion efficiency of photons to J, and θ (unitless) is a constant convexity factor describing the response of J to ILc. Leaf absorptance (α, unitless) is related to Chl (Evans, 1993):
| (13) |
Chloroplastic CO2 concentration depends on the steady-state of stomatal conductance (gsc, mol CO2 m−2 s−1) and mesophyll conductance (gm, mol CO2 m−2 s−1) to CO2:
| (14) |
where Ca (μmol CO2 mol−1) is atmospheric CO2 concentration, and gsc is calculated with species-specific constants of stomatal conductance, g0 and g1 (Chen et al., 2014), and leaf-to-air vapor pressure deficit (D, kPa, Medlyn et al., 2011):
| (15) |
Mesophyll conductance is expressed as a log-normal function of t (Chen et al., 2014), where gm first increases during leaf development and decreases during ageing (Flexas et al., 2008):
| (16) |
where tgm is the t when the maximum gm (gmmax, mol CO2 m−2 s−1) occurs and vgm is the standard deviation of the curve; gmmax is linearly related to Nph, since a similar relationship has been reported for C3 plants (e.g. Yamori et al., 2011a):
| (17) |
where rgm (mol CO2 mmol−1 N s−1) describes the rate of increase of gmmax in relation to Nph, and rgm0 (mol CO2 m−2 s−1) is the minimum gmmax.
The steady-state Ac was solved analytically with Eqs (9b), (14), and (15), and Aj with Eqs (9c), (14), and (15), following Moualeu‐Ngangue et al. (2016). Model variables and coefficients are listed in Tables 1–3.
Table 2.
List of model input and output variables
| Description | Variable | Unit | Equation | Type |
|---|---|---|---|---|
| Net photosynthetic rate | A | μmol CO2 m−2 s−1 | 9a | Output |
| RuBP carboxylation-limited A | A c | μmol CO2 m−2 s−1 | 9b | Output |
| RuBP regeneration-limited A | A j | μmol CO2 m−2 s−1 | 9c | Output |
| Leaf absorptance | α | — | 13 | Output |
| Atmospheric CO2 concentration | C a | μmol CO2 mol−1 | — | Input |
| Chloroplastic CO2 concentration | C c | μmol CO2 mol−1 | 14 | Output |
| Leaf chlorophyll per unit area | Chl | mmol m−2 | 2c | Output |
| Leaf-to-air vapor pressure deficit | D | kPa | — | Input |
| Protein degradation rate of N pool X | D X | °Cd−1 | 6 | Output |
| Factor for creating variation in N distribution | f d | — | 18 | Input |
| Factor for creating variation in N partitioning | f p | — | 19 | Input |
| Mesophyll conductance to CO2 | g m | mol CO2 m−2 s−1 | 16 | Output |
| Maximum gm | g mmax | mol CO2 m−2 s−1 | 17 | Output |
| Stomatal conductance to CO2 | g sc | mol CO2 m−2 s−1 | 15 | Output |
| PPFD at leaf | I Lc | μmol photons m−2 s−1 | — | Input |
| Daily photosynthetic photon integral at leaf | I Ld | mol photons m−2 d−1 | — | Input |
| Mean ILd during the last 4 d | I Ld4d | mol photons m−2 d−1 | — | Input |
| Electron transport rate | J | μmol e− m−2 s−1 | 12 | Output |
| Maximum electron transport rate | J max | μmol e− m−2 s−1 | 2b | Output |
| Leaf area | LA | m2 | — | Input |
| Total leaf photosynthetic N content in the canopy | N canopy | mmol N | — | Output |
| Leaf photosynthetic N content | N leaf | mmol N | — | Output |
| Leaf photosynthetic N per unit area | N ph | mmol N m−2 | 1 | Output |
| N concentration of nutrient solution | N s | mM | — | Input |
| Concentration of N pool X | N X | mmol N m−2 | 4 | Output |
| Concentration of N pool of light harvesting | N C | mmol N m−2 | 4 | Output |
| Concentration of N pool of electron transport | N J | mmol N m−2 | 4 | Output |
| Concentration of N pool of carboxylation | N V | mmol N m−2 | 4 | Output |
| Partitioning fraction of N pool X | p X | — | 3 | Output |
| Daytime respiration rate in the absence of photorespiration | R d | μmol CO2 m−2 s−1 | 10 | Output |
| Reduction factor of protein synthesis depending on N availability | r N | — | 8 | Output |
| Maximum protein synthesis rate | S max | mmol N m−2 °Cd−1 | 7 | Output |
| Protein synthesis rate of N pool X | S X | mmol N m−2 °Cd−1 | 5 | Output |
| Leaf age | t | °Cd | — | Input |
| Carboxylation rate | V c | μmol CO2 m−2 s−1 | 11 | Output |
| Maximum carboxylation rate | V cmax | μmol CO2 m−2 s−1 | 2a | Output |
Table 3.
List of model coefficients
| Description | Coefficient | Unit | Value (SE) | Reference |
|---|---|---|---|---|
| Conversion coefficient of chlorophyll per light harvesting N | χC | mmol Chl mmol−1 N | 0.03384 | Buckley et al. (2013) |
| Conversion coefficient of chlorophyll per electron transport N | χCJ | mmol Chl mmol−1 N | 4.64 × 10–4 | Buckley et al. (2013) |
| Conversion coefficient of electron transport capacity per electron transport N | χJ | μmol e− mmol−1 N s−1 | 9.48 | Buckley et al. (2013) |
| Conversion coefficient of carboxylation capacity per Rubisco N | χV | μmol CO2 mmol−1 N s−1 | 4.49 | Buckley et al. (2013) |
| Minimum gsc | g 0 | mol CO2 m−2 s−1 | 0.009 | Chen et al. (2014) |
| Species-specific coefficient of gsc | g 1 | — | 3.51 | Chen et al. (2014) |
| CO2 compensation point in the absence of dark respiration | Γ* | μmol CO2 mol−1 | 43.02 | Singsaas et al. (2004) |
| Michaelis–Menten constant of Rubisco for CO2 | K c | μmol CO2 mol−1 | 404 | Chen et al. (2014) |
| Michaelis–Menten constant of Rubisco for O2 | K o | mmol O2 mol−1 | 278 | Chen et al. (2014) |
| O2 concentration at the site of carboxylation | O | mmol O2 mol−1 | 210 | Chen et al. (2014) |
| Coefficient relating Nph to gmmax | r gm | mol CO2 mmol−1 N s−1 | 1.64 × 10–3 (5.27 × 10–4) | — |
| Minimum gmmax | r gm0 | mol CO2 m−2 s−1 | 0.140 (0.0345) | — |
| Coefficient related to the decrease in Rd by growth respiration | R g | m2 d °Cd−1 mol−1 photon | 4.16 × 10–4 (4.52 × 10–5) | — |
| Coefficient related to the increase in Rd by maintenance respiration | R m | μmol CO2 d °Cd−1 mol−1 photons s−1 | 1.88 × 10–4 (1.61 × 10–5) | — |
| Coefficient relating ILd to maximum Rd | R max | μmol CO2 μmol−1 photons s−1 | 0.308 (0.028) | — |
| Conversion efficiency of photons to J | ϕ | µmol e– µmol−1 photons | 0.340 (2.5 × 10–3) | — |
| Convexity coefficient | θ | — | 0.7 | Chen et al. (2014) |
| Leaf age when gmmax occurs | t gm | °Cd | 121 (8.1) | — |
| Standard deviation of the dependence of gm–t curve | v gm | — | 0.860 (0.063) | — |
Standard errors (SE) are indicated in parentheses.
Growth chamber experiment to investigate the dynamics of photosynthetic protein turnover
Cucumber (Cucumis sativus ‘Aramon’, Rijk Zwaan, De Lier, The Netherlands) plants were grown in two experiments at the Institute of Horticultural Production Systems, Leibniz Universität Hannover, Germany (latitude 52.4°N).
One growth chamber experiment was conducted from 21 October to 9 December 2016 with factorial combinations of three light and three nitrogen supply levels to parameterize the photosynthetic protein turnover model (see below). Cucumber seeds were sown in rock-wool cubes (36 × 36 × 40 mm) on 5 October. Eight days later, seedlings were transplanted to larger rock-wool cubes (10 × 10 × 6.2 cm) for another 8 d until the second true leaves appeared (leaf length ≥3 cm). Plants were transferred into 25 litre plastic containers (one plant per container) on 21 October and cultivated hydroponically with a 12 h light period and 24 °C day/20 °C night air temperature. Three nitrogen levels, 9.6, 4.6 and 2.3 mM, were supplied using Ca(NO3)2 and Ferty Basisdünger 1 (Planta GmbH, Regenstauf, Germany, 5.2 mM K, 1.3 mM P, 0.82 mM Mg in working solution). Nutrient solution was replaced weekly and adjusted to pH 6.0–6.5 two times a week. Three constant light conditions with daily photosynthetic photon integrals (DPI) of 28.9, 14.2, and 4.4 mol photons m−2 d−1 were provided using metal halide lamps. Four plants were grown under each treatment combination. Three leaves per plant (between leaf ranks four to eight, counted acropetally) were maintained horizontally and well exposed to incoming light using custom-made leaf holders, while the rest of the shoot was trained downward to avoid mutual shading. Gas exchange (see below) and relative chlorophyll content (SPAD-502; Minolta Camera, Japan) were measured at different thermal ages of the leaves, ranging from 45 °Cd to 558 °Cd, calculated by subtracting a base temperature of 10 °C (Savvides et al., 2016) from mean daily air temperature around the leaf. Air temperature was recorded continuously using data loggers (Tinytag; Gemini Data Loggers, Chichester, UK). After gas exchange measurements, leaves were harvested for leaf area and nitrogen analyses.
Greenhouse experiment to evaluate optimality of nitrogen distribution and partitioning
One greenhouse experiment was carried out from 4 April to 12 May 2017 under two light regimes and two nitrogen supply levels to evaluate the model performance and to collect input data for optimality analyses. Seeds were sown on 14 March and transplanted to larger rock-wool cubes on 22 March. After the third true leaves had appeared, plants were transferred onto rock-wool slabs on 4 April with plant density of 1.33 plants m−2 and supplied with two nitrogen concentrations, 10 mM (high nitrogen, HN) and 2.5 mM (low nitrogen, LN), by drip irrigation using the same fertilizers as described in the growth chamber experiment. During the experimental period, average nitrogen supply was calculated from the nitrogen concentration in the nutrient supply and rock-wool slabs, which was 8.2 and 2.0 mM for HN and LN, respectively. Plants were grown under either high light (HL) or low light (LL) regimes. The southern half of the greenhouse was unshaded as the HL regime. The LL regime was created in the northern half of the greenhouse by shading nets to reduce incoming light from top and sides, where PPFD was reduced on average to ca. 40% of that under HL (38 ± 1.3% under sunny and 42 ± 0.2% under cloudy condition). Average DPI above the canopy was 21.4 and 8.5 mol photons m−2 d−1 for HL and LL, respectively, during the experimental period. DPI during the experimental period was recorded by the weather station located above the greenhouse. An average light transmittance of 49.8% through the greenhouse structure was applied (39.2% on a sunny day and 60.4% on a cloudy day). Air temperature in the middle canopy was recorded continuously using data loggers and was significantly higher under HL (0.5 °Cd per day). Gas exchange measurements and harvests were conducted at four time points on 21 April, 28 April, 5 May, and 12 May at two different canopy layers with two replications. Leaf age at measurement ranged from 77 to 414 °Cd. Leaf elevation angle was obtained by a 3D digitizer (Fastrak; Polhemus, Colchester, VT, USA) according to Chen et al. (2014). Leaves were harvested after gas exchange measurements to determine leaf area index (LAI, m2 m−2).
Gas exchange measurements and estimation of photosynthetic parameters
Light-saturated net photosynthetic rate under PPFD of 1300 µmol photons m−2 s−1 (A1300, μmol CO2 m−2 s−1) and light response curves were measured using a portable photosynthesis system (LI-6400XT; Li-Cor Inc., Lincoln, NE, USA). All measurements were carried out under sample CO2 400 µmol mol−1, leaf temperature 25 °C and relative humidity 55–65%. Rd was estimated from the linear portion of the light response curve (Kok, 1948). Vcmax was estimated using the one-point method (Wilson et al., 2000; De Kauwe et al., 2016), and Jmax and ϕ by least squares fitting to a non-rectangular hyperbola (Ögren and Evans, 1993). Mesophyll conductance was estimated using the variable J method (Harley et al., 1992). Chlorophyll fluorescence was measured using the multiphase flash approach (Loriaux et al., 2013) following Moualeu‐Ngangue et al. (2017).
Nitrogen analyses and photosynthetic nitrogen partitioning estimation
Leaf samples obtained in the growth chamber experiment were freeze-dried and ground into a fine powder for nitrogen analyses. Total leaf nitrogen was analysed using the Kjeldahl method (Nelson and Sommers, 1980). Leaf chlorophyll was extracted with 96% ethanol and analysed colorimetrically (Lichtenthaler, 1987). Relationships between relative chlorophyll content (SPAD) and Chl were determined (Supplementary Fig. S2) for estimating Chl in the greenhouse experiment.
Model parameterization
The differential equations (4)–(6) were solved and the coefficients were quantified using R (version 3.3.0; R Foundation for Statistical Computing, Vienna, Austria) by using the packages ‘deSolve’ and ‘DEoptim’, which minimizes the sums of squares of the residuals between observations and simulations. The data obtained in the growth chamber experiment were used for the parameterization. Dr,X and td,X were first quantified for each pool using data of all treatments. With the determined values of Dr,X and td,X, Smax,X was then quantified for each treatment. Smm,X, kI,X, and kN,X were determined from Smax,X [Eqs (7) and (8)] by least squares fitting in SigmaPlot (version 11.0, Systat software GmbH, Erkrath, Germany) as well as the influences of t and ILd on Rd [Eq. (10)] and gm [Eqs (16) and (17)].
Dynamic leaf photosynthetic nitrogen simulation and model evaluation
Daily environmental information during the experimental period (Supplementary Fig. S3) and the canopy information obtained at the four harvests, including age and area of each leaf, were used as input to simulate photosynthetic nitrogen per unit leaf area (Nph, mmol N m−2), photosynthetic nitrogen per leaf (Nleaf, mmol N) and total leaf photosynthetic nitrogen content of the canopy (Ncanopy, mmol N). First, leaf elevation angle of each leaf and LAI were simulated empirically depending on t (Supplementary Fig. S4). Second, for each time step, the daily light interception ILd at the leaf was calculated and used in Eq. (7) to simulate protein turnover. Light interception was calculated by the Beer–Lambert law (Monsi and Saeki, 1953) with a light extinction coefficient of 0.695 and adjusted by the cosine of leaf elevation angle. For model evaluation, root mean squared deviation (RMSD) and accuracy (%) were determined for photosynthetic parameters, Nph, and pX predictions following Kahlen and Stützel (2011).
Simulating daily canopy carbon assimilation
Daily canopy carbon assimilation during daytime (DCA, mol CO2 d−1) was simulated using greenhouse canopy characteristics obtained at the last harvest as input (Supplementary Table S1; Supplementary Fig. S5). Leaf-to-air vapor pressure deficit (D) 1.2 kPa and Ca 400 μmol CO2 mol−1 were used in all simulations, similar to the environmental conditions during the gas exchange measurements. Scenarios with different DPI levels were defined for simulating DCA. Up to six DPI levels were taken as relative to the average DPI during acclimation (aDPI) to simulate the influence of day-to-day DPI fluctuation on DCA. To simulate DCA, diurnal PPFD above the canopy was simulated for a given DPI level with a time step of 0.1 h by a simple cosine bell function (Kimball and Bellamy, 1986) with 14.4 h day length.
Modifying photosynthetic nitrogen distribution and partitioning
To evaluate the effects of between-leaf distribution and within-leaf partitioning of Nph on DCA, a distribution factor fd was introduced into Eq. (5) to create variations in the rate of protein synthesis, and a partitioning factor fp,X was introduced into Eq. (7) to create variations in the maximum protein synthesis rate of different functional pools:
| (18) |
| (19) |
A control condition was defined with fd=1 and fp,X=1, when all coefficients in the synthesis process (Table 1) remained unmodified. Increasing fd accelerates the decrease in the rate of protein synthesis and enhances acropetal Nph reallocation. An increase in fp,X results in a higher rate of synthesis of NX and increases the partitioning to pool X. A modified partitioning pattern that maximized DCA was identified as optimal for several DPI levels, and the optimal values of fp,X were determined using the package ‘DEoptim’ in R. The change in DCA caused by modified distribution or optimal partitioning of Nph was compared with the control conditions. The ratios between optimal and control partitioning fractions of each pool X, as well as the contributions of daily leaf carbon assimilation (DLA) to the DCA increase were calculated along the canopy depth.
Results
Mechanistic model aims to quantify the environmental effects of light and nitrogen availabilities and developmental effects on photosynthetic protein turnover
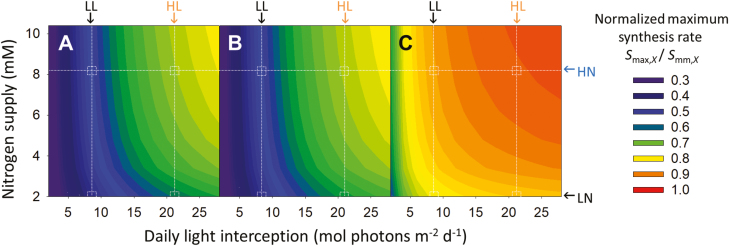
In the model, we assume that photosynthetic protein turnover is under genetic and environmental control. The genetic control is characterized by the potential maximum protein synthesis rate Smm, coefficient td, and protein degradation constant, Dr. The coefficient td affects the decrease in the rate of synthesis, and Dr contributes to the degradation rate, which together influence the developmental effect on protein turnover dynamics. The low value of td (0.001–0.002 °Cd−1, Table 1) suggests that the influence of ageing appears rather late in the leaf lifespan under a constant light environment. The coefficient Dr was found to be the same for the carboxylation pool (NV) and the electron transport pool (NJ), while the light harvesting pool (NC) had a lower Dr (Table 1). The genotypic sensitivities to light and nitrogen availabilities are characterized by kI and kN, respectively. Collectively, Smm, kI, and kN determine the maximum protein synthesis rate Smax in Eq. (7). When light was increased 2.5-fold (from LL to HL), Smax increased by 50% in NV and NJ, and by 10% in NC, while nitrogen level had less influence on Smax (<10%), which only occurred under low nitrogen concentration (<3.5 mM) and the higher light intensity (Fig. 1), showing that light had a major control of Smax. NC had the highest kI (Table 1); consequently, Smax,C approached saturation at lower light intensity than Smax,V and Smax,J (Fig. 1). Smax,V and Smax,J were well coordinated in response to light and nitrogen level (Fig. 1A, B), but the higher kI and kN of NV (Table 1) suggested that NV synthesis is more sensitive to the variation in light and nitrogen availabilities than NJ.
Fig. 1.
Simulated effects of daily light interception (ILd, mol photons m−2 d−1) and nitrogen supply level in the nutrient solution (NS, mM) on maximum protein synthesis rate (Smax,X) in Eq. (7) using coefficients from Table 1, of (A) the carboxylation, (B) the electron transport and (C) the light harvesting pools. The colors denote the normalized maximum protein synthesis rate, which is Smax,X normalized by the potential maximum protein synthesis rate (Smm,X) in Eq. (7). The data obtained in the growth chamber experiment were used for the parameterization. The arrows above and beside the figures indicate the corresponding average environmental conditions in the greenhouse experiment: high light (HL) 21.4 mol photons m−2 d−1; low light (LL) 8.5 mol photons m−2 d−1; high nitrogen (HN) 8.2 mM; low nitrogen (LN) 2.0 mM.
Effects of light and nitrogen availabilities on maximal protein synthesis rate explain the dynamics of photosynthetic acclimation
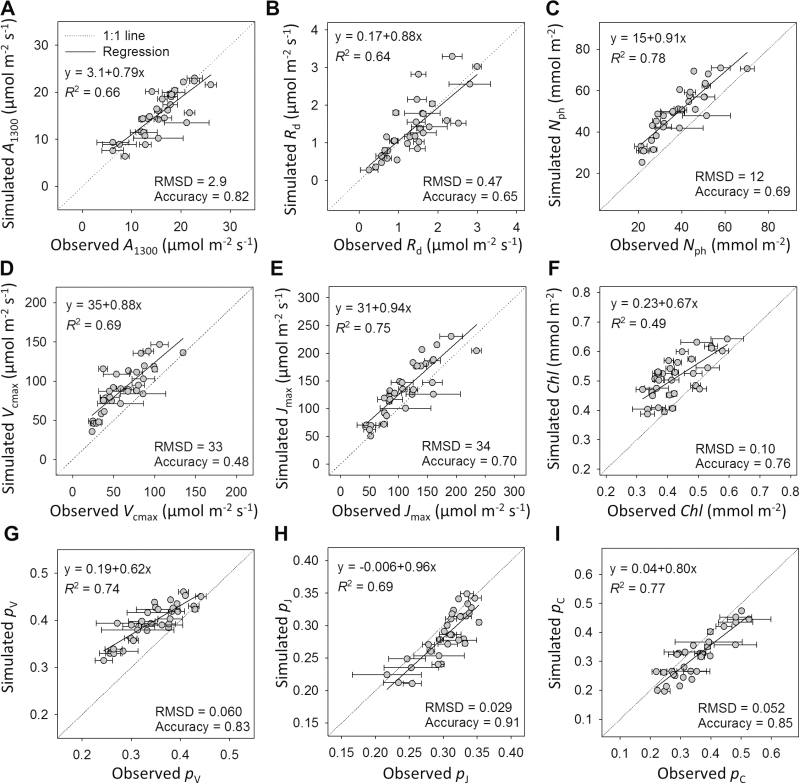
We evaluated the model using a greenhouse experiment, where leaves grown under combinations of two light regimes (HL and LL) and two nitrogen levels (HN and LN) were measured in two canopy layers weekly for four consecutive weeks. The model predicted leaf photosynthetic characteristics with high accuracy (70–91%, Fig. 2) and a trend of photosynthetic acclimation (Supplementary Fig. S6) similar to the experimental observations (Fig. 3), except for slight overestimations in photosynthetic nitrogen (Nph, Fig. 2C), carboxylation pool (Fig. 2D, G), and chlorophyll (Fig. 2F).
Fig. 2.
Comparisons between simulated and observed leaf photosynthetic parameters. (A) Light-saturated net photosynthetic rate under PPFD 1300 µmol photons m−2 s−1 (A1300, µmol CO2 m−2 s−1); (B) daytime respiration rate (Rd, µmol CO2 m−2 s−1); (C) leaf photosynthetic nitrogen (Nph, mmol N m−2); (D) maximum carboxylation rate (Vcmax, µmol CO2 m−2 s−1); (E) maximum electron transport rate (Jmax, µmol e− m−2 s−1); (F) chlorophyll (Chl, mmol Chl m−2); (G) partitioning fraction of the carboxylation pool (pV); (H) partitioning fraction of the electron transport pool (pJ); and (I) partitioning fraction of the light harvesting pool (pC). The observed data were obtained in the greenhouse experiment. The dotted grey lines are one-to-one lines. Root mean squared deviation (RMSD) and accuracy of the predictions are shown (see Materials and methods).
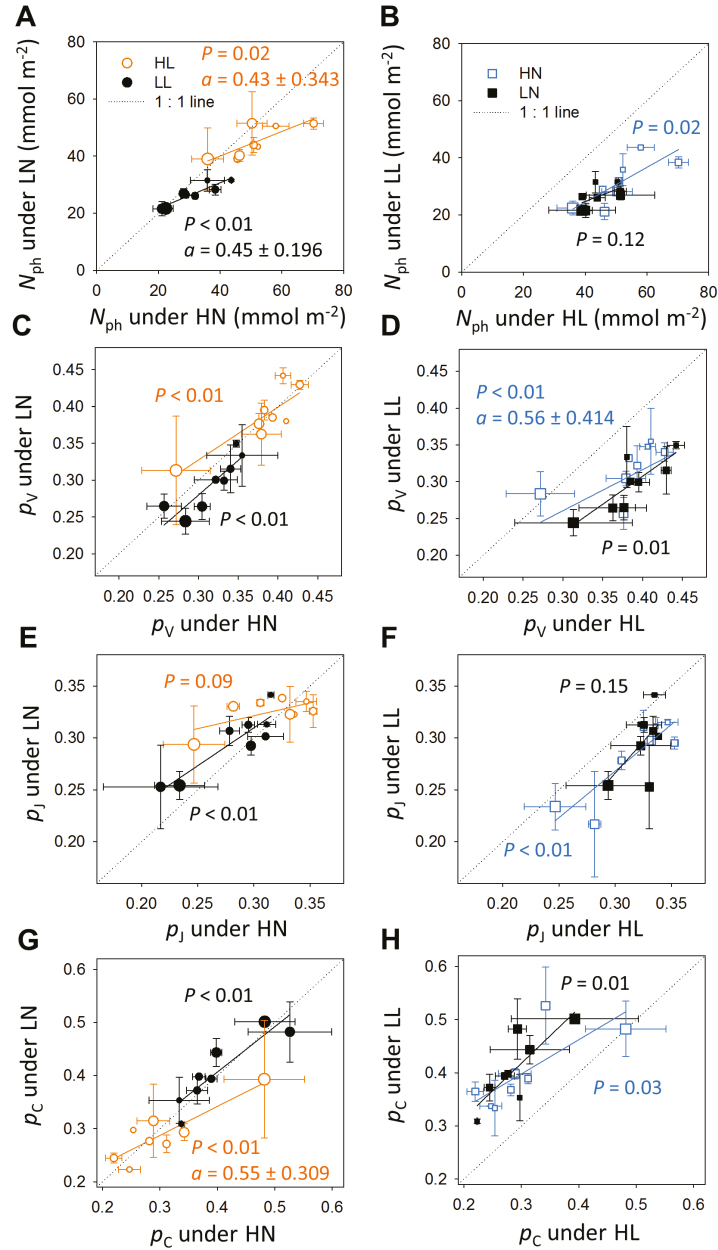
Fig. 3.
Comparisons of leaf photosynthetic nitrogen (Nph, mmol N m−2; A, B), partitioning fractions of the carboxylation pool (pV; C, D), the electron transport pool (pJ; E, F), and the light harvesting pool (pC; G, H) between high and low nitrogen supply (HN and LN, respectively; A, C, E, G) and between high and low light conditions (HL and LL, respectively; B, D, F, H). Each point represents the measurements in the greenhouse experiment obtained from a comparable canopy layer. The orange open circles indicate leaves grown under HL, the black closed circles indicate LL, the blue open squares indicate HN and the black closed squares indicate LN. The size of the circles increases with leaf age, ranging from 77 °Cd to 414 °Cd. The solid lines show the linear regression y=ax + b. The P values of the slope a are shown. The values of a are specified with 95% confidence intervals when they are significantly different from 1. The dotted grey lines are one-to-one lines.
Photosynthetic acclimation in the greenhouse canopies as influenced by the interplay between light, nitrogen level and leaf age was examined (Fig. 3). Light had positive effects on Nph (Fig. 3A), the partitioning fractions of NV (pV, Fig. 3C) and NJ (pJ, Fig. 3E) but negative effects on the partitioning fraction of NC (pC, Fig. 3G). This negative effect of light on pC can be explained by the high kI of NC (Table 1), which leads to an saturation of Smax,C under lower light (Fig. 1). The changes in Nph, pV, pJ, and pC with leaf age were similar to those with light (Fig. 3) due to the association in the gradients of age and light.
In comparison with HN, Nph under LN was significantly lower in the young leaves but similar in the old leaves (Fig. 3A). In the greenhouse, young leaves developed under high light intensity, which increased the sensitivity of Smax to nitrogen level (Fig. 1). During the simultaneous increase in leaf age and mutual shading, the effects of nitrogen supply on Smax became less prevalent (Fig. 1). Nitrogen level had less influence on functional partitioning (Fig. 3C, E, G) than light (Fig. 3D, F, H).
Photosynthetic nitrogen distribution is close to optimum and the effect of nitrogen reallocation is more prominent under limited nitrogen availability
The influence of Nph distribution pattern along the canopy depth on daily canopy carbon assimilation (DCA, mol CO2 d−1) was evaluated by introducing a distribution factor fd to create variations in the rate of protein synthesis. In our model, protein synthesis and degradation rates determined simultaneously (i) total leaf photosynthetic nitrogen content of the canopy (Ncanopy, mmol N), (ii) Nph distribution in the canopy, and (iii) Nph partitioning fractions of pools X (pX) in the leaf. Thus, it was impossible to modify single elements while maintaining the other two constant. Increasing fd led to a faster reduction of Nph during leaf ageing and more acropetal Nph reallocation. However, it also reduced Ncanopy and tended to increase pC (data not shown). Therefore, to obtain the leaf photosynthetic nitrogen content (Nleaf,i, mmol N in leaf i) with comparable Ncanopy, simulated Nleaf,i with fd=n (denoted as N′leaf,i) was adjusted proportionally to the ratio between Ncanopy calculated with fd=1 and with fd=n:
| (20a) |
p X,i was set equal to the control value:
| (20b) |
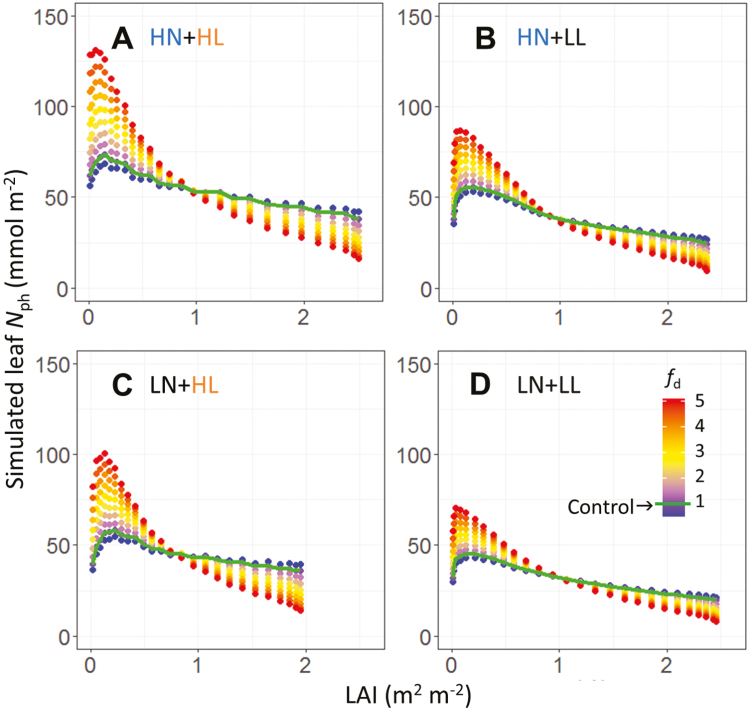
These adjustments assured the same amount of Ncanopy among the distribution patterns. The factor fd was varied between 0.5 and 5.0 at intervals of 0.5 in the simulation, which gave values of Nph comparable to those measured in cucumber leaves (22–135 mmol N m−2; Fig. 4). Canopy Nph distributions with enhanced acropetal reallocation were created by increasing fd (Fig. 4; Supplementary Fig. S7). In general, the distribution of Nph corresponded to the vertical light distribution except in the expanding leaves in the upper canopy, and the Nph distribution with light was steeper under LL (Supplementary Fig. S7).
Fig. 4.
Leaf photosynthetic nitrogen (Nph, mmol N m−2) distributions along the canopy depth, characterized by leaf area index (LAI, m2 m−2). Variations in nitrogen distribution were created using a distribution factor fd ranging from 0.5 to 5.0 at intervals of 0.5 in Eq. (18) under different growth conditions. (A) High nitrogen and high light (HN+HL); (B) high nitrogen and low light (HN+LL); (C) low nitrogen and high light (LN+HL); (D) low nitrogen and low light (LN+LL). Simulated control Nph distributions (fd=1) are indicated by the green lines.
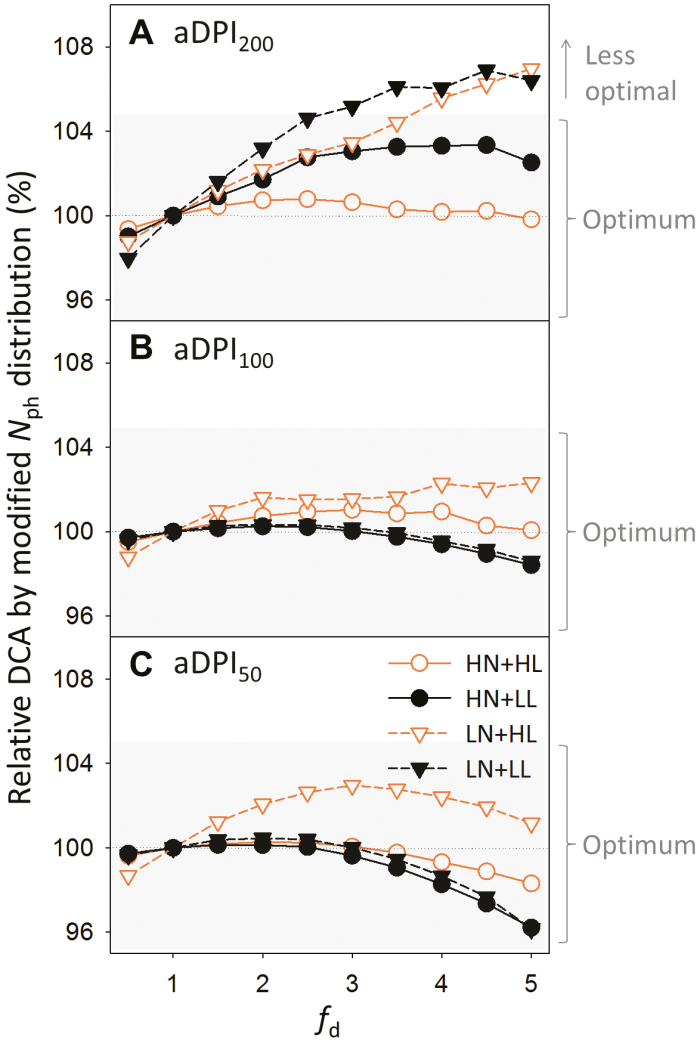
To simulate the natural fluctuations in light between days, three light levels representing 200% (aDPI200), 100% (aDPI100) and 50% (aDPI50) of average DPI during acclimation (aDPI) were used in the DCA simulation. Under aDPI100 and aDPI50, enhancing acropetal Nph reallocation did not significantly increase DCA (<5%), suggesting that Nph distribution was optimal under constant and decreasing DPI (Fig. 5B, C). More acropetal reallocation did not improve the optimality in Nph distribution in terms of maximizing DCA since a large proportion of leaf area was located in the middle-lower to lower canopy (Supplementary Fig. S5). However, enhancing Nph reallocation resulted in an increase in DCA by 7% under LN at aDPI200 (Fig. 5A), indicating that acropetal Nph reallocation was more important under LN than HN.
Fig. 5.
Effects of photosynthetic nitrogen (Nph) distributions with different values of fd (Fig. 4) on daily canopy carbon assimilation (DCA) under different daily photosynthetic photon integrals (DPI, mol photons m−2 d−1) relative to average DPI during acclimation (aDPI). (A) Two-fold aDPI (aDPI200); (B) aDPI (aDPI100); (C) half aDPI (aDPI200). Acropetal Nph reallocation increases with fd. Plants grown under high nitrogen and high light (HN+HL, orange open circles), under high nitrogen and low light (HN+LL, black closed circles), under low nitrogen and high light (LN+HL, orange open triangles), and under low nitrogen and low light (LN+LL, black closed triangles) are compared under given DPI. The relative change in DCA was calculated by dividing the DCA obtained with a given Nph distribution by the DCA obtained with the control Nph distribution (fd=1) under same DPI. A change within ±5% (grey shading) is considered insignificant.
It was observed that Nph was more overestimated in the older leaves than in the younger ones (Fig. 2C), which indicated that our model tended to underestimate the acropetal Nph reallocation when scaling up from leaf to canopy level. In order to maintain a constant light environment for the measured leaves in the growth chamber experiment, leaves younger than the sampled leaves were trained downward and their light interception, together with their nitrogen demand, was inevitably reduced; therefore, the model coefficients were obtained from the leaves with limited nitrogen reallocation. However, underestimating acropetal Nph reallocation would not affect our result that Nph distribution was close to optimum.
Suboptimal nitrogen partitioning is due to daily light fluctuation
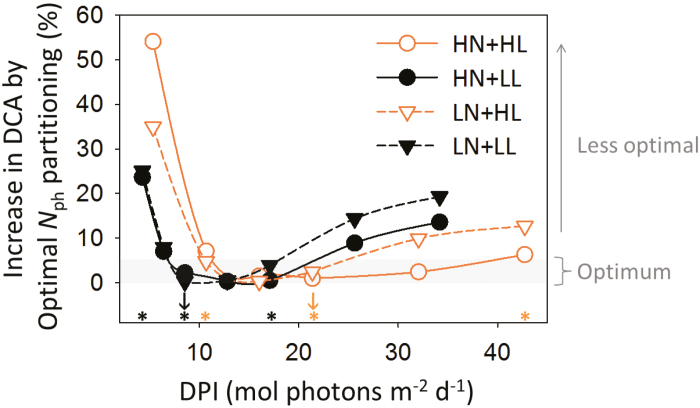
To find the optimal within-leaf Nph partitioning between functions, the potential maximal protein synthesis rate for pool X was modified by a factor fp,X, ranging from 0.2 to 2.0. Increasing fp,X resulted in higher protein synthesis rates, but it also increased Ncanopy and the proportion of nitrogen distributed in the upper canopy. After simulating nitrogen partitioning with a modified fp,X, Nleaf of each leaf was re-assigned to their control values that were obtained with fp,X=1. Partitioning patterns with maximal DCA at six DPI levels (25–400% aDPI) were identified as optimal and the maximal DCA was compared with control DCA (Fig. 6). The increase in DCA by optimal partitioning was insignificant (<5%) when DPI was close to aDPI (indicated by the arrows in Fig. 6). This suggested the ability of plants to maximize DCA by optimizing Nph partitioning to aDPI. Nph partitioning deviated further from optimum when DPI diverged from aDPI (Fig. 6). Therefore, strong day-to-day light fluctuation induced suboptimality in Nph partitioning and led to lower PNUE.
Fig. 6.
Increase in daily canopy carbon assimilation (DCA) by optimizing photosynthetic nitrogen (Nph) partitioning for different growth conditions under various daily photosynthetic photon integrals (DPI, mol photons m−2 d−1). The increase in DCA was the DCA with the optimal partitioning under a given DPI in comparison with the control partitioning [fp,X=1 in Eq. (19)]. An increase less than 5% (grey shading) is considered insignificant. The average DPI during acclimation (aDPI) is indicated by the orange arrow for HL (21.4 mol photons m−2 d−1) and by the black arrow for LL (8.5 mol photons m−2 d−1). The asterisks indicate the scenarios compared in Figs 7, 8 and Table 4 with 50%, 100% and 200% aDPI. The symbols and colors used here are the same as those in Fig. 5.
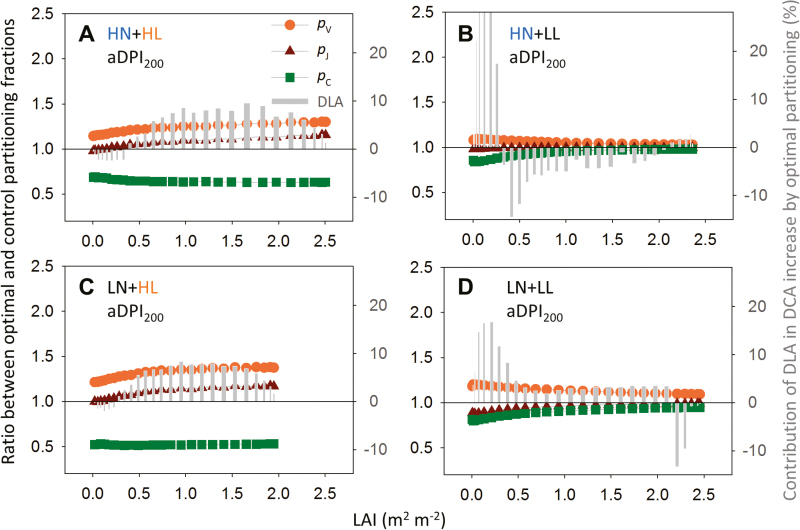
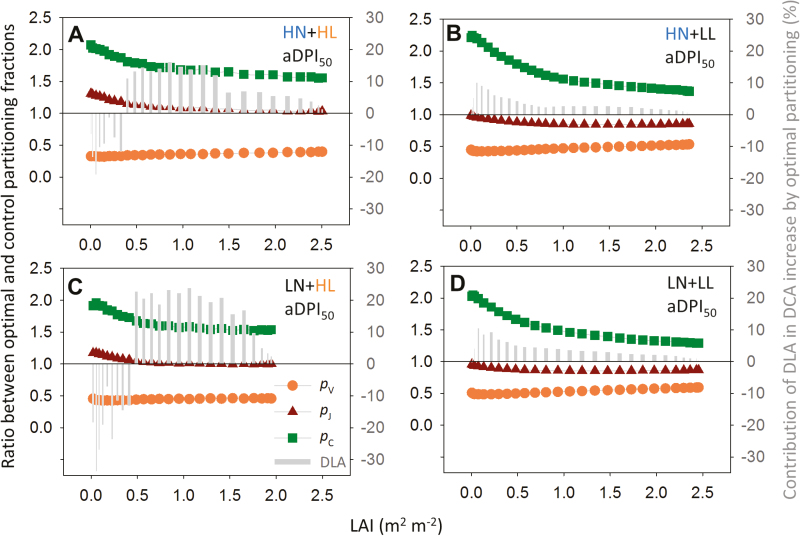
By optimizing Nph partitioning, DCA could be increased by nitrogen reinvestment in the limited functional pools. Under aDPI200, Nph partitioning was suboptimal under HL (Fig. 6), and this suboptimality was less under HN than under LN (Table 4). By reinvesting about half of NC into NV and NJ (Fig. 7A, C), DCA increased by 6% under HN and by 13% under LN (Table 4), as a result of increased carbon assimilation in the middle-lower canopy (Fig. 7A, C). Under aDPI50, HN did not reduce the suboptimality in Nph partitioning (Table 4) due to an underinvestment in the light harvesting function. Reinvesting NV into NC in the middle or upper canopy (HL, Fig. 8A; LL, 8B, 8D) increased DCA by 7–25% (Table 4).
Table 4.
Increase in the daily canopy carbon assimilation (DCA) by optimized photosynthetic nitrogen distribution or partitioning under various daily photosynthetic photon integrals (DPI, mol photons m−2 d−1) for canopies grown under different conditions
| Growth condition | Light level | Control DCA | Increase in DCA (%) by optimized | ||
|---|---|---|---|---|---|
| aDPI level (%) | DPI | (mol CO2 d−1) | Distribution | Partitioning | |
| HN+HL | 200 | 42.7 | 0.5467 | <5% | 6.3% |
| 100 | 21.4 | 0.3217 | <5% | <5% | |
| 50 | 10.7 | 0.1368 | <5% | 7.1% | |
| HN+LL | 200 | 17.1 | 0.2554 | <5% | <5% |
| 100 | 8.5 | 0.1195 | <5% | <5% | |
| 50 | 4.3 | 0.0259 | <5% | 23.6% | |
| LN+HL | 200 | 42.7 | 0.4011 | 7.0% | 12.7% |
| 100 | 21.4 | 0.2653 | <5% | <5% | |
| 50 | 10.7 | 0.1221 | <5% | <5% | |
| LN+LL | 200 | 17.1 | 0.2261 | 6.9% | <5% |
| 100 | 8.5 | 0.1108 | <5% | <5% | |
| 50 | 4.3 | 0.0215 | <5% | 25.0% |
Average DPI during acclimation (100% aDPI), 200% and 50% aDPI were tested. The increase in DCA for plants grown under the combinations of high nitrogen (HN), high light (HL), low nitrogen (LN), and low light (LL) was calculated by comparing the DCA between optimal and control distribution or partitioning.
Fig. 7.
Ratio between optimal and control partitioning fractions (optimal pX/control pX) of the carboxylation pool (pV, orange circles), the electron transport pool (pJ, red triangles), the light harvesting pool (pC, green squares), and contributions of daily leaf carbon assimilation (DLA) to the daily canopy carbon assimilation (DCA) increase by optimal partitioning (grey bars, right y-axis) along the canopy depth [leaf area index (LAI) m2 m−2] under 200% average daily photosynthetic photon integral during acclimation (aDPI200) for plants grown under (A) high nitrogen and high light (HN+HL), (B) high nitrogen and low light (HN+LL), (C) low nitrogen and high light (LN+HL), (D) low nitrogen and low light (LN+LL) conditions. Photosynthetic nitrogen partitioning is close to optimum for HN+LL and LN+LL under aDPI200, which corresponds to a DPI of 42.7 and 17.1 mol photons m−2 d−1 for HL and LL, respectively. See Table 4 for the increase in DCA by the optimal partitioning.
Fig. 8.
Ratio between optimal and control partitioning fractions (optimal pX/control pX), and contributions of daily leaf carbon assimilation (DLA) to the daily canopy carbon assimilation (DCA) increase by optimal partitioning (grey bars, right y-axis) along the canopy depth [leaf area index (LAI) m2 m−2] under 50% average daily photon integral during acclimation (aDPI50) for plants grown under (A) high nitrogen and high light (HN+HL), (B) high nitrogen and low light (HN+LL), (C) low nitrogen and high light (LN+HL), (D) low nitrogen and low light (LN+LL) conditions. Photosynthetic nitrogen partitioning is close to optimum for LN+HL under aDPI50, which corresponds to a DPI of 10.7 and 4.3 mol photons m−2 d−1 for HL and LL, respectively. The symbols and colors used here are the same as those in Fig. 7. See Table 4 for the increase in DCA by the optimal partitioning.
Discussion
This model is the first approach applying a dynamic protein turnover mechanism at the leaf level to assess the optimality and limitation in nitrogen use at the canopy level. Here, maximized canopy carbon assimilation is considered as a general indicator of maximizing fitness. The adaptation of the protein turnover mechanism gives reasonable predictions of optimal Nph and accurate predictions of leaf photosynthetic traits.
Mechanistic explanation of leaf nitrogen economics under a wide range of light and nitrogen availabilities
It is well documented that light has the major control of leaf economics. For example, specific leaf area, an integrative indicator of leaf structure that co-varies with leaf nitrogen content (Anten et al., 1998), shows more plastic responses to light than to nutrient availability (Poorter et al., 2009; Poorter et al., 2010). Mechanistic models can be used to interpret measured biological data (Chen et al., 2015, 2018), as in our model here, providing a quantitative explanation of the different plastic responses in leaf nitrogen economics (e.g. photosynthetic nitrogen per unit leaf area, Nph, and photosynthetic capacities) to light and to nitrogen by their effects on the maximum protein synthesis rate (Smax, Fig. 1). A 5-fold increase in light (4–20 mol photons m−2 d−1) doubled Smax of the carboxylation pool (NV) and electron transport pool (NJ; Fig. 1A, B), which is similar to the published values (Niinemets et al., 2015). In contrast, increasing nitrogen supply from 2 to 10 mM increased Smax of NV and NJ only by 20% and 16%, respectively. The effects of light on photosynthetic nitrogen can be quantitative (on Nph) or qualitative (on nitrogen partitioning, pX; Niinemets et al., 2006; Buckley et al., 2013), while nitrogen only affected Nph by restricting Smax (Figs 1, 3). Similar effects of light and nitrogen availabilities on the partitioning between electron transport and light harvesting functions were observed in spinach (Terashima and Evans, 1988). Our model of protein turnover explains the photosynthetic acclimation to light and nitrogen supply and provides a mechanistic insight into leaf nitrogen economics.
In a growing canopy, leaf age is associated with decreasing light availability (Niinemets et al., 2006, Chen et al., 2014). Therefore, leaf photosynthetic acclimation to light occurs together with leaf ageing, which is characterized by the protein degradation constant Dr and the constant td describing the decrease of protein synthesis rate in our model. The Dr values of NV and NJ fall within the range of in vivo quantifications reported by Peterson et al. (1973) and Li et al. (2017). The low value of td (Table 1) explains the modest influence of ageing on leaf photosynthetic capacity observed under constant light conditions (Pettersen et al., 2010a).
Besides light and nitrogen availability, temperature has effects on photosynthetic nitrogen content and partitioning (Yamori et al., 2005; Kattge and Knorr, 2007; Yamori et al., 2009). Temperature dependency of developmental processes and biochemical reactions is often described by exponential or Arhenius-type functions (Parent et al., 2010; Parent and Tardieu, 2012; Kahlen and Chen, 2015). In our model, temperature effects are considered partly by the temperature sum, which assumes a linear relationship between protein synthesis and leaf temperature. Since the exact temperature dependency of protein synthesis and degradation is unknown and our data are obtained from controlled environments with minimized temperature fluctuations, we apply the linear parsimonious approach to avoid speculation and overparameterization (Parent et al., 2016).
Above-optimum Rubisco investment can be a mechanism to adapt canopy photosynthesis to short-term light fluctuations
Under sufficient nitrogen availability, Rubisco can function as a storage protein, which means that the amount of Rubisco can exceed the requirements to support photosynthesis (Carmo-Silva et al., 2015). The Rubisco pool has the highest value of kN (Table 1), indicating that Rubisco synthesis reacts with higher sensitivity to increasing nitrogen availability than the other two pools. This explains the increase in the ratio between Vcmax and Jmax with nitrogen availability (Hikosaka, 2004; Yamori et al., 2011a), especially under LL (Fig. 3C, E). Under HN, Rubisco storage is advantageous since light-induced Rubisco activation, having a time constant of 3–5 min (Portis et al., 1986; Kaiser et al., 2018), is much faster than Rubisco synthesis. Therefore, Rubisco storage can be a mechanism for quick adaptation to a sudden increase in light. This explains why the plants grown under HN have wider ranges of DPI, at which nitrogen partitioning is optimal, than those under LN (Fig. 6; Table 4). Furthermore, excluding Rubisco activation [Vc=Vcmax in Eq. (9b)] in the DCA simulation resulted in a 4-fold above-optimum investment in NV even under aDPI (data not shown). Since Rubisco is not an especially inefficient catalyst in comparison with other chemically related enzymes (Bathellier et al., 2018), above-optimum Rubisco investment in the canopy can be rather a mechanism for adapting to short-term light fluctuation than a mechanism to overcome its enzymatic inefficiency.
Implications for crop model improvement and greenhouse management
Using plant models to understand crop performance requires knowledge of physiological mechanisms (Boote et al., 2013; Poorter et al., 2013). By integrating the known biological mechanism of protein turnover at the leaf level into a multi-layer model of canopy photosynthesis, we demonstrate the explanatory power of a mechanistic model for the measured biological data. Our simulations suggest that canopy photosynthesis can be increased by manipulating the functional pools related to photosynthesis. For example, investment in Rubisco and electron transport (Ishimaru et al., 2001; Yamori et al., 2011b) should be increased under increasing light (Fig. 7), and a larger antenna size for light harvesting (Masuda et al., 2003) is required under decreasing light availability (Fig. 8). It is clear that the pattern of optimal nitrogen partitioning depends strongly on light regime, and biosynthetic regulation is unlikely to keep up with daily light fluctuation (up to 4-fold difference; Supplementary Fig. S3).
In greenhouse cultivation, it is possible to achieve a more stable light environment using supplemental lighting. This can be a plausible solution to improve the vertical light distribution (Lu and Mitchell, 2016) and to minimize the suboptimality in nitrogen use induced by light fluctuation. Since carbon assimilation is the rate-limiting step for yield production of cucumber plants due to the indeterminate production of vegetative and generative organs (Wiechers et al., 2011), canopy carbon gain can be considered as an approximation for yield. Our simulation suggests that the suboptimal nitrogen partitioning induced by a 50% decrease in DPI can be compensated by reducing the light limitation of the shaded leaves using inter-row lighting during the high-light season (ca. 7% increase in DCA) and using top-lighting, possibly in combination with inter-lighting, during the low-light season (ca. 25% increase in DCA; Table 4; Fig. 8), similar to the reported increase in cucumber fruit yield (22%–31%) by inter-lighting in the winter season (Kumar et al., 2016). In the summer season, suboptimal nitrogen partitioning induced by sudden doubling in DPI can be overcome by pre-treatment of increasing nitrogen supply and inter-lighting (ca. 6% increase in DCA; Table 4), which maintains the biochemical capacity and reduces the biochemical limitation of the shaded leaves (Pettersen et al., 2010b; Trouwborst et al., 2010; Chen et al., 2014). These results provide a physiological explanation at canopy level for the observations of supplemental lighting experiments (Hovi et al., 2004; Hovi-Pekkanen and Tahvonen, 2008; Pettersen et al., 2010b; Trouwborst et al., 2010). Furthermore, the relationship between protein synthesis rate and intercepted light intensity is non-linear in our model [Eq. (7)], which may offer an explanation why the photoacclimatory responses of a leaf grown under natural within-day light fluctuation differ from that under constant light, as shown in a recent experimental study (Vialet-Chabrand et al., 2017).
Light fluctuations occur particularly in the lower canopy layer, where sunflecks cause strong and frequent variations in light, thereby increasing variations of Nph and pX in the older leaves (Fig. 3). Interestingly, leaves under HL seemed to prioritize their nitrogen investment in NJ over NC under LN with increasing leaf age (Fig. 3E), which might be explained by the reduced LAI development under LN+HL and, hence, the higher light interception of the older leaves (Figs S4C, S5). Since within-leaf and within-day light heterogeneity (e.g. sunflecks) were not described in the model, these variations observed in the greenhouse experiment could not be reproduced in the simulations (Supplementary Fig. S6). This can be improved by coupling the model with a 3D structural plant model and the use of shorter time steps in the simulations to capture more realistic response of photoacclimation.
Conclusions
We propose a mechanistic model to quantify the effects of leaf age, nitrogen and light availabilities on photosynthetic acclimation. The model predicts the observed photosynthetic acclimation under different combinations of nitrogen supply and light availability in the greenhouse. Model simulation indicates that photosynthetic nitrogen distribution is close to optimum and photosynthetic nitrogen partitioning can be optimal under constant light conditions. However, large fluctuation in light between days under natural conditions inevitably leads to suboptimal nitrogen partitioning. Our study provides insights into photosynthetic acclimation and the model can be used for crop model improvement and provides guidelines for greenhouse management.
Supplementary data
Supplementary data are available at JXB online.
Fig. S1. Schematic diagram of photosynthetic nitrogen turnover.
Fig. S2. Relationship between relative chlorophyll content and leaf chlorophyll concentration.
Fig. S3. Environmental input for the model evaluation and simulation.
Fig. S4. Relationships between leaf angle, LAI, and age.
Fig. S5. Leaf area distribution used as input in the daily canopy assimilation simulation.
Fig. S6. Comparisons of simulated photosynthetic nitrogen traits between nitrogen supply levels and between light conditions.
Fig. S7. Leaf photosynthetic nitrogen distributions with the vertical light distribution.
Table S1. Canopy characteristics used in the daily canopy assimilation simulation.
Acknowledgements
This work was supported by Deutsche Forschungsgemeinschaft (DFG). We thank Ilona Napp, Marlies Lehmann, Adjoa Sekyi-Appiah, Sanzida Akhter Anee and Felliesia Regina Halim for their assistance during the experiments.
Glossary
Abbreviations
- aDPI
average daily photosynthetic photon integral during acclimation
- Chl
chlorophyll per unit leaf area
- DCA
daily canopy carbon assimilation
- DPI
daily photosynthetic photon integral
- HL
high light
- HN
high nitrogen
- Jmax
maximum electron transport rate
- LL
low light
- LAI
leaf area index
- LN
low nitrogen
- NC
light harvesting pool of photosynthetic nitrogen
- NJ
electron transport pool of photosynthetic nitrogen
- Nph
photosynthetic nitrogen
- NV
carboxylation pool of photosynthetic nitrogen
- PNUE
photosynthetic nitrogen use efficiency
- PPFD
photosynthetic photon flux density
- Vcmax
maximum carboxylation rate
References
- Anten NP , Miyazawa K , Hikosaka K , Nagashima H , Hirose T. 1998. Leaf nitrogen distribution in relation to leaf age and photon flux density in dominant and subordinate plants in dense stands of a dicotyledonous herb. Oecologia 113, 314–324. [DOI] [PubMed] [Google Scholar]
- Anten NP , Schieving F , Werger MJ. 1995. Patterns of light and nitrogen distribution in relation to whole canopy carbon gain in C3 and C4 mono- and dicotyledonous species. Oecologia 101, 504–513. [DOI] [PubMed] [Google Scholar]
- Athanasiou K , Dyson BC , Webster RE , Johnson GN. 2010. Dynamic acclimation of photosynthesis increases plant fitness in changing environments. Plant Physiology 152, 366–373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bathellier C , Tcherkez G , Lorimer GH , Farquhar GD. 2018. Rubisco is not really so bad. Plant, Cell & Environment 41, 705–716. [DOI] [PubMed] [Google Scholar]
- Boote KJ , Jones JW , White JW , Asseng S , Lizaso JI. 2013. Putting mechanisms into crop production models. Plant, Cell & Environment 36, 1658–1672. [DOI] [PubMed] [Google Scholar]
- Buckley TN , Cescatti A , Farquhar GD. 2013. What does optimization theory actually predict about crown profiles of photosynthetic capacity when models incorporate greater realism? Plant, Cell & Environment 36, 1547–1563. [DOI] [PubMed] [Google Scholar]
- Carmo-Silva E , Scales JC , Madgwick PJ , Parry MA. 2015. Optimizing Rubisco and its regulation for greater resource use efficiency. Plant, Cell & Environment 38, 1817–1832. [DOI] [PubMed] [Google Scholar]
- Chen TW , Henke M , de Visser PH , Buck-Sorlin G , Wiechers D , Kahlen K , Stützel H. 2014. What is the most prominent factor limiting photosynthesis in different layers of a greenhouse cucumber canopy? Annals of Botany 114, 677–688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen TW , Nguyen TM , Kahlen K , Stützel H. 2015. High temperature and vapor pressure deficit aggravate architectural effects but ameliorate non-architectural effects of salinity on dry mass production of tomato. Frontiers in Plant Science 6, 887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen TW , Stützel H , Kahlen K. 2018. High light aggravates functional limitations of cucumber canopy photosynthesis under salinity. Annals of Botany 121, 797–807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Kauwe MG , Lin YS , Wright IJ , et al. 2016. A test of the ‘one-point method’ for estimating maximum carboxylation capacity from field-measured, light-saturated photosynthesis. New Phytologist 210, 1130–1144. [DOI] [PubMed] [Google Scholar]
- Dreccer MF , van Oijen M , Schapendonk AHCM , Pot CS , Rabbinge R. 2000. Dynamics of vertical leaf nitrogen distribution in a vegetative wheat canopy. Impact on canopy photosynthesis. Annals of Botany 86, 821–831. [Google Scholar]
- Evans JR. 1989. Partitioning of nitrogen between and within leaves grown under different irradiances. Functional Plant Biology 16, 533–548. [Google Scholar]
- Evans JR. 1993. Photosynthetic acclimation and nitrogen partitioning within a lucerne canopy. II. Stability through time and comparison with a theoretical optimum. Functional Plant Biology 20, 69–82. [Google Scholar]
- Falster DS , Westoby M. 2003. Leaf size and angle vary widely across species: what consequences for light interception? New Phytologist 158, 509–525. [DOI] [PubMed] [Google Scholar]
- Farquhar GD , von Caemmerer S , Berry JA. 1980. A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species. Planta 149, 78–90. [DOI] [PubMed] [Google Scholar]
- Field C. 1983. Allocating leaf nitrogen for the maximization of carbon gain: Leaf age as a control on the allocation program. Oecologia 56, 341–347. [DOI] [PubMed] [Google Scholar]
- Flexas J , Ribas-Carbó M , Diaz-Espejo A , Galmés J , Medrano H. 2008. Mesophyll conductance to CO2: current knowledge and future prospects. Plant, Cell & Environment 31, 602–621. [DOI] [PubMed] [Google Scholar]
- Harley PC , Loreto F , Di Marco G , Sharkey TD. 1992. Theoretical considerations when estimating the mesophyll conductance to CO2 flux by analysis of the response of photosynthesis to CO2. Plant Physiology 98, 1429–1436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hikosaka K. 2004. Interspecific difference in the photosynthesis-nitrogen relationship: patterns, physiological causes, and ecological importance. Journal of Plant Research 117, 481–494. [DOI] [PubMed] [Google Scholar]
- Hikosaka K. 2005. Nitrogen partitioning in the photosynthetic apparatus of Plantago asiatica leaves grown under different temperature and light conditions: similarities and differences between temperature and light acclimation. Plant & Cell Physiology 46, 1283–1290. [DOI] [PubMed] [Google Scholar]
- Hikosaka K. 2014. Optimal nitrogen distribution within a leaf canopy under direct and diffuse light. Plant, Cell & Environment 37, 2077–2085. [DOI] [PubMed] [Google Scholar]
- Hikosaka K. 2016. Optimality of nitrogen distribution among leaves in plant canopies. Journal of Plant Research 129, 299–311. [DOI] [PubMed] [Google Scholar]
- Hikosaka K , Anten NP , Borjigidai A , et al. 2016. A meta-analysis of leaf nitrogen distribution within plant canopies. Annals of Botany 118, 239–247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hikosaka K , Terashima I. 1996. Nitrogen partitioning among photosynthetic components and its consequence in sun and shade plants. Functional Ecology 335–343. [Google Scholar]
- Hirose T , Ackerly DD , Traw MB , Ramseier D , Bazzaz FA. 1997. CO2 elevation, canopy photosynthesis, and optimal leaf area index. Ecology 78, 2339–2350. [Google Scholar]
- Hirose T , Werger MJ. 1987. Maximizing daily canopy photosynthesis with respect to the leaf nitrogen allocation pattern in the canopy. Oecologia 72, 520–526. [DOI] [PubMed] [Google Scholar]
- Hollinger DY. 1996. Optimality and nitrogen allocation in a tree canopy. Tree Physiology 16, 627–634. [DOI] [PubMed] [Google Scholar]
- Hovi T , Näkkilä J , Tahvonen R. 2004. Interlighting improves production of year-round cucumber. Scientia Horticulturae 102, 283–294. [Google Scholar]
- Hovi-Pekkanen T , Tahvonen R. 2008. Effects of interlighting on yield and external fruit quality in year-round cultivated cucumber. Scientia Horticulturae 116, 152–161. [Google Scholar]
- Irving LJ , Robinson D. 2006. A dynamic model of Rubisco turnover in cereal leaves. New Phytologist 169, 493–504. [DOI] [PubMed] [Google Scholar]
- Ishimaru K , Kobayashi N , Ono K , Yano M , Ohsugi R. 2001. Are contents of Rubisco, soluble protein and nitrogen in flag leaves of rice controlled by the same genetics? Journal of Experimental Botany 52, 1827–1833. [DOI] [PubMed] [Google Scholar]
- Kahlen K , Chen TW. 2015. Predicting plant performance under simultaneously changing environmental conditions—The interplay between temperature, light, and internode growth. Frontiers in Plant Science 6, 1130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kahlen K , Stützel H. 2011. Modelling photo-modulated internode elongation in growing glasshouse cucumber canopies. New Phytologist 190, 697–708. [DOI] [PubMed] [Google Scholar]
- Kaiser E , Morales A , Harbinson J. 2018. Fluctuating light takes crop photosynthesis on a rollercoaster ride. Plant Physiology 176, 977–989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kattge J , Knorr W. 2007. Temperature acclimation in a biochemical model of photosynthesis: a reanalysis of data from 36 species. Plant, Cell & Environment 30, 1176–1190. [DOI] [PubMed] [Google Scholar]
- Kimball BA , Bellamy LA. 1986. Generation of diurnal solar radiation, temperature, and humidity patterns. Energy in Agriculture 5, 185–197. [Google Scholar]
- Kitao M , Kitaoka S , Harayama H , Tobita H , Agathokleous E , Utsugi H. 2018. Canopy nitrogen distribution is optimized to prevent photoinhibition throughout the canopy during sun flecks. Scientific Reports 8, 503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kok B. 1948. A critical consideration of the quantum yield of Chlorella photosynthesis. Enzymologia 13, 1–56. [Google Scholar]
- Kumar K , Hao X , Khosla S , Guo X , Bennett N. 2016. Comparison of HPS lighting and hybrid lighting with top HPS and intra-canopy LED lighting for high-wire mini-cucumber production. Acta Horticulturae 1134, 111–118. [Google Scholar]
- Li L , Nelson CJ , Trösch J , Castleden I , Huang S , Millar AH. 2017. Protein degradation rate in Arabidopsis thaliana leaf growth and development. The Plant Cell 29, 207–228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lichtenthaler HK. 1987. Chlorophylls and carotenoids: pigments of photosynthetic biomembranes. Methods in Enzymology 148, 350–383. [Google Scholar]
- Loriaux SD , Avenson TJ , Welles JM , McDermitt DK , Eckles RD , Riensche B , Genty B. 2013. Closing in on maximum yield of chlorophyll fluorescence using a single multiphase flash of sub-saturating intensity. Plant, Cell & Environment 36, 1755–1770. [DOI] [PubMed] [Google Scholar]
- Lu N , Mitchell CA. 2016. Supplemental lighting for greenhouse-grown fruiting vegetables. In: Kozai T, Fujiwara K, Runkle ES, eds. LED lighting for urban agriculture. Singapore: Springer, 219–232. [Google Scholar]
- Masuda T , Tanaka A , Melis A. 2003. Chlorophyll antenna size adjustments by irradiance in Dunaliella salina involve coordinate regulation of chlorophyll a oxygenase (CAO) and Lhcb gene expression. Plant Molecular Biology 51, 757–771. [DOI] [PubMed] [Google Scholar]
- Medlyn BE , Duursma RA , Eamus D , Ellsworth DS , Prentice IC , Barton CVM , Crous KY , De Angelis P , Freeman M , Wingate L. 2011. Reconciling the optimal and empirical approaches to modelling stomatal conductance. Global Change Biology 17, 2134–2144. [Google Scholar]
- Meir P , Kruijt B , Broadmeadow M , Barbosa E , Kull O , Carswell F , Nobre A , Jarvis PG. 2002. Acclimation of photosynthetic capacity to irradiance in tree canopies in relation to leaf nitrogen concentration and leaf mass per unit area. Plant, Cell & Environment 25, 343–357. [Google Scholar]
- Monsi M , Saeki T. 1953. Über den Lichtfaktor in den Pflanzengesellschaften und seine Bedeutung für die Stoffproduktion. Japanese Journal of Botany 14, 22–52. [Republished in English: Monsi M, Saeki T. 2005. On the factor light in plant communities and its importance for matter production. Annals of Botany 95, 549–567.] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moreau D , Allard V , Gaju O , Le Gouis J , Foulkes MJ , Martre P. 2012. Acclimation of leaf nitrogen to vertical light gradient at anthesis in wheat is a whole-plant process that scales with the size of the canopy. Plant Physiology 160, 1479–1490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moualeu-Ngangue DP , Chen TW , Stützel H. 2016. A modeling approach to quantify the effects of stomatal behavior and mesophyll conductance on leaf water use efficiency. Frontiers in Plant Science 7, 875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moualeu‐Ngangue DP , Chen TW , Stützel H. 2017. A new method to estimate photosynthetic parameters through net assimilation rate−intercellular space CO2 concentration (A−Ci) curve and chlorophyll fluorescence measurements. New Phytologist 213, 1543–1554. [DOI] [PubMed] [Google Scholar]
- Nelson DW , Sommers LE. 1980. Total nitrogen analysis of soil and plant tissues. Journal of the Association of Official Analytical Chemists 63, 770–778. [Google Scholar]
- Niinemets Ü. 2016. Leaf age dependent changes in within-canopy variation in leaf functional traits: a meta-analysis. Journal of Plant Research 129, 313–338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niinemets U , Cescatti A , Rodeghiero M , Tosens T. 2006. Complex adjustments of photosynthetic potentials and internal diffusion conductance to current and previous light availabilities and leaf age in Mediterranean evergreen species Quercus ilex. Plant, Cell & Environment 29, 1159–1178. [DOI] [PubMed] [Google Scholar]
- Niinemets Ü , Keenan TF , Hallik L. 2015. A worldwide analysis of within-canopy variations in leaf structural, chemical and physiological traits across plant functional types. New Phytologist 205, 973–993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ögren E , Evans JR. 1993. Photosynthetic light-response curves. Planta 189, 182–190. [Google Scholar]
- Parent B , Tardieu F. 2012. Temperature responses of developmental processes have not been affected by breeding in different ecological areas for 17 crop species. New Phytologist 194, 760–774. [DOI] [PubMed] [Google Scholar]
- Parent B , Turc O , Gibon Y , Stitt M , Tardieu F. 2010. Modelling temperature-compensated physiological rates, based on the co-ordination of responses to temperature of developmental processes. Journal of Experimental Botany 61, 2057–2069. [DOI] [PubMed] [Google Scholar]
- Parent B , Vile D , Violle C , Tardieu F. 2016. Towards parsimonious ecophysiological models that bridge ecology and agronomy. New Phytologist 210, 380–382. [DOI] [PubMed] [Google Scholar]
- Peterson LW , Kleinkopf GE , Huffaker RC. 1973. Evidence for lack of turnover of ribulose 1,5-diphosphate carboxylase in barley leaves. Plant Physiology 51, 1042–1045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pettersen RI , Torre S , Gislerød HR. 2010. a Effects of leaf aging and light duration on photosynthetic characteristics in a cucumber canopy. Scientia Horticulturae 125, 82–87. [Google Scholar]
- Pettersen RI , Torre S , Gislerød HR. 2010. b Effects of intracanopy lighting on photosynthetic characteristics in cucumber. Scientia Horticulturae 125, 77–81. [Google Scholar]
- Pons TL , Anten NP. 2004. Is plasticity in partitioning of photosynthetic resources between and within leaves important for whole‐plant carbon gain in canopies? Functional Ecology 18, 802–811. [Google Scholar]
- Poorter H , Anten NP , Marcelis LF. 2013. Physiological mechanisms in plant growth models: do we need a supra-cellular systems biology approach? Plant, Cell & Environment 36, 1673–1690. [DOI] [PubMed] [Google Scholar]
- Poorter H , Niinemets U , Poorter L , Wright IJ , Villar R. 2009. Causes and consequences of variation in leaf mass per area (LMA): a meta-analysis. New Phytologist 182, 565–588. [DOI] [PubMed] [Google Scholar]
- Poorter H , Niinemets U , Walter A , Fiorani F , Schurr U. 2010. A method to construct dose–response curves for a wide range of environmental factors and plant traits by means of a meta-analysis of phenotypic data. Journal of Experimental Botany 61, 2043–2055. [DOI] [PubMed] [Google Scholar]
- Portis AR , Salvucci ME , Ogren WL. 1986. Activation of ribulosebisphosphate carboxylase/oxygenase at physiological CO2 and ribulosebisphosphate concentrations by rubisco activase. Plant Physiology 82, 967–971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prieto JA , Louarn G , Perez Peña J , Ojeda H , Simonneau T , Lebon E. 2012. A leaf gas exchange model that accounts for intra-canopy variability by considering leaf nitrogen content and local acclimation to radiation in grapevine (Vitis vinifera L.). Plant, Cell & Environment 35, 1313–1328. [DOI] [PubMed] [Google Scholar]
- Qian T , Elings A , Dieleman JA , Gort G , Marcelis LF. 2012. Estimation of photosynthesis parameters for a modified Farquhar-von Caemmerer-Berry model using simultaneous estimation method and nonlinear mixed effects model. Environmental and Experimental Botany 82, 66–73. [Google Scholar]
- Retkute R , Smith-Unna SE , Smith RW , Burgess AJ , Jensen OE , Johnson GN , Preston SP , Murchie EH. 2015. Exploiting heterogeneous environments: does photosynthetic acclimation optimize carbon gain in fluctuating light? Journal of Experimental Botany 66, 2437–2447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Savvides A , Dieleman JA , van Ieperen W , Marcelis LF. 2016. A unique approach to demonstrating that apical bud temperature specifically determines leaf initiation rate in the dicot Cucumis sativus. Planta 243, 1071–1079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singsaas EL , Ort DR , Delucia EH. 2004. Elevated CO2 effects on mesophyll conductance and its consequences for interpreting photosynthetic physiology. Plant, Cell & Environment 27, 41–50. [Google Scholar]
- Song Q , Wang Y , Qu M , Ort DR , Zhu XG. 2017. The impact of modifying photosystem antenna size on canopy photosynthetic efficiency—Development of a new canopy photosynthesis model scaling from metabolism to canopy level processes. Plant, Cell & Environment 40, 2946–2957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suzuki Y , Makino A , Mae T. 2001. Changes in the turnover of Rubisco and levels of mRNAs of rbcL and rbcS in rice leaves from emergence to senescence. Plant, Cell & Environment 24, 1353–1360. [Google Scholar]
- Terashima I , Evans JR. 1988. Effects of light and nitrogen nutrition on the organization of the photosynthetic apparatus in spinach. Plant and Cell Physiology 29, 143–155. [DOI] [PubMed] [Google Scholar]
- Thornley JHM. 1998. Dynamic model of leaf photosynthesis with acclimation to light and nitrogen. Annals of Botany 81, 421–430. [Google Scholar]
- Trouwborst G , Hogewoning SW , Harbinson J , van Ieperen W. 2011. Photosynthetic acclimation in relation to nitrogen allocation in cucumber leaves in response to changes in irradiance. Physiologia Plantarum 142, 157–169. [DOI] [PubMed] [Google Scholar]
- Trouwborst G , Oosterkamp J , Hogewoning SW , Harbinson J , van Ieperen W. 2010. The responses of light interception, photosynthesis and fruit yield of cucumber to LED-lighting within the canopy. Physiologia Plantarum 138, 289–300. [DOI] [PubMed] [Google Scholar]
- Verkroost AW , Wassen MJ. 2005. A simple model for nitrogen-limited plant growth and nitrogen allocation. Annals of Botany 96, 871–876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vialet-Chabrand S , Matthews JS , Simkin AJ , Raines CA , Lawson T. 2017. Importance of fluctuations in light on plant photosynthetic acclimation. Plant Physiology 173, 2163–2179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walters RG. 2005. Towards an understanding of photosynthetic acclimation. Journal of Experimental Botany 56, 435–447. [DOI] [PubMed] [Google Scholar]
- Werger MJ , Hirose T. 1991. Leaf nitrogen distribution and whole canopy photosynthetic carbon gain in herbaceous stands. Vegetatio 97, 11–20. [Google Scholar]
- Wiechers D , Kahlen K , Stützel H. 2011. Dry matter partitioning models for the simulation of individual fruit growth in greenhouse cucumber canopies. Annals of Botany 108, 1075–1084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson KB , Baldocchi DD , Hanson PJ. 2000. Spatial and seasonal variability of photosynthetic parameters and their relationship to leaf nitrogen in a deciduous forest. Tree Physiology 20, 565–578. [DOI] [PubMed] [Google Scholar]
- Wright IJ , Leishman MR , Read C , Westoby M. 2006. Gradients of light availability and leaf traits with leaf age and canopy position in 28 Australian shrubs and trees. Functional Plant Biology 33, 407–419. [DOI] [PubMed] [Google Scholar]
- Yamori W , Evans JR , Von Caemmerer S. 2010. Effects of growth and measurement light intensities on temperature dependence of CO2 assimilation rate in tobacco leaves. Plant, Cell & Environment 33, 332–343. [DOI] [PubMed] [Google Scholar]
- Yamori W , Nagai T , Makino A. 2011. a The rate-limiting step for CO2 assimilation at different temperatures is influenced by the leaf nitrogen content in several C3 crop species. Plant, Cell & Environment 34, 764–777. [DOI] [PubMed] [Google Scholar]
- Yamori W , Noguchi KO , Terashima I. 2005. Temperature acclimation of photosynthesis in spinach leaves: analyses of photosynthetic components and temperature dependencies of photosynthetic partial reactions. Plant, Cell & Environment 28, 536–547. [Google Scholar]
- Yamori W , Noguchi K , Hikosaka K , Terashima I. 2009. Cold-tolerant crop species have greater temperature homeostasis of leaf respiration and photosynthesis than cold-sensitive species. Plant & Cell Physiology 50, 203–215. [DOI] [PubMed] [Google Scholar]
- Yamori W , Takahashi S , Makino A , Price GD , Badger MR , von Caemmerer S. 2011. b The roles of ATP synthase and the cytochrome b6/f complexes in limiting chloroplast electron transport and determining photosynthetic capacity. Plant Physiology 155, 956–962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu XG , Long SP , Ort DR. 2010. Improving photosynthetic efficiency for greater yield. Annual Review of Plant Biology 61, 235–261. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.