Design and Utility of a Point-of-Care Microfluidic Platform to Assess Hematocrit and Blood Coagulation

Abstract

Purpose

To develop a small volume whole blood analyzer capable of measuring the hematocrit and coagulation kinetics of whole blood.

Methods and Results

A co-planar microfluidic chamber designed to facilitate self-driven capillary action across an internal electrical chip was developed and used to measure the electric parameters of whole human blood that had been anticoagulated or allowed to clot. To promote blood clotting, select chip surfaces were coated with a prothrombin time (PT) reagent containing lipidated tissue factor (TF), which activates the extrinsic pathway of coagulation to promote thrombin generation and fibrin formation. Whole human blood was added to the microfluidic device, and voltage changes within the platform were measured and interpreted using basic resistor-capacitor (RC) circuit and fluid dynamics theory. Upon wetting of the sensing zone, a circuit between two co-planar electrodes within the sensing zone was closed to generate a rapid voltage drop from baseline. The voltage then rose due to sedimentation of red blood cells (RBC) in the sensing zone. For anticoagulated blood samples, the time for the voltage to return to baseline was dependent on hematocrit. In the presence of coagulation, the initiation of fibrin formation in the presence of the PT reagent prevented the return of voltage to baseline due to the reduced packing of RBCs in the sensing zone.

Conclusions

The technology presented in this study has potential for monitoring the hematocrit and coagulation parameters of patient samples using a small volume of whole blood, suggesting it may hold clinical utility as a point-of-care test.

Introduction

Hemostasis is a vital physiological response to vessel injury, involving a dynamically regulated process of thrombus formation at the blood vessel wall to halt blood loss and maintain organ perfusion.44,50,53 Thrombosis is a pathophysiological process involving excessive thrombus formation within blood vessels that may progress to vessel occlusion and potential organ ischemia.11,29 Both hemostasis and thrombosis rely on the intermingled activating and inhibitory pathways of platelets and coagulation factors within the bloodstream.3,6,27,28,36

A wide range of basic clinical tests exist to assess coagulation parameters, platelet function and blood cellularity (complete blood cell count, CBC) separately. However, these tests fail in part to account for the interlink between these parameters as well as the complexities of blood reactions in the framework of blood biorheology. Specifically, the red blood cell content of blood, or hematocrit, can play a major role in platelet availability at the vessel wall1 as well as the viscosity of blood.51,52 Clinically, decreased hematocrit has been shown to be predictive of bleeding,54 while increased hematocrit has been linked with thromboembolic complications.5 Furthermore, blood behaves as a complex non-Newtonian particle suspension, and blood rheology drastically differs between the setting of laminar or turbulent flows and varying shear flow gradients.6,47

Clinical coagulation tests, such as the prothrombin time (PT) and activated partial thromboplastin time (aPTT) are used to assess blood clotting function in patients. These tests are performed by assessing clotting of isolated platelet poor plasma (PPP) in a closed test system in the presence of known activators of the coagulation cascade via either the extrinsic pathway (lipidated tissue factor, TF, for PT) or the intrinsic pathway (silica or ellagic acid for aPTT). These tests can provide useful information for pinpointing specific coagulation factor deficiencies or monitor the drug effects of anticoagulant therapy. However, such tests currently require a sizable blood donation from a patient per test and the need for trained personnel to collect blood, isolate and test plasma, all of which may be time consuming and costly.

A number of miniaturized technologies reliant on microfluidic engineering have been designed for use with whole blood or blood products. Some of these have become commercially available for use in the hospital setting and serve as a popular means of bedside testing to facilitate rapid assessment of specific patient parameters (metabolite and protein levels, coagulation tests etc.).9,35,45,46 These technologies have become increasingly user friendly and provide fast turn-around, which can be vital for emergent situations or even at-home testing. However, additional considerations such as cost and requirements of separate cartridges and sometimes even computational modules make these technologies less accessible for at-home use at present.

In this study, we built upon our understanding of print electronics and microfluidic technologies to create a microfluidic platform that only requires picolitres of whole blood. The initial goal of this technology was to test blood flow dynamics of both anticoagulated blood and blood in the presence of coagulation, with a focus on assessing patient hematocrit and hematocrit-adjusted coagulation. Ultimately, we aim to produce a cartridge technology that is compatible with home-based software for testing of clinical parameters in whole blood.

Materials and Methods

Materials and Reagents

The prothrombin time (PT) reagent Dade^® Innovin^®, containing lipidated tissue factor (TF), was purchased from Siemens (Munich, Germany). Electronic chips were produced via high-throughput silica processing at HP, Inc (Corvallis, OR). All other materials were purchased from Sigma-Aldrich (St. Louis, MO) or previously named sources.57,58

Microfluidic Platform Design and Chip Parameters

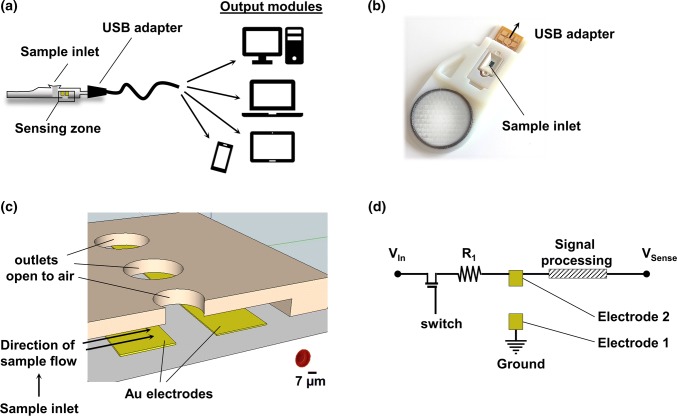
The platform was designed as a co-planar microfluidic device with an internal electronic chip supplied by direct current (DC). The microfluidic device connected a sample inlet and the sensing zone with an outlet open to the air (Figs. 1a–1c). The sensing zone of the chip included two co-planar electrodes, where electrode 1 (E1) was connected to ground, while electrode 2 (E2) was connected to an input voltage via a pullup resistor (R1) and a DC switch (Fig. 1d). E1 and E2 were designed to be separated by a physical gap and to remain electrically decoupled in a dry empty device. The electric current path between E1 and E2 was expected to be established upon wetting of the sensing zone with a sample.

Figure 1.

Design of a microfluidic platform for use with blood samples. (a) Illustration of the experimental setup. (b) Photograph of the assembled device. (c) Illustration of the sensing zone with two gold (Au) co-planar electrodes. (d) Basic circuit design in the absence of blood sample.

Functionalization of Microfluidic Devices with an Activator of the Extrinsic Pathway of Coagulation

Microfluidic devices were incubated with 1 µL of stock solution of tissue factor (TF)-containing PT reagent (Dade^® Innovin^®) for 1 h under rotation at room temperature. The introduction of PT reagent into the sensing zone corresponded with a drop in the measured voltage across co-planar electrodes E2 to E1. Next, devices were rinsed with phosphate buffered saline (PBS) pH 7.4 and dried by vacuum aspiration of liquid from the inlet and outlet. Surfaces were then blocked with 5 mg/mL denatured bovine serum albumin (BSA) for 1 h at room temperature, followed by a rinse with PBS and drying of the device.

Time Constant Approximation

Using Ohm’s Law, the voltage contribution due to red blood cell (RBC) sedimentation within the sensing zone was treated as RBC membranes acting as leaky capacitors,2,16,17,20,32,56 leading to an increase of measured voltage over time following an exponential growth (Figs. 3a and 3b), per the equation:

$$V_c=\epsilon (1-e^{-t/\tau }),$$ 1

where $V_c$ is the voltage rise due to the charging capacitor and $\epsilon$ is the full charge of a capacitor due to the property of the capacitor to charge from the supply voltage as time passes (Fig. 3b).10 Per Ohm’s law, each component in an RC circuit has a time constant, $\tau$, which is the product of resistance multiplied by capacitance and equal to the time it takes for the voltage across the circuit component to either rise or fall to $(1-e^{-1})$ of its final value, $\epsilon$. Substituting $\tau$ for time in Eq. (1) allows the calculation of the time $\tau$ to reach 63% of $\epsilon$ (Fig. 3b), while the time for the capacitor to reach a plateau approaches $5\tau$ (Fig. 3b).21

Figure 3.

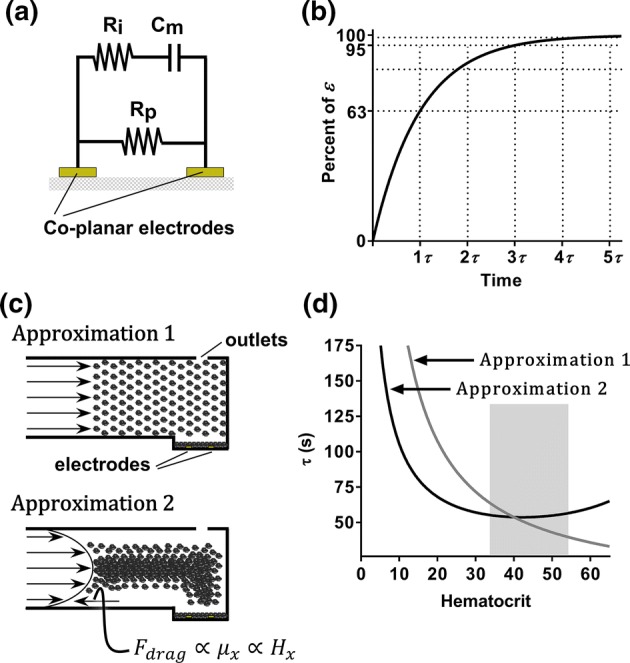
Estimation of microfluidic platform voltage sensitivity to hematocrit. (a) Model of a three component blood circuit between two co-planar electrodes. (b) Voltage profile of a RBC-capacitor contribution based on Ohm’s Law. (c) Illustration of RBC flow assumption for approximation of the time constant values (${\tau }_{H_x}$) as a function of hematocrit: Approximation 1 accounts for bulk flow of blood as a uniform colloid suspension, while Approximation 2 accounts for parabolic blood flow profiles and hematocrit-dependent viscosity. (d) Plot of approximated ${\tau }_{H_x}$ values as a function of hematocrit using Approximation 1 (grey line) or Approximation 2 (black line). The normal hematocrit range for men (40–54%) and women (36–48%) is highlighted with a grey box.

We assumed that in the absence of coagulation, after initial entry of the sample and drop of the measured voltage to ~ 2.1 V (Figs. 2a and 2b), RBCs are free to flow and sediment within the sensing zone, leading to the measured voltage increase as a function of time until the maximal packing capacity of RBCs within the sensing zone is achieved. Thus, the time to maximal packing capacity, $5\tau$, with voltage of $(2.1\text{V}+\epsilon )$ was assumed to be a function of hematocrit (ratio of the volume of RBCs to the total volume of blood). Using this assumption and initial experimental data, a basic approximation of the time constant, ${\tau }_{(H_x)}$, was derived for samples with increasing hematocrit (as described below) and compared to experimentally measured ${\tau }_{(H_x)}$ (Fig. 4b).

Figure 2.

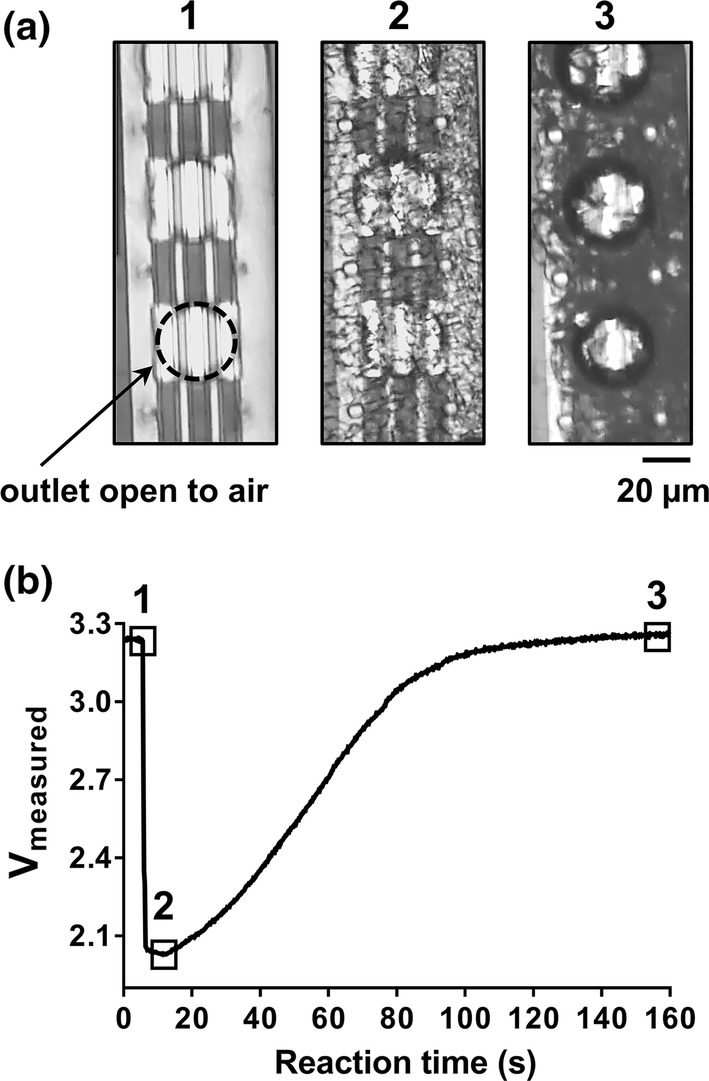
Microfluidic platform with anticoagulated whole human blood sample. Venous whole blood samples collected from a healthy human donor (Hematocrit of 43) were anticoagulated with bivalent direct thrombin inhibitor (40 µg/mL hirudin) and applied to the inlet of the microfluidic device. Real-time progression of blood sample within microfluidic device was (a) visualized with light microscopy with each pertinent transition point shown in panels (1–3) and (b) labeled on the voltage profile (1) dry sensing zone prior to blood entry, (2) entry of blood samples and (3) sedimentation of RBCs within sensing zone. Data representative of n > 30.

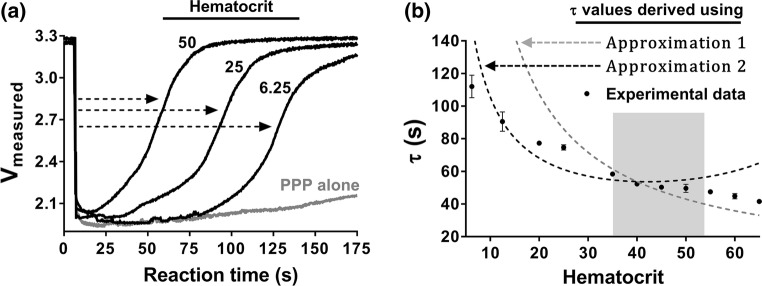
Figure 4.

Sensitivity of the microfluidic platform to hematocrit. Venous whole blood anticoagulated with a bivalent direct thrombin inhibitor (hirudin) was subjected to a series of centrifugation steps to isolate RBCs and platelet-poor plasma (PPP) fractions. The RBC pellet was resuspended with autologous PPP to specified levels of hematocrit and samples were perfused through BSA-coated microfluidic devices. (a) Representative ‘voltage vs. reaction time’ curves of real-time progression of resuspended RBCs at select hematocrits within the microfluidic device are shown, with ‘PPP alone’, which has a hematocrit of zero, used as a control. The dashed arrows indicate calculation of empirical time constant values (${\tau }_{H_x}$) for samples with increasing hematocrits. (b) Plot of empirical ${\tau }_{H_x}$ values for samples with select hematocrit content is shown as mean ± SD, n ≥ 3. Single experimental data points are compared with approximated ${\tau }_{H_x}$ values from Fig. 3 (dashed lines: Approximation 1—grey, Approximation 2—black). The normal hematocrit range for men (40–54%) and women (36–48%) is highlighted in grey.

Based on the measured voltage profile of a whole blood sample with a hematocrit of 43% (Fig. 2b), the sample flow rate was estimated as:

$$Q_{H43}=Volum{e}_{\mathit{Sensingzone}}/5{\tau }_{43},$$ 2

where $5{\tau }_{43}$ is the time required for the voltage to rise from transition point 2 to the final voltage plateau $(2.1\text{V}+\epsilon )$, transition point 3 (Fig. 2b).

$Volum{e}_{\mathit{Sensingzone}}$ was set as a constant volume of the sensing zone to be occupied by RBCs to achieve $(2.1\text{V}+\epsilon )$.

Knowing the fraction of RBCs within the sample, the bulk flow rate was estimated as:

$$Q=Q_{H43}\ast 100/43$$ 3

For “Approximation 1” of ${\tau }_{(H_x)}$, flow rates ($Q_{H_x}$) for samples with different hematocrits ($H_x$) were calculated by multiplying the bulk flow rate by the percent hematocrit fraction (Fig. 3c). Next, $Volum{e}_{\mathit{Sensingzone}}$ was divided by respective $Q_{H_x}$ to calculate $t_{\epsilon (H_x)}$. Using RC circuit theory, ${\tau }_x$ was approximated by dividing $t_{\epsilon (H_x)}$ by 5. This ‘Approximation 1’ ${\tau }_x$ vs. $H_x$ is depicted in Fig. 3d in grey.

For “Approximation 2” of ${\tau }_{(H_x)}$, we accounted for the parabolic flow profile of whole blood6,55 and effect of hematocrit on blood viscosity.18,19,41,51 Using Hatschet’s formula19 modified by Pirofsky,41 a relationship between hematocrit ($H_x$) and blood viscosity (${\mu }_x$) was expressed as follows:

$${\mu }_x=\frac{{\mu }_{\mathit{plasma}}}{1-H_x^{1/3}}$$ 4

Given that the flow rate of a particle (in this case, an RBC) is inversely proportional to the viscosity of the particle suspension (in this case, blood), the relationship can be given as:

$$Q_{H_{43}}\propto \frac{1}{{\mu }_x}$$ 5

To arrive at an adjusted bulk flow $Q^{\prime }$, bulk flow $Q$ (derived in Eq. (3)) was multiplied by the ${\mu }_x$ for a hematocrit of 43 and divided by viscosity of plasma (${\mu }_{\mathit{plasma}}$). Subsequently, ${\mu }_x$ and $Q_{H_x}^{\prime }$ for a range of hematocrits was derived and used to calculate adjusted $5{\tau }_{(H_x)}$ and ${\tau }_{(H_x)}$ as above. This “Approximation 2” ${\tau }_{(H_x)}$ vs. $H_x$ is depicted in Fig. 3d as a black curve.

Human Venous Blood Collection and Handling

Venous whole human blood was drawn by venipuncture from an anonymous pool of healthy adult volunteers into either a dry syringe, a syringe containing a bivalent direct thrombin inhibitor (hirudin, 40 µg/mL final) or trisodium citrate (0.38% w/v) in accordance with the Oregon Health and Science University Institutional Review Board. To isolate RBCs, whole blood was spun down at 1600 rpm for 10 min at RT in a Hermle Z300 centrifuge outfitted with rotor 221.12 V01 (Labnet, Edison, NJ). After the first spin, platelet rich plasma (PRP) was transferred into a new tube and, when appropriate, PRP was spun down again at 2500 rpm for 10 min to isolate platelet poor plasma (PPP). The RBC pellets were diluted with autologous PPP to select levels of hematocrit before use in the microfluidic devices. All blood products were used within 2 h of the blood draw.

Statistics

Data are shown as mean ± SEM. Statistical significance of differences between means, where noted, was determined by ANOVA. Probability values of p < 0.05 were selected to be statistically significant.

Results

Design of a Microfluidic Platform for Use with Blood Samples

The microfluidic blood analyzer platform was manufactured as a microfluidic device with an internal mass-printed electronic chip. The device was incased into insulating plastic, which allowed handling and connection of the platform to a range of output modules via a USB adapter (Figs. 1a and 1b). The co-planar microfluidic device consisted of a sample inlet connected to a sensing zone containing a number of outlets open to air to drive blood flow into the device by capillary action (Figs. 1a–1c). The sensing zone of the chip included two co-planar gold (Au) electrodes physically separated by a gap and electronically uncoupled, with electrode 1 (E1) connected to ground, while electrode 2 (E2) was connected to input voltage via a pullup resistor (R1) and a DC switch (Fig. 1d).

Microfluidic Platform with Anticoagulated Whole Human Blood Sample

We first studied the electrical parameters of buffers and anticoagulated whole human blood within our microfluidic platform. Microfluidic device surfaces were blocked with bovine serum albumin (BSA) and vacuum aspirated prior to addition of the blood sample (Fig. 2a, panel 1). Notably, the addition of buffer to the sensing zone resulted in a rapid drop in voltage from V_max (~ 3.3 V) to ~ 2.1 V; this voltage drop could be reversed by subsequent removal of buffer from the device by vacuum aspiration (data not shown).

Venous whole blood samples were collected from a pool of healthy human donors and anticoagulated with a bivalent direct thrombin inhibitor (40 µg/mL hirudin). Anticoagulated whole blood was added to the sample inlet and progressed quickly (within 5 s) by capillary action to the outlets within sensing zone (Fig. 1); the presence of red blood cells (RBCs) within the sensing zone was visualized with light microscopy Fig. 2a, panel 2).

Figure 2b shows a representative voltage profile of an anticoagulated whole sample from a donor with hematocrit of 43%. The wetting of the sensing zone with a blood sample produced a rapid drop in voltage from V_max to ~ 2.1 V (corresponding to the transition from point 1 to point 2 on the graph in Fig. 2b). With increasing time, RBCs would enrich within the sensing zone, resulting in decreased light transmittance through the sensing zone (Fig. 2a, panel 3) and an increase in measured voltage (Fig. 2b). Eventually, RBC packing would approach maximal capacity, as observed via microscopy as a lack of RBC movement; correspondingly, the voltage returned to near V_max (Fig. 2b, point 3).

Estimation of Microfluidic Platform Voltage Sensitivity to Hematocrit

We next approximated the dependence of voltage on the concentration of RBCs (hematocrit). For a proof-of-concept calculation, we used experimental observations of voltage measurements for a blood sample with a hematocrit of 43% (Fig. 2) and adapted a previously validated three-element-model of blood,26,30 in which blood components were modeled as an RC circuit comprised of two resistor components, corresponding to resistive properties of blood plasma (R_p) and intracellular components of blood cells (R_i), and a capacitor (C_m), corresponding to a collective capacitance of RBC membranes (Fig. 3a). Under laminar flow, human whole blood was assumed to be a non-Newtonian stable colloidal suspension of cells and proteins separated by electrostatic repulsion.8,15 We assumed that the experimentally measured rise in voltage (transition from point 2 to point 3 in Fig. 2b corresponded to RBC sedimentation into the sensing zone, with RBCs acting as leaky capacitors,2,16,17,20,32,40,56 resulting in an increase in measured voltage over time in accord with Ohm’s law (Fig. 3b). We further assumed that in the absence of coagulation, the maximal capacity of RBC packing would be equivalent, regardless of the initial hematocrit, thus leading to the same voltage rise ($\epsilon$) from ~ 2.1 V to V_max.

Using these assumptions, we were then able to interpret the experimental time evolution of the RBC-dependent voltage rise and time required to reach $(2.1V+\epsilon )$ for a sample with hematocrit of 43% ($5{\tau }_{\left(H43\right)}$).10,21 We next calculated the RC time constant, ${\tau }_{(H43)}$, which corresponds to the time required to reach $63\%\epsilon$ (Fig. 3b). Based on the total volume of the sensing zone, we derived a basic estimate of the flow rate of blood samples ($Q_{H43}$) by dividing the sensing zone volume by $5{\tau }_{\left(H43\right)}$.

For “Approximation 1” of ${\tau }_{(H_x)}$ as a function of hematocrit ($H_x$), RBCs in samples with different hematocrits were assumed to flow as a uniform colloid suspension and thus have equivalent flow profiles regardless of hematocrit (Fig. 3c). Using this assumption, the bulk flow rate was estimated by dividing the sample flow rate ($Q_{H43}$) by the RBC content (hematocrit percent). The flow rates of samples with different hematocrits were then calculated by multiplying the bulk flow rate by hematocrit percent. These values were then used to approximate the time to $(2.1\text{V}+\epsilon )$, $5{\tau }_{(H_x)}$, for a range of hematocrits and divided by 5 to estimate ${\tau }_{(H_x)}$ as a function of hematocrit. The resultant “Approximation 1” ${\tau }_{(H_x)}$ values were plotted (grey curve) as a function of hematocrit (Fig. 3d).

For “Approximation 2” of ${\tau }_{(H_x)}$ as function of hematocrit ($H_x$), the blood flow was assumed to follow a parabolic flow profile with a sample viscosity dependent upon the hematocrit (Fig. 3c).18,19,41,51 We divided the blood flow rate ($Q_{H43}$) by a viscosity factor that accounts for changes in viscosity due to RBCs,19,41 calculated for sample with a hematocrit of 43% using Hatchet’s formula19 modified by Pirofsky.41 The resultant flow rate ($Q_{H43}^{\prime }$) was then used to calculate an adjusted bulk flow rate. “Approximation 2” of ${\tau }_{(H_x)}$ as a function of hematocrit is shown in Fig. 3d (black curve). Both our approximations predict that ${\tau }_{(H_x)}$ should decrease with increasing hematocrit.

Sensitivity of the Microfluidic Platform to Hematocrit

We next experimentally evaluated the effect of hematocrit on the time constants measured by our device. We therefore prepared whole human blood samples with increasing hematocrit levels. Fresh whole human blood was collected by venipuncture and anticoagulated with a bivalent direct thrombin inhibitor (40 µg/mL hirudin). Blood was then subjected to a series of centrifugation steps to isolate RBC, platelet-rich plasma (PRP) and platelet-poor plasma (PPP) fractions. The RBC pellets were diluted with autologous PPP to select levels of hematocrit before use in the microfluidic devices. As a control, PPP and PRP alone were also tested.

Our experimental data shows that the time to reach 63$\%\epsilon$, or ${\tau }_{(H_x)}$, decreased as a function of hematocrit ($H_x$), with a longer ${\tau }_{(H_x)}$ observed with lower hematocrit (Fig. 4a). Notably, samples devoid of RBCs, PPP (Fig. 4a) or PRP (data not shown), produced a characteristic initial dip in measured voltage to ~ 2.1 V (as with whole blood or buffer); yet, a significant rise in voltage was not detected for PPP samples within the 400 s measurement time. These findings suggest that RBCs are primarily responsible for the voltage changes observed in our platform, and that ${\tau }_{(H_x)}$ correlates with hematocrit ($H_x$).

We next plotted mean ${\tau }_{(H_x)}$ ± standard deviation values of ${\tau }_{(H_x)}$ calculated from experimental voltage profiles as a function of hematocrit levels (Fig. 4b). We saw that the ${\tau }_{(H_x)}$ times calculated from experimental data decreased with hematocrit level. Next, we overlaid the approximated value curves of ${\tau }_{(H_x)}$ from Fig. 3 and saw that these approached the empirical values of ${\tau }_{(H_x)}$ within the physiological range of hematocrit (36–54%).4 As expected, experimental ${\tau }_{(H_x)}$ values fell closer to Approximation 2 values when the sample hematocrit was less than 45 in accord to Fahraeus effect limitations for flowing blood.12,14,37,42

Sensitivity of the Microfluidic Platform to Coagulation

We next assessed the sensitivity of our microfluidic platform to the initiation of coagulation. Select microfluidic devices were functionalized with PT reagent (Dade^® Innovin^®) containing lipidated tissue factor (TF), which activates the extrinsic pathway of coagulation, while the rest of the devices were coated with BSA alone. Venous whole blood was collected into an empty syringe and pretreated with either vehicle buffer control (anticoagulation = none) or a bivalent direct thrombin inhibitor (hirudin). Samples were added to microfluidic devices, and real-time voltage recordings were obtained (Fig. 5).

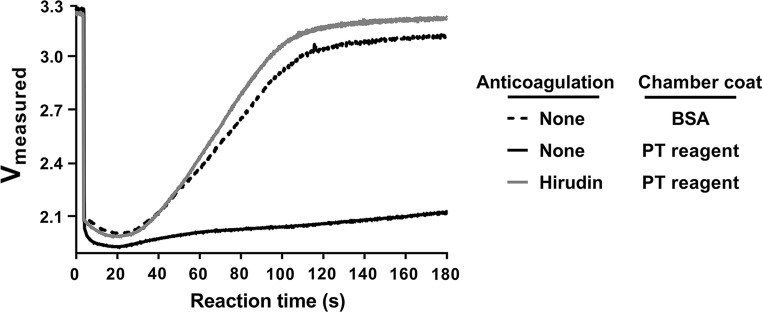
Figure 5.

Sensitivity of the microfluidic platform to coagulation. Non-anticoagulated venous whole blood was pretreated with either vehicle buffer control or a bivalent direct thrombin inhibitor (hirudin) and added to either BSA-coated or PT reagent-coated microfluidic device. The real-time progression of blood cells within cartridge was recorded using voltage measurements. Graphs are representative of results from n ≥ 4 repeats.

A near-instantaneous drop in voltage was observed following the introduction of non-anticoagulated or hirudin-anticoagulated blood into a device. After the initial voltage drop, non-anticoagulated blood filling the BSA-coated device produced a voltage rise (black dashed line) (Fig. 5). In contrast, the voltage remained depressed throughout the observation period for non-anticoagulated blood filling a device that had been coated with PT reagent (black solid line), presumably due to the fact that rapid fibrin formation slowed the blood flow and prevented RBCs from packing into the sensing zone. This effect was reversed when the blood was anticoagulated with the thrombin inhibitor hirudin (grey, solid line). Taken together, our data demonstrate that this device platform is sensitive to both RBC content as well as fibrin formation.

Discussion

The goal of this work was to develop a microfluidic platform utilizing an electrical chip design that facilitates testing of whole blood dynamics for hemostatic assessment. We have developed a rational microfluidic device design that allows the passive flow of a blood sample through the sensing zone coupled with a signal processing algorithm that helps to isolate a signature of red blood cell (RBC) sedimentation and packing. The platform allows for the evaluation of hematocrit using an RC circuit and fluid dynamic theory of RBC transport in whole blood. The platform is sensitive to the rate of thrombin generation and fibrin formation when the chip is functionalized with an initiator of the extrinsic pathway of coagulation (PT reagent). Together, this platform has the potential for a multiplexed analysis of a small volume of whole blood.

Whole blood is a complex sample to handle, study and quantify. Blood behaves as a non-Newtonian fluid, which means its viscosity changes with shear rate.33 It is a colloid suspension that adheres to Stokes theory of particle motion in viscous solution but only with a hematocrit of up to one percent.37 Some strides to understand particle motion in physiologically relevant hematocrit settings are emerging from the study of silica slurries; however, RBCs and other cells introduce other challenges that are difficult to account for in slurries. Whole blood in part follows the Fahraeus effect, which predicts that RBCs tend to migrate to the channel centerline and form a core that flows faster as compared to the rest of the blood (the basis of Approximation 2), thus contributing to higher “discharge” hematocrit ($H_d$) as compared to sample hematocrit ($H_x$).12,42 However, this relationship falls apart at hematocrits above 45%.14 Furthermore, RBC shape and potential shape changes, channel diameter and geometry, temperature and other aspects all play a role in flow dynamics of this viscoelastic and intricate fluid.18,47^–49

Clinically, it is vital to rapidly assess hemostasis in emergency situations. While classically used anticoagulants, such as warfarin, could be monitored with traditional tests including PT and aPTT, the effects of newer direct oral anticoagulants cannot be easily assessed.43 In patients presenting with acute major or central nervous system bleeding, point of care testing has the potential to quickly identify anticoagulated patients allowing providers to initiate appropriate reversal agents. Likewise, certain medical conditions such as end stage liver disease24 and antiphospholipid antibodies39 interfere with the accuracy of traditional coagulation tests. Point-of-care microfluidic platforms have the potential for utility to offer better assessment of these patients in real time.

RBCs play a key role in the delivery of oxygen and nutrients to organs; thus, monitoring hematocrit levels is an essential part of patient management. Moreover, hematocrit levels affect clotting associated with thrombosis and hemostasis7,38,52 and predict clinical bleeding.54 Thus, the capability to both assess the hematocrit level and the hematocrit-adjusted clotting properties of a whole blood patient sample (Fig. 6) may be of utility in monitoring patients with procoagulant and/or hemorrhagic risks.22,31 At the current stage of development, our platform is sensitive to the hematocrit of blood samples prepared by diluting RBC pellets with platelet poor plasma (PPP). With this consideration in mind, our platform may be of utility in the assessment of bleeding in the setting of anemia,54 as PPP clotting time tests alone are insufficient to assess global hemostasis.

Figure 6.

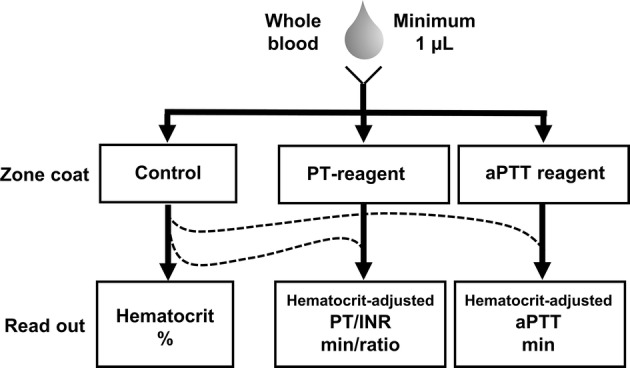
Schematic of possible blood measurements and readouts.

Cancer patients undergoing chemotherapy frequently suffer from bone marrow suppression and thus a drop in hematocrit, platelets and other related aspects of hemostasis. Yet, cancer patients are also predisposed to potentially dangerous thrombus formation due to cancer itself, immobility, tissue damage and other confounding factors.23,25 Thus, such populations, particularly when anticoagulation is needed, require continuous monitoring and therapy adjustment to mitigate potential thrombo-hemorrhagic complications. Importantly, due to bone marrow and thus immune system suppression, cancer patient populations are also vulnerable to the development of potentially lethal infections. Thus, the capability for home testing may be potentially beneficial from the perspective of limiting hospital visits and thus dangerous in-hospital exposures.

Several portable small volume blood analyzer platform designs have proven to be successful in the clinical point-of-care setting. Notably, Abbott’s iSTAT^® technology allows for rapid testing of blood parameters in emergency medicine and surgical settings. The iSTAT^®-specific computational module is compatible with a wide range of cartridges for bedside testing of basic coagulation as well as metabolic panels in non-anticoagulated venous blood.35,45 While use of these portable blood analyzers provides information used for immediate care, design of patient treatment plans typically requires analysis of blood samples in a routine clinical blood laboratory panel, including but not limited to PT/INR, CBC and levels of specific coagulation markers.35 Thus, there remains a need for a point-of-care technology that provides these values in emergency or surgical settings.

Roche and Alere have developed computational modules with cartridges compatible with capillary blood samples obtained via finger prick for the intended use by patients to assess their hemostatic state at home.34 Part of the goal of at-home testing devices is to reduce costs and exposures involved with frequent hospital visits for patients on chronic anticoagulation and with other types of hemostatic irregularities. After appropriate patient coaching by a physician, access to data from home tests can further provide a sense of comfort for both the patient and the provider. Currently marketed technologies to measure coagulation range in cost from $1000 to $2000 for the device and software; additional costs are incurred to purchase the test cartridges. These costs may prohibit the use of such technologies for fixed income patient population groups. Furthermore, since hemostasis is a complex process involving blood enzymes as well as cells, results from these devices may not account for flow-dependent parameters of blood clotting at distinct shear rates in different vessel beds. Specifically, for the assessment of anticoagulation therapy and other contributing factors to prothrombotic phenotypes such as inflammation or cancer, the failure to account for cellular components involved in whole blood clotting may underestimate the clotting kinetics, which may compromise the information patients use to adjust their therapy and lead to potentially deleterious health repercussions. This is in part why the Alere INRatio2^® home testing module-cartridge technology was recently recalled.13

The aim of this study was to develop a small-volume microfluidic platform design that is sensitive to cellular dynamics of blood samples which can be integrated with existing user computational modalities. The platform described in this study requires only a small volume (< 5 µL) to perform testing, compatible with blood collection procedures using a small lancet for a finger prick rather than venipuncture, potentially reducing the need for hospital visits, blood loss, and alternative sampling routes for patients with limited venous access. Ideally, this technology would be adapted for use with smart phone technologies to allow for both data collection and sharing, as appropriate. Our future studies will include testing and comparison of our device sensitivity within a larger cohort of donor populations to test naïve blood obtained by venous blood draw as well as capillary blood obtained by a finger prick. During this next phase of our point-of-care device technology research and development, we will compare the results from our platform to devices including the Roche Coaguchek^®,34 Abbot’s iSTAT cartridges and other commercially available point-of care devices.9,45 The ultimate goal is to develop this microfluidic point-of-care platform for analysis of whole blood samples in multiple patient populations.