Experimental implementation of a joint statistical image reconstruction method for proton stopping power mapping from dual‐energy CT data

Abstract

Purpose

To experimentally commission a dual‐energy CT (DECT) joint statistical image reconstruction (JSIR) method, which is built on a linear basis vector model (BVM) of material characterization, for proton stopping power ratio (SPR) estimation.

Methods

The JSIR‐BVM method builds on the relationship between the energy‐dependent photon attenuation coefficients and the proton stopping power via a pair of BVM component weights. The two BVM component images are simultaneously reconstructed from the acquired DECT sinograms and then used to predict the electron density and mean excitation energy (I‐value), which are required by the Bethe equation for SPR computation. A post‐reconstruction image‐based DECT method, which utilizes the two separate CT images reconstructed via the scanner’s software, was implemented for comparison. The DECT measurement data were acquired on a Philips Brilliance scanner at 90 and 140 kVp for two phantoms of different sizes. Each phantom contains 12 different soft and bony tissue surrogates with known compositions. The SPR estimation results were compared to the reference values computed from the known compositions. The difference of the computed water equivalent path lengths (WEPL) across the phantoms between the two methods was also compared.

Results

The overall root‐mean‐square (RMS) of SPR estimation error of the JSIR‐BVM method are 0.33% and 0.37% for the head‐ and body‐sized phantoms, respectively, and all SPR estimates of the test samples are within 0.7% of the reference ground truth. The image‐based method achieves overall RMS errors of 2.35% and 2.50% for the head‐ and body‐sized phantoms, respectively. The JSIR‐BVM method also reduces the pixel‐wise random variation by 4‐fold to 6‐fold within homogeneous regions compared to the image‐based method. The average differences between the JSIR‐BVM method and the image‐based method are 0.54% and 1.02% for the head‐ and body‐sized phantoms, respectively.

Conclusion

By taking advantage of an accurate polychromatic CT data model and a model‐based DECT statistical reconstruction algorithm, the JSIR‐BVM method accounts for both systematic bias and random noise in the acquired DECT measurement data. Therefore, the JSIR‐BVM method achieves good accuracy and precision on proton SPR estimation for various tissue surrogates and object sizes. In contrast, the experimentally achievable accuracy of the image‐based method may be limited by the uncertainties in the image formation process. The result suggests that the JSIR‐BVM method has the potential for more accurate SPR prediction compared to post‐reconstruction image‐based methods in clinical settings.

1. Introduction

An important advantage of proton‐beam therapy is that the high gradient dose fall‐off near the end of the proton range, which can improve dose conformality and normal tissue sparing if aligned accurately with the distal margin of the clinical target volume (CTV). However, in current clinical practice, additional 2–3.5% safety margins of the proton range are required to ensure adequate coverage of the distal CTV margin due to uncertainties in the proton range estimated from current state‐of‐the‐art single‐energy CT‐based stopping power ratio (SPR) mapping processes.^{1, 2, 3} To unlock the full potential of proton therapy, more accurate patient‐specific proton SPR maps are needed.

The current clinical practice for estimating patient‐specific SPR distributions is the single‐energy CT (SECT) stoichiometric calibration method,⁴ which utilizes a predetermined calibration curve between CT Hounsfield units (HUs) and SPRs for biological tissues. However, the achievable performance of SECT analysis may deteriorate if either the density or elemental composition of patient tissue deviates from the reference tissues used to determine the calibration curve because SPR exhibits different sensitivities to variations in density and elemental composition.^{5, 6} To solve this problem, dual‐energy CT (DECT) techniques have been proposed for determining SPR distributions. By scanning patients at two different energies, DECT techniques endeavor to extract two independent material properties (most commonly electron density ${\rho }_e$ and effective atomic number $Z_{\mathrm{eff}}$) from the CT measurements in order to more accurately resolve variations in CT intensity into variations in electron density and atomic composition, which leads to more robust SPR estimation compared to the SECT stoichiometric calibration method.^{5, 7, 8}

Most proposed DECT methods are image‐based decomposition analyses, in which the two material properties are extracted for each image voxel from the two corresponding HU values in separately reconstructed CT images acquired under different x‐ray source spectra.^{5, 7, 9, 10, 11, 12, 13, 14, 15, 16, 17} These post‐reconstruction methods are easy to implement because one can directly use the scanner’s SECT image reconstruction process, typically some form of filtered back projection (FBP). However, because the decomposition process is ill‐conditioned, DECT analyses based on separate FBP reconstructions are sensitive to both systematic and random variations of CT numbers in the separately reconstructed images, which may compromise the high accuracy that is theoretically achievable by DECT techniques.^{6, 8, 18, 19}

It has been shown that sinogram‐based methods, which decompose dual‐energy CT transmission sinograms into energy‐invariant projections before image reconstruction, are able to better compensate for the polychromatic nature of CT x‐ray beams and improve performance.^{20, 21} In addition, statistical image reconstruction methods have been investigated for dual‐energy and multi‐energy CT problems and have been shown to better suppress image noise and improve image quality compared to the conventional FBP approach.^{18, 22, 23, 24, 25, 26, 27, 28}

As alternative to the ${\rho }_e$–$Z_{\mathrm{eff}}$ parameterization, we have investigated a linear basis vector model (BVM) for tissue property parameterization,^{29, 30, 31} which exhibits high accuracy for approximating both monoenergetic photon cross‐sections and proton SPRs. This linear model enables an efficient model‐based joint statistical image reconstruction (JSIR) algorithm: the dual‐energy alternating minimization (DEAM) algorithm.^{26, 27} Based upon an accurate CT forward model, the DEAM algorithm is able to reconstruct quantitatively accurate images with moderate computational complexity. Our previous simulation study demonstrated that the JSIR‐BVM approach provides more accurate and precise proton SPR mapping compared to either image‐ or sinogram‐based decomposition approaches.³²

The goal of the present study is to assess the accuracy of proton SPR maps derived by the JSIR‐BVM method from experimentally acquired raw DECT exported from a commercial CT scanner. Two sizes of phantoms containing tissue surrogates of known densities and elemental compositions were scanned and analyzed by both the JSIR‐BVM method and a calibration‐based image‐domain decomposition method. The predicted proton SPR of each sample was then compared to the corresponding reference values computed from the known densities and elemental compositions. To our knowledge, our study is the first implementation of a joint statistical reconstruction algorithm for estimating SPR maps that operates simultaneously on two DECT sinograms extracted from a commercial scanner.

2. Materials and methods

2.A. Dual‐energy joint SIR approach

To link the proton SPR values and DECT measurements, the BVM parameterizes both the photon linear attenuation coefficients and the proton stopping power as a combination of two dissimilar reference materials.^{29, 30, 31} Images of two BVM weights are first reconstructed from the measured data via the DEAM algorithm. Electron density (${\rho }_e$) and mean excitation energy (I‐value) are then predicted from the two BVM component weights and used for computing proton stopping power $S_p$ via the Bethe equation³³ according to

$$S_p(E_p)=-\frac{\mathrm{d}{E}_p}{\mathrm{d}x}={\rho }_e\frac{k_1}{{\beta }^2}\left[\frac{1}{2}\text{ln}\frac{k_2{\beta }^2{T}_{\max }}{I^2(1-{\beta }^2)}-{\beta }^2\right],$$ (1)

where $E_p$ is the proton energy; $\beta =v_p/c$ is the proton speed relative to that of light, $T_{max}$ is the maximum energy transferred from the proton to a single electron, and $k_1$ and $k_2$ are products of physical constants. The density correction and the shell correction are ignored since they are negligible for the typical proton energy range used in proton therapy. The proton SPR is then computed by taking the ratio relative to that of water.

2.A.1. Joint statistical DECT image reconstruction

The DEAM algorithm^{26, 27} simultaneously reconstructs the two BVM component images from the two acquired sinograms. The reconstruction is based on a statistical, polychromatic CT data model and is formulated as a penalized maximum likelihood estimation (MLE) problem.

Let $d_j(y)$ be the acquired transmission sinograms (without the beam‐hardening correction), where j  ∈  {L, H} is the index for low‐ and high‐energy scans and y is the index of source‐detector pairs. For energy integrating detectors used in clinical CT scanners, it has been shown that the Poisson model is an accurate approximation of the statistics of the acquired signals.^{34, 35} Therefore, the transmission data $d_j(y)$ are assumed to be independently Poisson distributed with means of

$$Q_j(y:\mathit{\mu })=I_{0,j}(y)\sum _E{\psi }_j(y,E)e^{-{\sum }_{x}h(y|x)\mu (x,E)}+{\gamma }_j(y),$$ (2)

where ${\psi }_j(y,E)$ is the normalized detector‐response‐weighted spectrum of the jth scan and $I_{0,j}(y)$ is the corresponding unattenuated source intensity expressed in noise‐equivalent quanta (NEQ).^{34, 35} The source spectra and intensities are detector‐dependent because of the bow‐tie filter. ${\gamma }_j(y)$ represents the estimation of background events (i.e., scattered radiation), which is assumed to be prior knowledge. The system matrix, h(y|x), represents the effective length of the intersection between the ray path y and image pixel x. The photon energy E is discretized at 1 keV intervals in the reconstruction algorithm.

The BVM assumes that the energy‐dependent linear attenuation coefficients of normally occurring human tissues and tissue‐like materials can be represented by a linear combination of those of two basis materials, that is,

$$\mu (x,E)=c_1(x){\mu }_1(E)+c_2(x){\mu }_2(E),$$ (3)

where ${\mu }_i(E)$ are the linear attenuation coefficients of the two basis materials and $c_i(x)$ are the corresponding BVM component weights. In the present study, polystyrene and 23% ${\text{CaCl}}_2$ aqueous solution are used as the basis materials, which is able to parameterize linear attenuation coefficients with 1–2% accuracy in the 20 keV to 1 MeV energy range and 2–20 effective atomic number range.^{29, 30, 32}

Substituting Eq. (3) into Eq. (2), the mean of the transmission measurement can then be written as a function of the two BVM component images as

$$Q_j(y:\mathbf{c})=I_{0,j}(y)\sum _E{\psi }_j(y,E)e^{-{\sum }_{x}h(y|x){\sum }_{i=1}^2{c}_i(x){\mu }_i(E)}+{\gamma }_j(y).$$ (4)

To find the MLE of the two BVM component images, maximization of the Poisson log‐likelihood function is converted to the equivalent problem of minimizing the I‐divergence³⁶ between the measured transmission data ${\mathbf{d}}_j$ and the estimated mean values ${\mathbf{Q}}_j$ parameterized by ${\mathbf{c}}_i$. The I‐divergence is defined as

$$d_I({\mathbf{d}}_j\Vert {\mathbf{Q}}_j)=\sum _y\left(d_j(y)log\frac{d_j(y)}{Q_j(y)}-d_j(y)+Q_j(y)\right).$$ (5)

Additionally, a regularization term is employed to enforce image smoothness because of the ill‐conditioning of the dual‐energy reconstruction problem. The objective function of the minimization problem is then defined as

$$g({\mathbf{c}}_1,{\mathbf{c}}_2)=\sum _{j=\mathrm{L},\mathrm{H}}{d}_I({\mathbf{d}}_j\Vert {\mathbf{Q}}_j)+\mathrm{\lambda }\sum _{i=1}^{2}R({\mathbf{c}}_i),$$ (6)

in which a single scalar λ controls the trade‐off between data fitting and image smoothness. The spatial penalty function $R({\mathbf{c}}_i)$ is formulated as

$$R({\mathbf{c}}_i)=\sum _x\sum _{x^{\prime }\in \mathcal{N}(x)}{w}_{x,x^{\prime }}\varphi \left(c_i(x)-c_i(x^{\prime })\right),$$ (7)

where $\mathcal{N}(x)$ is the adjacent neighborhood of pixel x and $w_{x,x^{\prime }}$ is an inverse‐distance weight for each pixel‐pair. The value difference between neighboring pixels is penalized by the potential function

$$\varphi (t)=\delta \left(\left|\frac{t}{\delta }\right|-\text{ln}\left(1+\left|\frac{t}{\delta }\right|\right)\right),$$ (8)

which has a quadratic region for |t| ≪ δ and a linear region for |t| ≫ δ. The Huber‐type potential function helps preserve edges while suppressing image noise.³⁷

Because the direct minimization of Eq. (6) is difficult, the DEAM algorithm alternatively minimizes a decomposed surrogate function in each iteration, which ensures monotonic decrease of the original objective function. Details of the derivation of the DEAM algorithm can be found in O’Sullivan et al.²⁷ Acceleration techniques including ordered subsets³⁸ and heuristic step‐size adjustment are also used in the implemented DEAM algorithm to accelerate the convergence.

Implementing the proposed reconstruction algorithm method on a conventional CT scanner requires

• The ability to extract raw energy‐uncompensated projection data from the CT scanner.

• Knowledge of the system matrix of the CT scanner, h(y|x), which is computed for the scanner geometry.

• Knowledge of the energy‐fluence spectra and the wedge (bow‐tie filter) profile of the scanner, ${\mathrm{\Psi }}_j(y,E)$, which can be modeled by the equivalent spectrum method as described in Section 2.C.

• An estimate of the background events presented in the measured data, ${\gamma }_j(y)$, which are assumed to be zero for the narrow collimation used in our experiment.

2.A.2. Proton stopping power computation based on basis vector model

To compute the proton stopping power map, the electron density and mean excitation energy are predicted for each pixel from the two reconstructed BVM component images.

The electron density of a typical biological medium can be accurately estimated by the following linear combination,³⁰

$${\widehat{\rho }}_e(x)=c_1(x){\rho }_{e,1}+c_2(x){\rho }_{e,2},$$ (9)

where ${\rho }_{e,1}$ and ${\rho }_{e,2}$ are the known electron densities of the two basis materials. As an extension, this approximation can also be applied to non‐biological materials composed with elements similar to tissues, such as the those phantom materials used in the experiment.

On the other hand, the I‐value cannot be directly determined from CT image intensities. Thus, a commonly used method for estimating the I‐value is to employ an empirical relationship between the I‐value and some quantity that is related to the elemental composition and can be computed from CT data (most commonly the effective atomic number $Z_{\mathrm{eff}}$).^{5, 7, 11, 12} We hypothesize that for a constrained group of materials with highly similar compositions, the logarithm of the I‐value closely follows a linear relationship with the weighted‐component‐ratio defined as

$$r_c(x)=\frac{c_1(x){\rho }_{e,1}}{c_1(x){\rho }_{e,1}+c_2(x){\rho }_{e,2}},$$ (10)

and the estimate of I‐value is given as

$$\widehat{I}(x)=exp\left(a·r_c(x)+b\right),$$ (11)

where a and b are the fitting parameters. Details of the derivation and explanation of the I‐value parameterization can be found in Appendix B.

The empirical I‐value parameterization model is fit using 83 reference human tissues described in Woodard et al.³⁹ and White et al.⁴⁰ The reference I‐values were calculated by applying the Bragg additivity rule to the ICRU‐recommended elemental I‐values including the recommended gaseous to solid/liquid phase corrections.⁴¹ The reference BVM component weights for arbitrary material were computed via a spectrally weighted least‐squares‐fitting procedure of Eq. (3) to the tabulated attenuation coefficients⁴² as described in Appendix A, which ensures that the computed BVM weights agree with those derived from idealized image reconstruction. Figure 1 demonstrates that ln I is linearly related to $r_c$ for the reference human tissues with residual I‐value modeling errors less than 3% (except for the thyroid tissue). The detailed residual I‐value modeling error for each individual reference tissue can be found in Section S1 in Data S1.

Figure 1.

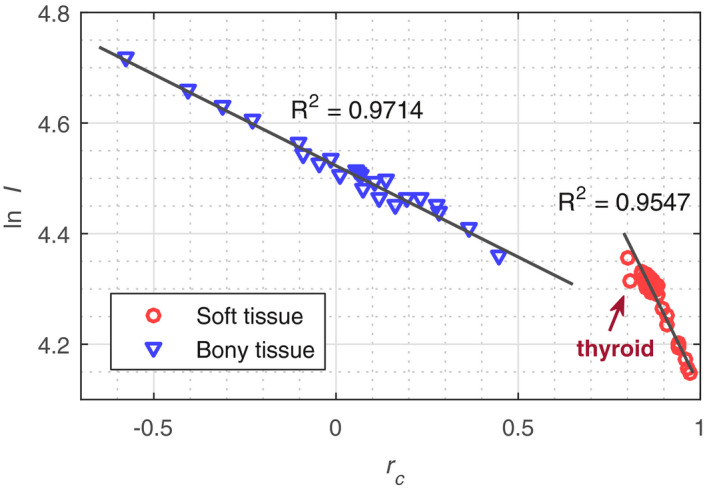
The relationship between logarithm of the I‐value ( ln  I) and weighted‐component‐ratio ($r_c$) for reference human tissue compositions. Thyroid is excluded in the linear fitting since it is an outlier due to the presence of iodine (Z = 53). [Color figure can be viewed at wileyonlinelibrary.com]

It can be seen that the soft tissues and bony tissues follow different linear relationships due to the dissimilarity between their compositions, that is, bony tissues contain a large fraction of calcium and phosphorous while soft tissues are mostly composed of elements with Z ≤ 8. Note that the proposed I‐value parameterization model, as is the case for all such models, can only approximate I‐values for materials with compositions similar to those used to derive the model. If the composition of a scanned object deviates from reference biological tissues, for example, the phantom tissue surrogates used in our experiment, a modified fit that better reflects the prior knowledge about the composition of the scanned objects should be adapted, regardless of which published I‐value parameterization model is used, to reduce the underlying SPR modeling error. The phantom‐specific I‐value parameterizations for both our JSIR‐BVM method and the investigated image‐domain method are discussed in Section 2.C.

2.B. Calibration‐based image‐domain decomposition approach

Several image‐domain methods have been reported for predicting SPRs from two images that are reconstructed separately using a conventional SECT reconstruction algorithm, typically the scanner’s reconstruction software. In the present study, we implemented the image‐domain decomposition method that is originally proposed by Hünemohr et al.⁷ and improved by Li et al.¹⁹ because it showed the best performance among three image‐domain methods in our previous simulation study.³²

Based on the Alvarez–Macovski photon cross‐section model,⁴³ the Hünemohr’s method builds the mathematical relationship between low‐ and high‐energy CT numbers and the material characteristics (i.e., ${\rho }_e$ and $Z_{\mathrm{eff}}$) as follows,

$$\frac{{\rho }_e}{{\rho }_{e,\mathrm{w}}}=c_e{u}_{\mathrm{L}}+\left(1-c_e\right)u_{\mathrm{H}},$$ (12)

$$\frac{Z_{\mathrm{eff}}}{Z_{\mathrm{eff},\mathrm{w}}}={\left[{\left(\frac{{\rho }_e}{{\rho }_{e,\mathrm{w}}}\right)}^{-1}\left(d_e{u}_{\mathrm{L}}+\left(1-d_e\right)u_{\mathrm{H}}\right)\right]}^{\frac{1}{n}},$$ (13)

where ${\rho }_{e,\mathrm{w}}$ and $Z_{\mathrm{eff},\mathrm{w}}$ are the electron density and effective atomic number of water, respectively; $u_{\mathrm{L}}$ and $u_{\mathrm{H}}$ are the modified HU of low‐ and high‐energy CT images defined as $u=\frac{\text{HU}}{1000}+1$; and $c_e$ and $d_e$ are the scanner‐specific calibration parameters. The effective atomic number is defined as

$$Z_{\mathrm{eff}}={\left[\frac{{\sum }_k{\omega }_k(Z_k/A_k)Z_k^n}{{\sum }_k{\omega }_k(Z_k/A_k)}\right]}^{\frac{1}{n}},$$ (14)

where ${\omega }_k$, $Z_k$, and $A_k$ are the mass fraction, atomic number, and atomic weight of element k, respectively. An n of 3.2 yielded the best fit for the elemental attenuation coefficients within the range Z = 2 − 20 and the CT spectra used in our experiment.

The original Hünemohr method requires only one calibration material other than water. To avoid the uncertainty related to the choice of calibration material and to account for the inaccuracy of reconstructed CT numbers that may occur in practice, Li et al.¹⁹ adapted the Saito method for ${\rho }_e$ estimation¹³ and modified the calibration model as

$$\frac{{\rho }_e}{{\rho }_{e,\mathrm{w}}}={\alpha }_1\left((1+{\alpha }_0)u_{\mathrm{H}}-{\alpha }_0{u}_{\mathrm{L}}\right)+{\alpha }_2,$$ (15)

$$\frac{Z_{\mathrm{eff}}}{Z_{\mathrm{eff},\mathrm{w}}}={\left[{\left(\frac{{\rho }_e}{{\rho }_{e,\mathrm{w}}}\right)}^{-1}\left({\beta }_1\left((1+{\beta }_0)u_{\mathrm{H}}-{\beta }_0{u}_{\mathrm{L}}\right)+{\beta }_2\right)\right]}^{\frac{1}{n}},$$ (16)

where the calibration parameters ${\alpha }_k$ and ${\beta }_k$ are determined via scanning the Gammex RMI 467 phantom (Gammex, Middleton, WI) with tissue substitutes of known compositions. The calibration parameters are optimized by fitting the known ${\rho }_e$ and $Z_{\mathrm{eff}}$ to the measured HUs. In the following sections, this modified method is referred to as the image‐based Hünemohr‐Saito (HS) method.

To estimate proton stopping power via the Bethe Equation [Eq. (1)], the I‐value is inferred from $Z_{\mathrm{eff}}$ by applying the empirical linear‐relationship that was first introduced by Yang et al.,⁵

$$\text{ln}I=a{Z}_{\mathrm{eff}}+b,$$ (17)

where the parameters a and b are predetermined separately for different material groups with highly similar compositions, for example, soft and bony tissues for patient imaging.

2.C. Phantom experiment

Two customized test phantoms of different sizes were used in our experiment to assess the performance of the proposed JSIR‐BVM approach. The head‐sized phantom has a cylindrical acrylic shell with a diameter of 215 mm and is filled with water. A separate acrylic body ring, which is elliptically shaped with major and minor axis diameters of 350 and 260 mm, respectively, was placed around the cylindrical phantom in order to imitate typical pelvic volume (shown in Fig. 2). In the following sections, the first phantom setup is referred to as the head phantom and the second one is referred to as the body phantom.

Figure 2.

Image of the test phantom used in the experiment (front view). The phantom consists of a water‐filled cylinder with a removable elliptical body‐ring. [Color figure can be viewed at wileyonlinelibrary.com

Liquid samples were contained in plastic bottles with a diameter of 31 mm (FEP bottle for acetone and HDPE bottles for the other samples) and then mounted to an out‐of‐field plate inside the phantom. The compositions and reference properties of all investigated samples are listed in Table 1. The compositions of aqueous solutions were determined via measuring the mass of the solutes and the volume of the water solvent. The densities were determined via measuring the mass of 50 mL of the samples.

Table 1.

Properties of fabricated test samples. The electron densities were computed by applying the mixture rule to their densities and atomic compositions, and I‐values were computed via the Bragg additivity rule. The concentration represents the mass fraction of the salt in aqueous solutions

Category	Material	Composition	ρ (g/mL)	${\rho }_e/{\rho }_{e,\mathrm{w}}$	I (eV)	SPR
soft	Water	${\mathrm{H}}_2\mathrm{O}$	0.998	1.000	75.3	1.000
	Acetone	${\mathrm{C}}_3{\mathrm{H}}_6\mathrm{O}$	0.788	0.784	66.1	0.796
	Ethanol	${\mathrm{C}}_2{\mathrm{H}}_5\text{OH}$	0.789	0.804	63.1	0.820
	n‐Propanol	${\mathrm{C}}_3{\mathrm{H}}_7\text{OH}$	0.803	0.821	61.5	0.841
	n‐Butanol	${\mathrm{C}}_4{\mathrm{H}}_9\text{OH}$	0.807	0.826	60.5	0.848
bony	CaCl‐1	${\text{CaCl}}_2$ (7.20%)	1.052	1.045	80.0	1.037
	CaCl‐2	${\text{CaCl}}_2$ (18.24%)	1.153	1.130	87.8	1.110
	CaCl‐3	${\text{CaCl}}_2$ (23.07%)	1.202	1.171	91.6	1.144
	KP‐1	${\mathrm{K}}_2{\text{HPO}}_4$ (9.37%)	1.075	1.066	80.2	1.058
	KP‐2	${\mathrm{K}}_2{\text{HPO}}_4$ (17.17%)	1.149	1.130	84.5	1.114
	KP‐3	${\mathrm{K}}_2{\text{HPO}}_4$ (29.26%)	1.273	1.235	91.9	1.206
	KP‐4	${\mathrm{K}}_2{\text{HPO}}_4$ (45.21%)	1.467	1.397	103.0	1.346

The phantom materials are divided into two groups: ${\text{CaCl}}_2$ and ${\mathrm{K}}_2{\text{HPO}}_4$ aqueous solutions are considered as bony tissue surrogates, while water and organic compounds are considered as soft tissue surrogates.

Because the elemental compositions of the phantom materials differ from those of typical human tissues, the I‐values of the phantom materials deviate from both $r_c$‐ and $Z_{\mathrm{eff}}$‐curve fits derived from reference human tissues. To minimize the underlying SPR modeling errors due to such differences, phantom material‐specific I‐value parameterizations were generated for both methods using a series of water–alcohol–acetone mixtures and water–${\text{CaCl}}_2$–${\mathrm{K}}_2{\text{HPO}}_4$ mixtures for soft and bony tissue surrogates, respectively.

The test phantoms and Gammex RMI 467 calibration phantom were scanned on a Philips Brilliance Big Bore CT scanner (Philips Medical Systems, Cleveland, OH) using an axial pelvis protocol with 0.75 mm × 4 collimation. The tube potentials were set to 90 kVp (600 mAs, ${\text{CTDI}}_{\mathrm{vol}}=28.5\text{mGy}$) and 140 kVp (200 mAs, ${\text{CTDI}}_{\mathrm{vol}}=31.6\text{mGy}$). The central axis spectra of the two energies were determined using the well‐validated equivalent spectrum method,^{44, 45, 46} in which the detector‐response weighted spectra were determined by fitting the Birch‐Marshall model⁴⁷ to the measured beam transmission profiles through stacks of high‐purity aluminum and copper filters with varying thickness. Details of the experimental setup for spectrum measurement are described by Evans et al.⁴⁶

The acquired sinograms were reconstructed using both the DEAM algorithm and the scanner’s standard reconstruction process with 0.98 mm × 0.98 mm pixel size and 3 mm slice thickness. For the DEAM reconstruction, the raw sinograms were exported from the scanner and were preprocessed by the tool provided by the vendor without the beam hardening correction process. The regularization parameters in the DEAM algorithm were set to δ = 0.01, λ = 15 and 4 for head and body phantoms, respectively, as a trade‐off between noise and resolution that ensures the spatial resolution is slightly higher than the scanner’s reconstruction for typical soft tissue contrast (75 HU). The background events ${\gamma }_j(y)$ are assumed to be zero for the narrow collimation protocols used in the experiment.

2.D. Performance assessment

The experimental estimates of the electron density, mean excitation energy, and proton SPR of each test sample were compared to the reference ground‐truth values listed in Table 1, which are computed from the known compositions and densities.

The estimation errors were evaluated for a region of interest (ROI) of 24 mm diameter within each homogeneous test sample. The mean and standard deviation of the estimation errors were computed for each test sample. Additionally, water equivalent path length (WEPL) was computed from the reconstructed SPR images for parallel beams from all directions. The differences between the WEPLs predicted from the two methods were compared.

3. Results

3.A. I‐value parameterization of phantom materials

The phantom material‐specific I‐value parameterizations were determined as

$$\text{ln}I=\left\{\begin{array}{cc}-1.746r_c+5.835& \text{for}{r}_c\ge 0.75,\\ -0.269r_c+4.551& \text{for}{r}_c<0.75,\end{array}\right.$$ (18)

and

$$\text{ln}I=\left\{\begin{array}{cc}0.147Z_{\mathrm{eff}}+3.222& \text{for}{Z}_{\mathrm{eff}}\le 8.5,\\ 0.055Z_{\mathrm{eff}}+3.890& \text{for}{Z}_{\mathrm{eff}}>8.5,\end{array}\right.$$ (19)

for the JSIR‐BVM method [Eq. (18)] and the image‐based HS method [Eq. (19)], respectively. Figure 3 compares the I‐value fitting curves derived from the two sets of materials (i.e., reference human tissue and mixtures of phantom materials) for the two methods. The I‐value residuals of the phantom material‐specific parameterization are comparable for the two methods, with the root‐mean‐square (RMS) of the residual I‐value errors being 2.36% and 2.61% for the JSIR‐BVM method and the image‐based HS method, respectively. On the other hand, applying the reference human tissue‐specific parameterization to the phantom materials would result in 4.84% and 6.19% residual errors for the JSIR‐BVM method and the image‐based HS method, respectively.

Figure 3.

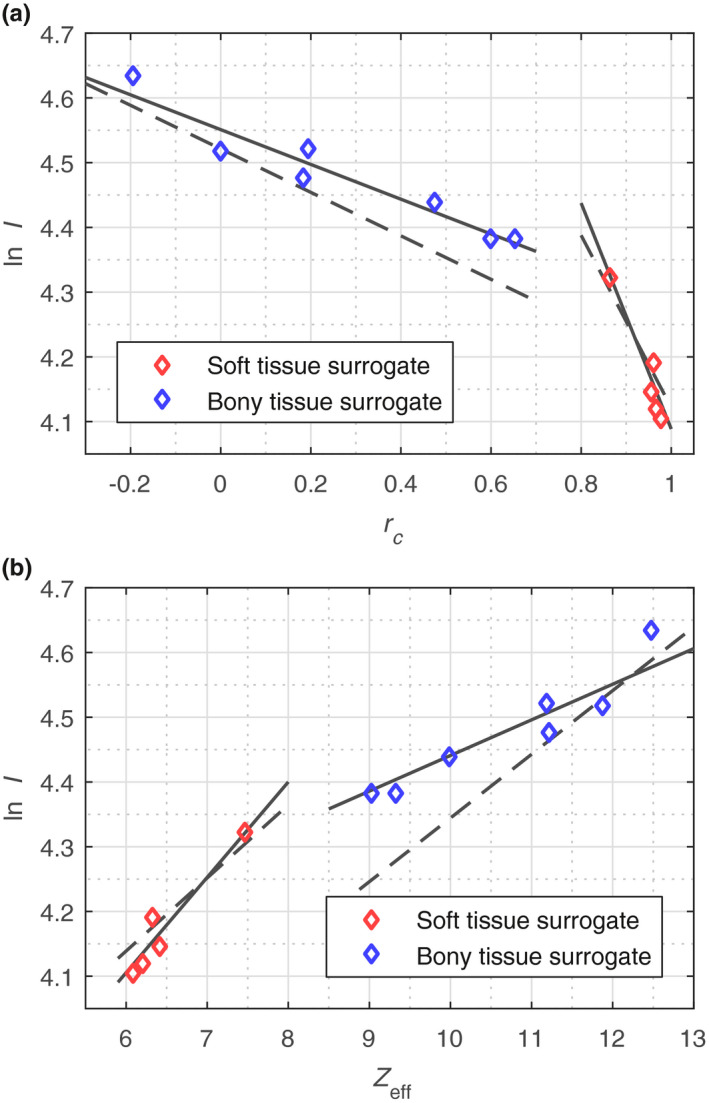
I‐value parameterization curves for the (a) JSIR‐BVM method and (b) image‐based HS method. The solid lines are the phantom material‐specific parameterizations that were used in the present study, while the dashed lines denote the parameterizations generated from reference human tissues. [Color figure can be viewed at wileyonlinelibrary.com

Based on the phantom material‐specific I‐value parameterization, the JSIR‐BVM method and the image‐based HS method show comparable SPR modeling accuracy for the phantom materials. The recovered proton SPRs are all within 0.8% of the ground truths. The RMS of the SPR modeling error is 0.3% and 0.4% for the JSIR‐BVM method and the image‐based HS method, respectively. The detailed modeling error for each individual phantom material can be found in Section S2 in Data S1.

3.B. Experimental estimates of proton SPR and WEPL

Figure 4 compares the estimation errors of the JSIR‐BVM method and the image‐based HS method for each test sample in the two phantom arrangements.

Figure 4.

Mean and standard deviation (1σ) of electron density [(a) and (b)], mean excitation energy [(c) and (d)], and proton SPR [(e) and (f)] estimation errors for all scanned samples in two phantoms of different sizes. The compositions and reference properties of the materials are shown in Table 1. The proton SPR was calculated at 200 MeV. [Color figure can be viewed at wileyonlinelibrary.com]

For the JSIR‐BVM method, the mean errors of the estimated electron density and proton SPR are within 0.6% and 0.7% of the theoretically computed ground truth shown in Table 1, respectively, for all test samples in both phantom settings, and the mean errors of estimated I‐values are all within 1.1% of the modeling residuals. The RMS of the mean estimation errors for electron density and proton SPR are 0.20% and 0.35%, respectively. The accuracy of the JSIR‐BVM method on the two different phantom sizes is comparable. The RMS of the mean SPR estimation errors for all test samples in the head and body phantoms are 0.33% and 0.37%, respectively.

In contrast, the image‐based HS method exhibits RMS of mean errors of 2.35% and 2.50% for electron density and proton SPR, respectively. The RMS of mean SPR errors for the head and body phantoms are 2.96% and 1.93%, respectively. The image‐based method overestimates the electron density for all bony tissue surrogates, which is mainly due to the dependence of CT numbers in the separately reconstructed images on phantom size caused by residual beam hardening effects.³² The ${\rho }_e$ estimation errors can be as much as 5.2% for bony samples in the head phantom, while the maximum ${\rho }_e$ error is 2.8% for the larger body phantom. The larger error on the smaller head phantom is mainly due to the larger size‐difference between the head phantom (215 mm in diameter) and the calibration phantom (330 mm in diameter). The overestimation of ${\rho }_e$ is the dominant contributor to the overestimation of SPR values up to 5.9% and 3.1% in the head and body phantoms, respectively. The largest difference between the mean I‐value estimation error and the modeling residual is 6.6% for the image‐based method.

The JSIR‐BVM method also achieves much smaller random errors in SPR values within homogeneous regions while exhibiting relatively higher spatial resolution. The standard deviation of the SPR estimates is approximately four‐ to sixfold less than those of the image‐based HS method. More details on the spatial resolution of the reconstructed SPR images can be found in Section S3 in Data S1.

Figure 5 shows the SPR images of the head and body phantoms reconstructed by the JSIR‐BVM method and the image‐based HS method. The difference between the WEPL computed by the two methods is also compared. The means of absolute discrepancies in WEPL are 0.54% and 1.02% for the head and body phantom, respectively.

Figure 5.

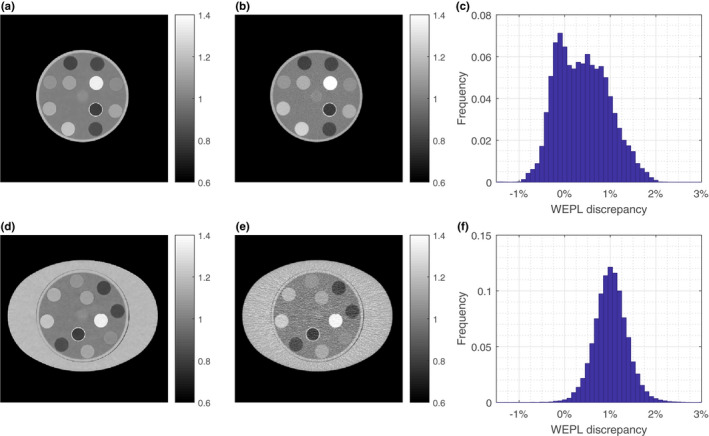
(a) and (b) show the SPR images of the head phantom reconstructed by the JSIR‐BVM method and the image‐based HS methods, respectively. (c) shows the distribution of the differences between WEPL computed from the two SPR images of the head phantom. (d) and (e) show the SPR images of the body phantom reconstructed by the JSIR‐BVM method and the image‐based HS methods, respectively. (f) shows the corresponding WEPL difference for the body phantom. The WEPL is computed for 150 parallel beams with width of 1 mm for every degree. [Color figure can be viewed at wileyonlinelibrary.com

Most of the WEPL values in the body phantom computed from the image‐based HS method are larger than that computed from the JSIR‐BVM methods, which is consistent with the result that the image‐based method overestimates SPRs for all test samples in the body phantom (as shown in Fig. 4). For the head phantom, there are two peaks of the difference between the two methods, which is due to the overestimation of SPR for bony tissue surrogates and underestimation for alcohols.

4. Discussion

4.A. Comparison with previous studies

Our results show that the proposed JSIR‐BVM method more accurately estimates proton SPRs for various materials and object sizes from the experimentally acquired DECT measurements than our implementation of the image‐based HS method. The JSIR‐BVM method achieves 0.35% RMS accuracy for all test samples and both phantom settings, which is comparable to the theoretical SPR modeling error, compared to 2.50% RMS accuracy for the image‐based HS method. The JSIR‐BVM method also achieves more than fourfold reduction in SPR image noise compared to the image‐based method for higher spatial resolution.

The image‐based method is vulnerable to uncertainties in the scanner‐reconstructed CT numbers including image noise, residual beam hardening effect, and imperfections in other data preprocessing steps. Because of the ill‐conditioning of the DECT decomposition problem, the random noise and the residual beam hardening effects in the CT images are amplified in the predicted SPR images. As previous studies show, the residual beam‐hardening effect in separately reconstructed images leads to size‐ and position‐dependence of the reconstructed CT numbers and therefore introduces uncertainties into predicted SPR values.^{19, 32} Our experimental implementation of the image‐based method overestimates the electron densities and SPRs for the higher $Z_{\mathrm{eff}}$ materials when the test object is much smaller than the calibration phantom, which is consistent with our previous simulation results.³²

It should be noted that the performances of all DECT methods depend on the scanning protocol. Our experiment used the 90 and 140 kVp energy‐pair, which is the maximum spectral separation available on the Philips Brilliance Big Bore CT scanner. Several studies have shown that a larger spectral separation can be realized via additional 0.4–0.8 mm Sn filters for the high‐energy beam, which reduces the ill‐conditioning of the DECT decomposition problem and improves the estimation accuracy of both image‐ and sinogram‐based methods.^{13, 48, 49} Garcia et al.¹² presented a 1.9% absolute‐mean error on electron density for an 80 and 140 kVp spectrum‐pair and a relatively small size‐difference, which is similar to our result on the body phantom, while Hünemohr et al.⁷ and Almeida et al.⁴⁹ showed the electron density estimation errors of all their test samples were within 1.2% for a 80 kVp and 140 kVp/Sn energy‐pair. Li et al.¹⁹ that under the largest achievable spectrum separation among current commercial DECT scanners (i.e., 80 kVp and 150 kVp/Sn), the CT number variations in similar head‐ and body‐sized phantoms can cause 0.9% and 1.8% SPR uncertainties for soft and bony tissues, respectively.

4.B. Assessment of SPR estimation uncertainty of JSIR‐BVM method

A limitation of our study is lack of a complete and rigorous assessment of the uncertainty of the comparison between the SPRs reconstructed from JSIR‐BVM imaging and the assumed ground‐truth SPRs that were computed from the measured densities and compositions. A full analysis must estimate Type A (statistical) and/or Type B (systematic) uncertainty for each of the following uncertainty sources,^{50, 51} which are independent and therefore can be separately considered:

1. Computation of ground‐truth SPRs from the measured densities and compositions via the Bethe equation.

2. SPR modeling: estimation of electron density, mean excitation energy, and SPR from the BVM model using the theoretical BVM component weights, ($c_1^{*}$, $c_2^{*}$), which are computed as in Appendix A.

3. Image formation: reconstruction of BVM component images, ($c_1(x)$, $c_2(x)$), from experimentally acquired sinograms, when compared to the theoretical BVM component weights ($c_1^{*}$, $c_2^{*}$).

For the first uncertainty source, the Type B uncertainties of the ground‐truth SPR values computed from measured densities and compositions are 0.1%, based upon the uncertainties in the mass and volume measurement, when assuming no errors in the Bethe equation or its parameters.

The SPR modeling uncertainties are inherent to all DECT approaches. One major component of the SPR modeling uncertainties arises from lack of a one‐to‐one correspondence between I‐value and the photon cross‐section modeling parameters, either $(c_1,c_2)$ or $({\rho }_e,Z_{\mathrm{eff}})$. To assess the SPR modeling errors associated with the JSIR‐BVM method, we followed the method Han et al.³⁰ to investigate the dependence of SPR estimates to deviation in tissue compositions from the reference compositions used to fit the BVM model. The major components of adipose‐like, muscle‐like, and trabecular bone tissues were varied over the ranges reported in the literature^{39, 40, 52, 53} (see Table 2). As shown in Fig. 6, the maximum SPR modeling error, which includes the inherent I‐value parameterization error, is 0.21%, 0.13%, and 0.45% for adipose‐like, muscle‐like, and trabecular bone tissues, respectively, over the whole range of tissue composition variations. This result demonstrates that the BVM maintains good theoretical modeling accuracy for even relatively large derivations of human tissue composition from the reference ones.

Table 2.

Variations in the component composition of soft and bony tissue (percentage by mass) considered in the present study. The red marrow in trabecular bone is represented by the fraction in total marrow

	Adipose‐like tissue	Muscle‐like tissue	Trabecular bone
Protein (%)	0–10	10–25
Lipid (%)	30–88	0–12
Water (%)	1.7–69.7	61.1–88.1
Carbohydrate (%)		1
Ash (%)	0.3	0.9
Osseous (%)			20–100
Red marrow (%)			0–100

Figure 6.

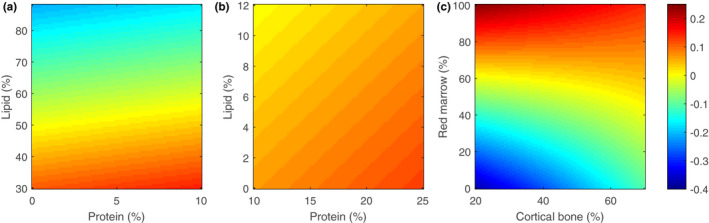
The percentage error of SPR computed by theoretical BVM component weights for (a) adipose‐like tissue, (b) muscle‐like tissue, and (c) trabecular bone as a function of the composition variation. The tissue‐specific I‐value parametrization in Fig. 1 was used. [Color figure can be viewed at wileyonlinelibrary.com]

In this paper, we neglect the approximation error of the tabulated I‐value computed by the Bragg additivity rule, which may dominate the uncertainty of theoretically computed SPR values.^{54, 55, 56} A meaningful assessment of JSIR‐SPR uncertainties due to I‐value uncertainties is not straightforward. Hence, we chose to defer a full analysis to future work.

The uncertainty of the BVM component weights due to image formation process also leads to the uncertainty of the SPR. By combining Eqs. (9), (10), and (18), the estimation of SPR in

$$\text{SPR}=\left\{\begin{array}{cc}1.056·c_1+0.973·c_2& \text{for}{r}_c\ge 0.75,\\ 1.033·c_1+1.154·c_2& \text{for}{r}_c<0.75.\end{array}\right.$$ (20)

for the phantom materials, or more generally,

$$\text{SPR}={\nu }_1{c}_1+{\nu }_2{c}_2.$$ (21)

By applying the law of propagation of uncertainty,⁵¹ the Type A or Type B image‐formation uncertainty of SPR, ${\sigma }_{\mathrm{SPR}}$, can be written as

$${\sigma }_{\mathrm{SPR}}^2={\nu }_1^2{\sigma }_{c_1}^2+{\nu }_2^2{\sigma }_{c_2}^2+2{\nu }_1{\nu }_2\text{cov}(c_1,c_2),$$ (22)

where ${\sigma }_{c_i}^2,i\in \{1,2\}$ is the uncertainty of $c_i$ and $\text{cov}(c_1,c_2)$ is the covariance of $c_1$ and $c_2$.

A full analysis of image‐formation uncertainties associated with the JSIR‐BVM method is likewise beyond the scope of this paper. A full analysis of the Type B uncertainty requires knowledge of uncertainties associated with x‐ray source spectra, scattered radiation, and tabulated photon attenuation coefficients, which are not currently available.

Insight into the impact of Type B uncertainties on estimated SPR can be gained by examining the bias of JSIR reconstructions for several ROIs. For each ROI, the Type B uncertainties lead to uncertainties in the bias of the reconstructed BVM component weights, and through Eq. (22) into uncertainties in SPR. Denote the bias of reconstructed BVM component weights by $\mathrm{\Delta }{c}_i={\overline{c}}_i-c_i^{*}$, where $c_i^{*}$ is the theoretical BVM weight of a single phantom material and ${\overline{c}}_i$ is the reconstructed BVM component weights averaged over the corresponding ROI of the material. The bias values for all ROIs in the head and body phantoms are shown in Fig. 7. The bias in SPR can be found simply as

$${\mathrm{\Delta }}_{\mathrm{SPR}}={\nu }_1\mathrm{\Delta }{c}_1+{\nu }_2\mathrm{\Delta }{c}_2,$$ (23)

which is less than 0.5% for all ROIs.

Figure 7.

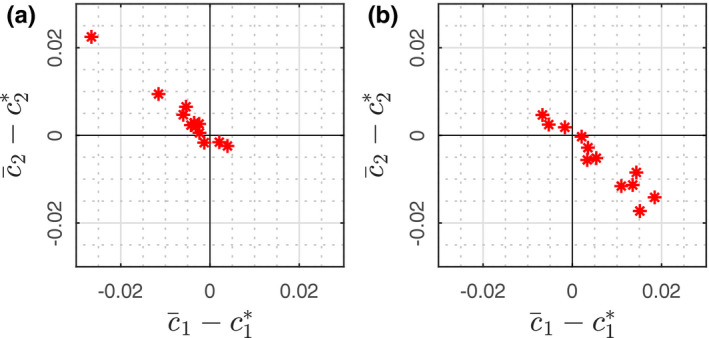
The bias of reconstructed BVM component weights relative to the theoretical values for each of the 12 ROIs in the (a) head and (b) body phantom. [Color figure can be viewed at wileyonlinelibrary.com

To estimate Type A image formation uncertainties, for each of the phantom inserts, the covariance matrix of reconstructed BVM component weights is computed as

$$\begin{array}{cc}& \left[\begin{array}{cc}{\sigma }_{c_1}^2& \text{cov}(c_1,c_2)\\ \text{cov}(c_1,c_2)& {\sigma }_{c_2}^2\end{array}\right]=\frac{1}{N}\sum _x\hfill \\ & \left[\begin{array}{cc}{(c_1(x)-{\overline{c}}_1)}^2& (c_1(x)-{\overline{c}}_1)(c_2(x)-{\overline{c}}_2)\\ (c_1(x)-{\overline{c}}_1)(c_2(x)-{\overline{c}}_2)& {(c_2(x)-{\overline{c}}_2)}^2\end{array}\right],\hfill \end{array}$$ (24)

where the indicated summation is over the N pixels in the ROI. Figure 8 graphically illustrates the covariance matrices of all phantom insert ROIs in head and body phantoms in terms of coverage factor k = 1 uncertainty ellipses.⁵⁷ In the case of JSIR image formation, the result indicates the Type A uncertainties of the BVM component weights exhibit high negative correlation. Evaluating Eq. (22) yields Type A uncertainties (k = 1) around 0.4% and 1.0% for head and body phantoms, respectively.

Figure 8.

The k = 1 uncertainty ellipse corresponding to the covariance matrix for each of the 12 ROIs in the (a) head and (b) body phantom. [Color figure can be viewed at wileyonlinelibrary.com]

5. Conclusions

The proposed JSIR‐BVM method is able to reconstruct proton SPRs from the DECT data exported from a clinical scanner with an overall RMS error of 0.35% and a maximum absolute error of 0.7% for the selected samples. In comparison, a state‐of‐art image‐based method exhibits overall RMS and maximum errors of 2.5% and 5.9%, respectively. The JSIR‐BVM method also reduces the random uncertainty by more than fourfold compared to the image‐based method for slightly higher spatial resolutions. The average differences between the JSIR‐BVM method and the image‐based method are 0.54% and 1.02% for the head and body phantoms, respectively.

By taking advantage of an accurate polychromatic CT data model and a model‐based DECT statistical reconstruction algorithm, the JSIR‐BVM method is able to account for both systematic bias correction and random noise suppression in the reconstruction, and therefore achieve quantitatively accurate SPR estimation for various materials and object sizes.

Conflicts of interest

The authors have no relevant conflicts of interest to disclose.

Supporting information

Data S1: Supplemental material for “Experimental implementation of a joint statistical image reconstruction method for proton stopping power mapping from dual‐energy CT data.”

Appendix A.

Theoretical BVM component weights

In this appendix, we derive the calculation of theoretical BVM component weights.

Assume that x‐ray beams of two different energy spectra pass through a thin layer of material with thickness l, where l is sufficiently small and the source intensities are sufficiently large (i.e., the noise can be ignored). Let ${\psi }_j(E)$ and $I_{0,j}$, j  ∈  {L, H} be the two spectra and the corresponding source intensities, respectively, and ${\mu }_x(E)$ and ${\mu }_i(E),i\in \{1,2\}$ be the linear attenuation coefficients of the scanned material and basis materials, respectively. The measured transmission is given by

$$d_j=I_{0,j}\sum _E{\psi }_j(E)e^{-l·{\mu }_x(E)},$$ (A1)

and the BVM‐modeled transmission is formulated as

$$Q_j=I_{0,j}\sum _E{\psi }_j(E)e^{-l·\left(c_1{\mu }_1(E)+c_2{\mu }_2(E)\right)}.$$ (A2)

Under the Poisson‐noise assumption, the DEAM algorithm finds $c_1$ and $c_2$ that minimize

$$\sum _j{d}_I(d_j\Vert Q_j)=\sum _j\left(d_{j}ln\frac{d_j}{Q_j}-d_j+Q_j\right).$$ (A3)

Applying the Taylor expansion to the objective function at l = 0 gives

$$\sum _j{d}_I(d_j\Vert Q_j)=\frac{l^2}{2}·{\left(A\left[\begin{array}{c}{c}_1\\ c_2\end{array}\right]-\mathbf{b}\right)}^{T}W\left(A\left[\begin{array}{c}{c}_1\\ c_2\end{array}\right]-\mathbf{b}\right)+o(l^2),$$ (A4)

where

$$A=\left[\begin{array}{c}{\mathit{\psi }}_{\mathrm{L}}\\ {\mathit{\psi }}_{\mathrm{H}}\end{array}\right]\left[\begin{array}{cc}{\mathit{\mu }}_1& {\mathit{\mu }}_2\end{array}\right],\mathbf{b}=\left[\begin{array}{c}{\mathit{\psi }}_{\mathrm{L}}\\ {\mathit{\psi }}_{\mathrm{H}}\end{array}\right]{\mathit{\mu }}_x,W=\left[\begin{array}{cc}{I}_{0,\mathrm{L}}& 0\\ 0& I_{0,\mathrm{H}}\end{array}\right].$$ (A5)

Thus, the theoretical BVM component weights are calculated as

$$\left[\begin{array}{c}{c}_1\\ c_2\end{array}\right]={\left(A^{T}WA\right)}^{-1}\left(A^{T}W\right)\mathbf{b}.$$ (A6)

Note that the theoretical BVM component weights depend slightly on the local spectrum. However, such impact is much less than that of SPR modeling error and image formation uncertainty. In the JSIR‐BVM method, the unattenuated central‐axis spectra were used for fitting the I‐value parameterization.

Appendix B.

I‐value parameterization

In this appendix, we derive the I‐value parameterization of the JSIR‐BVM method.

Assume that substance X consists of two components A and B. Let $w_A$ and $w_B$ be the mass fraction of the two components. By the result from Appendix A, the theoretical BVM component weights are given by

$$\left[\begin{array}{c}{c}_1\\ c_2\end{array}\right]=P\left[\begin{array}{c}{w}_A\\ w_B\end{array}\right],$$ (B1)

where

$$P={\left(A^{T}WA\right)}^{-1}\left(A^{T}W\right)\left[\begin{array}{c}{\mathit{\psi }}_{\mathrm{L}}^T\\ {\mathit{\psi }}_{\mathrm{H}}^T\end{array}\right]\left[\begin{array}{cc}{\mathit{\mu }}_A& {\mathit{\mu }}_B\end{array}\right].$$ (B2)

By the Bragg additivity rule, the I‐value of substance X is formulated as

$$\begin{array}{cc}\hfill ln{I}_x& =\frac{w_A{\rho }_{e,A}ln{I}_A+w_B{\rho }_{e,B}ln{I}_B}{w_A{\rho }_{e,A}+w_B{\rho }_{e,B}}\hfill \\ & \approx \frac{\left[\begin{array}{cc}{\rho }_{e,A}ln{I}_A& {\rho }_{e,B}ln{I}_B\end{array}\right]·\left[\begin{array}{c}{w}_A\\ w_B\end{array}\right]}{c_1{\rho }_{e,1}+c_2{\rho }_{e,2}}\hfill \\ & =\frac{\left[\begin{array}{cc}{\rho }_{e,A}ln{I}_A& {\rho }_{e,B}ln{I}_B\end{array}\right]P^{-1}\left[\begin{array}{c}{c}_1\\ c_2\end{array}\right]}{c_1{\rho }_{e,1}+c_2{\rho }_{e,2}}\hfill \end{array}.$$ (B3)

Then

$$ln{I}_x=a\frac{c_1{\rho }_{e,1}}{c_1{\rho }_{e,1}+c_2{\rho }_{e,2}}+b,$$ (B4)

where

$$\left[\begin{array}{cc}a& b\end{array}\right]=\left[\begin{array}{cc}{\rho }_{e,A}ln{I}_A& {\rho }_{e,B}ln{I}_B\end{array}\right]P^{-1}{\left[\begin{array}{cc}{\rho }_{e,1}& 0\\ {\rho }_{e,1}& {\rho }_{e,2}\end{array}\right]}^{-1}.$$ (B5)

The above result demonstrates that for a series of mixtures that are made up of the same two components,  ln  I is linear with the weighted‐component‐ratio $r_c=\frac{c_1{\rho }_{e,1}}{c_1{\rho }_{e,1}+c_2{\rho }_{e,2}}$. Moreover, for any constrained set of materials whose compositions can be accurately represented by two major principal components, such as the soft or bony tissues as discussed in a previous study by Lalonde et al.¹⁶,  ln  I closely follows a linear relationship with $r_c$.