Abstract
Purpose
The purpose of this study was to assess the performance of a novel dual‐energy CT (DECT) approach for proton stopping power ratio (SPR) mapping that integrates image reconstruction and material characterization using a joint statistical image reconstruction (JSIR) method based on a linear basis vector model (BVM). A systematic comparison between the JSIR‐BVM method and previously described DECT image‐ and sinogram‐domain decomposition approaches is also carried out on synthetic data.
Methods
The JSIR‐BVM method was implemented to estimate the electron densities and mean excitation energies (I‐values) required by the Bethe equation for SPR mapping. In addition, image‐ and sinogram‐domain DECT methods based on three available SPR models including BVM were implemented for comparison. The intrinsic SPR modeling accuracy of the three models was first validated. Synthetic DECT transmission sinograms of two 330 mm diameter phantoms each containing 17 soft and bony tissues (for a total of 34) of known composition were then generated with spectra of 90 and 140 kVp. The estimation accuracy of the reconstructed SPR images were evaluated for the seven investigated methods. The impact of phantom size and insert location on SPR estimation accuracy was also investigated.
Results
All three selected DECT‐SPR models predict the SPR of all tissue types with less than 0.2% RMS errors under idealized conditions with no reconstruction uncertainties. When applied to synthetic sinograms, the JSIR‐BVM method achieves the best performance with mean and RMS‐average errors of less than 0.05% and 0.3%, respectively, for all noise levels, while the image‐ and sinogram‐domain decomposition methods show increasing mean and RMS‐average errors with increasing noise level. The JSIR‐BVM method also reduces statistical SPR variation by sixfold compared to other methods. A 25% phantom diameter change causes up to 4% SPR differences for the image‐domain decomposition approach, while the JSIR‐BVM method and sinogram‐domain decomposition methods are insensitive to size change.
Conclusion
Among all the investigated methods, the JSIR‐BVM method achieves the best performance for SPR estimation in our simulation phantom study. This novel method is robust with respect to sinogram noise and residual beam‐hardening effects, yielding SPR estimation errors comparable to intrinsic BVM modeling error. In contrast, the achievable SPR estimation accuracy of the image‐ and sinogram‐domain decomposition methods is dominated by the CT image intensity uncertainties introduced by the reconstruction and decomposition processes.
Keywords: dual‐energy computed tomography, proton stopping power, proton therapy, statistical image reconstruction
1. Introduction
The clinical effectiveness of proton‐beam therapy has been demonstrated in several treatment sites due to its highly conformal dose distributions.1, 2, 3 To realize the full potential of proton therapy, the range of the proton beam, which is defined as the depth of the Bragg peak, needs to be accurately determined. However, in current clinical practice, a safety margin of 2–3.5% of the proton range is added to the distal boundary of the clinical target volume (CTV)4, 5, 6 to ensure CTV coverage in the face of proton range uncertainties, limiting dose sparing of surrounding healthy tissue. One of the dominant sources of range uncertainty is the limited accuracy with which proton stopping power ratios (SPRs) along the beam path are estimated using single‐energy computed tomography (SECT).7, 8
State‐of‐the‐art clinical practice for estimating patient‐specific SPR distributions is the SECT stoichiometric calibration method,9 which builds a one‐to‐one relationship between CT Hounsfield units (HUs) and SPRs for biological tissues by using a calibration phantom with tissue‐substitute inserts of known composition. However, the accuracy of SECT SPR mapping is limited by HU degeneracy in the presence of tissue composition and density variations. Since there is only one measurement per image pixel, SECT analysis is unable to disambiguate the HU dependency on density and elemental composition.8, 10
Numerous approaches have been proposed to estimate the SPR by dual‐energy CT (DECT) techniques with patient scans at two different energies. Theoretical analyses demonstrated that DECT techniques can achieve much better accuracy and robustness compared to the SECT stoichiometric calibration method.7, 10 Most proposed DECT methods for SPR estimation are postreconstruction image‐domain analyses of two separately reconstructed CT images acquired at different scanning energies.11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21 Based on a calibration process, two independent material properties (most commonly electron density ρ e and effective atomic number Z eff) can be extracted for each image pixel from corresponding HU values in the two CT images and then used to compute SPRs.13, 14, 15, 16, 17, 18 These two‐parameter DECT‐SPR models are theoretically highly accurate with as low as 0.2% root‐mean‐square (RMS) errors for human tissues.10 Other DECT‐SPR models that do not require explicit estimation of ρ e or Z eff have also been developed and show comparable theoretical accuracy.19, 20, 21, 22 However, random noise as well as residual systematic errors in the separately reconstructed CT images, for example, HU nonuniformity and dependence on patient size due to residual beam‐hardening and scatter artifacts, may cause accuracy of SPR estimates derived from image‐domain analyses to deteriorate in the clinical setting.10, 12, 23 Inappropriate calibration also introduces systematic errors into prediction results.23, 24
To compensate for the polychromatic nature of CT x‐ray beams, several approaches for decomposing dual‐energy and multienergy CT transmission sinograms into energy‐invariant projections before image reconstruction have been proposed.25, 26, 27, 28, 29, 30, 31, 32 These prereconstruction sinogram‐domain decomposition techniques either require knowledge of the x‐ray source spectra28, 29, 30, 31, 32 or use calibration‐based implicit spectral characterization.25, 26, 27 On the other hand, joint decomposition and reconstruction techniques, which incorporate a polychromatic CT forward model and simultaneously reconstruct two images, have also been investigated for dual‐energy and multienergy CT.33, 34, 35, 36, 37, 38
Recently, our group has investigated an alternative tissue property parameterization: a linear basis vector model (BVM) for photon cross section and proton SPR approximation.39, 40 This linear model not only exhibits theoretical accuracy comparable to more complex nonlinear ρ e −Z eff models but also enables an efficient DECT joint statistical image reconstruction (JSIR) algorithm called dual‐energy alternating minimization (DEAM) algorithm.41, 42, 43 Based on physically realistic signal formation models, the DEAM algorithm is able to reconstruct more quantitatively accurate and artifact‐free images.
This present study investigates the performance of our BVM‐based JSIR approach for SPR estimation,44, 45 which simultaneously reconstructs two energy‐invariant BVM component images with the statistical DEAM algorithm as well as image‐ and sinogram‐decomposition approaches based on the filtered back projection (FBP) algorithm in a simulation framework. The postreconstruction image‐domain decomposition approach extracts either (ρ e , Z eff) or BVM component weights (c 1, c 2) for each individual image pixel from the separately FBP‐reconstructed low‐ and high‐energy CT image intensities. The scanner‐specific mathematical relationship that converts two CT image intensities into material parameters is derived by scanning a calibration phantom consisting of tissue substitutes of known density and composition. In the prereconstruction sinogram‐domain decomposition approach, the low‐ and high‐energy polychromatic sinograms are first decomposed into two energy‐invariant component projections using the known source spectra, and then, each corresponding component image is reconstructed via FBP.31, 32 Three different DECT‐SPR models are implemented to fairly compare the different reconstruction and decomposition techniques.
2. Materials and methods
2.A. Proton stopping power estimation model
Within the energy range typically used in proton therapy, the proton stopping power at a given energy E p can be approximated by the Bethe equation,46
| (1) |
where k 1 and k 2 are products of physical constants; β = v p /c is the proton speed relative to that of light; T max is the maximum energy transferred from the proton to a single electron; and ρ e and I are the electron density and mean excitation energy of the medium, respectively. In clinical practice, the stopping power relative to water, SPR, is more commonly used and often assumed to be constant for different energies. Prior studies39 have demonstrated that the estimated to ground‐truth SPRs are nearly independent of energy. Hence, for all evaluations in this paper, the proton energy E p is set to 200 MeV.
Accurate SPR estimation from Eq. (1) requires exact knowledge of material characteristics, that is, ρ e and I‐value. Most DECT‐based methods assume that I‐value can be approximated by a function of effective atomic number, Z eff, for a constrained set of materials such as normally occurring human tissues. Several models have been proposed to link DECT image intensities with ρ e and I‐value.7, 15, 16, 17, 18 In the present work, we implemented two such DECT‐SPR models proposed by Hünemohr et al.14 and Bourque et al.16 for predicting ρ e and Z eff from the CT image intensities as well as the BVM model that was recently extended by Han et al.39 from photon cross section estimation26, 47 to direct approximation of ρ e and I‐value from the two BVM component weights.
2.A.1. Basis vector model
The BVM assumes that the energy‐dependent photon cross sections of biological media can be represented by linear combinations of those of two dissimilar basis materials:
| (2) |
where μ i (E) are the linear attenuation coefficients at photon energy E of the two basis materials and c i (x) are the corresponding component weights at image location x. In the present study, polystyrene and an aqueous CaCl2 solution (23% concentration by mass), which bracket the range of naturally occurring biological media, are used as the basis materials for all typical human tissues. The selection of basis materials has been discussed by Williamson et al.47
Once the two BVM component weights are determined from the CT scan data, the electron density and mean excitation energy of the unknown material are then predicted from the two BVM component weights as
| (3) |
| (4) |
where ρ e,i and I i are the electron densities and mean excitation densities of the two basis materials, respectively. A precomputed empirical correction function
| (5) |
is applied to mitigate residual I‐value estimation error. The parameters are computed using reference human tissue compositions recommended by International Commission on Radiation Units and Measurements (ICRU)48 and White et al.49 Separate corrections are used for soft tissues and bony tissues due to the dissimilarity between their compositions.39
2.A.2. Hünemohr's model
To build the mathematical relationship between the reconstructed low‐ and high‐energy CT numbers and the material characteristics, Hünemohr et al.14 adapted the photon cross‐section model from Alvarez and Macovski25 and developed the following formulas for calculating ρ e and Z eff:
| (6) |
| (7) |
where u L and u H are the modified HU defined as
| (8) |
which is proportional to the spectrally averaged attenuation coefficient. A similar mathematical formula for estimating ρ e had also been previously developed by Saito.12
The effective atomic number in Eq. (7) is defined as
| (9) |
where ω k , Z k , and A k are the mass fraction, atomic number, and atomic weight of the kth element in the material, respectively. In the present study, the optimal value of n was found to be 3.2 for the CT spectra assumed in our simulation by fitting the attenuation coefficients of elements for Z = 2−20.
The two model parameters, c e and d e , depend on the specific dual‐energy scanning protocol. To determine the two model parameters, a calibration phantom is required to be scanned under the same protocol as the patient scans. The two unknown model parameters are then calculated by fitting Equations. (6) and (7) to the measured CT intensities, using the known material properties of the calibration materials.
To extract SPR estimates from the ρ e and Z eff images, Hünemohr et al.14 used the empirical relationship between I‐value and Z eff that is first introducted by Yang et al.7:
| (10) |
where the parameters are derived from linear fitting for ICRU‐recommended soft and bony human tissue compositions48, 49 using the CT spectra assumed in the simulation.
2.A.3. Bourque's model
Bourque et al.16 developed a dual‐energy stoichiometric calibration process to convert u L and u H into electron density and effective atomic number. In their model, spectrally averaged elemental electronic cross sections are fit to a polynomial function, , of their atomic numbers, Z. Then, the spectrum‐dependent effective atomic number for an arbitrary mixture is defined as . The parametric ρ e −Z eff model is given by
| (11) |
| (12) |
where c k and b m,L/H are scanner‐specific model parameters, which need to be determined from a calibration phantom scan just as in Hünemohr's method. The orders of polynomial fitting used in the present study is consistent with the original work, that is, K = M = 6.
When applying this model, Z eff is first calculated via Eq. (11). Two separate estimations of ρ e are calculated via Eq. (12) from images of low and high energies, respectively, and then averaged to obtain the final estimate of ρ e . The I‐value is parameterized as a piecewise polynomial function of Z eff for ICRU‐recommended human tissue compositions.48, 49
2.B. DECT image reconstruction and decomposition approaches
2.B.1. Image‐domain decomposition approach
In the image‐domain decomposition approach, the two CT sinograms from different source spectra are reconstructed separately based on the assumption that the beam‐hardening correction applied to the sinogram during preprocessing successfully transforms the raw sinogram into monochromatic projections. In our implementation, a water‐based beam‐hardening correction50, 51 was applied to each synthetic polychromatic sinogram before reconstruction via the FBP algorithm.
After image reconstruction, the two ρ e −Z eff models are applied to the two single‐energy CT images pixel by pixel. The model parameters are determined by the calibration process for each technique. Following common practice,12, 13, 16, 17, 18 a conventional Gammex RMI 467 (Gammex, Middleton, WI) phantom with 13 tissue‐substitute inserts of known compositions is used for the calibration in our implementation. Note that Hünemohr et al.14 suggested a single material for calibration, while we use all Gammex inserts to calibrate both the Hünemohr's and Bourque's methods.
To implement the BVM‐based image‐domain decomposition method, a phantom containing the two BVM basis materials, polystyrene and 23% CaCl2 solution, is used for the calibration.52 Two BVM component weights for an unknown material at image pixel x are then determined from
| (13) |
where are the modified HUs of the basis materials obtained from calibration images.
2.B.2. Sinogram‐domain decomposition approach
The sinogram‐domain decomposition approach31, 32 attempts to extract two component line integrals (i.e., projections) that are invariant to the spectra before the image reconstruction process. The two corresponding component images are then reconstructed via the FBP algorithm after the decomposition.
Let such that ∑ E ψ j (y, E) = 1 be the detector response‐weighted spectrum of the low‐ and high‐energy scans for photon energy E and source–detector pair y, which is discretized at 1 keV intervals, and I 0,j (y) be the corresponding detector response in the absence of a scan subject (i.e., air scan) expressed in noise‐equivalent quanta (NEQ). For an attenuating object, the expected transmission sinogram can be modeled as
| (14) |
where μ(x, E) is the photon linear attenuation coefficient of energy E at image pixel x and h(y|x) is the point‐spread function of the scanner system representing the effective length of the intersection between the beam path y and image pixel x. Note that in most situations, ψ j (y, E) and I 0,j (y) are detector dependent because of the bow‐tie filter.
In the sinogram decomposition process, the energy‐uncompensated (i.e., uncorrected for beam hardening) measurement d j (y) is assumed to equal the expected mean Q j (y). Moreover, based on the BVM model [Eq. (2)], two line integrals corresponding to the two bases are defined as
| (15) |
implying that
| (16) |
The two BVM component line integrals L i (y) are solved from Eq. (16) for each source–detector pair y independently via Newton's method. After the decomposition, the two corresponding images of BVM component weights, c i (x), are obtained from L i (y) using the FBP algorithm.
The ρ e and I‐value can then be predicted by plugging the reconstructed BVM component weights into Equations. (3) and (4). Moreover, to comprehensively compare with the image‐domain decomposition approach, the two calibration‐based ρ e −Z eff models are also extended into the sinogram‐domain decomposition approach31 via computing two monochromatic HU images at the effective energies of low‐ and high‐energy scans (55 and 69 keV for the 90 and 140 kVp spectra, respectively) for both calibration and test phantoms.
2.B.3. Dual‐energy joint SIR approach
Our JSIR‐BVM method for SPR estimation is based on the DEAM algorithm41, 42 that reconstructs the two images of BVM component weights directly and simultaneously from the two energy‐uncompensated sinograms d L(y) and d H(y). Unlike the sinogram‐domain decomposition approach that finds the exactly decomposed line integrals, the reconstruction process in the DEAM algorithm is based on a statistical model of CT data and formulated as a penalized maximum likelihood estimation (MLE) problem.
Although the signal statistics of energy‐integrating detectors theoretically follows a compound Poisson model, our prior work shows that for clinical CT, the modified Poisson model is an accurate approximation.53, 54 Thus, the measured transmission data d j (y) are assumed to be independently Poisson distributed with the expected mean parameterized by BVM component weights as
| (17) |
The DEAM algorithm finds the two BVM component images by minimizing the following objective function:
| (18) |
The first term in the objective function is the data‐fitting term. Based on the assumption of Poisson statistics, maximization of the log‐likelihood of c i is equivalent to minimization of the I‐divergence55 between the measured transmission data d j and the estimated mean values Q j over c i ,42, 56
| (19) |
The second term in the objective function is a regularization term that penalizes the difference between neighboring pixels in order to enforce smooth images. The spatial penalty function R(c i ) is formulated as
| (20) |
where
| (21) |
is the adjacent neighborhood of pixel x, and w x,k is an inverse distance weight for each pixel pair. The Huber‐type potential function ϕ(t) has a quadratic region for |t| < 1/δ and a linear region for |t| > 1/δ, which is able to preserve edges while suppressing noise.57 The parameter λ in the objective function [Eq. (18)] controls the trade‐off between data fitting and image smoothness. A larger λ produces images with smaller noise level but lower resolution.
The optimization problem is solved iteratively by minimizing a surrogate function in each iteration. Details of the derivation and implementation of the DEAM algorithm can be found in O'Sullivan et al.42 Acceleration techniques such as ordered subsets58 and heuristic step‐size are also used in our implementation to speed up the convergence of the algorithm.
2.C. Performance assessment
2.C.1. Intrinsic SPR modeling accuracy
The accuracy with which the three different two‐parameter models reproduce SPRs was tested by comparing the theoretical model predictions against the computed ground truth of SPRs for the tabulated mass densities and element compositions of 34 ICRU reference human tissues.48, 49
The photon linear attenuation coefficients were computed by applying the mixture rule to the elemental mass attenuation coefficients from the National Institute of Standards and Technology (NIST) XCOM database.59 To evaluate the two ρ e −Z eff models, the theoretical CT numbers were then calculated by taking the average over the known x‐ray energy‐fluence spectrum ψ(E) as
| (22) |
where μ(E) and μ water(E) are the attenuation coefficients of the scanned material and water, respectively. The BVM component weights were estimated via Eq. (2) by least‐square‐fitting weighted by the source spectrum.
Figure 1 shows the low‐ and high‐energy spectrum that were computed by the Birch–Marshall model60 for 90 and 140 kVp tube potentials with 12 mm Al filtration.
Figure 1.
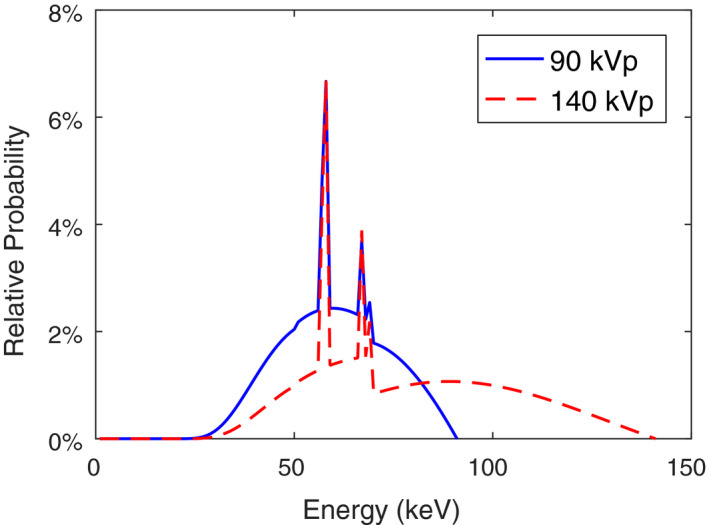
The normalized detector response‐weighted spectra of the two CT scans used in the simulation. [Color figure can be viewed at wileyonlinelibrary.com]
Ground‐truth SPR values were computed by the Bethe equation [Eq. (1)] for various tissues, where electron densities were computed by applying the mixture rule to their known densities and atomic compositions, and I‐values were obtained by applying the Bragg additivity rule to the ICRU‐recommended elemental I‐values including the recommended gaseous to solid/liquid phase corrections.61
2.C.2. Simulation of DECT sinograms
A series of synthetic sinograms were generated for test phantoms containing the 34 reference human tissues to evaluate the accuracy of different SPR mapping approaches and models in the presence of image noise and other uncertainties inherent in the CT reconstruction process. The proprietary geometry of the Philips Brilliance Big Bore CT scanner (Philips Medical Systems, Cleveland, OH) was used throughout the simulation. The same 90 and 140 kVp spectra used for the theoretical calculation are assumed for the sinogram simulation. The spectra were mathematically hardened using the known geometry and density of the TeflonTM bow‐tie filter giving rise to detector‐dependent spectra, ψ j (y, E). Image reconstructions were processed with 1 × 1 mm pixel size and 3 mm slice thickness.
Scatter‐free transmission sinograms were generated for virtual phantoms with different levels of Poisson noise. Noiseless sinograms that represent the ideal case of infinite source intensity were generated via Eq. (14). The noise level was varied by adjusting the absolute source intensities in the CT data model, while keeping the relative source intensities of the low‐ and high‐energy scans equal. The reference source intensity level (i.e., 100%) was set to 300 and 90 mAs for 90 and 140 kVp, respectively, which were chosen to reproduce the sinogram noise level typical of a clinical adult abdomen scan. A low‐noise case and a high‐noise case were simulated with 200% and 50% source intensities, respectively.
The geometry of the virtual phantoms was designed based on the Gammex RMI 467 phantom, which consists of a cylindrical solid water background of 330 mm diameter with 17 cylindrical inserts of 30 mm diameter (as shown in Fig. 2). Two different realizations were required to include all 34 ICRU human tissue inserts. The standard Gammex tissue substitutes16 were used as the calibration material for the two ρ e −Z eff models in both image‐ and sinogram‐domain decomposition approaches, while a Gammex‐like phantom with polystyrene and CaCl2‐solution inserts was used for calibrating the BVM‐based image‐domain decomposition method. The detailed insert arrangements for each individual phantom can be found in Table 1.
Figure 2.
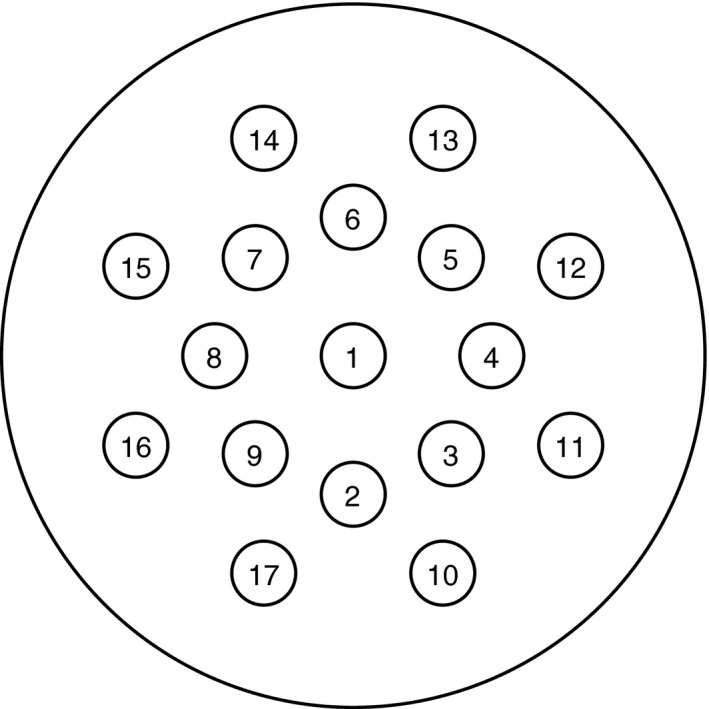
Illustration of the phantom geometry. The insert materials are shown in Table 1.
Table 1.
Arrangement of inserts in the virtual phantoms. The insert locations inside the phantoms are shown in Fig. 2
| No. | Test phantom | Calibration phantom | ||
|---|---|---|---|---|
| Tissue #1 | Tissue #2 | Gammex | BVM basis | |
| 1 | Adipose | Lymph | Solid water | – |
| 2 | Blood (whole) | Brain | Solid water | – |
| 3 | Breast | Cell nucleus | CB2 50% CaCO3 | Polystyrene |
| 4 | Eye lens | GI tract | AP6 adipose | – |
| 5 | Heart (blood filled) | Kidney | SR2 brain | CaCl2 solution |
| 6 | Liver | Lung (deflated) | SB3 cortical bone | – |
| 7 | Lung (inflated) | Muscle | BR12 breast | Polystyrene |
| 8 | Ovary | Pancreas | Water | – |
| 9 | Cartilage | Red marrow | CB2 30% CaCO3 | CaCl2 solution |
| 10 | Yellow marrow | Skin | Solid water | CaCl2 solution |
| 11 | Thyroid | Femur | IB3 inner bone | – |
| 12 | Cranium | Mandible | Solid water | Polystyrene |
| 13 | Humerus | Pelvic sacrum | LN300 lung | – |
| 14 | Spleen | Testis | Solid water | CaCl2 solution |
| 15 | Ribs 10th | Ribs 2nd, 6th | LN450 lung | – |
| 16 | Cortical bone | Spongiosa | B200 mineral bone | Polystyrene |
| 17 | Vertebral C4 | Vertebral D6,L3 | LV1 liver | – |
The impact of object size variations on the estimation accuracy was evaluated by scaling the 330 mm diameter test phantoms to 250 mm diameter (i.e., about 25% smaller than the calibration phantom) with proportionally scaled insert sizes and positions, while calibration processes were based on 330 mm calibration phantoms. Additionally, a series of test phantoms with cortical bone inserts at different positions (i.e., different distances to the phantom center) were generated to assess the impact of position dependence. Only noiseless sinograms were used in these comparisons in order to avoid the impact of random uncertainties.
The simulated sinograms were processed using the three distinct approaches described in Section 2.B. The three different DECT‐SPR models described in Section 2.A were applied to the reconstruction results in both the image‐ and sinogram‐domain decomposition approaches, while only the BVM was applied in the JSIR approach. For the image‐ and sinogram‐domain decomposition methods, the images were reconstructed using the FBP algorithm with a ramp filter modified by a 1.5 mm Gaussian kernel.62 For the JSIR‐BVM method, the regularization parameters in the DEAM algorithm were set to δ = 100 and λ = 6. The parameters were selected to achieve similar resolutions for typical soft tissue contrast from different reconstruction algorithms.62 The DEAM algorithm was run for 600 iterations. Table 2 summarizes the seven combinations of reconstruction approaches and DECT‐SPR models that are investigated in the present study.
Table 2.
Summary of investigated methods
| Approach | Model | Calibration | |
|---|---|---|---|
| img‐BVM | Image‐domain | BVM | Yes |
| img‐HM | Image‐domain | Hünemohr's | Yes |
| img‐BM | Image‐domain | Bourque's | Yes |
| Sino‐BVM | Sinogram‐domain | BVM | No |
| Sino‐HM | Sinogram‐domain | Hünemohr's | Yes |
| sino‐BM | Sinogram‐domain | Bourque's | Yes |
| JSIR‐BVM | Joint SIR | BVM | No |
To quantify the accuracy of the predicted proton SPR image of these virtual test phantoms, relative SPR estimation error is evaluated for all pixels within a region of interest (ROI) of 24 mm diameter inside each homogeneous tissue insert, and then, the average estimation error is calculated for each tissue's ROI. The mean error, the RMS of tissue‐specific average errors (i.e., RMS‐average error), and RMS error over all ROI pixels are then computed as
| (23) |
| (24) |
| (25) |
where N is the number of pixels in each ROI, R k is the ROI of the kth tissue, e x is the relative SPR estimation error at pixel x, and is the average estimation error for the kth tissue. The mean error shows the overall bias of the SPR estimates, while the RMS‐average error measures the variation of the systematic estimation error for different tissues. The RMS error reflects the pixel‐to‐pixel variation in the SPR image.
3. Results
3.A. Intrinsic SPR modeling accuracy
Figure 3 shows the prediction error for each of the three two‐parameter DECT‐SPR models for each reference tissue using the theoretically computed CT numbers and BVM component weights. The minimum, maximum, and RMS errors are summarized in Table 3.
Figure 3.
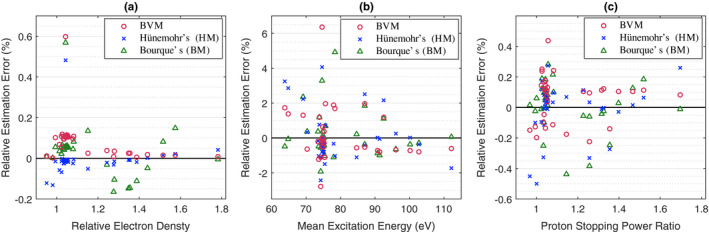
Theoretical residual errors of the three investigated DECT‐SPR models for each reference human tissue, shown as the prediction errors relative to the reference values for (a) electron density relative to water, (b) mean excitation energy, and (c) proton SPR at 200 MeV. The reference tissues are listed in the second and third columns of Table 1. The deflated lung is not shown because it has the same composition as the inflated lung. [Color figure can be viewed at wileyonlinelibrary.com]
Table 3.
Statistics of the theoretical residual errors predicted using the three investigated DECT‐SPR models
| Relative electron density | Mean excitation energy | Proton SPR | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Min (%) | Max (%) | RMS (%) | Min (%) | Max (%) | RMS (%) | Min (%) | Max (%) | RMS (%) | |
| BVM model | 0.00 | 0.59 | 0.13 | −2.79 | 6.36 | 1.55 | −0.23 | 0.44 | 0.16 |
| Hünemohr's model | −0.13 | 0.48 | 0.09 | −2.43 | 4.06 | 1.46 | −0.50 | 0.27 | 0.17 |
| Bourque's model | −0.16 | 0.56 | 0.12 | −1.92 | 4.92 | 1.30 | −0.44 | 0.28 | 0.16 |
All three models show comparable modeling accuracy under idealized conditions. The predicted SPRs of all tissue types are within 0.5% of the reference value and the RMS errors are less than 0.2%. The electron‐density estimation errors are within 0.2% for all tissues with the exception of thyroid tissue. The relatively high‐modeling error for thyroid is mainly due to the existence of iodine (Z = 53), which lies outside the range of typical elements of biological tissues.40
3.B. Impact of reconstructed image intensity uncertainties on SPR estimation
Figure 4 shows the reconstructed CT images from the 100% source intensity‐level synthetic sinograms for the BVM‐based image‐domain decomposition, sinogram‐domain decomposition, and JSIR methods. The image noise levels associated with each method for different levels of source intensity are shown in Fig. 5. All CT images were computed at 60 keV, which is approximately the mean of effective energies of low‐ and high‐energy scans.
Figure 4.

Monochromatic CT images (60 keV) of the tissue #1 phantom reconstructed by the BVM‐based (a) image‐domain decomposition, (b) sinogram‐domain decomposition, and (c) JSIR methods from 100% source intensity sinograms. The display window is set to [−200 HU 200 HU]. The profiles across a bone insert (rib 10th) in the above three images indicated by the solid line are shown in (d). [Color figure can be viewed at wileyonlinelibrary.com]
Figure 5.

Comparison of the image noise level of 60 keV monochromatic CT images from different reconstruction approaches. The image noise level is calculated as the one standard deviation (1σ) of HU values for pixels within selected regions inside the solid water background. [Color figure can be viewed at wileyonlinelibrary.com]
The DEAM‐reconstructed images in the JSIR‐BVM method are fourfold less noisy than the FBP reconstructions in either the image‐ or sinogram‐domain decomposition methods while preserving image sharpness at the high‐contrast insert boundaries. Compared to the image‐domain decomposition method, both the sinogram‐domain decomposition and the JSIR method are able to reduce the streak artifacts between bony inserts in the images. The JSIR method more effectively suppresses such artifacts and achieves more accurate reconstructions. Both CT image noise and residual beam‐hardening artifacts are propagated into the converted SPR images as shown in Fig. 6. The quality of the SPR images derived from the FBP‐based image‐ and sinogram‐domain decomposition methods are compromised by the high image noise.
Figure 6.
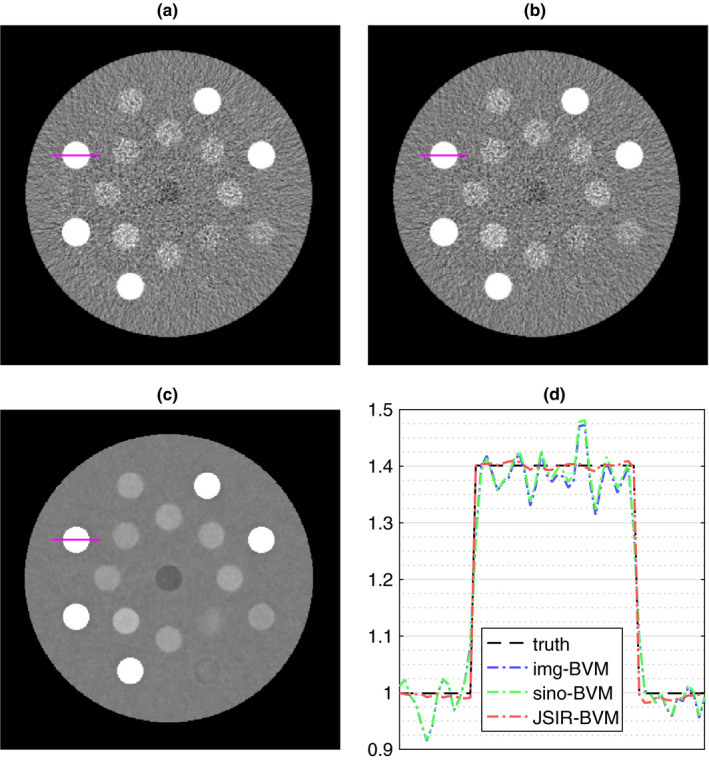
SPR images (200 MeV) of the tissue #1 phantom estimated by the BVM‐based (a) image‐domain decomposition, (b) sinogram‐domain decomposition, and (c) JSIR methods from 100% source intensity sinograms. The display window is set to [0.8 1.2]. The profiles across a bone insert (rib 10th) in the above three images indicated by the solid line are shown in (d). [Color figure can be viewed at wileyonlinelibrary.com]
The systematic difference of the results derived from different methods is much smaller than the insert‐background contrast and therefore difficult to visualize on the images. To more quantitatively compare these methods, Fig. 7 summarizes the estimation accuracy of all seven investigated methods under different source intensity levels. In the noiseless case, all methods achieve small mean errors, that is, less than 0.1% for all except the BVM‐based image‐domain decomposition method. The RMS‐average errors of the sinogram‐domain decomposition and JSIR methods are comparable to the intrinsic modeling error, while those of the image‐domain decomposition methods are approximately twice of the modeling error. The higher estimation errors of the image‐domain decomposition methods in noiseless case can be explained by the systematic image intensity errors, such as the HU nonuniformity due to the impact of residual beam‐hardening effects.
Figure 7.

Relative SPR estimation errors for human tissues from each investigated method as a function of sinogram source intensity levels: (a) mean error for all pixels within ROIs, which equals the mean of average estimation errors for different tissues; (b) RMS of average estimation errors for different tissues (RMS‐average error); and (c) RMS errors for all pixels within ROIs. The seven methods are listed in Table 2. [Color figure can be viewed at wileyonlinelibrary.com]
Among the seven methods, the JSIR‐BVM method has the best performance, which achieves mean and RMS‐average errors of less than 0.05% and 0.3%, respectively, for all noise levels. These errors are close to the intrinsic BVM modeling accuracy. For the same source intensity level, the RMS errors of the JSIR‐BVM method are less than 1/6 of those of all the other six methods, which indicate that the JSIR‐BVM method has much smaller pixel‐to‐pixel SPR variations inside homogeneous regions compared to the other two approaches. Thus, the JSIR‐BVM method achieves high mean estimation accuracy under different noise levels as well as dramatically reduces the statistical uncertainty of SPR estimates.
For all six image‐ and sinogram‐domain decomposition methods, the pixel‐wise variations of SPR estimates are approximately twice as large as the corresponding 60 keV monochromatic CT image noise. The BVM and Hünemohr's model‐based methods exhibit similar noise propagation from the sinogram to the SPR image. Bourque's model‐based methods, however, result in at least 30% larger RMS error than the other methods for the same noise level. Besides introducing random uncertainty into SPR images, sinogram noise also lead to systematic errors for most image‐ and sinogram‐domain decomposition methods. The RMS‐average errors monotonically increase with the sinogram noise level. The mean errors exhibited by both Bourque's and Hünemohr's model‐based methods also increase with increased noise level, while those of BVM‐based methods remain relatively low for all noise levels. The BVM‐based sinogram‐domain decomposition method is the most robust among the six image‐ and sinogram‐domain decomposition methods in the presence of noise.
The sinogram‐domain decomposition methods based on BVM and Hünemohr's model generally achieve lower mean and RMS‐average errors than the corresponding image‐domain decomposition methods. Bourque's model‐based sinogram‐domain decomposition method, however, is the least robust of all the methods. We note that both of the Bourque's model‐based methods show increased mean and RMS‐average errors at high noise levels.
3.C. Impact of test object geometry on SPR estimation
For the scaled 250 mm phantoms, Fig. 8 shows the differences of the mean SPR estimates to the 330 mm test phantoms for various tissue inserts.
Figure 8.
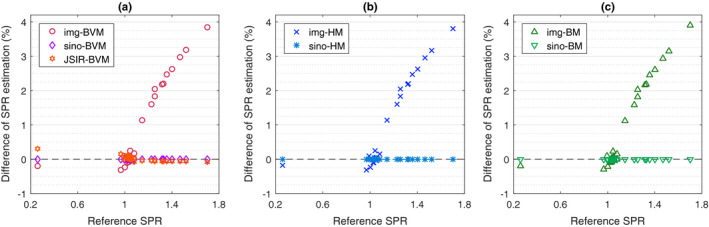
Percent difference of mean SPR estimate for each tissue sample, indexed as functions of reference SPR, due to the test phantom size being changed from 330 mm to 250 mm for (a) BVM model, (b) Hünemohr's ρ e −Z eff model, and (c) Bourque's ρ e −Z eff model in different reconstruction approaches. All calibration curves are derived from the 330 mm calibration phantoms. No noise was added to the sinograms. [Color figure can be viewed at wileyonlinelibrary.com]
As indicated by the results, both the JSIR‐BVM method and the sinogram‐domain decomposition methods, which jointly reconstruct spectrum‐invariant component images, are almost unaffected by the size change. The mean SPR differences between the test phantoms of the two different sizes are less than 0.1% for the same tissue (except for the low‐density deflated lung tissue in the JSIR‐BVM method).
All image‐domain decomposition methods, however, are sensitive to phantom size due to dependence of residual beam‐hardening effects on scan object size, leading to size‐dependent CT numbers in the separately reconstructed images. This effect leads to overestimation of bony tissue SPRs of 1–4% in the 250 mm phantom compared to the 330 mm phantom. Bony tissues with higher Z eff tend to exhibit a larger difference in SPR estimates due to the sensitivity to beam‐hardening effects. It is worth noting that for bony tissues, the reference SPR, which is shown as the x‐axis in Fig. 8, is positively correlated with Z eff. SPR estimates of low‐Z eff tissues, such as the adipose tissue, are reduced about up to 0.3% on the smaller test phantom. This pattern of errors is nearly identical for all three methods. This suggests that the HU differences caused by the residual beam‐hardening effects in the single‐energy reconstructed images are the dominant contribution to the systematic variation of SPR estimates.
We chose the BVM‐based image‐domain decomposition method to further analyze the impact of object geometry. As Fig. 9 shows, both the reconstructed CT image intensities and predicted SPR values of cortical bone tissue depend on both of the phantom size and the radial distance from the phantom center. In the two separately reconstructed images, the CT numbers of the smaller phantom are generally higher than those on the larger phantom. On the same phantom, the CT numbers also increase with the distance to the phantom center. This is due to the fact that the equivalent spectrum passing through the center of a large phantom is harder than that passing through the border of a small phantom. The difference of CT numbers between the central and the peripheral inserts can be as much as 40 HU (i.e., around 1.5%) in both low‐ and high‐energy CT images, which leads to more than 2% increase in the predicted SPR. Similar results are also obtained for the other two image‐domain decomposition methods. On the other hand, the position‐dependent HU variations in the sinogram‐domain decomposition and the JSIR methods are less than 2 HU; thus, the two approaches are able to achieve uniform SPR estimates with less than 0.05% variation across the whole phantom.
Figure 9.
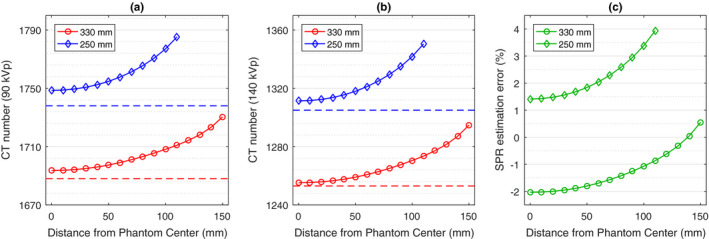
The average CT numbers of the cortical bone sample on the (a) 90 kVp and (b) 140 kVp images reconstructed via FBP and (c) the corresponding relative SPR estimation error from the BVM‐based image‐domain decomposition method as a function of the distance between the center of insert and the center of the phantom. Each phantom contains only one cortical bone insert. The dashed lines in (a) and (b) indicate the expected CT numbers for the cortical bone insert located at the center of 250 and 330 mm phantoms. [Color figure can be viewed at wileyonlinelibrary.com]
4. Discussion
The performance of DECT‐based SPR estimation methods are compromised by two main sources of uncertainties. The first is the material characterization error, which refers to the relationship between material parameters from which SPRs are inferred (i.e., ρ e and I‐value) and the two idealized DECT image intensity measurements. The second class of uncertainties is the error introduced during CT sinogram acquisition and image formation processes, including image noise and systematic uncertainties due to incomplete correction for scatter and beam hardening. Bär et al.10 and Han et al.39 have shown that most currently available DECT models support relatively low intrinsic SPR prediction errors (0.16–0.41% RMS errors). Consistent with the literature, our investigation demonstrates that the three selected material characterization models are able to model the SPR of human tissues with less than 0.2% RMS error. However, we also demonstrate that such high accuracy is not achievable in clinical settings due to the aforementioned image‐formation uncertainties including measurement noise propagation and residual beam‐hardening effects. Moreover, the impact of random noise on method performance is model specific. In our analysis, BVM is the most robust one, while Bourque's model shows the most sensitivity to the noise level. This is possibly due to the high degree of nonlinearity of Bourque's model, which employs three fifth‐order polynomial fittings using only 13 distinct tissue substitutes in the calibration process.
As our results demonstrate, the widely accepted image‐domain decomposition approach is vulnerable to image formation uncertainties. Although it is assumed that the scanning conditions of the calibration phantoms can be identically reproduced for the test phantoms and patients, the anatomy, size, ROI location, and composition of patients may differ from those of the calibration phantoms. Our study shows that even simple dissimilarities, such as size scaling variations or ROI position changes, yield CT number variations that cannot be fully accounted for by the calibration process and thus introduce systematic errors into SPR estimates. Since these image‐domain decomposition methods rely on two separately reconstructed CT images, residual beam‐hardening effects introduce image intensity uncertainties as well as other image artifacts, leading to systematic SPR estimation error much larger than the intrinsic modeling error, thereby limiting the benefit of DECT in mitigating proton range uncertainty. Similar issues caused by uncorrected systematic variations have also been discussed in previous studies.12, 63 Besides the test object variability, CT number variations of the calibration phantoms can also introduce noticeable uncertainties into the SPR estimates of the test objects. Figure 10 shows that rearrangement of the Gammex inserts in the calibration phantom alters soft and bony tissue SPR estimates by as much as 0.4% and 0.8%, respectively. Li et al.23 have also shown that the selection of calibration materials may affect the estimation results.
Figure 10.

Comparison of average SPR estimation error for each tissue sample of Hünemohr's model‐based image‐domain decomposition method calibrated by Gammex phantom with two different insert arrangements. The original arrangement is listed in Table 1 and the modified arrangement is perturbed by exchanging the inner ring and outer ring of inserts. [Color figure can be viewed at wileyonlinelibrary.com]
Although sinogram‐domain decomposition methods suffer less from the systematic uncertainties introduced by geometry changes, they may also show degraded estimation performance in the presence of random noise in the measurement data. Likewise, image‐domain decomposition methods are also vulnerable to noise in the images. Due to the DECT decomposition process being ill‐conditioned, the random sinogram noise is amplified in both image‐ and sinogram‐domain decomposition methods. Moreover, Bär et al.10 have suggested that the impact of random noise cannot be canceled via averaging and may introduce systematic errors into the proton range computation. Our current study confirms that mean errors and RMS‐average errors of most image‐ or sinogram‐domain decomposition methods increase with the elevated sinogram noise.
Our JSIR‐BVM method accounts for both systematic bias correction and random noise suppression and thus shows a robust response to the inherent uncertainties of the acquired sinogram data. Unlike step‐wise methods that perform the two‐parameter estimation on reconstructed HU images, the JSIR‐BVM method directly solves the intertwined problem of the material characterization and image reconstruction. The underlying DEAM algorithm along with a well‐established CT data model dramatically reduces both systematic uncertainties and random noise.42, 43, 62 Based on the linear, separable BVM model, the DEAM algorithm achieves superior estimation accuracy with moderate computational complexity. The result demonstrates that the JSIR‐BVM method supports accurate SPR mapping for various object geometries and outperforms other investigated methods in terms of robustness to noise. As far as we know, our study is the first to investigate the impact of a joint statistical reconstruction method for SPR estimation.
One of the advantages of sinogram‐based and joint reconstruction methods over image‐based methods is that they are able to circumvent the influence from unaccounted beam‐hardening effects. However, all of these methods require an accurate polychromatic forward model, that is, the capacity to compute the expected mean of CT measurement given a known scan object. An important component of forward‐modeling uncertainties is that of the x‐ray spectrum modeling.60, 64, 65, 66, 67 In previous experimental realizations of polychromatic reconstruction methods implemented by our group,43, 52 we have utilized the well‐validated equivalent spectrum method60, 64 to measure the x‐ray spectrum. It was demonstrated that the experimentally determined spectra of all available energies on the Philips Brilliance Big Bore scanner were able to support polychromatic reconstruction of image intensities within 0.5% of the expected ground truth for a variety of object materials and geometries.52 In the present simulation framework, the spectrum‐related errors, including both the assumed spectra for sinogram‐based and JSIR methods as well as the beam‐hardening calibration for image‐based methods, are ignored and thus have no impact on the reported results. While our preliminary results suggest that uncertainties in x‐ray spectra and in‐air profiles only slightly compromise SPR estimates, definitive error analyses have not yet been reported. Realistic assessment of the impact of the spectrum and related forward‐modeling uncertainties on the extracted SPR values is currently underway in our laboratory.
There are several ways in which this study can be made more general and clinically applicable. First, the 90 and 140 kVp x‐ray beams used throughout this work have the same level of external filtration. Additional filters, such as 0.4–0.8 mm tin filters, are used for the high‐energy beam in some commercial DECT scanners to increase the energy separation between the two spectra. It has been shown that this technique is able to partially curb the ill‐conditioning of the DECT decomposition problem and helps improve the estimation results.12, 23, 68, 69 However, the effects of energy pair selection on the SPR uncertainties have not been fully studied. Further simulation studies may include optimization of the energy pair choice and its impact on the performance of proton SPR estimation. Second, the present study neglects the effect of scatter. Unaccounted scatter has been shown to cause artifacts in the reconstructed images,56, 70 which can compromise the performance of quantitative DECT. The evaluation and correction for scatter in both simulation and experimental settings will remain an important topic for our future study. Third, our simulations are based on the exact knowledge of elemental compositions of calibration phantoms. In the clinical setting, uncertainties of actual composition and density of calibration tissue substitutes may also impact the performance of calibration‐based methods. It is recommended for calibration‐based methods that an accurate determination of density and elemental composition of the calibration phantom should be performed at least once prior to calibration scans to mitigate such uncertainties.
5. Conclusion
A novel JSIR‐BVM method for proton SPR mapping, which is built on an iterative statistical reconstruction algorithm integrating the processes of image reconstruction and material decomposition, was introduced and compared against six different image‐ and sinogram‐domain decomposition methods.
Our simulation study shows that though DECT‐SPR models are highly accurate under the idealized conditions, the achievable SPR estimation accuracy is dominated by the systematic uncertainties as well as random noise introduced during the CT reconstruction stage. Among all the investigated methods, the JSIR‐BVM method performs the best. This method demonstrates its immunity to variations of object size and noise level. The mean and RMS‐average errors are well below 0.05% and 0.3%, respectively, and the pixel‐wise variation is reduced by sixfold compared to the other methods.
Conflicts of interest
The authors have no conflicts of interest to disclose.
Acknowledgments
This study was supported by NIH R01 CA 149305, NIH R01 CA 212638, and NIH 5T32EB01485505. We would like to thank Bruce R. Whiting, Tianyu Zhao, and Mariela A. Porras‐Chaverri for their valuable discussions. We would also like to thank Philips, in particular Mr. Paul Khlar, for sharing the proprietary specifications of the Brilliance Big Bore scanner with our group.
References
- 1. Munzenrider JE, Liebsch NJ. Proton therapy for tumors of the skull base. Strahlenther Onkol. 1999;175:57–63. [DOI] [PubMed] [Google Scholar]
- 2. Lomax A, Boehringer T, Coray A, et al. Intensity modulated proton therapy: a clinical example. Med Phys. 2001;28:317–324. [DOI] [PubMed] [Google Scholar]
- 3. Slater JD, Rossi CJ, Yonemoto LT, et al. Proton therapy for prostate cancer: the initial Loma Linda University experience. Int J Radiat Oncol Biol Phys. 2004;59:348–352. [DOI] [PubMed] [Google Scholar]
- 4. Moyers MF, Miller DW, Bush DA, Slater JD. Methodologies and tools for proton beam design for lung tumors. Int J Radiat Oncol Biol Phys. 2001;49:1429–1438. [DOI] [PubMed] [Google Scholar]
- 5. Paganetti H. Range uncertainties in proton therapy and the role of Monte Carlo simulations. Phys Med Biol. 2012;57:R99–R117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Park PC, Zhu XR, Lee AK, et al. A beam‐specific planning target volume (PTV) design for proton therapy to account for setup and range uncertainties. Int J Radiat Oncol Biol Phys. 2012;82:e329–e336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Yang M, Virshup G, Clayton JE, Zhu XR, Mohan R, Dong L. Theoretical variance analysis of single‐ and dual‐energy computed tomography methods for calculating proton stopping power ratios of biological tissues. Phys Med Biol. 2010;55:1343–1362. [DOI] [PubMed] [Google Scholar]
- 8. Yang M, Zhu XR, Park PC, et al. Comprehensive analysis of proton range uncertainties related to patient stopping‐power‐ratio estimation using the stoichiometric calibration. Phys Med Biol. 2012;57:4095–4115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Schneider U, Pedroni E, Lomax A. The calibration of CT Hounsfield units for radiotherapy treatment planning. Phys Med Biol. 1996;41:111–124. [DOI] [PubMed] [Google Scholar]
- 10. Bär E, Lalonde A, Royle G, Lu H‐M, Bouchard H. The potential of dual‐energy CT to reduce proton beam range uncertainties. Med Phys. 2017;44:2332–2344. [DOI] [PubMed] [Google Scholar]
- 11. Bazalova M, Carrier J‐F, Beaulieu L, Verhaegen F. Dual‐energy CT‐based material extraction for tissue segmentation in Monte Carlo dose calculations. Phys Med Biol. 2008;53:2439–2456. [DOI] [PubMed] [Google Scholar]
- 12. Saito M. Potential of dual‐energy subtraction for converting CT numbers to electron density based on a single linear relationship. Med Phys. 2012;39:2021–2030. [DOI] [PubMed] [Google Scholar]
- 13. Landry G, Seco J, Gaudreault M, Verhaegen F. Deriving effective atomic numbers from DECT based on a parameterization of the ratio of high and low linear attenuation coefficients. Phys Med Biol. 2013;58:6851–6866. [DOI] [PubMed] [Google Scholar]
- 14. Hünemohr N, Krauss B, Tremmel C, Ackermann B, Jäkel O, Greilich S. Experimental verification of ion stopping power prediction from dual energy CT data in tissue surrogates. Phys Med Biol. 2014;59:83–96. [DOI] [PubMed] [Google Scholar]
- 15. Hünemohr N, Paganetti H, Greilich S, Jäkel O, Seco J. Tissue decomposition from dual energy CT data for MC based dose calculation in particle therapy. Med Phys. 2014;41:061714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Bourque AE, Carrier J‐F, Bouchard H. A stoichiometric calibration method for dual energy computed tomography. Phys Med Biol. 2014;59:2059–2088. [DOI] [PubMed] [Google Scholar]
- 17. Garcia LIR, Azorin JFP, Almansa JF. A new method to measure electron density and effective atomic number using dual‐energy CT images. Phys Med Biol. 2016;61:265–279. [DOI] [PubMed] [Google Scholar]
- 18. Lalonde A, Bouchard H. A general method to derive tissue parameters for Monte Carlo dose calculation with multi‐energy CT. Phys Med Biol. 2016;61:8044–8069. [DOI] [PubMed] [Google Scholar]
- 19. Farace P. Experimental verification of ion stopping power prediction from dual energy CT data in tissue surrogates. Phys Med Biol. 2014;59:7081–7084. [DOI] [PubMed] [Google Scholar]
- 20. Taasti VT, Petersen JB, Muren LP, Thygesen J, Hansen DC. A robust empirical parametrization of proton stopping power using dual energy CT. Med Phys. 2016;43:5547–5560. [DOI] [PubMed] [Google Scholar]
- 21. Saito M, Sagara S. Simplified derivation of stopping power ratio in the human body from dual‐energy CT data. Med Phys. 2017;44:4179–4187. [DOI] [PubMed] [Google Scholar]
- 22. Kanematsu N, Inaniwa T, Koba Y. Relationship between electron density and effective densities of body tissues for stopping, scattering, and nuclear interactions of proton and ion beams. Med Phys. 2012;39:1016–1020. [DOI] [PubMed] [Google Scholar]
- 23. Li B, Lee HC, Duan X, et al. Comprehensive analysis of proton range uncertainties related to stopping‐power‐ratio estimation using dual‐energy CT imaging. Phys Med Biol. 2017;62:7056–7074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Saito M, Tsukihara M. Exploring the limit for the conversion of energy‐subtracted CT number to electron density for high‐atomic‐number materials. Med Phys. 2014;41:071701. [DOI] [PubMed] [Google Scholar]
- 25. Alvarez RE, Macovski A. Energy‐selective reconstructions in X‐ray computerised tomography. Phys Med Biol. 1976;21:733–744. [DOI] [PubMed] [Google Scholar]
- 26. Lehmann L, Alvarez R, Macovski A, et al. Generalized image combinations in dual KVP digital radiography. Med Phys. 1981;8:659–667. [DOI] [PubMed] [Google Scholar]
- 27. Chuang K‐S, Huang H. Comparison of four dual energy image decomposition methods. Phys Med Biol. 1988;33:455–466. [Google Scholar]
- 28. Schlomka J, Roessl E, Dorscheid R, et al. Experimental feasibility of multi‐energy photon‐ counting k‐edge imaging in pre‐clinical computed tomography. Phys Med Biol. 2008;53:4031–4047. [DOI] [PubMed] [Google Scholar]
- 29. Huh W, Fessler JA. Iterative image reconstruction for dual‐energy X‐ray CT using regularized material sinogram estimates. In: Proc. IEEE Int. Symp. Biomed. Imag. Nano to Macro. Chicago, IL: IEEE; 2011:1512–1515. [Google Scholar]
- 30. Schirra CO, Roessl E, Koehler T, et al. Statistical reconstruction of material decomposed data in spectral ct. IEEE Trans Med Imag 2013;32:1249–1257. [DOI] [PubMed] [Google Scholar]
- 31. Tremblay J‐É, Bedwani S, Bouchard H. A theoretical comparison of tissue parameter extraction methods for dual energy computed tomography. Med Phys. 2014;41:081905. [DOI] [PubMed] [Google Scholar]
- 32. Vilches‐Freixas G, Taasti VT, Muren LP, et al. Comparison of projection‐and image‐based methods for proton stopping power estimation using dual energy ct. Phys Imag Radiat Oncol. 2017;3:28–36. [Google Scholar]
- 33. Yan CH, Whalen RT, Beaupre GS, Yen SY, Napel S. Reconstruction algorithm for polychromatic CT imaging: application to beam hardening correction. IEEE Trans Med Imag. 2000;19:1–11. [DOI] [PubMed] [Google Scholar]
- 34. Heismann B, Balda M. Quantitative image‐based spectral reconstruction for computed tomography. Med Phys. 2009;36:4471–4485. [DOI] [PubMed] [Google Scholar]
- 35. Ivakhnenko VI. A novel quasi‐linearization method for CT image reconstruction in scanners with a multi‐energy detector system. IEEE Trans Nucl Sci. 2010;57:870–879. [Google Scholar]
- 36. van Abbema JK, van Goethem M‐J, Greuter MJ, van der Schaaf A, Brandenburg S, van der Graaf ER. Relative electron density determination using a physics based parameterization of photon interactions in medical DECT. Phys Med Biol. 2015;60:3825–3846. [DOI] [PubMed] [Google Scholar]
- 37. Sukovic P, Clinthorne NH. Penalized weighted least‐squares image reconstruction for dual energy x‐ray transmission tomography. IEEE Trans Med Imag. 2000;19:1075–1081. [DOI] [PubMed] [Google Scholar]
- 38. Huh W, Fessler JA, Alessio AM, Kinahan PE. Fast kVp‐switching dual energy CT for PET attenuation correction. In: Nuclear Science Symposium Conference Record (NSS/MIC), 2009 IEEE. Orlando, FL: IEEE; 2009:2510–2515. [Google Scholar]
- 39. Han D, Siebers JV, Williamson JF. A linear, separable two‐parameter model for dual energy CT imaging of proton stopping power computation. Med Phys. 2016;43:600–612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Han D, Porras‐Chaverri MA, O'Sullivan JA, Politte DG, Williamson JF. On the accuracy of parametric two‐parameter photon cross‐section models in dual‐energy CT applications. Med Phys. 2017;44:2438–2446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. O'Sullivan JA, Benac J, Williamson JF. Alternating minimization algorithm for dual energy X‐ray CT. In: Proc. IEEE Int. Symp. Biomed. Imag. Nano to Macro. Vol. 1; 2004:579–582. [Google Scholar]
- 42. O'Sullivan JA, Benac J. Alternating minimization algorithms for transmission tomography. IEEE Trans Med Imag. 2007;26:283–297. [DOI] [PubMed] [Google Scholar]
- 43. Chen Y, O'Sullivan JA, Politte DG, et al. Line integral alternating minimization algorithm for dual‐energy X‐ray CT image reconstruction. IEEE Trans Med Imag. 2016;35:685–698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Zhang S, Han D, Politte DG, et al. Basis vector model based method for proton stopping power estimation from experimental dual energy CT data. Med Phys. 2016;43:3756. [Google Scholar]
- 45. Zhang S, Han D, Politte DG, Williamson JF, O'Sullivan JA. Comparison of integrated and post‐reconstruction dual‐energy ct proton stopping power ratio estimation approaches. Med Phys. 2017;44:3004. [Google Scholar]
- 46. Bethe H. Zur theorie des durchgangs schneller korpuskularstrahlen durch materie. Ann Phys. 1930;397:325–400. [Google Scholar]
- 47. Williamson JF, Li S, Devic S, Whiting BR, Lerma FA. On two‐parameter models of photon cross sections: application to dual‐energy CT imaging. Med Phys. 2006;33:4115–4129. [DOI] [PubMed] [Google Scholar]
- 48. ICRU . Tissue substitutes in radiation dosimetry and measurement. Report No. 44. ICRU, Bethesda, MD; 1989.
- 49. White D, Woodard H, Hammond S. Average soft‐tissue and bone models for use in radiation dosimetry. Br J Radiol. 1987;60:907–913. [DOI] [PubMed] [Google Scholar]
- 50. Herman GT, Trivedi SS. A comparative study of two postreconstruction beam hardening correction methods. IEEE Trans Med Imag. 1983;2:128–135. [DOI] [PubMed] [Google Scholar]
- 51. Herman GT. Correction for beam hardening in computed tomography. Phys Med Biol. 1979;24:81–106. [DOI] [PubMed] [Google Scholar]
- 52. Evans JD, Whiting BR, Politte DG, O'Sullivan JA, Klahr PF, Williamson JF. Experimental implementation of a polyenergetic statistical reconstruction algorithm for a commercial fan‐beam CT scanner. Phys Med. 2013;29:500–512 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Whiting BR. Signal statistics in X‐ray computed tomography. In: Proc. SPIE 4682, Med. Imag; 2002:53–60.
- 54. Lasio GM, Whiting BR, Williamson JF. Statistical reconstruction for X‐ray computed tomography using energy‐integrating detectors. Phys Med Biol. 2007;52:2247–2266. [DOI] [PubMed] [Google Scholar]
- 55. Csisáar I. Why least squares and maximum entropy? an axiomatic approach to inference for linearinverse problems. Ann Stat. 1991;19:2032–2066. [Google Scholar]
- 56. Williamson JF, Whiting BR, Benac J, et al. Prospects for quantitative computed tomography imaging in the presence of foreign metal bodies using statistical image reconstruction. Med Phys. 2002;29:2404–2418. [DOI] [PubMed] [Google Scholar]
- 57. Stevenson R, Delp E. Fitting curves with discontinuities. In: Proc. the first international workshop on robust computer vision; 1990:127–136.
- 58. Degirmenci S, Politte DG, Bosch C, Tricha N, O'Sullivan JA. Acceleration of iterative image reconstruction for X‐ray imaging for security applications. In: Proc. SPIE 9401, Comput. Imag; 2015:94010C.
- 59. Berger M, Hubbell J, Seltzer S, et al. XCOM: Photon cross section database (version 1.5). Tech. Rep. National Institute of Standards and Technology Gaithersburg, MD; 2010.
- 60. Birch R, Marshall M. Computation of bremsstrahlung X‐ray spectra and comparison with spectra measured with a Ge (Li) detector. Phys Med Biol. 1979;24:505–517. [DOI] [PubMed] [Google Scholar]
- 61. ICRU . Stopping powers for electrons and positrons. Report No. 37 ICRU, Bethesda, MD; 1984.
- 62. Evans JD, Politte DG, Whiting BR, O'Sullivan JA, Williamson JF. Noise‐resolution tradeoffs in x‐ray CT imaging: a comparison of penalized alternating minimization and filtered backprojection algorithms. Med Phys. 2011;38:1444–1458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63. Yang M, Virshup G, Clayton JE, Zhu XR, Mohan R, Dong L. Does kV–MV dual‐energy computed tomography have an advantage in determining proton stopping power ratios in patients?. Phys Med Biol. 2011;56:4499–4515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64. Boone JM. The three parameter equivalent spectra as an index of beam quality. Med Phys. 1988;15:304–310. [DOI] [PubMed] [Google Scholar]
- 65. Poludniowski GG, Evans PM. Calculation of x‐ray spectra emerging from an x‐ray tube. Part I. Electron penetration characteristics in x‐ray targets. Med Phys. 2007;34:2164–2174. [DOI] [PubMed] [Google Scholar]
- 66. Poludniowski GG. Calculation of x‐ray spectra emerging from an x‐ray tube. Part II. X‐ray production and filtration in x‐ray targets. Med Phys. 2007;34:2175–2186. [DOI] [PubMed] [Google Scholar]
- 67. Poludniowski GG, Landry G, DeBlois F, Evans P, Verhaegen F. SpekCalc: a program to calculate photon spectra from tungsten anode x‐ray tubes. Phys Med Biol. 2009;54:N433. [DOI] [PubMed] [Google Scholar]
- 68. Primak A, Ramirez Giraldo J, Liu X, Yu L, McCollough CH. Improved dualenergy material discrimination for dual‐source CT by means of additional spectral filtration. Med Phys. 2009;36:1359–1369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69. Vilches‐Freixas G, Létang JM, Ducros N, Rit S. Optimization of dual‐energy ct acquisitions for proton therapy using projection‐based decomposition. Med Phys. 2017;44:4548–4558. [DOI] [PubMed] [Google Scholar]
- 70. Glover GH. Compton scatter effects in CT reconstructions. Med Phys. 1982;9:860–867. [DOI] [PubMed] [Google Scholar]


