Model Driven Optimization of Magnetic Anisotropy of Exchange-coupled Core-Shell Ferrite Nanoparticles for Maximal Hysteretic Loss

Abstract

This study provides a guide to maximizing hysteretic loss by matching the design and synthesis of superparamagnetic nanoparticles to the desired hyperthermia application. The maximal heat release from magnetic nanoparticles to the environment depends on intrinsic properties of magnetic nanoparticles (e.g. size, magnetization, and magnetic anisotropy), and extrinsic properties of the applied fields (e.g. frequency, field strength). Often, the biomedical hyperthermia application limits flexibility in setting of many parameters (e.g. nanoparticle size and mobility, field strength and frequency). We show that core-shell nanoparticles combining a soft (Mn ferrite) and a hard (Co ferrite) magnetic material form a system in which the effective magnetic anisotropy can be easily tuned independently of the nanoparticle size. A theoretical framework to include the crystal anisotropy contribution of the Co ferrite phase to the nanoparticles total anisotropy is developed. The experimental results confirm that this framework predicts the hysteretic heating loss correctly when including non-linear effects in an effective susceptibility. Hence, we provide a guide on how to characterize the magnetic anisotropy of core-shell magnetic nanoparticles, model the expected heat loss and therefore, synthesize tuned nanoparticles for a particular biomedical application.

INTRODUCTION

Current research on magnetic nanoparticles (MNP) is motivated by biomedical applications utilizing their heat generation capacity in alternating magnetic fields to induce tumor necrosis, remotely release drugs, or stimulate cellular signaling or gene transcription^1-3. These applications require the design and synthesis of MNPs with maximal heat loss, while limiting some experimental parameters. Possible damage to tissue without MNP (i.e., by eddy current heating) limits the product of magnetic field frequency and strength limits⁴. Typically the magnetic field frequency is kept below 1 MHz, and the field strength below 20kA/m. To allow the MNPs to diffuse freely between cells, their hydrodynamic diameter after biocompatible coating should be below 30 nm, limiting their magnetic core to less than 20 nm. This leaves the MNP’s saturation magnetization (M_s) and the effective magnetic anisotropy to maximize the specific loss power (SLP)⁵.

Core-shell MNPs designed to merge the advantageous magnetic properties of soft and hard magnetic materials^6,7 have shown excellent SLP values and promise tunability of the magnetic anisotropy. Among them, manganese and cobalt substituted ferrites meet the physical requirements to build up exchange-coupled magnetic single domains where the magnetic properties must be averaged over the entire particle volume ^8,9. Customizing this anisotropy to maximize the SLP requires a reliable and predictive theoretical framework. Hence, we develop a theory on how to integrate the magnetic properties of the bulk Mn- and Co-ferrites in one core-shell MNP, and demonstrate its validity on a set of MNPs with diameters around 14 nm. This set includes pure Mn- and Co-ferrite MNPs and three core-shell assemblies: one with Co-ferrite core and Mn-ferrite shell (denoted as Co@Mn) and two with Mn-ferrite and Co-ferrite shell of varying thicknesses (Mn@Co and Mn@Co-TL /Thin Layer).

EXPERIMENTAL SECTION

Materials

iron(III) acetylacetonate (99%), cobalt(II) acetylacetonate (97%), manganese(II) acetylacetonate (99%) or manganese(II) chloride (98%), 1,2-hexadecanediol (90%), oleic acid (98%), oleylamine (70%), benzyl ether (99%) and dioctyl ether (99%) were purchased from Sigma-Aldrich and used as received without purification.

Synthesis

Core-shell ferrites were synthesized by adapting seed-growth methods of metal precursors (Fe, Co and/or Mn)¹⁰. Seeds, core-shell and single-phase magnetic nanoparticles (MNPs) were produced by thermal decomposition of metal precursors (i.e., iron(III) acetylacetonate, cobalt(II) acetylacetonate, manganese(II) acetylacetonate or manganese(II) chloride) in the presence of 1,2-hexadecanediol, oleic acid and oleylamine, in high boiling point organic solvents (benzyl ether or dioctyl ether), following largely protocols for single-phase MNPs^11,12 or core-shell ferrite MNPs². In order to produce colloids with the desired sizes and structure (single-phase or core-shell), we combined and adapted existing methods, except for the production of Mn ferrite MNPs with d ~ 14 nm, which followed ¹². (See the supporting information for details).

The MNPs were transferred to the aqueous phase by coating with an amphiphilic polymer (dodecyl-grafted-poly-(isobutylene-alt-maleic-anhydride / PMA), which confers colloidal stability in high ionic strength media¹³, and provides carboxylic groups for further functionalization with other macromolecules.

Characterization

Gel electrophoresis in an agarose gel (2% w/w) electrophoresis (100 V, 200 mA and 60 min) was used to inspect the monodispersity of the sample and to separate polymer-coated MNPs from empty polymer micelles following published procedures¹³. Sample images were acquired in a JEM-1230 transmission electron microscope and an ORIOUS SC1000 4008×2672 pixels CCD camera (Gatan UK, Abingdon Oxon, UK). In order to estimate the thickness of the PMA shell we performed TEM with Uranyl acetate negative staining. Samples were prepared on carbon film 400 copper mesh grids purchased from Electron Microscopy Sciences (Hatfield, USA), which were treated with glow-discharge under air plasma for 20 s (2.0·10-1 atm and 35 mA). Dynamic Light Scattering (DLS) and ζ-potential of the as synthesized MNPs (i.e., coated with aliphatic chains) and PMA-coated hydrophilic NPs were analyzed using a Zetasizer Nano-ZS, Malvern Instruments. The composition of the MNPs was analyzed by induction coupled plasma mass spectrometry (ICP-MS, Agilent 7500 Series). Magnetic characterization has been performed directly in colloidal suspensions (M vs H measurements at RT) and in samples obtained by drying the colloidal dispersion on semi-permeable filter paper (M vs H and M vs T measurements). Hysteresis loops at 5 K and 300 K to a maximum field of 6.5 T and the measurements of magnetization versus temperature (at 1 mT and 10 mT in the temperature range of 5-300 K) have been carried out using a Quantum Design MPMS-7 SQUID magnetometer. Hysteresis loops at RT in colloidal samples were performed in a custom built VSM magnetometer up to a maximum field of 1.8 T with high low field resolution. Specific Power Loss measurements were performed using a custom build, water-cooled coil driven by a power supply from MSI Automation Inc. (Wichita, Kansas). The coil’s mean radius was 2.4cm and had 6 turns. The sample temperature was recorded using a fiber optic temperature sensor (T1S-03-WNO-B05) and an analogue to digital converter (ReFlex) from Neoptix (Quebec, Canada). The sample holder was doubled walled glass, sealed with a plastic cap. Annular air gaps between the glass walls of the sample holder and between the sample holder and the coil ensured near adiabatic conditions for small temperature changes. The samples, water-based suspensions of each synthesized MNP, were subjected to magnetic field for 15 s and the temperature rise was simultaneously recorded. The mean magnetic flux density along the sample column (1 cm) was (22.4 kA/m) at 412.5 kHz for all the samples.

RESULT AND DISCUSSION

The diameter of the resulting inorganic MNPs (d_in) shows good monodispersity (~10%) (Table 1, Figure S1). Their hydrodynamic diameter (d_h) measured by dynamic light scattering increased due to the polymer coating by 2.7 ± 0.7 nm (Table S2), consistent with the shell thickness (d_s) observed by negative staining (Figure 1f). The chemical composition of Mn and Co ferrite phases calculated from ICP-MS data (Table3S in S.I.) was found to be similar in all samples, about Mn_0.3Fe_2.7O₃ and Co_0.5Fe_2.5O₃ respectively

Table 1.

Size, composition, and magnetic properties of the core-shell samples

Sample	din ±σα (nm)	dcore±σα (nm)	Co α % vol	Ms(RT) α (Am2/kg)	Mr/Ms α (5K)	μ0Hcα (5K) (T)
Mn	13.9±1.9	13.9±1.9	0	90.5	0.47	0.026
Co@Mn	12.9±1.4	6.7±1.0	14	87	0.75	0.505
Mn@Co-TL	14.3±1.5	10.2±1.1	63	84	0.80	1.268
Mn@Co	13.8±1.3	7.3±1.0	85	82	0.87	2.20
Co	15.3±1.6	15.3±1.6	100	80	0.88	1.84

^αDiameter of the inorganic MNP (core + shell) and of the inorganic core (d_core); Co ferrite volume fraction in the core-shell structure, saturation magnetization (M_s) at RT, reduced remanence (M_r/M_s) at 5°K and coercive field (μ₀H_c ) at 5°K.

Figure 1.

a-e) TEM micrographs of PMA-coated MNPs, i.e., Mn, Co@Mn, Mn@Co-TL, Mn@Co and Co ferrites. f) Negative staining TEM micrograph of Mn@Co-TL, which shows a homogeneous coating around the MNPs of ca. 3 nm.

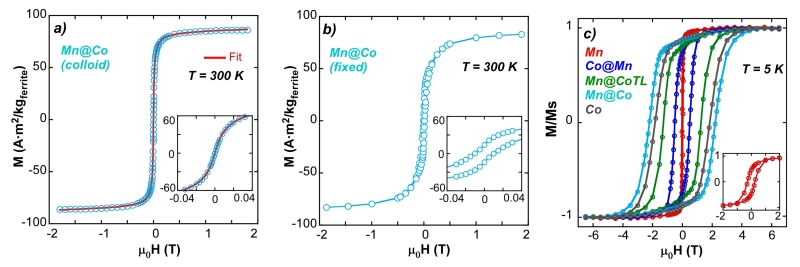
The magnetization versus field measurements of the MNPs rich in Co ferrite (pure Co, Mn@Co and Mn@Co-TL) show significant hysteresis at room temperature (RT) in fixed, dried samples (Figures 2b, S3 and S4). However, the same measurements obtained directly in colloidal suspension show no hysteresis (inset Figure 2a) as then the Co ferrite rich NPs are free to orient themselves to a slowly varying external magnetic field. Thus, the magnetic response is almost perfectly superparamagnetic behavior, because only the magnetostatic term ($-\overrightarrow{m}\cdot \overrightarrow{B}$, where $\overrightarrow{m}$ is the total magnetic moment) contributes to the total energy at thermal equilibrium. This means that these M(H) curves in colloidal suspension are also described by a Langevin function and provide an easy way to estimate an effective magnetic size (see S.I.), which is also obviously true for the other intrinsically superparamagnetic samples (Mn and Co@Mn). The average magnetic diameter obtained this way are between 13 and 15 nm (d_MvsH in Table 2, see S.I.)). The good agreement with the physical size of the inorganic part (d_in) proves that core and shell act as an exchange couple MNP. Moreover, the saturation magnetization (M_s) values obtained in powder samples are consistent with the average volume fraction of both pure ferrites, and therefore with the formation of core-shell particles (Table 1, see S.I.).

Figure 2.

Magnetization versus field measurements at low temperature and RT and for immobilized and freely rotating MNPs. a) M(H) curve of Mn@Co at RT and colloidal sample and the corresponding Fit b) M(H) curve at RT of Mn@Co colloidal sample deposited on filter paper (fixed NPs). c) M(H) curves at 5K of the 5 samples (fixed NPs)

Table 2.

Magnetic variables from the magnetization versus magnetic field curves (MvsH) and ZFC branch

Sample	dMvsH±σMvsHα (nm)	dZFC±σZFCα (nm)	K0 α (kJ/m3)	K1α (kJ/m3)	Q α (meV)	Keff_RTα (kJ/m3)	SLPcal.α (W/g)	SLPexpα (W/g)
Mn	13.4±1.7	13.7±2.2	20	6	3.4	15	190±60	184±2
Co@Mn	12.3±1.5	12.8±1.5	117	117	10.5	39	560±50	553±10
			2μ0μBHe (meV)	αλ (meV)	a (meV)	Keff_RT (kJ/m3)
Mn@Co-TL	14.4±1.4	14.1±1.6	30	12.8	17.6	53	340±50	291±1
Mn@Co	13.5±4.3	13.8±1.6	30	13.0	17.1	85	320±40	302±15
Co	15.6±3.4	15.0±1.9	50	13.1	21.0	95	280±30	316±9

^αd_MvsH and σ_MvsH (in colloidal samples at RT). d_ZFC, σ_ZFC and K_eff at RT for the 5 samples; K₀, K₁ and activation energy (Q) for Mn and Co@Mn samples; and the strength of the exchange field (2μ₀μ_BH_e), the L-S coupling (αλ) and the crystal field perturbation (a) for Mn@Co-TL, Mn@Co and Co samples; calculated SLP values from Figure 4 for the corresponding d_in of each sample (uncertanties are estimated from the experimental error of d_in, σ, d_h, M_s, and fixed to 3% for K_eff); experimental SLP together with its experimental error.

The magnetic anisotropy in nanoscale materials composed of single magnetic domains is typically determined from the thermal dependence of the magnetization ^14,15. In the simplest approximation, the activation temperature (T_bl, blocking temperature) of the superparamagnetic state (SPM) becomes proportional to the energy barrier E_B between equivalent easy directions:

$$T_{bl}=E_B∕ln({\tau }_m∕{\tau }_0)k_B$$ (1)

where k_B is the Boltzmann constant and τ₀ is the inverse of the so-called frequency of jump attempts, usually between 10⁻⁹ and 10⁻¹¹ s, assuming an Arrhenius-type time relaxation where τ_m represents the time window of the experiment. The effective magnetic anisotropy, K_eff, is defined by E_B = K_effV, with V being the particle volume and is affected by the shape of the MNP and by the magneto-crystalline anisotropy (K_c) of its material, including surface effects. Equation (1) allows estimating the effective anisotropy by measuring the magnetization versus temperature after cooling the sample in zero field (zero field cooling (ZFC)). At temperatures close to the maximum of the ZFC, the term ln(τ_m/τ₀) is typically approximated to 25 (assuming τ_m = 100 s and τ₀ = 10⁻⁹ s). However, at any other temperature some extrapolation and additional modeling concerning the thermal dependence of the anisotropy are needed^16,17. This is particularly critical in Co containing NPs, where the effective anisotropy determined at low temperature becomes useless for reliable predictions of SLP at room temperature, for instance.

Often, there exists only one easy direction, either because the crystal has one axis with high symmetry, or because the shape anisotropy (proportional to ${\mu }_0{M}_s^2$) dominates the system as MNP are rarely perfectly spherical and the magneto-crystalline anisotropy (K_c) is small^18,19. In those cases the anisotropy is called uniaxial (K_eff = K_u). Examples are magnetite and soft magnetic materials, such as pure Mn-ferrite. However, in Co-ferrite the magneto-crystalline anisotropy (K_c) is positive, expected to be cubic and very large compare to Mn-ferrite, and K_eff becomes K_c/4 ²⁰. As observed in the Figure 3c, hysteresis loops at 5K of Co rich core-shell MNPs show indeed quite large coercive fields (>1.5 T) and remnant magnetizations above 0.8 M_s (see Table 1), pointing to a predominantly magneto-crystalline cubic character in the Co richest MNPs²¹

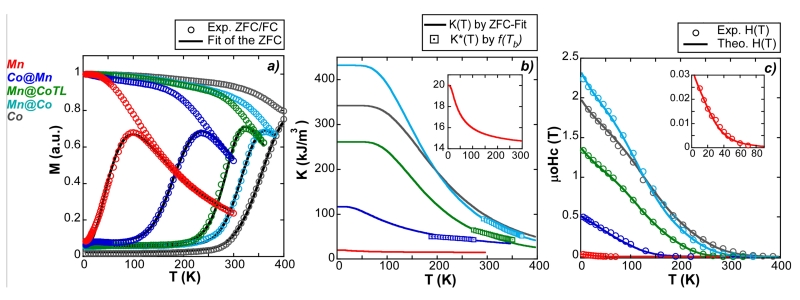
Figure 3.

a) Experimental ZFC/FC measurements at 1 mT (circular markers) with the fit of the ZFC branch (solid line). b) K_eff(T). obtained from the fit of the ZFC (solid line) and K_eff^*(T) from the statistical approach (square markers); the inset gives a closer look of the Mn curve. c) Experimental thermal dependence of coercive field (μ₀H) (circular markers) and theoretical H(T) function (solid line) calculated by equation (5) and using the obtained K_eff(T).

The challenge in modeling the magnetic properties and the SLP of Co-/Mn-ferrite is how to account for the Co’s phase contribution to the total anisotropy. We show here that in a core-shell geometry, contrary to mixed Co-/Mn-ferrite MNPs ²², the contribution of both phases can be weighted by volume to combine an effective anisotropy with minor corrections for interface effects between the two phases, and how a temperature description of K_eff allows prediction of SLP data.

In inverse spinel ferrites, Co²⁺ cations at octahedral or B sites contribute strongly to the cubic magneto-crystalline anisotropy because their ground state retains some orbital degeneracy and is embedded in a crystal field of reduced symmetry²³ , due to the trigonal arrangement of the six next nearest cation neighbours at B sites The theoretical basis of the anisotropy in Co containing ferrites dates back to the 1950s explaining many bulk material observations ^24,25. In short, the expression for K_c(T) calculated by Tachiki ²⁶ depends on three free parameters that measure the strength of the exchange field (molecular field) (2μ₀μ_BH_e) , the L-S coupling (αλ) and a crystal field perturbation (a), which accounts for the reduced symmetry originated by the presence of different cations in the octahedral sites. This perturbation (a), that reduces the anisotropy according to the ratio: ~ αλ/a, acts as soon as octahedral B sites are occupied by different atomic species. For instance, it means that each Co²⁺ ion contributes less to the anisotropy as the Co content increases in Co-substituted magnetite ^27,28 or in chemically mixed ferrites ²⁹. Ultimately the model for the cubic anisotropy constant in pure Co-ferrite is a thermally activated process of the form:

$$K_c(\alpha \lambda ,a,T)=F(\alpha \lambda ,a,T)-G(\alpha \lambda ,a,T)e^{-2{\mu }_0{\mu }_B{H}_e∕k_{B}T}$$ (2)

where $\mathcal{F}$ and $\mathcal{G}$ are explicit functions of the L-S coupling, crystal field splitting and temperature (details in S.I) and K_c goes to zero in the limit T = ∞. For Co ferrite rich samples we propose to weight contributions proportional to the phases’ volume: K_eff(T) = (%Co)×K_c/4, where K_c is given by equation 2 with, for simplicity, only one type of neighbor configuration, due to Co²⁺ and Fe³⁺, included. Under this approach, all the effects of the crystal field, including surfaces/boundaries effects and off-stoichiometry effects, are implicitly included in an effective crystal field parameter, a. Other contributions to the anisotropy due to Mn⁺², Fe⁺³ and shape are neglected.

Testing the quantitative validity of this approach in MNPs is greatly facilitated if the theoretical K_eff(T) can be implemented in a simple framework as the non-interacting single domain theory³⁰. Then, the magnetization versus temperature (ZFC) can be fitted to an explicit function of temperature composed of two terms, corresponding to the thermally activated (first) and blocked MNPs (second) as follows:

$$M_{ZFC}\left(T\right)={\int }_0^{V_c(K_{eff},T)}{M}_{s}L\left(\frac{MVH}{k_{B}T}\right)f\left(V\right)dV+{\int }_{V_c(K_{eff},T)}^{\infty }{M}_s\frac{MH}{3K_{u,c}}f\left(V\right)dV$$ (3)

where, L(x) is the Langevin function, and M and M_s represent respectively the domain and the saturation magnetizations and f(V, σ_v ) is the size distribution of the MNPs. The integrals are distinguished by the critical volume function V_c = V_c(K_eff,T), which describes the volume fraction of thermally activated MNPs at a certain temperature³¹. Possible interparticle interactions are not taken into account because the average interparticle distance is large in the dilute aqueous colloidal suspensions used for the measurements (>50 nm). This assumption is supported by the insensitivity of ZFC/FC to the strength of the applied field (1 or 10 mT) (Figure S5) ^32,33.

The peak ZFC magnetization of the core-shell and pure Mn and Co ferrite MNPs (Figure 3a) shift to higher temperatures and sharpen with increasing Co-ferrite content. The superimposed black lines in Figure 3a represent fits using equation (3), whose outputs are the function K_eff(T), mean diameter (d_ZFC) and standard deviation (σ_ZFC).; the latter are found to be consistent with TEM analysis in all cases (Table 2). For Co ferrite-rich MNPs (Mn@Co-TL, Mn@Co and pure Co) with ${\mu }_0{M}_s^2$ ≪ K_c(0), the fits use the Tachiki model (equation 2), extracting direct physical conclusions. The L-S coupling is similar in the three samples (αλ~13 meV), which is expected as it is affected by the local symmetry around the Co⁺² cations. The strengths of interactions described in equation (2), (μ_BH_e, αλ, a), are found to be similar in the two core-shell Co richest samples Mn@Co-TL and Mn@Co, being that the resulting K_eff(T) is fully consistent with the known core/shell volume fraction (60 and 85 % respectively). This discards the existence of significant mixing of Mn and Co phases²² and fits perfectly in the core-shell model, where the magnetic anisotropies are additive effect, mostly proportional to the Co ferrite volume fraction. The resulting exchange or molecular field of pure Co ferrite MNPs μ_BH_e~50meV) is comparable to that reported for bulk Co ferrite, while becoming smaller in Mn@Co-TL and Mn@Co (~30 meV). This reflects a weaker exchange interaction, which is expected in Mn ferrite containing MNPs due to the low Curie temperature of this material ³⁴. It also stresses that K_c(0 K) in pure Co ferrite MNPs is calculated as 1360 kJ/m³, which is 30% lower than that of bulk Co_xFe_3-xO₄ for x=1 (1960 kJ/m³, ²⁴ Such reduction can be likely related to off-stoichiometric effects: the Co content (x~0.5) of our Co ferrite phase lies within the range x=0 to x=0.7, where the anisotropy is expected to grow very quickly ^27,28 and is therefore highly sensitive to x. In Mn@Co-TL and Mn@Co, this is significantly smaller (~30 meV), reflecting a weaker the exchange interaction, which is a expected in Mn ferrite containing MNPs, due to the low Curie temperature of this material ³⁴.

The Mn@Co and Mn@Co-TL core-shell MNPs show changes of the effective crystal field perturbation (a) relative to pure Co ferrite MNPs, which are likely caused by boundary/surface effects considering that both shell interfaces are contributing. As a consequence the anisotropy at 0 K increases (K_c ≈ 1600 kJ/m³ in Mn@Co) and drops faster with temperature than in pure Co ferrite (Figure 3b).

In pure Mn-ferrite MNPs the shape anisotropy is expected to dominate over K_c(0 K), ${\mu }_0{M}_s^2∕K_c\left(0\right)$ ≈ 1.5 (K_c(0) ≈ 22kJ/m³ taking from³⁵). For Co@Mn uniaxial and cubic anisotropies have to be considered because ${\mu }_0{M}_s^2∕K_c\left(0\right)$ ≈ 0.15 if K_c(0) is estimated from the average over relative volumes of Mn and Co. The Tachiki model (equation (2)) cannot be applied to these two systems and a more phenomenological approach has been used instead, similar to that proposed in bulk magnetite³⁶. In this, the effective anisotropy decreases with temperature following a pure activation process in the form: K_eff(T) = K₀ − K₁e^−Q/k_BT, where Q represents the activation energy. Best fits yield K_eff(T) = 22 − 7.5e^−3/k_BT in the Mn sample and K_eff(T) = 117 − 117e^−10.5/k_BT in Co@Mn. It means that in the latter the reduction of the anisotropy between 0 and 300 K is less than in the other core-shell ferrites (~66% versus 75%) and K_eff(T) tends also to zero at high T, as in equation (2).

As the real MNP size distribution is critical for the fit of the magnetic parameters, we also validated the modeling of the anisotropy by comparing the size distribution deduced from TEM (f′(V)) with that contained in the ZFC/FC (blocking temperature distribution, f(T_bl)). As explained by Yoon and Krishnan³¹, the percentage of thermal activated MNPs at a certain temperature, obtained from f(T_bl), must equal the percentage to those whose size is below a certain critical volume, V_c, calculated from f′(V). This determines numerically a critical volume function V_c = V_c(T) that when inserted in equation (1), allows for the calculation of the effective anisotropy, say $K_{eff}^{\ast }\left(T\right)$. This approach is especially useful if the anisotropy reduction effect is strong, as in the three core-shell systems. As observed in Figure 3b, this estimation leads to$K_{eff}^{\ast }$ values (shown as squared markers), almost overlapping with the functions K_eff(T) obtained from the fits of the ZFC branch (see S.I.).

The analysis of the coercive field is a useful opportunity to examine the validity of the magnetic anisotropy modelling. In the non-interacting Stoner-Wohlfarth theories, both properties are directly related: μ₀H_c(0K) = c(2K_eff(0K)/M_s), where M_s is the saturation magnetization and the pre-factor c depends on the type of anisotropy: it is equal to 0.48 for uniaxial and 1.3 for cubic anisotropy (or 0.32×K_c = 0.32×(4 K_eff)) ^37-39. When the thermal energy comes into play, determination of the coercive field for T ≠ 0 in a real poly-dispersed assembly of MNPs is challenging because it cannot be calculated as a simple superposition of the individual contributions. Following the approach of Nunes et al. ⁴⁰, the problem can be addressed in a simplified form as a two phase system, where the relative fractions of SPM and blocked MNPs change with temperature. If the demagnetization curve is approximated by a straight line ⁴¹, the resultant coercive field is:

$$H_c\left(T\right)=H_{cbl}\left(T\right)\left[M_r\right(T)∕({\chi }_{sp}\left(T\right)H_{cbl}\left(T\right)+M_r\left(T\right)\left)\right]$$ (4)

which is mainly determined by the coercive field of the blocked phase H_cbl(T), being χ_sp(T) the SPM susceptibility that vanishes at low temperatures and M_r(T) the remnant magnetization. The difficulty is further reduced by assuming that the thermal relaxation of magnetization causes the coercive field to decrease as [1 − (T/〈T_bl〉_T)^e]. The exponent e is widely fixed to 0.5 in the literature but several calculations suggest instead that it tends to 0.75-0.8 in monodisperse uniaxial randomly distributed MNPs ^21,42. In this way, H_cbl can be written as:

$$H_{cbl}\left(T\right)=c\frac{2K_{eff}\left(T\right)}{{\mu }_{0}M}\left[1-{\left(\frac{T}{\langle T_b{\rangle }_T}\right)}^e\right]$$ (5)

The thermal dependence of the coercive field is presented in Figure 3c (circular markers) where solid lines correspond to the calculation by equations (4) and (5) by using the functions K_eff(T) of Figure 3b and leaving c and e as free parameters. The whole picture shows a good agreement to the experiment with c = 1.4 and e = 0.85 for the Co ferrite rich samples (Co, Mn@Co-TL and Mn@Co), with c = 1.2 and e = 0.85 for Co@Mn and c = 0.48 and e = 0.75 for Mn ferrite. The value of c in the first group matches very well to the theoretical value of 1.32 for randomly oriented single domains with cubic anisotropy, while it is equal to the uniaxial case (0.48) in Mn ferrite. The coercive field of Co@Mn lies between pure uniaxial and cubic behaviors, as happens with the remnant magnetization.

The previous analysis was motivated by the need for a theoretical framework to predict the performance of these core-shell MNPs as heat generators. The experimental determination of the SLP has been carried out in colloidal samples (PMA-coated MNPs) in aqueous suspension (see S.I), where the power dissipation arises from the interaction of magnetization with both the lattice (internal) and the surrounding liquid molecules (external). The prevalent dissipation mechanism can be determined by estimating the characteristic relaxation times of pure internal processes (referred as Neel relaxation, given by τ_N ≈ τ₀e^K_effV/k_BT) and external (Brown relaxation, given by ${\tau }_N\approx \pi \eta d_h^3∕2k_{B}T$; where η is the viscosity). The available set of values (K_eff, d_in, d_h ) in the five samples indicates that in the hard Co-ferrite MNPs (samples Mn@Co-TL, Mn@Co and Co) the Brown mechanism dominates: τ_N/τ_B > 10³. It is just the opposite in the Mn sample (τ_N/τ_B ≈ 2×10³), while Co@Mn is between both limits (τ_N/τ_B ≈ 1). The contribution of the Brownian dissipation was tested experimentally by attaching proteins to the surface of Mn and Mn@Co samples to increase the hydrodynamic diameter d_h. After the addition of albumin, the SLP of the Mn sample remains almost unchanged (from 184 W/g to 196 W/g); on the contrary, the SLP of the Mn@Co sample is reduced from 302 W/g to 78 W/g.

Size, magnetization and anisotropy constitute the basic elements for any SLP calculation regardless of the framework used. In our particular case there is no one approach fully compatible with the whole set of samples: for instance, the determination of the dynamical hysteresis loops, by resolving the Landau-Lifshitz-Gilbert equation that includes the thermal effects⁴³ encounters the difficulty of implementing the Brownian relaxation mechanism, predominant in our Co rich NPs. This fact also prevents the use of simpler approximations as the Stoner-Wolhfart based models⁴²), which are applicable to these high anisotropic NPs. On the other side the linear response theory (LRT) could lead to strongly overestimate the absorption because the field used in the experiments is in general above the limit of the linear response regime. This limit is in practice determined by the ratio of the external field to the anisotropy field (H₀/H_k); therefore, the non-linear effects might be stronger in the Mn sample as compared with the more anisotropic Co containing samples. With the aim of making a more reliable estimation of the power absorption, the initial susceptibility can be substituted by the so called chord susceptibility that depends on the amplitude of the applied external field H₀, following the approach of Rossenweig⁴⁴ (χ_c = ML(x)/H₀). This corrected Linear Response Theory (c-LRT) works as a simplifying way to keep the amplitude of the response within more realistic limits, where the susceptibility is still a constant and the linear response equations are used for calculation. This model has been widely used² and proven to give correct estimation for case where the applied field amplitude is small compared to the anisotropy field^36,39,45, especially considering the uncertainty of some key variables, such as concentration of MNPs, polydispersity, diameter, and calculated effective anisotropies. In the particular case of Mn sample, where the Brownian mechanism is negligible, this approach (cLRT) can be contrasted with a more robust model based on the dynamical hysteresis loop calculation.

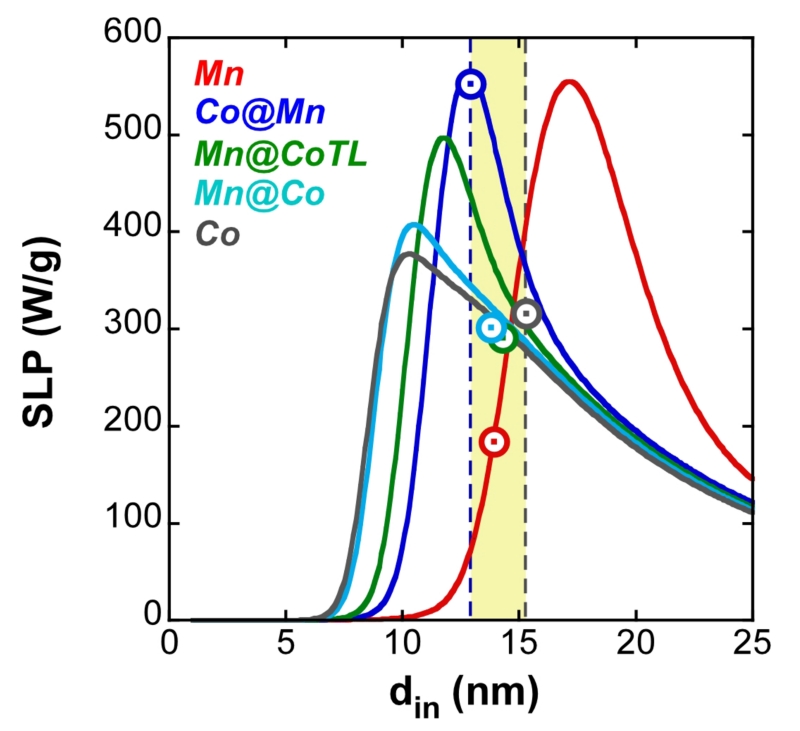
The comparison of experimental and theoretical SLP indicates that the cLRT approach predicts accurately the heat generation capacity. Figure 4 presents the calculated SLP functions of mean diameter, obtained by fixing the effective anisotropies (at RT) to those calculated in the previous section for each sample and assuming a constant dispersity (taken from TEM data). The experimental SLP values (Table 2) are represented by open circles, whose size is larger than the estimated experimental error (184 ± 2 W/g for Mn, 553 ± 10 W/g for Co@Mn, 290 ± 1 W/g for Mn@Co-TL, 302 ± 15 for Mn@Co and 280 ± 9 W/g for Co). In the Mn sample the SLP deduced from the calculated hysteresis loop match with the simplest estimation made by cLRT within the uncertainty (see S.I. for details). The representation of Figure 4 provides an overview of which size approaches the best theoretical SLP, for this kind of core-shell NPs and at the specific excitation condition used, and shows how the magnetic anisotropy can be finely tuned to maximize the SLP at room temperature by adjusting the content of Co while keeping the size constant. The Co@Mn sample (15% of Co ferrite in the core) approaches the optimal anisotropy and size under the excitation used (412.5 kHz and 22.4 kA/m). The higher SLP reported by Lee² is largely a result of high field strength and frequency (500 kHz and 37.3 kA/m). To enable comparing different experiments, Parnkhurst⁴⁶ suggested to normalize the SLP to the field strength and frequency to derive the Intrinsic Loss Power $ILP={10}^3\ast SLP\left(\frac{W}{g}\right)∕(f\ast H_{Ac}^2)$, which within the validity of the linear response regime is a constant independent of the field parameters. The ILP of our 13-nm Co@Mn is 2.7 nHm²/kg, while the one of Lee’s 15-nm Co@Mn is 3.0 nHm²/kg². They reported smaller size dispersivity than our samples (0.05 versus our 0.11), possibly due to their use of the solvent trioctylamine. Our simulations show that if our NP had a dispersity of 0.05, their SLP and ILP would rival the one shown by Lee et al.. had which more than accounts for the difference in SLP and ILP.

Figure 4.

Simulation of SLP versus d_in by the quasi-linear approach (solid lines), using the experimental values of M_s, d_in, σ, d_h (d_in+d_s) and previously determined K_eff at RT have been used. The experimental SLP values are superimposed for comparison (circular markers, , magnetic field of 412.5 kHz and 22.4 kA/m).

CONCLUSION

In summary, we present here a model calculating the magnetic anisotropy of core-shell particles composed of Co ferrite in a whole range of temperatures quantitatively, which allows correct prediction of their SLP. This model relies on theories well established in bulk materials, and we have experimentally tested its power in predicting the thermal dependence of basic magnetic properties, such as the susceptibility and coercive field of randomly oriented single domains of small size dispersivity. We conclude that the anisotropy of these exchange-coupled core-shell MNPs is mostly determined by the relative fraction of Co ferrite, whose increase determines a gradual transition to systems with cubic magnetic anisotropy. The correct prediction of the magnetic properties of these MNPs enables designing core-shell MNPs with optimized heat generation for a particular complex biomedical application.

ABBREVIATIONS

MNP

magnetic nanoparticle

SLP

specific loss power

ZFC

zero-field cooling

PMA

poly (isobutylene-alt-maleic anhydride

K

anisotropy

M

magnetization