Layer-specific activation of sensory input and predictive feedback in the human primary somatosensory cortex

Using laminar fMRI, we show that prediction and sensory inputs activate specific layers in human primary somatosensory cortex.

Abstract

When humans perceive a sensation, their brains integrate inputs from sensory receptors and process them based on their expectations. The mechanisms of this predictive coding in the human somatosensory system are not fully understood. We fill a basic gap in our understanding of the predictive processing of somatosensation by examining the layer-specific activity in sensory input and predictive feedback in the human primary somatosensory cortex (S1). We acquired submillimeter functional magnetic resonance imaging data at 7T (n = 10) during a task of perceived, predictable, and unpredictable touching sequences. We demonstrate that the sensory input from thalamic projects preferentially activates the middle layer, while the superficial and deep layers in S1 are more engaged for cortico-cortical predictive feedback input. These findings are pivotal to understanding the mechanisms of tactile prediction processing in the human somatosensory cortex.

INTRODUCTION

When humans process unexpected environmental stimuli, their brains integrate sensory input and learned expectations of the world (1–3). For example, when fingers are touched in a sequence, the actual cortical inputs from sensory receptors are processed differently depending on the next anticipated touch. Any potential mismatch between the sensory input and the expectation can be used to update future expectations and improve the accuracy of upcoming somatosensory predictions. A mechanistic model of this hierarchical framework is the so-called predictive coding principle (2, 4). The primary somatosensory cortex (S1) is expected to play a crucial role in the predictive coding of the somatosensory information. However, it is poorly understood how well the predictive coding is applicable to explain somatosensation. Furthermore, it is not known which neural circuit mechanisms are used to integrate sensory feedforward inputs and feedback signals.

Current research studies are starting to map out the neural circuits underlying sensory processing. Anatomical and physiological data indicate that S1 is composed of a stack of six neuronal layers (5–7), with different layers harboring different neuron types with distinct feedforward inputs and feedback projections (8). Inputs from thalamic projects preferentially terminate on layer 4 (L4) neurons in the middle layer, and layer 2/3 (L2/3) and layer 5/6 (L5/6) neurons have secondary functions in cortical processing of these feedforward inputs (9). L2/3 pyramidal neurons are also critical for receiving prediction signals from other high-level areas, and interlaminar connections within L2/3 and L5/6 neurons support the temporal integration of feedforward inputs and feedback signals to predict future sensations (9–11). Thus, L2/3 and L5/6 are an important part of the predictive coding framework, as they are poised to organize learned sensation and associate these sensations with prediction signals (schematically depicted in Fig. 1A). However, in human S1, the precise contribution of specific layers to sensory input and prediction has not been investigated to date.

Fig. 1. Model of the expected laminar activity in the human somatosensory cortex (area 3b).

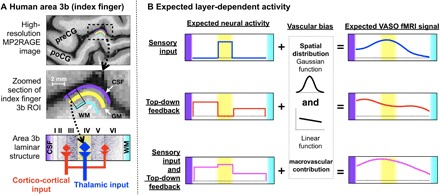
(A) Anatomical location of human area 3b for one participant and the model of layer-dependent circuitry based on previous animal studies. (B) Expected layer-dependent activity and corresponding fMRI signal for the task conditions used here. preCG, precentral gyrus; poCG, postcentral gyrus; CSF, cerebrospinal fluid; WM, white matter; ROI, region of interest; VASO, vascular space occupancy.

To explore the layer contributions of sensory input and prediction in human S1, we acquired high-resolution (0.7 mm) functional magnetic resonance imaging (fMRI) at 7T and sought to identify layer-specific activity in area 3b. Area 3b is a subdivision of the S1. It is viewed as a purely somatosensory structure and acquires cutaneous signals through the sensory thalamus, and from there, these signals propagate to areas 1 and 2 (12). Human area 3b is just starting to be explored with layer fMRI (13), and such investigations face considerable technical challenges. Area 3b has a particularly small cortical thickness of only 2 mm and a relatively fine-scale organization (14), where individual fingers are represented in only a few voxels.

Here, we aim to acquire and analyze blood oxygen level–dependent (BOLD) and cerebral blood volume (CBV)–based layer fMRI using vascular space occupancy (VASO) as a function of layers across cortical depths (15, 16). The conventional BOLD signal is limited by its spatial specificity at high resolutions, since it tends to be dominated by large veins toward the pial surface. Furthermore, conventional gradient-echo (GE) BOLD depends on nonlinear interactions between physiological variables that can differ across cortical depths, making a quantitative interpretation difficult. VASO, on the other hand, is less biased toward superficial depths and provides more quantitative signals; however, it suffers from a lower contrast-to-noise ratio. In short, BOLD is more sensitive, while VASO is more specific. We discriminate the laminar activity patterns in area 3b while participants receive predictable or unpredictable stroking on their fingers by using concurrent measurements of VASO and BOLD at 7T. Our hypothesis is that the prediction of touch evokes feedback activity in the superficial and deep layers without engaging the middle layers (see Fig. 1B). In contrast, an unpredictable touch sequence eliminates the anticipation of the next stroke, such that the superficial and deep layers rarely receive prediction signals.

RESULTS

Finger somatotopic mapping run

The tactile stroking elicited fMRI signal changes along the anterior bank of the postcentral gyrus in all participants. Both the BOLD and VASO signal changes suggested functional activity modulations in area 3b. The BOLD finger representation map of one participant can be seen in the left of Fig. 2A, and the group average laminar activity is shown in the right of Fig. 2A. All participants’ individual results are shown in fig. S5. We localized the somatotopic representations for each participant based on their activation and extracted laminar activity of each of the four fingers’ (D1, index; D2, middle; D3, ring; and D4, pinky) representations in area 3b. The group average laminar activity shows that, during stroking of the corresponding fingertip, a peak response in the VASO signal changes occurs in the middle layers of each finger region. However, no activity is detectible if stroking is performed on a different fingertip (Fig. 2A. The peak signature in the middle layers was visible in all participants and was markedly stronger than in the superficial and deep layers (fig. S5).

Fig. 2. Representative results of a finger somatotopic mapping run and acquisition methods.

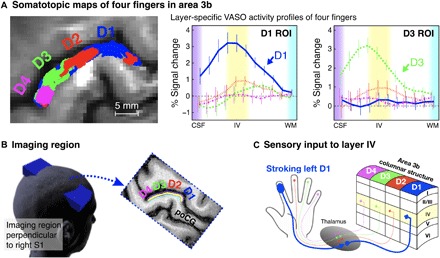
Left panel of (A) shows the boundaries of activation evoked in the somatosensory cortex by stroking each finger for one participant, with the right panel showing the average (n = 10) cortical profiles using VASO contrast in D1 and D3 ROIs. Here, n = 10 represented the number of individually conducted experiment session (eight participants with two retests). Error bars refer to the SEM. (B) The imaging slice is aligned perpendicular to the cortical surface of the left hand representation in the right primary somatosensory cortex (S1), and slices are tilted as indicated by the blue box. (C) Illustration of laminar structures and four-finger columnar structure (D1, index; D2, middle; D3, ring; D4, pinky) in area 3b.

Prediction task runs

Prediction task–induced fMRI signal change in the area 3b was found in all participants. Layer-dependent activity was highly reproducible across participants. All participants’ individual results are shown in fig. S4. Depth-dependent activity for BOLD-fMRI modulations across tasks could be detected in representative participant’s individual activation maps with and without smoothing along the cortical depths (Fig. 3A, and with corresponding zoomed sections of the index finger “omega” shape (Fig. 3B). As shown in Fig. 3B, the BOLD activity in the superficial and deep cortical layers differed across conditions. Specifically, prediction with sensory input [stroking Four fingers in Predictable order (FP) condition] evoked strong activation across all layers. Prediction without sensory input [stroking Three fingers in Predictable order (TP) condition] showed a clear increase in activity in the superficial cortical layers and a clear reduction of the response in the middle cortical layers, presumably due to the reduced input from the thalamus. Nonprediction with sensory input [stroking Four fingers in Random order (FR) condition] evoked increases in the middle input layers only. Nonprediction without sensory input [stroking Three fingers in Random order (TR) condition] did not evoke any positive response.

Fig. 3. Illustration of the used stroking and prediction, with the corresponding activation maps of a representative participant.

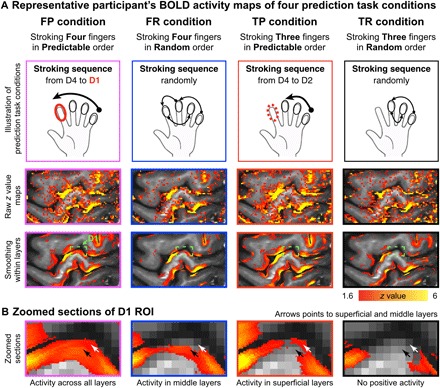
(A) The first row illustrates the four different task conditions. The second row represents the unsmoothed activation maps (FSL z statistic maps, clusters determined by z > 1.6) of the four different conditions for one participant. For visualization, the third row represents the activation maps with smoothing in each layer (no smoothing was applied across layers). (B) Zoomed sections of the index finger ROI are shown. It can be seen that the four conditions have a different distribution of activity across the layers in the index finger region of area 3b. Note that the depicted data refer to the BOLD contrast. Although BOLD is generally less layer specific than VASO, some individual participants’ data showed indications of differentially activated layers in the single-slice data. To identify differentially activated layers in VASO, signal pooling across multiple voxels in a patch of cortex was necessary.

Averaged profiles of layer-dependent VASO responses for the four task conditions in the D1 region are shown in Fig. 4A. The trends of activity in different layers of four prediction conditions were highly consistent with the activity map as shown in Fig. 3B. Specifically, sensory input evoked the strongest activity in the middle cortical layers regardless of whether prediction was present (for FP-TP, P < 0.004; for FR-TR, P < 0.001). Predictive top-down feedback produced a clear activity increase in the superficial layers (for FP-FR, P < 0.001; for TP-TR, P < 0.012) and deep layers [for FP-FR, P < 0.01; for TP-TR, the P value of the lamina nearest the white matter (WM) was 0.156, but all others were <0.036]. For a full list of statistical comparisons, see table S1. The BOLD responses showed mostly similar patterns, but the distinction between layers was less clear (for detail, see fig. S3), presumably due to venous signal leakage.

Fig. 4. Cortical profiles of VASO activity changes in the ROIs of the index finger (D1) and the ring finger (D3) in area 3b.

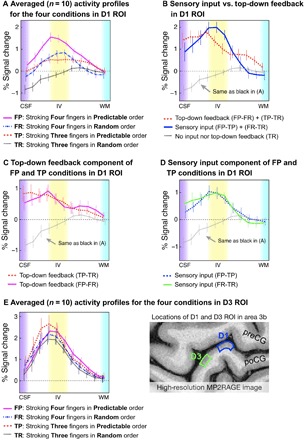
(A) The four tasks results in modulated cortical activity profiles in D1 ROI. (B) Top-down feedback modulated activity was dominant in the superficial and deep layers, while sensory input activity was strongest in the middle layers. (C) and (D) compare different task contrasts. (E) The different layer-dependent activity profiles of the four task conditions from D3 ROI. Since the modulation of sensory input and prediction activity was designed for D1, we did not expect substantial changes across the four conditions. For all graphs, 0 on the y axis refers to the average response during rest periods. Here, n = 10 represented the number of individually conducted experiment session (eight participants with two retests). Error bars refer to the SEM.

Specific laminar activity of sensory input and top-down feedback

To quantify the layer-dependent sensory input and top-down feedback activity, we contrasted signal changes between the four conditions using the model depicted in Fig. 1B. The results are shown in Fig. 4B. The contrast between sensory input (blue line) [(FP-TP) + (FR-TR)] and top-down feedback (red dashed line) [(FP-FR) + (TP-TR)] shows that sensory input caused the strongest activation in the middle layers, at the presumed location of the thalamic input. Top-down feedback, on the other hand, caused two peaks of activation in the superficial and deep layers, at the presumed location of cortico-cortical feedback input. When we directly compared these two profiles in Fig. 4B, we found that, in the middle layers, sensory input raised stronger activation than prediction input (P < 0.046). In the deep layers, however, we found that prediction input raised stronger activation than sensory input (P < 0.049), but not in the superficial layers (P > 0.227). The specific profiles for each contrast are shown in Fig. 4 (C and D).

To confirm that the different layer-dependent activity for prediction input was specific to the D1 region, we also extracted the profiles for all conditions from a control region (the part of area 3b representing D3). As shown in Fig. 4E, the laminar profiles of the four conditions in the D3 region do not represent activity changes for prediction input. Instead, the activity in the control condition can be explained by sensory feedforward input only. The activity in cortical layers showed mostly similar patterns across conditions. All four conditions evoked the strongest activity in the middle layers.

DISCUSSION

The precise roles of S1 in the hierarchy of neural circuits for predictive coding of the world and our perception within it have been debated for several decades (17). However, to make sense of such cortical systems, accurate measurements of laminar activity are required. These measurements would allow for the causal investigation of the integration of sensory input and associated expectations in the context of predictive coding. While there have been some findings from invasive animal studies, there have been no direct observations of laminar activity in the human S1. In this study, our investigation of the precise modulation of sensory input and prediction input enabled us to pinpoint the contribution of specific layers to sensory input and prediction input in the somatosensory system. Our results demonstrated that sensory input to area 3b evoked activity in the middle layers, while prediction input yielded activity in the superficial and deep layers (Fig. 4B). Together, our findings revealed the existence of clear laminar contributions underlying sensory input and prediction input. To the best of our knowledge, this is the first report of functional laminar specificity in the human somatosensory system.

Here, we confirmed that ascending sensory input terminates in middle layers in area 3b. We found one peak of increased activity in middle layers for sensory input, regardless of whether prediction input was present (Fig. 4D). According to previous anatomical findings, sensory input activity comes mostly from the thalamus via thalamo-cortical connections (18). This laminar functional activity pattern is expected from previous structural studies (19).

Our findings are consistent with other evidence demonstrating that responses in the human S1 reflect the influences of top-down processes, including prediction, expectation, and anticipation (20, 21). However, our results extend beyond those of other studies by revealing the layer-dependent activation of the prediction input to the superficial and deep layers during the representation of a series of tactile stimuli in area 3b. Furthermore, our layer-dependent analysis enabled us to observe the layer-specific nature of change in area 3b. Namely, we find that the superficial and deep layers become more responsive to temporal rhythmic-related predictive feedback when the series of tactile stimuli is associated with rhythmic input (i.e., the FP condition) compared with when it is not (i.e., the FR condition).

This layer-dependent activity of sensory input and prediction input as observed in the present study may be interpreted using several theoretical frameworks. According to one, the somatosensory system may represent hierarchical Bayesian inference (2, 4, 22, 23), where area 3b integrates priors (top-down feedback) with current sensory input (bottom-up input) to infer the likelihood of the future input. Although numerous previous studies have proposed that this Bayesian inference may be implemented in the human brain (23), it is necessary to provide more layer-specific neural evidence to support the suggested theoretical framework. In the present study, previous knowledge of the temporal rhythm (i.e., in the FP and TP conditions) provides the additional constraints necessary to improve the understanding of a rhythmic stroking sequence. Our findings further provided layer-specific evidence of this Bayesian inference in the somatosensory system, in which the middle layers respond to current sensory input, while the superficial and deep layers respond to predictive feedback and integrate previous information with current sensory input as a coherent whole.

Another possible interpretation of our findings is related to other top-down effects such as attention or imagination. These effects might occur because the participants pay attention to stroked finger (in the FP and FR conditions) or the expected location where it will be stroked even when no actual stroking occurs (in the TP condition). For example, attentional effects have been previously extensively investigated in the nonhuman primate (24) and in layer-dependent fMRI in humans from the de Lange group (25–27). However, the attentional effects may not be an alternative to the predictive effect that arises from learning the temporal rhythm within other fingers in the tasks (25). Namely, the attentional effects cannot be used to explain why there is no different activity between the FP and FR conditions in the superficial and deep layers of the D3 region (Fig. 4E). For example, comparing the FP to the FR condition, our results showed stronger activity at the superficial and deep layers of the D1 region (Fig. 4B). If it would be the case that attentional effects were the major driver of the layer-dependent activity modulation in the FP condition, then the top-down attentional process would be dominant for D1 and reduced for D3 (28). On the other hand, if attentional effects would be the driving force of the activity modulations in the FR condition, then they would be equal for all fingers rather than reduced for D3. Since the results depicted in Fig. 4 do not show such a finger-specific activity signature and rather show that the activities of the FP and FR conditions were the same in the D3 region (Fig. 4E), we suggest that these attentional effects play a negligible contribution here.

Prediction and attention are not mutually exclusive phenomena: The expectation of a stimulus on a specific finger can lead to expectation-driven attention at that location (25, 29). Mechanistically speaking, attentional effects cannot simply be separated from the prediction process, but they can be graded in intensity by comparing the four associated conditions. In the experimental instruction of the FP condition, participants were asked to direct their attention to the stroking on each finger and then predict when D1 will be stroked on the basis of the temporal rhythm learned from D4, D3, and D2. In this case, the right decision was based on the temporal rhythm from the earlier three fingers and the prediction of the timing of the last D1 stroke. Conversely, in the FR condition, the participants were only asked to direct their attention to the stroking on each finger but not to predict any pattern. Thus, the FP versus FR contrast (the pink solid line in Fig. 4C) was expected to subtract the attentional effect and show more of the prediction effect, which would induce changes in the superficial and deep layers of the D1 region. On the other hand, in the TP condition, the participants were asked to alter their attention to the stroking on each finger and then predict when D1 will be stroked even if no actual stroking was happening. In this case, the accounts of the TP condition would include prediction and also expect-driven attention to D1, but no actual sensory input. Thus, the TP versus TR contrast may reflect top-down effects, including prediction and attention on D1 (red dashed line in Fig. 4C). The similarity of the FP versus FR and TP versus TR contrasts in D1 provides further evidence that the observed effects are due to prediction rather than attention. Note that it is not established in the field whether touch predictions would result in fMRI signal increase or decrease in the feedback layers (27, 30, 31). Our results show a stronger fMRI signal increase for predicted stroking compared with unpredicted stroking, suggesting that the predictive feedback is amplifying the fMRI signal.

From a methodological perspective, we used an advanced laminar investigation system by using VASO in place of the conventional GE-BOLD contrast. BOLD has a limited spatial specificity and is biased toward the superficial layers and large draining veins (32). Thus, GE echo-planar imaging (EPI) may not be as suitable for brain activity investigations across cortical layers compared to VASO-EPI. While spin-echo (SE) BOLD fMRI can reduce the relative sensitivity to pial veins, unsegmented SE-EPI in humans can still contain considerable unwanted T₂* sensitivity (33) due to the BOLD signal arising from the intravascular blood. In the layer-dependent applications of the human primary visual cortex (26, 34, 35), primary auditory cortex (36), dorsolateral prefrontal cortex (37), and motor cortex (15), these venous contaminations may be partly circumvented by refraining from the interpretation of cortical activity profiles directly and restricting neuroscientific interpretations to differences between conditions. In this study, we exploited the superior depth-dependent localization specificity of VASO fMRI (38, 39). VASO was shown to have a lower sensitivity compared with GE-BOLD; however, its higher specificity allowed for a clearer interpretation of layer-dependent activity changes compared with GE-BOLD (compare Fig. 4 and fig. S3).

Moreover, we should point out that VASO is not completely independent of macrovascular bias toward the pial surface. As discussed previously (16, 40), the larger vascular density of diving arterioles and microvessels in the superficial and the middle layers may result in higher signal changes compared to the deep layers. Thus, the fact that the red dashed line in Fig. 4B (layer profile of prediction) is larger in the superficial layers compared with deep layers may represent the vascular density gradient across the cortical depth and should not be taken as evidence that the superficial layers have a stronger activity for this condition than deep layers (41). Because of this sensitivity to layer-dependent vascular density, all neuroscientific interpretations in this study were not based on the comparisons between the different layers within the same condition but are based solely on differential activity strengths within layers across different conditions.

To explore the laminar mechanisms of prediction processing in human S1, we used an index finger prediction task that consisted of sequential finger stroking. Completing this task required learning a set of sensory stimuli and mentally chaining them together in chronological order. By changing the sequence order, our design allowed us to test how a parametric change in temporal prediction feedback modulated the laminar representation in area 3b. In addition, the use of ultrahigh-resolution fMRI, which is specific and sensitive enough to reveal functional laminar activity (15, 16, 40), allowed us to focus on the activation patterns at different cortical depths. Our findings provide evidence that sensory flow–guided predictions are related to feedback input in the superficial and deep layers in area 3b. Furthermore, we observed prediction-related activation in the superficial and deep layers, supporting the idea that a core function of the human S1 is to aid in the prediction of the next stimulus based on the learned expectations of the world. Future studies will focus on improving the laminar fMRI imaging technique, allowing the variation of prediction and attention on a trial-by-trial basis to better elucidate these predictions in the human brain.

MATERIALS AND METHODS

Human participants

Eight healthy right-handed volunteers (age 20 to 47 years) participated after granting informed consent under a National Institutes of Health Combined Neuroscience Institutional Review Board–approved protocol (93-M-0170, ClinicalTrials.gov identifier: NCT00001360) in accordance with the Belmont Report and U.S. Federal Regulations that protect human subjects. Five participants were males, and three participants were nonpregnant females. Because two (one male and one female) of them were reinvited to participate in an additional session (different day) to confirm the reproducibility, the number of individually conducted experiment sessions was treated as n = 10. The research was conducted as part of the National Institute of Mental Health Intramural Research Program (no. ZIA-MH002783).

Scan session setup and image acquisition

Each session consisted of one finger somatotopic mapping run of 9.9-min duration and two or three prediction task runs of 12-min duration. No participant was in the scanner for longer than 120 min per session.

Here, the same fMRI sequence and image reconstruction pipeline were used as in previously published work (16). In short, slice-selective slab-inversion VASO (38) was used on a 7T scanner (Siemens Healthineers, Erlangen, Germany), equipped with a 32-channel radiofrequency (RF) coil (Nova Medical, Wilmington, MA, USA) and a SC72 body gradient coil. Third-order B0 shimming was performed with three iterations. The timing of the acquisitions was TI1/TI2/TR = 1100/2845/3490 ms. The coil-combined data consist of interleaved BOLD and VASO contrasts, obtained as separate yet simultaneous time series. These time series are corrected for rigid volume motion and are separated by contrast with the effective temporal resolution of TR = 3.49 s for each individual contrast. The nominal resolution was 0.71 mm across cortical depths with 1.8-mm-thick slices perpendicular to the postcentral bank of the right central sulcus. VASO contrast was corrected for BOLD contaminations by the division of blood-nulled MR signal and not-nulled MR signal across consecutive TRs [for details, see (42)]. Imaging slice position and slice angle were adjusted individually for every participant to be perpendicular to the finger region of S1. This was performed on the basis of one to four short EPI test runs with five measurements (approximately 22 s per test scan) and their online depiction in the vendor-provided three-dimensional (3D) viewer.

If time permitted, slab-selective high-resolution (0.437 mm × 0.438 mm × 1.2 mm) anatomical data were collected covering the right S1 with MP2RAGE (Fig. 1A) (43). Those anatomical data were not used in the pipeline for generating cortical profiles. They were used to compare the approximate position of the cytoarchitectonically defined cortical layers to the 11 reconstructed cortical depths, in which the data were processed.

Experimental paradigm and procedures

All the participants were asked to perform one finger somatotopic mapping run, followed by two or three prediction task runs using their left four fingertips (D1, index; D2, middle; D3, ring; and D4, pinky) while we imaged the activity of the right S1 (specifically, area 3b).

Finger somatotopic mapping run

To select the precise regions of interest (ROIs) for each participant, first, we localized the finger area of their hand in the contralateral area 3b (Fig. 2A) by using an on-off block design. The duration of each on phase (i.e., stimulation phase) was 17.5 s, followed by a 10.5- or 14-s duration off phase. An experimenter was located at the entrance of the scanner bore, where they could easily reach and stroke the participant’s fingers using the custom-built MR-safe finger stroking device (fig. S2). During the stimulation phase, each of the four fingers was randomly and independently stroked at a frequency of 4 to 5 Hz, and each finger was stroked five times. The participants were instructed to “keep your attention on the left stroked fingertip during the stimulation phase.”

Prediction task run

To investigate cortical layer–dependent brain responses reflecting the sensory input and prediction activity, we then instructed the participants to perform two or three prediction task runs. Each prediction task run (Fig. 5A) consisted of four conditions (2 × 2 design), which were designed to include prediction/nonprediction and sensory input/non-input conditions. All the tasks alternated between 27-s “on” and 20-s “off,” and each condition was repeated four times (Fig. 5B). All the participants were asked to look at the on screen from the start to the end of each run. At first, a line drawing hand-shaped picture was presented at the center of the screen. When a red solid circle appeared on the index finger, the participant was asked to pay attention to the stroking on each finger and then predict when the index finger would be stroked. In contrast, if an empty circle appeared on the index finger, then the participant was asked to pay attention to the stroking on each finger without any prediction.

Fig. 5. Experimental design of the prediction task run.

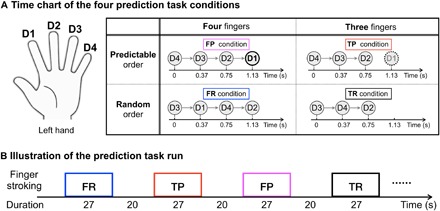
(A) Time chart of the four prediction task conditions. For the FP condition, an isochronous rhythmic stroking sequence from D4 to D1 was used. Participants were instructed to “Pay attention to the stroking on each finger and predict when your left index finger will be stroked based on the temporal rhythm.” For the TP condition, the same isochronous rhythmic stroking sequence from D4 to D2 was used as in condition FP, and D1 was not actually stroked. The participants were instructed to “Pay attention to the stroking on each finger and predict when the left index finger will be stroked even if no actual stroking is happening.” For the two control conditions (FR and TR), a random stroking across the four (or three) fingers was used. Participants were instructed to “Pay attention to the stroking on each finger, but do not try to predict any pattern.” (B) Illustration of the prediction task run. All those conditions alternated between 27-s on and 20-s off, and each condition was repeated four times for each run.

Stroking Four fingers in Predictable order (FP)

For the prediction condition with sensory input, an isochronous rhythmic stroking sequence from D4 to D1 was used. The participants were instructed with the following text on the screen: “Pay attention to the stroking on each finger and predict when your left index finger will be stroked based on the temporal rhythm.” The actual sensory stimuli involved the experimenter stroking the four fingers of the participant in an ordered fashion from D4 to D3 to D2 to D1, with an interval of approximately 0.37 s between each stroke. This condition was expected to evoke strong thalamic input into the D1 region in area 3b. Furthermore, by using a consistent order, it was expected to evoke strong cortico-cortical feedback signals in the D1 region in area 3b, since stimulus-driven activity was expected to evoke a strong prediction of the index finger stroke at the end of the sequence.

Stroking Four fingers in Random order (FR)

For the nonprediction condition with sensory input, a random stroking across the four fingers was used. The participants were instructed with the following text on the screen: “Pay attention to the stroking on each finger, but do not try to predict any pattern.” In this control condition, the actual sensory stimuli involved the experimenter stroking the four fingers (D4, D3, D2, and D1) of the participant in a random order, with an interval of approximately 0.37 s between each stroke. By presenting a random order, it was expected that the stimulus-driven prediction for the next stroking position would be eliminated. This was used to provide thalamic input to the D1 region in area 3b without a stimulus-driven prediction.

Stroking Three fingers in Predictable order (TP)

For the prediction condition without sensory input, the same isochronous rhythmic stroking sequence from D4 to D2 was used as in condition FP, but the experimenter did not really stroke D1. The participants were instructed with the following text on the screen: “Pay attention to the stroking on each finger and predict when the left index finger will be stroked even if no actual stroking is happening.” The actual sensory stimuli involved the experimenter stroking the three fingers of the participant in an ordered fashion from D4 to D3 to D2, with an interval of approximately 0.37 s between each stroke. Although no stimulus on D1 occurred, we kept the one beat time of 0.37 s to allow for the participants to predict it. This was used to evoke a similar cortico-cortical feedback signal as the FP condition, without sensory input into the D1 region in area 3b from the thalamus.

Stroking Three fingers in Random order (TR)

For the nonprediction condition without sensory input, a random stroking across three fingers was used. The participants were instructed with the following text on the screen: “Pay attention to the stroking on each finger, but do not try to predict any pattern.” In this control condition, the actual sensory stimuli involved the experimenter stroking the three fingers (D4, D3, and D2) of the participant in a random order, with an interval of approximately 0.37 s between each stroke. This was performed to provide a basic baseline with neither sensory input nor prediction into the D1 region in area 3b.

Data analysis

Motion correction

Motion estimation and realignment were conducted with SPM12 (Functional Imaging Laboratory, University College London, UK) using a fourth-order spline interpolation. To minimize errors on the motion estimation due to nonlinear motion at air-tissue interfaces, the motion parameter estimation was restricted to a manually drawn ROI of the central sulcus (weight option in SPM12).

Anatomical reference methods

To avoid additional resolution loss due to repeated resampling steps and to avoid any errors of the distortion correction and registration, we did not register the functional data to an anatomical reference dataset. Instead, we used the functional data directly as an anatomical reference as was performed previously.

General linear model analysis

After the motion correction, a general linear model (GLM) was fitted to the fMRI data for each participant per run with FSL5.0.9 (the FMRIB Software Library, University of Oxford, UK). VASO and BOLD signals for all runs were modeled with a BLOCK function convolved with the canonical hemodynamic response function using the FEAT tool of FSL. For the somatotopic mapping run, the design matrix for each participant included one run with four regressors, corresponding to the onset timing of each finger. The activity of each finger is defined as the mean signal difference between the stimulation phase and the off phase (difference of GLM βs). The activation maps of each finger were used to define the individual index finger ROI in area 3b. The data of prediction runs used the same analysis procedure but different block design matrices corresponding to each condition. Then, we used the 3dcalc function in AFNI (Analysis of Functional NeuroImages, National Institute of Mental Health, Bethesda, MD) to calculate the percent signal change maps for each condition.

Layering methods and profile extraction

The borderlines between cerebrospinal fluid, gray matter, and WM were used as the basis to define cortical depths (also known as layers). The equivolume layering approach (44) was implemented in C++ for its application to EPI data with a restricted field of view (https://github.com/layerfMRI). To avoid singularities at the edges in angular voxel space, the cortical depths were defined on a fivefold finer grid than the original EPI resolution. Eleven equivolume lines were calculated across the cortical depth. Please note that with a nominal 0.71-mm resolution and an approximate cortical thickness of 2 mm in area 3b, the effective resolution allows the detection of only three independent data points. Hence, the defined 11 cortical depths do not represent the MRI effective resolution. After we defined the index finger area 3b ROI for each participant per run, we extracted the cortical depth–dependent area 3b profiles of four prediction conditions (fig. S4). Furthermore, for visualization purposes, cortical depth–specific smoothing was applied in one participant, as shown in the lower part of Fig. 3 (A and B). Cortical profiles were evaluated from the unsmoothed data.

For the interpretation of the functional depth profiles according to known feedforward and feedback layers, knowledge of the approximate location of underlying cytoarchitectonically defined layers I to VI is vital. To estimate the approximate location of the outer band of Baillarger, we followed the approach outlined earlier (45). First, we identified the MR-sensitive landmarks and layer signatures in 20-μm resolution multimodal postmortem data. Second, we used those features as markers of the cyto- and myeloarchitectonic landmarks in the in vivo data. Dips and peaks in ex vivo T₁ and T₂* profiles were assigned to cytoarchitectonic layers based on SMI 311 stained histology slices at the same position (fig. S1C). In S1, deep layer III comes along with a peak/dip and layer IV coincides with a gradient of T₁ and T₂* values (yellow band in fig. S1). This T₁ and T₂* gradient next to the layer III peak can be used as a landmark in the in vivo EPI data to estimate the correspondence of CBV peaks to cytoarchitectonically defined cortical layers.

Statistical analysis

The difference between any pair of task conditions (e.g., FP-TP) across the layers (i.e., 11 cortical depths) was statistically assessed through a linear mixed effects (LME) modeling approach using the R package nlme. With the pair-wise difference at each layer from each experiment session (n = 10, two from the same participants) as the data for the response variable, the LME model was formulated with no intercept, with layers as a fixed effects factor and with a random intercept for cross-sessions variability. The LME model is

$$y_{\mathit{ij}}=d_i+e_{\mathit{ij}}$$

where y_ij is the jth participant’s effect difference between two task conditions, for example, FP and FR, at the ith layer (i = 1, 2, …, 11; j = 1, 2, …, 10), d_i is the effect difference at the group level between two task conditions, for example, FP and FR, at the ith layer, and e_ij is the residual term. Since no intercept is included in the LME model above, the F statistic from the LME model for the composite null hypothesis H0: d₁ = d₂ … d₁₁ = 0 tests whether there is statistical evidence at any of the 11 layers.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/5/eaav9053/DC1

Fig. S1. Assignment of functional layer fMRI activity to the location of cytoarchitectonically defined cortical layers by comparison between high-resolution postmortem and in vivo data.

Fig. S2. Custom-designed, metal-free, 3D-printed finger stimulation device.

Fig. S3. Cortical profiles of BOLD activity changes in ROI of the index finger in area 3b.

Fig. S4. Stability and repeatability of prediction task results across participants.

Fig. S5. Stability and repeatability of functional localizer across participants.

Table S1. Summary statistics of difference between task condition pairs of the VASO signal in each layer.