Abstract
Introduction
To predict the rate of prostate cancer detection on prostate biopsy more accurately, the performance of deep learning using a multilayer artificial neural network was investigated.
Methods
A total of 334 patients who underwent multiparametric magnetic resonance imaging before ultrasonography guided transrectal 12-core prostate biopsy were enrolled in the analysis. Twenty-two non-selected variables, as well as selected ones by least absolute shrinkage and selection operator (Lasso) regression analysis and by stepwise logistic regression analysis, were input into the constructed multilayer artificial neural network (ANN) programs; 232 patients were used as training cases of ANN programs and the remaining 102 patients were for the test to output the probability of prostate cancer existence, accuracy of prostate cancer prediction, and area under the receiver operating characteristic (ROC) curve with the learned model.
Results
With any prostate cancer objective variable, Lasso and stepwise regression analyses selected 12 and nine explanatory variables, respectively, from 22. Using trained ANNs with multiple hidden layers, the accuracy of predicting any prostate cancer in test samples was about 5–10% higher compared to that with logistic regression analysis (LR). The area under the curves (AUC) with multilayer ANN were significantly larger on inputting variables that were selected by the stepwise LR compared with the AUC with LR. The ANN had a higher net benefit than LR between prostate cancer probability cutoff values of 0.38 and 0.6.
Conclusions
ANN accurately predicted prostate cancer without biopsy marginally better than LR. However, for clinical application, ANN performance may still need improvement.
Introduction
Prostate cancer was the third most common cancer diagnosed in men and the sixth most common cause of cancer death in Japan in 2017.1 Prostatic biopsy is indicated when a patient is suspected of having prostate cancer, mainly based on elevated serum prostate-specific antigen (PSA) and/or digital rectal examination (DRE). Nevertheless, based on the Surveillance, Epidemiology, and End Results (SEER) data, the rate of detecting prostate cancer upon biopsy was 32%.2 Recently, magnetic resonance imaging (MRI)-targeted biopsy enhanced the rate of detecting any prostate cancer to 51–66%.3–6 If the existence of prostate cancer can be predicted more accurately before biopsy, unnecessary and invasive procedures can be avoided.
Recent advances in artificial intelligence are now being applied to various fields in society and science. A neural network simulates the pattern recognition capabilities of a biological brain. It has strength in non-linear classification, including complex regression problems. Here, we have predicted the rate of prostate cancer detection on prostate biopsy by deep learning using a multilayer artificial neural network (ANN) as an application to the urological field.
Methods
A total of 334 patients who underwent 3-Tesla multiparametric magnetic resonance imaging (mpMRI) before ultrasoundguided MRI targeted transrectal 12-core prostate biopsy between 2013 and 2017 were enrolled in the analysis. MRI was viewed before biopsy and the MRI-identified lesion was cognitively targeted. Upon biopsy, the sample sites from the prostatic peripheral zone were bilateral from the apex, mid-gland, to base. Two additional cores from the far posterior, lateral peripheral zone and one core from the transition zone of each lobe were also biopsied. Exceptionally, seven patients with prostate-specific antigen (PSA) values from 32–725 ng/ml, positive DRE, and positive MRI findings were administered sextant biopsy and prostate cancer was detected in all. Patient and clinical characteristics are described in Table 1.
Table 1.
Clinical characteristics
| Median (range) | |
|---|---|
| Age, years | 70 (44–88) |
| BH, cm | 167 (152–180) |
| BW, kg | 64 (39–111) |
| BMI | 24 (14–37) |
| WBC, /μL | 5800 (3000–13 900) |
| Hb, g/dL | 14.4 (6.9–19.9) |
| Alb, mg/dL | 4.4 (2.2–5.0) |
| Tchol, mg/dL | 197 (85–308) |
| TG, mg/dL | 126 (35–497) |
| BS, mg/dL | 107 (72–278) |
| eGFR, mL/min | 68 (3.9–110) |
| GPT, unit/L | 20 (4–78) |
| CRP, mg/dL | 0.06 (0.003–4.45) |
| PSA, ng/Ml | 30 (10–274) |
| PV, mL | 0.3 (0.04–47) |
| PSAD | |
| n (%) | |
| DRE | 59 (18) |
| MRI_PZ_T2-positive | 157 (47) |
| MRI_PZ_DWI-positive | 154 (46) |
| MRI_TZ_T2-positive | 131 (39) |
| MRI_TZ_DWI-positive | 130 (39) |
| Previous biopsy | |
| 0 | 287 (86) |
| 1 | 31 (9) |
| 2 | 9 (3) |
| 3 | 6 (2) |
| 4 | 0 (0) |
| 5 | 1 (0) |
| Gleason score | |
| 6 | 51 (15) |
| 7 | 37 (11) |
| 8 | 53 (16) |
| 9 | 24 (7) |
| 10 | 4 (1) |
DRE and MRI findings were recorded as one if prostate cancer was suspected; otherwise 0. Alb: serum albumin; BH: body height; BMI: body mass index; BS: blood sugar; BW: body weight; CRP: serum C-reactive protein; DRE: digital rectal examination; DWI: diffusion-weighted imaging; eGFR: estimated glomerular filtration rate; GPT: serum glutamic pyruvic transaminase; Hb: hemoglobin; MRI: magnetic resonance imaging; PSA: prostate-specific antigen; PSAD: PSA density; PV: prostate volume (calculated by transabdominal ultrasonography); PZ: prostatic peripheral zone; Tchol: total cholesterol; TG: triglycerides; T2: T2-weighted imaging; TZ: transition zone; WBC: white blood cell counts.
The library to construct deep leaning programs was tensorflow (Google) and the programming language was python. Twenty-two variables (Table 2) of patients who underwent prostate biopsy were initially enrolled with continuous variables standardized ([value-average]/standard_deviation). Appropriate variables were selected by least absolute shrinkage and selection operator (Lasso) regression analysis7 and by stepwise logistic regression analysis using data from all 334 samples with the glmnet 2.0–10 and the glm packages for R version 3.2.4 (Table 2). Then, 22 non-selected variables, as well as automatically selected ones, were input into the constructed multilayer ANN programs with five-fold cross-validation and were also analyzed with the conventional logistic regression analysis (LR). In brief, 232 patients for whom the last digits of their patient identification (ID) number was 0–6 were used as training cases in ANN programs and the remaining 102 patients were for the test to output the probability of prostate cancer detection, accuracy of prostate cancer prediction, and area under the receiver operating characteristic (ROC) curve with the learned model. When the output probability of prostate cancer detection in a patient was more than 0.5, it was regarded as prostate cancer and vice versa, as a discrete classifier. The parameter of ROC curves was the probability of prostate cancer detection to be evaluated as a probabilistic classifier.
Table 2.
Variable selection by the Lasso and stepwise regression analyses
| Lasso coef | Stepwise coef | |
|---|---|---|
| Intercept | 0.338 | −0.050 |
| Age | 0.047 | 0.461 |
| Previous biopsies | −0.070 | −0.740 |
| BH | 0.741 | |
| BW | −1.189 | |
| BMI | 0.006 | 1.319 |
| WBC | ||
| Hb | ||
| Alb | ||
| Tchol | −0.009 | |
| TG | −0.001 | |
| BS | −0.008 | |
| eGFR | ||
| GPT | ||
| CRP | ||
| PSA | 0.002 | |
| PV | −0.040 | −0.245 |
| PSAD | 3.835 | |
| DRE | 0.269 | 2.139 |
| MRI_PZ_T2 | ||
| MRI_PZ_DWI | 0.258 | 1.031 |
| MRI_TZ_T2 | 0.027 | |
| MRI_TZ_DWI | 0.016 |
Lasso coef and Stepwise coef were coefficients of remaining variables by Lasso and stepwise regression analysis, respectively. Alb: serum albumin; BH: body height; BMI: body mass index; BS: blood sugar; BW: body weight; CRP: serum C-reactive protein; DRE: digital rectal examination; DWI: diffusion-weighted imaging; eGFR: estimated glomerular filtration rate; GPT: serum glutamic pyruvic transaminase; Hb: hemoglobin; MRI: magnetic resonance imaging; PSA: prostate-specific antigen; PSAD: PSA density; PV: prostate volume (calculated by transabdominal ultrasonography); PZ: prostatic peripheral zone; Tchol: total cholesterol; TG: triglycerides; T2: T2-weighted imaging; TZ: transition zone; WBC: white blood cell counts.
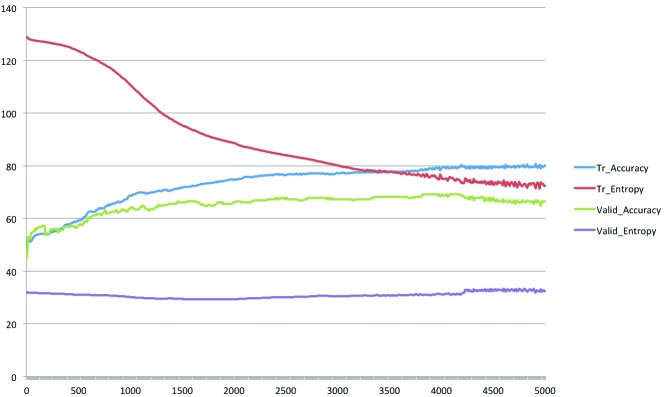
Two to five hidden layers of ANN were composed of five neurons for each layer, the activation function of hidden layers was the ReLu function, loss function was cross entropy error function, back propagation algorithm was gradient descent, and output function was softmax function. Validation of the training of ANNs was performed with the five-fold cross-validation method (results are shown in Fig. 1). The learning rate of each step was 0.0001 and the L2 regularization penalty of scale 0.005 was added to cross entropy to avoid over-fitting; those values had been adopted in a preliminary evaluation of ANNs.
Fig. 1.
Accuracy and cross entropy in training, and cross-validation of the artificial neural network (ANN) model. The representative ANN model was composed of five hidden layers with five neurons per layer and was input variables selected by stepwise regression analysis. The horizontal axis represents step cycles; the vertical axis is the % for accuracy and values for cross entropy. Tr: training; valid: cross-validation.
LR with 22 non-selected variables and variables selected by Lasso and stepwise regression was also performed with R 3.2.4 and the glm package, inputting variables of the training samples described above (Table 3). Using the obtained coefficients, the probability of prostate cancer detection, accuracy of prostate cancer prediction, and area under the ROC curve (AUC) were output from test samples. When the probability of prostate cancer detection in a patient was more than 0.5, it was regarded as prostate cancer and vice versa, as described above.
Table 3.
Logistic regression analysis of training samples with non-selected 22 variables and variables selected by the Lasso and stepwise regression
| Coefficients | All | Lasso | Stepwise |
|---|---|---|---|
| Intercept | 0.51±0.65 | 0.23±0.56 | 0.84±0.61 |
| Age | 0.43±0.28 | 0.17±0.20 | 0.29±0.21 |
| Previous biopsies | −0.58±0.34 | −0.60±0.34 | −0.55±0.32 |
| BH | −0.10±0.48 | −0.07±0.41 | |
| BW | 0.68±0.87 | 0.16±0.74 | |
| BMI | 0.19±0.76 | 0.61±0.21** | 0.46±0.65 |
| WBC | 0.23±0.22 | ||
| Hb | −0.42±0.29 | ||
| A1b | 0.41±0.25 | ||
| Tchol | −0.03±0.20 | −0.03±0.19 | |
| TG | −0.09±0.21 | −0.14±0.2 | |
| BS | −0.21±0.20 | −0.11±0.17 | |
| eGFR | 0.22±0.20 | ||
| GPT | 0.12±0.23 | ||
| CRP | −0.48±0.31 | ||
| PSA | 3.87±3.78 | 6.46±2.19** | |
| PV | −0.17±0.24 | −0.26±0.15 | 0.07±0.15 |
| PSAD | 5.67±5.65 | 10.17±3.25** | |
| DRE | 3.87±1.15*** | 3.49±1.08** | 3.36±1.07** |
| MRI_PZ_T2 | −0.38±0.92 | ||
| MRI_PZ_DWI | 2.08±0.92* | 1.66±0.38*** | 1.27±0.35*** |
| MRI_TZ_T2 | −0.86±0.83 | −0.41±0.76 | |
| MRI_TZ_DWI | 1.54±0.85 | 1.03±0.76 |
Values: estimate±standard error.
p<0.05;
p<0.01;
p<0.001.
All: 22 non-selected variables; Lasso: variables selected by Lasso regression analysis; stepwise: variables selected by stepwise regression analysis. Alb: serum albumin; BH: body height; BMI: body mass index; BS: blood sugar; BW: body weight; CRP: serum C-reactive protein; DRE: digital rectal examination; DWI: diffusion-weighted imaging; eGFR: estimated glomerular filtration rate; GPT: serum glutamic pyruvic transaminase; Hb: hemoglobin; MRI: magnetic resonance imaging; PSA: prostate-specific antigen; PSAD: PSA density; PV: prostate volume (calculated by transabdominal ultrasonography); PZ: prostatic peripheral zone; Tchol: total cholesterol; TG: triglycerides; T2: T2-weighted imaging; TZ: transition zone; WBC: white blood cell counts.
ROC curves were constructed and depicted using R 3.2.4 with the ROCR package for prostate cancer detection upon biopsy to assess the usefulness of the algorithm-output probability of prostate cancer detection as a parameter, and AUCs were statistically compared by R 3.2.4 with the pROC package. Net-benefit curves were depicted by R 3.2.4 with the rmda package.
Results
Variable selection with Lasso and stepwise regression analyses
With any prostate cancer objective variable, Lasso and stepwise regression analyses selected 12 and nine explanatory variables, respectively, from 22, as shown in Table 2. In common between them, age at biopsy, findings on DRE, findings in the peripheral zone on MRI diffusion-weighted imaging (MRI_PZ_DWI), and body mass index (BMI) were positively influential variables, while numbers of previous prostatic biopsy and prostate volume were negatively influential.
Prediction of prostate cancer with multilayer ANN
Using trained ANNs with multiple hidden layers, the accuracy of predicting any prostate cancer in test samples was about 5–10% higher compared with that with LR, as shown in Table 4 (p value not below 0.05 by Pearson Chi-square test compared with corresponding LR, odds ratio [OR] 1.49). Variable selection with Lasso and stepwise regression analyses enhanced the accuracy of prostate cancer prediction and AUCs. Five thousand learning steps reduced the accuracy compared with 2000 steps, possibly due to over-fitting. The AUCs with multilayer ANN were significantly larger on inputting variables that were selected by the stepwise logistic regression compared with the AUC with LR. The number of hidden layers slightly enhanced the AUCs.
Table 4.
Performance of multilayer artificial neural network and logistic regression analysis
| Any prostate cancer prediction in test samples | ||||||
|---|---|---|---|---|---|---|
|
| ||||||
| Test_set_accuracy (%) | Area under ROC curve | |||||
|
| ||||||
| Analytical method | Step1000 | Step2000 | Step5000 | Step1000 | Step2000 | Step5000 |
| 22_variable_logistic_regression | 59.8 | 59.8 | 59.8 | 0.67 | 0.67 | 0.67 |
| 22_variable_ANN_2_hidden_layers | 66.7 | 64.7 | 57.8 | 0.72 | 0.70 | 0.64 |
| 22_variable_ANN_3_hidden_layers | 66.7 | 64.7 | 55.9 | 0.71 | 0.66 | 0.62 |
| 22_variable_ANN_4_hidden_layers | 65.7 | 60.8 | 57.8 | 0.70 | 0.66 | 0.61 |
| 22_variable_ANN_5_hidden_layers | 66.7 | 63.7 | 59.8 | 0.71 | 0.67 | 0.62 |
| Lasso_logistic_regression | 61.8 | 61.8 | 61.8 | 0.68 | 0.68 | 0.68 |
| Lasso_ANN_2_hidden_layers | 68.6 | 70.6 | 69.6 | 0.74 | 0.70 | 0.69 |
| Lasso_ANN_3_hidden_layers | 68.6 | 71.6 | 64.7 | 0.75 | 0.72 | 0.69 |
| Lasso_ANN_4_hidden_layers | 67.7 | 71.6 | 68.6 | 0.73 | 0.72 | 0.70 |
| Lasso_ANN_5_hidden_layers | 66.7 | 71.6 | 67.7 | 0.73 | 0.71 | 0.72 |
| Stepwise_logistic_regression | 61.8 | 61.8 | 61.8 | 0.68 | 0.68 | 0.68 |
| Stepwise_ANN_2_hidden_layers | 65.7 | 65.7 | 61.8 | 0.74 | 0.72 | 0.71 |
| Stepwise_ANN_3_hidden_layers | 64.7 | 68.6 | 62.8 | 0.73 | 0.75* | 0.67 |
| Stepwise_ANN_4_hidden_layers | 62.8 | 68.6 | 66.7 | 0.73 | 0.75* | 0.72 |
| Stepwise_ANN_5_hidden_layers | 65.7 | 70.6 | 67.7 | 0.74 | 0.76* | 0.74 |
Test_set_accuracy: prediction accuracy of test samples by artificial neural network (ANN) and logoistc regsression (LR) when threshold set at 0.5; step: step cycles of ANN, ignore for LR; 22_variable: 22 non-selected variables; Lasso: variables selected by Lasso regression analysis; stepwise: variables selected by stepwise regression analysis.
p<0.05 by pROC compared with corresponding.
ROC: receiver operating characteristic.
The multilayer ANN that showed the largest AUC, i.e., ANN with five hidden layers using variables selected by stepwise regression analysis after 2000 steps (Stepwise_ ANN_5_hidden_layers in Table 4, its ROC curve in Fig. 2), was precisely compared with the corresponding LR, as shown in Table 5. With a prostate cancer probability threshold of 0.3 for example, the ANN prevented 48% of patients without actual prostate cancer from having to undergo needless prostate biopsy, while LR prevented 44%. The ANN missed 16% of any prostate cancer and 6% of prostate cancer with Gleason score (GS) ≥7, while LR missed 18% and 9%, respectively. Negative predictive values (NPV) for any prostate cancer were 76% and 72% with ANN and LR, respectively. NPVs for prostate cancer with GS ≥7 were 94% and 91%, respectively. As shown in Fig. 3, net-benefit curves for any prostate cancer detection indicated that the ANN had a higher net benefit than LR between prostate cancer probability cutoff values of 0.38 and 0.6.
Fig. 2.
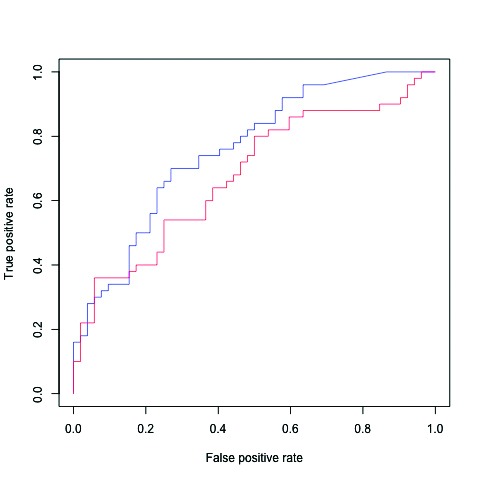
Receiver operating characteristic (ROC) curves for the actual detection of prostate cancer on biopsy to assess the usefulness of the algorithm-output probability of prostate cancer in test samples. Blue: artificial neural network (ANN) with five hidden layers using variables selected by stepwise regression analysis after 2000 steps; red: logistic regression analysis using the same variables. p<0.05.
Table 5.
Comparison of performance of ANN and the corresponding LR
| Model | Probability cutoff, % | Biopsies performed, n (%) | Biopsies not performed, n (%) | Biopsies not performed in men without PCa, n (%) | Any PCa detected, n (%) | Any PCa missed, n (%) | NPV for any PCa (%) | PCa GS ≥7 detected, n (%) | PCa GS ≥7 missed, n (%) | NPV for PCa GS ≥7 (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| ANN | 102 | NA | 50 | NA | 100 | 35 | NA | 100 | ||
| 30 | 69 (68) | 33 (32) | 25 (48) | 42 (84) | 8 (16) | 76 | 33 (94) | 2 (6) | 94 | |
| 40 | 61 (60) | 41 (40) | 29 (56) | 38 (76) | 12 (24) | 71 | 29 (83) | 6 (17) | 85 | |
| 50 | 48 (47) | 54 (53) | 38 (73) | 34 (68) | 16 (32) | 70 | 28 (80) | 7 (20) | 87 | |
| LR | 102 | NA | 50 | NA | 100 | 35 | NA | 100 | ||
| 30 | 70 (69) | 32 (31) | 23 (44) | 41 (82) | 9 (18) | 72 | 32 (91) | 3 (9) | 91 | |
| 40 | 62 (61) | 40 (39) | 27 (52) | 37 (74) | 13 (26) | 68 | 31 (89) | 4 (11) | 90 | |
| 50 | 51 (50) | 51 (50) | 32 (62) | 31 (62) | 19 (38) | 63 | 28 (80) | 7 (20) | 86 |
ANN: ANN with five hidden layers using variables selected by stepwise regression analysis after 2000 steps. GS: Gleason score; LR: logistic regression analysis (using the same variables); NA: not available; NPV: negative predictive value; PCa: prostate cancer.
Fig. 3.
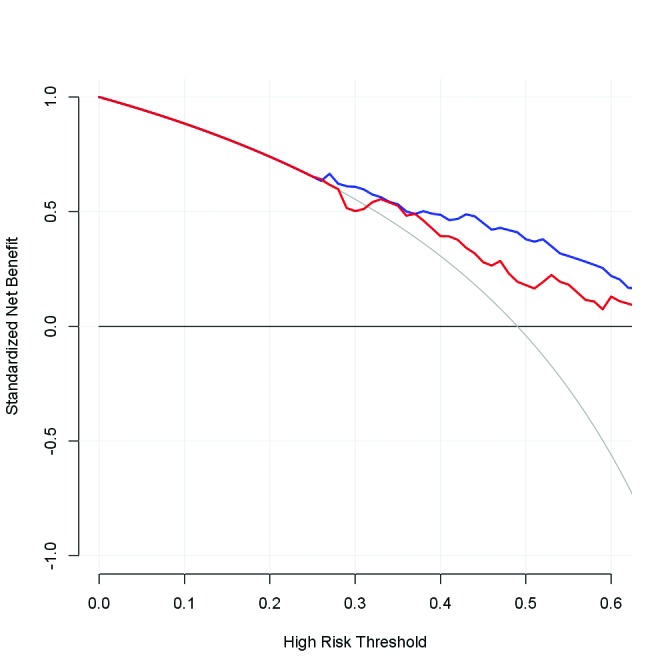
Net-benefit curves for any prostate cancer detection. Horizontal axis: cutoff value for probability of prostate cancer existence; blue: artificial neural network (ANN) with five hidden layers using variables selected by stepwise regression analysis after 2000 steps; red: logistic regression analysis using the same variables.
Discussion
Multilayer ANN could predict prostate cancer with a 5–10% higher accuracy than conventional LR when used as a discrete classifier at a cutoff probability of 0.5. This superiority was also supported by the fact that the AUCs with ANN, of which the parameter was the probability of prostate cancer existence, were larger than with LR when used as a probabilistic classifier. Thus, multilayer ANN may be a promising tool to predict the existence of prostate cancer.
However, with precise investigation, the difference between ANN and LR was still marginal for the prevention of unnecessary prostate biopsy, missing prostate cancer, and NPV. Accurate prediction of prostate cancer with a high GS is clinically more important, as it tends to become castration-resistant, metastasize, and become life-threatening. The marginal difference also applies to high GS (≥7) prostate cancer.
Several trials have been undertaken to predict the presence of prostate cancer without prostate biopsy using LR,8–15 leading to excellent performance. LR is already very accurate in its prediction of prostate cancer and it may retain this effectiveness even in comparison with ANN. ANN and LR missed less than 20% of all prostate cancer and less than 10% of high GS prostate cancer on setting the cutoff value of probability as 0.3. This rate of missed cancer detection may be acceptable or remain controversial when ANN and LR are used to screen candidates for prostate biopsy.
Conclusion
The ANN predicting the existence of prostate cancer is novel and still preliminary. The accuracy of predicting the existence of prostate cancer without biopsy is good, but there is still room for improvement. The highly effective ANN shows a higher rate of classification accuracy and larger AUC. There are ways to improve the capacity of ANNs to predict prostate cancer.
Increasing the sample size may improve the performance of multilayer ANN as a result of more sufficient training. In this study, the sample size was limited and training with 10 to 100 times more samples would work better. If the sample size is increased, ANNs with more hidden layers and neural nodes can perform better, avoiding early over-fitting. Adding more variables that are appropriate for predicting prostate cancer may be another good way for ANN to perform better. For example, genetic factors and excellent biomarkers may be candidates in addition to standard clinical and imaging parameters. Tuning of hyper-parameters, such as the learning rate, regularization penalty scale, and leaning cycles, would be less effective than those factors described above. In conclusion, ANN accurately predicted prostate cancer without biopsy marginally better than LR. However, for clinical application, ANN performance may still need improvement.
Footnotes
Competing interests: This article appears in bioRxiv 291609; https://doi.org/10.1101/291609 as a preprint dated March 29, 2018. The authors report no competing personal or financial interests related to this work.
This paper has been peer-reviewed.
References
- 1.Cancer Information Service. Projected cancer statistics, 2018. [Accessed June 30, 2018]. Available at: https://ganjoho.jp/en/public/statistics/short_pred.html.
- 2.Welch HG, Fisher ES, Gottlieb DJ, et al. Detection of prostate cancer via biopsy in the Medicare-SEER population during the PSA era. J Natl Cancer Inst. 2007;99:1395–400. doi: 10.1093/jnci/djm119. [DOI] [PubMed] [Google Scholar]
- 3.Haffner J, Lemaitre L, Puech P, et al. Role of magnetic resonance imaging before initial biopsy: Comparison of magnetic resonance imaging-targeted and systematic biopsy for significant prostate cancer detection. BJU Int. 2011;108:E171–8. doi: 10.1111/j.1464-410X.2011.10112.x. [DOI] [PubMed] [Google Scholar]
- 4.Porpiglia F, Manfredi M, Mele F, et al. Diagnostic pathway with multiparametric magnetic resonance imaging vs. standard pathway: Results from a randomized prospective study in biopsy-naive patients with suspected prostate cancer. Eur Urol. 2017;72:282–8. doi: 10.1016/j.eururo.2016.08.041. [DOI] [PubMed] [Google Scholar]
- 5.Moore CM, Kasivisvanathan V, Eggener S, et al. Standards of reporting for MRI-targeted biopsy studies (START) of the prostate: Recommendations from an International Working Group. Eur Urol. 2013;64:544–52. doi: 10.1016/j.eururo.2013.03.030. [DOI] [PubMed] [Google Scholar]
- 6.Baco E, Rud E, Eri LM, et al. A randomized controlled trial to assess and compare the outcomes of two-core prostate biopsy guided by fused magnetic resonance and transrectal ultrasound images and traditional 12-core systematic biopsy. Eur Urol. 2016;69:149–56. doi: 10.1016/j.eururo.2015.03.041. [DOI] [PubMed] [Google Scholar]
- 7.Tibshirani R. Regression shrinkage and selection via the lasso. J Royal Stat Soc Series B (Methodological) 1996;58:267–88. doi: 10.1111/j.2517-6161.1996.tb02080.x. [DOI] [Google Scholar]
- 8.Bjurlin MA, Rosenkrantz AB, Sarkar S, et al. Prediction of prostate cancer risk among men undergoing combined MRI-targeted and systematic biopsy using novel pre-biopsy nomograms that incorporate MRI findings. Urology. 2018;112:112–20. doi: 10.1016/j.urology.2017.09.035. [DOI] [PubMed] [Google Scholar]
- 9.Dong F, Kattan MW, Steyerberg EW, et al. Validation of pretreatment nomograms for predicting indolent prostate cancer: Efficacy in contemporary urological practice. J Urol. 2008;180:150–4. doi: 10.1016/j.juro.2008.03.053. [DOI] [PubMed] [Google Scholar]
- 10.Kattan MW, Eastham JA, Wheeler TM, et al. Counselling men with prostate cancer: A nomogram for predicting the presence of small, moderately differentiated, confined tumours. J Urol. 2003;170:1792–7. doi: 10.1097/01.ju.0000091806.70171.41. [DOI] [PubMed] [Google Scholar]
- 11.Hansen J, Auprich M, Ahyai SA, et al. Initial prostate biopsy: Development and internal validation of a biopsy-specific nomogram based on the prostate cancer antigen 3 assay. Eur Urol. 2013;63:201–9. doi: 10.1016/j.eururo.2012.07.030. [DOI] [PubMed] [Google Scholar]
- 12.Lopez-Corona E, Ohori M, Scardino PT, et al. A nomogram for predicting a positive repeat prostate biopsy in patients with a previous negative biopsy session. J Urol. 2003;170:1184–8. doi: 10.1097/01.ju.0000087451.64657.fa. [DOI] [PubMed] [Google Scholar]
- 13.Chun FK, Briganti A, Graefen M, et al. Development and external validation of an extended repeat biopsy nomogram. J Urol. 2007;177:510–5. doi: 10.1016/j.juro.2006.09.025. [DOI] [PubMed] [Google Scholar]
- 14.Zaytoun OM, Kattan MW, Moussa AS, et al. Development of improved nomogram for prediction of outcome of initial prostate biopsy using readily available clinical information. Urology. 2011;78:392–8. doi: 10.1016/j.urology.2011.04.042. [DOI] [PubMed] [Google Scholar]
- 15.Benecchi L, Pieri AM, Melissari M, et al. A novel nomogram to predict the probability of prostate cancer on repeat biopsy. J Urol. 2008;180:146–9. doi: 10.1016/j.juro.2008.03.043. [DOI] [PubMed] [Google Scholar]