A novel modelling technique to predict resource ­requirements in critical care – a case study

ABSTRACT

Modelling is an under-used tool in the NHS operationally; this is primarily due to a lack of familiarity, but also due to the complex nature of the healthcare system, lack of sufficiently detailed data, and difficulties trying to distil the heterogeneity of individual patient experience into manageable groups.

 This paper describes a model of patient flow and resource use on the critical care unit at Bradford Royal Infirmary, ­produced using a novel technique which helps avoid these issues by using genuine routinely collected historical data in lieu of trying to model individual patients. This has had ­unexpected benefits in terms of engagement with the model as it is much easier to justify its validity when it is based directly on real people.

 Going forward, we will use this approach to model an entire hospital.

Introduction

Over winter 2015–16, Bradford Royal Infirmary (BRI) critical care unit (CCU) dealt with an unprecedented level of demand which led to many patients having to be transferred elsewhere and a large number of elective operations being cancelled or deferred.

The BRI is a teaching hospital with approximately 900 beds. The CCU takes general medical, and acute and elective surgical patients, and works to the Guidelines for the Provision of Intensive Care Services (GPICS) standards.¹ Nominally, capacity is eight intensive care unit (ICU) patients (GPICS level 3, where advanced respiratory support or multiple organ support is required) and eight high dependency unit (HDU) patients (GPICS level 2, with only single organ support or close observation), but where possible staff are used flexibly so long as a nurse:patient ratio of 1:2 for HDU and 1:1 for ICU can be maintained.

In 2016, the CCU comprised a main unit with 12 beds, all capable of taking ICU patients but normally configured as eight ICU / four HDU, and a secondary unit with four HDU beds. The building of a new ICU with 16 ICU-capable beds in one location presented an opportunity for expansion, but it was not clear whether the winter's events were a statistical fluke or a predictable consequence of demand.

We decided to build a model of resource use and patient flow to test this, and also to explore the effects of nursing staffing, bed-base changes, and other changes to working which might impact on flow through the unit.

There are a variety of ways in which ICU capacity, and other hospital processes, can be modelled. These can be categorised into two main types: top-down (often ‘system dynamics’ or ‘time series’), and bottom-up (usually ‘discrete event’ or ‘agent-based’) approaches.^2,3

Top-down approaches model the healthcare system at an aggregate level, such as modelling wards or even an entire hospital.^4,5 They treat patients as a continuous mass rather than as complex individuals and can be very useful to guide understanding of a complicated system and the effect of perturbations. They are most useful for high-level decision guidance,² but due to their lower data requirements have been used for the specifics of resource allocation.⁶

Bottom-up approaches are much more commonly used in resource-allocation modelling.^7–9 Patients are modelled as discrete entities passing through activities according to defined decision rules. Approaches include Markov chain models,¹⁰ where a patient may arrive on the ICU in one state, and at each time point have a probability of moving to another (eg deteriorating, improving, or requiring some resource), or simply distributing a patient's resource requirements based on a classification system.^11,12 These approaches are very powerful, but are in general enormously data-driven and require substantial work.

Methods

An initial exploration was made of top-down modelling using time-series analysis,¹³ targeting an output of the total numbers of patients across time, feeding in numbers from previous days and modifying by external events such as day/season etc. However, we rapidly rejected this approach as it treats patients as equivalent and interchangeable when there is a predictable difference between a stable patient admitted after elective surgery and one arriving as an unstable emergency. The possible amendment of subcategorising the patients was considered, but an attempt at categorising patients in similar UK hospitals resulted in anywhere between 13 and 39 categories, with the majority having a length of stay interquartile range greater than the median.¹² This amendment was therefore also rejected as the low numbers and high variation in each category would make the error term dwarf the predictive value of the model.

Therefore, the best approach seemed to be a bottom-up one, treating patients as individuals and using each one's resource use to drive the model. The Markov chain approach is powerful, but generation of this model would have required massive amounts of data to estimate the probabilities. Even worse, these probabilities would have changed depending on facts about the patient or their history – leading again to the ‘explosion of categories’ problem. Large amounts of categories without large amounts of data would lead to the problem of over-fitting, where each category is based on such a small sample that it essentially replicates what happened to those people rather than uncovering a more general trend.

Like most ICUs in the UK our unit participates in the Intensive Care National Audit & Research Centre (ICNARC) audit which involves routine collection of basic data about each patient and their resource use. The data collected thus represent as full a sample as could be reasonably used to generate distributions for use in any bottom-up modelling approach, so rather than processing these data in an intermediate step to build a ‘representative patient’, a Monte-Carlo approach can use the data directly.¹⁴ Therefore, the model simulates inputs to the ICU in a more traditional statistical fashion but when the process calls for a new patient to be input, a genuine patient is selected from anonymised historical data in a random fashion which accounts for the fact that patients arriving in different ways or on different days may have different needs. The outputs of interest are then generated directly from the interaction of the sampled historic data within the model.

This approach on its own it does not easily allow calculation of best- and worst-case scenarios, or ranges of what is likely. Each run of the model, like real life, gives only one of the many potential paths such a complex system can undertake. However, in another Monte-Carlo approach the model can be run many times over,^14,15 and each path recorded, to allow capture of the likely range of possibilities and give an estimated distribution of the outcomes of interest.

The purpose of this model was to look at the effects of limited capacity; therefore, the outcomes chosen for the report aimed to reflect the effects of the unit being unable to meet the demands placed on it. Occupancy rates are commonly quoted as an early warning of under-resourcing when they rise above 80%.¹⁶ The model calculates these using the ‘calendar date’ method which is used as a standard regionally.¹⁷ This counts a bed twice if it is occupied by two patients on the same day (and therefore can rise above 100%), but also considers a bed ‘empty’ even if it has been closed to free up nurses to temporarily increase ICU capacity. Cancelled elective surgery is the main control clinicians can exert on demand, so this statistic is also reported. Acute non-clinical transfers to other hospitals are the main ‘relief valve’ for an overloaded system; these are difficult for the model to accurately predict as clinicians may adopt more stringent standards for admission when the unit is full.⁹ Other subcategories are also reported to show whether cancellations are due to physical bed or nursing capacity, or the use of ‘staffing up’ if it is selected as an option in the model. All statistics are reported as medians with quartiles to illustrate the range of possibilities in each scenario.

As a service improvement project using anonymised routinely-collected data, and without generalisable results, our director of research agreed that this was not research and formal ethical approval was not required.

Results

Initial runs of the model using the real setup at BRI plausibly matched real-life occupancy data (Fig 1) and rates of cancelled surgery and non-clinical transfers for the year, and showed that the events of winter 2015–16 were not so unpredictable. This ‘least worst’ modelling option chosen turned out to have powerful benefits; a major potential criticism of modelling of this type is that the process used to model each patient does not represent reality, but each ‘data point’ in the model was grounded in genuine historic data from real people.

Fig 1.

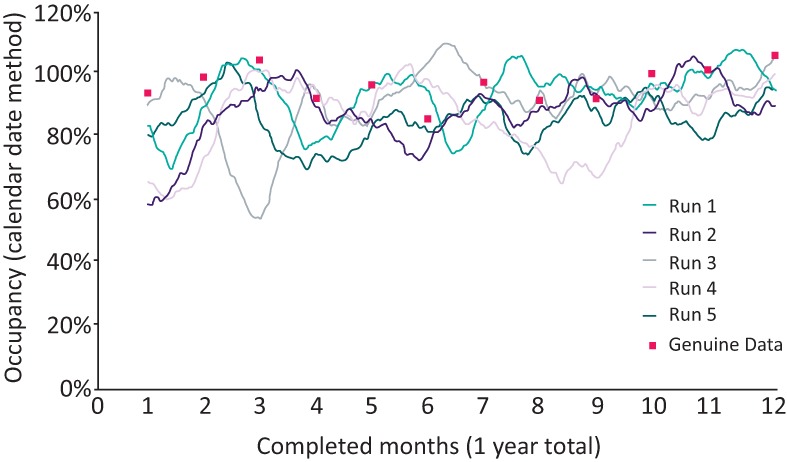
Illustrative graph of 30-day bed occupancy from five model runs of the baseline unit, with real data for comparison.

Having established that the model was useful, hypothetical scenarios could be tested. These are shown in Table 1. ‘Baseline’ represents the old unit as described in 2016, with 12 nurses on a shift directly caring for patients. The main flexibility in this scenario comes from ‘staffing up’ by bringing in an extra nurse where required to avoid a cancelled elective operation, represented in the second row.

Table 1.

Hypothetical scenarios tested. Values are numbers of patients per year, median + interquartile range

Scenario	Cancelled elective surgery	Acute transfers out	Occupancy
Baseline	57 (34–121)	43 (27–64)	0.92 (0.81–1.01)
Baseline + staffing up for electives	27 (19–41)	38 (23–56)	0.93 (0.82–1.02)
New unit	60 (40–92)	42 (26–53)	0.93 (0.83–1.01)
New unit + staffing up for electives	31 (22–44)	41 (31–62)	0.91 (0.81–1.01)
New unit + 2 HDU beds + 0 nurses	47 (28–82)	35 (19–49)	0.81 (0.73–0.90)
New unit + 2 HDU beds + 1 nurse	32 (19–46)	24 (13–36)	0.83 (0.74–0.91)
New unit + 2 HDU beds + 2 nurses	14 (8–24)	8 (4–13)	0.81 (0.72–0.90)
New unit + 4 HDU beds + 2 nurses	11 (6–17)	9 (5–15)	0.75 (0.65–0.84)
New unit + 1 nurse	34 (20–69)	24 (12–39)	0.93 (0.83–1.02)
New unit + overnight PACU	30 (21–41)	37 (25–55)	0.88 (0.78–0.97)
New unit + no delayed discharges	54 (37–98)	33 (23–75)	0.86 (0.78–0.96)

HDU = high dependency unit; PACU = post anaesthetic care unit

The new unit offered additional flexibility as all 16 beds could be used for ICU patients – with some hoping that this might prevent the issues experienced in 2015–16 from recurring. The modelling suggested otherwise, even with ‘staffing up’. The use of an overnight recovery (post anaesthetic care unit) for some elective surgical patients who would normally be discharged the following day helped slightly to avoid cancelled surgery, but only patients who demanded the least resource were suitable so the total pressure on the unit changed little. Equally, solving the problem of delayed discharges would help little. The only modelled solutions to ease pressures on the unit was an increase in the number of staffed HDU beds and predictions from the model have been used in a business case to support this.

Discussion

This technique sidesteps many of the issues with more conventional modelling approaches, and has advantages in terms of explicability and acceptance, making it potentially very useful operationally. However, as a short-cut technique it has its limitations. The real patient data used as an input may not include some rare outliers, who might spend a great deal of time on the unit, whereas a Markov chain model would be capable of generating these. While they could be manually generated, it would sacrifice the explainability of the model. Other more general changes, such as an aging population or an expansion in a certain patient type, could be dealt with by resampling the underlying data which is likely to be less contentious. Quality measures at the patient level cannot easily be tested – for example the effects on readmission rates of being able to keep patients a day longer, but this is a limitation of most modelling types.

The abilities of technique are also very reliant on the type of data used to drive it. ICNARC resource use is at the level of individual days, so the ‘tick rate’ in the model had to match. This generated most of the fuzziness in the outputs, as it was never clear whether an arrival would occur before or after a discharge. However, on the real unit elective surgery usually arrives later in the day and it is possible to delay arrivals by the temporary use of recovery areas, so the model was configured to assume this was possible – but to note down when it occurred as a possible marker of pressure.

Similar difficulties exist around the concept of acute transfers out as clinicians may behave differently when the unit is full.⁹ The figure therefore represents a total of patients who in real life came to the unit, but in the modelled scenario would have to be cared for elsewhere – whether by transfer to another hospital, or in some cases remaining in the same hospital but with extra support.

The main advantage of this technique is that it relies on relatively small amounts of routinely collected data, and little analysis is required to build the model. However, building the model and encoding the decision processes is more complex. Commercial tools exist which could speed up the process but their cost may dissuade NHS trusts from embarking on modelling as part of improvement practice. The free statistical environment R can perform modelling of this type and the NHS is developing an R community with skills in this language, so the opportunity exists to use modelling like this at low cost, outside of a research setting.

Another operational benefit is the possibility of breaking down the simulation to ask specific questions around flow – tracking individual variables which may not have been present in source data used for time series analysis or similar. For example, this could be used to determine the best day for scheduling elective surgery to avoid cancellations. It should also be possible to allow the model to ‘pick up’ from live genuine data to allow short-term forecasting of demand, and efficient resource allocation.

The approach described is clearly applicable to critical care in the UK, where ICNARC data are readily available. Admission, discharge and transfer data are computerised in most hospitals, and for a basic model of bed use this may be sufficient. And as the NHS becomes increasingly digital and patient journeys are recorded with ever-finer granularity – this technique will become increasingly powerful.

Conclusion and next steps

This is a useful modelling technique for complex situations where attempts to use traditional statistical techniques would either need too much data, or risk over-fitting due to large numbers of categories. It also has particular benefits during the engagement phase, allowing focus to remain on the model and its predictions rather than justifying its assumptions.

This technique could consider the specialist case of intensive care across the whole country, as ICNARC has data for the majority of the UK's intensive care units. A model could be created which accounts for the fact that a ‘transfer out’ of one patient is actually a ‘transfer in’ somewhere else. This could help inform ICU resource provision around the country and could even go further by resampling data to predict the future need for ICU resource.

As our next step we will expand this approach to generate a full-hospital model. This will require more varied data inputs, but this technique is surprisingly ‘data light’ and we feel that we are already at the point where this technique should be possible. Once a whole-hospital model is built it can be used for strategic planning; in particular, we will focus on potential responses to winter pressures – allowing ideas to be tested prior to implementation, and allowing potentially less intuitive methods to be considered. We intend to make our efforts available for others to build upon, and we would hope to develop more user-friendly tools to make this modelling technique easier within the NHS.

Author contributions

Tom Lawton was responsible for the design, modelling and first draft of the manuscript. Michael McCooe contributed to management and revisions of the text.