Oxygen consumption in human, tissue-engineered myobundles during basal and electrical stimulation conditions

Abstract

During three-dimensional culture of skeletal muscle in vitro, electrical stimulation provides an important cue to enhance skeletal muscle mimicry of the in vivo structure and function. However, increased respiration can cause oxygen transport limitations in these avascular three-dimensional constructs, leading to a hypoxic, necrotic core, or nonuniform cell distributions in larger constructs. To enhance oxygen transport with convection, oxygen concentrations were measured using an optical sensor at the inlet and outlet of an 80 μl fluid volume microphysiological system (MPS) flow chamber containing three-dimensional human skeletal muscle myobundles. Finite element model simulations of convection around myobundles and oxygen metabolism by the myobundles in the 80 μl MPS flow chamber agreed well with the oxygen consumption rate (OCR) at different flow rates, suggesting that under basal conditions, mass transfer limitations were negligible for flow rates above 1.5 μl s⁻¹. To accommodate electrodes for electrical stimulation, a modified 450 μl chamber was constructed. Electrical stimulation for 30 min increased the measured rate of oxygen consumption by the myobundles to slightly over 2 times the basal OCR. Model simulations indicate that mass transfer limitations were significant during electrical stimulation and, in the absence of mass transfer limitations, electrical stimulation induced about a 20-fold increase in the maximum rate of oxygen consumption. The results indicate that simulated exercise conditions increase respiration of skeletal muscle and mass transfer limitations reduce the measured levels of oxygen uptake, which may affect previous studies that model exercise with engineered muscle.

INTRODUCTION

Skeletal muscle tissue engineering holds great promise for drug screening,^1,2 regenerative medicine,^3,4 soft robotic devices,⁵ and the study of muscle development, disease, growth, and metabolism.^6–10 However, current skeletal muscle tissue engineered constructs lack the complex cellular and molecular organization, mature muscle protein expression, and adequate functional output characteristic of native muscle.¹¹ Specific contractile forces produced by engineered muscles are 10–100 times less than the values measured for native adult muscles in vivo.⁶ A number of factors are responsible for the lower forces in vitro including inadequate myofiber density and orientation, presence of fetal forms of myosin, and/or the absence of innervation during culture. Electrical stimulation has beneficial effects on myoblast cell fusion, as well as myotube alignment, hypertrophy, expression of contractile proteins, myokines, electrical excitability, and force generation.^12–18

Recently, we measured the myobundle oxygen consumption rate (OCR) using the OROBOROS O2k system,¹⁹ providing the first results for oxygen consumption by engineered human skeletal muscle. The O2K system is highly accurate but is not well-suited for studies of skeletal muscle that is electrically stimulated. Measurements in the O2K system break sterility and cannot be used for repeated long-term studies with the same engineered myobundles. Furthermore, the O2K system cannot accommodate electrodes to repetitively contract engineered muscle bundles. Flow of media around the myobundles in a microphysiological system (MPS) flow chamber enables the real-time, nondestructive measurement of oxygen metabolism with and without electrical stimulation. These added advantages enable the measurement of oxygen consumption in myobundles under simulated exercise conditions that could previously only be studied in human or animal subjects.

Electrical stimulation of engineered muscle can increase oxygen consumption, leading to hypoxic regions in engineered tissue. This is due to myofibers relying on diffusion within the construct, which is not fast enough to meet the metabolic demand when the size or cell density is too large.²⁰ Even in the absence of electrical stimulation, oxygen gradients prevent uniform cell densities in thicker myobundles.²¹

Convection is an effective way to overcome external mass transfer limitations, while decreasing the construct size reduces the diffusion time within the engineered tissue.²⁰ Flow has enabled the culture of larger avian, rat, and C2C12 muscle constructs.^22,23 These beneficial effects of flow and perfusion result in improved structural organization and functional properties of engineered muscles.¹¹ Addition of mixing by rocking cells during culture enhances cell density and differentiation within myobundles, leading to higher contractile forces.¹⁰ The establishment of a functional vasculature is needed to ensure that such systems can retain function after implantation and incorporating endothelial cells in myobundles before implantation accelerates this process. Elimination of oxygen transport limitations would improve methods to chronic stimulate engineered muscle in vitro, leading to increased skeletal myobundle survival and mimicry of the in vivo structure and function.

In this study, we created an MPS flow chamber to measure the myobundle oxygen consumption rate and validated using the O2K system. The flow system was then modified to accommodate electrodes for electrical stimulations of myobundles. To estimate the maximum rate of oxygen consumption in the myobundles and mass transfer effects, oxygen transport and myobundle oxygen consumption were modeled using COMSOL.

RESULTS

Myobundle oxygen transport during basal respiration

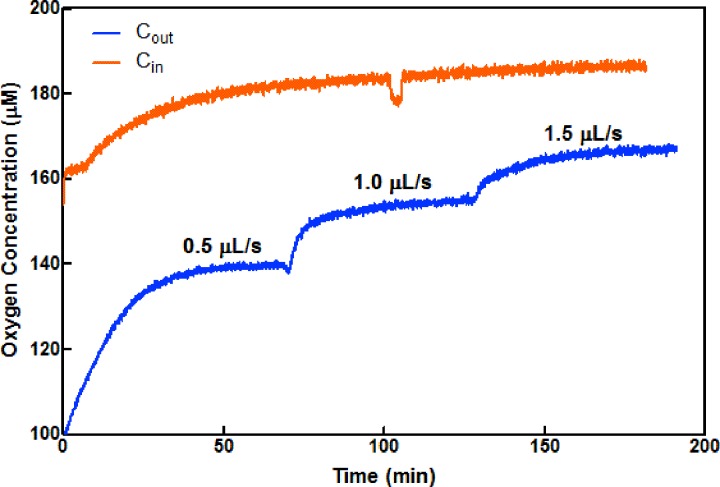
Oxygen consumption rates in myobundles under resting conditions were measured in an 80 μl MPS flow chamber (Figs. 1 and S1A) at varying flow rates in the absence of electrical stimulation. The myobundle was attached to a porous nylon frame to maintain tension and rests slightly above the bottom of the 80 μl chamber to enable flow around the myobundle. Shown in Fig. 2 are representative upstream and downstream traces of oxygen at different flow rates. (The delay time in reaching the steady state was due to thermal equilibration times in the incubator. We minimized such delays after the initial start of flow by adjusting flow rates with the incubator door closed. The small change in the inlet concentration at 110 min is an artifact.) Once the steady state was reached, the upstream concentration did not change with the flow rate and approached the value for saturated oxygen in the culture media at 37 °C. Downstream, the oxygen concentration increased as the flow rate increased, suggesting improved fluid phase mass transfer.

FIG. 1.

Custom perfusion system design and assembly. (a) Exploded view of the acrylic perfusion chamber housing the muscle bundle construct. Arrows denote the direction of flow. The final chamber volume is 80 μl after top fits within the bottom through a lock-and-key mechanism. The myobundle is attached to the porous nylon frame which rests on the bottom of the chamber. Fluid flows above and below the myobundle. (b) Side view of the chamber, showing the placement of the muscle bundle. (c) Photograph of upper and lower halves of the perfusion chamber, showing the 80 μl reservoir where the myobundle is located. (d) Photograph of the assembled chamber with the myobundle.

FIG. 2.

Trace of oxygen concentration vs time in the inlet (orange) and outlet (blue) of the 80 μl chamber for flow rates of 0.5, 1.0, and 1.5 μl s⁻¹. Outlet concentrations of oxygen increase as the flow rate increases, consistent with a reduction in mass transfer resistance in the fluid phase.

The oxygen consumption rate (OCR) through the flow chamber was calculated from the steady state mass balance equating the change in the concentration between the inlet of the chamber (C_in) and the outlet of the chamber (C_out) multiplied by the flow rate

$$\text{OCR}=\mathrm{Q}\left({\mathrm{C}}_{\text{out}}-{\hspace{0.17em}\mathrm{C}}_{\text{in}}\right).$$ (1)

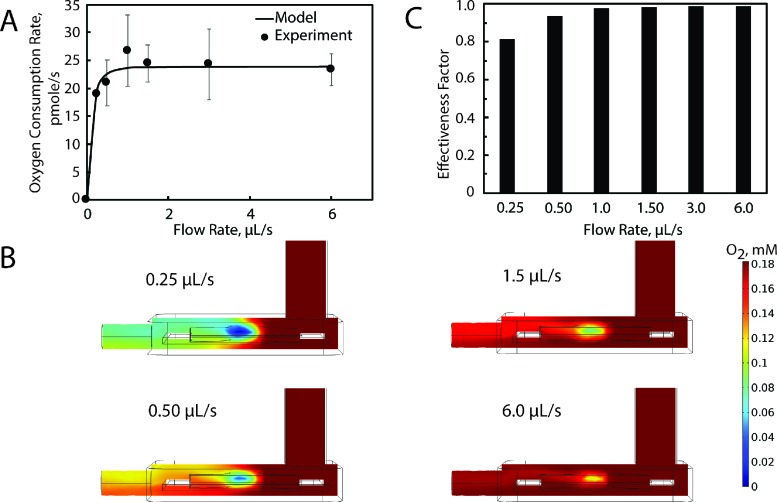
In the 80 μl microphysiological flow chamber, the myobundle OCR became independent of the flow rate for flow rates above 1.5 μl s⁻¹ [Fig. 3(a)]. To estimate R_{max_Basal} and assess mass transfer limitations in the system, we developed a model of oxygen transport and compared model simulations with experimental results. The model included convection and diffusion (D_{O2_media}) in the fluid flowing through the MPS chamber and Michaelis-Menten oxygen metabolism (R_{max_Basal} is the maximum rate of O₂ metabolism under resting conditions, and K_m is the Michaelis constant), diffusion (D_{O2_myobundle}), and porous media flow in the myobundle. Parameter values are listed in Table I. The myobundle shape and thickness were based on representative measured values, and R_{max_Basal} was obtained from values in the O2k system [pmol s⁻¹ (10⁶ nuclei)⁻¹]¹⁹ multiplied by the number of nuclei per myobundle volume. There was excellent agreement between the experimental results and model simulations [Fig. 3(a)].

FIG. 3.

Theoretical and experimental oxygen transport for myobundles' basal respiration. (a) Comparison between experimental and computational values for myobundle basal respiration over a range of flow rates. The oxygen consumption rate (pmol s⁻¹) was calculated from the product of the average reaction rate in the bundle multiplied by the bundle volume. Experimental data are mean±SEM from 3 donors with 2 biological replicates per donor. (b) Colorimetric plot denoting changes in the oxygen concentration in the myobundle and perfusion chamber for flow rates of 0.25, 0.50, 1.50, and 6.0 μl s⁻¹. Flow enters the chamber from the upper right and exits on the left port. (c) Change in the effectiveness factor with the flow rate.

TABLE I.

Computational model parameters.

Parameter	Value or equation	Description	References
Chamber and myobundle dimensions
Ainlet_basal	0.01 [cm2]	Cross-sectional area of the basal perfusion chamber inlet	Measured
Ainlet_ES	0.015875 [cm2]	Cross-sectional area of the electrical stimulation perfusion chamber inlet	Measured
PSA	0.1102 [cm2]	Projected surface area (PSA) of the representative myobundle	19
T	5.3 × 10-2 [cm]	Thickness of the myobundle	19
		Range:0.025-0.075 cm
Volume	PSA*t	Volume of the myobundle
Fluid transport values
Q	0.25–100 [μl s−1]	Flow rate	Measured
uinlet	Q/Ainlet	Inlet velocity
ρ	1.0 [g cm−3]	Media density	20
Oxygen transport values
Rmax_Basal	–4.12 × 10-6 [M s−1]	Basal respiration maximum reaction rate	19
Km	1.33 × 10–6 [mol L−1]	Michaelis constant	30
DO2_mybundle	2.0 × 10–5 [cm2 s−1]	Diffusion coefficient of O2 in the myobundle	29
DO2_media	2.4 × 10–5 [cm2 s−1]	Diffusion coefficient of O2in culture media	27
T	293.15 [K]	Temperature	Measured
ϵp	0.99	Porosity	32
K	1 × 10–8 [cm2]	Permeability	33

Fluid streamlines showed that fluid moved in a uniform manner above and below the myobundle (Fig. S2). Although the myobundles were porous, the average velocity in the myobundle (⟨u_M⟩=1.19 × 10⁻⁷ m s⁻¹ for a flow rate of 6 μl s⁻¹) is several orders of magnitude less than fluid velocity and the Peclet number in the myobundles (⟨u_M⟩t/D_{O2_myobundle}) is ≪1 (0.031 for a flow rate of 6 μl s⁻¹).

At 0.5 μl s⁻¹, model simulations showed that the media dissolved oxygen concentration was depleted along the flow direction, due to the myobundle oxygen consumption. Increasing the flow rate to 1.5 μl s⁻¹ improved oxygen delivery, and oxygen concentration gradients were confined to regions within the myobundles. Increasing the fluid flow rate increased the myobundle oxygen concentration, which resulted in an increase in myobundle respiration [Fig. 3(b)].

This trend was also apparent in the effectiveness factor [Fig. 3(c)], which is the ratio of the average myobundle rate of oxygen consumption to the maximum myobundle rate of reaction if the concentration were equal to the inlet concentration.²⁰ This measure assesses the reduction in the reaction rate due to both internal and external oxygen transport. Although there are significantly lower oxygen concentrations at low flow rates, the effectiveness factor does not drop too much below 1 because K_m is still much smaller than the oxygen concentration and the rate declines modestly from R_{max_Basal}. The effectiveness factor was 0.99 for a flow rate of 1.5 μl s⁻¹, which indicates that flow rates at and above this value do not lead to internal mass transport limitations.

To validate the custom microphysiological flow chamber respiration results, respiration rates from two myobundles from each of the 3 different donors measured in the flow system at a flow rate of 1.5 μl s⁻¹ were measured in the O2K system. The oxygen consumption rates for both methods were comparable with the average difference being 15.7% (p = 0.94; Fig. S3). OCR values obtained with the O2k system are similar to what we reported previously.¹⁹

Contractile force measurements of myobundles under electrical stimulation and flow

Since the carbon electrodes could not fit within the 80 μl chamber, a new chamber was designed to produce the smallest chamber volume (450 μl), which enabled handling and placement of the electrodes and myobundles (Figs. S1B and S1C). Due to the larger size of the 450 μl chamber, two myobundles were placed in each chamber to ensure that a measurable concentration difference between the inlet and the outlet could be obtained. A stimulation regimen of 5 ms biphasic pulses at 5 Hz with a 50-ms delay between trains of pulses was chosen to mimic a moderate exercise regime. Previous studies have used up to 10 Hz stimulation and 1 mA,^24–26 and did not lead to damage of myobundles or 2D muscle cultures.

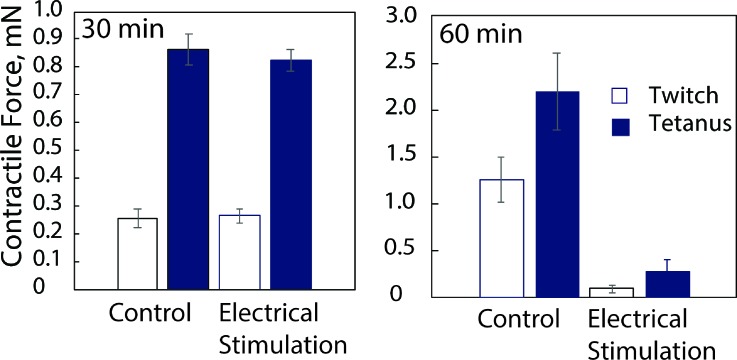
Myobundles were perfused in chambers at 3 μl s⁻¹ and stimulated for 30 or 60 min, and the contractile force was measured as described previously.² A 30-min stimulation period did not affect the force, while a 60-min stimulation caused a significant force decline (Fig. 4). The decline in force after the longer stimulation period may be due to fatigue since a longer rest between pulses enables myobundles to be stimulated chronically for 7 days.^17,25 Based on these results, oxygen consumption rates were determined during a 30-min period of electrical stimulation.

FIG. 4.

Twitch and tetanus contractile force after exposure to 5 Hz stimulation for 30 min (mean ± SEM, N = 4 myobundles per condition) or 60 min (N = 2 myobundles per condition).

Oxygen consumption rate of myobundles under electrical stimulation and flow

For the 450 μl chamber, a flow rate of 3 μl s⁻¹ was used to produce some mass transfer limitations under basal conditions, whereas a flow rate of 12 μl s⁻¹ was expected to minimize fluid phase mass transfer limitations since the residence time was less than that in the 80 μl channel at 1.5 μl s⁻¹. Streamlines indicated that the flow patterns on the two myobundles are very different (Fig. S4) which affected oxygen transport. In order to compare basal conditions between the 80 μl and 450 μl microphysiological flow systems, the results are presented for the average OCR per 10⁶ nuclei in the myobundles measured under basal respiration followed by electrical stimulation.

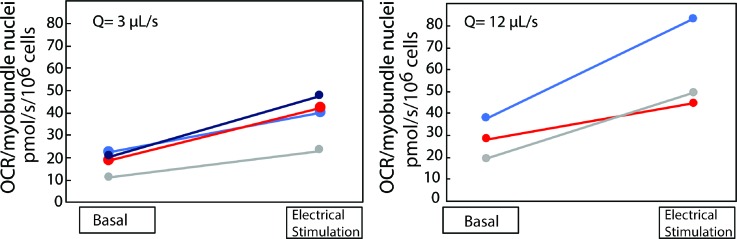
Each pair of myobundles exhibited an increase in OCR after 30 min of electrical stimulation with an average change of 2.1 ± 0.2 at 3 μl s⁻¹ (mean ± SD, N = 4 donors) and 2.10 ± 0.5 at 12 μl s⁻¹ (mean ± SD, N = 3 donors) (Fig. 5). Increasing the flow rate seemed to have a similar effect on OCR for basal (1.59-fold increase) and exercise (1.55-fold increase) conditions. Thus, the increased demand on the muscle to sustain contractions produced an increase in the rate of oxygen consumption.

FIG. 5.

Oxygen consumption by myobundles under basal and simulated exercise conditions at Q = 3 μl s⁻¹ (n = 4 replicates; 2 myobundles per replicate) and Q = 12 μl s⁻¹ (n = 3 replicates; 2 myobundles per replicate) in the 450 μl perfusion system. In order to compare basal conditions with the results in the 80 μl volume perfusion system, the results are presented for the average per chamber measured under basal respiration followed by electrical stimulation. Each pair is connected by a line showing the specific change in oxygen consumption.

Maximal oxygen reaction rate and mass transfer limitations under basal and simulated exercise conditions

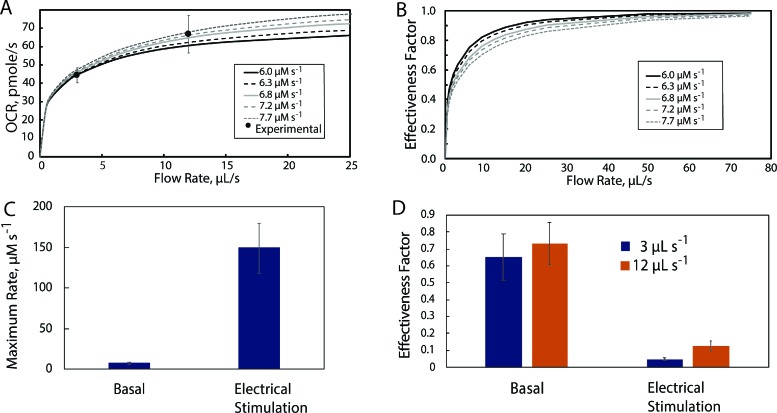
The finite element COMSOL model was used to simulate oxygen uptake as a function of flow rate and R_{max_basal} in the 450 μl microphysiological flow system [Fig. 6(a)]. Under basal conditions, the values of R_{max_Basal} between 70 and 90 pmol s⁻¹ (6.0–7.7 μM s⁻¹) overlapped with the measured values [Fig. 6(a)]. As a result, the effectiveness factor [Fig. 6(b)] is below 1 for 3 and 12 μl s⁻¹ and only rises above 0.90 for all reaction rates at flow rates above 30 μl s⁻¹. Consistent with the lower effectiveness factors, significant concentration gradients are present in the myobundles for a flow rate of 3 μl s⁻¹ (Fig. S5). While the gradients at 12 μl s⁻¹ were smaller than at 3 μl s⁻¹, the gradients in the fluid were not minimized until flow rates above 25 μl s⁻¹ (Fig. S3). Thus, even under basal conditions, mass transfer limitations arise in the fluid and myobundle in the 450 μl chamber unless the flow rate is relatively high.

FIG. 6.

Estimation of R_{max_basal} and mass transfer effects under basal conditions in the 450 μl perfusion chamber. (a) Comparison of experimental results at flow rates of 3 and 12 μl s⁻¹ with simulations for values of R_{max_Basal} between 6.0 and 7.7 μM s⁻¹; (b) Effect of the flow rate and R_{max_Basal} upon the effectiveness factor. (c) Values of R_{max_Basal} and R_{max_Exercise} determined by matching the model results with the measured values for OCR. (d) Effectiveness factors for basal and exercise conditions at flow rates of 3 μl s⁻¹ and 12 μl s⁻¹.

The two myobundles are exposed to different concentrations due to their placement and the direction of flow (Fig. S3). While the shape of the myobundle provides a greater exchange area from the upper and lower surfaces (aspect ratio ∼2), the placement of the upstream myobundle directly below the inlet resulted in different flow patterns relative to the downstream myobundle (Fig. S4) and caused the upstream myobundle to be exposed to a differential in oxygen concentration on the upper and lower surfaces, resulting in more severe oxygen gradients than the downstream myobundle, even at higher flow rates.

Given the presence of mass transfer limitations at the flow rates of 3 and 12 μl s⁻¹, we adjusted the value of R_max under basal and exercise conditions to yield the observed OCR and computed the effectiveness factor. For both flow rates, all model values for R_{max_Basal} yielded values of OCR within 0.2% of the measured values. The values of the maximum rate under electrical stimulation, R_{max_Exercise}, were an average of 19.6 times higher than R_{max_Basal} [Fig. 6(c)]. The effectiveness factor was reduced 25%–35% under basal conditions but was dramatically reduced during electrical stimulation [Fig. 6(d)]. Thus, in the 450 μl chamber, significant mass transfer limitations arise in the fluid and myobundle, reducing the observed oxygen consumption rate under basal and simulated exercise conditions.

The values of D_{O2_media,}^27,28 D_{O2_tissue,}²⁹ t,¹⁹ and K_M^30,31 were in the midrange of published values (Table I). Collagen and fibrin gels are generally very porous³² with high values of hydraulic peremeability.³³ We performed a sensitivity analysis to assess the effect of the range of these variables on the effectiveness factor for a flow rate of 12 μl/s (Table II). The effectiveness factor was most sensitive to the thickness and least sensitive to D_{O2_tissue}. The inverse trend of the effectiveness factor with the magnitude of D_{O2_tissue} arises from the increased external mass transfer relative to internal mass transfer, which compensates for the relative increase in the metabolic rate relative to diffusion in the myobundle.

TABLE II.

Percent change in the effectiveness factor for a 50% change in the parameter value.

Myobundle diffusion coefficient, cm2/s	1 × 10−5	2 × 10−5	3.0 × 10−5
Effectiveness factor	0.099	0.091	0.088
Percent change	8.9	…	−3.3
Media diffusion coefficient, cm2/s	1.2 × 10−5	2.4 × 10−5	3.6 × 10−5
Effectiveness factor	0.07388	0.091	0.103
Percent change	–18.8	…	13.1
KM, μM	0.67	1.33	2.66
Effectiveness factor	0.099	0.091	0.084
Percent change	8.46	…	−7.52
Thickness, cm	0.025	0.053	0.075
Effectiveness factor	0.135	0.091	0.073
Percent change	47.7	…	−19.5

DISCUSSION

In this study, we showed that short periods of electrical stimulation that mimic exercise conditions increased the oxygen consumption rate, and appreciable oxygen concentration gradients were present in the media and myobundles limiting oxygen metabolism. Previous efforts to incorporate electrical stimulation into a culture protocol have focused mainly on measuring alterations in contractile force and structural organization.^{24,25,34–36} To date, none of these studies have examined oxygen consumption during electrical stimulation. Thus, we have provided new information on the maximum respiration rates under electrical stimulation and a modeling framework to design in vitro systems.

In the larger MPS flow chamber, the rate of oxygen transport limits the rate of oxygen metabolism, particularly under electrical stimulation. In the absence of electrical stimulation, flow rates above 1.5 μl s⁻¹ in the 80 μl chamber and 30 μl s⁻¹ in the 450 μl chamber minimized oxygen gradients and provided accurate measures of cellular respiration rates. The increase in uptake imposed by the simulated exercise conditions increased the energy turnover and thus the myobundle oxygen demand. In vivo, this increased demand is met through myoglobin,³⁷ increased cardiovascular oxygen supply to the muscles, and glycolysis. While electrical stimulation produced a twofold increase in the measured oxygen consumption rate in the larger 450 μl chamber, model results showed that oxygen gradients in the myobundles and the microphysiological flow chamber limited the OCR. If the gradients could be eliminated, the model results showed that the OCR would be ten times higher than observed.

Most published values for oxygen uptake by skeletal muscle in vivo are reported under basal conditions on the basis of the total cell mass or protein mass. However, the results based on a tissue volume basis, summarized in Ref. 6, are between 0.3 and 6 μM s⁻¹ for resting conditions and rise to values as high as 275 μM s⁻¹ under exercise. In vivo values are often estimated from entire limb measurements and vary among specific muscles. The increasing oxygen demand is met by the increased blood flow rate to muscle and opening of muscle capillaries, but mass transfer limitations appear for consumption rates above 200 μM s⁻¹.³⁰ The results from this study, corrected for mass transfer limitations [Fig. 6(c)], are on the high end of this range, given the lower cell volume fraction in the engineered muscle (50% to 60% in engineered muscle vs 95% in vivo). The value of R_{max_Estim} on a per nuclei basis, 366 pmole s⁻¹(1 × 10⁶ nuclei)⁻¹, is similar to the values obtained for liver hepatocytes in vitro, 450 pmol s⁻¹(1 × 10⁶ nuclei)⁻¹,³⁸ another highly metabolic tissue.

The overall system design enabled the measurement of oxygen uptake and subsequent determination of contractile force, as well as fatigue and force-length or force velocity relations. The system can be modified to incorporate the inline measurement of force using deformable posts³⁵ or an elastic membrane in series with the myobundle,³⁴ providing important information about oxygen consumption during conditions that model exercise.

The larger 450 μl chamber reduced the effectiveness factor under basal conditions relative to the 80 μl chamber at the flow rates used. Since the system volume is limited by the electrode size, smaller electrodes or optogenetic stimulation^35,36 could be incorporated to reduce the chamber volume. If the oxygen concentration drop between the inlet and the outlet is too small to measure accurately, local oxygen concentrations near myobundles could be measured with a ruthenium-based oxygen sensitive dye together with a reference dye,³⁸ although a bead-based system may be necessary for continuous monitoring.

Even if the chamber volume were reduced or mixing enhanced such that the oxygen concentration on the surface of the myobundle equaled the solubility of oxygen in culture media, model results suggest that the higher OCR after electrical stimulation would still produce significant concentration gradients within the myobundles. Given the cell density requirement of 10⁷ cells ml⁻¹ to ensure myotube formation, even a 20-fold reduction in the myobundle thickness to 26 μm would still generate significant oxygen gradients limiting oxygen consumption. Thus, almost all systems currently used to simulate exercise conditions with engineered skeletal muscle may have mass transfer limitations affecting oxygen consumption. Under such conditions, the engineered muscle may compensate by increasing glycolysis, as was observed when lactate concentrations increased 50% after electrical stimulation for 24 h.²⁵

CONCLUSIONS

We presented a method to measure respiration rates during electrical stimulation under flow. This in vitro noninvasive tool enables the investigation of human muscle physiology during exercise, an advantage over existing commercial systems. A numerical model of oxygen transport showed that significant gradients existed in the culture media and myobundles, limiting the rate of oxygen consumption. The respiration rates obtained with engineered human myobundles should guide future design of engineered muscle and microphysiological flow chambers and study metabolism under simulated exercise conditions.

METHODS

Primary human myoblast culture

Muscle biopsies were obtained using Duke IRB approved protocols (exempt protocol Pro00054162 4/24/2014). Human skeletal muscle myoblasts were isolated according to previously described methods.^2,8 Biopsy samples were minced, washed in phosphate buffered saline (PBS), and enzymatically digested in 0.05% trypsin for 30 min. Muscle samples were collected by centrifugation, preplated for 2 h, and transferred to a Matrigel (BD Biosciences, San Jose, CA) coated flask for attachment. Myoblasts were cultured in human growth media (hGM) containing 1 g l⁻¹ glucose (LG) Dulbecco's Modified Eagles Medium (DMEM, GIBCO/Invitrogen) and supplemented with 8% fetal bovine serum (Hyclone), 1× antibiotic-antimycotic, and SkGM SingleQuots (Lonza, Basel) without insulin or Gentamicin/Amphotericin-B.

Human tissue-engineered skeletal muscle bundle culture

Myobundles were assembled as previously described.^2,8 Myoblasts cultured on T75 flasks were dissociated in 0.025% trypsin-EDTA to a single cell solution and then encapsulated in a 20–25 mg/ml fibrinogen (Akron, Boca Raton, FL) and matrigel solution attached to laser cut Cerex frames within polydimethylsiloxane (PDMS) molds at 7.5 × 10⁵ cells/myobundle. The cell/hydrogel mixture was polymerized for 30 min at 37 °C with 50 unit/ml thrombin in 0.1% bovine serum albumin (BSA) in PBS (Sigma, St. Louis, MO). To promote myoblast growth, human muscle bundles were cultured in hGM containing aminocaproic acid (ACA) on a rocker (0.33 Hz) at 37 °C. On day 4, the medium was switched to differentiation medium (hDM) consisting of LG-DMEM supplemented with 2% adult horse serum (HS), 100 μM fatty acids (1:1 oleate: palmitate) conjugated to 0.14% BSA, 100 μM carnitine, 2 mg ml⁻¹ of ACA, and 1× antibiotic-antimycotic.

Human skeletal muscle bundle respirometry

After 1 week of differentiation, the mitochondrial respiratory function was determined in myobundles using an Oxygraph-O2k high resolution respirometer (Oroboros Instruments) and a custom flow chamber. The O2k system was considered the reference standard, and a Viton O-ring was added to the chamber to inhibit interaction of myobundles with the stir bar.¹⁹ The myobundle was then transferred into the respiration chamber in 2 ml of hDM. Oxygen flux was monitored in real-time following standardized instrumental and chemical background calibrations using Datlab software.^39,40

Calibration of oxygen sensors

An optical sensor based on luminescence quenching was used to detect oxygen concentrations in culture media (Parts FTCM-PSt1-L2.5-VAL1/16″-TF-OIW; PreSens Precision Sensing GmBH; Regensburg, Germany). Output from the oxygen sensor was interfaced with an Electro-Optical Module (EOM, PreSens) connected to a computer with Labview software (National Instruments). The sensor surface was 140 μm in diameter and was attached to a thin, glass fiber optic cable. The housing surrounding the sensor surface has a fluid volume of 2.1 μl. Using custom software for the EOM, sensors were calibrated using a two-point calibration, by first perfusing with humidified air, and then humidified nitrogen gas. This calibration was adjusted to ensure that the reading for the oxygen concentration in culture media was 0.19 mM for a solubility of 1.08 (atm l mmol⁻¹) at 37 °C.⁴¹ The half time for the response following addition of 0.0625 mg sulfite is 5.3 ± 1.5 s, yielding a time to reach 90% of a change in oxygen equal to 15.3 ± 4.3 s, which is similar to specifications provided by PreSens.

Custom microphysiological flow chamber design and respiration measurements

A custom microphysiological flow chamber consists of an upper piece that fits within the lower piece using a lock-and-key mechanism, thus creating an 80 μl reservoir [Figs. 1(a)–1(c) and supplementary material, Fig. S1A]. The flow chamber was situated within a flow loop between a pump and an oxygen sensor at the chamber outlet. Since the calibration curves of different sensors exhibited considerable variability, we used the same sensor for upstream and downstream readings. Initially, the sensor was placed downstream to the flow chamber. At the end of each experiment, the sensor was moved to the inlet of the chamber.

In order to enable electrical stimulation of the myobundles during flow, the flow chamber volume was increased to 450 μl to fit the electrodes [supplementary material, Figs. S1B and S1C]. PDMS posts were added to pin the myobundles in the reservoir. Carbon flat electrodes (BMK Designs) were about 20 mm in length, 3 mm in height, and 1 mm in thickness. The working distance between electrodes was about 10 mm.

Contractile function assessment

After two weeks of differentiation, myobundles were loaded into a custom-made force measurement apparatus as previously described.² Samples were stimulated (40 V cm⁻¹) to recreate twitch (1 Hz for 10 ms) and tetanic (20 Hz for 1 s) contraction with a Grass stimulator. Contractile force traces were analyzed for peak twitch and tetanus force using a custom MATLAB program.²

Electrical stimulation during flow

The regimen used consists of 5 ms pulses, 5 Hz at 100 V, with a 50 ms delay in-between each train of pulses, with biphasic stimulation to minimize electrolysis in the medium.²⁶ The stimulation lasted for 30 min, while oxygen uptake was measured. The regimen was chosen based on the range of conditions studied previously in vitro.^{17,24–26,42,43} Although a biphasic stimulation pattern was used, oxygen concentrations declined after the onset of stimulation. To compute the oxygen consumption rate, a mass balance was performed in which the change in moles of oxygen in the flow chamber equaled the balance between flow of oxygen into and from the flow chamber, oxygen consumption by the myobundle (OCR), and reaction with the electrodes

$$V\frac{\mathit{dC}}{\mathit{dt}}=Q\left(C_{\mathit{out}}-C_{\mathit{in}}\right)-\mathit{OCR}-R_{\mathit{electrodes}}.$$ (2)

The reaction rate with the electrodes, R_electrodes, was determined in the absence of myobundles from the initial slope of the outlet concentration vs time.

DNA isolation and quantification

To efficiently determine the number of nuclei per myobundle, human myoblasts were used to create a standard curve based on absorbance. Standard curves were created in triplicate from ten samples with increasing, known numbers of myoblasts from each of the 7 donors. Samples were lysed in a 9:1 buffer including ATL/proteinase K solution (Qiagen). Each sample or standard was combined with an equal volume of Hoechst dye in a 96-well plate. After a 5-min incubation period at room temperature, absorbances were measured for 350 nm (excitation) and 486 nm (emission). Nuclei quantification was determined by comparing absorbance of the donor-specific linear standard curve with readings of the bundle samples with subtraction of the matrix background readings.

Statistical analysis

Data are presented as mean ± SEM, where N represents the number of donors tested per experiment with 2 biological replicates (myobundles) per condition. Statistical analyses were carried out using an unpaired t-test (Graphpad Prism 5). Statistical significance is shown as *p < 0.05, **p < 0.01, #p < 0.001.

Myobundle geometry

The cross-sectional area was determined from a representative myobundle by taking an aerial image and sketching the outline using Solidworks (Dassault Systems). The myobundle thickness was measured using ImageJ (FIJI) from 3 different donors (0.53 ± 0.15 mm).

Computational model

A three-dimensional finite element model was implemented in COMSOL Multiphysics 5.2a (COMSOL Inc). The model incorporates both oxygen and momentum transport. Culture medium flow is modeled as an incompressible, isothermal, Newtonian fluid [Eq. (3)]. The myobundle was considered a porous domain, and medium flow through the domain was described by the Brinkman equation [Eq. (4)], where u is the fluid velocity in the culture media, u_M denotes the fluid velocity field in the myobundle, p is the pressure, ϵ_p is the porosity, K is the permeability, and μ is the viscosity

$$\mathbf{0}=-\mathbf{\nabla }\mathit{p}+\mathbf{\nabla }·\left(\mathit{\mu }\left(\mathbf{\nabla }\mathit{u}+{\left(\mathbf{\nabla }\mathit{u}\right)}^{\mathbf{T}}\right)\right),$$ (3)

$$\mathbf{0}=-\mathbf{\nabla }\mathit{p}+\frac{\mathit{\mu }}{{\mathit{ϵ}}_{\mathit{p}}}\mathbf{\nabla }·\left(\mathbf{\nabla }{\mathit{u}}_{\mathit{M}}+{\left(\mathbf{\nabla }{\mathit{u}}_{\mathit{M}}\right)}^{\mathit{T}}\right)-\left(\frac{\mathit{\mu }}{\mathit{K}}\right){\mathit{u}}_{\mathit{M}}.$$ (4)

The fluid was assumed to be incompressible, $\mathbf{\nabla }·\mathit{u}=0$.

No-slip boundary conditions were specified for all the walls and the frame ($\mathit{u}=0$). At the inlet, the velocity was specified.

Oxygen transport is described by the general form of the conservation of mass for dilute solutions in an incompressible fluid in the steady state

$$\mathbf{0}={\mathit{D}}_{\mathbf{O}\mathbf{2}}{\mathbf{\nabla }}^{\mathbf{2}}{\mathit{C}}_{\mathbf{O}\mathbf{2}}-\mathbf{u}·\mathbf{\nabla }{\mathit{C}}_{\mathbf{O}\mathbf{2}}+{\mathit{R}}_{\mathbf{O}\mathbf{2}},$$ (5)

where C_O2 denotes the oxygen concentration [M, mole l⁻¹], D_O2 is the diffusion coefficient [cm²·s⁻¹] of oxygen, and R_O2 is the reaction rate [M s⁻¹]. The myobundle is assumed as a porous domain with oxygen volumetric consumption, R_O2, and diffusion coefficient, D_{O2_myobundle}. Oxygen consumption was assumed to follow Michaelis-Menten kinetics^44–46

$${\mathrm{R}}_{\mathrm{O}2}=\left({\mathrm{R}}_{\text{max}}{\mathrm{C}}_{\mathrm{O}2}\right)/\left(K_m+{\mathrm{C}}_{\mathrm{O}2}\right),$$ (6)

where R_max is the maximum reaction rate (M s⁻¹) based on the myobundle volume and K_m is the Michaelis constant (M). The boundary conditions imposed included a maximum saturation of 0.190 × 10⁻³ M at the inlet, no flux conditions at all walls, and mass conservation at the inlet and the outlet.

Calculated values

Similar to the experimental data, the oxygen consumption rate was measured by taking the product of the oxygen concentration difference of the flow chamber inlet and outlet and the perfusate flow rate. The effectiveness factor η represents the ratio of the average reaction rate in the myobundle to the reaction rate if the concentration through the flow chamber and myobundle were at the inlet oxygen concentration C_inlet (0.190 mM). As a result, the OCR is related to the effectiveness factor as

$$\mathit{OCR}={\overline{R}}_{{\mathrm{O}}_2}V=\eta \frac{R_{\mathit{max}}V{C}_{\mathit{inlet}}}{K_m+C_{\mathit{inlet}}},$$ (7)

where ${\overline{R}}_{{\mathrm{O}}_2}$ is the average reaction rate determined by integrating Eq. (5) over the volume of the myobundle.

Mesh generation

A mesh independence study was used to determine the number of elements in each model.⁴⁷ Specifically, we successively increased the number of mesh elements by a factor of 1.5 to 2 until the evolution of the myobundle average volumetric oxygen consumption rate showed a relative difference of less than 1% from one mesh iteration to another. The mesh independence study for the basal chamber resulted in a total of 1 170 694 triangular elements and a mesh density of 7758 elements mm⁻³. For the electrical stimulation chamber, the mesh consisted of a total number of 5 372 609 triangular elements and a mesh density of 5300 elements mm⁻¹.

SUPPLEMENTARY MATERIAL

See supplementary material for five figures with images of the microphysiological flow chambers, comparison of oxygen uptake measured in the flow chamber and the O2k system, and plots of the oxygen concentration in the 450 μl flow chamber.