Abstract
Realistic modeling of biomolecular systems requires an accurate treatment of electrostatics, including electronic polarization. Due to recent advances in physical models, simulation algorithms and computing hardware, biomolecular simulations with advanced force fields at biologically relevant time scales are becoming increasingly promising. These advancements have not only led to new biophysical insights but also afforded opportunities to advance our understanding of fundamental intermolecular forces. This work describes the recent advances and applications, as well as future directions, of polarizable force fields in biomolecular simulations.
Keywords: molecular dynamics simulation, polarizable force field, protein, nucleic acid, QM/MM
Introduction
Molecular dynamics (MD) simulations are indispensable tools for investigating physical properties of proteins, nucleic acids and designing new molecules and materials.(30, 83, 127) Due to recent advances in computing hardware and improved simulation methods, the time and length scales of molecular dynamics simulations have been greatly extended. Noticeably, by combining GPU computing(8, 21, 103) and enhanced sampling methods,(23, 24, 42) molecular simulations are approaching the time scale of milliseconds and beyond, enabling the study of macromolecular interactions and dynamics with high fidelity. These advances not only lead to more reliable interpretation and predictions by computer simulations but also crucial for examining and improving the underlying physical models and simulation methods.
There has been much effort devoted to improving the potential-energy functions used in MD simulations, also called force field (FF). It is believed in biology that amino acid sequences determine the structure, which then determines the function. Similarly, the physical driving forces underlying biomolecular structure and interactions are encoded in the potential energy surface. Force fields usually consist of several empirical energy terms including short-ranged bonded interactions and non-bonded interactions such as repulsion, dispersion and electrostatics. Electrostatics is both important and computationally expensive due to its long-range nature. To enable simulations of biomolecules with modest computational power, traditional force fields (FFs) use fixed point charge placed at atomic centers to represent the electrostatic interactions. The limitations of the fixed point-charge force fields have been well recognized.(5, 13, 55, 78, 87, 100) One significant approximation in traditional force fields is the omission of polarization, i.e. the response of the charge distribution to environment. This is problematic when applying the same set of charge parameters to different environments, such as aqueous solution, protein cavity, cell membrane and heterogeneous interfaces, where the charge distribution is expected to change accordingly. Another approximation is the atom-centered point-charge model, whereas the realistic charge distribution should be smooth and anisotropic. To capture anisotropic features such as σ-holes, lone pairs and π-bonding, it is necessary to adopt higher-order multipolar electrostatics models (32, 43, 49, 50, 121) and/or adding off-center sites.(32, 55) The effect of having atomic multipoles beyond fixed charges is of the same magnitude as the effect of polarization, suggesting that both should be included in force field development.(43)
Previously a number of reviews on polarizable force fields have been published.(5, 13, 37, 55, 90, 93, 100, 134) In this review, we will provide an update on recent progress in biomolecular force field development, particularly advanced electrostatic modeling, simulation algorithms, and recent applications of polarizable force fields in biomolecular simulations.
Electrostatic Models and Force Field Parameterization
Electrostatic interactions are essential for the recognition and stability of biomolecules.(13, 100) More realistic treatment of electrostatics is the main feature that distinguishes polarizable force fields from fixed-charge ones. In addition to explicit treatment of polarization, improving the permanent electrostatic component in force fields is as important, even though not often discussed. The permanent electrostatic interaction is not only the dominant intermolecular force in many biomolecules, but also directly affects the polarization behavior.
Permanent Electrostatics
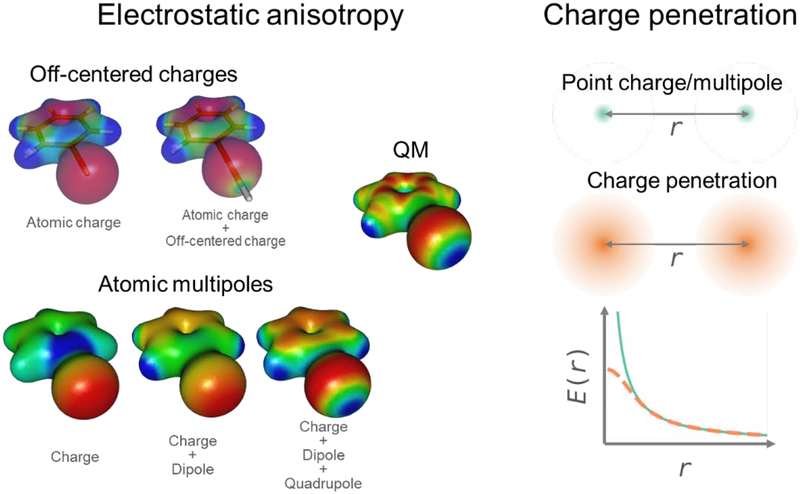
Permanent electrostatics can be viewed as the interaction between fixed charge densities of molecular fragments without induction effect. In traditional force fields, the permanent electrostatics is represented by atom-centered point charges. This representation has two major shortcomings: the inabilities to model anisotropic charge distribution and the charge penetration effect that occurs when atomic electron clouds overlap. These effects are critical in determining equilibrium geometry and energy of molecular complexes. Examples of the importance of anisotropic charge distribution include σ-holes, lone-pairs, and aromatic systems, which are usually involved in highly specific interactions. For example, σ-hole is a region with positive electrostatic potential on halogen atoms, which can interact with a lone pair on a heteroatom, forming a halogen bond. While in the point-charge representation, the halogen atom has a spherical negative electrostatic potential (Figure 1). One ad hoc remedy for the σ-hole model is to attach an off-centered positive charge to the halogen atom.(47, 64) This approach is effective and easy to implement. Similarly, the off-centered charges, or virtual interaction sites, have been employed to model electron lone pairs.(55) In principle, this approach can also be used to model π-bonding by attaching two negative charges to each heavy atom, although it is computationally inefficient. A systematic approach to improve the description of anisotropic charge distribution is the use of atomic multipoles.(13, 93, 100) Multipoles are a series expansion that can represent arbitrary angular distributions. Atomic multipole truncated at quadrupole is sufficient to model common chemistries including σ-holes, lone-pairs and π-bonding.
Figure 1.
Electrostatic anisotropy and charge penetration effects in permanent electrostatics. Two models for electrostatic anisotropy, off-centered charges and atomic multipoles can be used to represent the σ-hole in halogen-containing compounds such as bromobenzene. Atomic multipoles up to quadrupole can also effectively reproduce the π-bonding character. Charge penetration weakens the electrostatic interaction compared to that between point charges, which is usually represented by an effective damped interaction.
Charge penetration arises from the interaction between overlapping charge distributions, which softens the electrostatic interaction at short range compared to that between point charges. Charge penetration can be modelled via empirical damped functions,(133) or integral of interaction between charge densities represented by Gaussian-type or Slater-type basis functions.(19, 27)
Charge penetration models can be combined with the above anisotropic electrostatic model, by placing charge densities on bonds or lone pairs,(91) or by using damping functions for atomic multipoles.(99)
Two classes of approaches can be used to derive electrostatic parameters. The first one is directly fitting to electrostatic potential.(9, 130) The second one is partitioning of ab initio charge distributions into atomic contributions, including Stone’s distributed multipole analysis (DMA), the Hirshfeld partitioning,(39) the Iterative Stockholder Analysis and their derivatives.(81, 116) The mathematical and chemical properties of selected methods are summarized in a recent paper by Heidar-Zadeh et al.(39)
It is recognized that atomic multipole parameters have some degree of redundancy, which causes computational overhead and overfitting.(44) Jensen and coworkers showed that the number of multipole parameters can be reduced to twice the number of atoms without affecting the accuracy of the electrostatic potential.(44) In a similar fashion, Meuwly and coworkers developed a minimal distributed charge model (MDCM), in which a minimal number of off-centered point charges is determined to approximate the reference electrostatic potential.(121)
Electronic Polarization
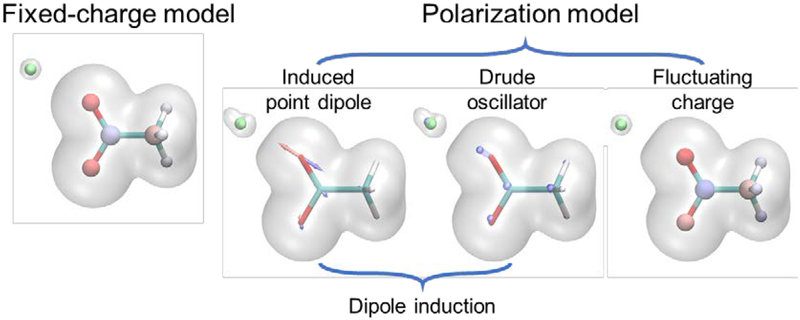
A significant advancement in modeling biomolecular electrostatics over the past decade is the explicit treatment of the polarization effect, allowing electrostatics to respond to chemical environments. Classical polarization models can be classified into two categories, one characterizing the charge redistribution within each atom, by either induced dipole(93) or Drude oscillator(55) (also called charge-on-spring, shell model) and the other based on charge flow between atoms such as the fluctuation charge model (also known as charge equilibration, or chemical potential equilibration) (see Figure 2).(104)
Figure 2.
Electron cloud represented by fixed-charge model and polarization models. Both the induced point dipole and the Drude oscillator can represent the deformation of electron cloud. The fluctuating charge model can represent the re-distribution of charges within a molecule, while to represent the electron deformation of monoatomic ions and out-of-plane polarization, a dipole induction model is needed.
In the induced dipole model, each polarizable site can have an induced dipole moment μind in response to external electric field E, μind = αE where α is the polarizability.(93) The induced dipoles also contribute to the total electric field, so the polarization is non-additive and often solved iteratively via self-consistent field (SCF). In the Drude oscillator model,(55) a Drude particle carrying part of the atomic charge is attached to the core atom via a harmonic spring. The displacement of Drude particle creates induced dipole moment. The positions of the Drude particles also need to be solved iteratively via SCF to ensure that the Drude particles are at ground state, although extended Lagrangian method has been employed in MD simulations to approximate the exact solution. The fluctuating charge (FQ) model is based on the electronegativity equalization principle. The atomic charges are redistributed to equalize the electronegativity/chemical potential at each site.(10, 104)
Due to the nature of polarization, these three polarization models have similar functional forms. The total electrostatic energy is a sum of Coulomb energy between all the charges and dipoles in the system and a self-energy term corresponding the work needed to change the charge distribution, which is usually quadratic.
| (Eq. 1a) |
| (Eq. 1b) |
| (Eq. 1c) |
| (Eq. 1d) |
Where Eelst, Eself and ECoulomb are the total electrostatics energy, the self- and Coulomb energy, respectively. The expressions for the self-energy in the induced dipole model, the Drude oscillator model and the fluctuating charge model in their simplest forms are given in Eq. 1b–1d, respectively. αi and μi are the atomic polarizability and induced dipole of atom i, and di are the force constant and displacement of the Drude particle, and χi, ηi and qi are the electronegativity, chemical hardness and partial charge of atom i. The charge distribution is solved to minimize the total energy. The difference between these models is the way that the charge distribution can change. Both the induced dipole and the Drude oscillator models allow a dipole to be generated at each site. Since the displacement of the Drude oscillator is usually very small, it is approximately a point dipole. Recently, Huang et al. numerically established the equivalence of Drude oscillator and induced dipole models.(41) The fluctuating charge model allows charges to flow between atoms. The simple fluctuating charge model does not take into account out-of-plane polarization or the polarization of monoatomic ions. These effects can be represented by the charge fluctuating model with additional virtual sites around each atom,(145) although this becomes less efficient.
Since there are subtle differences between the polarization of atomic charge distribution and the charge flow among atoms, incorporation of both effects can potentially make a model more accurate. However, such a model is more prone to parameter optimization issues such as overfitting, in addition to an increased computational cost. Stern et al. developed a five-site water model combining fluctuation charge and induced dipole, and found that allowing charge flow between oxygen and lone pairs would improve the agreement with gas-phase QM calculations but decrease the performance in condensed phase simulations.(115) Also, there is no unique way to separate the two effects. Mei et al. found that the contribution of fluctuating charge to polarization obtained from nine different population analysis schemes has large variations from 59.9% to 96.2%.(80) In practice, most polarizable force fields only model the polarization of atomic charge distribution, through either induced dipole or Drude oscillator.
Similar to charge penetration, special care is given to short-range polarization at equilibrium and compressed regions. In both induced dipole and Drude oscillator models, the Thole damping function is commonly used to damp the polarization according to a smeared charge distribution.(55, 93) Recent studies have revealed the inadequacies of Thole damping function.(17, 76) By studying water-water, water-ion, and water-trimers, the Thole damping was shown to produce non-perfect distance dependence for polarization when compared with energy decomposition analysis (EDA). Liu et al. proposed to improve the accuracy of Thole damping for many-body energies by optimizing the exponent in the function.(68)
Besides the explicit polarization models, methods for effective polarization in the framework of fixed-charge force fields have also been developed. Leontyev and Stuchebrukhov proved that if simulations involve only structurally similar configurations, polarizable molecular systems can be described by equivalent non-polarizable fixed-charge models by scaling the partial charges by a constant.(58) It is recognized that simple scaling is not a replacement of a well-built real-time polarizable force field.(58) More rigorous ways to account for solvent polarization and reference self-energy in fixed-atomic charges have also been published. (9, 16, 118)
Atomic Polarizability Parameters
Like atomic charges, the atomic polarizabilities are not actual observables while the molecular polarizabilities can be measured. Therefore, the atomic polarizability parameters in polarizable force fields are often empirically chosen to reproduce the molecular responses. However, the atomic polarizabilities may not be uniquely determined by this approach, and the molecular polarizabilities are less sensitive to the atomic polarizabilities than the polarization energy is.(101) Wang et al. proposed to calculate the atomic polarizabilities by fitting to the response of the electrostatic potentials (ESPs) under external electric field obtained from quantum mechanical (QM) calculations,(128) which is analogous to the electrostatic potential fitting approach to determine atomic charges. The molecular polarizability obtained from this method is comparable to those from directly fitting to molecular polarizabilities. Verstraelen et al. developed a DFT-based method to compute the polarization parameters directly as expectation values of an electronic wave function.(124)
For polar molecules such as water, polarization is highly anisotropic. To account for the anisotropy of polarizability, atomic polarizability tensors are used.(14, 116, 122) The use of gas-phase clusters for deriving atomic polarizabilities can overestimate polarization in condensed phase.(125) Vosmeer et al. used a combined QM/MM approach to estimate condensed-phase polarization.(126) The obtained polarizabilities for water and ethanol were found to be close to those used in previous water and methanol models.(126)
Parametrization of Polarizable Force Field
In principle, polarizable force fields are more accurate and transferable than non-polarizable force fields when applied to contrasting dielectric environments, as evidenced by the better agreement with QM on gas-phase interaction energies and successful applications in various problems such as ion solvation,(36) protein-ligand binding(45) and pKa prediction.(74) However, there exist cases where certain results given by polarizable force fields are comparable to or even worse than non-polarizable force fields, likely due to the poor quality of parameters in the polarizable force fields, in addition to potential sampling issues.(5, 124) Generally, optimization of force field parameters is challenging due to the large parameter space, non-linear interdependencies of parameters and limitation in the amount and quality of experimental and ab initio reference data.(131) The problem could be even more pronounced for polarizable force fields because of the additional parameters. On the other hand, by improving the physics and utilizing high-level QM data, the parameterization process can be made more robust,(119, 124) leading to more accurate, transferable and reproducible force fields. Nonetheless, due to the limitation of ab initio methods, recently biological force fields have heavily relied on experimental data such as NMR data to refine their parameters for proteins and nucleic acids.(56, 110, 144)
Significant efforts have been made to design systematic and automatic approaches for the parameterization of force fields. Typically, the development of a force field consists of determining reference data (QM and experimental properties), defining an objective function to measure the quality of force field, and optimizing a large set of parameters to improve the objective function. When the nonlinear interdependency between parameters is nontrivial, sophisticated optimization methods can be utilized. Methods in artificial intelligence, such as evolutionary algorithms, have been applied to optimize force field parameters.(60, 129) Wang et al.(131) developed the ForceBalance software to tackle several problems in force field development. Specially tuned objective function, regularization and gradient-based optimization algorithm were used to improve the optimization results.(131) To choose subset of parameters to optimize, one can utilize sensitivity analysis or test optimization using cheaper objective functions.(132, 142) These automated algorithms can save substantial human efforts. However, the quality of resulting force fields depends critically on the reference data set and various “weights” assigned to different reference properties typically determined based on empirical knowledge, due to the imperfection of the underlying models. Overfitting can also potentially lead to problems in transferability.
Efficient methods for polarizable MD simulations
Algorithms for Computing Long Range Electrostatics
Particle Mesh Ewald (PME) is an efficient algorithm for calculating electrostatics interactions under periodic conditions. Recently, several groups have developed generalized and efficient PME algorithms for electric multipoles (EMP) of arbitrary order.(28, 65, 112) Simmonett et al.(112) and Giese et al.(28) independently developed a PME algorithm based on spherical tensors. The algorithm when applied to quadrupoles only slows down the calculation by 1.5 to 2 times compared to a charge-only model, in part because a shorter real-space cutoff is possible with fast-decaying higher multipole moments. The result is quite encouraging considering that the charge-dipole-traceless quadrupole model has nine degrees of freedom for each atom.(28) This manifests the advantage of point multipole over an equivalent representation by a set of point charges. An efficient algorithms based on Cartesian tensors has also been developed, which bypass the need for coordinate transformation at each step.(63) Other algorithms suitable for homogenous systems or non-periodic systems have recently been extended to atomic multipoles.(7, 138)
Algorithms for Evaluating Polarization
Self-consistent field (SCF) iterations provides rigorous solution to polarization energy and gradient at the group state, which is needed for structure optimization, QM/MM application and energy conservation in MD simulations etc. However, full SCF calculation is computationally demanding. To speed up the SCF calculation, several groups have developed efficient algorithms for solvation polarization. One class of methods is based on extended Lagrangian. Extended Lagrangian is an alternative method where an additional set of electronic degrees of freedoms is propagated to approximate the SCF solution. Due to stability issues, early extended Lagrangian methods only permit small integration time step of 1 fs or less. Recently, Albaugh et al. introduced an iteration-free method, inertial extended Lagrangian with 0 SCF (iEL-0SCF). (2, 3) In this scheme, the auxiliary dipoles drive the time evolution of real dipoles that stays close to the true SCF solution. This method allows for 6 fs time step for single-point polarizable rigid water.(2) When used to simulate the flexible AMOEBA water model with the same 1.0 fs time step, iEL-0SCF is twice as fast as standard SCF algorithm.(3) Another approach is to use fixed number of iterations to approximate the exact solution. Brooks and coworkers developed an empirical extrapolation scheme based on perturbation theory.(113) They showed that the fourth order perturbation method (OPT4) achieves the best compromise between accuracy and efficiency, with a cost similar to that of three SCF iterations. The truncated conjugate gradient (TCG) method allows users to choose the number of iterations while giving analytical solution for force, which is free from stability issues of approximate methods. (4) Tests on various systems demonstrate that three to four iterations provide excellent accuracy. These methods also produce analytical forces of the corresponding energy, and thus avoid energy drift and permits large time steps in MD.(4) Both OPT4 and TCG have been implemented in highly optimized software packages.(38, 52)
Enhanced Molecular Dynamics and Sampling Algorithms
Enhanced sampling techniques are needed for achieving the necessary sampling efficiency of biomolecular systems regardless of how force fields are used.(23) Several efforts have been made in recent years to accelerate the simulations of polarizable force fields. Multiple time step algorithms have been developed to allow for very large time steps in molecular dynamics simulations.(61, 77, 82) In the extreme case, the computation speed can be accelerated by 10 to 20 times.(77) Dual force field approach introduced by Schnieders and coworkers,(85) takes advantage of the sampling efficiency of the fixed-point charge model (OPLS-AA) and accuracy of polarizable force fields (AMOEBA) to compute the absolute crystal decomposition thermodynamics. A similar procedure was used by Shirts and coworkers(20) to indirectly calculate the free energy of three benzene polymorphs by AMOEBA.(20) There have also been significant advances in thermodynamic and kinetic reweighting methods,(11, 135) which can in principle be combined with the dual-force field methods. Orthogonal space random walk (OSRW) and orthogonal space tempering (OST) by Yang and coworkers(73) allows more effective sampling of conformational transitions in aqueous solution, and has been utilized on crystal(108) and host-guest (6) systems with AMOEBA force field.
Recent Development of Polarizable Force Fields for Biomolecules
Over the past decades, several polarizable force fields have been developed for biological systems, including AMBER,(12, 129) AMOEBA,(89, 93) CHARMM Drude,(55) CHARMM fluctuating charge,(15, 104) SIBFA, GEM,(32) and ABEEMσπ.(67, 141) Their coverage and software implementation are summarized in Table 1. Most of the force fields are supported on GPU platforms,(8, 21, 38, 40, 103) which provides two orders of magnitude acceleration compared to CPU and permits routine access to the microsecond time scale. Tinker-HP is a massively parallel package for polarizable MD simulations of large systems on CPU based supercomputers.(52) Below we will only overview some of recent developments, and the readers are referred to the respective literature for more details.
Table 1.
Polarizable force fields for biomolecules and available software
| Force field | Polarization | Electrostatics | Coverage | Software | |||||
|---|---|---|---|---|---|---|---|---|---|
| Penetration | Anisotropy | Protein | DNA | RNA | Sugar | Lipid | |||
| AMBER | Induced dipole |
N/A | N/A | Yes | Yes | Yes | No | No | AMBER |
| AMOEBA | Induced dipole |
N/A | Multipole | Yes | Yes | Yes | No | Yes | TINKER, AMBER, OpenMM |
| CHARMM-Drude | Drude | N/A | Distributed charges | Yes | Yes | No | Yes | Yes | CHARMM, NAMD, AMBER, GROMACS, OpenMM |
| CHARMM-FQ | Fluctuating charge | N/A | N/A | Yes | No | No | No | Yes | CHARMM |
| SIBFA | Induced dipole | Yes | Multipole | Yes | No | No | No | No | TINKER |
| ABEEMσπ | Fluctuation charge | N/A | Distributed charges | Yes | Yes | No | No | No | TINKER |
AMBER
AMBER ff02pol(12) is one of the earliest polarizable force fields for proteins and nucleic acids. Point charge and simple induced dipole model with no damping were employed in ff02pol. Later ff12pol with Thole-style damping functions was developed to improve the accuracy of intermolecular interaction energies.(129)
AMOEBA
The AMOEBA polarizable force fields employ atomic induced dipole to model polarization and atomic multipoles up to quadrupole to represent the permanent electrostatics. AMOEBA force fields have been applied to simulate water, ions, organic molecules and proteins.(36, 76, 101, 102, 110, 136) Mu et al. showed that the σ-hole effect can be captured by AMOEBA.(84) Recently, Zhang et al. developed the AMOEBA force field for DNA and RNA.(144) The force field was extensively validated through 35 microseconds of MD simulations. The simulated solution and crystal structures of DNA duplexes, RNA duplexes and hairpins agree with NMR structures with RMSDs < 2.0 Å. Notably, the interconversion between A- and B-form DNAs was observed in ethanol-water mixtures, indicating a balanced description of the stabilities of different forms.
Clavaguéra and coworkers developed the AMOEBA force field for Fe(II) and the heme cofactor in ferrous and ferric form.(109, 137) The parameters were validated for energy calculation of larger clusters and MD simulations of cytochromes, showing good agreement with DFT and NMR data. To match the energy components from ab initio calculations, Xia et al. incorporated an explicit charge-transfer term into the AMOEBA force field for Fe(III).(139) For the transition metal ions Cu2+ and Zn2+, AMOEBA-VB model was derived.(140) This model generates correct ion-ligand geometry and energetics for both QM gas-phase clusters and the coordination of first solvation shell structure of their aqueous solutions. To better model the water ligand exchange rate around Mg2+, Kurnikov and Kurnikova (51) treated the polarizability of AMOEBA water as variables according to the distance between water and Mg2+.
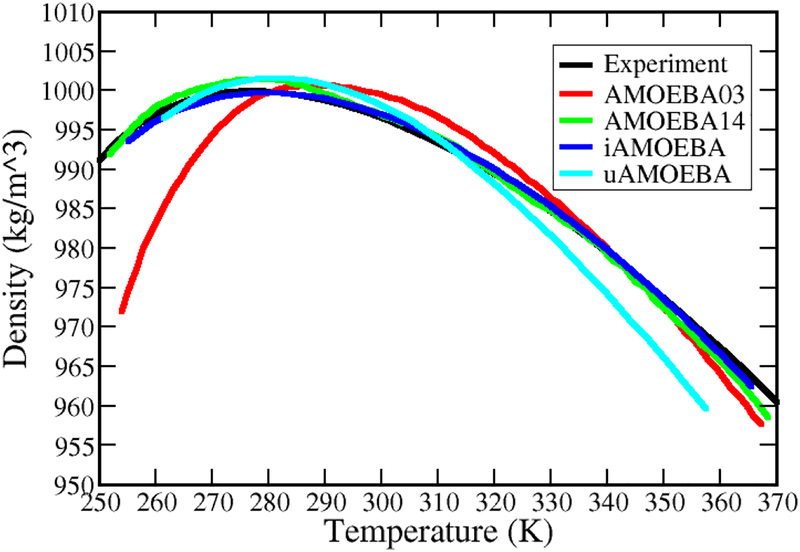
An automatic and systematic approach for the parameterization of AMOEBA using the ForceBalance package(131) has been explored. The AMOEBA water model reparameterized (AMOEBA14)(53) by using ForceBalance better reproduces high-level quantum mechanical (QM) data and experimental condensed-phase properties compared to the original AMOEBA03. Faster water models, including the direct polarization (iAMOEBA)(131) and united atom models (uAMOEBA),(95) were also devised and parameterized using this approach. Both iAMOEBA and uAMOEBA have comparable accuracy to AMOEBA03 for predicting gas-phase and liquid properties. As an example, the liquid densities over a wide temperature range predicted by different water models are compared in Figure 3.
Figure 3.
Density of liquid water over the temperature range of ~250–370 K at atmospheric pressure. The data were reproduced from the original papers by using WebPlotDigitizer (https://automeris.io/WebPlotDigitizer).
Ongoing work to develop the next-generation AMOEBA force field focuses on calibrating each energy component to high-level QM energy decomposition such as Symmetry-Adapted Perturbation Theory (SAPT), and using automated optimization methods(131) for parameterization at large scales. This promises to improve the accuracy and transferability and mitigate the tedious parameterization process. Although previous AMOEBA force fields for metal ions have utilized energy decomposition analysis,(92) it is only recently when EDA methods become sufficiently accurate and feasible for large molecular fragments so that force field development can be systematically based on EDA. For permanent electrostatic interactions, the charge-penetration effect can be captured by empirical damping functions either for charge-charge interactions only (133) or including higher order multipoles.(99) For polarization, the Thole damping function used in AMOEBA(93) was improved to better capture the explicit many-body interactions for a range of molecules at different intermolecular distances.(68) The polarization model also offers a way to separate the polarization energy from the charge-transfer energy in a physically consistent way. For vdW interactions, the buffered-14–7 potential used in AMOEBA is parametrized by targeting the SAPT exchange-repulsion and dispersion energy.(96)
CHARMM Drude force field
The CHARMM Drude force fields utilize the Drude oscillator model for polarization and off-center charges to represent anisotropic charge distributions.(55) The Drude force field covers the majority of biomolecules, including small organic molecules, protein/peptide, DNA,(56) and lipid.(59) (See Ref(55) and references therein) Lin et al. improved the Drude force field for both aliphatic and aromatic halogenated molecules by including off-site charges, anisotropic polarizability on halogen and vdW parameter on the Drude particle.(64) The Drude model for DNA has been refined to resolve problems of the previous version Drude-2013, such as the weak base stacking in A- and B-DNA, and the unwinding of Z-DNA.(56) Ions and water models have been adjusted to obtain better compatibility with DNA model by fitting to QM energy profiles and aqueous solution properties.(55) Similar strategies were used to develop the ion-protein model.(72)
SIBFA
SIBFA(32) (Sum of Interaction Between Fragments Ab Initio) is an ab initio polarizable force field formulated as a sum of electrostatic multipole, short-range repulsion, polarization, charge transfer and dispersion contributions, each of which is designed to reproduce its QM counterpart. It was first developed to deal with divalent cations metalloproteins(33) but extended halogen compounds(22) and nucleic acids.(34) SIBFA has been implemented into Tinker-HP(52) for massively parallel MD simulations. Recent developments include the Gaussian electrostatic model (GEM), which provides a more faithful representation of ab initio electron density.(32) GEM has been combined with SIBFA(32) and AMOEBA.(19)
Recent Application of Polarizable Force Field
Metal ion solvation and binding thermodynamics
Early successes of polarizable force fields have been demonstrated on the calculation of ion solvation thermodynamics. Although fixed-charge force field can be parameterized to reproduce the hydration free energy and solvation shell structure,(97) the parameters are unlikely to be transferable to a different environment, such as protein binding pockets or organic solvents. In these cases, polarization is crucial for obtaining correct thermodynamics.
Solvation of salt ions in the non-aqueous solvent has significant implications for understanding ion transport in cellulose. Noskov and coworkers performed combined experimental and computational analysis of the solvation of LiCl salt in N-methyl-acetamide (NMA). They found that polarizable Drude oscillator model could energetics and geometries of the gas-phase clusters, and yielded qualitative agreement with experimental data on the concentration-dependence of solvation enthalpies. Polarization also has a dramatic impact on the computed potential of mean force (PMF) for ion permeation.(75)
Divalent metal ions such as Mg2+, Ca2+ and Zn2+ are integral to various regulatory and catalytic process in biology. Simulation studies of the binding of divalent metal ions may provide insights into their functions. Since fixed-charge force fields for metal ions often target experimental hydration free energy, the permanent electrostatics interaction of divalent ions must be artificially stronger to capture the polarization effect. When divalent ions bind to anions or proteins, the electrostatics interaction will be too strong, which leads to significant overestimation of the binding free energies. For example, it was shown that the binding free energy between Mg2+ and H2PO4− determined by AMOEBA, CHARMM fixed-charge force field, and QM with mixed explicit/continuum solvent model were are −2.23, −41.0 and −3.3 kcal/mol, respectively, compared to the experimental value of −1.7 kcal/mol.(105)
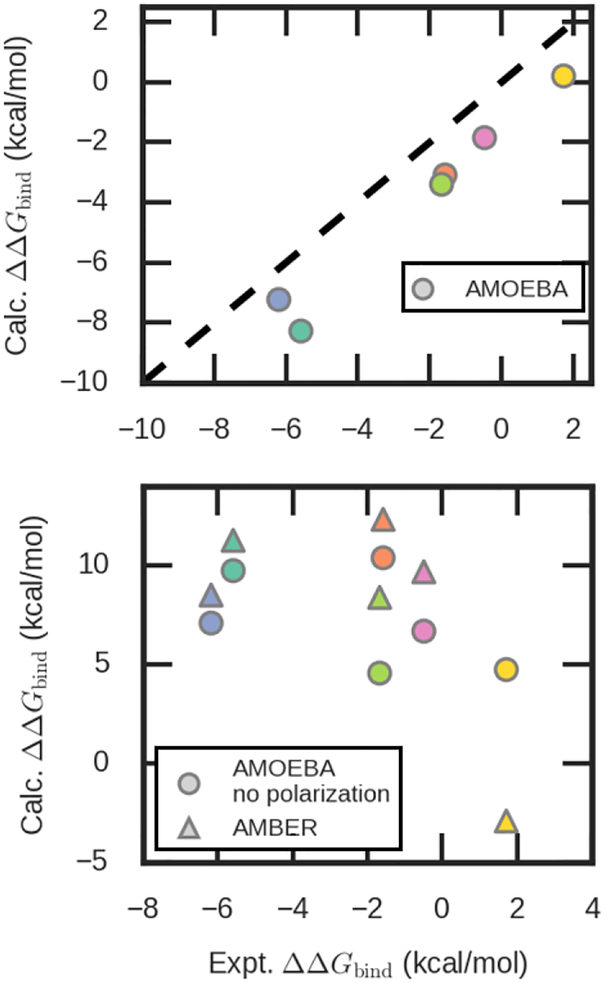
The interactions between ions and proteins have been extensively studied by polarizable force fields. With the Drude polarizable force field, the secondary coordination shells of proteins were shown to be perturbed in cation-dependent manner, with significant delocalization and long-range effects of charge transfer and polarization on Ca2+ binding.(86) Mehandzhiyski et al. showed that near equilibrium distance, charge transfer between metal ions and deprotonated carboxylic acids are significant.(79) The AMOEBA force field was employed to calculate the relative binding free energies between Mg2+ and Ca2+ for a series of proteins.(46) The results correlate well with experimental measurements with a correlation coefficient of 0.97. (Figure 4) Further, it was shown that the intriguing question of Ca2+ selectivity in proteins can be explained by the many-body polarization effect. (41, 46) In contrast, fixed-charge force fields predicted wrong sign of the relative binding free energies.(46)
Figure 4.
Relative binding free energies between Mg2+ and Ca2+ for a series of proteins calculated by polarizable and fixed-charge force fields. . Green, orange, navy blue, magenta, light green and yellow are proteins with PDB ID 5CPV, 1B8L, 4ICB, 2CHE and 1ZOO, respectively.(46)
Ion channels and membrane
The permeation of ions and small molecules through cell membrane is a precisely controlled dynamic process. Since the membrane has a different dielectric constant from plasma, polarizable force fields are expected to be helpful for improving the accuracy of simulations.
2D Free energy profiles for Zn-binding to a voltage-gated proton channel (Hv1) calculated with the Drude force field were consistent with the voltage clamp fluorometry data, supporting the existence of two Zn2+-binding sites and the involvement of different amino acid residues in the two binding sites.(98)
Polarization effects are essential for capturing ion transport as shown by calculating the potential of mean force of Li transport through a narrow ion channel (75). The free energy path for an oxygen molecule to travel along E. Coli AlkB tunnels has been determined with AMBER and AMOEBA. Both PMFs indicate passive transport of O-2 from the surface of the protein. However, the inclusion of explicit polarization shows a very large barrier for diffusion of the co-substrate out of the active site, compared with the non-polarizable potential. Also, the results suggest that the mutation of a conserved residue along the tunnel, Y178, has dramatic effects on the dynamics of AlkB and the transport of O-2 along the tunnel.(120)
By explicitly introducing the multipole terms and polarization into the electrostatic potentials, the permeation free energy barrier of K+ through the gA channel is considerably reduced compared to the overestimated results obtained from the fixed-charge model. Moreover, the estimated maximum conductance, without any corrections, for both K+ and Na+ passing through the gA channel is much closer to the experimental results than any classical MD simulations, demonstrating the power of AMOEBA in investigating the membrane proteins.(89)
Voltage-gated sodium (Na-v) channels play vital roles in the signal transduction of excitable cells. Upon activation of a Nav channel, the change of transmembrane voltage triggers conformational change of the voltage sensing domain, which then elicits opening of the pore domain and thus allows an influx of Na+ ions. Description of this process with atomistic details is in urgent demand. In this work, the partial activation process of the voltage sensing domain of a prokaryotic Nav channel using a polarizable force field was simulated. It was not only observed the conformational change of the voltage sensing domain from resting to preactive state, but also rigorously estimated the free energy profile along the identified reaction pathway. Comparison with the control simulation using an additive force field indicates that voltage-gating thermodynamics of Na-v channels may be inaccurately described without considering the electrostatic polarization effect.(117)
Roux and coworkers investigated the properties of an ion channel from the Gram-positive bacterium Tsukamurella paurometabola with a selectivity filter formed by an uncommon proline-rich sequence. Electrophysiological recordings show that it is a non-selective cation channel and that its activity depends on Ca2+ concentration. In the crystal structure, the selectivity filter adopts a novel conformation with Ca2+ ions bound within the filter near the pore helix where they are coordinated by backbone oxygen atoms, a recurrent motif found in multiple proteins. The binding of Ca2+ ion in the selectivity filter controls the widening of the pore as shown in crystal structures and in molecular dynamics simulations. The structural, functional and computational data provide a characterization of this calcium-gated cationic channel.(18)
Zhu et al. studied the permeation behavior of 2-aminoethoxydiphenyl borate (2-APB), a broad-spectrum modulator for some membrane proteins. They showed that the protonation state and therefore the polarity of the drug is critical for its partition, and that the drug is likely to switch between different protonation states along its permeation pathway. By changing the degrees of freedom, protonation further affects the thermodynamic of the permeation pathway of 2-APB, leading to different entropic contributions. A survey of 54 analog structures with the similar backbone to 2-APB showed that delicate balance between entropy and polarity plays an important role in the potency of drugs.(146)
Several apical iodide translocation pathways have been proposed for iodide efflux out of thyroid follicular cells, including a pathway mediated by the sodium-coupled monocarboxylate transporter 1 (SMCT1), which remains controversial. Vergara-Jaque et al. evaluated the structural and functional similarities between SMCT1 and the well-studied sodium-iodide symporter (NIS) that mediates the first step of iodide entry into the thyroid. These results suggest that wild-type hSMCT1 in the inward-facing conformation may bind iodide only very weakly, which may have implications for its ability to transport iodide.(123)
Protein-ligand binding
MD simulations have been widely used to understand the mechanism of protein-ligand binding and to predict the binding affinities. Accurate modeling with polarizable force fields have allowed us to gain new insights.
The protonation state of phosphate bound the phosphate binding protein (PBP) has been controversial. Biochemical assays determined similar binding affinities at pH 4.5 and 8.5, and based on the data it was argued that PBP could bind to both 1H and 2H phosphates with similar affinities. However, a later sub-angstrom X-ray study only observed 1H phosphate. Qi et al. showed that after considering the interaction with buffer solution, the AMOEBA force field could accurately predict the binding free energy at both pHs, with 1H phosphate being the dominant bound species. (94) The similar binding affinities at both pH results from the competition between buffer ligand and pH. This study demonstrates that polarizable force fields are useful for deciphering the subtle effects in protein-ligand binding.
Preorganization of a ligand to the bound conformation has been a useful concept for designing ligands with favorable binding entropy and free energy. However, experimental studies of a series of unconstrained and constrained ligands binding to an SH2 domain revealed that the constrained ligands have less favorable binding entropy than the unconstrained ligands. The AMOEBA force field was used to study this paradox.(111) Both the binding free energies and entropies predicted by AMOEBA were in line with experimental values. It was found that the unconstrained ligand formed a macrocyclic structure in solution, stabilized by the interaction between phosphate and amide groups, while the constrained ligand adopted an extended conformation. Therefore, the conformational preference in unbound states must also be considered when designing ligands.
Protein and Peptide Structures
Due to cooperative effect, polarization plays a stabilization role for ordered structures such as α-helices. MacKerell and coworkers showed that polarization enhancing the dipole moment of peptide bonds in helices.(55, 88) Mutations altering the local peptide-bond dipole moments can cause destabilization of the alpha-helix, and induce unfolding of amyloid A-beta peptide.(54)
Polarizability of nonpolar solvent also affects the protein stability. With polarization, the alpha-helix is stabilized compared to beta-hairpin by about 1 kJ mol−1 per residue for methanol and chloroform and by about 2 kJ mol−1 per residue for carbon tetrachloride. This highlights the importance of polarizability in models for less polar and nonpolar solvents or protein environments.(65) Additionally, an MD study of alkali-acetate solutions at various concentrations indicated that polarizable force fields may be needed to accurately capture behavior of protein in electrolyte solutions using MD simulations. (1)
There have been limited kinetics studies of proteins by polarizable force fields due to the computational cost. Lin et al. showed that the relaxation rate of proteins was overestimated by one order of magnitude by fixed-charge force fields; while relaxation can be slowed down by using polarizable FF (AMBER12pol), it cannot make up for the gap in timescales between experiments and simulations.(62) To improve the description of kinetics, energies of conformational transition states may be considered in force field development.(48)
Nucleic Acids
Nucleic acids involve complicated intermolecular interactions such as strong polarization, π-π stacking and hydrogen bonds, which require accurate treatment of both permanent electrostatics and polarization in force fields. Numerous studies have been devoted to the benchmark of force fields for modeling these interactions. The importance of polarization for capturing the flexibility and stacking behavior of nucleic acids with ions has been noted in several works.(35, 106, 144) Gresh et al. showed that multipoles and explicit representation of lone pairs in SIBFA is essential to account for coulomb anisotropies and exchange repulsion when studying the stacking of cytosine dimers and a doubly H-bonded dimer. (35) Gao et al. showed that orbital overlap is vital for capturing short hydrogen bonding.(26)
With physically sound models for these interactions, polarizable force fields can better describe the conformational states of nucleic acids with less iterative tuning of the force field parameters. Simulations with CHARMM Drude polarizable force field yielded near-quantitative agreement with experimental measurements of the equilibrium between the base-paired and flipped states. Free energy barriers to base flipping are reduced by changes in dipole moments of both the flipped bases that favor solvation of the bases in the open state and water molecules adjacent to the flipping base.(57) The Drude force field also better reproduced experimental solution X-ray scattering for DNA compared to non-polarizable AMBER parmbsc0 and CHARMM36 force fields. The simulations indicate that the conformational properties of DNA in solution are sensitive to the type of monovalent ion. The primary conformational mode associated with the variations is a contraction of the DNA minor groove width with decreasing cation size.(107). The AMOEBA force field also shows good agreement with experimental NMR measurements for DNA duplexes, RNA duplexes and hairpins. Starting from unstacked conformation, the RNA CAAU tetramer can be folded into A-form structure.(144)
Song et al. showed that polarization of the nucleobases by K+ enhanced electrostatic attraction between the base and ions.(114) This increased attractive interaction is critical to stabilizing the stem-loop junction ions in G-DNA. With non-polarizable force fields, the top and bottom cations would be released into the solvent within just a few nanoseconds, and an incorrect bifurcated bonding geometry of G-DNA will be adopted which is not observed in experiments. Polarization effects are also significant when introducing a second ion to a G-stem quadruplex, which indicates a delicate balance between electrostatics and polarization.(29)
While the conformational sampling for nucleic acids has been a grand challenge, and therefore it is unclear how good polarizable force fields are for modeling large DNA and RNA molecules, protein-nucleic acid binding and global structural transitions, these initial applications are quite promising. When combined with enhanced sampling methods, polarizable force fields will open new opportunities for the study of nucleic acids.
QM/MM
QM/MM has greatly facilitated the study of reactive processes and quantum effects. However, QMM/MM has been mainly used with fixed-charge force field, which does not response to the changes in the electronic structure of the QM region. Recently polarizable force fields (e.g. AMOEBA, GEM and CHARMM-Drude) have been applied to the hybrid QM/MM method to better describe the environment of the QM region.(25, 31, 66, 70, 71, 143) The methods have been implemented in software interfaces, such as Gaussian/TINKER,(71) Psi4/TINKER(31), Q-Chem/CHARMM.(143) The use of polarizable force field improves both ground-state energy and structure(31, 71) and excited-state spectral properties.(69, 71, 143) Loco et al. used QM/MM simulations with B3LYP and AMOEBA to study the color tuning in Carotenoid pigment-crustacyanin complexes.(69) It was found that polarizable force field and MD simulations are necessary to obtain quantitative predictions of the spectrum. The high color tunability of the pigment-protein complex was explained by the bond length alternation in the long-chain carotenoids modulated by the dynamical protein environment.
Summary and Outlook
Polarizable force fields have been growing steadily during the past few years in terms of computational efficiency, model accuracy and applications to biomolecular systems.
Recent works from different groups have led to notable improvements and better understanding of the underlying physical models. The connection between different models have facilitated the adoption of novel algorithms and techniques across different force fields. For example, the Thole damping model has been used in both induced dipole model and Drude oscillator model. The accelerated polarization solvers, initially developed for the induced dipole model, can be used for other polarization models. This also helps separate the effect of models from that of parameterization schemes and objectively compare different force fields.
Advances in polarization algorithms and computing hardware, especially GPU computing, have significantly reduced the computational overhead of polarizable force fields compared to fixed-charge force field. Microsecond MD simulations with polarizable force fields are now routinely accessible.
The accuracy and coverage of polarizable force fields have also improved in recent years. The AMOEBA force field that has recently been extended to DNA and RNA shows an improved description of the conformational ensemble in different environments. The CHARMM Drude force field has recently been refined for DNA and extended to carbohydrates and halogenated molecules.
The applications of polarizable force fields have provided many new insights. Recent studies using polarizable force fields have demonstrated the critical role of polarization for the stability of nucleic acids and proteins, base-pair flipping, ion distribution around DNA, diffusion and permeation of small molecules. In general, simulations with polarization force fields agree better with experiments. When comparing general biomolecular force fields (polarizable or nonpolarizable), it is important to consider a wide range of properties and systems and we are confident that better physical foundation will lead to better force fields.
There is a need to further improve the underlying physical models, particularly for short-range interactions such as charge penetration(99, 133) and charge transfer. Such models will allow systematic calibration of energy components based on ab initio EDA and significantly better accuracy and transferability with little additional computational cost. Better models combined with systematic parameterization methods will also reduce human efforts and errors and improve reproducibility. These effort will benefit from the continuous advancement in QM methods and machine learning approaches that are increasingly adopted in chemistry. In addition, validation and application of polarizable force fields to long simulations of biomolecules. An exciting opportunity is to combine polarizable force fields with enhanced sampling methods such as orthogonal space sampling (OSS),(73) Markov state models (MSMs) and Milestoning,(23, 42) to significantly extend the time and length scales of PFF simulations to areas such as protein and nucleic acids conformational dynamics. These studies would provide crucial feedback to force field development and to our understanding of the intermolecular forces and how they affect the structure and properties of biomolecular systems.
Acknowledgement
We are grateful for support by the National Institutes of Health (Nos. R01GM106137 and R01GM114237), the Robert A. Welch Foundation (No. F-1691) and CPRIT(RP160657).
Literature Cited
- 1.Ahlstrand E, Zukerman Schpector J, Friedman R. 2017. Computer simulations of alkali-acetate solutions: Accuracy of the forcefields in difference concentrations. J Chem Phys 147: 194102. [DOI] [PubMed] [Google Scholar]
- 2.Albaugh A, Head-Gordon T. 2017. A New Method for Treating Drude Polarization in Classical Molecular Simulation. Journal of Chemical Theory and Computation 13: 5207–16 [DOI] [PubMed] [Google Scholar]
- 3.Albaugh A, Niklasson AMN, Head-Gordon T. 2017. Accurate Classical Polarization Solution with No Self-Consistent Field Iterations. The Journal of Physical Chemistry Letters 8: 1714–23 [DOI] [PubMed] [Google Scholar]
- 4.Aviat F, Levitt A, Stamm B, Maday Y, Ren P, et al. 2017. Truncated Conjugate Gradient: An Optimal Strategy for the Analytical Evaluation of the Many-Body Polarization Energy and Forces in Molecular Simulations. Journal of Chemical Theory and Computation 13: 180–90 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Baker CM. 2015. Polarizable force fields for molecular dynamics simulations of biomolecules. Wiley Interdisciplinary Reviews: Computational Molecular Science 5: 241–54 [Google Scholar]
- 6.Bell DR, Qi R, Jing Z, Xiang JY, Mejias C, et al. 2016. Calculating binding free energies of host-guest systems using the AMOEBA polarizable force field. Physical Chemistry Chemical Physics 18: 30261–69 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Boateng HA. 2017. Mesh-free hierarchical clustering methods for fast evaluation of electrostatic interactions of point multipoles. The Journal of Chemical Physics 147: 164104. [DOI] [PubMed] [Google Scholar]
- 8.Carsten K, Szilárd P, Martin F, Ansgar E, dGB L, Helmut G 2015. Best bang for your buck: GPU nodes for GROMACS biomolecular simulations. Journal of Computational Chemistry 36: 1990–2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Cerutti DS, Rice JE, Swope WC, Case DA. 2013. Derivation of Fixed Partial Charges for Amino Acids Accommodating a Specific Water Model and Implicit Polarization. The Journal of Physical Chemistry B 117: 2328–38 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Chen J, Martínez TJ. 2007. QTPIE: Charge transfer with polarization current equalization. A fluctuating charge model with correct asymptotics. Chemical Physics Letters 438: 315–20 [Google Scholar]
- 11.Chodera JD, Swope WC, Noé F, Prinz J-H, Shirts MR, Pande VS. 2011. Dynamical reweighting: Improved estimates of dynamical properties from simulations at multiple temperatures. The Journal of Chemical Physics 134: 244107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Cieplak P, Caldwell J, Kollman P. 2001. Molecular mechanical models for organic and biological systems going beyond the atom centered two body additive approximation: aqueous solution free energies of methanol and N‐methyl acetamide, nucleic acid base, and amide hydrogen bonding and chloroform/water partition coefficients of the nucleic acid bases. Journal of Computational Chemistry 22: 1048–57 [Google Scholar]
- 13.Cisneros GA, Karttunen M, Ren P, Sagui C. 2014. Classical Electrostatics for Biomolecular Simulations. Chemical Reviews 114: 779–814 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Das AK, Demerdash ON, Head-Gordon T. 2018. Improvements to the AMOEBA Force Field by Introducing Anisotropic Atomic Polarizability of the Water Molecule. Journal of Chemical Theory and Computation [DOI] [PubMed] [Google Scholar]
- 15.Davis JE, Patel S. 2009. Charge Equilibration Force Fields for Lipid Environments: Applications to Fully Hydrated DPPC Bilayers and DMPC-Embedded Gramicidin A. The Journal of Physical Chemistry B 113: 9183–96 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Debiec KT, Cerutti DS, Baker LR, Gronenborn AM, Case DA, Chong LT. 2016. Further along the Road Less Traveled: AMBER ff15ipq, an Original Protein Force Field Built on a Self-Consistent Physical Model. Journal of Chemical Theory and Computation 12: 3926–47 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Demerdash O, Mao Y, Liu T, Head-Gordon M, Head-Gordon T. 2017. Assessing many-body contributions to intermolecular interactions of the AMOEBA force field using energy decomposition analysis of electronic structure calculations. J Chem Phys 147: 161721. [DOI] [PubMed] [Google Scholar]
- 18.Dhakshnamoorthy B, Rohaim A, Rui H, Blachowicz L, Roux B. 2016. Structural and functional characterization of a calcium-activated cation channel from Tsukamurella paurometabola. Nature Communications 7: 12753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Duke RE, Starovoytov ON, Piquemal J-P, Cisneros GA. 2014. GEM*: A Molecular Electronic Density-Based Force Field for Molecular Dynamics Simulations. Journal of Chemical Theory and Computation 10: 1361–65 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Dybeck EC, Schieber NP, Shirts MR. 2016. Effects of a More Accurate Polarizable Hamiltonian on Polymorph Free Energies Computed Efficiently by Reweighting Point-Charge Potentials. Journal of Chemical Theory and Computation 12: 3491–505 [DOI] [PubMed] [Google Scholar]
- 21.Eastman P, Swails J, Chodera JD, McGibbon RT, Zhao Y, et al. 2016. OpenMM 7: Rapid Development of High Performance Algorithms for Molecular Dynamics. bioRxiv [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.El HK, Jean‐Philip P, Zeina H, G. MR, Nohad G 2013. Could an anisotropic molecular mechanics/dynamics potential account for sigma hole effects in the complexes of halogenated compounds? Journal of Computational Chemistry 34: 1125–35 [DOI] [PubMed] [Google Scholar]
- 23.Elber R 2016. Perspective: Computer simulations of long time dynamics. The Journal of Chemical Physics 144: 060901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Faradjian AK, Elber R. 2004. Computing time scales from reaction coordinates by milestoning. The Journal of Chemical Physics 120: 10880–89 [DOI] [PubMed] [Google Scholar]
- 25.KE G, WA R, Louis L, Filippo L, Jean‐Philip P, G. AC. 2016. LICHEM: A QM/MM program for simulations with multipolar and polarizable force fields. Journal of Computational Chemistry 37: 1019–29 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Gao XC, Hao Q, Wang CS. 2017. Improved Polarizable Dipole-Dipole Interaction Model for Hydrogen Bonding, Stacking, T-Shaped, and X-H…pi Interactions. J Chem Theory Comput 13: 2730–41 [DOI] [PubMed] [Google Scholar]
- 27.Ghahremanpour MM, van Maaren PJ, Caleman C, Hutchison GR, van der Spoel D. 2018. Polarizable Drude Model with s-Type Gaussian or Slater Charge Density for General Molecular Mechanics Force Fields. Journal of Chemical Theory and Computation 14: 5553–66 [DOI] [PubMed] [Google Scholar]
- 28.Giese TJ, Panteva MT, Chen H, York DM. 2015. Multipolar Ewald Methods, 1: Theory, Accuracy, and Performance. Journal of Chemical Theory and Computation 11: 436–50 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Gkionis K, Kruse H, Platts JA, Mladek A, Koca J, Sponer J. 2014. Ion Binding to Quadruplex DNA Stems. Comparison of MM and QM Descriptions Reveals Sizable Polarization Effects Not Included in Contemporary Simulations. J Chem Theory Comput 10: 1326–40 [DOI] [PubMed] [Google Scholar]
- 30.Goh BC, Hadden JA, Bernardi RC, Singharoy A, McGreevy R, et al. 2016. Computational Methodologies for Real-Space Structural Refinement of Large Macromolecular Complexes. Annual Review of Biophysics 45: 253–78 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Gökcan H, Kratz E, Darden TA, Piquemal J-P, Cisneros GA. 2018. QM/MM Simulations with the Gaussian Electrostatic Model: A Density-based Polarizable Potential. The Journal of Physical Chemistry Letters 9: 3062–67 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Gresh N, Cisneros GA, Darden TA, Piquemal J-P. 2007. Anisotropic, Polarizable Molecular Mechanics Studies of Inter- and Intramolecular Interactions and Ligand−Macromolecule Complexes. A Bottom-Up Strategy. Journal of Chemical Theory and Computation 3: 1960–86 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Gresh N, Perahia D, de Courcy B, Foret J, Roux C, et al. 2016. Complexes of a Zn‐metalloenzyme binding site with hydroxamate‐containing ligands. A case for detailed benchmarkings of polarizable molecular mechanics/dynamics potentials when the experimental binding structure is unknown. Journal of Computational Chemistry 37: 2770–82 [DOI] [PubMed] [Google Scholar]
- 34.Gresh N, Sponer JE, Devereux M, Gkionis K, de Courcy B, et al. 2015. Stacked and H-Bonded Cytosine Dimers. Analysis of the Intermolecular Interaction Energies by Parallel Quantum Chemistry and Polarizable Molecular Mechanics. The Journal of Physical Chemistry B 119: 9477–95 [DOI] [PubMed] [Google Scholar]
- 35.Gresh N, Sponer JE, Devereux M, Gkionis K, de Courcy B, et al. 2015. Stacked and H-Bonded Cytosine Dimers. Analysis of the Intermolecular Interaction Energies by Parallel Quantum Chemistry and Polarizable Molecular Mechanics. J Phys Chem B 119: 9477–95 [DOI] [PubMed] [Google Scholar]
- 36.Grossfield A, Ren P, Ponder JW. 2003. Ion Solvation Thermodynamics from Simulation with a Polarizable Force Field. Journal of the American Chemical Society 125: 15671–82 [DOI] [PubMed] [Google Scholar]
- 37.Halgren TA, Damm W. 2001. Polarizable force fields. Current Opinion in Structural Biology 11: 236–42 [DOI] [PubMed] [Google Scholar]
- 38.Harger M, Li D, Wang Z, Dalby K, Lagardère L, et al. 2017. Tinker‐OpenMM: Absolute and relative alchemical free energies using AMOEBA on GPUs. Journal of Computational Chemistry 38: 2047–55 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Heidar-Zadeh F, Ayers PW, Verstraelen T, Vinogradov I, Vöhringer-Martinez E, Bultinck P. 2018. Information-Theoretic Approaches to Atoms-in-Molecules: Hirshfeld Family of Partitioning Schemes. The Journal of Physical Chemistry A 122: 4219–45 [DOI] [PubMed] [Google Scholar]
- 40.Huang J, Lemkul Justin A, Eastman Peter K, MacKerell Alexander D. 2018. Molecular dynamics simulations using the drude polarizable force field on GPUs with OpenMM: Implementation, validation, and benchmarks. Journal of Computational Chemistry 0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Huang J, Simmonett AC, Pickard FC, MacKerell AD, Brooks BR. 2017. Mapping the Drude polarizable force field onto a multipole and induced dipole model. The Journal of Chemical Physics 147: 161702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Husic BE, Pande VS. 2018. Markov State Models: From an Art to a Science. Journal of the American Chemical Society 140: 2386–96 [DOI] [PubMed] [Google Scholar]
- 43.Jakobsen S, Jensen F. 2014. Systematic Improvement of Potential-Derived Atomic Multipoles and Redundancy of the Electrostatic Parameter Space. Journal of Chemical Theory and Computation 10: 5493–504 [DOI] [PubMed] [Google Scholar]
- 44.Jakobsen S, Jensen F. 2016. Searching the Force Field Electrostatic Multipole Parameter Space. Journal of Chemical Theory and Computation 12: 1824–32 [DOI] [PubMed] [Google Scholar]
- 45.Jiao D, Golubkov PA, Darden TA, Ren P. 2008. Calculation of protein–ligand binding free energy by using a polarizable potential. Proceedings of the National Academy of Sciences 105: 6290–95 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Jing Z, Liu C, Qi R, Ren P. 2018. Many-body effect determines the selectivity for Ca2+ and Mg2+ in proteins. Proceedings of the National Academy of Sciences 115: E7495–E501 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Jorgensen WL, Schyman P. 2012. Treatment of Halogen Bonding in the OPLS-AA Force Field: Application to Potent Anti-HIV Agents. Journal of Chemical Theory and Computation 8: 3895–901 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Kaminsky J, Jensen F. 2016. Conformational Interconversions of Amino Acid Derivatives. J Chem Theory Comput 12: 694–705 [DOI] [PubMed] [Google Scholar]
- 49.Kolář MH, Hobza P. 2016. Computer Modeling of Halogen Bonds and Other σ-Hole Interactions. Chemical Reviews 116: 5155–87 [DOI] [PubMed] [Google Scholar]
- 50.Kramer C, Spinn A, Liedl KR. 2014. Charge Anisotropy: Where Atomic Multipoles Matter Most. Journal of Chemical Theory and Computation 10: 4488–96 [DOI] [PubMed] [Google Scholar]
- 51.Kurnikov IV, Kurnikova M. 2015. Modeling Electronic Polarizability Changes in the Course of a Magnesium Ion Water Ligand Exchange Process. The Journal of Physical Chemistry B 119: 10275–86 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Lagardere L, Jolly L-H, Lipparini F, Aviat F, Stamm B, et al. 2018. Tinker-HP: a massively parallel molecular dynamics package for multiscale simulations of large complex systems with advanced point dipole polarizable force fields. Chemical Science 9: 956–72 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Laury ML, Wang L-P, Pande VS, Head-Gordon T, Ponder JW. 2015. Revised Parameters for the AMOEBA Polarizable Atomic Multipole Water Model. The Journal of Physical Chemistry B 119: 9423–37 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Lemkul JA, Huang J, MacKerell AD. 2015. Induced Dipole–Dipole Interactions Influence the Unfolding Pathways of Wild-Type and Mutant Amyloid β-Peptides. The Journal of Physical Chemistry B 119: 15574–82 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Lemkul JA, Huang J, Roux B, MacKerell AD. 2016. An Empirical Polarizable Force Field Based on the Classical Drude Oscillator Model: Development History and Recent Applications. Chemical Reviews 116: 4983–5013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Lemkul JA, MacKerell AD. 2017. Polarizable Force Field for DNA Based on the Classical Drude Oscillator: I. Refinement Using Quantum Mechanical Base Stacking and Conformational Energetics. Journal of Chemical Theory and Computation 13: 2053–71 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Lemkul JA, Savelyev A, MacKerell AD. 2014. Induced Polarization Influences the Fundamental Forces in DNA Base Flipping. The Journal of Physical Chemistry Letters 5: 2077–83 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Leontyev IV, Stuchebrukhov AA. 2014. Polarizable molecular interactions in condensed phase and their equivalent nonpolarizable models. The Journal of Chemical Physics 141: 014103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Li H, Chowdhary J, Huang L, He X, MacKerell AD, Roux B. 2017. Drude Polarizable Force Field for Molecular Dynamics Simulations of Saturated and Unsaturated Zwitterionic Lipids. Journal of Chemical Theory and Computation 13: 4535–52 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Li Y, Li H, Pickard FC, Narayanan B, Sen FG, et al. 2017. Machine Learning Force Field Parameters from Ab Initio Data. Journal of Chemical Theory and Computation 13: 4492–503 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Liberatore E, Meli R, Rothlisberger U. 2018. A Versatile Multiple Time Step Scheme for Efficient ab Initio Molecular Dynamics Simulations. Journal of Chemical Theory and Computation 14: 2834–42 [DOI] [PubMed] [Google Scholar]
- 62.Lin B, Gao Y, Li Y, Zhang JZ, Mei Y. 2014. Implementing electrostatic polarization cannot fill the gap between experimental and theoretical measurements for the ultrafast fluorescence decay of myoglobin. J Mol Model 20: 2189. [DOI] [PubMed] [Google Scholar]
- 63.Lin D 2015. Generalized and efficient algorithm for computing multipole energies and gradients based on Cartesian tensors. The Journal of Chemical Physics 143: 114115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Lin F-Y, MacKerell AD. 2018. Polarizable Empirical Force Field for Halogen-Containing Compounds Based on the Classical Drude Oscillator. Journal of Chemical Theory and Computation 14: 1083–98 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Lin Z, van Gunsteren WF. 2015. Effects of Polarizable Solvent Models upon the Relative Stability of an α-Helical and a β-Hairpin Structure of an Alanine Decapeptide. Journal of Chemical Theory and Computation 11: 1983–86 [DOI] [PubMed] [Google Scholar]
- 66.Lipparini F, Lagardère L, Raynaud C, Stamm B, Cancès E, et al. 2015. Polarizable Molecular Dynamics in a Polarizable Continuum Solvent. Journal of Chemical Theory and Computation 11: 623–34 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Liu C, Li Y, Han B-Y, Gong L-D, Lu L-N, et al. 2017. Development of the ABEEMσπ Polarization Force Field for Base Pairs with Amino Acid Residue Complexes. Journal of Chemical Theory and Computation 13: 2098–111 [DOI] [PubMed] [Google Scholar]
- 68.Liu C, Qi R, Wang Q, Piquemal J-P, Ren P. 2017. Capturing Many-body Interactions with Classical Dipole Induction Models. Journal of Chemical Theory and Computation 13: 2751–61 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Loco D, Buda F, Lugtenburg J, Mennucci B. 2018. The Dynamic Origin of Color Tuning in Proteins Revealed by a Carotenoid Pigment. The Journal of Physical Chemistry Letters 9: 2404–10 [DOI] [PubMed] [Google Scholar]
- 70.Loco D, Lagardère L, Caprasecca S, Lipparini F, Mennucci B, Piquemal J-P. 2017. Hybrid QM/MM Molecular Dynamics with AMOEBA Polarizable Embedding. Journal of Chemical Theory and Computation 13: 4025–33 [DOI] [PubMed] [Google Scholar]
- 71.Loco D, Polack É, Caprasecca S, Lagardère L, Lipparini F, et al. 2016. A QM/MM Approach Using the AMOEBA Polarizable Embedding: From Ground State Energies to Electronic Excitations. Journal of Chemical Theory and Computation 12: 3654–61 [DOI] [PubMed] [Google Scholar]
- 72.Lopes PEM, Huang J, Shim J, Luo Y, Li H, et al. 2013. Polarizable Force Field for Peptides and Proteins Based on the Classical Drude Oscillator. Journal of Chemical Theory and Computation 9: 5430–49 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Lv C, Li X, Wu D, Zheng L, Yang W. 2016. Predictive Sampling of Rare Conformational Events in Aqueous Solution: Designing a Generalized Orthogonal Space Tempering Method. Journal of Chemical Theory and Computation 12: 41–52 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.MacDermaid CM, Kaminski GA. 2007. Electrostatic Polarization Is Crucial for Reproducing pKa Shifts of Carboxylic Residues in Turkey Ovomucoid Third Domain. The Journal of Physical Chemistry B 111: 9036–44 [DOI] [PubMed] [Google Scholar]
- 75.Manin N, da Silva MC, Zdravkovic I, Eliseeva O, Dyshin A, et al. 2016. LiCl solvation in N-methyl-acetamide (NMA) as a model for understanding Li(+) binding to an amide plane. Phys Chem Chem Phys 18: 4191–200 [DOI] [PubMed] [Google Scholar]
- 76.Mao Y, Demerdash O, Head-Gordon M, Head-Gordon T. 2016. Assessing Ion-Water Interactions in the AMOEBA Force Field Using Energy Decomposition Analysis of Electronic Structure Calculations. J Chem Theory Comput 12: 5422–37 [DOI] [PubMed] [Google Scholar]
- 77.Margul DT, Tuckerman ME. 2016. A Stochastic, Resonance-Free Multiple Time-Step Algorithm for Polarizable Models That Permits Very Large Time Steps. Journal of Chemical Theory and Computation 12: 2170–80 [DOI] [PubMed] [Google Scholar]
- 78.Marshall GR. 2013. Limiting assumptions in molecular modeling: electrostatics. Journal of Computer-Aided Molecular Design 27: 107–14 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Mehandzhiyski AY, Riccardi E, van Erp TS, Koch H, Astrand PO, et al. 2015. Density Functional Theory Study on the Interactions of Metal Ions with Long Chain Deprotonated Carboxylic Acids. J Phys Chem A 119: 10195–203 [DOI] [PubMed] [Google Scholar]
- 80.Mei Y, Simmonett AC, Pickard FC, DiStasio RA, Brooks BR, Shao Y. 2015. Numerical Study on the Partitioning of the Molecular Polarizability into Fluctuating Charge and Induced Atomic Dipole Contributions. The Journal of Physical Chemistry A 119: 5865–82 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Misquitta AJ, Stone AJ, Fazeli F. 2014. Distributed Multipoles from a Robust Basis-Space Implementation of the Iterated Stockholder Atoms Procedure. Journal of Chemical Theory and Computation 10: 5405–18 [DOI] [PubMed] [Google Scholar]
- 82.Morrone JA, Markland TE, Ceriotti M, Berne BJ. 2011. Efficient multiple time scale molecular dynamics: Using colored noise thermostats to stabilize resonances. The Journal of Chemical Physics 134: 014103. [DOI] [PubMed] [Google Scholar]
- 83.Mortier J, Rakers C, Bermudez M, Murgueitio MS, Riniker S, Wolber G. 2015. The impact of molecular dynamics on drug design: applications for the characterization of ligand–macromolecule complexes. Drug Discovery Today 20: 686–702 [DOI] [PubMed] [Google Scholar]
- 84.Mu X, Wang Q, Wang L-P, Fried SD, Piquemal J-P, et al. 2014. Modeling Organochlorine Compounds and the σ-Hole Effect Using a Polarizable Multipole Force Field. The Journal of Physical Chemistry B 118: 6456–65 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Nessler IJ, Litman JM, Schnieders MJ. 2016. Toward polarizable AMOEBA thermodynamics at fixed charge efficiency using a dual force field approach: application to organic crystals. Physical Chemistry Chemical Physics 18: 30313–22 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Ngo V, da Silva MC, Kubillus M, Li H, Roux B, et al. 2015. Quantum effects in cation interactions with first and second coordination shell ligands in metalloproteins. J Chem Theory Comput 11: 4992–5001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Omar D, Lee‐Ping W, Teresa HG. 2018. Advanced models for water simulations. Wiley Interdisciplinary Reviews: Computational Molecular Science 8: e1355 [Google Scholar]
- 88.Ouyang JF, Bettens RP. 2016. When are Many-Body Effects Significant? J Chem Theory Comput 12: 5860–67 [DOI] [PubMed] [Google Scholar]
- 89.Peng X, Zhang Y, Chu H, Li Y, Zhang D, et al. 2016. Accurate Evaluation of Ion Conductivity of the Gramicidin A Channel Using a Polarizable Force Field without Any Corrections. Journal of Chemical Theory and Computation 12: 2973–82 [DOI] [PubMed] [Google Scholar]
- 90.Piotr C, François-Yves D, Yong D, Junmei W. 2009. Polarization effects in molecular mechanical force fields. Journal of Physics: Condensed Matter 21: 333102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Piquemal J-P, Cisneros GA, Reinhardt P, Gresh N, Darden TA. 2006. Towards a force field based on density fitting. The Journal of Chemical Physics 124: 104101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Piquemal J-P, Perera L, Cisneros GA, Ren P, Pedersen LG, Darden TA. 2006. Towards accurate solvation dynamics of divalent cations in water using the polarizable amoeba force field: From energetics to structure. The Journal of Chemical Physics 125: 054511. [DOI] [PubMed] [Google Scholar]
- 93.Ponder JW, Wu C, Ren P, Pande VS, Chodera JD, et al. 2010. Current Status of the AMOEBA Polarizable Force Field. The Journal of Physical Chemistry B 114: 2549–64 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Qi R, Jing Z, Liu C, Piquemal J-P, Dalby KN, Ren P. 2018. Elucidating the Phosphate Binding Mode of PBP: The Critical Effect of Buffer Solution. The Journal of Physical Chemistry B [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Qi R, Wang L-P, Wang Q, Pande VS, Ren P. 2015. United polarizable multipole water model for molecular mechanics simulation. The Journal of Chemical Physics 143: 014504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Qi R, Wang Q, Ren P. 2016. General van der Waals potential for common organic molecules. Bioorganic & Medicinal Chemistry 24: 4911–19 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Qiao B, Skanthakumar S, Soderholm L. 2018. Comparative CHARMM and AMOEBA Simulations of Lanthanide Hydration Energetics and Experimental Aqueous-Solution Structures. Journal of Chemical Theory and Computation 14: 1781–90 [DOI] [PubMed] [Google Scholar]
- 98.Qiu F, Chamberlin A, Watkins BM, Ionescu A, Perez ME, et al. 2016. Molecular mechanism of Zn2+ inhibition of a voltage-gated proton channel. Proceedings of the National Academy of Sciences 113: E5962–E71 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Rackers JA, Wang Q, Liu C, Piquemal J-P, Ren P, Ponder JW. 2017. An optimized charge penetration model for use with the AMOEBA force field. Physical Chemistry Chemical Physics 19: 276–91 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Ren P, Chun J, Thomas DG, Schnieders MJ, Marucho M, et al. 2012. Biomolecular electrostatics and solvation: a computational perspective. Quarterly Reviews of Biophysics 45: 427–91 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Ren P, Ponder JW. 2003. Polarizable Atomic Multipole Water Model for Molecular Mechanics Simulation. J. Phys. Chem. B 107: 5933–47 [Google Scholar]
- 102.Ren P, Wu C, Ponder JW. 2011. Polarizable Atomic Multipole-Based Molecular Mechanics for Organic Molecules. Journal of Chemical Theory and Computation 7: 3143–61 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Salomon-Ferrer R, Götz AW, Poole D, Le Grand S, Walker RC. 2013. Routine Microsecond Molecular Dynamics Simulations with AMBER on GPUs. 2. Explicit Solvent Particle Mesh Ewald. Journal of Chemical Theory and Computation 9: 3878–88 [DOI] [PubMed] [Google Scholar]
- 104.P Sandeep, L. BC. 2004. CHARMM fluctuating charge force field for proteins: I parameterization and application to bulk organic liquid simulations. Journal of Computational Chemistry 25: 1–16 [DOI] [PubMed] [Google Scholar]
- 105.Satpati P, Clavaguéra C, Ohanessian G, Simonson T. 2011. Free Energy Simulations of a GTPase: GTP and GDP Binding to Archaeal Initiation Factor 2. The Journal of Physical Chemistry B 115: 6749–63 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Savelyev A, MacKerell AD. 2014. All‐atom polarizable force field for DNA based on the classical drude oscillator model. Journal of Computational Chemistry 35: 1219–39 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Savelyev A, MacKerell AD. 2015. Differential Impact of the Monovalent Ions Li+, Na+, K+, and Rb+ on DNA Conformational Properties. The Journal of Physical Chemistry Letters 6: 212–16 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Schnieders MJ, Baltrusaitis J, Shi Y, Chattree G, Zheng L, et al. 2012. The Structure, Thermodynamics, and Solubility of Organic Crystals from Simulation with a Polarizable Force Field. Journal of Chemical Theory and Computation 8: 1721–36 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Semrouni D, Isley WC, Clavaguéra C, Dognon J-P, Cramer CJ, Gagliardi L. 2013. Ab Initio Extension of the AMOEBA Polarizable Force Field to Fe2+. Journal of Chemical Theory and Computation 9: 3062–71 [DOI] [PubMed] [Google Scholar]
- 110.Shi Y, Xia Z, Zhang J, Best R, Wu C, et al. 2013. Polarizable Atomic Multipole-Based AMOEBA Force Field for Proteins. Journal of Chemical Theory and Computation 9: 4046–63 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Shi Y, Zhu CZ, Martin SF, Ren P. 2012. Probing the Effect of Conformational Constraint on Phosphorylated Ligand Binding to an SH2 Domain Using Polarizable Force Field Simulations. The Journal of Physical Chemistry B 116: 1716–27 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Simmonett AC, P FC IV, S HF III, Brooks BR. 2014. An efficient algorithm for multipole energies and derivatives based on spherical harmonics and extensions to particle mesh Ewald. The Journal of Chemical Physics 140: 184101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Simmonett AC, P FC IV, Ponder JW, Brooks BR. 2016. An empirical extrapolation scheme for efficient treatment of induced dipoles. The Journal of Chemical Physics 145: 164101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Song J, Ji C, Zhang JZH. 2013. The critical effect of polarization on the dynamical structure of guanine quadruplex DNA. Physical Chemistry Chemical Physics 15: 3846–54 [DOI] [PubMed] [Google Scholar]
- 115.Stern HA, Rittner F, Berne BJ, Friesner RA. 2001. Combined fluctuating charge and polarizable dipole models: Application to a five-site water potential function. The Journal of Chemical Physics 115: 2237–51 [Google Scholar]
- 116.Stone A 2016. The Theory of Intermolecular Forces: Oxford University Press, USA [Google Scholar]
- 117.Sun R-N, Gong H. 2017. Simulating the Activation of Voltage Sensing Domain for a Voltage-Gated Sodium Channel Using Polarizable Force Field. The Journal of Physical Chemistry Letters 8: 901–08 [DOI] [PubMed] [Google Scholar]
- 118.Swope WC, Horn HW, Rice JE. 2010. Accounting for Polarization Cost When Using Fixed Charge Force Fields. I. Method for Computing Energy. The Journal of Physical Chemistry B 114: 8621–30 [DOI] [PubMed] [Google Scholar]
- 119.Tazi S, Molina JJ, Rotenberg B, Turq P, Vuilleumier R, Salanne M. 2012. A transferable ab initio based force field for aqueous ions. The Journal of Chemical Physics 136: 114507. [DOI] [PubMed] [Google Scholar]
- 120.Torabifard H, Cisneros GA. 2017. Computational investigation of O2 diffusion through an intra-molecular tunnel in AlkB; influence of polarization on O2 transport. Chemical Science 8: 6230–38 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 121.Unke OT, Devereux M, Meuwly M. 2017. Minimal distributed charges: Multipolar quality at the cost of point charge electrostatics. The Journal of Chemical Physics 147: 161712. [DOI] [PubMed] [Google Scholar]
- 122.Van Vleet MJ, Misquitta AJ, Schmidt JR. 2018. New Angles on Standard Force Fields: Toward a General Approach for Treating Atomic-Level Anisotropy. Journal of Chemical Theory and Computation 14: 739–58 [DOI] [PubMed] [Google Scholar]
- 123.Vergara-Jaque A, Fong P, Comer J. 2017. Iodide Binding in Sodium-Coupled Cotransporters. Journal of Chemical Information and Modeling 57: 3043–55 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 124.Verstraelen T, Vandenbrande S, Ayers PW. 2014. Direct computation of parameters for accurate polarizable force fields. The Journal of Chemical Physics 141: 194114. [DOI] [PubMed] [Google Scholar]
- 125.Vosmeer CR, Kiewisch K, Keijzer K, Visscher L, Geerke DP. 2014. A comparison between QM/MM and QM/QM based fitting of condensed-phase atomic polarizabilities. Physical Chemistry Chemical Physics 16: 17857–62 [DOI] [PubMed] [Google Scholar]
- 126.Vosmeer CR, Rustenburg AS, Rice JE, Horn HW, Swope WC, Geerke DP. 2012. QM/MM-Based Fitting of Atomic Polarizabilities for Use in Condensed-Phase Biomolecular Simulation. Journal of Chemical Theory and Computation 8: 3839–53 [DOI] [PubMed] [Google Scholar]
- 127.Walsh TR, Knecht MR. 2017. Biointerface Structural Effects on the Properties and Applications of Bioinspired Peptide-Based Nanomaterials. Chemical Reviews 117: 12641–704 [DOI] [PubMed] [Google Scholar]
- 128.Wang H, Yang W. 2016. Determining polarizable force fields with electrostatic potentials from quantum mechanical linear response theory. The Journal of Chemical Physics 144: 224107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 129.Wang J, Cieplak P, Li J, Cai Q, Hsieh M-J, et al. 2012. Development of Polarizable Models for Molecular Mechanical Calculations. 4. van der Waals Parametrization. The Journal of Physical Chemistry B 116: 7088–101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 130.Wang J, Wolf Romain M, Caldwell James W, Kollman Peter A, Case David A. 2004. Development and testing of a general amber force field. Journal of Computational Chemistry 25: 1157–74 [DOI] [PubMed] [Google Scholar]
- 131.Wang L-P, Head-Gordon T, Ponder JW, Ren P, Chodera JD, et al. 2013. Systematic Improvement of a Classical Molecular Model of Water. The Journal of Physical Chemistry B 117: 9956–72 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 132.Wang L-P, McKiernan KA, Gomes J, Beauchamp KA, Head-Gordon T, et al. 2017. Building a More Predictive Protein Force Field: A Systematic and Reproducible Route to AMBER-FB15. The Journal of Physical Chemistry B 121: 4023–39 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 133.Wang Q, Rackers JA, He C, Qi R, Narth C, et al. 2015. General Model for Treating Short-Range Electrostatic Penetration in a Molecular Mechanics Force Field. J. Chem. Theory Comput 11: 2609–18 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 134.Warshel A, Kato M, Pisliakov AV. 2007. Polarizable Force Fields: History, Test Cases, and Prospects. Journal of Chemical Theory and Computation 3: 2034–45 [DOI] [PubMed] [Google Scholar]
- 135.Wu H, Paul F, Wehmeyer C, Noé F. 2016. Multiensemble Markov models of molecular thermodynamics and kinetics. Proceedings of the National Academy of Sciences [DOI] [PMC free article] [PubMed] [Google Scholar]
- 136.Wu JC, Chattree G, Ren P. 2012. Automation of AMOEBA polarizable force field parameterization for small molecules. Theoretical Chemistry Accounts 131: 1138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 137.Wu X, Clavaguera C, Lagardère L, Piquemal J-P, de la Lande A. 2018. AMOEBA Polarizable Force Field Parameters of the Heme Cofactor in Its Ferrous and Ferric Forms. Journal of Chemical Theory and Computation 14: 2705–20 [DOI] [PubMed] [Google Scholar]
- 138.Wu X, FC P IV, Brooks BR. 2016. Isotropic periodic sum for multipole interactions and a vector relation for calculation of the Cartesian multipole tensor. The Journal of Chemical Physics 145: 164110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 139.Xia M, Chai Z, Wang D. 2017. Polarizable and Non-Polarizable Force Field Representations of Ferric Cation and Validations. The Journal of Physical Chemistry B 121: 5718–29 [DOI] [PubMed] [Google Scholar]
- 140.Xiang JY, Ponder JW. 2013. A valence bond model for aqueous Cu(II) and Zn(II) ions in the AMOEBA polarizable force field. Journal of Computational Chemistry 34: 739–49 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 141.Yang Z-Z, Wang JJ, Zhao D-X. 2014. Valence state parameters of all transition metal atoms in metalloproteins - Development of ABEEMσπ fluctuating charge force field [DOI] [PubMed] [Google Scholar]
- 142.Yin J, Fenley AT, Henriksen NM, Gilson MK. 2015. Toward Improved Force-Field Accuracy through Sensitivity Analysis of Host-Guest Binding Thermodynamics. The Journal of Physical Chemistry B 119: 10145–55 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 143.Zeng Q, Liang W. 2015. Analytic energy gradient of excited electronic state within TDDFT/MMpol framework: Benchmark tests and parallel implementation. The Journal of Chemical Physics 143: 134104. [DOI] [PubMed] [Google Scholar]
- 144.Zhang C, Lu C, Jing Z, Wu C, Piquemal J-P, et al. 2018. AMOEBA Polarizable Atomic Multipole Force Field for Nucleic Acids. Journal of Chemical Theory and Computation 14: 2084–108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 145.Zhao D-X, Liu C, Wang F-F, Yu C-Y, Gong L-D, et al. 2010. Development of a Polarizable Force Field Using Multiple Fluctuating Charges per Atom. Journal of Chemical Theory and Computation 6: 795–804 [DOI] [PubMed] [Google Scholar]
- 146.Zhu Q, Lu Y, He X, Liu T, Chen H, et al. 2017. Entropy and Polarity Control the Partition and Transportation of Drug-like Molecules in Biological Membrane. Scientific Reports 7: 17749. [DOI] [PMC free article] [PubMed] [Google Scholar]