Utility of Covalent Labeling Mass Spectrometry Data in Protein Structure Prediction with Rosetta

Abstract

Covalent labeling mass spectrometry experiments are growing in popularity and provide important information regarding protein structure. Information obtained from these experiments correlates with residue solvent exposure within the protein in solution. However, it is impossible to determine protein structure from covalent labeling data alone. Incorporation of sparse covalent labeling data into the protein structure prediction software Rosetta has been shown to improve protein tertiary structure prediction. Here, covalent labeling techniques were analyzed computationally to provide insight into what labeling data is needed to optimize tertiary protein structure prediction in Rosetta. We have successfully implemented a new scoring functionality that provides improved predictions. We developed two new covalent labeling based score terms that use a “cone”-based neighbor count to quantify the relative solvent exposure of each amino acid. To test our method, we used a set of 20 proteins with structures deposited in the Protein Data Bank. Decoy model sets were generated for each of these 20 proteins and the normalized covalent labeling score versus RMSD distributions were evaluated. Based on these distributions, we have determined an optimal subset of residues to use when performing covalent labeling experiments in order to maximize the structure prediction capabilities of the covalent labeling data. We also investigated how much false negative and false positive data can be tolerated without meaningfully impacting protein structure prediction. Using these new covalent labeling score terms, protein models were rescored and the resulting models improved by 3.9 Å RMSD on average. New models were also generated using Rosetta’s AbinitioRelax program under the guidance of covalent labeling information and improvement in model quality was observed.

Graphical Abstract

Introduction

Full understanding of protein function requires knowledge of protein tertiary structure. In cases when high-resolution experimental structure determination techniques (such as X-ray crystallography, NMR and cryo-EM) fail to comprehensively characterize protein structure, a plethora of more sparse techniques can yield important structural information. One such set of tools are covalent labeling (CL) experiments coupled with mass spectrometry (MS), a growing set of methods that yield valuable information on the three-dimensional structure of proteins.¹ Experiments using covalent labeling techniques involve either amino acid specific or non-specific probe molecules (labeling reagents) that are exposed to the protein in solution and covalently bind to the side-chains that are solvent accessible and not involved in any other inter- or intramolecular interactions. Structural information is derived from the assumption that a residue that is exposed to the solvent will be accessible to the reagent and hence labeled, whereas a residue that is buried within the protein (or occluded by a bound ligand or protein subunit) would be inaccessible and hence unlabeled. For structural interpretation, the labeled protein is routinely mass analyzed using a combination of proteolysis and mass spectrometry and information regarding the relative location of some of the residues can be elucidated.^2–4

Many different labeling reagents exist, each with their own advantages and disadvantages. For non-specific amino acid labeling, one of the most commonly used methods is oxidative labeling (also known as hydroxyl radical footprinting or HRF). This method utilizes hydroxyl radicals to label the solvated protein.^5–7 Theoretically, 19 of the 20 amino acid types can be labeled, but only a few types provide useful information for structure determination.^8–10 Another reagent used to non-specifically label amino acids is diethylpyrocarbonate (DEPC).¹¹ DEPC primarily reacts with histidine, but is also capable of labeling lysine, tyrosine, cysteine, threonine, and serine. Reagents that only modify specific amino acid types comprise the other major class of covalent labels.^{1, 12, 13} In practice, only eight different amino acid types have been predominantly used in conjunction with mass spectrometry techniques to study structure. These residues are arginine, aspartic acid, glutamic acid, cysteine, histidine, lysine, tryptophan, and tyrosine. A large variety of different reagents have been successfully used to label and probe tertiary structure for each of those eight commonly labeled amino acid types. A few examples include: biotin N-hydroxysuccinimide derivatives for labeling lysine;¹⁴ iodoacetamide and its derivatives along with iodacetic acid N-alkylmaleimides have been used for cysteines;^{15, 16} methylglyoxal and 1,2-cyclohexandione for arginines.^{4, 17, 18} A more extensive overview of all the amino acid specific labeling techniques and their applications is provided in a review by Mendoza and Vachet.¹

Despite the relative success of structure elucidation using covalent labeling techniques, many challenges still exist. It can be difficult to find labeling reagents that successfully modify a protein but do not cause conformational changes. In addition, reagents that are capable of labeling amino acid types different from those listed above are crucial to successfully analyze tertiary structure. However, most notably, the information obtained from covalent labeling experiments cannot directly provide tertiary structure without interpretation utilizing computational protein structure algorithms (or further experimentation). Two recent examples of hybrid computation-CL methods include our previous study on HRF-guided modeling and the work of Xie and co-workers.^{8, 10} In our study, we showed that hydroxyl radical footprinting MS data can be successfully used to predict tertiary structure when combined with the computational macromolecular modeling tool Rosetta. We developed a new score term for the Rosetta energy function that was used to rescore ab initio models for four benchmark proteins and improve the accuracy of the predicted models. The work by Xie and co-workers successfully demonstrated a correlation between experimental HRF data and the absolute average solvent exposure. Using this exposure measure, it was possible to differentiate between low and high RMSD models for two benchmark proteins: lysozyme and myoglobin. Over the years, Rosetta has also proven to be an excellent tool for the incorporation of other sparse experimental data for use in structure prediction.^19–28

So far, however, the computational methods have predominantly been used to interpret the covalent labeling data, not to direct the experiments with the intention of improving their structure predictive capabilities. Here we show that CL-guided protein structure prediction algorithms such as Rosetta have the potential to inform on yet unanswered questions such as: Which amino acid types provide the most useful structural information? How many labeled residues are needed to accurately discriminate between different models? How much error can be tolerated? We argue that answering these questions has the potential to design better covalent labeling experiments that yield optimal information for protein structure prediction using covalent labeling techniques. Crecca and Roitberg performed a similar analysis regarding the utility of inter-residue distances for protein structure prediction.^{29, 30} Additionally, we are also exploring whether a covalent labeling score term is more effective when used to bias the generation of models, rather than we used to simply rescore pre-built models as demonstrated in our previous HRF modeling work.⁸

In this study, we developed the methodology to incorporate information from covalent labeling experiments into Rosetta’s protein structure prediction protocol. To accomplish this, we have analyzed 6,165 proteins obtained from the Protein Data Bank with solvent exposure metrics with the goal of identifying a measure of solvent exposure that accurately characterizes relative solvent accessibility of each residue. Two new score terms for Rosetta were derived from this information and used to identify the ideal subset of residue types to be used for model discrimination based upon a benchmark set of 20 proteins. The tolerance of our prediction algorithm towards false negative and false positive data points was also explored. Protein models were rescored with the new scoring framework and the resulting distributions were analyzed. Finally, new sets of models were generated under the guidance of covalent labeling data.

Methods

Generation of a Protein Set from the Protein Data Bank

The proteinsused for the various aspects of this work consisted of protein structures extracted from the Protein Data Bank (PDB). All monomer, single chain proteins, with at most 50% sequence identity were downloaded (15,000 total). The goal was to create a set of protein structures that served as a non-redundant representation of single chain monomers in the PDB. From this initial set, structures with missing residues that were not part of either the C- or N- terminus were filtered out, due to potential problems when calculating per residue solvent exposure. Not only would the solvent exposure of the missing residues be impossible to determine, the exposure of neighboring residues would be calculated incorrectly. After filtering, the protein set contained 6,185 protein structures. From this set, a benchmark set of 20 structures was created. The 20 structures in the benchmark set were randomly selected from the total decoy set and were between 50 and 200 amino acids in length. To confirm that the benchmark set was truly a representative subset of the protein set, distributions of the total number of residues, secondary structure content, and contact order (both absolute and relative) were analyzed. The distributions can be found in Figure S1. The proteins that comprise the benchmark set are summarized in Table S1. From the original set of 6,185 structures, a set of 6,165 structures were used to determine the correlation between various solvent exposure metrics.

Solvent Exposure Metrics

The goal of this work is to provide insight into how the results of covalent labeling experiments can improve protein tertiary structure prediction. For this purpose, a procedure of correlating relative solvent exposure for a given residue to the data provided from experiment is necessary. Studies have previously shown that residue solvent exposure correlates with experimentally derived protection factors.^{8–10, 31, 32} The general trend observed has been that a more solvent exposed residue is more likely to be labeled whereas a more buried residue is less likely to be labeled. Several different approaches for assessing solvent exposure from the tertiary structure have been reported.

The most accurate method of determining solvent exposure is through the calculation of the solvent accessible surface area (SASA). Despite its popularity, calculating the SASA for every residue in a protein is computationally expensive.^{33, 34} The amount of solvent exposure determinations needed for tertiary structure prediction renders SASA impractical for these purposes. An alternative, and computationally less expensive, method for solvent exposure determination comes in the form of a per residue neighbor count. By counting the number of neighboring residues that are present surrounding a target residue, an inference into the solvent exposure can be made. The more neighbors a residue has, the less solvent exposed it is. Using this idea, we developed a neighbor count measure that is composed of both a distance criterion and an angle criterion. A graphical schematic of this is shown in Figure 1. This is a more sophisticated version of the neighbor count used in our previous work.⁸ In this version, the directional approach of the label through the solvent is taken into account, as opposed to accounting for neighbors in all directions equally in the old neighbor count version. Two different versions of this neighbor count were developed: one that utilizes a low-resolution centroid representation of the protein in Rosetta (all of the backbone atoms are explicitly present, but the entire side-chain is represented as a single point referred to as a centroid) and a full-atom representation (all atoms explicitly defined). To calculate the neighbor count residue i (NeighborCount_i) in the centroid representation both the distance in Angstroms (r_ij) between the Cα of residue i and the CEN of residue j with j ≠ i and the angle in radians (θ_ij) enclosed by the CEN_j-Cα_i-CEN_i vectors were assessed. The full atom version, depicted in Figure 1A, is similar to the centroid version in that the CEN coordinates were replaced with the respective residue Cβ coordinates (or Hα in the case of glycine). The respective distance and angle were then used as functional inputs to a product of two sigmoidal functions, defined as D(r_ij) and A(θ_ij) respectively, to determine each neighboring residue’s overall contribution to the total neighbor count, NeighborCount_i (ranging from 0 to 1). Details regarding the definitions of D(r_ij) and A(θ_ij) can be found in Figures 1B and 1C respectively. Each product was then summed over all the residues in the protein to yield a total neighbor count for residue i. Functionally, this is represented in eq 1, where N is the total number of residues in the protein:

$$NeighborCoun{t}_i=\sum _{j\ne i}^{N}D\left(r_{ij}\right)A\left({\theta }_{ij}\right)=\sum _{j\ne i}^N\frac{1}{1+\exp \left(r_{ij}-9\right)}.\frac{1}{1+\exp \left(2\pi \left({\theta }_{ij}-\pi \right)\right)}$$ (1)

Figure 1.

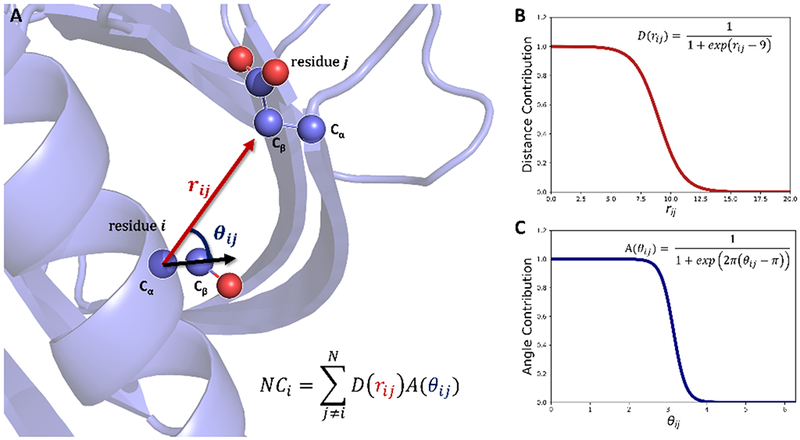
(A) Diagram of the “cone” neighbor count method using the full-atom definition. The neighbor count of residue i is defined as the product of the distance contribution (D(r_ij)) and the angle contribution (A(θ_ij)) summed over all residues j ≠ i. The distance r_ij is defined as the length of the vector between the Cα of residue j and the Cβ of residue j and the angle θ_ij is defined as the angle between the vector between the Cα of residue i and the Cβ of residue j and the vector between the Cα and Cβ of residue i. (B) Functional form of the distance contribution, D(r_ij). (C) Functional form of the angle contribution, A(θ_ij).

In order to calculate the neighbor counts, we developed the per_residue_solvent_exposure Rosetta pilot application. This application takes a PDB as input and calculates the neighbor count using eq 1. To examine the distribution of solvent exposure as a function of residue type, both the per-residue SASA and neighbor counts were calculated for each of the 6,165 proteins downloaded from the Protein Data Bank. The SASA calculations were performed using NACCESS.³⁵

Decoy Model Generation from the Benchmark Set

In order to test the effectiveness of covalent labeling in improving Rosetta tertiary structure prediction, decoy sets containing both low and high RMSD protein models were necessary. A total of 9,700 models were generated for each of the 20 benchmark set proteins using the following three methods: full-atom relaxation of the PDB (5 models), ab initio structure prediction (5,000 models) and threading (4,695 models).

Five models were generated by relaxing the PDB structures for each of the 20 proteins. The relaxation was performed with Rosetta using the Ref2015 score function.³⁶ The relax application within Rosetta provided a simple full-atom refinement that did not dramatically alter the backbone conformation of the protein.^{37, 38}

The 5,000 ab initio models per protein were generated using the standard Rosetta AbinitioRelax protocol.^39–44 The fragment files were generated using the Robetta webserver.⁴⁵ The fragment assembly stage is broken down into four separate stages that vary in the centroid-based score functions and the fragment size applied. The final full-atom refinement stage used the Ref2015 score function.³⁶

The 4,695 threaded models per protein were generated using RosettaCM.⁴⁶ Each of the 20 target protein sequences were threaded onto the tertiary structure of 4,695 template structures from the set of 6,165 proteins (only the proteins with a length greater than or equal to 90 residues were used for the threading). EMBOSS Needle, which uses the Needleman-Wunsch alignment algorithm, was used to generate the sequence alignments between the target protein sequence and each of the templates.⁴⁷ A gap open penalty of 10.0 and an end gap penalty of 10.0 were applied to the alignment in order to minimize the gaps in the sequence alignments. Following the standard RosettaCM protocol, each of the target sequences were threaded onto each of the template structures using the alignments and then the gaps were constructed using the Rosetta Hybridize Mover followed a full-atom relaxation.

covalent_labeling_cen and covalent_labeling_fa Score Terms

Two new Rosetta score terms, covalent_labeling_cen and covalent_labeling_fa, were developed to calculate the agreement between a model’s solvent exposure (evaluated as a neighbor count) and the corresponding native structure’s solvent exposure. The native structure was defined as the experimental structure of the protein as deposited in the PDB. The neighbor counts were evaluated using eq. 1 and calculations were performed in both a centroid and full atom representation of the structure. The need for two separate forms of the score term arose from Rosetta’s AbinitioRelax protocol. The protocol is divided into two primary stages: a low-resolution centroid fragment assembly stage and a high-resolution full atom refinement/relaxation. In order to use the score term in both stages, two separate forms were necessary. The centroid version of the score term was evaluated as shown in eq 2:

$$\text{covalent\_labeling\_cen=}\sum _i^{\#labeledresidues}\frac{1}{1+\exp \left(10\left({\left|diff\right|}_i-2\right)\right)}$$ (2)

where |diff|_i is the absolute difference of the neighbor count for residue i (calculated using a centroid representation) of the model and the corresponding input average centroid and full-atom native neighbor counts. Each labeled residue contributes a score ranging from −1 (perfect agreement between the model and experiment) and 0 (complete disagreement). The score as shown in eq. 2 is represented as the sum of the score contributions calculated as a sigmoidal function for the labeled residues. A tolerance neighbor count of +/− 2 was included to allow for experimental error. In other words, for values of 0 ≤ |diff|_i ≤ 2 a full per residue score value of −1 was assigned. The other score term, covalent_labeling_fa, was defined functionally identically to eq 2 with the only difference being that |diff|_i was evaluated using the full atom representation.

Summary of Validation Methods

In order to validate the ability of our new score terms to discriminate between low and high RMSD models, three different methods were used. The first was an evaluation of the performance (defined by the shape, discriminatory power, and funnel-like quality) of the score term (covalent_labeling_cen) itself, in the absence of any other Rosetta score terms. This involved calculating the size normalized covalent labeling score for all 9,700 benchmark decoy models. We refer to this method as the analysis of the “covalent labeling score distribution” throughout the remainder of this work. The second validation method was a rescoring of decoy models generated with Rosetta using covalent_labeling_fa. Unlike the previous method, this “rescoring” method results in a score that is a linear combination of the Rosetta Ref15 score and our newly developed covalent labeling score. Finally, the third validation method we employed was using the score term in conjunction with Rosetta to generate new models, which is referred to as “folding in the presence of covalent labeling”.

As part of the analysis of the covalent labeling score distribution, several different metrics were used to evaluate the performance of our new score terms, covalent_labeling_cen and covalent_labeling_fa. The simplest metric used was the RMSD of the best scoring model. If the score terms were able to accurately predict the native model, the best scoring model should have a low RMSD relative to the native structure. This metric corresponded to what is typically done when evaluating distributions generated using Rosetta. In practice, the native structure is unknown, so one way to differentiate between models is to compare their Rosetta score.

The second evaluation metric utilized was a goodness-of-energy-funnel metric, developed by Bhardwaj and co-workers, dubbed P_Near.⁴⁸ The value of P_Near is a single value that represents the overall “funnel-ness” of a Rosetta score vs. RMSD distribution. P_Near ranges from 0 (no funnel like character) to 1 (perfect funnel). It is defined as shown in eq 3.:

$$P_{Near}=\frac{{\sum }_{m=1}^N\exp \left(-\frac{RMS{D}_m^2}{{\lambda }^2}\right)\exp \left(-\frac{E_m}{k_{B}T}\right)}{{\sum }_{m=1}^N\exp \left(-\frac{E_m}{k_{B}T}\right)}$$ (3)

where N is the total number of models in the distribution and E_m and RMSD_m are the score and RMSD of model m, respectively. The two remaining parameters, λ and k_BT, represent how similar the RMSD of a model to the native to be considered native-like and the depth of the funnel, respectively. The values used for these parameters follow the conventions set forth by Bhardwaj and co-workers in their work developing this metric.⁴⁸ For all evaluations of P_Near, a value of 2.0 Å was used for λ. The value used for k_BT depended on the type of distribution being analyzed. For total Rosetta score vs. RMSD distributions (as seen in the rescoring and refolding validation tests), k_BT was assigned a value of 1.0. As part of the analysis of the covalent labeling score distributions, the normalized covalent_labeling_cen score (dividing the score by the total number of labeled residues) vs. RMSD distributions for the set of models were evaluated and k_BT was assigned an empirically determined value of 0.001, to account for the change in relative scale of the scores.

Residue Type Sets

To answer the question of which residue type exposures provided the most structural information for protein structure prediction, we broke down the set of 20 amino acid types into several subsets. The subsets are summarized in Figure 2. A total of six subsets were used for this study. The first consisted of all 20 amino acid types. This set represents the ideal scenario where information regarding the solvent exposure of every amino acid type could be utilized. The next two subsets consisted of the amino acid types that are typically labeled and analyzed with hydroxyl radical footprinting and DEPC respectively.^8–11 The hydroxyl radical (HRF) set contained the following amino acids: I, L, P, F, W, Y, E, and H. The DEPC set contained Y, H, K, S, T, and C. The fourth subset was made up of the amino acid types that are most commonly targeted in covalent labeling experiments.¹ This subset, which we denote the “common” subset, contained W, Y, D, E, R, H, K, and C. In order to experimentally label all of these amino acids, several different labeling reagents would have to be used. We generated the final two subsets ourselves. The “most varied” subset consisted of the eight amino acid types (A, L, V, F, W, Y, C, and M) that were identified during the neighbor count calculations of the 6,165 PDB structures. These amino acids exhibited the greatest variation (i.e. had wide neighbor count distributions; at least 50% of those residues had neighbor counts ranging from 15 to approximately 30 neighbors). The final subset was identified as being the most optimal subset of residue types based on their ability to discriminate between low and high RMSD models in our covalent labeling score distribution analysis. This “optimal” subset was composed of G, L, V, F, D, R, H, S, and T.

Figure 2.

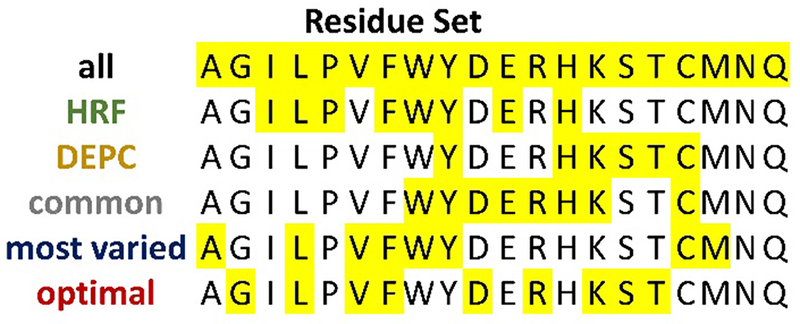
Amino acid types that comprise the different residue type sets.

To determine the subset of amino acids for the “optimal” type set, the size normalized version of covalent_labeling_cen was calculated for the 194,100 decoy models ((5,000 ab initio models + 4,695 threaded models + 5 relaxed native models) × 20 proteins) along with the RMSD for each model to its respective native. The normalized version was used so that the scores could be compared across the 20 proteins, regardless of their size. The residue types used to evaluate the scores were systematically varied and the value of P_Near was calculated for the resulting distributions. Starting with all of the combinations of pairs of amino acids as different subsets (190 total combinations), the covalent labeling score vs. RMSD distributions were generated and evaluated using P_Near. The top 5, based upon P_Near, combinations (GS, GY, GV, ER, and GR) were used as seeds for the various combinations of 3 amino acids. The top 5 combinations of 3 were used as seeds for combinations of 4, and so on. This process was continued until a subset of amino acids yielded a size-normalized covalent labeling score vs. RMSD distribution and P_Near that was comparable to the distribution of the set containing all 20 amino acids.

Incorporation of Experimental Noise

From a modeling standpoint, one of the main issues with data obtained from covalent labeling experiments is that it contains noise, as does all experimental data. In an ideal situation, every solvent exposed residue that could be labeled (i.e. that is not participating in any non-covalent interactions, and that is of the type that can be labeled with the given reagent) would be labeled and provide structural information. In practice, this rarely occurs, and thus solvent-exposed residues sometimes appear to be unlabeled. This can be thought of as an incomplete experimental sampling or false negative data points. The other type of experimental noise exists in the form of false positive data where buried residues appear to be labeled.

False Negative Data

In order to simulate false negative data (the noise due to incomplete sampling) and also to determine how many labeled data points are needed to differentiate between low and high RMSD models, different percentages of the total number of potential data points were removed from the total set of data points. For each of the 20 proteins, percentages ranging from 0-50% of the total number of residues that could be labeled were removed from the total set of residues. To determine which residues to remove from the data set, we utilized inverse transform sampling of the native neighbor count solvent exposed residue (centroid based neighbor count < 15) distribution. By doing this, we effectively simulated what occurs experimentally when residues that are solvent exposed provide ambiguous data or are not labeled and are thus not used for any further analysis. The resulting set of residues were used as simulated experimental inputs for the covalent labeling score distribution validation method. covalent_labeling_cen vs. RMSD distributions were generated and analyzed using the metrics described in the Summary of Validation Methods section. This was done for all of the residue type sets defined in the previous section. The maximum percentage of removed data points that demonstrated model discrimination that was comparable to the case of no removed points was identified.

False Positive Data

The other type of experimental noise examined was that of false positive or incorrect data points. These are residues that should not have been labeled due to low solvent exposure but were experimentally labeled. To determine the percentage of false positive data points that could be tolerated, a similar approach to the incorporation of false negative data was taken. Various percentages ranging from 0-25% of the total number of buried residues (neighbor count > 15) were selected using inverse transform sampling from the native neighbor count distribution for each protein. These residues were then assigned a new neighbor count obtained by performing inverse transform sampling on the neighbor count distribution ranging from a neighbor count of 0 to 15. This procedure simulated a buried residue providing incorrect labeling information suggesting that it should be solvent exposed. Along with the set of labeled data points determined after incorporating false negative data points, these false positive data points were used as covalent labeling inputs to validate the covalent labeling score distributions.

Rescoring of Rosetta ab initio Models

As the second test for evaluating the effectiveness of the covalent labeling based score term, the method of “rescoring” was used. Two separate sets of proteins were used for this validation: six of the proteins whose ab initio distribution contained sub 5 Å RMSD models and nine of the proteins whose threaded distributions contained sub 5 Å models. The rationale behind our decision to truncate the 20-protein set and only focus on six and nine proteins, respectively, with high quality models was that the covalent labeling score term should be able to distinguish between high quality models (RMSD ≤ 5Å) and low-quality models (RMSD ≥ 10Å). The covalent labeling score term was not designed to distinguish between two low quality models. For rescoring to be able to theoretically select a high-quality model, at least one of those had to be present in the set of models that were rescored. The six proteins selected from the ab initio set were PDB ID 1tpm, 2klx, 2nc2, 2y4q, 3iql, and 4omo. The nine proteins selected from the threaded set were the six from the ab initio with the addition of 1fgy, 2kr9, and 4k47.

For each model (5,000 total for the six ab initio proteins and 4,695 total for the nine threaded proteins), the covalent_labeling_fa score was evaluated using a simulated experimental input file containing the average neighbor counts (average of the centroid and full atom versions of the neighbor count as defined in eq 1) for 65% of the solvent exposed residues (randomly selected). Additionally, 10% of the buried residues (randomly selected) were included as false data points. Input files were created in triplicate for each of the residue type sets defined in Residue Type Sets. The resulting input files were used to calculate the covalent_labeling_fa score for each model and the score was added to the overall Rosetta Ref15 score with a weight of 6.0.

Generating Rosetta ab initio Models with covalent_labeling_cen and covalent_labeling_fa

In addition to rescoring existing models, a new set of models for each of the 20 proteins were generated using the standard Rosetta AbinitioRelax protocol with the addition of the two new score terms: covalent_labeling_cen and covalent_labeling_fa. The Rosetta AbinitioRelax protocol is divided into two main stages: a low-resolution fragment assembly stage where all backbone atoms are expressed explicitly with the side-chains represented as single spheres and a high-resolution full-atom refinement where the side-chain coordinates are explicitly accounted for. The centroid version of the score term was used in the fragment assembly stages of the protocol. A weight of 0.3 was assigned to covalent_labeling_cen in all five centroid scoring phases. The full-atom version was used only in the refinement/relaxation stage with a weight of 6.0. Input files were generated using the average neighbor counts (average between centroid and full atom neighbor counts per residue) including 65% of the solvent exposed residues (or 35% false negatives) and 10% of the buried residues (with false positive neighbor counts). Input files were generated in triplicate for the following residue type sets: all, common, and optimal. A total of 5,000 models were generated and scored with the Rosetta Ref15 score function plus covalent_labeling_fa for each protein using each of the triplicate input files. This resulted in a total ensemble of 15,000 models for each of the residue type sets. In addition, 15,000 models were generated using the standard Rosetta protocol as a control. In addition to using RMSD to quantify the accuracy of the predicted models, the fraction of correctly predicted contacts was calculated using a Python script with a distance threshold between Cβ atoms (Cα for Glycine) of 8Å.

Results and Discussion

Cone-Based Neighbor Count Provided a More Consistent, Computationally Inexpensive Measure of Solvent Exposure than SASA

In order to use the information from CL-based experiments to aid protein structure prediction, it is necessary to efficiently and accurately determine the per residue solvent exposure for a given protein model. The most common method for calculating residue solvent exposure is evaluating the residue SASA. However, we found in our previous work with HRF experimental data that the neighbor count provided a stronger correlation to experimentally derived protection factors and was less computationally expensive.⁸ Using the 6,165-protein set as a representative set of non-redundant protein subunit structures, we evaluated the solvent exposure for all residues in each protein using both SASA and a cone-based neighbor count, as defined in eq 1. The distributions of the SASA and a cone-based neighbor count for each amino acid type are shown in Figure S2. Larger neighbor counts or lower SASA values indicate a higher solvent exposure, as shown by the correlation in Figure S2 panel C. The overall solvent exposure trends per residue match expectations. The charged residues (D, E, R, K), which most commonly appear on the protein surface, do have among the highest solvent exposure. This trend is most pronounced in the SASA distribution and can also be seen with the neighbor count metric. The percentage of charged residues (D, E, R, and K) that have a neighbor count less than 15 were 79.6%, 82.1%, 75.2%, and 82.6%, respectively, indicating a relatively high solvent exposure. Indeed, the charged residues constituted four of the six most solvent exposed residue types, with the remaining two being N and Q. Based upon the overall distribution of the neighbor counts, a threshold of 15 was determined as a cutoff for differentiating between a residue being solvent exposed (neighbor count less than 15) or buried (neighbor count greater than 15).

Ultimately, we decided to use the neighbor count as the metric to define solvent exposure. The computational cost of calculating SASA would be too expensive to calculate for every residue at each step of the Rosetta AbinitioRelax protocol.^{33, 34} Using the neighbor count distributions as a guide, a set of residue types were selected that had the most even distribution of residues that were considered solvent exposed and buried. The residues selected were A, L, V, F, W, Y, C, and M. In the following, we are referring to this residue type set as the “most varied” type set. Our hypothesis was that labeling information on residues that had an equal likelihood of being solvent exposed and buried should provide the most guidance with regards to tertiary structure prediction.

In practice, when evaluating covalent labeling experiments, information is generally only used from the residues that are labeled. Data on protein residues that are not labeled (but are of the type of amino acid that can be labeled by the reagent being used) is generally not used to deduce protein structure. These unlabeled residues could either be buried within the protein and not exposed to solvent, or, the residues could be participating in some type of non-covalent interaction such as a salt bridge or hydrogen bond. Because it is not obvious how to interpret the lack of labeling in terms of the proteins structure, we decided to not include information from what could be considered buried residues based upon their neighbor counts. This decision was made to better simulate what is actually obtained from experiment. Any residue whose neighbor count was above the determined threshold of 15 was excluded from any further analysis.

Optimal Subset of Nine Amino Acid Types that Provided the Most Discriminatory Information for Structure Prediction

One of the primary questions that arises in conjunction with covalent labeling experiments for protein structure determination is which amino acid types should be labeled to obtain structural information. Ideally, all 20 residue types would be labeled. To test this presumption, we calculated the normalized covalent labeling score for each of 194,100 decoy models and calculated the resulting score versus RMSD distributions P_Near. The distributions for all of the investigated residue type sets can be found in Figure S3. An important observation from these distributions is that regardless of the residue type set used, the covalent labeling score was able to score poorly very high RMSD models (RMSD > 20Å). These poor-quality models did not agree with the residue exposure pattern of even a subset of the residues and could be easily discarded by the score term. The ideal case of using all 20 residue types exhibited a P_Near of 0.87 (as shown in both Figure S3 and Figure 3A). However, there is currently not a single reagent that can reliably label all protein side chains. Hence, either a single reagent that can label a limited number of residues can be selected with the hope that the residues that are labeled provide enough information or multiple reagents can be used to label a larger number of amino acid types. The most commonly labeled residues (W, Y, D, E, R, H, K, and C) that would require multiple reagents make up the “common” residue type set whose normalized covalent labeling distribution had a P_Near of 0.81. Thus, the discriminatory power of the covalent labeling score of the “common” residue type set was almost as high as that of the “all” residue type set. In order to obtain labeling information for all eight residues in the “common” residue type set, as few as four different labeling reagents could be used (for example: phenylglyoxal for arginine; EDC for aspartic and glutamic acids; DEPC for histidine, lysine, tyrosine, and cysteine; Koshland’s reagent for tryptophan).¹ Two of the residue type sets we examined, HRF and DEPC, both utilize a single reagent to label multiple residue types. HRF and DEPC gave P_Near values of 0.78 and 0.60, respectively. Although these were lower than those observed for “all” and “common”, the results are still encouraging given that both only require a single labeling reagent, which minimizes experimental labeling effort. The “common” and HRF residue type sets were almost as accurate as the ideal case of using all 20 residue types, but there is still room for improvement. The final residue type set that we identified as the “most varied” (A, L, V, F, W, Y, C, and M) provided a P_Near of 0.50. The “most varied” and DEPC residue sets performed the worst with the lowest P_Near. The results for the “most varied” set were surprising, since the residues in that set were selected solely based on their highly variable solvent exposure observed in trends from the Protein Data Bank. Upon further investigation, we found that these amino acid types only cover 36.2% of the average protein sequence.⁴⁹ This implies that the low sequence coverage of the “most varied” set outweighed the highly variable solvent exposure of its constituent residues.

Figure 3.

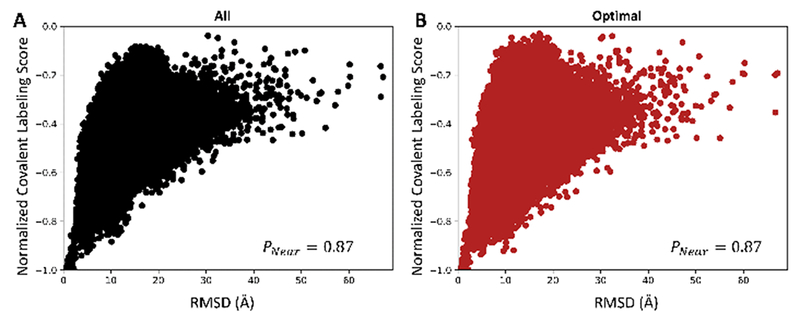
Normalized covalent labeling score distributions for the combined 194,100 decoy models. Panel (A) shows the distribution using all 20 amino acid types to calculate the normalized covalent_labeling_cen and panel (B) shows the “optimal” distribution containing only the residues G, R, K, L, T, F, S, V, and D.

Labeling experiments are costly and time-consuming, making it desirable to perform experiments with a labeling strategy optimized to maximize the amount of structural information obtained. Using computational methods, here we identified an optimized set of residue types, referred to as the “optimal” type set, that provided the best discriminatory behavior in terms of tertiary structure prediction. In order to identify this “optimal” residue type set, the covalent labeling score distribution was evaluated for all 20 residues types. This distribution, as shown in Figure 3A, exhibited a P_Near value of 0.87 and was used as the baseline. The goal of our analysis was to find the combination of the fewest residue types that gave a P_Near comparable to 0.87. By following the procedure described in Materials and Methods, an optimal subset of nine residue types was identified. The amino acid types that comprise this “optimal” subset were G, R, K, L, T, F, S, V, and D. The corresponding normalized covalent labeling score vs RMSD distribution is depicted in Figure 3B and had a P_Near of 0.87, identical to that of the baseline. With just nine amino acid types, we are able to generate a distribution that was just as funnel-like as the total set. The “optimal” type set is composed of charged (R, K, D), hydrophobic (L, F, V), polar uncharged (T, S) amino acid types and glycine (G). There are amino acid types in this set that represent the various different groups of amino acids. Because of this, we speculate that because of the wide spread of representation of amino acid types, this subset provided structural information on par with using all amino acid types. Based upon the average distribution of amino acid types, these nine amino acid types make up 56.2% of the average protein sequence.⁴⁹ For the 20 protein benchmark set used for this work, the respective amino acids made up 53.9% of the sequences. The fact that they cover over half of the average protein sequence makes these amino acid types very attractive for use in covalent labeling experiments. Out of this set of nine amino acid types, we identified two subsets of just four residues that provided the most information: 1) L, S, G, and R and 2) L, S, G, and V. These two subsets gave distributions with P_Near values of 0.70 and 0.64 respectively. The subset of five amino acid types composed of the union of these two subsets (L, S, G, R, V) had a distribution with a P_Near of 0.77. In addition to providing P_Near values close to that of the total optimal set, these five residues account for 35.3% of the average protein sequence coverage. These five amino acids are also among the top seven most prevalent amino acid types in the average proteins (the other two being A and Q). Because of this, we hypothesize that these core amino acids are the most useful to label for structure prediction.

In order to demonstrate that not all subsets of nine amino acids provided equally useful information, the same procedure was performed again, but this time taking the top five worst sets at each iterative step. The final result was a subset that had a P_Near of 0.03 and was comprised of the following amino acid types: C, I, F, M, W, P, V, A, and S. This distribution can be found in Figure S4. Clearly, the ability of subsets of nine amino acids varies widely in their abilities to produce funnel-like distributions.

Up to 35% of Solvent Exposed Residues can be Tolerated as False Negatives in Tertiary Structure Prediction

In an ideal scenario, all 20 amino acid types could be labeled and data was collected on every residue in the protein. This would provide the most information regarding protein tertiary structure. In practice, this rarely occurs and solvent-exposed residues frequently appear to be unlabeled. One of the main questions we sought to answer in this work was the question of how many unlabeled residues can be tolerated while still accurately differentiating between low and high RMSD protein models. To do this, a normalized covalent labeling score was calculated for the 194,100 decoy models. The normalized neighbor score was defined as the covalent_labeling_cen score divided by the total number of residues in the given protein. By normalizing the score in this way, the covalent_labeling_cen scores of the 20 different benchmark proteins could be compared to each other.

Starting with the “all” residue type set (containing all 20 amino acid types) and only using the residues that had a native neighbor count less than 15, a size normalized covalent labeling score distribution was generated. This distribution, shown in Figure S5A, represented the ideal baseline. A P_Near of 0.87 was calculated for this distribution, indicating a high-quality funnel. Sets of false negative residues were determined by identifying fractions of the solvent exposed residues starting at 0% and continuing until 50% at increments of 5%. These false negative data points were then removed from the set of labeled residues and P_Near values for the resulting distributions were calculated for each of the residue type sets. This process was repeated in triplicate due to the random element introduced in the selection of the removed residues and the results were averaged (as summarized in Table 1 and Figure S5B). As was expected, the P_Near values decreased as the number of false negative data points increased, indicating less funnel-like distributions. The “all” residue type set provided distributions with the best P_Near values at almost all percentages of residues removed and did not show a dramatic decrease in funnel-like quality. The other residue type sets showed more pronounced decreases in quality as larger percentages of solvent exposed residues were removed. The HRF and DEPC residue sets decreased in quality by changes in P_Near from 0.78 to 0.36 and 0.60 to 0.15, respectively, when comparing 0% to 50% of the solvent exposed residues being treated as false negatives. This indicated that these residue sets are less tolerable to false negative data points. On the other hand, the “optimal” type set only decreased by a P_Near of 0.15 (from 0.87 to 0.73) when increasing false negative data from 0% to 50%. Unlike HRF and DEPC, this demonstrated a stronger tolerance to false negatives, which is a necessary condition for selecting residue types to label. The “most varied” type set changed in P_Near from 0.50 to 0.11 when increasing the false negative percentage from 0% to 50%. This type set did not perform well in the absence of any false negative data and only got worse upon inclusion of the data. The “common” type set on the other hand only decreased in P_Near from 0.81 to 0.53. While this type set performed well in the absence of any false negative data it did exhibit a noticeable decline in discrimination power upon the addition of false negative points.

Table 1.

Average P_Near values for the normalized covalent labeling score versus RMSD distributions (in triplicate) for the 20 benchmark proteins at various percentages of false negative data points.

	% False Negative Data Points
Residue Type Set	0%	5%	10%	15%	20%	25%	30%	35%	40%	45%	50%
All	0.87	0.88	0.88	0.87	0.87	0.85	0.87	0.85	0.86	0.85	0.81
HRF	0.78	0.78	0.74	0.74	0.70	0.73	0.56	0.55	0.48	0.41	0.36
DEPC	0.60	0.61	0.56	0.53	0.48	0.42	0.41	0.37	0.33	0.18	0.15
Common	0.81	0.81	0.78	0.79	0.77	0.72	0.76	0.71	0.69	0.62	0.53
Most Varied	0.50	0.51	0.38	0.47	0.36	0.30	0.26	0.27	0.16	0.17	0.11
Optimal	0.87	0.87	0.87	0.85	0.86	0.84	0.83	0.81	0.80	0.75	0.73

In summary, we identified 35% of the solvent exposed residues removed and treated as false negatives, to be the maximum percentage that maintained sufficient funnel-likeness as seen in the “all”, “common” and “optimal” residue type sets. This suggests that protein structure prediction from covalent labeling data can tolerate up to 35% of false negative data points if suitable labels are used. This assumed level of false negative data agrees with the assumptions made by MacCallum and co-workers as part of their MELD method.⁵⁰ Additionally, there are multiple covalent labeling studies that reported false negative labeling rates below 35%.^{14, 18} Distributions of each of the residue type sets with 35% of the solvent exposed residues removed from the normalized covalent labeling score calculation can be found in Figure S5 panels C-H.

10% of Buried Residues can be Tolerated as False Positive Data Points

In addition to identifying the maximum number of tolerable false negative data point, we sought to identify how many incorrect data points could be tolerated. This was done by using 65% of the solvent exposed residues (assuming a false negative data rate of 35%) and then adding into this set a percentage (ranging from 0-25%) of “buried” residues with assigned incorrect neighbor counts smaller than 15. This generated a certain percentage of buried residues that were incorrectly labeled as exposed. The introduction of false positive data resulted in an overall decrease in the funnel-like quality of the distributions for all residue type sets, as shown in Table 2 and Figure S6 A. We observed more variability in the distributions as additional incorrect data was added. This was expected since the ability to discriminate between different quality models diminishes as the amount of false positive information is increased.

Table 2.

Average P_Near values for the normalized covalent labeling score versus RMSD distributions (in triplicate) for the 20 benchmark proteins with 35% false negatives at various percentages of false positives.

	% False Positive Data Points
Residue Type Set	0%	5%	10%	15%	20%	25%
All	0.85	0.86	0.61	0.56	0.58	0.57
HRF	0.51	0.40	0.43	0.20	0.25	0.23
DEPC	0.34	0.35	0.28	0.16	0.27	0.26
Common	0.73	0.71	0.62	0.62	0.68	0.61
Most Varied	0.25	0.18	0.06	0.03	0.06	0.09
Optimal	0.81	0.83	0.84	0.40	0.57	0.54

Because the distributions were generated using only 65% of the solvent exposed residues (as opposed to the ideal case of all solvent exposed residues), the best possible distribution was the “all” residue type set with 0% false positive residues which had an average P_Near of 0.85. Based on the average P_Near values calculated for the “all” residue type set, a major decrease in the funnel-like quality was observed between 5 and 10% of buried residues added as false positives (P_Near decreased from 0.86 to 0.61). The largest decrease in P_Near occurred between 10 and 15% for the “optimal” type set, with the P_Near dropping from 0.84 to 0.40. The values for P_Near when going from 0% to 10% false positive data points only decreased from 0.73 to 0.62 for “common”. The final two residue type sets decreased in P_Near from 0.51 to 0.43 for HRF, and from 0.34 to 0.28 for DEPC. Although the absolute decrease in P_Near for these two sets is the smallest among all of the sets, the relative decrease in P_Near for HRF and DEPC are significant. Based upon this, we concluded that an addition of up to 10% of a protein’s buried residues as false positives can be tolerated while still being able to differentiate between low and high RMSD models for most of the possible labeled residue types. The resulting normalized covalent labeling score distributions with 35% of the solvent exposed residues removed (false negative data) and 10% of the buried residues included as false positive data points are shown in Figures S6 B-G.

Rescoring Decoy Set with covalent_labeling_fa Significantly Improved RMSD of Best Scoring Models

In the previous sections we demonstrated that the covalent labeling score itself can effectively discriminate between low and high RMSD protein models, even in the presence of false positive and false negative data. In practice, the covalent labeling score will be used in conjunction with the entire Rosetta score function (Ref15) to assess protein models. Here we tested the ability of the covalent_labeling_fa score term to improve protein model selection by rescoring the ab initio and threaded decoy models (5,000 and 4,655 totals, respectively, per protein) with the new score term incorporated into the standard Ref15 Rosetta energy function.

Rescoring existing protein models does not change model RMSD values, but only reevaluates the relative scores of models. The desired goal of the covalent labeling score term was discrimination between low RMSD (sub 5 Å) and high RMSD (greater than 10 Å) structural models. It was, for example, not designed to differentiate between a 10 Å RMSD model and a 20 Å RMSD model. In both cases, the model the model should be considered inaccurate. As such, we did not rescore the decoy sets for all 20 proteins, but only the decoy sets of proteins that had models with sub 5 Å RMSD. Because of this, a total of six proteins (1tpm, 2klx, 2nc2, 2y4q, 3iql, and 4omo) were selected from the ab initio decoy sets and nine proteins (1fgy, 1tpm, 2klx, 2kr9, 2nc2, 2y4q, 3iql, 4k47, and 4omo) were selected from the threaded decoy sets to be rescored.

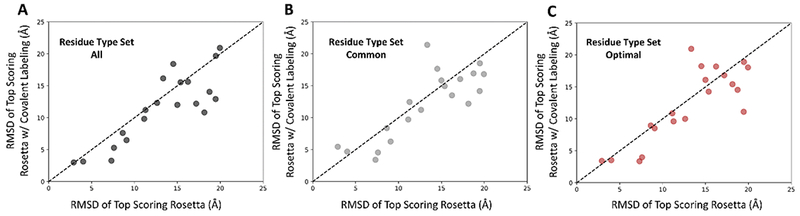
Input files for covalent_labeling_fa included the average neighbor counts (average between the centroid and full-atom version defined in eq 1) for 65% of the given proteins’ solvent exposed residues and 10% of the buried residues as false positives. The covalent_labeling_fa score was calculated for each of the decoy models and was subsequently weighted and added to the Ref15 score. This was done for weights ranging from 1.0 to 15.0. The resulting average differences between the RMSD of the top scoring models scored with Ref15 alone and with Ref15 plus covalent_labeling_fa are summarized in Figure 4A and 4C. At every weight tested, there was on average improvement, with the greatest improvement seen for the “all”, “optimal”, and “common” residue type sets. This was in agreement with our prior analysis on the discrimination power of the covalent labeling score term itself. We observed that as the weight increased, the degree of improvement initially also increased, eventually stabilizing starting around a weight of 4.0. From a weight of 4.0 to approximately 12.0, the results were fairly stable. The average RMSD improvements at each weight for each residue type set can be found in Table S2. Each data point in Figure 4A and 4C is shown as a pie chart representing the fraction of proteins (out of either six for ab initio or nine for threaded) that exhibited a top scoring model with either an improved or the same RMSD upon rescoring with covalent_labeling_fa. All of the fractions were close to 100%, indicating that the average improvement seen in the RMSDs did not come from a single protein at the expense of the others getting worse. The majority of the proteins demonstrated some degree of improvement. A weight of 6.0 was selected as the optimal weight for rescoring. This weight was the lowest weight that demonstrated a significant improvement in the top scoring RMSD for all of the residue type sets in both decoy protein sets. It also corresponded to the optimal weight we identified in our previous work using experimental HRF data.⁸ The average RMSD improvements for each of the residue type sets at a weight of 6.0 are depicted in Figure 4B and 4D. As expected from the analysis leading up to this point, the “all” and “optimal” type sets had the greatest RMSD improvement for the six ab initio proteins, with average improvements of 4.1 Å and 3.7 Å at the weight of 6.0, respectively. The average improvements for the threaded proteins were not as significant, but again the average improvements in the “all” and “optimal” sets were the greatest (1.8 Å and 1.3 Å, respectively). Overall, rescoring the ab initio decoy models demonstrated a greater improvement in the top scoring RMSD than the threaded models (average improvement of 4.1 Å for “all” type set as compared to 1.8 Å). In 6 of the 9 threaded model proteins used, the RMSD difference between the top scoring model and the lowest RMSD was less than 2 Å prior to rescoring, whereas only 1 of the 6 ab initio model proteins had a difference less than 2 Å. In other words, low RMSD threaded models frequently already scored well in Ref15 in the absence of covalent labeling data. Because of this, there was not nearly as much room for improvement for the threaded models as there was with the ab initio models. In summary, by rescoring the models with the incorporation of covalent labeling data, we were successful in significantly improving the quality of the models selected from the structure ensemble when combined with Ref15.

Figure 4.

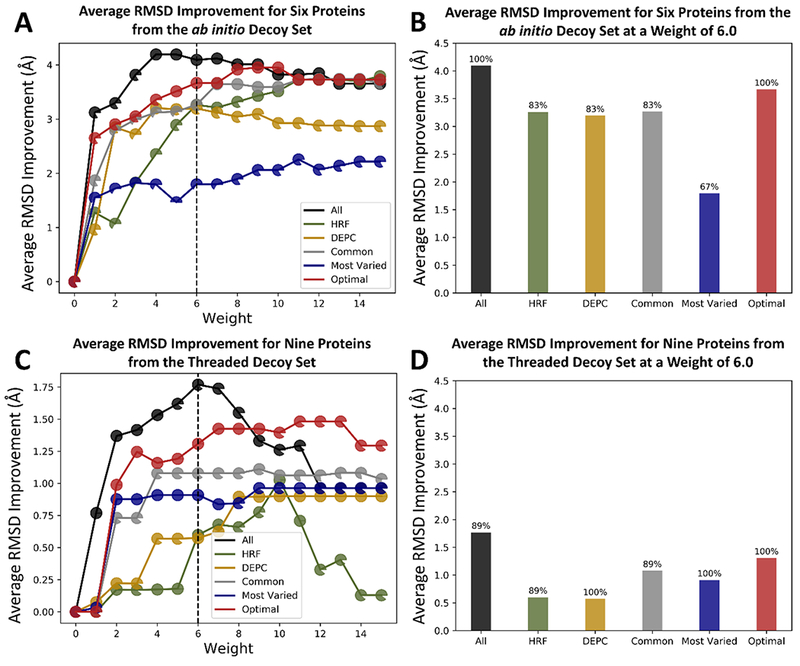
Plots of the average RMSD improvement for (A) the six ab initio proteins and (C) the nine threaded proteins with sub 5Å RMSD models before and after rescoring with covalent_labeling_fa at various weights for each of the residue type sets. Each data point is shown as a pie chart representing the fraction of proteins that exhibited either an improved or the same RMSD upon rescoring with covalent_labeling_fa. Panels (B) and (D) show the average RMSD improvement for the six ab initio and nine threaded proteins, respectively, at a weight of 6. The fraction of proteins that improved or stayed the same is represented as the percentage above each bar.

Generating Models with Rosetta and Covalent Labeling Data Resulted in Improvement of Best Scoring Model RMSDs

Above, we explored the ability of the covalent labeling score to improve protein model quality by rescoring existing protein models in conjunction with the entire Rosetta score function. Here, we tested the ability of a covalent labeling derived score term to accurately predict protein tertiary structure by using it to guide ab initio model generation. Rosetta’s AbinitioRelax protocol is broken into two major stages: a low-resolution fragment assembly stage and a high-resolution full-atom refinement/relaxation. Hence, two versions of the score term were necessary and required different weights for each stage. An optimized weight of 0.3 was used for covalent_labeling_cen in all five scoring phases of the fragment assembly stage. Similar to the weight selection process for the rescoring, the weight of 0.3 was empirically selected from a set of weights ranging from 0.01 to 40.0. The impact of the weight on the prediction results is shown in Figure S7. For the full-atom relaxation stage, a weight of 6.0 was used for covalent_labeling_fa. This weight was chosen based on the rescoring results. New models were generated for the “all”, “common”, and “optimal” residue type sets. In addition, sets of 15,000 models were generated using the standard Rosetta protocol as a control.

For each of the residue type sets, triplicate versions of the input neighbor counts were created. A total of 5,000 models were generated using each input file resulting in a total ensemble of 15,000 models per protein per residue type set. Summarized in Table 3 are the average (across all 20 proteins) minimum RMSDs of the ensemble of structures, the average RMSD of the top scoring model, and the average RMSD of the top 10 scoring models. On average, the “all” residue type set demonstrated the most improvement in all three categories. The top scoring RMSD model improved by an average of 1.6 Å, indicating that there is a positive effect of including information from covalent labeling. The minimum RMSD improved by 0.2 Å, while the average RMSD of the top 10 scoring models improved by 0.8 Å. Improvements of 0.8 Å and 0.9 Å in the RMSD of the top scoring model were seen for the “common” and “optimal” residue type sets, respectively. Additionally, for these two residue type sets, the average RMDS of the top 10 scoring models improved by 0.4 Å and 0.3 Å, respectively.

Table 3.

Average minimum RMSD, top scoring RMSD, and average RMSD of the top 10 scoring for the 20 benchmark proteins generated guided by covalent labeling as compared to those generated without.

	Minimum RMSD (Å)		Top Scoring RMSD (Å)		Avg. RMSD of Top 10 Scoring (Å)
Residue Type Set	Rosetta	Rosetta + CL	Rosetta	Rosetta + CL	Rosetta	Rosetta + CL
all	7.0	6.8	13.1	11.5	12.9	12.1
optimal	7.0	7.1	13.1	12.3	12.9	12.5
common	7.0	7.1	13.1	12.2	12.9	12.6

Furthermore, we investigated the RMSD improvement for each protein individually. The RMSD of the top scoring model for each protein was plotted by analyzing the ensemble of 15,000 models (as opposed to averaging the metrics across the 5,000 models from three trials) as shown in Figure 5. Out of the 20 proteins, 14 demonstrated an improvement in the top scoring RMSD for the all three residue type set. The specific protein RMSD improvements and fractions of correctly predicted contacts can be found in Table S3. The amount of improvement varied greatly among the 20 proteins and the three residue type sets used for the covalent labeling-guided folding. The magnitude of the improvement for the “all” residue type set ranged from a maximum improvement of 7.3 Å to a decrease in RMSD by 3.9 Å. The “common” and “optimal” residue type sets exhibited maximum improvements of 8.4 Å and 5.9 Å, respectively. Despite demonstrating improvements similar to the “all” set, both sets also showed occurrences of major decreases in RMSD (up to 7.7 Å decrease for “common” and 8.1 Å decrease for “optimal”). Although, not all of the 20 proteins improved, on average, there was a net positive increase in the quality of the top scoring models. The P_Near-driven optimization scheme employed when developing the covalent labeling score focused not just on the best scoring model but on all models, thus implicitly accounting for the overall ruggedness of the energy landscape. To account for other measures beyond model RMSD, we analyzed the fraction of correctly predicted contacts for each of the top scoring models. We observed the same general trend as observed for the RMSD. For example, 2n28 showed an improvement in RMSD for the “all” residue type set (from 17.2 to 12.2 Å) and it also demonstrated an increased fraction of correct contacts (from 0.94 to 0.97). In the cases where the RMSD did not improve, such as in 2kr9, the fraction of correct contacts remained unchanged indicating that the quality of the models did not deteriorate significantly despite decreases in RMSD. Four of the proteins that showed improvement with the “all” residue type set are presented in detail in Figure 6. Figure 6 shows the RMSD frequency distributions of the top 1% scoring models, the Rosetta score versus RMSD plots, and the top scoring models overlaid with the native structure, with Rosetta alone in teal and Rosetta plus covalent labeling in indigo. Out of all 20 proteins, 2n28 exhibited the greatest improvement in the overall quality of the models generated, as shown in the distributions, although the top scoring model still had a relatively high RMSD of 12.2 Å. The largest absolute improvement in the RMSD of the top scoring model was observed for 1jfm, with an improvement of 7.4 Å. 2klx and 4omo both improved in their top scoring models (improvements of 2.6 Å and 4.0 Å, respectively). The overall score versus RMSD plots also presented more funnel-like distributions. The score versus RMSD plots and RMSD frequency distributions for all 20 benchmark proteins generated using each of the three residue type sets (“all”, “common”, and “optimal”) can be found in Figures S8 – S13.

Figure 5.

The top scoring RMSD, minimum RMSD, and average RMSD of the top 10 scoring models for each of the 20 proteins calculated using Rosetta Ref15 alone (x-axis) and with covalent labeling (y-axis) for the (A) “all”, (B) “common”, and (C) “optimal” residue type sets.

Figure 6.

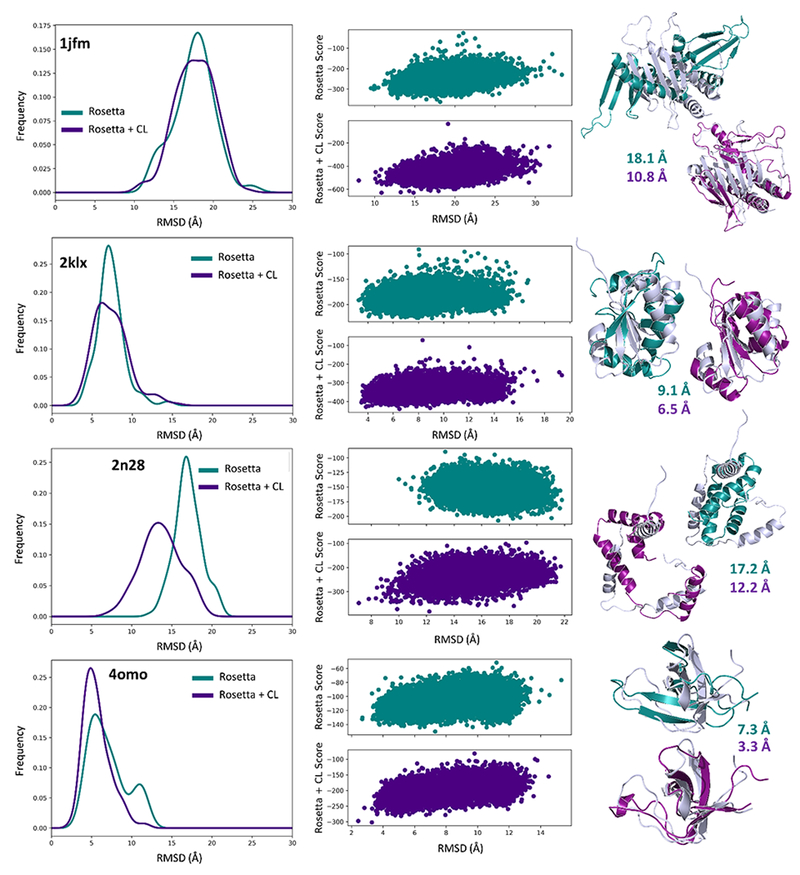
Distributions of the top 1% of scoring models (150 total) with (indigo) and without (teal) covalent labeling (“all” residue type set) for 1jfm, 2klx, 2n28, and 4omo. Also plotted are the Rosetta score versus RMSD to native distributions as well as the top scoring models (colored) compared to the native (gray).

Using covalent labeling information to guide protein structure prediction was successful. The average RMSD improvement appeared to be lower than for the model rescoring analysis. However, the rescoring results were obtained by averaging only six or nine proteins (for the ab initio and threaded proteins, respectively), as opposed to all 20. These subsets had a predisposition for proteins that worked well in Rosetta protein structure prediction. Additionally, rescoring existing models precludes observing improvements in the RMSD ranges sampled as was seen for 2n28 (see Figure 6). Rescoring is incapable of improving the best RMSD model generated. Finally, rescoring models requires increased computational and user effort. Additional, post processing steps are necessary whereas guided model generation only requires a single pre-protocol step of generating the necessary input file.

Conclusion

In this work, covalent labeling techniques were analyzed computationally to provide insight into what labeling data is needed to optimize tertiary protein structure prediction in Rosetta. Using the Protein Data Bank (PDB), statistics were gathered regarding various per residue solvent exposure metrics. Based on these results, a “cone”-based neighbor count metric was selected as the best predictor of solvent exposure. A benchmark set of 20 proteins randomly selected from the PDB was used to generate decoy models that were then scored with a normalized covalent labeling score derived from the neighbor counts. Various sets of residue types were evaluated as potential experimental labeling targets and an “optimal” set (composed of G, R, K, L, T, F, S, V, and D) was identified as being the subset that provided model discrimination as accurate as using all 20 residue types. The normalized covalent labeling score was then used to determine the false negative and false positive data point tolerance. Two new score terms were created, covalent_labeling_cen and covalent_labeling_fa, to be used within Rosetta’s AbinitioRelax protocol. Models generated with Rosetta were rescored with covalent_labeling_fa and a new set of models were generated by using the AbinitioRelax protocol guided by both new score terms. As a result, improvements in the model quality and accuracy were seen upon both rescoring and guiding model generation.

In conclusion, we would like to make several recommendations to those looking to perform covalent labeling experiments with the goal of tertiary structure prediction. Ideally, one would try to label as many residue types as possible, given that our results using all 20 residue types provided the strongest predictions. However, in the likely scenario that all 20 residue types could not be labeled, we would recommend using the set of eight residues that are most commonly labeled (W, Y, D, E, R, H, K, and C) or the set we identified as optimal (G, R, K, L, T, F, S, V, and D). For the most commonly labeled residues, a combination of the following reagents can be used to perform labeling experiments: phenylglyoxal, 1-ethyl-3-(3-dimethylaminopropyl) carbodiimide hydrochloride (EDC), diethylpyrocarbonate (DEPC), and 2-hydroxy-5-nitrobenzyl bromide (Koshland’s regent).¹ Seven out of the nine residue types in the “optimal” residue type set can be labeled using known labeling reagents: L and F with HRF, D with EDC, R with phenylglyoxal, and DEPC can be used to label K, S, and T. Additionally, HRF is theoretically capable of labeling G and V but those have a relatively low reactivity.^{1, 51} We hypothesize that the residue types identified as the “optimal” residue type set were identified based on their above-average sequence coverage in proteins. This set contains a core set of five amino acid types (L, G, R, V, and R) that contributed the most to the covalent labeling score’s ability to discriminate models. These five amino acid types are among the seven most abundant residue types. Thus, we believe that maximizing sequence coverage is a key factor when selecting residue types to label with the intention of tertiary structure prediction. We have also determined that for accurate protein structure prediction, there is a tolerance of about 35% of the maximum possible number of labeled residues (i.e. solvent exposed) that can be excluded as false negatives and 10% of residues inaccessible to labeling (i.e. buried) can be introduced as false positives. Encouragingly, these values seem to be in agreement with common levels of experimental error.

Future work will focus on improving the guidance capability of covalent labeling within Rosetta. We also plan on extending this methodology to quaternary structure and protein-ligand complexes.