Active superelasticity in three-dimensional epithelia of controlled shape

Abstract

Fundamental biological processes are carried out by curved epithelial sheets enclosing a pressurized lumen. How these sheets develop and withstand three-dimensional deformations has remained unclear. By combining measurements of epithelial tension and shape with theoretical modeling, here we show that epithelial sheets are active superelastic materials. We produce arrays of epithelial domes with controlled geometry. Quantification of luminal pressure and epithelial tension reveals a tensional plateau over several-fold areal strains. These extreme tissue strains are accommodated by highly heterogeneous cellular strains, in seeming contradiction with the measured tensional uniformity. This phenomenology is reminiscent of superelasticity, a behavior generally attributed to microscopic material instabilities in metal alloys. We show that this instability is triggered in epithelial cells by a stretch-induced dilution of the actin cortex and rescued by the intermediate filament network. Our study unveils a new type of mechanical behavior -active superelasticity- that enables epithelial sheets to sustain extreme stretching under constant tension.

Epithelial tissues enable key physiological functions, including morphogenesis, transport, secretion and absorption¹. To perform these functions, epithelia often adopt a three-dimensional architecture consisting of a curved cellular sheet that encloses a pressurized fluid-filled lumen^2,3. The loss of this three-dimensional architecture is associated with developmental defects, inflammatory conditions, and cancer^4,5.

The acquisition of a three-dimensional shape by epithelial sheets requires a tight control of cellular deformation, mechanical stress, and luminal pressure. How these mechanical variables are tuned together to sculpt three-dimensional epithelia is unknown, however, because current techniques to map epithelial mechanics are largely restricted to two-dimensional layers seeded on a flat substrate^6,7 or freely standing between cantilevers⁵. Here we report direct measurements of traction, tension, pressure and deformation in three-dimensional epithelial monolayers of controlled size and shape. These measurements establish that epithelial monolayers exhibit active superelasticity, an unanticipated mechanical behavior that enables extreme deformations at nearly constant tension.

Micropatterning epithelial domes

To shape epithelial monolayers in 3D, we used transmural pressure as morphogenetic driving force. We seeded MDCK cells on a soft PDMS substrate that was homogeneously coated with fibronectin except for micropatterned non-adhesive areas of precise geometry (Fig. 1a). A few hours after seeding, cells covered the adherent regions of the gel and, with time, they invaded the non-adherent areas^8,9. Since MDCK cells are known to actively pump osmolites in the apico-basal direction^10,11, we reasoned that fluid pressure should build-up in the interstitial space between cells and the impermeable substrate, leading to tissue delamination from the substrate in the non-adherent regions. In agreement with this rationale, we observed the spontaneous formation of multicellular epithelial domes closely following micropatterned shapes such as circles, rectangles and stars (Fig. 1b-e, Extended Data fig. 1a-d). In contrast to spontaneous doming by delamination^10,11, control of dome footprint gave us access to large variations in dome aspect ratio (Fig. 1c-e).

Figure 1. Generation of epithelial domes of controlled size and shape.

a, Scheme of the process of dome formation. b, Top view of an array of 15×15 epithelial domes (n=10). Scale bar, 1 mm. c-e, Confocal x-y, y-z and x-z sections of MDCK-LifeAct epithelial domes with a circular basal shape and varying spacing (n=10). Scale bar, 100 μm.

Measurement of dome mechanics

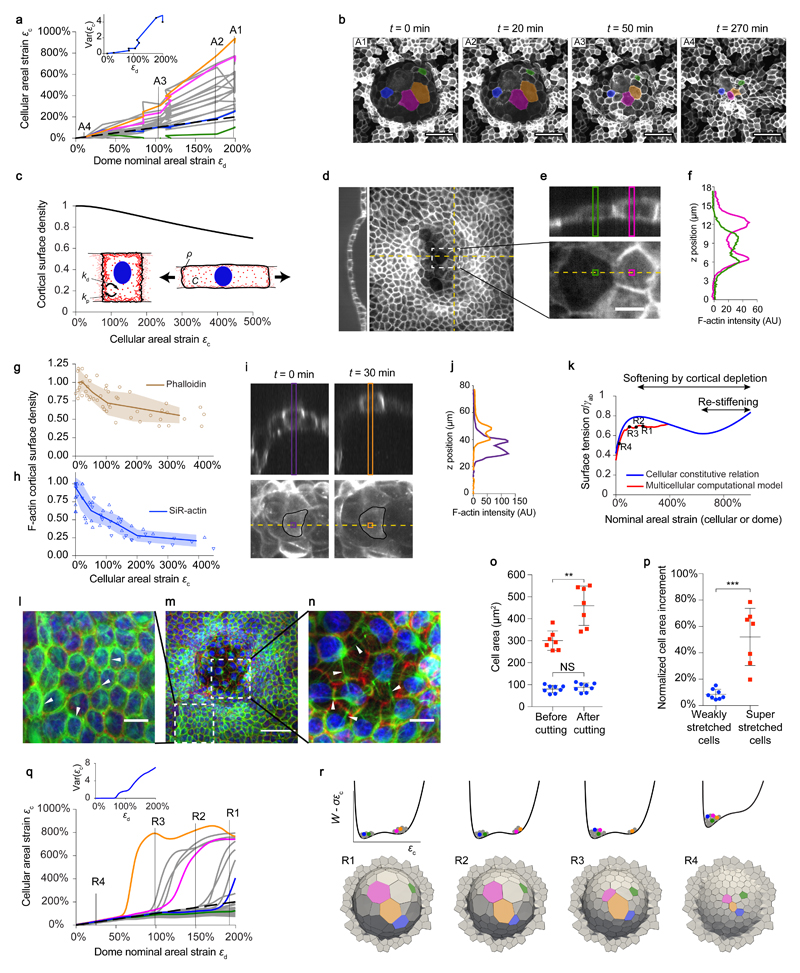
To measure dome mechanics, we focused on circular patterns and implemented 3D traction microscopy to determine the three components of tractions at the surface of the PDMS substrate (Fig. 2a,b). Tractions in adherent regions showed large fluctuations without a clear spatial pattern (Fig. 2b). By contrast, non-adherent areas exhibited systematic normal and nearly uniform negative tractions that indented the substrate. In a narrow annular region at the margin of the dome footprint, the traction vector consistently exhibited a positive normal component pulling the substrate upward. These observations, along with the morphology of the domes, established that the lumen was in a state of hydrostatic pressure, and that the free-standing part of the monolayer sustained tension to balance this pressure (Fig. 2a).

Figure 2. Measurement of luminal pressure and dome tension.

a, Scheme of dome mechanics. The lumen is under uniform pressure ΔP (black arrows) and the free-standing monolayer is under surface tension σ (yellow arrows). b, Traction vectors of a dome of MDCK-LifeAct cells. Top: lateral view. Bottom: 3D traction maps overlaid on a top view of the dome. Yellow arrows represent in-plane components and the color map represents the vertical component. Scale bar, 50 μm. Scale arrows, 150 Pa (representative of n=13 domes). c, d, Tractions exerted by MDCK-LifeAct cells before (control) and after 5 min incubation with 30 μM of Y-27632. Scale bar, 50 μm. Scale arrows, 75 Pa. e-g, Time evolution of dome volume and curvature (e), pressure (f) and tension (g) before (control) and after adding Y-27632. The time points corresponding to panels c and d are labelled in e-g (representative of n=3 domes).

We then wondered if we could map the tensional state of the dome, even though constituent cells did not directly generate tractions on the substrate. Epithelial domes very closely followed a spherical cap geometry (Fig. 2b), which implies that their surface tension σ was isotropic, uniform and obeyed Laplace’s law 2σ = R ΔP, where ΔP is the transmural pressure and R the radius of curvature of the dome (Supplementary note 1). This equation allowed us to measure epithelial tension of the domes since the normal traction in the non-adherent regions provides a direct readout of ΔP, and R could be measured from confocal stacks. We found tissue tensions in the mN/m range, similar to previous measurements in 2D monolayers^5,7.

To test the principle behind our tension measurement, we perturbed the system with Rho Kinase inhibitor Y-27632, known to reduce tissue tension. Because the epithelial barrier has finite permeability to water, the enclosed volume, and hence R, cannot change instantaneously upon this perturbation. Consequently, Laplace’s law requires tension relaxation be paralleled by a pressure drop. This prediction was confirmed by our measurements (Fig. 2c-g, Extended Data fig. 2a-c, Supplementary video 1). We also examined water transport by subjecting domes to hyper-osmotic shocks (Supplementary note 2). Volume dynamics under osmotic perturbations were consistent with a simple physical picture in which the epithelium behaves like a semi-permeable membrane actively pumping osmolites at nearly constant rate.

Constitutive relation between dome tension and strain

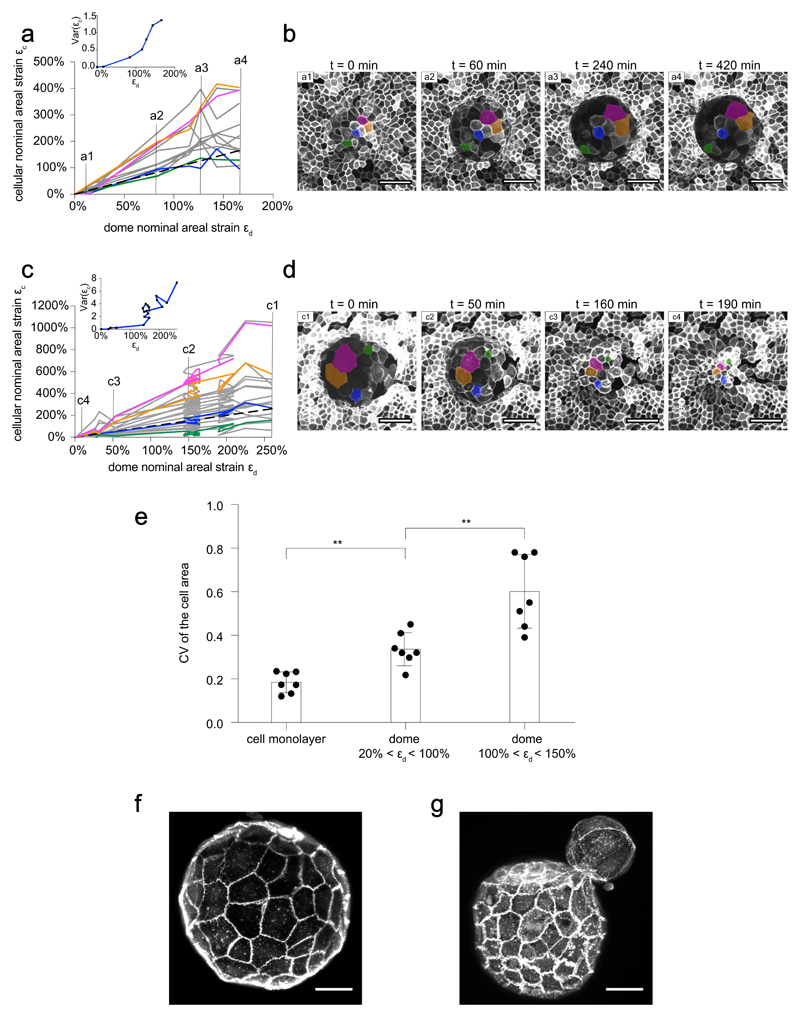
In the absence of pharmacological or osmotic perturbations and over timescales of hours, epithelial domes exhibited large volume fluctuations (Fig. 3a, Supplementary Video 2). These fluctuations involved periods of slow swelling and deswelling combined with sudden volume drops, often up to total dome collapse and subsequent rebirth. The magnitude of collapse events, presumably caused by localized disruptions of epithelial integrity, and the duration of swelling phases exhibited high variability (Fig. 3a-b and Extended Data fig. 3). During these spontaneous fluctuations, we tracked luminal pressure and dome geometry, which provided a measurement of epithelial tension at different degrees of swelling (Fig. 3c-e, Supplementary video 2). To examine these data, we represented tension in the free-standing tissue as a function of nominal areal strain of the dome ε_d = (h/a)², defined as the difference between the actual area of the dome π(h²+a²) and the area of the non-adhesive region π a², normalized by the latter (see Fig. 2b for a definition of h and a). All domes exhibited tensions of ~1 mN/m at small strains. At moderate strains (below 100%), tension progressively increased following a highly reproducible law. Beyond this point, tension exhibited larger scatter but reached a plateau at ~2 mN/m for areal strains up to 300% (Fig. 3e, Extended Data fig. 4a). The existence of this plateau is remarkable, as it reveals that epithelial domes maintain tensional homeostasis while undergoing deformations that change their area by up to 4-fold. Human epithelial colorectal adenocarcinoma cells (Caco-2) showed a plateau at similar tension but lower strain (Extended Data fig. 4b,c; see Supplementary Table 1 for a list of cell lines known to form domes).

Figure 3. Constitutive relation between dome tension and strain.

a, Spontaneous time evolution of tractions in a MDCK-LifeAct dome (y-z section). Scale bar, 50 μm. Scale arrows, 150 Pa. Regions in the dome monolayer lacking fluorescence signal correspond to unlabeled cells, not to gaps. b-d, Time evolution of spontaneous fluctuations in dome volume (b), pressure ΔP (c) and surface tension σ (d) (representative of n=9 domes). e, Surface tension in the free-standing sheet as a function of nominal areal strain of the dome ε_d (n = 9 domes, each sampled over various time points). The solid line and shaded area indicate mean ± SD obtained by binning the data (n = 14 points per bin). f, Normalized dome surface tension as a function of areal strain calculated with the vertex model. The dashed blue line represents the cellular constitutive relation in Eq. (1), based on a sheet of identical hexagonal cells under uniform strain (ε_d = ε_c). The solid red line is the result of a multicellular computational vertex model for a dome with an initial geometry obtained experimentally. Insets: computed dome shape at 50% and 300% nominal areal strain. g, Scheme of an idealized monolayer undergoing uniform equi-biaxial stretching, representing model assumptions leading to Eq(1).

A number of mechanisms could contribute to such tensional homeostasis, including directed¹² or accelerated¹³ cell division, junctional network rearrangements¹⁴, and cell exchange between domes and the adjacent adhered tissue. Visual examination of the domes showed that cell division and extrusion were rare (Supplementary videos 3 and 4). Moreover, the number of cells in the dome remained constant during the several-fold increases in dome area (Extended Data fig. 1f). We thus concluded that the tension-strain response of the tissue had to depend on the mechanics of cell stretching.

To understand the tension-strain relation of the dome monolayer, we developed a theoretical vertex model in 3D^15,16. The model is based on the well-established observation that the major determinant of epithelial cell mechanics is the actin cortex¹⁷. In the time-scales of our experiments, this thin cytoskeletal network behaves like a fluid gel, capable of developing contractile tension thanks to myosin motors¹⁷. In 3D vertex models, these active tensions act along lateral (γ_l) and apico-basal (γ_ab) faces of polyhedral cells (Fig. 3g, Supplementary note 3). Assuming constant cell volume⁵ and idealizing cells as regular hexagonal prisms of uniform thickness under uniform equibiaxial strain, this model predicts that the effective surface tension of the tissue depends on cellular areal strain ε_c as

$$\sigma ={\gamma }_{ab}-k\frac{{\gamma }_l}{{\left(1+{\epsilon }_c\right)}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}},$$ (1)

where k is a non-dimensional constant. Remarkably, this active constitutive relation recapitulates the initial increase in tension and the subsequent plateau at larger areal strain observed experimentally (Fig. 3e,f). The tendency of tension to plateau at large strains emerges naturally from the fact that the area of lateral faces decreases with cell stretching and, hence, tissue tension converges to apico-basal tension. To theoretically examine tissue stretching by dome swelling, we developed a computational version of the vertex model shown in Fig. 3g (Supplementary note 3). The tension-strain law evaluated using this computational approach closely matched the analytical constitutive relation in Eq. 1 (Fig. 3f).

Although this simple theoretical framework captured the tension-strain relationship, it missed a remarkable experimental feature; during swelling and de-swelling, we systematically observed cells that barely changed area coexisting with others that reached cellular areal strains up to 1000%, five times greater than the average dome strain (Fig. 4a,b, Extended Data fig. 5a-e, Supplementary videos 5, 6 and 7). This extreme strain heterogeneity is reminiscent of that observed in highly stretched epithelia in vivo such as the trophoblast in human and mouse blastocysts^18,19 (Extended Data fig. 5f,g). Both in epithelial domes and blastocysts, strain heterogeneity would seem in contradiction with their spherical shape, which implies tensional uniformity. Interestingly, heterogeneity of cellular strain increased sharply beyond areal strains of ~100% (Fig. 4a, Extended Data fig. 5). This strain threshold coincides with the onset of the tensional plateau and with the increase in the scatter of tissue tension (Fig. 3e).

Figure 4. Epithelial domes exhibit superelasticity.

a, Cell strain ε_c versus dome strain ε_d during a deflation event for a subset of cells. Colored curves correspond to cells labelled in b. Dashed line: ε_c = ε_d. Variance of ε_c versus ε_d (inset). b, MDCK-CAAX deflating dome. Scale bar, 50 μm. c, Model prediction of stretch-induced cortical dilution. d, Sum of intensity projection and confocal section of a dome stained for F-Actin (phalloidin). Scale bar, 50 μm. e, Zoom of representative cells. Scale bar, 10 μm. f, F-actin intensity along the bands marked in e. g, Normalized cortical F-Actin density (phalloidin) versus cellular strain (n=68 cells from 5 domes). h, Normalized cortical F-Actin density (SiR-actin) versus cellular strain during swelling (upward triangles) and deswelling (downward triangles). n=26 cells from 7 domes. Solid line and shaded area in (g) and (h) indicate mean ± SD. i, Live imaging of the cortex (SiR-actin) at two instants during swelling. j, Intensity profiles along bands shown in i. k, Non-monotonic cellular constitutive relation predicted by the vertex model, accounting for softening by cortical depletion and re-stiffening at extreme cellular strains (blue line). Dome tension-strain relationship for the multicellular computational version of the same model (red line). r1 to r4 correspond to panels shown in q and r. l-n, MDCK keratin-18 (green) dome stained for F-Actin (phalloidin, red), and nuclei (Hoechst, blue) (n=3). Scale bar in m, 50 μm. Scale bar in l,n, 10 μm. o,p, Changes in cell area following laser cuts of keratin bundles for weakly stretched (blue, n=8) and superstretched cells (red, n=7), represented as cell area before and after cuts (o, **P=0.0023; ns, non-significant, P=0.3282) and as normalized cell area increment (p, ***P<0.0003). Two-tailed Mann-Whitney tests. Mean ± SD. q, ε_c versus ε_d from the vertex model. Variance of ε_c versus ε_d (inset). r, (bottom) Computed geometries during deflation. (top) Effective potential energy landscape of active origin. Tilted by tissue tension, this landscape exhibits two wells at sufficiently high tension, corresponding to barely stretched and superstretched cellular states.

Epithelial domes exhibit superelastic behavior

Taken together, our experiments show that epithelial domes exhibit large reversible deformations and a tensional plateau during which superstretched constitutive elements coexist with barely stretched ones. These uncommon material features are defining hallmarks of superelasticity, a behavior observed in some inert materials such as Nickel-Titanium alloys²⁰. These materials are able to undergo large and reversible deformations at constant stress by heterogeneously switching between low- and high-strain phases²⁰. The microscopic trigger of superelasticity is a mechanical instability resulting from a decreasing branch in the stress-strain relation of the material (strain-softening). We reasoned that, in analogy with this behavior, cell monolayers might behave as superelastic materials by switching from barely stretched to superstretched cellular states at constant tension. To explore this possibility further, we sought a strain-softening mechanism that would explain the mechanical instability underlying the transition between low and high-strain phases.

Since cellular deformations increased the surface area of the actin cortex by over 3-fold, we hypothesized that strain-softening arose from the limited availability of cytoskeletal components²¹. Indeed, scarcity of cytoskeletal components could lead to stretch-induced cortical dilution, which could impair the ability of the cortex to generate active tension²² (Supplementary note 3). To test this hypothesis, we incorporated cortical dynamics to the 3D vertex model. As the main cortical component we focused on actin, although cortical depletion could also affect actin cross-likers, polymerization agents and molecular motors. In our model, cortical thickness (or equivalently cortical surface density ρ) is determined by a balance between polymerization at the plasma membrane and depolymerization in the bulk of the actin gel²³. If the availability of cytoskeleton components ready for polymerization is infinite, this model predicts that cortical density ρ and hence cortical tension γ are constant and independent of strain, leading to Eq. 1. If free cytoskeleton components are limited, however, the model predicts a progressive depletion of cortical density ρ with cellular areal strain, and hence strain-softening when the cortex becomes sufficiently thin²² (Fig. 4c). To test this physical picture, we measured cortical surface density ρ in cells located at the apex of fixed domes, and represented it as function of cell strain ε_c. These experiments showed that superstretched cells systematically exhibited less dense cortices (Fig. 4d-g, Extended Data fig. 6). Moreover, live imaging of cells labelled with SiR-actin showed that the actin cortex became progressively and reversibly diluted with cell stretching (Fig. 4h-j, Supplementary Video 8).

We exogenously interfered with cell-cell junctions and the actin cytoskeleton (Extended Data fig.2, Extended Data fig.7). Notably, we locally triggered actin depolymerization using a photo-activatable derivative of cytochalasin D. Upon activation, targeted cells increased their area without noticeable changes in the overall shape of the dome (Extended Data fig. 8, Supplementary Video 9), indicating that cortical dilution is sufficient to cause large increases in cell area. Taken together, these results are consistent with our hypothesis that cortical dilution underlies cellular superstretching.

Besides strain-softening, superelasticity also requires re-stiffening at large strains to confine the high-strain phase. Without such mechanism, the first cell reaching the softening regime would easily deform further, relaxing neighboring cells and eventually localizing deformation unboundedly²⁴ (Supplementary note 3, Supplementary Video 10). Multiple mechanisms could stiffen cells subjected to extreme stretching, including exhaustion of the plasma membrane reservoir²⁵, crowding of adhesion molecules in shrinking cell-cell adhesions²⁶, confinement of the nucleus between tensed cortices, or load transfer to the otherwise relaxed intermediate filament cytoskeleton⁵. Our experiments do not rule out any of these possibilities but they support the latter, as intermediate filaments in superstretched cells appeared unusually straight, suggesting load bearing (Fig. 4l-n, Extended Data fig. 9). To further test this mechanism, we laser-ablated keratin-18 filaments. In weakly stretched cells, laser ablation did not induce changes in cell area. By contrast, laser ablation in superstretched cells resulted in a rapid increase in cell area, indicating that intermediate filaments in superstretched cells, but not in relaxed cells, bear tension (Fig. 4o,p, Extended Data fig. 10). By introducing re-stiffening at large strains into our computational vertex model, we were able to recapitulate our most salient experimental observations (Supplementary Videos 11,12). At low levels of dome stretching, tissue tension increased with strain and cellular strain heterogeneity was low (Fig. 4k,q,r). By contrast, at high levels of stretching, the domes reached a tensional plateau and cellular strain heterogeneity rose sharply. Thus, strain-softening by stretch-induced depletion of cortical components followed by re-stiffening at extreme stretches configure an effective bistable energy landscape of active origin that explains the emergence of a stable high-strain phase of superstretched cells under sufficiently large tension (Fig. 4r and Supplementary note 3).

Active superelasticity provides a mechanism for epithelial tissues to undergo extreme and reversible deformations at nearly constant tension by progressive switching of individual cells to a superstretched state. Because the underlying subcellular mechanisms are generic, our study suggests a broad applicability in vivo. For example, epithelial superelasticity may mediate the spreading of superstretched extraembryonic tissues and their subsequent rapid compaction²⁷. Active superelasticity may also enable extreme cellular strains in the trophectoderm during swelling and hatching of mammalian blastocysts^18,19. Besides providing a framework to understand epithelial mechanics and morphogenesis in vivo, the material laws established here set the stage for a rational manipulation of cell monolayers in organoids and organ-on-a-chip technologies²⁸.

Methods

Fabrication of soft silicone gels (soft PDMS)

Soft elastomeric silicone gels were prepared using a protocol based on previous publications^29–32. Briefly, a silicone elastomer was synthesized by mixing a 1:1 weight ratio of CY52-276A and CY52-276B polydimethylsiloxane (Dow Corning Toray). After degassing for 5 min, the gel was spin-coated on glass bottom dishes (35 mm, No. 0 coverslip thickness, Mattek) for 90 s at 400 rpm. The samples were then cured at 80 °C for 1 h. The substrates were kept in a clean, dust-free and dry environment and they were always used before 4 weeks from fabrication.

Coating the soft PDMS substrate with fluorescent beads

After curing, the soft PDMS was treated with APTES ((3-Aminopropyl)triethoxysilane, Sigma-Aldrich, cat. No. A3648) diluted at 5% in absolute ethanol for 3 min, rinsed 3 times with ethanol 96%, and dried in the oven for 30 min at 60 °C. Samples were incubated for 5 min with a filtered (220 nm) and sonicated solution of 200-nm-diameter red fluorescent carboxylate-modified beads (FluoSpheres, Invitrogen) in sodium tetraborate (3.8 mg/mL, Sigma-Aldrich), boric acid (5 mg/mL, Sigma-Aldrich) and 1-ethyl-3-(3-dimethylaminopropyl)carbodiimide (EDC, 0.1 mg/mL, Sigma-Aldrich), as described in Style et al²⁹. Next, gels were rinsed 3 times with type-1 water and dried in the oven for 15 min at 60 °C. Beads were passivated by incubating the samples with tris-buffered saline (TBS, Sigma-Aldrich) solution for 20 min at room temperature. Finally, substrates were rinsed again 3 times with type-1 water and dried in the oven for 15 min at 60 °C.

Soft PDMS stiffness measurements

Gel stiffness was measured by indenting the gel with a large metal sphere (diameter, 1000 μm) of known mass. The indentation caused by the weight of the sphere was determined using confocal microscopy. From the measured indentation and sphere mass, we obtained Young’s modulus by applying Hertz theory corrected for the finite thickness of the gel³³. We found a Young’s Modulus of 2.9± 0.5 kPa (mean ±SD, n=6), in good agreement with published data^{29–32,34,35}.

Cell patterning on soft PDMS

PDMS patterning stamps were incubated with a fibronectin solution at 40 μg/mL (Fibronectin from human plasma, Sigma-Aldrich) for 1 h. Next, the protein was transferred to Poly Vinyl Alcohol (PVA, Sigma-Aldrich) membranes which were then placed in contact with the gel surface for 1 h. Membranes were dissolved and the surface was passivated at the same time using Pluronic F127 (Sigma-Aldrich) 0.2% w/v overnight at 4 °C. Afterwards, the soft silicone gels were washed with Phosphate-Buffered Saline (PBS, Sigma-Aldrich) and incubated with cell culture medium for 30 min. For cell seeding, the culture medium was removed and a 70 μl drop containing ~150,000 cells was placed on the soft PDMS. 50 min after seeding, the unattached cells were washed away using PBS and more medium was added. Cells were seeded at least 48 h before experiments.

PDMS patterning stamps

Polydimethylsiloxane (PDMS, Sylgard, Dow Corning) stamps for micropatterning were fabricated. Briefly, SU8-50 masters containing cylinders of 80 μm or 100 μm in diameter were raised using conventional photolithography. Uncured PDMS was poured on the masters and cured for 2 h at 65 °C. PDMS was then peeled off from the master and kept at room temperature in a clean and dust-free environment until use.

3D traction microscopy

3D traction forces were computed using traction microscopy with finite gel thickness^36,37. To account for both geometrical and material nonlinearities, finite element method (FEM) solution was implemented. Confocal stacks of the fluorescent beads covering the gel surface were taken with z-step = 0.3 μm and total depth of 15 μm. A 3D displacement field of the gel’s top layer between any experimental time point and its relative reference image (obtained after cell trypsinization) were computed using home-made particle imaging velocimetry software based on an iterative algorithm with a dynamic interrogation window size and implementing convergence criteria based on image intensity as described in previous publications³⁸. Results for the normal traction inside the dome were compared to analytical solutions for a liquid droplet over an elastic substrate with finite thickness^39–42.

Cell culture

Madin Darby canine kidney (MDCK) strain II and human epithelial colorectal adenocarcinoma (Caco-2) were used. To visualize specific cell structures the following stable fluorescent cell lines were used: MDCK expressing expressing LifeAct-GFP (MDCK-LifeAct) to visualize the actin cytoskeleton, MDCK expressing CIBN-GFP-CAAX to visualize the plasma membrane (MDCK-CAAX), MDCK expressing keratin-18-GFP (MDCK-K18) to visualize intermediate filaments. All MDCK lines were cultured in minimum essential media with Earle’s Salts and L-glutamine (Gibco) supplemented with 10% v/v fetal bovine serum (FBS; Gibco), 100 μg/ml penicillin and 100 μg/ml streptomycin. Selection antibiotic geneticin (ThermoFisher Scientific) was added at 0.5 mg/ml to LifeAct stable cell lines. Cells were maintained at 37 °C in a humidified atmosphere with 5% CO₂. Live imaging of F-actin was performed by incubating cells (12 h, 100 nM) using Live Cell Fluorogenic F-actin Labelling Probe (SiR-actin, Spirochrome). Caco-2 were imaged using Bodipy FL C16 dye (1 μM, 1h incubation, Thermo Fisher Scientific). MDCK-LifeAct cells were obtained from Prof Benoit Ladoux's lab. MDCK keratin-18-GFP cells were obtained from G. Charras lab. MDCK-CAAX were obtained by viral infection of CIBN-GFP-CAAX. CACO-2 cells were bought at Sigma Aldrich (86010202). Cell lines tested negative for mycoplasma contamination. All MDCK cell lines were authenticated by providing laboratories. CACO-2 cells were authenticated by the provider (Sigma Aldrich, from the ECACC).

Pharmacological interventions and osmotic shocks

To perturb actomyosin contractility cells were treated with Rho Kinase inhibitor Y-27632 (InSolution™ Calbiochem, Merck-Millipore, 30 μM, 5 min incubation). To inhibit ARP2/3 complex cells were treated with CK666 (Sigma Aldrich, 100 μM, 1 h incubation). To perturb the osmolarity, D-mannitol (Sigma-Aldrich, final concentration 100 mM) was added to the medium. To weaken cell-cell junctions EGTA (Sigma Aldrich, final concentration 2 mM, 30 min) was added to the medium.

Cell immunofluorescence

MDCK cells were fixed with 4% paraformaldehyde in PBS for 10 min at room temperature and permeabilized using 0.1% Triton X100 (Sigma-Aldrich) in PBS for 10 min at room temperature. Cells were blocked in 1% Bovine Serum Albumin (BSA, Sigma-Aldrich) in PBS for 1 h (at room temperature). Phalloidin (Alexa Fluor™ 555 Phalloidin, ThermoFisher Scientific) was then added at 1:1000 dilution in PBS and incubated for 30 min at room temperature. To identify nuclei, cells were then incubated for 10 min in a Hoechst solution (Hoechst® 33342, ThermoFisher Scientific) at 1:2500 dilution in PBS. Images were acquired with a Spinning Disk confocal microscope using a Nikon 60x oil 1.4 Numerical Aperture (NA) lens.

Time-lapse microscopy

Multidimensional acquisition for traction force measurements was performed using an inverted Nikon microscope with a spinning disk confocal unit (CSU-W1, Yokogawa), Zyla sCMOS camera (Andor, image size 2,048 x 2,048 pixels) using a Nikon 40× 0.75 NA air lens. The microscope was equipped with temperature control and CO₂ control, using Andor iQ3 or Micro-Manager software⁴³.

Laser ablation

The set-up used is described in Colombelli et al⁴⁴. Briefly, MDCK keratin-18-GFP cells were cultured on thin PDMS micropatterned substrates and allowed to form domes. We then used a sub-nanosecond UV pulsed laser to ablate individual filament bundles in weakly-stretched and superstretched cells. Immediately after ablation we monitored the time evolution of keratin filaments and we obtained bright field images of the domes to measure cell area. Experiments were performed at 37 °C and 5% CO₂.

Photoactivatable Cytochalasin D

We used a phototriggerable derivative of Cytochalasin D (CytoD) that includes a nitroveratryloxycarbonyl (Nvoc) photoremovable group located at the hydroxyl group at C7 of CytoD. Attachment of the chromophore renders CytoD temporarily inactive. Upon light exposure, CytoD becomes active and causes local depolymerization of the actin cytoskeleton. For experiments, MDCK-CAAX domes were incubated with SiR-actin to visualize the cortical cytoskeleton. Individual cells were illuminated with a 405nm laser to activate CytoD. After the pulse, the cell area and actin cytoskeleton were visualized using time lapse microscopy (63× oil, Zeiss LSM 880).

Image analysis

ImageJ/Fiji software was used to perform the image analysis⁴⁵. The pairwise stitching plugin was used to create 3D montages, the maximum intensity z-projection and the sum slices z-projection were used where appropriate. Actual cell areas were computed from z-projections using the methodology described in Supplementary note 4.

Code availability

Matlab analysis procedures can be made available upon request to the corresponding author.

Data availability

The data that support the findings of this study are available from the corresponding author on reasonable request.

Animals

Animal care and experiments were carried out according to protocols approved by the Ethics Committee on Animal Research of the Science Park of Barcelona (PCB), Spain (Protocol number 7436). Outbred B6CBAF1/JRj mice (male and females of 5-6 weeks of age) were obtained from Janvier Labs. Mice were kept in a 12 h light/dark cycle (lights on 7:00 a.m.-7 p.m.) with ad libitum access to food and water.

Embryo collection and in vitro culture

For embryo collection, superovulation was induced in B6CBAF1/JRj females by intraperitoneal injection of 7.5 I.U. of pregnant mare serum gonadotropin (PMSG) followed, after 48h, by 7.5 I.U. of human chorionic gonadotropin (hCG). Superovulated females were then paired with male mice, and subsequently euthanized by cervical dislocation 20 h after hCG injection. Then, one-cell stage embryos (zygotes) were collected from the excised oviducts into medium containing 0.1% (w/v) hyaluronidase (Sigma) to remove cumulus cells under a dissection microscope. Recovered zygotes were cultured in micro-droplets of culture medium covered with mineral oil at 37°C and 5% CO₂ until the blastocyst stage. No randomization nor blinding were performed as experiments did not involve comparisons between groups. Experiments were reproduced four times.

Blastocyst immunofluorescence

Blastocysts at different degrees of development were fixed with 4% paraformaldehyde (PFA) (Aname) for 20 min at room temperature (RT). Then, fixed blastocysts were washed three times with PBS containing 1% bovine serum albumin (Sigma), 2% goat serum (Sigma) and 0.01% Triton X-100 (Sigma), referred as blocking buffer. Next, blastocysts were permeabilized with 2.5% Triton X-100 (Sigma) in PBS for 30 min at RT and subsequently washed three times with blocking buffer. Blastocysts were incubated overnight at 4°C in anti-E-Cadherin primary antibody (610181, BD Biosciences) diluted 1:50 in blocking buffer. The following day, blastocysts were washed three times with blocking buffer and incubated for 90 min at 37°C in Alexa Fluor (A) 488-conjugated secondary antibody (A21202, Thermo Fisher) diluted 1:200 in blocking buffer. Nuclei were counterstained with DAPI (D1306, Life Technologies) for 30 min. Image acquisition was performed in a SP5 Leica microscope or a Zeiss LSM780 confocal microscope using a plan-apochromat 40x/ oil DIC M27 objective.

Extended Data

Extended Data figure 1. The number of cells in the domes does not change significantly in time.

a-c, Confocal x-y, y-z and x-z sections of domes with rectangular basal shapes and varying size. MDCK-CAAX cells. Scale bar, 100 μm (representative of n=3 micropatterned substrates). d, Time evolution (0, 60 and 120 min) of a representative dome with a star-shaped footprint. The patterned footprint (yellow) was obtained from images of the fibrinogen-labelled substrate. Each row shows a different z-plane (labelled by doted yellow lines in the x-y profiles in e (representative of n=3 micropatterned substrates). Scale bar, 50 μm. e, Time evolution (0, 60, 120 min) of the same star-shaped dome showing the rare delamination of a single cell (red rectangle) at one tip of the star. Images are maximum intensity projections with confocal x-z and y-z sections along the yellow dashed lines (representative of n=3 micropatterned substrates). Scale bar, 50 μm. f, Quantification of the number of cells in circular domes at two time points 12 h apart (n=4 domes). ns, not significant (P = 0.4571), two-tailed Mann-Whitney test. Data shown as mean ± SD.

Extended Data figure 2. Dome response to inhibition of tension and weakening of cell-cell adhesion.

a, Time evolution of surface tension and volume of a representative dome in response to Y27632 (30 μM, added at t = 0 min). b, Cellular areal strain ε_c as a function of dome nominal areal strain ε_d during dome swelling. Only a subset of cells is represented and most cells with ε_c < ε_d have been omitted for clarity. Colored lines represent the cells labelled in c. Dashed line represents the relation ε_c = ε_d. The inset represents the variance of ε_c within the dome as a function of ε_d. c, Maximum intensity projection and x-z and y-z confocal sections of an epithelial dome of MDCK-CAAX cells before (-1 min) and after (12 min, 26 min) addition of Y27632 (30 μM, added at t = 0 min). The time evolution of colored cells is depicted in b using the same color code. Scale bars, 50 μm. Data are representative of n=3 experiments. d, Maximum intensity projection and corresponding x-z and y-z profiles showing the collapse of a MDCK-CAAX dome after treatment with EGTA 2mM (30 min and 35 min after EGTA addition). Data representative of n=3 experiments. Scale bar, 50 μm. e, After dome collapse, gaps (red arrowheads) were apparent at tricellular junctions. Scale bar, 10 μm.

Extended Data figure 3. Dome volume dynamics during spontaneous fluctuations.

a, c, Time evolution of the dome volume in experiments that last 12 h and 6 h respectively. Cells are MDCK-LifeAct. b, d, Confocal x-z sections of domes during these experiments. Data representative of n=10 experiments. Scale bars, 50 μm.

Extended Data figure 4. Tension-strain relations in MDCK-CAAX and Caco2 cells.

a, Relation between surface tension and areal strain for MDCK-CAAX cells. Data include measurements at different time points from n = 9 domes. The tension/strain relation is qualitatively similar to the one obtained for MDCK-LifeAct cells (Fig. 3e), with small quantitative differences. The solid line and shaded area indicate the mean ± SD obtained by binning the data (n = 14 points per bin). b, Image of a representative Caco2 cell dome labelled with Bodipy FL C16 dye (n = 3 micropatterned substrates). (Confocal x-y, x-z and y-z sections). Scale bar, 50 μm. c, Relation between surface tension and areal strain for Caco2 cells. Data include measurements at different time points from n = 6 domes. Caco2 cells show a tensional plateau throughout the probed strain range. The solid line and shaded area indicate the mean ± SD obtained by binning the data (n = 10 points per bin).

Extended Data figure 5. Dome cells exhibit large strain heterogeneity.

a, Cellular areal strain ε_c as a function of dome nominal areal strain ε_d during dome swelling. Only a subset of cells is represented and most cells with ε_c < ε_d have been omitted for clarity. Colored lines represent the cells labelled in b. Dashed line represents the relation ε_c = ε_d. The inset represents the variance of ε_c within the dome as a function of ε_d. b, Maximum intensity projection of an epithelial dome of MDCK-CAAX cells at 4 different time-points of the swelling event described in a. The time evolution of colored cells is depicted in a using the same color code. Scale bars, 50 μm. c and d represent the same as a and b for a different dome of MDCK-CAAX cells during slow deflation. e, Coefficient of variation (CV, defined as standard deviation divided by mean) of MDCK-CAAX cells in a 2D adherent cell monolayer, in weakly inflated domes (20%-100% areal strain), and in highly inflated domes (100%-150%). The coefficient of variation is a non-dimensional indicator of heterogeneity. The CV was calculated by measuring area of 10 cells in n = 7 cell monolayers, n = 7 weakly inflated domes, and n = 7 highly inflated domes (**P= 0.0041, **P=0.0041 from left to right, two-tailed Mann-Whitney test). Data are shown as mean ± SD. f, g, Mouse blastocysts (E-cadherin labelled) exhibiting cell area heterogeneity in the trophectoderm, particularly during hatching (g) (n=4). Scale bars, 25 μm.

Extended Data figure 6. Superstretched cells display lower F-Actin cortical surface density.

a-f, Sum of intensity projection of epithelial domes stained for F-Actin (phalloidin), n=5. Scale bars, 50 μm.

Extended Data figure 7. Inhibition of ARP2/3 does not affect area heterogeneity in MDCK domes.

a, Coefficient of variation of the cell area (CV, defined as standard deviation divided by the mean) in MDCK-CAAX domes treated with CK666 (100 μM for 60 minutes), compared to control domes. The coefficient of variation is a non-dimensional indicator of heterogeneity. The CV was calculated by measuring area of 10 cells in n = 6 domes treated with CK666 and in n = 14 control domes. ns, not significant (P = 0.1256). Two-tailed Mann-Whitney test. Data are shown as mean ± SD. b, Dome nominal areal strain in MDCK-CAAX domes treated with CK666 (100 μM for 60 minutes, n=6), compared to control domes (n=14). ns, not significant, P = 0.7043. Two-tailed Mann-Whitney test. Data are shown as mean ± SD c, Maximum intensity projections and x-z sections of a representative control dome (left) and the same dome treated with CK666 100 μM (1 h). Scale bar, 25 μm.

Extended Data figure 8. Local perturbation of the actin cortex using photoactivatable Cytochalasin D increases cell area.

a Time evolution of the normalized cell area in response to local photoactivation of Cytochalasin D (black line, activation at t = 0 min, see methods, n = 5 domes). The blue line shows the time evolution of control cells (same illumination protocol but no photoactivatable Cytochalasin D in the medium, n = 8 domes). Area was normalized to the first time point. Solid lines and shaded areas indicate mean ± SD. At t = 21 min, normalized cell areas were significantly different (*P = 0.0159, two-tailed Mann-Whitney test). b, Normalized cell area 21 minutes after photoactivation in three experimental conditions: photoactivated cells (black circles, n = 19 cells from 5 domes), cells subjected to the same illumination protocol but without photoactivatable Cytochalasin D in the medium (blue squares, n = 19 cells from 8 domes), and cells with photoactivatable Cytochalasin D in the medium but without illumination (red triangles, n = 24 cells from 9 domes). Data include the immediate neighbors of the targeted cells because Cytochalasin D quickly diffused after activation. (****P<0.0001, ****P<0.0001, ns not significant, P = 0.4130, from left to right, two-tailed Mann-Whitney test. Data are shown as mean ± SD. c, Representative photoactivation experiments showing the apex of one dome before (-12 min) and after (6 min, 21 min) photoactivation of the cell marked with a yellow dashed rectangle (n=5). Top panels show the fluorescently labelled membrane and bottom panels show the SiR-actin channel. Note the increase in cell area and granulation in the SiR-actin channel (white arrowheads), indicating disruption of the actin cortex. Scale bar, 15 μm. d, Control experiment in which one cell at the apex of the dome (yellow dashed line) was subjected to the illumination protocol of c without photoactivatable Cytochalasin D in the medium (n=8). Top panels show the fluorescently labelled membrane and bottom panels show the SiR-actin channel. Scale bar, 15 μm. See also Supplementary Video 9.

Extended Data figure 9. Intermediate filaments reorganize in superstretched cells.

a-f, Immunofluorescence micrographs (Methods), represented using maximum intensity projection, of domes of MDCK keratin-18-GFP (in green) cells stained for F-Actin (phalloidin, red), and nuclei (Hoechst, blue), n=3. Scale bars, 50 μm. a, d, Zoomed area (marked with a dashed white square in b) showing that the keratin-18 filament network links neighboring cells and localizes at cell boundaries (white arrowheads). Scale bars, 10 μm. c, f, Zoomed area (marked with a dashed white square in e) showing that keratin-18 filaments are taut (white arrowheads) and have reorganized, with nodes at the cell center connecting different cells. Scale bars, 10 μm.

Extended Data figure 10. Intermediate filaments stabilize cell shape in superstretched cells.

a, Representative MDCK keratin-18-GFP superstretched cell at the apex of a dome before (0 s) and after (90 s) laser cutting the keratin filament bundle marked in b with a white arrowhead. The yellow line marks the outline of the cell measured with bright field imaging. Scale bar, 10 μm. b, Magnified view of the region labelled in a with a doted magenta rectangle. Scale bar, 5 μm. c, Representative MDCK keratin-18-GFP weakly stretched cell at the apex of a dome before (0 s) and after (90 s) laser cutting the keratin filament bundle shown in d. The yellow line marks the outline of the cell measured with bright field imaging. Scale bar, 10 μm. d, Magnified view of the region labelled in c with a doted magenta rectangle. The same laser cutting protocol and laser power were used to cut filaments in superstretched and weakly stretched cells. n=5. Scale bar, 5 μm. See Fig. 4o,p for quantification and statistics.