Internal Models in Biological Control

Abstract

Rationality principles such as optimal feedback control and Bayesian inference underpin a probabilistic framework that has accounted for a range of empirical phenomena in biological sensorimotor control. To facilitate the optimization of flexible and robust behaviors consistent with these theories, the ability to construct internal models of the motor system and environmental dynamics can be crucial. In the context of this theoretic formalism, we review the computational roles played by such internal models and the neural and behavioral evidence for their implementation in the brain.

1. Introduction

Over the last half century, the hypothesis that the nervous system constructs predictive models of the physical world to guide behavior has become a major focus in neuroscience [1, 2, 3]. In his 1943 book, Craik was perhaps the first to suggest that organisms maintain internal representations of the external world and provide a rationale for their use [4]:

If the organism carries a “small-scale model” of external reality and of its own possible actions within its head, it is able to try out various alternatives, conclude which is the best of them, react to future situations before they arise, use the knowledge of past events in dealing with the present and future, and in every way to react in a much fuller, safer, and more competent manner to the emergencies that face it.

K. Craik, p61, The Nature of Explanation.

In this cognitive view of prospective simulation, an internal model allows an organism to contemplate the consequences of actions from its current state without actually committing itself to those actions. Since Craik’s initial proposal, internal models have become widely implicated in various brain sub-systems with a diverse range of applications in biological control. Beyond facilitating the rapid and flexible modification of control policies in the face of changes in the environment, internal models provide an extraordinary range of advantages to a control system, from increasing the robustness of feedback corrections to distinguishing between self- and externally-generated sensory input. However, there tends to be confusion as to what exactly constitutes an internal model. This confusion has likely arisen because the internal model hypothesis has independently emerged in distinct areas of neuroscientific research prompted by disparate computational motivations. Furthermore, there are intricate interactions between various types of internal models maintained by the brain. Here, we aim to provide a unifying account of biological internal models, review their adaptive benefits, and evaluate the empirical support for their use in the brain.

In order to accomplish this, we describe various conceptions of internal models within a common computational formalism based on the principle of rationality. This principle posits that an agent will endeavor to act in the most appropriate manner according to its objectives and the “situational logic” of its environment [5, 6] and can be formally applied to any control task and dataset. It provides a parsimonious framework in which to study the nervous system and the mechanisms by which solutions to sensorimotor tasks are generated. In particular, probabilistic inference [7] and optimal feedback control [8] together provide parsimonious computational accounts for many sensory and motor processes in biological control. In Section 2, we describe how these theories characterize optimal perception and action across a wide variety of scenarios. Recently, technical work has integrated these two theories into a common probabilistic framework by developing and exploiting a deeper theoretic equivalence [9, 10]. This will provide the mathematical architecture necessary to integrate putative internal modeling mechanisms across a range of research areas, from sensorimotor control to behavioral psychology and cognitive science. In Section 3, we review theoretical arguments and experimental evidence supporting the contribution of internals models to the ability of nervous systems to produce adaptive behavior in the face of noisy and changing environmental conditions at many spatiotemporal scales of control.

2. Internal Models in the Probabilistic Framework

Bayesian inference and optimal control have become mainstream theories of how the brain processes sensory information and controls movement, respectively [11]. Their common theme is that behavior can be understood as an approximately rational solution to a problem defined by task objectives and a characterization of the external environment, sensory pathways, and musculoskeletal dynamics—that is they are normative solutions. In this section, we contextualize these theories in each of their respective domains of perception and action and review the experimental techniques employed to acquire evidence supporting their implementation in the nervous system.

2.1. Bayesian Inference in the Brain

In Bayesian inference, probabilities are assigned to each possible value of a latent state variable z one wishes to estimate, reflecting the strength of the belief that a given value represents the true state of the world [7]. It is hypothesized that the brain encodes a prior p(z) reflecting its beliefs regarding the state z before any sensory information has been received, as well as a probabilistic internal model describing the dependency of sensory signals y on the latent state z known as a generative model in computational neuroscience [12]. On receiving sensory information y, this probabilistic internal model can be used to compute a likelihood p(y|z) that quantifies the probability of observing the signals y if a particular state z is true. Using these probabilistic representations of state uncertainty, Bayes rule prescribes how the prior p(z) and likelihood p(y|z) are combined in a statistically optimal manner to produce the posterior probability distribution p(z|y):

$$\text{p}\left(z|y\right)=\frac{\text{p}\left(y|z\right)\text{p}\left(z\right)}{\text{p}\left(y\right)}$$ (1)

where p(y) = Σ_z p(y|z)p(z) is known as the evidence for the observation y. In the context of sensory processing, Bayesian inference is proposed as a rational solution to the problem of estimating states of the body or environment from sensory signals afflicted by a variety of sources of uncertainty (Fig. 1, Perception). Sensory signaling is corrupted by noise at many points along the neural pathway including transduction, action potential generation, and synaptic transmission [13]. Furthermore, relevant state variables are typically not directly observable and therefore need to be inferred from stochastic, statistically dependent, observations drawn from multiple sensory modalities.

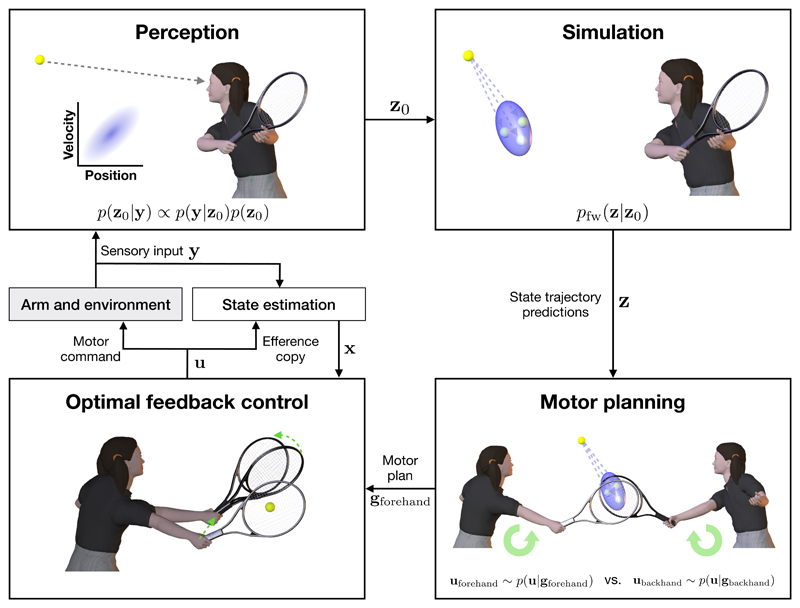
Figure 1. The roles of internal models in sensorimotor control.

Perception. Sensory input y is used to estimate the ball’s state z₀ which is uncertain due to noise along the sensory pathway and the inability to directly observe the full state of the ball (e.g. its spin and velocity). Bayes rule is used to calculate the posterior (an example of a posterior over one component of position and velocity shown in inset). Simulation. An internal dynamical model p_fw simulates the forward trajectory z of the ball. At short timescales, this internal modeling is necessary to overcome delays in sensory processing, while at longer timescales, the predictive distribution p_fw(z|z₀) of the ball’s trajectory can be used for planning. Motor planning. Internal simulation of the ball’s trajectory along with prospective movements are evaluated in order to generate an action plan. The player may have to decide between re-orienting their body in order to play a forehand or backhand. Optimal feedback control. Once a motor plan has been specified, motor commands u are generated by an optimal feedback controller which uses a state estimator to combine sensory feedback and forward sensory predictions (based on an efference copy of the motor command) in order to correct motor errors online in task-relevant dimensions (green arrows).

Several lines of behavioral evidence suggest that humans and other animals learn an internal representation of prior statistics, and integrate this with knowledge of the noise in their sensory inputs, in order to generate state estimates through probabilistic inference. First, many studies have applied a known prior (e.g. the location of an object or duration of a tone) to a subject performing a task and shown that the prior is internalized and reflected in behavior [14, 15, 16, 17]. Importantly, as predicted by Bayes rule this bias is greater when the stimulus is less reliable and thus more uncertain. Second, other studies have assumed a reasonable prior so as to explain a range of phenomena and illusions as rational inferences in the face of uncertainty. For example, a prior over the direction of illumination of a scene [18, 19, 20] or over the speed of object motion[21] can explain several visual phenomena such as how we extract shape from shading or perceive illusory object motion.

Beyond the sensorimotor domain, Bayesian methods have also been successful in explaining human reasoning. In the cognitive domain, the application of Bayesian principles using relatively complex probabilistic models has provided normative accounts of how humans generalize from few samples of a variable [22], make inferences regarding the causal structure of the world [23], and derive abstract rules governing the relationships between sets of state and sensory variables [24]. Behavioral analyses which estimate high-dimensional cognitive prior representations from low-dimensional (e.g. binary) responses have been used to demonstrate that humans maintain a prior representation for faces and that this naturalistic prior is conserved across tasks [25].

2.1.1. Bayesian forward modeling

Bayesian computations can be performed with respect to the current time or used to predict future states as hypothesized by Craik. Consider the problem of tracking a ball during a game of tennis (see Fig. 1, Perception). The response of any given photoreceptor in our retina can only provide delayed, noisy signals regarding the position y of the ball at a given time. From the probabilistic point of view, this irreducible uncertainty in the reported ball position is captured by a distribution p(y). Since a complete characterization of the state z of the tennis ball, including velocity, acceleration, and spin, is not directly observable, this information must be inferred from position samples transduced from many photoreceptors at different timepoints in concert with the output of an internal model. Given a previously inferred posterior p(z_t|y_:t) over possible ball states z_t based on previous sensory input y_:t up to time t, an internal forward model p_fw(z_t+1|z_t) can be used to predict the state of the ball at the future timestep t + 1 (Fig. 1, Prediction):

$$\text{p}\left(z_{t+\text{1}}|y_{:t}\right)={\displaystyle {\int }_{zt}{\text{p}}_{\text{fw}}\left(z_{t+1}|z_t\right)\text{p}\left(z_t|y_{:t}\right)dz}$$ (2)

The internal forward dynamical model p_fw must take physical laws, such as air resistance and gravity, into account. From a perceptual point of view, new sensory information y_t+1 can then be integrated with this predictive distribution in order to compute a new posterior distribution at time t + 1:

$$\text{p}\left(z_{t+1}|y_{:t+1}\right)\propto \text{p}\left(y_{t+1}|z_{t+1}\right)\text{p}\left(z_{t+1}|y_{:t}\right)$$ (3)

This iterative algorithm, known as Bayesian filtering, can be used to track states z_t, z_t+1, … of the body or the environment in the presence of noisy and delayed signals for the purposes of state estimation (see Section 3.2). The extrapolation of latent states over longer timescales can be used to predict states further into the future for the purposes of planning movement (see Section 3.3). The results of such computations are advantageous to the tennis player from the control perspective. On a short timescale, it enables the player to predictively track the ball with pursuit eye movements, while on a longer timescale, the player can plan to move into position well in advance of the ball’s arrival in order to prepare their next shot.

In the brain, the dichotomy between the prediction step, based on a forward model and the observation step is reflected, at least partially, in dissociated neural systems. With respect to velocity estimation, a detailed analysis of retinal circuitry has revealed a mechanism by which target velocity can be estimated at the earliest stages of processing [26]. Axonal conductance delays endow retinal cells with spatio-temporal receptive fields which integrate information over time and fire in response to a preferred target velocity. Furthermore, the retina contains a rudimentary predictive mechanism based on the gain control of retina ganglion cell activity whereby the initial entry of an object into a cell’s receptive field causes it to fire but then the activity is silenced [27]. However, more complex predictions (e.g. motion under gravity) require higher order cortical processing.

2.1.2. Neural implementation

Theories have been developed regarding how neuronal machinery could perform the requisite Bayesian calculations. These theories fall into two main classes: population coding mechanisms in feedforward network architectures [28, 29, 30, 31] and recurrently connected dynamical models [32, 33, 34]. In the former, neural receptive fields are proposed to “tile” the sensory space of interest such that their expected firing rates encode the probability (or log-probability [29]) of a particular value of the encoded stimulus. For example, this implies that each neuron in a population would stochastically fire within a limited range of observed positions of a reach target and fire maximally for its “preferred” value. Importantly, the variability in neural activity can then be directly related to the uncertainty regarding the precise stimulus values that generated the input in a manner consistent with Bayesian theory [28]. Thus, across neurons, the population activity would reflect the posterior probability distribution of the target position given sensory input. This neural representation can then be fed forward to another layer of the network in order to produce a motor response. It has been shown that such population codes are able to implement Bayes rule in parsimonious network architectures and account for empirical neural activity statistics during sensorimotor transformations [30], Bayesian decision-making [35], and sensory computations such as cue integration [28], filtering [36], and efficient stimulus coding [31].

Although the functional implications of population codes can be directly related to Bayesian calculations, they do not incorporate the rich dynamical interactions between neurons in cortical circuits nor model the complex temporal profiles of neural activity which follow transient stimulus input [37, 38]. These considerations have motivated the development of dynamical models of cortex with recurrent connectivity which approximate Bayesian inference [32, 34] though the characterization of this class of models from a computational point of view remains an ongoing challenge [39]. In contrast to the probabilistic population coding approach, it has been postulated that neural variability across time reflects samples from a probability distribution based on a “direct-coding” representation [40]. In this model, population activity encodes sensory variables directly (as opposed to the probability of a particular variable value) such that the variability of neural activity across time reflects the uncertainty in the stimulus representation. When sensory input is received, it is suggested that neural circuits generate samples from the posterior distribution of inferred input features. In the absence of external input, spontaneous activity corresponds to draws from the prior distribution which serves as an internal model of the sensory statistics of the environment. In support of this theory, the change in spontaneous visual cortical activity during development has been shown to be consistent with the gradual learning of a generative internal model of the visual environment whereby spontaneous activity adapted to reflect the average statistics of all visual input [41].

2.2. Optimal Feedback Control

Bayesian inference is the rational mathematical framework for perception and state estimation based on noisy and uncertain sensory signals. Analogously, optimal control has been a dominant framework in sensorimotor control to derive control laws which optimize behaviorally relevant criteria and thus rigorously comply with the principle of rationality[11] (Fig. 1, Optimal feedback control). Understanding how natural motor behavior arises from the combination of a task and the biomechanical characteristics of the body has driven the theoretic development of optimal control models in the biological context [42, 43]. Initially, models were developed which posited that given a task, planning specified either the desired-trajectory or the sequence of motor commands to be generated. These models typically penalized lack of “smoothness” such as the time derivative of hand acceleration (known as “jerk”) [44] or joint torques [45]. The role of any feedback was, at best, to return the system to the desired trajectory. These models aimed to provide a normative explanation for the approximately straight hand paths and bell-shaped speed profiles of reaching movements. However, these models are only accurate for movement trajectories averaged over many trials and do not account for the richly structured trial-to-trial variability observed in human motor coordination [8].

A fundamental characteristic of biological control is the number of effector parameters to be optimized far exceeds the dimensionality of the task requirements. For example, infinitely many different time series of hand positions or joint angles can be used to achieve a task such as picking up a cup. Despite the plethora of possible solutions motor behavior is stereotypical both across a population and within a person suggesting that the nervous system selects actions based on a prudent set of principles. How the brain chooses a particular form of movement out of the many possible is known as the “degrees of freedom” problem in motor control [46]. A ubiquitous empirical observation in goal-directed motor tasks is that effector states tend to consistently covary in a task-dependent manner [47, 8, 48, 49, 50]. In particular, these covariances tend to be structured in such a way as to minimize movement variance along task-relevant dimensions while allowing variability to accumulate in task-irrelevant dimensions.

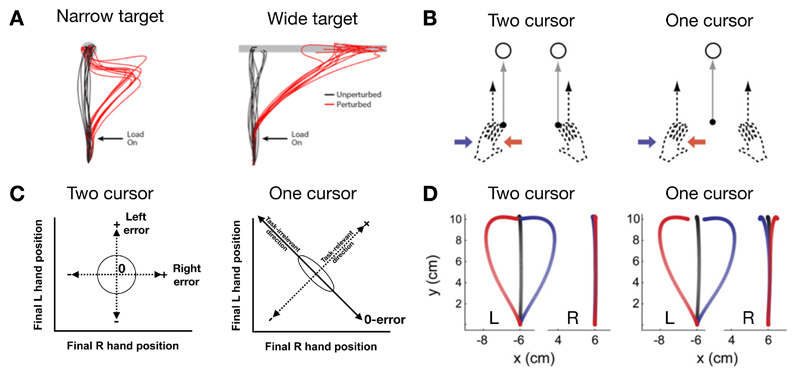
Optimal feedback control (OFC) was introduced [8, 11] in the motor control context in order to provide a normative solution to the “degrees of freedom” problem of motor coordination and, in particular, to develop a broad account of effector covariance structure and motor synergy as a function of task requirements. In this class of control laws, the core distinction with respect to optimal (feedforward or desired trajectory) control, is that sensory feedback is integrated into the production of motor output. Optimal feedback control policies continually adapt to stochastic perturbations (for example, due to noise within the motor system [51]) and therefore predict temporal patterns of motor variability which have been widely tested in behavioral experiments. An emergent property of OFC, known as the minimum intervention principle, explains the correlation structures of task-oriented movements [8]. Simply put, as movements deviate from their optimal trajectories due to noise, OFC specifically predicts that only task-relevant deviations will be corrected [8]. For example, when reaching to a target which is either narrow or wide subjects tend to make straight line movements to the nearest point on the target (Fig. 2A, black trajectories). However, when the hand is physically perturbed early in the movement, corrections are only seen when reaching towards the narrow target and not the wide target as the perturbation does not affect task success in the latter case, so there is no reason to intervene (Fig. 2A, red trajectories). Intervening would be counterproductive as it typically requires more energy and adds noise into the reach.

Figure 2. Minimum intervention principle and exploitation of redundancy.

A. Unperturbed movements (black traces show individual hand movement paths) to narrow or wide targets tend to be straight and to move to the closest point on the target. Hand paths during the application of mechanical loads (red traces in response to a force pulse that pushes the hand to the right) delivered immediately after movement onset, which disrupt the execution of the planned movement, obey the principle of minimum intervention. That is, for a narrow target (left), the hand paths correct to reach the target whereas, for a wide target (right), there is no correction and the hand just reaches to another point on the target. B. Participants make reaching movements to targets. In a two-cursor condition, each hand moves its own cursor (black dots) to a separate target. In a one-cursor condition, the cursor is displayed at the average location of the two hands and participants reach with both hands to move this common cursor to a single target. During the movement, the left hand could be perturbed with a leftward (red) or rightward (blue) force field or remain unperturbed (black). C. When each hand controls its own cursor there is only one combination of final hand positions for which there is no error (center of circle). Optimal feedback control predicts that there will be no correlation between the endpoint positions (black circle shows a schematic distribution of errors). When the two hands control the position of a single cursor, there are many combinations of final hand positions which give zero error (black diagonal line; task-irrelevant dimension). Optimal control predicts correction in one hand to deviations in the other leading to negative correlations between the final locations of the two hands, so that if one hand is too far to the left the other compensates by moving to the right (black ellipse). D. Movement trajectories shown for the left and right hand for perturbations shown in B (one-cursor condition). The response of the right hand to perturbations of the left hand shows compensation only for the one-cursor condition in accord with the predictions of optimal feedback control. In addition, negative correlations in final hand positions can be seen in unperturbed movements for the one-cursor but not two-cursor condition (not shown). Modified with permission from [52] (A) and [53] (B-D).

In sensorimotor control, the specification of a particular behavioral task begins with a definition of what constitutes the relevant internal state x (which may include components corresponding to the state of the arm and external environment) and control signals u. In general, the state variables should include all the variables, which together with the equations of motion describing the system dynamics and the motor commands, are sufficient to predict future configurations (in the absence of noise). A discrete-time stochastic dynamics model can then be specified which maps the current state x_t and control inputs u_t to future states x_t+1. This model is characterized by the conditional probability distribution p_env(x_t+1|x_t, u_t). For reaching movements, for example, the state x could correspond to the hand position, joint angles and angular velocities and the control signals u might correspond to joint torques. Given these dynamics, the aim of optimal control is to minimize a cost function which includes both control and state costs. The state cost Q “rewards” states that successfully achieve a task (such as placing the hand on a target), while R represent an energetic cost such as that required to contract muscles (see Box: Costs, Rewards, Priors, and Parsimony for a discussion of cost function specification in the biological context). In order to make predictions regarding motor behavior, a control policy π (a mapping from states to control signals u_t = π(x_t)) is optimized to minimize the total cumulative costs expected to be incurred. This objective V_π (x_t) is known as a cost-to-go function of a control policy (in control theory) or value function (in reinforcement learning where it typically quantifies cumulative expected rewards rather than costs):

$$V_{\pi }\left(x_t\right)=Q\left(x_t\right)+R\left(\pi \left(x_t\right)\right)+{𝔼}_{x_{t+1\sim {\text{p}}_{\text{env}}\left(\cdot |x_t,\pi \left(x_t\right)\right)}}\left[V_{\pi }\left(x_{t+1}\right)\right].$$ (4)

This characterization of the value function, known as a Bellman equation, intuitively implies that the optimal controller balances the instantaneous costs in the current state x_t with the minimization of expected future cumulative costs in the subsequent state x_t+1.

This formulation is quite general. When applied to motor behavior, costs are often modeled as a quadratic function of states and control signals while the dynamics model p_env(x_t+1|x_t, u_t) typically takes the form of a linear equation with additive Gaussian noise [43]. Furthermore, the noise term is adapted to scale with the magnitude of the control input; as found in the nervous system [51]. This signal-dependent noise arises through the organization of the muscle innervation. The force that a single motor neuron can command is directly proportional to the number of muscle fibres that it innervates. When small forces are generated, motor neurons that innervate a small number of muscle fibres are active. When larger forces are generated, additional motor neurons that innervate a larger number of muscle fibres are also active. This is known as Henneman’s size principle. By recruiting larger number of muscle fibres from a single alpha motoneuron (the final neuronal output of the motor system) the variability of output is increased leading to variability in the force that is proportional to the average force that is produced by that muscle [54, 55]. This OFC problem formulation provides a reasonable balance between capturing the essential features of the sensorimotor task and enabling the accurate computation of optimal control policies; linear-quadratic-Gaussian problems with signal-dependent noise can be solved by the iteration of two matrix equations which converges exponentially fast [43].

Variants of this OFC model have been tested in many experiments involving a variety of effectors, task constraints, and cost functions [49, 48, 56, 57, 58, 59]. For example, studies have examined tasks in which the two hands either each control their own cursor to individual targets or control a single cursor (whose location is the average position of the two hands) to a single target (Fig. 2B). The predictions of OFC differ for these two scenarios (Fig. 2C). In the former, perturbations to each arm can only be corrected by that arm so that a perturbation to one arm should only be corrected by that arm. However, in the latter situation both arms could contribute to the control of the cursor so that perturbations to one arm should also be corrected by the other arm. Indeed, force perturbations of one hand resulted in corrective responses in both hands consistent with an implicit motor synergy as predicted by OFC (Fig. 2D). Moreover, in a directed force production task, a high-dimensional muscle space controls a low dimensional finger force. Electromyography recordings revealed task-structured variability in which the task-relevant muscle space was tightly controlled and the task-irrelevant muscle space showed much greater variation, again confirming predictions of OFC [57].

OFC is also a framework in which active sensing can be incorporated. Although engineering models typically assume state-independent noise, in the motor system the quality of sensory input can vary widely. For example, our ability to localize our hand proprioceptively varies substantially over the reaching workspace. By including state-dependent noise in OFC the quality of sensory input will depend on the actions taken. The OFC solution leads to a trade-off between making movements which allow one to estimate the state accurately and task achievement. The predictions of the optimal solution match those seen in human participants when they are exposed to state-dependent noise [60].

Recent work has focused on the adaptive feedback responses within an OFC framework. One way to measure the magnitude of the visuomotor response (positional gain) is to apply lateral visual perturbations to the hand during a reaching movement. Typically on such a visually perturbed trial a robotic interface is used to constrain the hand within a simulated mechanical channel so that the forces into the channel are a reflection of the visuomotor reflex gain. Such studies have shown that reflex gains are sensitive to the task and that the gains increase or decrease respectively depending on whether the perturbation is task relevant or not [56]. Moreover, the reflex gain varies throughout a movement in a way that qualitatively agrees with the predictions of OFC [59]. Reflexive responses due to muscle stretch caused by mechanical perturbation can be decomposed into short-latency (<50 ms) and long-latency (50-100 ms) components, both of which occur before the onset of volitional control (>100 ms) [61]. The former are generated by a spinal pathway (i.e. the transformation of proprioceptive feedback into motor responses occurs at the level of spinal cord) while the latter are transcortical in nature (i.e. cortex is involved in modulating the reflex). It has been shown that the long-latency response specifically can be “voluntarily” manipulated based on the behavioral context [62] and it has been suggested that this task-based flexibility is consistent with an optimal feedback controller operating along a pathway through primary motor cortex (M1) [63]. Neural activity in primary motor cortex has been shown to reflect both low-level sensory and motor variables [64] while also being influenced by high-level task goals [65]. This diversity of encoding is precisely what one would expect from an optimal feedback controller [66]. Further evidence in favor of this hypothesis includes the fact that M1 neurons appear to encode the transformation of shoulder and elbow perturbations into feedback responses [67].

2.3. Duality Between Bayesian Inference and Optimal Control

Classically, a control policy u = π(x) deterministically maps states to control signals. However, in the probabilistic framework, it is more natural to consider stochastic policies p(u|x) representing distributions over possible control commands conditioned on a given state. Furthermore, it is impossible for the brain to represent a deterministic quantity with perfect precision and therefore probabilistic representations may be a more appropriate technical language in the sensorimotor control context [75]. This perspective will allow us to review a general duality between control and inference. It has long been recognized that certain classes of Bayesian inference and optimal control problems are mathematically equivalent or dual. Such an equivalence was first established between the Kalman filter and the linear-quadratic regulator [76] and has recently been generalized to nonlinear systems [77, 9]. The intuition is as follows. Suppose somebody is performing a goal-directed reaching movement and wants to move their hand to a target. The problem of identifying the appropriate motor commands can be characterized as the minimization of a value function (Eqn. 4). However, an alternative but equivalent approach, can be considered. Instead, the person could fictively imagine their hand successfully reaching the target at some point in the future and infer the sequence of motor commands that were used to get there. The viewpoint transforms the control problem into an inference problem.

More technically, the duality can be described parsimoniously using trajectories of states x ≔ (x₁, …, x_T) and control signals u ≔ (u₀, …, u_T–1) up to a horizon T. Consider the conditional probability defined by p (g|x) ∝ exp [−Q (x)] where $Q\left(\text{x}\right):={\displaystyle {\sum }_{i=0}^{T}Q\left(x_t\right)}$ is the aforementioned state-dependent cost encoding the desired outcome (Eqn. 4). The variable g can be thought as as an “observation” of a successfully completed task. The task is “more likely” to be successful if less state costs are incurred. The control cost $R\left(\mathbf{\text{u}}\right):={\displaystyle {\sum }_{i=0}^{T-1}R\left(u_t\right)}$ can be absorbed in a prior over control signals p(u) ∝ exp [−R (u)] with more costly control commands (large R(u)) being more unlikely a priori. Bayesian inference can then be employed to compute the joint probability of motor outputs u and state trajectories x given the “observation” of a successful task completion g:

$$\text{p}\left(\mathbf{\text{x}},\mathbf{\text{u}}|\mathbf{\text{g}}\right)\propto {\text{p}}_{\text{env}}\left({\mathbf{\text{x}}|\mathbf{\text{x}}}_0,\mathbf{u}\right)\text{p}\left(\mathbf{\text{g}}|\mathbf{\text{x}}\right)\text{p}(\mathbf{u})={\text{p}}_{\text{env}}\left({\mathbf{\text{x}}|\mathbf{\text{x}}}_0,\mathbf{u}\right)e^{-Q\left(\mathbf{\text{x}}\right)}{e}^{-R\left(\mathbf{\text{u}}\right)}$$ (5)

It is observed that the posterior probabilities of control signals u which are “most likely” to lead to a successful completion of the task g along a particular state trajectory x are proportional to the expected cumulative costs as in the optimal control perspective (Eqn. 4). By marginalizing over state trajectories x, one obtains the posterior p(u|g) as a“sum-over-paths” of the costs incurred [78]. This perspective has led to theoretic insights within a class of control problems known as Kullback-Leibler control [10] or linearly solvable Markov decision processes [79] where the control costs take the form of a KL-divergence. In particular, this class of stochastic optimal control problems is formally equivalent to graphical model inference problems [10] and is a relaxation of deterministic optimal control [80]. Thus, approximate inference methods, which have provided inspiration for neural and behavioral models of the brain’s perceptual processes, potentially may also underpin the algorithms used by the brain during planning (see Section 3.3).

2.4. What Constitutes an Internal Model in the Nervous System?

In neuroscience, neural representations of our body or environment, that is internal models, are conceptualized in a wide range of theories regarding how the brain interprets, predicts, and manipulates the world. Most generally, one may consider a representation of the joint distribution p(x, z, y, u) between time series of sensory inputs y, latent states z, internal states x, and motor signals u. Together the latent states z and internal states x reflect the state of the world and the body but we separate them conceptually to reflect a separation between external and internal states. This probabilistic representation can be considered a “complete” internal model. Such a formulation contains within it various characterizations of internals models from different disciplines of neuroscience as conditional densities. Therefore, the phrase internal model can be used for markedly different processes and we suggest it is important for researchers to be explicit about what type of internal model they are investigating in a given domain. Here we attempt to non-exhaustively categorize the elements which can be considered part of an internal model in sensorimotor control:

1. Prior models. Priors over sensory signals, p(y), and states of the world, p(z). The world is far from homogeneous and numerous studies have shown that people are adept at learning the statistical regularities of sensory inputs and the distributions of latent states (for a review see [40]).

2. Perceptual inference models. These form a class of internal models which are postulated to be implemented along higher-order sensory pathways. These models compute latent world states (for example objects) given sensory input, p(z|y). Conversely, generative models are models which describe processes which generate sensory data. This may be captured by the joint distribution between sensory input and latent variables, p(y, z), or computed from the product of a state prior and the conditional distribution of sensory inputs given latent world states, p(y|z). Given sensory input, the generative model can be “inverted” via Bayes rule to compute the probabilities over the latent states which may have generated the observed input. Further uses of such generative models are predictive coding [81] and reafference cancellation (see section 3.1).

3. Sensory and motor noise models. The brain is sensitive to the noise characteristics and reliability of our sensory and motor apparatus [13]. On the sensory side, to calculate p(y|z) not only involves a transformation but also knowledge of the noise on the sensory signal y itself. In motor control, the control output u is also corrupted by noise, and knowledge of this noise can be used to refine the probability distribution of future states x. Maintaining such noise models aids the nervous system in accurately planning and implementing control policies which are robust to sensory and motor signal corruption [82].

4. Forward dynamical models. In general, we think of a forward dynamical model as a neural circuit that can take the present estimated state, x₀, and predict states in the future. This could model the passive dynamics, p(x|x₀), of the system or also use the current motor output to predict the state evolution, p(x|x₀, u).

5. Cognitive maps, latent structure representation, and mental models. Abstract relational structures between state variables (e.g. pertaining to distinct objects in the world) may be compactly summarized in the conditional probability distributions, p(z_n|z₁, …, z_n−1), of a graphical model. Such representations can also be embedded in continuous internal spaces such that a metric on the space encodes the relational strength between variables. These models can be recursively organized in hierarchies, thus facilitating the low-dimensional encoding of control policies and the transfer of learning across contexts (for a review of latent structure learning in the context of motor control, see [83]).

The probabilistic formalism allows one to relate internal models across a range of systems within the brain. However, it leaves many aspects of the internal models unspecified. Internal models can be further defined by a structural form which links inputs and outputs. For example, internal models may capture linear or nonlinear relationships between motor outputs and sensory inputs such as in the relationship between joint torques and future hand positions. Internal models may contain free parameters which can be quickly adapted in order to adapt to contextual variations; for example, the length and inertia of our limbs during development. Internal models can be further specified by the degree of approximation in the model implementation. Consider the problem of predicting the future from the past. At one extreme, one can generate simulations from a rich model containing internal variables which directly reflect physically relevant latent states such as gravitational forces and object masses. On the other hand, a mapping from current to future states can be learned directly from experience without constructing a rich latent representation. Such mappings can be encapsulated compactly in simple heuristic rules which may provide a good trade-off between generalizability and efficiency. Finally, internals models span a range of spatio-temporal resolution. Some internal models, such as those involved in state estimation compute forward dynamics on very short spatio-temporal scales such as centimeters and milliseconds (see section 3.2), while other internal models, such as those used during planning, simulate over timescales which may be longer by several orders of magnitude (see section 3.3).

2.5. Probabilistic Forward and Inverse Models

In the sensorimotor context, internal models are broadly defined as neural systems which mimic musculoskeletal or environmental dynamical processes [84, 85]. An important feature of putative internal models in sensorimotor control is their dynamical nature. This distinguishes internal models from other neural representations of the external world that the brain maintains such as generative and recognition models as studied in perception. This is reflected in the brain computations associated with internal models. Whether contributing to state estimation, reafference cancellation, or planning, internal inverse and forward models relate world states across a range of temporal scales. Recalling the previously described example of tennis, internal models may be used to make anticipatory eye movements in order to overcome sensory delays in tracking the ball. Incorporating a motor response, internal models can be used to simulate the ballistic trajectory of a tennis ball after it has been struck. This leads to a classical theoretic dissociation of internal models into different classes [85]. Internal models which represent future states of a process (ball trajectories) given motor inputs (racquet swing) are known as forward models. Reversing this mapping, models which compute motor outputs (the best racquet swing) given the desired state of the system at a future timepoint (a point-winning shot) are known as inverse models.

In the probabilistic formalism, the internal forward model p_fw(x_t+1|x_t, u_t) can be encapsulated by the distribution over possible future states x_t+1 given the current state x and control signals u. A prediction regarding a state trajectory x ≔ (x₁, …, x_T) can be made by repeatedly applying the forward model ${\text{p}}_{\text{fw}}\left({\text{x}|\text{x}}_0,\mathbf{\text{u}}\right)={\displaystyle {\prod }_{t=1}^T{\text{p}}_{\text{fw}}\left(x_t|x_{t-1},u_{t-1}\right)}.$ By combining a forward model p_fw and a prior over controls p(u), the inverse model p_inv can be described in the probabilistic formalism. Consider the problem of computing the optimal control signals which implement a movement towards a desired goal state g. This state could be, for example, the valuable target position of a reach movement. An inverse model is then a mapping from this desired state to a control policy u* which can be identified with the posterior probability distribution computed via control inference (Eqn. 5):

$${\text{p}}_{\text{inv}}(\mathbf{\text{u}}|\text{g})\propto {\displaystyle {\int }_{\mathbf{\text{x}}}{\text{p}}_{\text{fw}}(\mathbf{\text{x}}|{\text{x}}_0,\mathbf{\text{u}})\text{p}}(\mathbf{\text{g}}|\mathbf{\text{x}})\text{p}(\mathbf{\text{u}})d\mathbf{\text{x}}$$ (6)

$${\mathbf{\text{u}}}^{*}=\begin{array}{c}\text{argmax}\\ \mathbf{\text{u}}\end{array}{\text{p}}_{\text{inv}}(\mathbf{\text{u}}|\mathbf{\text{g}})$$ (7)

Typically, in the sensorimotor control literature, a mapping from desired states at each point in time to the control signals u* is described as the “inverse model”. This mapping requires the explicit calculation of a desired state trajectory x*. This perspective can be embedded within the probabilistic framework by setting p(g|x*) = 1 and p(g|x) = 0 for all other state trajectories x ≠ x*. In contrast, in optimal feedback control and reinforcement learning, motor commands are generated based on the current state without the explicit representation of a desired state trajectory. The two concepts can be related by noting that the optimal deterministic control policy u* is the mode of the probabilistic inverse model p_inv.

3. The Roles of Internal Models in Biological Control

3.1. Sensory Reafference Cancellation

Sensory input can be separated into two streams of input: afferent information which is information arising from the external world and reafferent information which is sensory input that is causes by our own actions. From a sensory receptors point of view these sources cannot be separated. However, it has been proposed that forward models are a key component that allows us both to determine whether the sensory input we receive is a consequence of our own actions and to filter out the components arising from our own actions so as to be more attuned to external events which tend to be more behaviorally important [86]. To achieve this, a forward model receives a signal of the outgoing motor commands and uses this so-called efference copy in order to calculate the expected sensory consequences of an ongoing movement [87]. This predicted reafferent signal (known as the corollary discharge in neurophysiology although this term is now often used synonymously with efference copy), can then be removed from incoming sensory signals leaving only sensory signals due to environment dynamics.

This mechanism plays an important role in stabilizing visual perception during eye movements. When the eyes make a saccade to a new position, the sensory representation of the world shifts across the retina. In order for the brain to avoid concluding that the external world has been displaced based on this “retinal flow”, a corollary discharge is generated from outgoing motor commands and integrated into the visual processing of the sensory input [88]. A thalamic pathway relays signals about upcoming eye movements from the superior colliculus to the frontal eye fields where it causally shifts the spatial receptive fields of target neurons in order to cancel the displacement due to the upcoming saccade [89]. Furthermore, the resulting receptive field shifts are time-locked by temporal information pertaining to the timing of the upcoming saccade carried by the corollary discharge.

Perhaps the best worked-out example of the neural basis of such a predictive model is in the cerebellum-like structure of the weakly electric fish [90]. These animals generate pulses (or waves) of electrical discharge into the water and can then sense the field that is generated to localize objects. However, the field depends on many features that the fish controls such as timing of the discharge, movement and posture of the fish. The cerebellum-like structure learns to predict sensory consequences (i.e. the expected signals generated by the electrical field) based on both sensory input and motor commands and removes this from incoming signals so that the residual signals reflects an unexpected input which pertains to objects in the environment. The detailed mechanism of synaptic modulation (anti-hebbian learning) and the way that the prediction is built up from a set of bases functions has recently been elucidated [91].

3.2. Forward State Estimation for Robust Control

An estimate of the current state of an effector is necessary for both motor planning and control. There are only three sources of information which can be used for state estimation: sensory inputs, motor outputs and prior knowledge. In terms of sensory input, the dominant modality for such state estimation is proprioceptive input (i.e. from receptors in the skin and muscles). While blind and deaf people people have close to normal sensorimotor control, the rare patients with loss of proprioceptive input are severely impaired in their ability to make normal movements [92, 93]. The motor signals that generate motion can also provide information about the likely state of the body. However, to link the motor commands to the ensuing state requires a mapping between the motor command and the motion, that is a forward dynamic model [2], in an analogous fashion to many “observer models” in control theory. There are at least two key benefits of such an approach. First, the output of the internal model can be optimally combined with sensory inflow via Bayesian integration (Section 2.1) resulting in a minimization of state estimation variance due to noise in sensory feedback [94]. Second, combining the motor command (which is available in advance of the change in state), together with the internal model, makes movement more robust with respect to errors introduced by the unavoidable time delays in the sensorimotor loop. Feedback-based controllers with delayed feedback are susceptible to destabilization since control input optimized for the system state at a previous time-point may increase, rather than decrease, the motor error when applied in the context of the current (unknown) state [85]. Biological sensorimotor loop delays can be on the order of 80–150 ms for proprioceptive to visual feedback [61]. However, a forward model which receives an efferent copy of motor outflow and simulates upcoming states can contribute an internal feedback loop in order to effect feedback control before sensory feedback is available [2, 3].

3.2.1. State estimation and sensorimotor control

Predictive control is essential for the rapid movements commonly observed in dexterous behavior. Indeed, this predictive ability can be demonstrated easily with the “waiter task”. If you hold a weighty book on the palm of your hand with an outstretched arm and use your other hand to remove the book (like a waiter removing objects from a tray) the supporting hand remains stationary. This shows our ability to anticipate events caused by our own movements so as to generate the appropriate and exquisitely timed reduction in muscle activity necessary to keep the supporting hand still. In contrast, if someone else removes the book from your hand, even with vision of the event, it is close to impossible to maintain the hand stationary even if the removal is entirely predictable [95].

Object manipulation also exhibits an exquisite reliance on anticipatory mechanisms. When an object is held in a precision grip, enough grip force must be generated to prevent the object from slipping. The minimal grip force depends on the object load (i.e. weight at rest) and the frictional properties of the surface. Subjects tend to maintain a small safety margin so that if the object is raised the acceleration causes an increase in the load force requiring an increase in the grip force to prevent slippage. Recordings of the grip and load force in such tasks show that the grip force increases with no lag compared to the load force even in the initial phase of movement thus ruling out the possibility that grip forces were adapted based on sensory feedback [96, 97]. Indeed, such an anticipatory mechanism is very general with no lag in grip force modulation observed if one jumps up and down while holding the object. In contrast, if the changes in load force are externally generated, then compensatory changes in grip force lag by around 80 ms suggesting a reactive response mechanism [98].

In contrast to internal models which estimate the state of the body based on efferent copies, internal models of the influence of external environmental perturbations are also utilized in state estimation. An analysis of postural responses to mechanical perturbations showed that long-latency feedback corrections were consistent with a rapid Bayesian updating of estimated state based on forward modeling of delayed sensory input [99]. Furthermore, trial-to-trial changes in the motor response suggested that the brain rapidly adapted to recent perturbation statistics reflecting the ability of the nervous system to flexibly alter its internal models when exposed to novel environmental dynamics. Although forward modeling can be based on both proprioceptive and visual information, the delays in proprioceptive pathways can be several tens of milliseconds shorter than those in visual pathways. During feedback control, the brain relies more heavily on proprioceptive information than visual information (independent of the respective estimation variances) consistent with an optimal state estimator based on multisensory integration [100].

Some actions can actually make state estimation easier and there is evidence that people may expend energy so as to reduce the complexity of state estimation. For example, in a task similar to sinusoidally translating a coffee cup without spilling its contents, people choose to move in such a way as to make the motion of the contents more predictable despite the extra energetic expense [101]. Such a strategy has the potential to minimize the computational complexity of the internal forward modeling and thereby reduce errors in state estimation.

3.2.2. Neural substrates

Extensive research has been conducted with the aim of identifying the neural loci of putative forward models for sensorimotor control. Two brain regions in particular have been implicated: the cerebellum and the posterior parietal cortex. It has long been established that the cerebellum is important for motor coordination. Although patients with cerebellar damage can generate movement whose gross structure matches that of a target movement, their motions are typically ataxic and characterized by dysmetria (typically the overshooting or undershooting of target positions during reaching) and oscillations when reaching (intention tremor) [102]. In particular, these patients experience difficulty in controlling the inertial interactions among multiple segments of a limb. This results in greater inaccuracy of multi-joint versus single-joint movements. An integrative theoretic account [2, 103] suggested that these behavioral deficits could be caused by a lack of internal feedback and thus that the cerebellum may contain internal models which play a critical role in stabilizing sensorimotor control. A range of investigation across multiple disciplines has supported this hypothesis including electrophysiology [104, 105, 106], neuroimaging [97], lesion analysis [107, 103], and noninvasive stimulation [108]. In particular, the aforementioned ability of humans to synchronize grip force with lift, which provided indirect behavioral evidence of an internal forward model, is impaired in patients with cerebellar degeneration [107]. Optimal control models have enabled researchers to estimate impairments of the forward dynamic models in cerebellar patients making dysmetric reaching movements [109]. Hypermetric patients appeared to overestimate arm inertia resulting in their movements overshooting the target while hypometric patients tend to underestimate arm inertia resulting in the opposite pattern of deviations from optimality. Consequently, dynamic perturbations could be computed which artificially increased (for hypermetric patients) or decreased (for hypometric patients) arm inertia and thus compensating for the idiosyncratic biases of individual patients [109]. This study highlights the contribution of optimal control and internal models towards a detailed understanding of a particular movement disability and the possibility of therapeutic intervention.

The parietal cortex has also been implicated in representing forward state estimates. A sub-region of the superior parietal lobule, known as the posterior parietal cortex (PPC), contains neural activity consistent with forward state estimation signals [110] which may be utilized for the purposes of visuomotor planning [111]. Indeed, transcranial magnetic stimulation of this region, resulting in transient inhibition of cortical activity, impaired the ability of subjects to error-correct motor trajectories based on forward estimates of state [112]. In another study, following intracranial electrical stimulation of PPC, subjects reported that they had made various physical movements despite these movements not having been performed, nor any muscle activity having been detected using electromyography [113]. This illusory awareness of movement is consistent with the activation of a forward state representation of the body. A study based on focal parietal lesions in monkeys reported a double dissociation between visually-guided and proprioceptively-guided reach movement impairments and lesions of the inferior and superior parietal lobules respectively [114]. This suggests that forward representations of state are localized to different areas of the PPC depending on the sensory source of state information.

3.3. Learning and Planning Novel Behaviors

The roles of internal models described thus far operate on relatively short timescales and do not fit Craik’s original conception of their potential contribution to biological control. This concerned the internal simulation of possible action plans, over longer timescales, in order to predict and evaluate contingent outcomes. Viewing his hypothesis through the computational lens of optimal control, Craik’s fundamental rationale for internal modeling falls within the broad domain of algorithms by which the brain can acquire new behaviors which we review in this section.

3.3.1. Reinforcement learning and policy optimization

Control policies can be optimized using a range of conceptually distinct, but not mutually exclusive, algorithms including reinforcement learning [115] and approximate inference [116]. Reinforcement learning provides a suite of iterative policy-based and value-based optimization methods which have been applied to solve optimal feedback control problems. Indeed, initial inspiration for reinforcement learning was derived from learning rules developed by behavioral psychologists [117]. Theoretical and empirical analyses of reinforcement learning methods indicate that a key algorithmic strategy which can aid policy optimization is to learn estimates of the value function V_π introduced in Section 2.2. Once V_π is known, the optimal controls u*(x_t) are easily computed without explicit consideration of the future costs (by selecting the control output which is most likely to lead to the subsequent state x_t+1 with minimal V_π (x_t+1)). A related, and even more direct, method is to learn and cache value estimates (known as “Q-values”) associated with state-action combinations [115]. Thus, value estimates are natural quantities for the brain to represent internally as theory are the long-term rationale for being in a given state and define optimized policies.

In many reinforcement learning algorithms, a key signal is the reward prediction error which is the difference between expected and actual rewards or costs. This signal can be used to iteratively update an estimate of the cost-to-go and is guaranteed to converge to the correct cost-to-go values (although the learning process may take a long time) [115]. Neural activity in the striatum of several mammalian species (including humans) appears to reflect the reinforcement learning of expected future reward representations [118, 119]. Indeed reward-related neurons shift their firing patterns in the course of learning, from signalling reward directly to signalling the expected future reward based on cues associated with later reward, consistent with a reward prediction error based on temporal differences [118].

The main shortcoming of such “model-free” methods for learning optimal control policies is that they are prohibitively slow. When applied to naturalistic motor control tasks with high-dimensional, non-linear and continuous state-spaces (corresponding to the roughly 600 muscles that are controlled by the nervous system) potentially combined with complex object manipulation, it becomes clear than human motor learning is unlikely to be based on these methods alone due to the time it takes to produce control policies with human-level performance. Furthermore, environment dynamics can transform unexpectedly and the goals of an organism may change depending on a variety of factors. Taken together, this suggests that humans and animals must integrate alternative algorithms in order to flexibly and rapidly adapt their behavior. In particular, internal forward models can be used to predict the performance of candidate control strategies without actually executing them as originally envisaged by Craik [4] (Fig. 1, Motor planning). These internal model simulations and evaluations (which operate over relatively long timescales compared to the previously discussed internal forward models) can be smoothly integrated with reinforcement learning [115] and approximate inference methods [120]. Thus, motor planning may be accomplished much faster, and more robustly, using internal forward models. Indeed, trajectory “roll-outs” [121] and local searches [122] form key components of many state-of-the-art learning systems.

3.3.2. Prediction for planning

Planning refers to the process of generating novel control policies internally rather than learning favorable motor outputs from repeated interactions with the environment (Fig. 1, Motor planning). Internal forward modeling on timescales significantly longer than those implemented in state estimation, contribute significantly at this point in the sensorimotor control process. Ultimately, once a task has been specified and potential goals identified, the brain needs to generate a complex spatiotemporal sequence of muscle activations. Planning this sequence at the level of muscle activations is computationally intractable due to the curse of dimensionality [124]. Specifically, the number of states (or volume in the case of a continuous control problem) which must be evaluated scales exponentially with the dimensionality of the state-space. This issue similarly afflicts the predictive performance of forward dynamic models where state-space dimensionality is determined by the intricate structure and nonstationarity of the musculoskeletal system and the wider external world. Biological control hierarchies have been described across the spectrum of behavioral paradigms from movement primitives and synergies in motor control [125] to choice “fragments” in decision-making [126]. From a computational efficiency perspective, this allows low-level, partially automated, components to be learned separately but also flexibly combined in order to generate broader solutions in a hierarchical fashion thus economising control by enabling the nervous system to curtail the number of calculations it need make [127]. For example, one does not learn to play the piano note-by-note but practices layers and segments of music in isolation before combining these fluent “chunks” together [128].

Given the hierarchical structure of the motor system, motor commands may be represented, and thus planned, at multiple levels of abstraction. Different levels of abstraction are investigated in distinct fields of neuroscience research which focus on partially overlapping sub-systems. However, here we take a holistic view and do not focus on arbitrary divisions between components of an integrated control hierarchy. At the highest level, if multiple possible goals are available, a decision may be made regarding which is to be the target of movement. Neuroimaging [129] and single-unit recordings [130] suggest that scalar values associated with goal states are encoded in an area of the brain known as the ventromedial prefrontal cortex. Then, by comparing such value signals, a target is established. Selections between food options is often used to study neural value representation since food is a primary reinforcer. In such an experiment, when confronted with novel goals which have never been encountered before, the brain synthesizes value predictions from memories of related goals in order to make a decision [131]. The precise mechanism by which this is accomplished is still under investigation, but these results require an internal representation that is sensitive to the relational structure between food items, possibly embedded in a feature space of constitute nutrients, and a generalization mechanism with which new values can be constructed. Such an internal representation and mechanism can be embedded within the probabilistic rationality framework. Let x be a vector of goal features, then the value v can be modeled as the latent variable to be inferred. Based on this representation, a “value recognition” model p(v|x) can be trained using experienced goal/value pairs and used to infer the value of a novel item. Analogously, in the example of tennis, a player who has scored points from hitting to the backhand as well as performing a dropshot, may reasonably infer that a dropshot to the backhand will be successful.

In psychology and neuroscience, the process by which decision variables in value-based and perceptual decision-making are retrieved and compared is described mechanistically by evidence integration or sequential sampling models [132]. Within the probabilistic framework elaborated in section 2, these models can be considered as iterative approximate inference algorithms [133]. There is both neural [36] and behavioral [134] evidence for their implementation in the brain. These sampling processes have been extended to tasks which require sequential actions over multiple states of control [135]. A network of brain structures, primarily localized to prefrontal cortical areas, has been hypothesized to encode an internal model of the environment at the “task-level” which relates relatively abstract representations of states, actions, and goals [136, 137]. From a probabilistic perspective, this internal model can then be “inverted” via Bayesian inference in order to compute optimal actions [133]. In order to accomplish this, one heuristic strategy is to simply retrieve memories of past environment experiences based on state similarity as a proxy for internal forward modeling. In the human brain, this process appears to be mediated by the hippocampus [138].

Once a goal has been established, the abstract kinematic structure of a movement and the final state of the end effector (e.g. hand) may be planned, a stage which may be referred to as action selection. One line of evidence for the existence of such motor representations is based on the “hand path priming effect” [139]. In these studies, participants are required to make obstacle-avoiding reaching movements. However, when cued to do so in the absence of obstacles, they appear to take unnecessarily long detours around the absent obstacle as before. Such suboptimal movements are inconsistent with optimal feedback control but are thought be due to the efficient re-use of the abstract spatiotemporal form of the previously used movements. When such representations are available in the nervous system (as in the hand-path priming task), it is possible that they may be re-used in forward modeling simulations during motor planning. When combined with sampling strategies [120], the retrieval of abstract motor forms could provide a computational foundation for the mental rehearsal of movement and may be relatively efficient when applied at a high level of abstraction in the motor hierarchy.

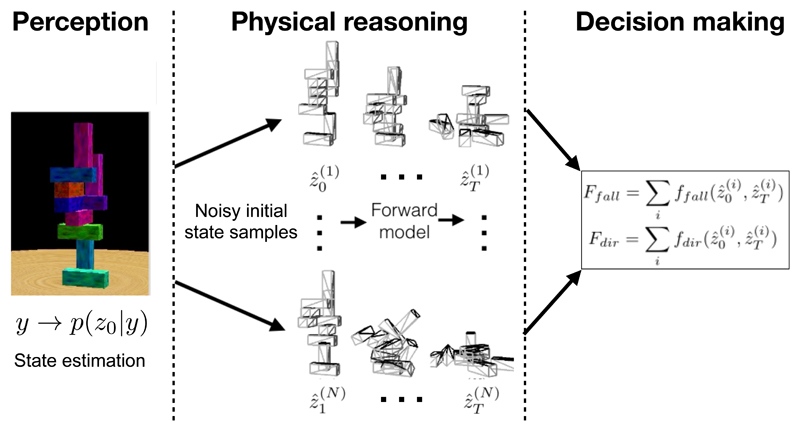
In tasks involving complex object interactions, it may be particularly important to internally simulate the impact of different control strategies on the environment dynamics in order to avoid catastrophic outcomes as envisaged by Craik. Recent research has shown that human participants were able to make accurate judgments regarding the dynamics of various visual scenes involving interacting objects under the influence of natural physical forces (Fig. 3). This putative “intuitive physics engine” [123], which combines an internal model approximating natural physics with Monte Carlo sampling procedures, could be directly incorporated into motor planning within the probabilistic framework. Consider, for example, the problem of carrying a tray piled high with unstable objects. By combining internal simulations of the high-level features of potential movement plans with physical reasoning about the resulting object dynamics, one would be able to infer that it is more stable to grip the tray on each side rather than in the center and thus avoid having the objects fall to the floor. Thus, internal forward models can make a crucial contribution at the planning stage of control by simulating future state trajectories conditional on motor commands. In addition, it may be necessary to implement this processing at a relatively high level of the motor hierarchy in order to do so efficiently given the complexity of the simulations. In the context of the tray example, the critical feature of the motor movement in evaluating the stability of the objects is the manner in which the tray is gripped. Thus, simulating the large number of possible arm trajectories which move the hand into position is irrelevant to the critical success of the internal modeling. Identifying the essential abstract features of movement to input into a forward modeling process may be a crucial step in planning complex and novel movements.

Figure 3. Physical reasoning.

Participants must decide if a complex scene of blocks will fall and if so the direction of the fall. A model of their performance combines perception, physical reasoning, and decision-making. Left. A Bayesian model of perception uses the sensory input y to estimate participant’s belief p(z₀|y) regarding environment states such as the position, geometry, and mass of the blocks. Middle. Stochastic simulations based on samples from the posterior are performed using a noisy and approximate model of the physical properties of the world. The simulations use a forward model to sample multiple (superscripts) state trajectories over time (subscripts) ${\widehat{\mathbf{\text{z}}}}^{(i)}=({\widehat{z}}_0^{(i)},\dots ,{\widehat{z}}_T^{(i)}).$ Right. The outputs of this “intuitive physics engine” can then be processed to make judgments, such as the probability that the tower block will fall (F_fall) and the direction of the fall (F_dir). Experiments have indicated that humans are adept at making rapid judgments regarding the dynamics of such complex scenes and these judgments are consistent with predictions generated using this model which includes approximate Bayesian methods combined with internal forward models. Modified with permission from [123].

4. Conclusions and Future Directions

We have presented a formal integration of internal models with the rationality frameworks of Bayesian inference and optimal feedback control. In doing so we have used the probabilistic formalism in order to review the various applications of internal models across a range of spatiotemporal scales in a unified manner. Although many aspects of the computations underpinning processes such as sensory reafference cancellation and state estimation are well understood, the motor planning process remains poorly understood at a computational level. OFC provides a principled way in which a task can be associated with a cost leading to an optimal control law that takes into account the dynamics of the body and the world as well as the noise processed involved in sensing and actuation. The theory is consistent with a large body of behavioral data. OFC relies on state estimation which itself relies on internal models which are also of general use in a variety of processes and for which there is accumulating behavioral and neurophysiological evidence.

There are still major hurdles to understanding OFC in biology. First, it is unclear how a task specifies a cost function. While for a simple reaching movement it may be easy to use a combination of terminal error and energy, the links to cost are much less transparent in many real-world tasks. For example, when a person needs to remove keys from their pocket or tie shoelaces, specifying the correct cost function is itself a difficult calculation to make. Second, although OFC can consider arbitrarily long (even infinite) horizon problems, people clearly plan our actions under finite horizon assumptions by establishing a task-relevant temporal context. It is unclear how the brain temporally segments tasks and the extent to which each task is solved independently [127]. Third, given a task context and a cost function or goal specification, fully solving OFC in a reasonable amount of time for a complex system such as the body is intractable. The brain must use approximations to the optimal solution which are as yet unknown although there are a variety of machine learning methods [140] which may provide inspiration for such investigations. Fourth, the representation of state is critical for OFC but how state is constructed and used is largely unknown though there are novel theories, with some empirical support, regarding how large state spaces could be modularized hierarchically to make planning and policy encoding efficient [75]. Finally, the neural basis of both OFC and internal models is still in its infancy. However, the elaboration of optimal feedback control within the brain will take advantage of new techniques for dissecting neural circuitry such as optogenetics, which have already delivered new insights into the neural basis of feedback-based sensorimotor control [141, 142].

Although some behavioral signatures and neural correlates of the computational principles by which plans are formed have been identified, this has primarily occurred in tasks containing relatively small state and action spaces such as sequential decision-making and spatial navigation. In contrast, the processes by which biological control solutions spanning large and continuous state-spaces are constructed remains relatively unexplored. Future investigations may need to embed rich dynamical interactions between object dynamics and tasks goals in novel and complex movements. Such task manipulations may generate new insights into motor planning since the motor planning process may then depend on significant cognitive input. This may reveal a more integrative form of planning across the sensorimotor hierarchy.

Costs, Rewards, Priors, and Parsimony.

Critics of optimal control theories of motor control point out that one can always construct a cost function to explain any behavioral data (at the extreme the cost can be the deviations of the movement from the observed behavior). Therefore, to be a satisfying model of motor control, it is crucial that the assumed costs, rewards, and priors be well-motivated and parsimonious. Initial work on optimal motor control used cost functions which did not correspond to ecologically relevant quantities. For example, extrinsic geometric “smoothness” objectives such as “jerk” [44] or the time derivative of joint torque [45] do not directly relate to biophysically important variables. In contrast, OFC primarily penalizes two components in the cost. The first component is an energetic or effort cost. Such costs are widespread to modelling animal behavior and provide well-fitting cost functions when simulating muscle contractions [68] and walking [69, 70] suggesting that such movements tend to minimize metabolic energy expenditure. By representing effort as energetic cost discounted in time it is possible to account for both the choices animals make and the vigor of their movements [71]. The second component quantifies task success is typically represented by a cost on inaccuracy. When explicit costs or rewards are placed by experimenters on a task element (such as a target position), people are usually able to adapt their control to be close to optimal in terms of optimizing such explicit objectives [72, 73, 74]. The parsimony and the experimental benefits of a model where experimenter specifies costs at the task-level are not present in “oracular” motor control models, which requires an external entity to provide a detailed prescription for motor behavior. Early theories of biological movement were often inspired by industrial automation. Research tended to focus on how reference trajectories for a particular task were executed rather than planned. For any given task, there are infinitely many trajectories that reach a desired goal, and infinitely many others that do not, and the problem of selecting one is off-loaded to a trajectory oracle reminiscent of industrial control engineers serving as the “deus ex machina”. As a theory of biological movement, this is problematic. Oracles can select movement trajectories, not necessarily to “solve” the task in an optimal manner (as would be the goal in industrial automation), but to fit movement data.

Summary Points.

1. Optimal feedback control and Bayesian estimation are rational principles for understanding human sensorimotor processing.

2. Internal models are necessary to facilitate dexterous control.

3. Forward models can assist in sensory filtering, state estimation and planning.

4. Modular internal models can mitigate the curse of dimensionality in sensorimotor control.

Future Issues.

1. Given a motor task, how are a state representation and cost function constructed?

2. What are the neural algorithms by which the solution to optimal feedback control is approximated?

3. How are internal models structured?

4. Are similar circuit mechanisms implemented across different prediction timescales?