Analytical study of the numerical aperture of cone-shaped optical fibers: A tool for tailored designs

Abstract

In this work, a set of analytical expressions to tailor the numerical aperture of cone-shaped step optical fibers is proposed. The expressions are derived from the geometrical study of light-ray tracing at the cone-shaped tip of a regular step-index optical fiber. Analysis of the different physical phenomena that can take place at the tip of the fiber led to numerical apertures ranging from 0 to 1.5 which can be achieved via a variety of cone angles, providing great versatility in the design of light sources or light collecting devices based on step-index optical fibers.

1. Introduction

The numerical aperture (NA) is a parameter to measure the capabilities of an optical system to gather light; the larger the NA, the wider the angle in which the system can accept light. When the optical system is utilized for illumination purposes, the NA tells the user about the emitting angle of the light projected by the imaging system. Likewise, the larger the NA, the wider the illumination angle.

In the case of optical fibers, the NA has the same meaning as in any optical system, telling about the capabilities of the optical fiber to gather and/or to emit light. In either case, gathering or emission of light, an optical fiber with the largest possible NA to guarantee the largest accepting or emitting cones of light is desired. As for the case of step index optical fibers, the numerical aperture is determined by the refractive index of the core $n_{co}$ and the cladding $n_{cl}$, namely $NA=n\sin \beta =\sqrt{n_{co}^2-n_{cl}^2}$, being $\beta$ the semi-angle of emission or gathering of light, and $n$ the refractive index of the surrounding medium. From this equation, it can be deducted that the difference between the refractive indexes must be maximized to have that largest possible NA. Commercially, ultra-high NA optical fibers are limited up to 0.35, which leads to a cone of acceptance or emission of the order of just 41. This figure could be quite small for many applications [1, 2, 3, 4]; therefore, different options have been utilized to increase the numerical aperture: photonic-crystal fibers [5, 6, 7], or shaped optical fibers [8, 9, 10]. In the former, the NA is increased thanks to an increment of the effective refractive index of the core. In the latter, the distal end of the optical fiber is geometrically modified.

Owing to the elaborated engineering process to produce photonics-crystal fibers, shaping is the most accessible method to increase the NA of the optical fibers. Multiple techniques have been reported to modify the geometry of the optical fiber tip; these include mechanical [11, 12, 13, 14], thermal [15], laser-aided [16, 17], and chemical etching processes [18, 19, 20, 21, 22, 23].

Despite of the great spectrum of applications of cone-shaped optical fibers [11, 20, 23, 24, 25] and the multiple options that have been reported to produce them [1, 2, 3, 4, 5, 6, 7], up to the best knowledge of the authors there has not been an in-depth analysis on how the geometry of the distal end of the optical fiber is linked to the NA. Only a brief description has been reported elsewhere [26], and a preliminary ray-tracing analysis that does not account for all the phenomena that can take place in the cone-shaped surface has been carried out in [27]. For this reason, in this work we present an analytical design to tailor the numerical aperture of cone-shaped step optical fibers which can be utilized as a guideline for their production.

2. Analysis

The numerical aperture $NA=n\text{sin}\beta$ demands an unambiguous definition of the angle $\beta$ as the light is gathered or emitted. In the case of cone-shaped optical fibers aimed to be used as illumination sources, $\beta$ is the angle measured with respect to the cone axis of the refracted-out ray in the core-surrounding medium interface, as illustrated in Fig. 1. For sake of simplicity, only the sagittal plane is represented in figure. A coarse light-ray analysis on this plane shows that the angle $\beta$ varies according to the phenomena that the incident ray on that cone-shaped surface suffers; (a) a simple refraction, (b) one total internal reflection, or (c) multiple total internal reflections. These cases are the phenomena that are finally controlled by the incident angle,${\theta }_i$ of the incoming ray over the cone-shaped surface; this latter angle is measured as illustrated in Fig. 1. In the same figure, one can realize that the incident angle ${\theta }_i$ can be controlled by the semi-angle of the cone tip, $\alpha$, measured with respect to the optical axis of the step optical fiber. In summary, the NA, namely the angle$\beta$if the fiber is immersed in a refractive index $n=1$, can be engineered as a function of the semi-angle of the tip in a step optical fiber for each of the phenomena that can take place on the cone-shape surface.

Fig. 1.

Step optical Fiber with a cone-shaped tip. $n$, $n_{cl}$ and $n_{co}$ are the refractive indexes of the surrounding medium, the cladding, and the core, in that order. A ray incident on the cone-shaped surface can suffer, depending on ${\theta }_i$, (a) a simple refraction, (b) one total internal reflection, or (c) multiple total internal reflections.

For the light to impinge at the cone-shaped surface, initially it must be guided by the step optical fiber. Since the mode coupling could significantly change the characteristics of the light propagating along the fiber, this proposed analytical study can be used only for short fiber lengths (a few meters in plastic optical fibers or few hundred of meters in silica optical fibers) [28, 29]. In consequence, a step-index optical fiber is considered in this study. The light guiding is only possible if a total internal reflection takes place at the core-cladding interface. This mandatory condition leads to the rule

$$\theta \ge {\theta }_c=\text{arcsin}\frac{n_{cl}}{n_{co}}$$ (1)

with $\theta$ measured as shown in Fig. 1. Effective coupling and propagation of the launched beam at the input facet of the optical fiber is assumed. Upon these assumptions, any ray reaching the cone-shaped surface must impinge the core-cladding interface at most at the critical angle, which is only possible for rays within the acceptance angle of the of the optical fiber; namely for rays within the NA of step-index optical fibers. Light-ray guided in the optical fiber impinges on the cone-shaped surface at an angle of ${\theta }_i=\theta -\alpha$, which for the limit-case in Eq. (1) turns into

$${\theta }_i={\theta }_c-\alpha \text{.}$$ (2)

On the cone-shaped surface, the ray can suffer any of the three aforementioned phenomena which are analyzed in the following subsections. It should be emphasized that a propagated or guided ray undergoes one of the three phenomena depending exclusively on the angle of the cone-shaped surface with no dependence on the size of the illumination at the input facet of the optical fiber.

2.1. Simple refraction

In this first case, the light-ray at the cone-shaped surface should impinge at an angle such that it does not experience total internal reflection at the core-medium interface, as shown in Fig. 2, namely

$${\theta }_i<{\theta }_c^{\text{'}}=\text{arcsin}\frac{n}{n_{\text{co}}}\text{.}$$ (3)

Fig. 2.

Scheme of a cone-shaped step optical fiber with tapered tip at an angle α such that$\alpha >arcsin\left(n_{cl}/n_{co}\right)-arcsin\left(n/n_{co}\right).$ Under this condition the incident ray suffers a simple refraction at the cone-shaped surface.

Considering that $\alpha ={\theta }_c-{\theta }_i,$the semi-angle of the cone-shaped tip must be

$$\alpha >{\theta }_c-{\theta }_c^{\text{'}}.\alpha >\arcsin \frac{n_{\text{cl}}}{n_{\text{co}}}-\arcsin \frac{n}{n_{\text{co}}}.$$ (4)

Eq. (4) expresses the angle of the cone-shaped step optical fiber in terms of the index of refraction of the core, the cladding, and the surrounding medium of the step optical fiber, something that is highly wanted in engineering. Now, to connect the cone-shaped angle $\alpha$ with the numerical aperture $NA=n\text{sin}\beta$, requires Snell's law to be applied at the core-medium interface, which can be expressed as

$$\text{sin}\left({\theta }_c-\alpha \right)=n\text{sin}\left(\frac{\pi }{2}-\beta -\alpha \right)\text{,}$$ (5)

which after some algebra allows the numerical aperture for a cone-shaped step optical fiber with a tip angle $\alpha >\text{arcsin}{n}_{\text{cl}}/n_{\text{co}}-\text{arcsin}n/n_{\text{co}}$ to be expressed as

$$\text{NA}\left(\alpha \right)=n\text{cos}\left\{\alpha +\text{arcsin}\left[\frac{n_{\text{co}}}{n}\text{sin}\left(\arcsin \frac{n_{\text{cl}}}{n_{\text{co}}}-\alpha \right)\right]\right\}\text{.}$$ (6)

In Fig. 3, a plot of Eq. (6) for a commercial multi-mode step optical fiber (Thorlabs® FG025LJA, 1.4577 $n_{\text{cl}}$/$1.4611n_{\text{co}}$, pure silica core/fluorine-doped silica cladding) surrounded by air is shown. From this figure, it can be seen that by tuning the angle of the cone-shaped optical fiber from $\alpha =42.9°$to $\alpha =90°$, numerical apertures ranging from 0 to 0.64 can be achieved.

Fig. 3.

Plot of NA vs. semi-angle α for a commercial multi-mode fiber FG025LJA with a cone-shaped such that $\alpha >arcsin\left(n_{cl}/n_{co}\right)-arcsin\left(n/n_{co}\right).$

2.2. One total internal reflection

As for the case of one total internal reflection on the cone-shaped surface, the incident angle ${\theta }_i$ at ① must fulfill the condition given by

$${\theta }_i\ge {\theta }_c^{\text{'}}=\text{arcsin}\frac{n}{n_{\text{co}}}.$$ (7)

Once again, accounting for the fact that $\alpha ={\theta }_c-{\theta }_i$, to have one total internal reflection on the surface ①, the semi-angle of the cone-shape tip must be

$$\alpha \le {\theta }_c-{\theta }_c^{\text{'}}.\alpha \le \arcsin \frac{n_{\text{cl}}}{n_{\text{co}}}-\arcsin \frac{n}{n_{\text{co}}}.$$ (8)

After this total internal reflection on the cone-shaped surface ①, the light ray must be refracted out on the cone-shaped surface ②. For this refraction to happen at the core-medium interface, the cone semi-angle $\alpha$ must be chosen such that the incident angle ${\theta }_i^{\text{'}}$, see Fig. 4, fulfills the condition ${\theta }_i^{\text{'}}<{\theta }_c^{\text{'}}=\text{arcsin}n/n_{\text{co}}$. From Fig. 4, ${\theta }_i^{\text{'}}={\theta }^{\text{'}}-2\alpha$ or ${\theta }_i^{\text{'}}={\theta }_c-3\alpha .$

Fig. 4.

Scheme of a cone-shaped step optical fiber with tapered tip at a semi-angle α such that $\left(arcsin\left(n_{cl}/n_{co}\right)-arcsin\left(n/n_{co}\right)\right)/3<\alpha \le arcsin\left(n_{cl}/n_{co}\right)-arcsin\left(n/n_{co}\right).$Under this condition the incident ray suffers one total internal reflection on the cone-shaped surface ① and it is refracted out at the cone-shaped surface ②.

According to the latter expression, the condition ${\theta }_i^{\text{'}}<{\theta }_c^{\text{'}}=\text{arcsin}n/n_{\text{co}}$ is equivalent to:

$$\alpha >\left(\text{arcsin}\frac{n_{\text{cl}}}{n_{\text{co}}}-\text{arcsin}\frac{n}{n_{\text{co}}}\right)/3\text{.}$$ (9)

Eqs. (8) and (9) determine the limits that the semi-angle of the cone-shaped tip must fulfill for the guided light-ray to suffer one single internal reflection and thereafter be refracted out from the cone-shaped step optical fiber, namely:

$$\left(\text{arcsin}\frac{n_{\text{cl}}}{n_{\text{co}}}-\text{arcsin}\frac{n}{n_{\text{co}}}\right)/3<\alpha \le \left(\text{arcsin}\frac{n_{\text{cl}}}{n_{\text{co}}}-\text{arcsin}\frac{n}{n_{\text{co}}}\right)\text{.}$$ (10)

On applying Snell's law at the core-medium interface ② with the use of auxiliary angles shown in Fig. 4, the numerical aperture can be expressed as a function of the cone-shaped semi-angle $\alpha$ as:

$$\text{NA}\left(\alpha \right)=n\text{cos}\left\{\alpha +\text{arcsin}\left[\frac{n_{\text{co}}}{n}\text{sin}\left(\arcsin \frac{n_{\text{cl}}}{n_{\text{co}}}-3\alpha \right)\right]\right\}\text{.}$$ (11)

In Fig. 5, Eq. (8) is plotted for a commercial multi-mode fiber (Thorlabs FG025LJA) surrounded by air. Numerical apertures ranging from 0 to 1 can be achieved by tuning the angle of the cone-shaped optical fiber from $\alpha =14.3°$ to $\alpha =42.9°$ which shows the opportunity to obtain step optical fibers with actual high numerical apertures.

Fig. 5.

Plot of NA vs. semi-angle α for a commercial multi-mode fiber (Thorlabs FG025LJA) with a conical tip when $\left(arcsin\left(n_{cl}/n_{co}\right)-arcsin\left(n/n_{co}\right)\right)/3<\alpha \le arcsin\left(n_{cl}/n_{co}\right)-arcsin\left(n/n_{co}\right).$

2.3. Multiple internal reflections

The third phenomenon that can arise at the cone-shaped tip of the step index optical fiber is the occurrence of multiple internal reflections. This manuscript presents the situation where only two internal reflections happen. The first total internal reflection happens at cone-shaped surface ① and the second on the cone-shaped surface ②. Thereafter, the light-ray is refracted out on the cone-shaped surface ①, as shown Fig. 6. For total internal reflection to occur on the cone-shaped surface ②, after being totally internally reflected at surface ①, the incident angle ${\theta }_i^{\text{'}}$ must fulfill the condition

$${\theta }_i^{\text{'}}\ge {\theta }_c^{\text{'}}=\text{arcsin}\frac{n}{n_{\text{co}}}.$$ (12)

Fig. 6.

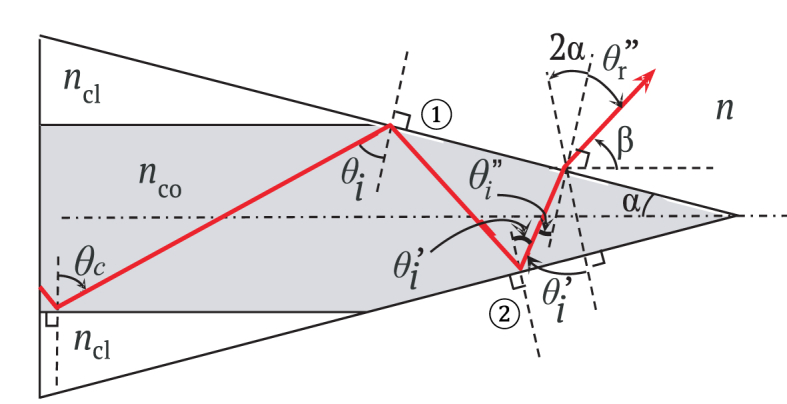
Scheme of a cone-shaped step optical fiber with tapered tip at a semi-angle α such that $\frac{\left(\text{arcsin}\left(n_{\text{cl}}/n_{\text{co}}\right)-\text{arcsin}\left(n/n_{\text{co}}\right)\right)}{5}<\alpha \le \frac{\left(\text{arcsin}\left(n_{\text{cl}}/n_{\text{co}}\right)-\text{arcsin}\left(n/n_{\text{co}}\right)\right)}{3}.$Under this condition the incident ray suffers one total internal reflection on the cone-shaped surface ①, one total internal reflection on the cone-shaped surface ②, and thereafter is refracted out at the cone-shaped surface ①.

Eq. (12) implies that $\alpha <\frac{\left(\text{arcsin}\left(n_{\text{cl}}/n_{\text{co}}\right)-\text{arcsin}\left(n/n_{\text{co}}\right)\right)}{3}$ as aforementioned for the case of a one total internal reflection.

Note that for the light-ray refracted out on the cone-shaped surface ①, cone semi-angle $\alpha$ must be chosen such that the incident angle ${\theta }_i^{\text{'}\text{'}}$ fulfills the condition ${\theta }_i^{\text{'}\text{'}}<{\theta }_c^{\text{'}}=\text{arcsin}n/n_{\text{co}}$. After some algebra with the geometry and the auxiliary angles illustrated in Fig. 6, one can arrive to the condition ${\theta }_i^{\text{'}}={\theta }_c-5\alpha$, which leads to an extra limit to the value of semi-angle cone-shaped tip

$$\alpha >\left({\theta }_c-{\theta }_c^{\text{'}}\right)/5\text{.}$$ (13)

Thus, the limits that the semi-angle cone-shaped tip must fulfill for the light-ray guided ray to suffer two internal reflections and thereafter being refracted out from the cone-shaped step optical fiber are given by

$$\frac{\left(\text{arcsin}\frac{n_{\text{cl}}}{n_{\text{co}}}-\text{arcsin}\frac{n}{n_{\text{co}}}\right)}{5}<\alpha \le \frac{\left(\text{arcsin}\frac{n_{\text{cl}}}{n_{\text{co}}}-\text{arcsin}\frac{n}{n_{\text{co}}}\right)}{3}\text{.}$$ (14)

Again, using Snell's law at the core-medium interface ② with the auxiliary angles shown in Fig. 6, the numerical aperture in this case is expressed as a function of the semi-angle cone-shaped $\alpha$ as

$$\text{NA}\left(\alpha \right)=n\text{cos}\left\{\alpha +\text{arcsin}\left[\frac{n_{\text{co}}}{n}\text{sin}\left(\arcsin \frac{n_{\text{cl}}}{n_{\text{co}}}-5\alpha \right)\right]\right\}\text{.}$$ (15)

The equations that have been derived in this paper also show the opportunity to surround the cone-shape optical fiber with mediums with higher refractive indexes than air to increase even further the achieved numerical apertures. To use this possibility, Eq. (15) has been plotted for a multi-mode fiber (Thorlabs FG025LJA) surrounded by different mediums, air (n = 1), water (n = 1.33), and immersion oil for microscopy (n = 1.515). Results are shown in Fig. 7. In this particular case, it can be noted that by choosing the angle of the cone-shaped optical fiber from $\alpha =8.58°$ to$\alpha =14.3°$, numerical apertures up to 0.77 for air, up to 1.12 for water, and up to 1.31 for immersion oil can be achieved, providing great versatility in the design of this kind of light sources or light collecting devices. As was expected, the surrounding of the cone-shape optical fiber with mediums with refractive indexes higher than one leads to the very wanted option of numerical apertures also higher than one, a feature very much wanted in many applications.

Fig. 7.

The plot of NA versus α for the commercial multi-mode fiber Thorlabs FG025LJA with tapered tip at an angle α such $\frac{\left(\text{arcsin}\left(n_{\text{cl}}/n_{\text{co}}\right)-\text{arcsin}\left(n/n_{\text{co}}\right)\right)}{5}<\alpha \le \frac{\left(\text{arcsin}\left(n_{\text{cl}}/n_{\text{co}}\right)-\text{arcsin}\left(n/n_{\text{co}}\right)\right)}{3}$.

The results of the carried out geometrical analysis that allowed Eq. (6), Eq. (11), and Eq. (15) to be obtained, allow a generalization to be made for the case of more than two total internal reflections. After a said number $m$ of total internal reflections, the numerical aperture, expressed as a function of the semi-angle cone-shaped $\alpha$, can be written as

$$NA\left(\alpha \right)=n\text{cos}\left\{\alpha +\text{arcsin}\left[\frac{n_{\text{co}}}{n}\text{sin}\left(\arcsin \frac{n_{\text{cl}}}{n_{\text{co}}}-\left(2m+1\right)\alpha \right)\right]\right\}.$$ (16)

Where $m=\mathrm{1,2,3},\dots ,N$. For a value of $m$, this equation is valid for the range of $\alpha$ values that satisfy the condition:

$$\left(\text{arcsin}\frac{n_{\text{cl}}}{n_{\text{co}}}-\text{arcsin}\frac{n}{n_{\text{co}}}\right)/\left(2m+1\right)<\alpha <\left(\text{arcsin}\frac{n_{\text{cl}}}{n_{\text{co}}}-\text{arcsin}\frac{n}{n_{\text{co}}}\right)/m.$$ (17)

The parametric Eq. (16) can be used to design cone-shaped optical fibers with a specific numerical aperture after the light-ray being totally internal reflected $m$ times. Fig. 8 shows the NA for a commercial multi-mode fiber (Thorlabs FG025LJA) surrounded by air, vs. semi-angle $\alpha$, whose ranges of values are determined for the total internal reflections of $m$ = 0, $m$ = 1, $m$ = 2 and $m$ = 3, according to the condition imposed by Eq. (17). It can be seen that it is possible to obtain the same numerical aperture for different cone angles. The number $m$ is chosen at the designer's convenience. A number $m=0$ corresponds with cone tips with large angles, $m=1$ allows the largest numerical apertures to be achieved, while $m=2$and $m=3$exhibit changes dramatically in the numerical aperture with small variations of the cone angle, and therefore, a precise control in the cone fabrication would be required to ensure the desired value of NA.

Fig. 8.

Plot of NA vs. semi-angle $\alpha$ for a commercial multi-mode fiber (Thorlabs FG025LJA) surrounded by air.

3. Conclusions

A simple and compact design equation to tailor the numerical aperture of cone-shaped optical fibers was presented in this work. This parametric equation can be used to design illumination sources or light gathering systems based on cone-shaped optical fibers with a specific numerical aperture. According to the analytic design, cone-shaped optical fibers with numerical apertures up to 1 for air, up to 1.33 for water, and up to 1.5 for immersion oil can be achieved from the convenient selection of the cone angle.

The presented design equations provide the production of a cone-shaped optical with a given numerical aperture through a variety of cone semi-angles. This feature allows the user to select the angle that fits better with the design needs according to the manufacturing capabilities available.

Declarations

Author contribution statement

Brayan Patiño-Jurado: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Juan F. Botero-Cadavid, Jorge Garcia-Sucerquia: Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Funding statement

This work was supported by Convocatoria nacional para el apoyo al desarrollo de tesis de posgrado o de trabajos finales de especialidades en el área de la salud, de la Universidad Nacional de Colombia 2017-2018 and Colciencias through the calling 761 of 2016 –Program of Young Researchers.

Competing interest statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.