Indirect, referent control of motor actions underlies directional tuning of neurons

Abstract

Many neurons of the primary motor cortex (M1) are maximally sensitive to “preferred” hand movement directions and generate progressively less activity with movements away from these directions. M1 activity also correlates with other biomechanical variables. These findings are predominantly interpreted in a framework in which the brain preprograms and directly specifies the desired motor outcome. This approach is inconsistent with the empirically derived equilibrium-point hypothesis, in which the brain can control motor actions only indirectly, by changing neurophysiological parameters that may influence, but remain independent of, biomechanical variables. The controversy is resolved on the basis of experimental findings and theoretical analysis of how sensory and central influences are integrated in the presence of the fundamental nonlinearity of neurons: electrical thresholds. In the presence of sensory inputs, electrical thresholds are converted into spatial thresholds that predetermine the position of the body segments at which muscles begin to be activated. Such thresholds may be considered as referent points of respective spatial frames of reference (FRs) in which neurons, including motoneurons, are centrally predetermined to work. By shifting the referent points of respective FRs, the brain elicits intentional actions. Pure involuntary reactions to perturbations are accomplished in motionless FRs. Neurons are primarily sensitive to shifts in referent directions, i.e., shifts in spatial FRs, whereas emergent neural activity may or may not correlate with different biomechanical variables depending on the motor task and external conditions. Indirect, referent control of posture and movement symbolizes a departure from conventional views based on direct preprogramming of the motor outcome.

INTRODUCTION

Since the classical studies by Georgopoulos and colleagues, it is known that many neurons of the primary motor cortex (M1) are maximally sensitive to specific, “preferred” directions of arm movement and generate progressively less activity during movements in other directions (Amirikian and Georgopoulos 2000; Ashe and Georgopoulos 1994; Caminiti et al. 1990, 1991; Fu et al. 1995; Georgopoulos and Carpenter 2015; Georgopoulos et al. 1982, 1983, 1988; Kalaska et al. 1989; Moran and Schwartz 1999a, 1999b; Schwartz 2016; Schwartz and Moran 1999; Sergio et al. 2005). This property of neurons is described by a directional tuning curve usually approximated by a cosine function of the angular deflection of the preferred from the actual direction of arm movement. Preferred directions differ for different neurons. Neurons are also sensitive to the direction of isometric forces when the hand is pushing against a motionless joystick (Georgopoulos and Carpenter 2015; Sergio and Kalaska 1998; Sergio et al. 2005). For clarity, in this review, the term “motor direction” will refer to both movement and isometric tasks. The term “motor commands” will only refer to the output activity of α-motoneurons (MNs) or electromyographic (EMG) activity recorded from muscles. Directional sensitivity is also characteristic of neurons of other brain areas and α-MNs (e.g., Brink et al. 1984). The integral activity of a population of direction-sensitive neurons is usually characterized by a neuronal population vector comprising individual contributions of neurons to the chosen hand motor direction. These contributions (weights) are determined from the tuning curves. With some exceptions (Kurtzer and Herter 2007; Scott et al. 2001; Sergio et al. 2005) discussed by Georgopoulos et al. (2007), the population vector of M1 neurons usually points to the motor direction.

Depending on the motor task, M1 activity can also correlate with other aspects of motor actions, particularly the movement extent, speed, motor commands (EMG patterns), muscle torques, grip forces, and composite kinematic variables characterizing interjoint coordinations–synergies (Cabel et al. 2001; Cheney et al.1985; Evarts 1968; Fetz and Cheney 1980; Georgopoulos et al. 1992; Hatsopoulos 2005; Hepp-Reymond et al. 1999; Holdefer and Miller 2002; Humphrey et al. 1970, 1978; Kalaska et al. 1989; Lemon and Mantel 1989; Maier et al. 1993; Park et al. 2004; Poliakov and Schieber 1999; Sergio and Kalaska 1997, 2003; Smith et al. 1975; Taira et al. 1996).

Neurophysiological findings in studies of brain function in the control of motor actions are predominantly interpreted in a standard biomechanical framework based on the assumption that the nervous system preprograms and directly specifies one or a combination of kinematic and kinetic variables or EMG patterns describing the motor outcome. For instance, based on the analysis of arm reaching, it was hypothesized that as a group, M1 neurons directly code motor actions by predetermining aspects of motor trajectories (direction, velocity profile, and extent) that are transformed into requisite motor commands at the level of the neuromuscular periphery, including spinal networks (Georgopoulos 1996; Georgopoulos and Carpenter 2015). Based on studies of other motor tasks, researchers also proposed that the M1 directly specifies EMG patterns, muscle forces, or combinations of kinematic and kinetic variables that meet the task demand (Omrani et al. 2017).

Most researchers analyzing M1 activity do not consider the alternative possibility that neurophysiological variables underlying the control of motor actions may not be found within the biomechanical framework. This possibility follows from the empirically derived equilibrium-point hypothesis, now advanced to the theory of indirect, referent control of action and perception (Feldman 2015). Strong support to this theory as well as for indirect control of motor actions by M1 is derived from recent findings that corticospinal influences can be decorrelated from kinematic and kinetic variables, including EMG patterns, such that these influences only predetermine where, in the spatial domain or frame of reference (FR), α-MNs can be activated without predetermining the motor outcome (Ilmane et al. 2013; Raptis et al. 2010; Sangani et al. 2011; Turpin et al. 2016; Zhang et al. 2017, 2018). Thus, although directional sensitivity of M1 neurons is an experimental fact, the assumption that these neurons directly predetermine the direction of hand movement or isometric force remains controversial. Also controversial is the notion that M1or other brain areas directly preprogram the motor outcome. This notion was retained in the computational framework in which the motor outcome is preprogrammed with the help of emulators (internal models) of physical and physiological laws (Hollerbach 1982). Correlations of activity of different brain areas with motor outcome variables have been considered as evidence for the computational theory (Shidara et al. 1993), although correlations do not necessarily imply causality and therefore are not sufficient for deriving conclusions on how posture and movement are controlled (see also Shah et al. 2004).

NONLINEAR, THRESHOLD PROPERTIES OF NEURONS

The lack of a physiological explanation of directional sensitivity of neurons may be another major reason for the existing controversy in the understanding of the role of the motor cortex in the control of posture and movement. The present review addresses this issue by considering how sensory and central influences are integrated in neurons having a fundamental nonlinearity, electrical threshold, i.e., a specific membrane potential that is necessary to exceed to recruit neurons. The term “fundamental nonlinearity” in this context means that because of the abrupt response to input signals (“all or nothing”) and the ability to autonomously sustain rhythmic discharges (plateau potentials; Heckmann et al. 2005; Hultborn 1999; Kiehn and Eken 1997), neurons cannot be considered as linear entities even for small changes in input signals. Threshold functions are thus different from many nonlinear functions that can be considered as locally linear. For instance, y = x³ is a nonlinear function, but locally, at any point (e.g., x = 1), it can be considered as linear. Threshold input/output functions are also irreversible; i.e., knowing that a neuron discharges, say, 20 times per second, one cannot determine which combination of synaptic inputs to this neuron was responsible for this outcome. It will be suggested that many important aspects of neural control of posture and movement, including directional tuning of neurons, cannot be understood without considering fundamentally nonlinear properties of MNs and other neurons.

Role of Sensory Information

In addition to threshold properties, many neurons have sensory inputs from the neuromuscular periphery and supraspinal (e.g., visual and vestibular) systems as well as central inputs that can be independent of sensory influences. Some sensory signals can transmit information about spatial variables characterizing motion of the whole body or its segments. For example, α-MNs are neurons that receive signals from muscle spindle afferents about changes in a spatial variable, the muscle length. These spatial signals can be modified via efferent inputs from γ-MNs to muscle spindle receptors (Matthews 1972). Other neurons may receive spatial signals that reflect the body configuration (“body schema”), allowing humans and animals, for example, to localize and scratch irritated spots on the body. Spatial signals may also reflect the location of the entire body or its part (e.g., hand) in the environment or the orientation of the body with respect to the gravitational vertical (Feldman et al. 2011; Mullick et al. 2018; Zhang et al. 2018). The direction of isometric pressure of the hand on a motionless joystick is a spatial variable. Indeed, spatial signals received by neurons can be combined with other signals that can be independent of spatial variables.

Spatial Frames of Reference

Directional tuning of M1 neurons can be explained by assuming that they function in a spatial FR representing possible hand positions in the environment. This statement needs to be clarified by considering the notion of spatial FR in a physiological context.

Since Descartes (1596–1650; see Descartes 2001), FRs or systems of coordinates have been used to describe natural phenomena. In an abstract, mathematical sense, a FR consists of elements, locations of which (coordinates) are determined from a specific point (or axes) called the origin or referent point. Once a referent point is chosen, coordinates are measured from this point by using a scale (metrics) that depends on FR geometry. It has been suggested that motor actions are accomplished in appropriate, most often spatial, FRs (Arbib 1991; Blouin et al. 1993; Colby 1998; Feldman and Levin 1995; Flash and Sejnowski 2001; Gross and Graziano 1995; Paillard 2005; Rizzolatti et al. 1997; Saltzman 1979), but this assumption may remain a mathematical abstraction unless we identify how FRs with their attributes (referent points, metrics and geometry) originate in the nervous system and how they are used to produce motor actions. First steps in this direction have been made (Feldman 2015; Feldman and Levin 1995), but additional efforts are necessary to explain the origin of directional sensitivity of neurons.

A major goal of this review is to integrate available experimental data to show that neurons function in spatial FRs and that the FR origin or referent points can be shifted by neural control levels. The metrics of FRs can likely be changed as well (e.g., due to physical exercises, muscle or neural fatigue, or growth of the organism). Some motor actions (e.g., somersaults) likely result from rotations of FRs. In the absence of experimental material verifying these hypotheses, only shifts in referent points are considered in this review. By shifting referent points, control levels elicit intentional motor actions that emerge in a predetermined spatial FR without preprogramming. If necessary, referent shifts are modified to adjust the emergent action and meet the task demand. The term referent control refers to this ability of the nervous system. In contrast, pure involuntary, uncorrected reactions to external perturbations can be produced in motionless FRs (Ilmane et al. 2013). Therefore, shifts in spatial FRs are tools for indirect control of intentional motor actions. Such FRs can be called physical (Feldman and Levin 1995), to distinguish them from abstract, mathematical FRs used in computations or representations of experimental data: the choice of one mathematical FR or another can only influence our description of behavior but not the behavior itself.

It will be shown that neurons are primarily tuned to referent directions, i.e., directions of shifts of spatial FRs. With indirect, referent control of motor actions, the emerging activity of neurons may or may not correlate with the motor direction or other kinematic or kinetic variables, including EMG patterns, depending on external conditions and the type of motor tasks, confirming that correlations do not necessarily imply causality. In this way, the controversy associated with the existence of two alternative theories seems to be resolved by benefiting referent control, rather than the computational theory of action control. Moreover, this analysis helps resolve several problems in motor control and identify some limitations of classical, physiological views, particularly on the relationship between central and peripheral (reflex) mechanisms in the production of motor actions.

MOTONEURONS FUNCTION IN A SPATIAL FRAME OF REFERENCE AND ARE CONTROLLED BY SHIFTING THE ORIGIN (REFERENT) POINT OF THIS FRAME

The notion of physical FRs can be clarified by considering basic properties of α-MNs. Experimental data initially obtained by Matthews (1959) and Feldman and Orlovsky (1972) in animals and by Asatryan and Feldman (1965) in humans are sufficient to assert that each α-MN as well as the pool of α-MNs of a single muscle, function in one-dimensional FR and are controlled by shifting the referent point of this frame (Feldman and Levin 1995). It is important to illustrate that α-MNs and other neurons such as M1 neurons, likely also function in spatial FRs.

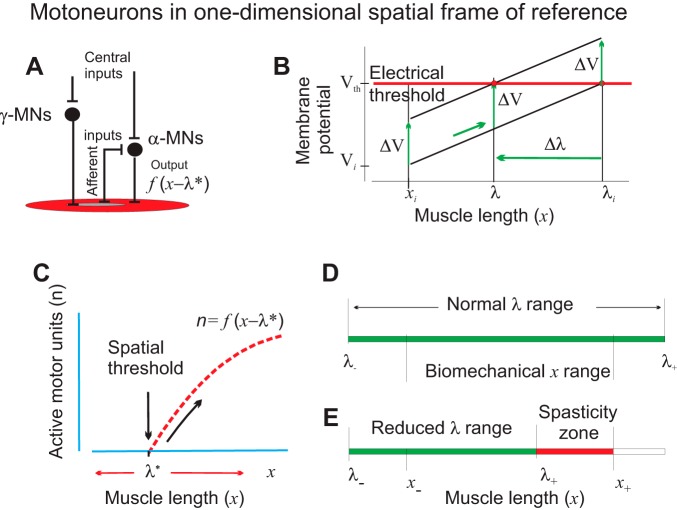
A single α-MN receives peripheral (afferent) influences from proprioceptors and central influences that can be independent of afferent influences (Fig. 1A). Both types of influences can be transmitted mono- and poly-synaptically to the MN. Central influences can also change afferent influences on the MN due to efferent innervation of muscle spindles by γ-MNs. During muscle stretching, the α-MN is facilitated predominantly from afferents of muscle spindles sensitive to muscle lengthening. This facilitation increases with increasing muscle length, x, provided that efferent influences on muscle spindles from γ-MNs remain unchanged (Fig. 1B). Therefore, starting from some initial muscle length, x_i, the membrane potential of this α-MN will monotonically increase depending on x (Fig. 1B, low diagonal line). At some value of the muscle length, called the threshold length, λ_i, the electrical threshold is reached, and the neuron starts generating rhythmic discharges, the frequency of which increases with the increasing difference between x and λ_i. If this MN has the lowest spatial threshold, other α-MNs innervating the same muscle will be recruited gradually with the increasing difference between x and λ_i (Fig. 1C). This behavior reflects the principle of rank-ordered recruitment of α-MNs expressed in terms of spatial thresholds, rather than the size of MNs (Henneman et al. 1965; McPhedran et al. 1965).

Fig. 1.

Referent (threshold) control of α-motoneurons (MNs). A: simplified diagram of central and peripheral inputs to α-MNs transmitted mono- and polysynaptically via interneurons and γ-MNs. B: in the presence of afferent feedback, central electrical changes in the membrane potential (ΔV) of α-MNs are converted into changes in the spatial threshold (Δλ) at which the MN begins to be recruited. C: motor units of a given muscle begin to be recruited when the difference between the actual (x) and the dynamic (velocity dependent) threshold muscle length (λ*) becomes positive. The number of recruited motor units (n) and the muscle force increase (diagonal arrow) with this difference (x − λ*). Intentional control of muscle activation results from shifts in λ. D: normally, the range of central regulation of the threshold (λ₋, λ₊) for each muscle exceeds the biomechanical range (x₋, x₊) of the muscle length, allowing muscle activation or relaxation at any point within the biomechanical range. E: a stroke-related decrease in the range of threshold control results in the inability of subjects to relax the muscle at lengths exceeding this limit (spasticity zone). Reproduced with modifications from Pilon et al. (2007) and Mullick et al. (2018) with permission.

Now consider influences on the MN (facilitation/inhibition) that are independent of afferent feedback. For example, in certain conditions, influences descending from M1 can be independent of afferent feedback (Ilmane et al. 2013; Raptis et al. 2010). Such influences can be transmitted to the α-MN directly (monosynaptically) or indirectly (via interneurons or γ- MNs). These influences are delivered to inputs of the MN, and their primary effect is a change in the MN membrane potential (ΔV), which may or may not lead to activation of the MN. In other words, independent central influences are also independent of what occurs at the MN output. This independent change in the membrane potential is added to its length-dependent changes, which means that the diagonal line in Fig. 1B will be shifted vertically. For example, if these influences depolarize the MN, then ΔV is positive and the diagonal line is shifted upward (Fig. 1B, vertical arrows). As a result, the threshold position for recruitment of the α-MN will be shifted by Δλ (Fig. 1B, horizontal arrow).

This means that in the presence of proprioceptive feedback, the electrical measure (ΔV) of independent central inputs to the MN is converted into changes (Δλ) in the spatial threshold at which the MN begins to be recruited. Thereby, recruitment of the MN is conditional: at muscle length x_i, the MN remains silent in response to central depolarization ΔV that shifts threshold by Δλ but becomes recruited at a higher muscle length (Fig. 1B, right vertical arrow). The shift in the spatial threshold will depend on the sensitivity, s, of the membrane potential to synaptic inputs (the slope of diagonal lines in Fig. 1B). It also depends on the sensitivity of muscle spindle afferents to lengthening. The slope of these lines increases with the increasing speed of changes in x. Therefore, the value of s and changes in the spatial threshold are velocity dependent. However, if s is measured as the ratio of steady-state (static) changes in the membrane potential over changes in the spatial coordinate, x, then the effect of central influences can be expressed as a velocity-independent shift (Δλ) in the spatial threshold for activation of the MN:

$$s\Delta \lambda =-\Delta V$$ (1)

The spatial threshold can be shifted even if the electrical threshold remains unchanged as in Fig. 1B, but Eq. 1 also defines shifts in λ when ΔV includes central changes in the electrical threshold, the possibility established for α-MNs in several studies (e.g., Krawitz et al. 2001). Further details about spatial threshold control of MNs can be found in previous publications (e.g., Feldman 1986, 2015). In dynamics, the activation threshold is velocity dependent (Feldman 1986). In the following text, an asterisk (*) is added to respective variables to emphasize that they are velocity dependent. The dynamic threshold, λ*, decreases with increasing muscle stretch velocity (Feldman 1986). Being an independent measure of central influences, shifts in the spatial threshold can affect not only sub- but also suprathreshold state of MNs. By setting the activation threshold (λ₊) beyond the upper biomechanical limit of muscle length (x₊), the muscle can be relaxed in the entire biomechanical range of muscle lengths (Fig. 1D). On the other hand, one can activate muscle at the biomechanically minimal length (x₋) by setting the threshold, λ, below x₋. This means that the range of central regulation of spatial threshold exceeds the biomechanical range of change in the actual muscle length. In some neural pathologies, the range of central regulation of thresholds can be abnormally diminished, resulting in motor deficits, such as, for example, spasticity often observed in poststroke subjects (Fig. 1E; Levin et al. 2000). Delays in afferent and central pathways to α-MNs indeed influence the time when α-MNs are recruited or derecruited. However, with spatial threshold control, stability of posture and movement is guaranteed even for delays substantially exceeding their physiological values (Pilon and Feldman 2006).

Simple as it is, Eq. 1 has far-reaching implications for the understanding of how α-MNs are controlled. It shows that in the presence of spatial sensory inputs and electrical thresholds, independent electrochemical influences transmitted to α-MNs (facilitation and/or inhibition) are converted (“decoded”) into changes in a spatial variable (λ) that indicate the muscle length and respective position of the body segments at which the MN begins to be recruited. In this way, electrochemical control influences on MNs are placed in the context of the body schema. Moreover, central influences delineate the spatial (length) range within which the muscle begins to be activated and proprioceptive inputs become effective from the range within which the muscle can be silent. In addition, independent central influences on α-MNs acquire a specific measure, a shift in the spatial threshold, i.e., a shift in the position at which MNs begin to be recruited. In this way, independent central influences only specify where, in the spatial domain, α-MNs can be activated without predetermining motor commands or muscle forces to be produced. In other words, independent central influences do not carry any information or instructions on which output signals (EMG patterns) they should generate. This conclusion has the most serious implication for the conventional biomechanical views or their extension, computational theories of motor control in which the brain directly preprograms motor actions and specifies motor commands or muscle forces to execute these actions: conventional motor control theories are inconsistent with basic, threshold properties of α-MNs, a concept that has been disregarded in studies of brain activity for more than half a century since the experimental demonstration of threshold position control in humans (Asatryan and Feldman 1965). Equally physiologically unfeasible are theories in which preprogramming of kinematics and motor commands (Harris and Wolpert 1998) or muscle forces (Todorov and Jordan 2002) is based on optimality criteria, since one cannot optimize programs or preprograms that physiologically cannot be actualized. This does not mean that motor actions are not optimized; they are, but not in ways suggested in computational theories. To clarify, it is known that laws of mechanics and quantum mechanics can be derived from an optimality principle, the principle of least action (e.g., Landau and Lifshitz 1958) equally applied to movements of stones and biological systems. It would be pseudoscientific to say that there is some computational mechanism in stones or in biological systems that forces them to move according to this optimality principle: optimal motion results from obeying the physical law. Examples of optimal behavior will be described in this review, but, as in the case of the principle of least action, such behavior simply results from obeying physical laws without any efforts of the nervous system. Indeed, much of biological life's operation is outside of the domain of motor behavior. Outside this domain, the system can mentally “break” laws of physics. As an example, we defy physical laws when flying in our dreams or making fantastic things in tales. However, it should be emphasized that as long as physical, motor actions are concerned, the system cannot violate laws of physics. In the realm of motor actions, there is no reason to doubt the statement that mechanical laws and the principle of least action are equally applied to movements of stones and animals.

Because any influences on MNs result in a shift in the spatial threshold, hybrid theories in which spatial (referent) control is combined with full or partial preprogramming of motor commands or muscle forces are also physiologically unfeasible. These conclusions should be recognized even though computational theories are successfully implemented in robotics (see also discussion).

An important consequence of spatial threshold control refers to the problem of the relationship between posture and movement. Most researchers (e.g., Cluff and Scott 2016; Cullen 2004) accept von Holst’s view that reflexes are suppressed by efference copy when movements are produced to prevent reflex resistance to deflections from an initially stabilized posture (von Holst 1954). Von Holst was a remarkable neuroscientist, but this fact should not prevent us from a critical evaluation of his solution of the posture-movement problem. He did not consider the physical rule that neither posture nor movement can be stable in the absence of position- and velocity-dependent reactions to perturbations. By suppressing reflexes, the system would deprive itself of the reflex mechanisms that are physically necessary for movement stability. His proposal is reminiscent of the idiom “throwing the baby out with the bathwater”: by suppressing reflexes, the ability of the system to resist external perturbations during any intentional movement including gait would be sharply reduced, as exemplified by severely impaired movement stability following the loss of proprioceptive reflexes in deafferented patients (Blouin et al. 1993). Thus von Holst’s proposal is inconsistent with the basic physical principles defining stability of posture and movement. We need to look for another solution, without relying on the idea of reflex suppression. Strange as it may seem, we need to do so despite numerous observations that MNs can be inhibited at some phases of movements, resulting in low or absent EMG responses to perturbations (e.g., Duysens et al.1990). Although such observations are often cited as evidence of von Holst’s proposal, there is an alternative explanation. According to the notion of referent control, the system elicits movement by shifting the place where reflexes can function without suppressing them as such. In other words, inhibition of responses to perturbation just signifies that these responses were tested when full reflex functionality had already been transferred to a new posture, as was illustrated in experiments recently conducted by Turpin et al. (2016). Not only proprioceptive but also other (e.g., vestibular) reflexes cannot be suppressed without destabilizing head or whole body movements (cf. Cullen 2004). In the referent control framework, by shifting spatial thresholds, the system does not suppress reflexes but shifts their spatial thresholds and thus transfers balance and stability to a new posture and elicits motion without any loss of stability. This is an optimal behavior that implies that posture and movement are seamlessly controlled by a single mechanism. Neither von Holst’s proposal nor computational theories, including those postulating behavioral optimality (e.g., Harris and Wolpert 1998; Todorov and Jordan 2002). solve the posture-movement problem. One can also say that by resetting spatial thresholds, the system converts posture-stabilizing to movement-producing mechanisms. In other words, threshold (referent) control manifests as the ability of the nervous system to transfer balance (equilibrium) and stability from an initial to a final posture of a limb segment or of the whole body (Feldman 2015; Feldman et al. 2011; see also discussion).

Production of Movement Through Referent Control

Many neural systems have access to threshold control. Specifically, as follows from experiments in animals and humans, shifts in λ are produced by different descending pathways that mediate central direct (monosynaptic) or indirect post- or presynaptic inputs to α-MNs via interneurons and γ-MNs, as well as by intermuscular reflexes such as crossed-extensor reflexes and reflex reciprocal inhibition between agonist and antagonist muscles (Feldman and Orlovsky 1972; Matthews 1959). Intentional movements in humans also result from shifts in the spatial thresholds, i.e., the referent point of the FR (Asatryan and Feldman 1965). A series of recent experimental studies has specifically focused on changes in spatial thresholds in the control of posture and movement in humans (Foisy and Feldman 2006; Ilmane et al. 2013; Mullick et al. 2018; Raptis et al. 2010; Sangani et al. 2011; Turpin et al. 2017; Zhang et al. 2017, 2018).

A motor goal may require a decrease in λ to activate the muscle, i.e., an increase in the difference x − λ*. In response, the neuromuscular periphery tends to diminish this difference by producing muscle contraction, i.e., a decrease in the muscle length x, and thus diminish the emergent muscle activity. This tendency is called “the minimization principle.” Passive muscle stretches elicit position- and velocity-dependent active muscle resistance (stretch reflexes). This is another manifestation of the minimization principle.

The minimization process is limited by external forces and the task demand. In other words, achieving the motor goal is prioritized over the tendency to optimize motor behavior. This is especially obvious during isometric torque production in which the position (x) remains the same but the value of λ is set below this position to elicit the desired isometric force: the greater the difference between x and λ, the greater the isometric force. The tendency to minimize the difference between x and λ and thus minimize muscle activity can be seen during isometric force production as well. In the presence of vision, subjects can continuously maintain the required level of isometric force, thus preventing a decrease in x − λ. However, soon after the vision is blocked, the muscle activity and force begin to decline (Reschechtko and Latash 2018), manifesting a gradual increase in the activation thresholds of agonist muscles, thus diminishing the difference x − λ.

The dependency of muscle activation on x − λ* also implies that α-MNs are maximally sensitive to the hand motor directions that affect this difference the most. The explanation of isometric force production reinforces the notion that parameter λ should not be confused with the targeted position during reaching a motor goal. Also, in contrast to some studies (Sergio et al. 2005), referent control should not be confused with “positional” control, nor can it be confused with servo-, force, feedback gain, stiffness, or impedance control (cf. Schwartz 2016) but should be considered as it is, as a tool for shifting the spatial FR in which the muscle is constrained to work.

Neurons in Multidimensional Space: Tuning to Referent Directions

In one-dimensional space, a central shift in the membrane potential is associated with a unique shift in the spatial threshold (Eq. 1). In contrast, in neurons that integrate multidimensional spatial information delivered via sensory inputs, the same change (ΔV) in the membrane potential can be composed of different shifts in spatial thresholds, i.e., along one or several coordinates. For each coordinate, the change in the spatial threshold is defined by Eq. 1, but the sensitivity s and the magnitude of change in the spatial threshold may be different for different coordinates. Mathematically, this notion can be described using vectors. Let us s be a vector of sensitivities of a neuron to changes in the coordinates of the hand position in space and Δh be a vector comprising respective shifts in the spatial thresholds. The change ΔV in the membrane potential associated with different shifts in spatial thresholds is then described by Eq. 1 in which the left part is replaced with a scalar (dot) product of vectors s and Δh:

$$s\cdot \Delta h=-\Delta V$$ (2)

This equation refers to a space of any dimension, but referent control will first be considered in terms of planar, two-dimensional hand movements or isometric force production in coordinates x and y. In this case, according to Eq. 2,

$$s_x\Delta h_x+s_y\Delta h_y=-\Delta V$$ (3)

where subscripts refer to components of respective vectors.

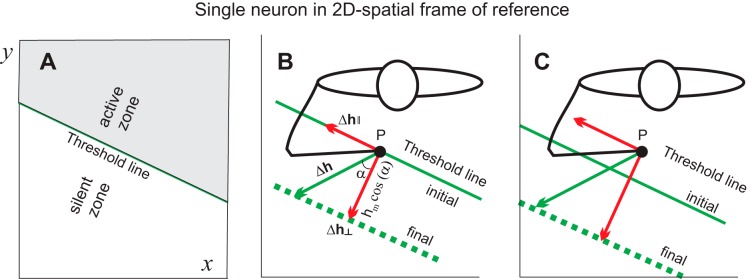
Geometrically, according to Eq. 3, all possible combinations of spatial shifts in thresholds (Δh_x, Δh_y) responsible for a given change in the membrane potential of this neuron comprise a line (“threshold line”) in space (x, y) with a slope defined by coefficients s_x and s_y that represent weights of synaptic inputs to this neuron (Fig. 2A, diagonal line). With respective definition of coordinates, the neuron will be active at any point (x, y) above the threshold line (Fig. 2A, active zone) but silent at any point below this line (silent zone).

Fig. 2.

Neurons are tuned to referent directions of shifts of the spatial frame of reference in which they function. A: a neuron receives afferent influences from the position (x, y) of the hand in the environment. The same change in the membrane potential can result from different changes in the threshold positions of the hand, comprising a single threshold line. The neuron can be active or silent at positions above or below this line, respectively. B: a central change in the membrane potential results in a shift in the threshold line. The referent (threshold) hand position is shifted to a certain point on this line (vector Δh; p is the initial hand position). Only the component of this vector orthogonal to the threshold line (Δh_⊥) affects the membrane potential and activity of this neuron. Δh_‖, component of vector Δh along the initial (parallel) threshold line; h_m, orthogonal projection of vector Δh where subscript m refers to the length of Δh. C: in the case when the neuron is active at position p, only the orthogonal component of shifts in the spatial thresholds affects the activity of the neuron.

Consider that the initial hand position, p, coincides with a certain point just below an initial threshold line (Fig. 2B, closed circle). At this hand position, the neuron will be silent. Different changes in the membrane potential can be considered as shifts from one threshold line to another (e.g., from solid to dashed line in Fig. 2B). A specific combination of central changes in the threshold positions can be visualized as a vector (Δh) from the initial point to a point on another, parallel threshold line. Reaction of this neuron to threshold shifts will be direction dependent. If the shift is directed to the active zone, the initial hand position, p, becomes remote from this zone, and defacilitated, the neuron will remain silent. Only shifts in the opposite direction, toward the silent zone, will activate the neuron, but in this case the effect of the shift will also be direction dependent. Consider a shift in thresholds represented by vector Δh in Fig. 2B. It can be decomposed in two orthogonal components: Δh_‖, which changes spatial thresholds along the initial threshold line, and Δh_⊥, which changes thresholds in the orthogonal direction. Apparently, the first component only rearranges the combination of synaptic inputs to this neuron, leaving its membrane potential unchanged such that this component will not influence the activity of the neuron. In contrast, the orthogonal component will facilitate the neuron, eliciting its activation. One can see that the neuron will be activated maximally when thresholds are shifted directly away from the initial threshold line to the silent zone. This referent (threshold) shift direction can be considered as “preferred” for this neuron. The effect of threshold shifts will progressively be diminished as a cosine function of the deflection (α) of vector Δh from the preferred direction (Fig. 2B):

$$\Delta h_{\perp }=h_{m}cos\left(\alpha \right)$$ (4)

where h_m is the orthogonal projection of vector Δh (subscript m refers to the length of Δh).

A similar conclusion can be made if the initial hand position is within the active zone when the neuron generates rhythmical discharges (Fig. 2C). Each neuron will have not only a preferred direction in the case of central control (Fig. 3A) but an opposite preferred direction with respect to passive changes in the hand position when the same spatial thresholds are maintained (Fig. 3B). Sensitivities of neurons to changes in coordinates and, as a result, the slope of the threshold line can be different for different neurons.

Fig. 3.

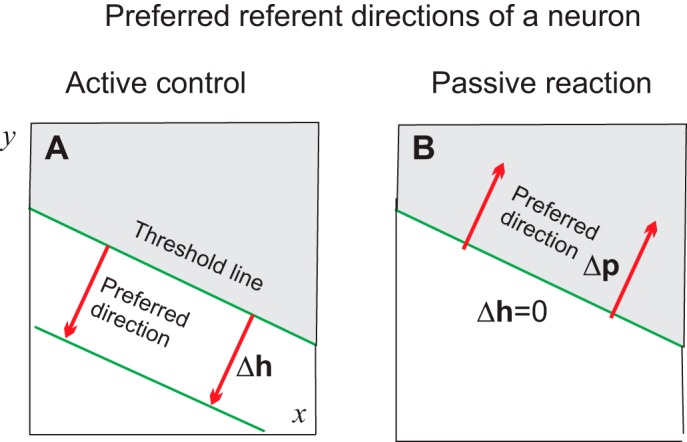
Preferred directions to intentional referent shifts (A) and to passive hand displacements (B). In both cases, preferred directions are orthogonal to the threshold line but opposite in signs. Δh is a vector comprising the respective shift in the spatial threshold; Δp is a vector indicating hand position.

Thus directional tuning of neurons can be interpreted as a consequence of their functioning in a spatial FR. It should be emphasized, however, that according to this analysis, neurons are tuned to shifts in the referent hand direction. As for α-MNs, the activity of such neurons (called h-neurons) will depend on p − h*, i.e., on the difference between the actual hand position (p) and velocity-dependent threshold position (h*). It follows that the emergent, actual motor direction does not necessarily coincide with the referent direction, because the former is not directly related to the latter but also depends on the dynamics of the interaction of the arm with external forces and biomechanical constraints.

During isometric force production, when the hand position p practically remains the same and movement speed is zero, the activity of neurons defined by p − h* will mainly depend on the timing of shifts in the spatial thresholds, h(t). Consistent with findings by Sergio et al. (2005) is the prediction that changes in the activity of neurons in isometric conditions will be more strongly correlated with the force dynamics, compared with hand motion, the dynamics of which is complicated by changes in the arm position, limb inertia, Coriolis forces, and movement speed.

Indeed, in three-dimensional space, instead of a threshold line there will be a threshold plane, and the preferred direction for activation of the respective neuron will be orthogonal to this plane. The activity of this neuron will progressively be diminished during hand movements in other directions, also as a cosine function of the angular deflection of hand movement from the preferred referent direction.

Given the natural variability of neuronal properties and a possible nonlinear dependency of shifts in the membrane potential on the muscle length (λ-dependent changes in coefficient s in Eqs. 1 and 2), the threshold line and plane may be curved, and the preferred direction of the neuron can be different for different hand locations (Kakei et al. 1999). The tuning curve may deviate from the “ideal” cosine function (see Sergio et al. 2005). However, these features do not affect the major conclusion that directional sensitivity of neurons is a consequence of their functioning in spatial FRs.

Equation 3 was derived by assuming that the neuron receives sensory information about the current hand position in space. Independent central inputs to this neuron then transmit shifts in the referent hand position. This rule can be generalized for neurons that instead of, or in addition to, spatial information gather multimodal sensory information. Independent central influences to such neurons then set a referent (threshold) value for the combination of sensory inputs received by this neuron. This combination can be called the “referent image.” One can say that MNs detect the difference between the current and referent muscle length. Similarly, one can say that neurons receiving multisensory information compare the current sensory image with the referent one and are activated when the two images are matched. In other words, such neurons function in multimodal and multidimensional FRs, and activation of such neurons symbolizes image recognition; i.e., such neurons have cognitive functions.

REFERENT CONTROL OF HAND MOTION OR ISOMETRIC FORCE (EXPERIMENTAL EXAMPLES)

Referent Control of Movement Adaptation to External Loads

Before going into further details on functioning of neurons in spatial FRs, experiments illustrating that the nervous system does not and cannot directly predetermine movement trajectories will be described. Instead, by accomplishing shifts in the referent position of body segments, the system allows motor action to emerge depending on external conditions in the FR predetermined by referent control. Thereby, the system reserves the possibility of corrections of referent shifts if afferent feedback signals that the emerging action is going to be in error.

The experiments are analogous to driving a boat across a river with a fast-running current. Instead of heading directly to the opposite shore, to prevent the boat being swept down the river with the current, it would be necessary to drive the boat along a diagonal path to compensate for the influence of the current.

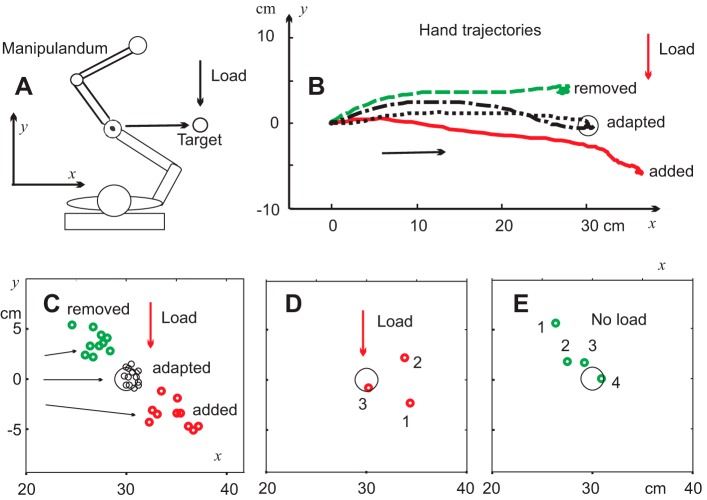
This concept was used in experiments in which sitting subjects rapidly moved a handle of a double-joint manipulandum to a target despite an external load acting orthogonally to the target direction (Foisy and Feldman 2006; Fig. 4). In terms of referent control, this was achieved by shifting the referent hand position in a diagonal direction, away from the target position, but under the influence of the load, the arm was deflected from the diagonal direction, moving the hand directly to the target. One can predict that if the load was not introduced in a randomly selected (“catch”) trial, the hand would move in a diagonal direction, close to the referent one, resulting in a positional error. This error was observed in the experiment when subjects were instructed to produce movements without making corrections until the trial is finished (Fig. 4B).

Fig. 4.

Shifts in the referent hand position underlie arm pointing movement. A: subjects moved the handle of a double-joint manipulandum in a frontal direction to reach a remembered target in the presence of a spring-like load increasing with increasing distance from the initial hand position and acting transversally to the hand movement direction. B: after several training trials, subjects reached the target (circle) and continued to do so in subsequent trials (adapted trajectories). When the load was suddenly not introduced in a randomly selected trial, the hand moved in another direction (green trajectory), resulting in a movement error that was corrected in subsequent trials without a load. When movement was adapted to zero load after several trials, the load was introduced again, preventing the hand from reaching the target (red trajectory). C: in all movements adapted to a load or to a zero load, the hand reached the remembered target (black circles), but the final hand positions in the first trials in which the load was unexpectedly added or removed were outside the targets (red and green circles, respectively). D and E: examples of adaptation to the new load condition. Numbers show the hand positions in sequential trials after unexpected changes in the load condition. Reproduced with modifications from Foisy and Feldman (2006) with permission.

In subsequent trials, the load remained zero and subjects gradually corrected the movement error from trial to trial (Fig. 4, B and C), implying that subjects changed the referent diagonal direction to one that brought the hand straight to the target. After adaptation of movement to the no-load condition, the load was introduced again in a randomly selected trial, and, indeed, the hand moved in another diagonal direction, resulting in a positional error of the opposite sign. The errors were corrected in several subsequent trials (Fig. 4, D and E).

Such experiments illustrate that the nervous system controls motion by specifying referent hand shifts and adjusts them depending on external conditions so that the hand moves directly to the target. Indeed, the choice of referent shifts in each trial is task specific; i.e., based on previous experience and recognition of the external conditions, the system anticipates that in response to the previous referent shifts, the emerging action will meet the task demand. If not, the system corrects the referent direction, rate, and durations in subsequent trials to eventually meet the task demand. This strategy does not rely on memory of motor commands, because specification of motor commands would only create problems, such as the posture-movement problem in reaching the motor goal. It also does not require an internal modeling of the force field during learning, because referent control is condition specific and the system just needs to recognize whether or not the conditions remain the same and, if they do not, to accordingly adjust, memorize, and reproduce new referent variables. As in the case of driving the boat, this is done empirically, i.e., without computations, by gradually adjusting the referent direction without the knowledge of the load.

The experiment also showed that in movements adapted to zero loads, the referent and actual movement directions were close to each other, but they were different in movements adapted to a non-zero load. Results of such experiments also show that, depending on external conditions, control, referent shifts may, in trials adapted to zero loads, or may not correlate with the actual movement direction. Thus observations of correlations are not sufficient for deriving hypotheses on how motor actions are controlled.

Although these demonstrations of referent control were not based on cellular analysis, they justify the general conclusion that the controversy in the interpretation of the population activity of M1 neurons may have resulted from disregarding the empirically derived notion of indirect, referent control of motor actions. Changes in referent variables are independent of, but have influence on, output variables, including hand motor direction. Thus motor outcome may not be preprogrammed, but results suggest that it emerges depending on external conditions in the spatial FR predetermined by referent variables. The absence of preprogrammed, direct specification of motor outcome implies that, depending on external conditions, activity of neurons may or may not correlate with different characteristics of this outcome, which is likely the case for M1 or other neurons (see discussion).

Timing of Referent Shifts

Starting from changes in the subthreshold state of MNs, referent control can also be completed before the end of the emergent movement. In this way, the system can initiate referent corrections of the previous action or initiate referent shifts to produce a new motor action before the offset of the previous action. The term “predetermined control” is used for this phenomenon, instead of the previously used term “feedforward control,” which may be misleading due to its engineering and computational connotations.

To encompass the predetermined nature of referent control, it has been suggested that changes in the referent hand position can be produced by specifying the rate (r_h) of referent shifts during time T that together define the extent of referent shifts (Adamovich et al. 1984):

$$\Delta h=r_h\cdot T$$ (5)

There are several rationales for the proposed timing of referent control. Referent control implies that shifts in the threshold position are gradual, resembling the finding of gradual shifts in the equilibrium position during reaching movement (Bizzi et al. 1982). By changing the value of r_h and T, the system can influence the emergent movement direction, speed, and extent. The movement extent is not predetermined beforehand: based on current sensory feedback, the system may diminish or prolong the duration T of referent shifts to minimize movement errors or prolong or shorten the speed and extent of motor action. The system can also change the direction of the rate vector, for example, to avoid an obstacle. Arm motion continues for some time after the end of referent shifts, and the gap between the end of the referent shift and the end of the resulting movement increases with movement speed. By accomplishing referent shifts rapidly, the system may initiate new referent shifts without waiting for the end of the emerging motor action, which is especially important in the generation of rapid movement sequences (e.g., in piano playing). In other words, at the level of referent control, the system can obtain continuous sensory information about the emerging motor action, but once a decision to correct or produce another motor action is made, referent control is performed in an open-loop way, i.e., independently of sensory feedback until the necessity of referent changes arises (piecewise control strategy). This control process is comparable with the generation of set of saccades produced in an open-loop way when vision is blocked until it becomes available at the end of each saccade (Bridgeman et al. 1975).

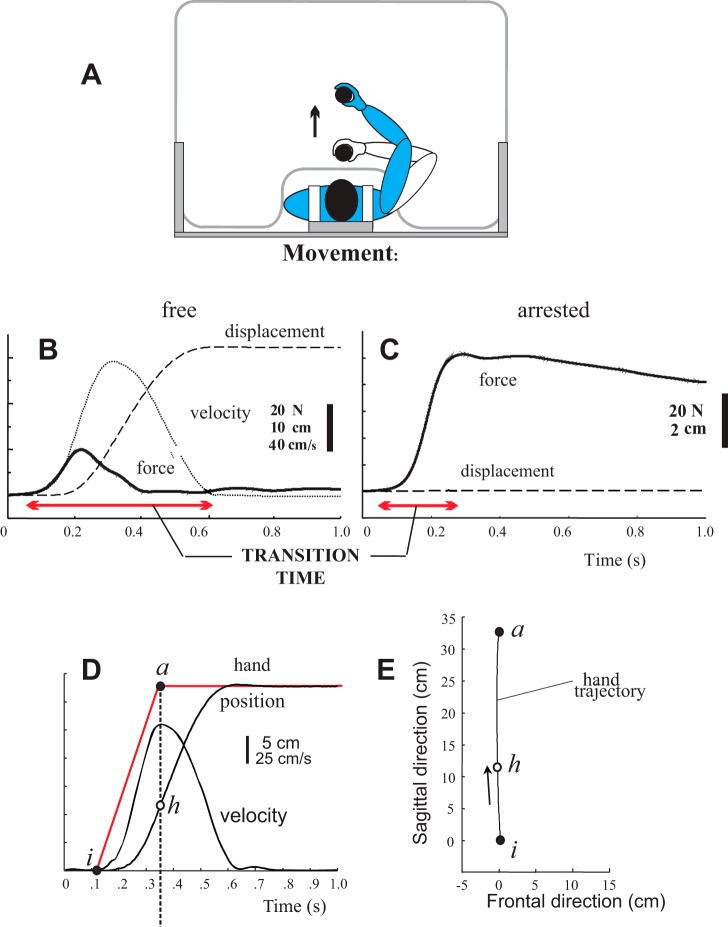
The hypothesis that the referent shifts underlying fast arm movements from one position to another cease to change long before the movement offset was tested by mechanically blocking the arm movements and thus transforming them into isometric torques (Ghafouri and Feldman 2001). This was done to eliminate inertial, centrifugal, and Coriolis forces that prolong the duration of unobstructed movements. If the hypothesis was correct and the original pattern of the referent shifts remained unchanged, it would take less time for the isometric force to reach a steady state compared with the time to reach the final position in unobstructed movements. This prediction was confirmed (Fig. 5, B and C). Thereby, the isometric force reached its final, steady-state value at the time when unobstructed movements had only reached their peak velocity (Fig. 5D).

Fig. 5.

Referent shifts are finished substantially before the offset of the resulting hand movement. A: subjects moved a vertical handle with an electromagnetic plate on a smooth surface of a table. In randomly selected trials, the handle motion was prevented by activating the electromagnet hidden underneath the table surface, thus converting hand motion into isometric force production. B and C: compared with free movement (B), the time of reaching the final isometric force (C) was substantially smaller (compare horizontal arrows in B and C). D and E: relationship between referent shifts and resulting kinematics of hand motion, by assuming that the duration of time of isometric force production (B) was close to the duration of referent shifts underlying unobstructed hand motion. Referent shifts (red line in D) were finished when the hand (h) reached the peak velocity (D) or covered only approximately one-third of the total movement extent (E); i is the initial hand position and a is the final hand position. Reproduced with modifications from Ghafouri and Feldman (2001) with permission.

This finding suggests that referent shifts underlying fast arm movements are completed substantially before the movement offset, approximately at the time or when the hand had covered approximately one-third of the movement distance (Fig. 5E), which was also confirmed in computer simulations (Pilon and Feldman 2006; Zhang et al. 2016). This experiment and simulations (see also Gribble et al. 1998) resolved the controversy regarding the other shapes and durations of equilibrium shifts underlying fast uncorrected arm movements suggested in other studies (Gomi and Kawato 1996; Latash and Gottlieb 1991).

Graphically, Eq. 5 represents a ramp-and-hold function with the holding phase starting before the end of emergent motion (Fig. 5D, thin line). Physiologically, this function can result from propagation of excitation along some neural ensemble. Propagation of excitation in the motor cortex during movements (Takahashi et al. 2011) may be related to the timing of referent shifts. The monotonic nature of referent shifts is fundamental for empirical (noncomputational) solution of the mapping problem.

Mapping Problem in Reaching the Motor Goal

In everyday life, we have no difficulty in setting appropriate control variables (whatever they are) to reach a motor goal, e.g., to establish a desired position of body segments. The understanding of how this is achieved by the nervous system is considered as a major “mapping problem” in behavioral neuroscience. The empirical, noncomputational nature of referent control allows referent variables to be monotonically changed until the goal is reached. To clarify, suppose one wants to establish a certain elbow angle in the presence of unknown external resistance (constant, monotonically or nonmonotonically dependent on the joint angle). Even if the resistance characteristic is unknown, the system can monotonically change the referent joint angle until some sensory feedback (vision, sound, kinesthetic sense, etc.) indicates that the desired final position is reached.

In pointing movements, the mapping problem can also be solved empirically. By monotonically changing the referent hand direction (see Eq. 5), one can establish the desired direction of the emergent hand motion, and by gradually changing the duration T and/or the rate of referent shifts, one can establish the desired hand movement speed and extent. Although some information about the external resistance can be helpful in accelerating the process, the required motor goal can be reached without such information.

In contrast, in the computational framework, the nervous system directly preprograms motor commands and muscle forces that are required for reaching the desired position. This cannot be done unless the resistance characteristic is known; the system needs to have an internal model of the “force field.” In any case, computations only yield symbolic values of motor commands that should be produced at the MN output. These symbolic values should be converted into real input synaptic potentials delivered to MNs. Such an “inverse dynamic” conversion is physically and mathematically impossible because input/output functions of MNs are irreversible (see motoneurons function in a spatial frame of reference). Therefore, despite numerous claims, computational theories fail to solve the mapping problem (see also discussion).

What Does the System Memorize During Motor Learning?

In the experiments described above, the nervous system adjusts the referent direction, its rate of change, and its duration in repeated trials to eventually meet the task demand. This strategy does not rely on memory of motor commands because this would only create problems, such as the posture-movement problem, in reaching the motor goal. It also does not require an internal modeling of the force field (see mapping problem in reaching the motor goal). However, the system needs to recognize whether the load condition remains unchanged in the current trial. The system can also anticipate a change in the load in the forthcoming trial and, if the load changed, correct referent variables. Based on analysis of adaptation to changes in external load in the above or similar experiments (Weeks et al. 1996), it was concluded that the system most often uses the recurrent control strategy, by memorizing referent shifts that resulted in successful performance in the previous trial and reproducing these shifts without anticipating changes in the load condition in the subsequent trial and by correcting the referent shifts if the load was changed. In other words, motor memory retains task-specific referent shifts, a fundamental but uninvestigated aspect of motor memory.

Corticospinal Influences Convey Referent Shifts and Can Be Decorrelated from Variables Describing the Motor Outcome

In addressing how motor actions are controlled, researchers basically focus on correlations of neural activity with kinematic and kinetic patterns as well as EMG timing. The predetermined and piecewise nature of referent control implies that it influences and therefore may correlate with variables that describe the motor outcome, but it virtually remains independent of these variables. This means that with changes in external conditions, correlations may disappear. This prediction of referent control was tested in several studies employing transcranial magnetic stimulation (TMS) of M1 in humans.

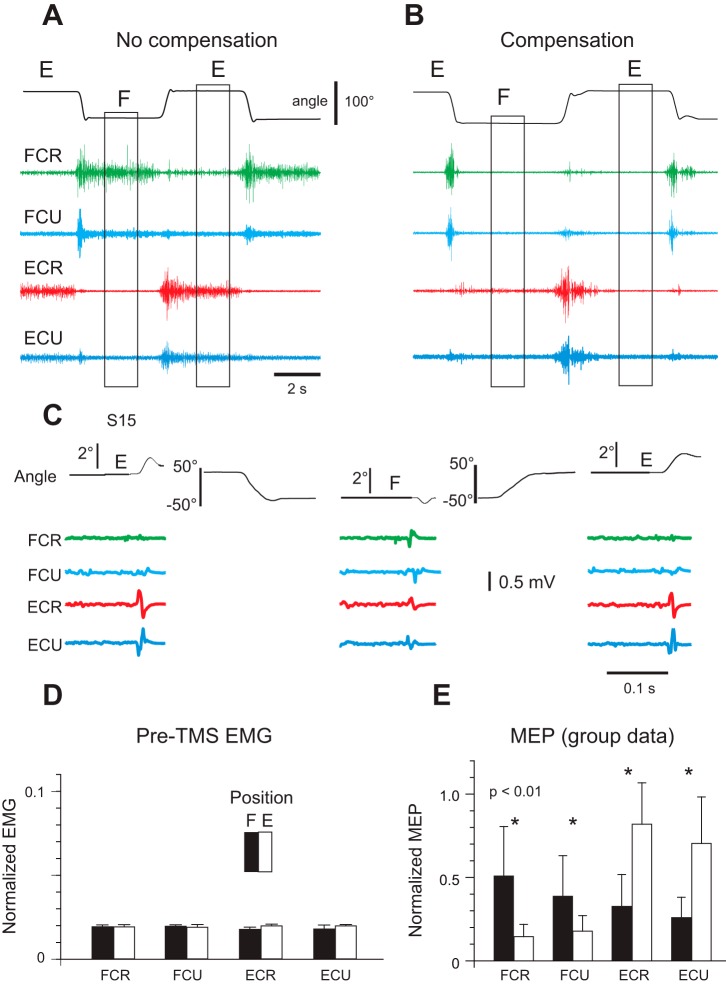
In healthy subjects, wrist flexors were more active when the wrist was held in flexion (F) than in extension (E), whereas wrist extensors were more active in extension (Fig. 6A, position E; Raptis et al. 2010). Tonic muscle activity was necessary to compensate for passive torques of antagonist muscles in each wrist position. By applying a small spring-like torque, tonic EMG levels were equalized at a near-zero (threshold) level in the two wrist positions (Fig. 6B). By testing reflex responses in these positions, it was shown that the threshold position was reset when intentional movement was made. If the specification of EMG patterns is controlled directly by the corticospinal system, the excitability of this system would be similar at positions E and F. Alternatively, if the cortical system transmits shifts in spatial activation thresholds, its excitability would be different at the two wrist positions. Because mechanical and EMG responses to TMS were different at the two positions (Fig. 6, C–E), findings were consistent with referent control.

Fig. 6.

Corticospinal influences reset the referent (threshold) position underlying intentional wrist motion without being directly involved in the specification of electromyographic (EMG) patterns. A: when subjects intentionally changed wrist position from extension (E) to flexion (F) or vice versa, wrist flexors (flexor carpi radialis, FCR; flexor carpi ulnaris, FCU) were tonically active in the flexion (F) position and extensors (extensor carpi radialis, ECR; extensor carpi ulnaris, ECU) in the extension (E) position. B: by compensating passive muscle torques with a torque motor, the tonic EMG activity of wrist muscles at F and E positions was equalized at near-zero (threshold) levels, showing that the threshold position at which muscles begin to be activated was reset with the changes in wrist position. C: although EMG activity was equalized, transcranial magnetic stimulation (TMS) of the primary motor cortex at the E position elicited a small extensor jerk (top curves, left and right) and at the F position, a flexor jerk (top curve, middle). Motor evoked potentials (MEPs) elicited by TMS also changed reciprocally for wrist flexors and extensors with the transition from one wrist position to another. D and E: group data for 16 subjects, showing that although EMG activity was similar at F and E positions (D), MEPs for wrist flexors and extensors were substantially different at F and E positions (E), implying that the referent (threshold) position was shifted when the intentional wrist motion was produced. Reproduced with modifications from Raptis et al. (2010) with permission.

One can assume that descending systems can maintain the same referent thresholds by allowing the neuromuscular periphery to generate uncorrected responses to external perturbations in a stationary spatial FR. Consistent with this hypothesis was the finding that corticospinal influences on α-MNs of wrist muscles remained unchanged despite involuntary changes in the wrist joint angle and EMG levels in response to unloading of preloaded wrist muscles (Ilmane et al. 2013), further showing that the corticospinal influences originated from M1 do not carry information about biomechanical variables describing the motor outcome.

REASSESSING CLASSICAL VIEWS ON CENTRAL AND PERIPHERAL (REFLEX) MECHANISMS IN MOTOR CONTROL

In the pathological condition of complete deafferentation, the spatial threshold vanishes, although MNs can still be activated via central inputs. In other words, following deafferentation, the spatial FR in which α-MNs normally function is damaged or destroyed, resulting in numerous deficits in action and perception, especially in humans (Blouin et al. 1993). Deafferentation also destroys the functional hierarchy in the relationship between central and peripheral (reflex) influences on α-MNs identified in section on MNs.

Deafferentation experiments were motivated by the assumption that central and peripheral (reflex) influences additively contribute to EMG patterns, implying a linear MN system. No doubt, deafferentation experiments were valuable in showing that there are central generators rhythmically influencing α-MNs even in the absence of reflexes. However, the usual assumption that in the presence of afferent feedback, these generators are directly involved in the specification of EMG patterns is questionable, because in intact systems the activation of MNs is conditional. The observations of a similarity between EMG patterns of rhythmical movements before and after deafferentation just demonstrates the possibility of rhythmical generation of movements in the absence of reflexes (Grillner and Zangger 1975), but this observation cannot be considered as evidence that central generators in intact systems are directly involved in the specification of motor commands to muscles. The notion of indirect, referent control of motor actions implies that the classical concept of central pattern generator (CPG) should be reassessed. Historically, the CPG concept resulted from the observation by Brown (1911) that the spinal cord can generate locomotor-like rhythmic activity after deafferentation. The notion that neural networks can generate organized rhythmical activity is not in question. However, in intact biological systems, not this activity, but referent shifts are responsible for the translation of the body balance and stability in the environment, which is the essence of locomotion. Indeed, not only the CPG concept, but other concepts, such as neural modules and synergies, should also be reassessed by considering that neurons function in spatial FRs selected and shifted in task-specific ways. Attempts to consider synergies in the context of referent control have also been made (e.g., Reschechtko and Latash 2018).

REFERENT CONTROL OF NEURON POPULATIONS

It is interesting to address the question of how an entire population of h-neurons with different preferred referent directions can be controlled as a coherent unit to produce desired motor outcomes. The following is an attempt to advance the referent control theory beyond its present point. Specific aspects of the theory from this point could be clarified by experimental testing.

Preferred directions are different for different h-neurons that function in the same spatial FR because of differences in the slopes of their threshold lines. A direction that is preferred for one neuron can be nonpreferred for another neuron. Let us assume that h-neurons that receive sensory information about coordinates of the hand in space occupy a part of the brain (“column” of neurons) with preferred referent directions uniformly distributed in the angular range of 0–360° for planar x, y space considered here (Fig. 7A). In three-dimensional space, the distribution of directions would be spherical.

Fig. 7.

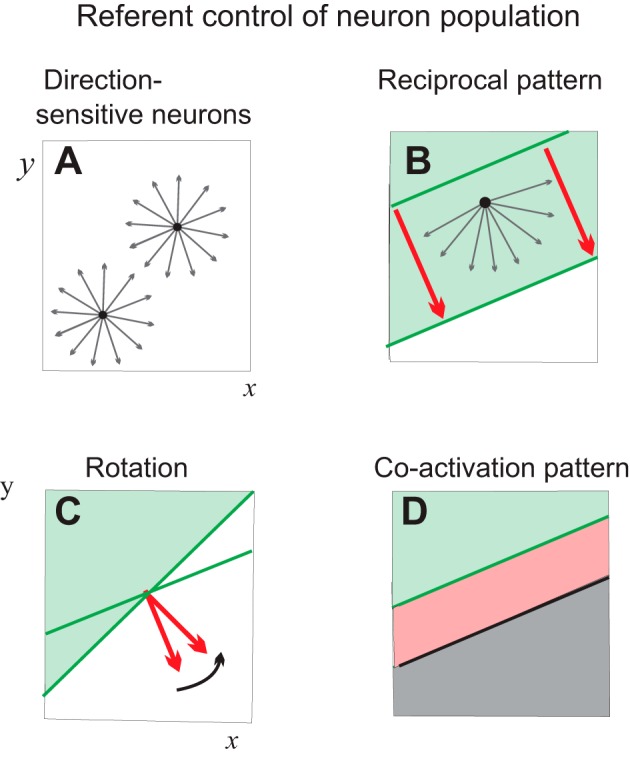
Possible reactions of a population of neurons sensitive to referent hand directions to external central influences (2-dimensional space). A: it is assumed that each point (x, y) of the hand space is represented by a column of neurons with a uniform distribution of referent directions (arrows). B: the required task-specific referent shift (red arrows) influences the whole neuronal population. Only neurons with positive referent projections to the global referent shifts are activated, whereas other neurons are defacilitated (reciprocal pattern). The line orthogonal to the global referent shifts separates these subgroups of neurons (note that the meaning of this line is different from the lines in Figs. 2 and 3). C: the population can react to rotation of the global input. D: cofacilitation of the 2 subgroups can result in activation of neurons in a part of space (x, y).

One can assume that the decision to reach a specific motor goal is formed at a level of neurons that transmit task-specific hand referent shifts to all direction-sensitive h-neurons (Fig. 7B, thick arrows). Each h-neuron will or will not be activated depending on the projection of its preferred referent direction to the global referent direction specified at a hierarchically higher level. All h-neurons with positive projections (Fig. 7B, thin arrows) will be facilitated, and those with negative projections will be defacilitated or inhibited, i.e., a reciprocal pattern. The line orthogonal to the global referent shift will separate neurons with opposite reactions (Fig. 7B, thick lines). Facilitations or inhibition of neurons can be visualized as motion of the separating line (note that this line is not a threshold line defined for individual h-neurons). The separating line can be shifted without changes in direction, meaning that a global shift in the preferred direction of the h-population could be maintained during a motor action (Fig. 7B). The line can also be rotated (Fig. 7C), and the state of all neurons would be modified accordingly.

The global reciprocal and rotation patterns are not the only possible patterns in the control of the population. Neurons could be cofacilitated such that in a part of space, all neurons will be coactivated (Fig. 7D). The reciprocal and cofacilitatory patterns could be combined (not illustrated). Thereby, the extent of the cofacilitation (Fig. 7C) zone could be regulated independently of the reciprocal command. Being a major tool in producing intentional motor actions, the reciprocal command could also shift the spatial zone in which neurons can be coactive.

Once a combination of reciprocal and cofacilitatory influences on the population is predetermined, as for α-MNs, changes in the activity (ΔH) of the neuronal population can be considered as an increasing function of the difference between the actual hand position p and the velocity-dependent referent threshold position (H*) of all active neurons.

Transitions Between Different Frames of Reference

The output activity of h-neurons could be used in different ways, e.g., for perception of hand position (Feldman 2016) or production of arm movements. In the latter case, the output activity of these neurons should be transmitted directly or indirectly (via interneurons) to appropriate α- and γ-MNs to elicit hand motion in the desired direction specified at the hierarchically higher level.

To address this issue, consider how the nervous system controls multiple muscles of the body and the entire body configuration in the referent control framework. It has been suggested, with experimental support (Feldman 2011, 2015; Lestienne et al. 2000; St-Onge and Feldman 2004; Mullick et al. 2018), that such control involves neurons that receive sensory (cutaneous, proprioceptive, kinesthetic) signals about the current body configuration (Q) and function in a spatial FR with the origin point, called the referent body configuration (R). It represents the body configuration at which all muscles across the body reach their minimal activity restricted by the level of coactivation of agonist and antagonist muscles. In a set of experimental studies listed above, it was shown that the difference Q − R* is a global factor influencing the activity of all muscles, in addition to other (local) factors characteristic of each muscle. Acting together, muscles tend to minimize this difference in limits restricted by external forces and the motor task. In preparation for reaching, subjects establish the required hand position (see mapping problem in reaching the motor goal to get an idea of how this can be done without any computations). It is suggested (Fig. 8) that there are two separate neural layers: the layer of h-neurons and the layer of R-neurons that receive direct inputs from h-neurons. Changes in the output of h-neurons (ΔH) can be considered as a signal that is independent of afferent signals transmitted to the R-neuron. According to the general rule, independent signals shift the referent position at which the host neurons begin to be activated. Therefore, this change in the output activity of h-neurons automatically results in proportional, with some coefficient k, changes (ΔR) in the referent arm configuration:

$$\Delta H=k\Delta R$$ (6)

Because of this arrangement, changes in the activity of h-neurons automatically modify the activity of R-neurons responsible for changes in the arm joint angles, moving the hand to the target in the direction specified at the level of h-neurons. The reader may consult three experimental studies that can be used to suggest how reach-to-grasp arm movements within and beyond the arm reach are produced: Pilon et al. (2007), Rossi et al. (2002), and Yang and Feldman (2010).

Fig. 8.

Schematic diagram showing layers of h- and R-neurons. It is assumed that h-neurons are directly projected to the R-neurons, responsible for changes in the referent arm configurations (R) responsible for changes in the arm joint angles moving the hand in the direction specified at the h level. R-neurons produce shifts in the spatial thresholds of α-motoneurons, resulting in the hand motion. R_m is the maximal change in the referent arm configuration during reaching within the arm reach. When changes in R exceed R_m, the trunk is involved. With further increase in R, subjects move from sitting to standing (S) and eventually begin to walk to the target if the latter is far from the body. Further explanations are provided in the text.

Specific details of the relationship between neurons working in different spatial FRs can be clarified with further development of the theory. For now, the most important point is that the output of neurons of one FR in the control hierarchy predetermines referent shifts for neurons in the subordinate FR (Figs. 8 and 9).

Fig. 9.

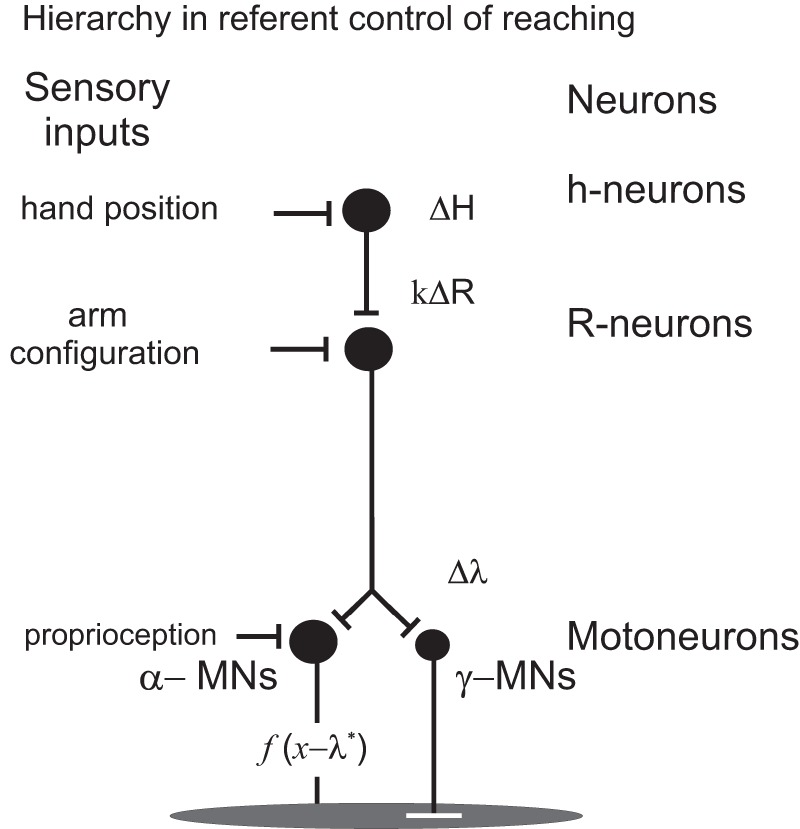
The output of each neuronal population plays the role of referent shifts for neurons in the subordinate frame of reference. Note the difference in sensory inputs to neurons at hierarchically different levels. See also Fig. 8. ΔH, change in output activity of h-neurons; k, coefficient; ΔR change in the referent arm configuration; Δλ, change in the spatial threshold; f(x − λ*), function of difference between the actual (x) and velocity-dependent threshold muscle length (λ*) as in Fig. 1C.

This analysis also addresses the question of how the movement direction in external space is transformed into appropriate changes in arm joint angles (internal space) and eventually into motor commands to muscles. In computational approaches, this is achieved by transformation of the coordinates of one FR to those of another, an operation involving Jacobian matrixes. In contrast, in the referent control theory, neurons dealing with motor directions and joint coordinations comprise separate spatial FRs. It is possible that both types of FRs are presumably localized in the motor cortex, as indirectly follows from findings that the motor cortex contains not only direction-sensitive neurons but also neurons sensitive to interjoint synergies (Capaday et al. 2013). The output activity of neurons in the hierarchically superior FR defines referent shifts of the subordinate FRs and, eventually, shifts in spatial thresholds of α-MNs (Fig. 9). In other words, to relay the performance from one FR to another, the system uses the output of neurons of one FR to shift the referent point of the subordinated FR (Figs. 8 and 9). This process does not require any computation or coordinate transformation and is done without learning, as has been shown for pointing in humans (Ghafouri et al. 2002).

Testing and Advancing the Referent Control Theory

It would be helpful to explicitly test that M1 neurons are involved in referent control. For example, one can analyze activity of these neurons in experiments in animals with hand movements adapted to a load acting transversally to the hand trajectory (Fig. 4). Consistent with referent control would be the observation that in the presence of such a load, the population vector would point in a diagonal direction that coincides with the direction of this vector in trials in which the load was suddenly removed but the animal does not produce corrective reactions.

By analyzing the navigation of birds and insects (Pritchard and Healy 2018), one can also test that they specify a referent direction that in the presence of deflecting winds does not coincide with the actual flight direction. To test this suggestion, one can attach an insect to a motionless surface while blowing the wind to evoke rhythmical motion of the wings. The actual and referent directions of the flight can be manipulated by changing the direction of air flow, as in experiments with loads deflecting the hand from the intended direction during pointing in humans (Fig. 4). One can also test the suggestion that direction-sensitive M1 neurons (h-neurons in Fig. 8) are projected to M1 neurons that change the arm configuration (R-neurons that are responsible for hand motion to the target).

External forces (loads, wind, etc.) deflect motion from the referent direction, resulting in an actual motor direction. Indeed, given the historical tradition of considering motor control in a standard biomechanical framework, it is difficult to acknowledge that the system does not preprogram, nor does it compute the actual movement direction. By trying to justify the traditional approach, one can argue that the population vector does represent the actual movement direction that can be “biased” by external forces. This reasoning would return us to the tenets of the standard biomechanical framework within which neurophysiological, referent variables underlying the control of motor actions cannot be found.

The present analysis shows that the understanding of the role of M1 neurons and neurons of other brain areas can be advanced by identifying spatial and cognitive FRs in which neurons function. While conducting research in the referent framework, one can address several questions: how neurons within each FR interact with relevant sensory inputs, how the control function is transferred from one spatial FR to another, how referent signals are used in perception, and how these signals are projected to MNs to produce motor actions. Presently, some of these questions have been answered for α-MNs on the basis of existing empirical data, but not for M1 and other neurons, studies of which were largely grounded in the conventional idea of preprogramming and direct specification of motor outcome. Finally, it would be important to analyze how task-specific referent shifts are retained in the motor memory and reproduced.

Further Implications of Referent Control

The referent control theory has been used to address the question of action-perception coupling with an explanation of kinesthesis and visual space constancy (Feldman 2016). The theory can be developed further by using Eq. 2 to suggest that in addition to or instead of spatial FRs, neurons can function in cognitive, multimodal FRs, which may allow the brain to recognize multidimensional patterns of events. This development can be done with formulations of testable predictions. The language of referent control might be helpful in conducting theory-driven research, as exemplified by several experimental studies reviewed in this article.

DISCUSSION

The present analysis suggests that, embedded in a sensory and central context, many neurons, including α-MNs, function in spatial FRs. These FRs are shifted to produce intentional motor actions but may remain motionless during involuntary, uncorrected reactions to external perturbations.

The present analysis confirms the significance of the finding of directional tuning of neurons by Georgopoulos and colleagues. An important outcome of this analysis is the conclusion that neurons are tuned to a referent direction underlying motor actions. In other words, motor actions are controlled indirectly, without predetermining motor direction or other kinematic or kinetic characteristics of the motor outcome. These characteristics emerge due to the interaction with the environment in predetermined spatial FRs. Referent control influences these characteristics, and based on sensory feedback, the system can decide whether referents should be changed, but once a decision is made, referent control is accomplished in an open-loop way until a next decision.

Empirical vs. Computational Theories of Motor Control

A fine point of the present analysis is that input signals to MNs (excitation/inhibition) predetermine the angular position at which MNs can begin to be recruited, but they do not and cannot carry any information about MN output, EMG signals, muscle forces, or kinematic variables. For some readers, this conclusion may come as a surprise because it cannot be reconciled with the conventional view that the brain directly preprograms the motor outcome. This view underlies the computational framework in which motor actions are presumably preprogrammed with the help of emulators of physical and physiological laws (internal models). In the same framework, it is assumed that, of many actions that meet the task demands, the system choses a specific action for which a cost function is minimal (e.g., Todorov and Jordan 2002). The idea of computation has become so pervasive that it is fashionable to call all processes in the brain “computations.” We need to disregard this fashion and evaluate different theories of motor control based on rigorous, scientific criteria. It is hardly too much to demand that a model, theory, or view of biological motor control should 1) be consistent with natural, physical laws, 2) be physiologically feasible, and 3) provide a logical structure for solving at least some classical problems (e.g., the posture-movement problem). It is necessary to emphasize, once again, that these criteria refer to theories of biological motor actions, because outside the realm of such actions (e.g., during mental processes), organisms are not constrained by physical and physiological laws (criteria 1 and 2). However, in the realm of motor actions, only theories that pass the three criteria can be considered as scientifically meaningful. We can ask, first, whether the existing computational theories of direct preprogramming of the motor outcome meet these criteria. We can then ask whether referent variables can be specified on the basis of some computational strategies. As far as the existing computational motor control theories are concern, they violate several physical laws or principles. Researchers might be not aware of such laws, because these are specific laws that are not described in standard textbooks, but as we know, ignorance of law excuses no one: conventional computational theories violate the principle of parametric control of equilibrium states identified in physics (Glansdorff and Prigogine 1971), dynamical systems theory (e.g., Andronov et al. 1987), and physiology (see below). Specifically, when changing the posture of the entire body or its segments, the system shifts equilibrium and stability to a final posture. Although equilibrium implies balance of forces (torques), the principle of parametric control states that the choice between different equilibrium positions is defined not by forces, torques, or other biomechanical variables characterizing the motor outcome but by system parameters that are independent of biomechanical variables. Such parameters, threshold positions at which muscles begin to be activated, have been identified by Matthews (1959) and Feldman and Orlovsky (1972) in animals and by Asatryan and Feldman (1965) in humans. The principle of parametric control of motor actions underlies the equilibrium-point hypothesis (EPH) and its extension, referent control. The same principle underlies the solution of the posture-movement problem (see motoneurons function in a spatial frame of reference). Strong support for the notion of parametric control of motor actions came from recent findings that corticospinal influences can be decorrelated from kinematic and kinetic variables, including EMG patterns, such that these influences only predetermine where, in the spatial domain or FR, α-MNs can be activated without any computation or predetermining of the motor outcome (Ilmane et al. 2013; Raptis et al. 2010; Sangani et al. 2011; Turpin et al. 2016; Zhang et al. 2017, 2018).

In contrast, by postulating direct preprogramming of motor outcome, conventional theories violate the principle of parametric control of motor actions. Such theories also violate the principle of causality, a major impetus of scientific enquiry (Planck 1949). Causality is inherent in laws of mechanics. In usual, inertial FRs, it is forces that cause changes in kinematic variables. In standard computational schemes, the system computes forces according to the desired kinematic characteristics of motion, thus inverting the causality of mechanical laws (Ostry and Feldman 2003; see also Sergio et al. 2005). There is no problem with this in mathematical computations: in fact, the Runge-Kutta solution of dynamic equations of motion is based on such an inversion. The causality is also inverted in artificial systems relying on mathematical computations (e.g., in robotics; see below). In contrast, the idea of inverting causality of mechanical laws in the production of physical movements can only be entertained in science fiction (e.g., Raspe 2012).

Indeed, the violation of natural, physical laws is unacceptable in any theory of motor control, but this is not the only “sin” of computational motor control theories: the fundamental nonlinearity of MNs and neurons also cannot be reconciled with such theories. For instance, on the basis of correlation between grip force and the load held between fingers during arm movement, Flanagan and Wing (1997) assumed that an anticipatory increase in the grip force during arm motion is preprogrammed and specified with the help of an internal model. By accepting this proposal, we need to explain how, physiologically, the preprogrammed grip forces can be specified. In other words, we need to show that the system can deliver input signals to MNs to force them to produce motor commands (EMG levels) resulting in the preprogrammed muscle forces. The system can use some EMG-force relationship to compute motor commands (EMG signals) required for production of the preprogramed muscle forces. When this is done, we still need to explain how the system can determine and physically deliver synaptic signals to MNs to force them to generate the requisite output EMG signals. The system should convert the output (EMG signals) of MNs into input (synaptic signals to MNs). Such conversion is physically and mathematically impossible because input/output functions of MNs are irreversible (see motoneurons function in a spatial frame of reference). Therefore, the proposal that grip forces are preprogrammed on the basis of an internal model is physiologically untenable, not to mention that it also violates the physical principle of parametric control and the causality principle. An anticipatory increase in grip forces was simulated in a dynamic model based on the notion of referent control (Pilon et al. 2007). The existence of an internal model for grip force production was motivated by the finding of grip force-load force coupling during arm motion, but this motivation is not convincing because it was shown (Pilon et al. 2007) that such coupling results from passive finger-object mechanical interaction via elastic finger pads.

Equally untenable are other proposals based on the idea of preprogramming of muscle forces, such as that by Todorov and Jordan (2002) in which the nervous system supposedly preprograms muscle forces to minimize a required cost function. The model by Harris and Wolpert (1998) is based on the hypothesis that the system specifies motor commands to minimize the variability of movement. This model is also physiologically unrealistic, because of the irreversibility of input/output functions of MNs. One can see that both models that postulate behavioral optimality have a common problem: they assume that the system optimizes programs or preprograms that cannot be actualized physiologically (see motoneurons function in a spatial frame of reference on how the system can and cannot optimize motor actions in the referent control framework).

Blakemore et al. (1998) proposed a computational scheme in which internal models are used to predict sensory consequences of our own actions. In this scheme, to reproduce sensory sensations, the system should specify the values of all kinematic and kinetic variables associated with the sensorimotor context estimation. In other words, like other computational schemes, this proposal implies direct specification of biomechanical variables, which is as physiologically and physically untenable as the proposal by Flanagan and Wing (1997). In contrast, by memorizing and reproducing referent variables, the system can repeat not only the desired motor actions but also sensations associated with them. In addition to the problems described above, computational schemes do not provide any clue to explain the origin of directional tuning of neurons; i.e., these schemes lack the capacity to explain the important dynamical aspect of neuronal behavior. Apparently, the formal use of the word “dynamics” in the descriptions of computational theories does not make them dynamical in the standard understanding of this notion.

All three criteria described above are met by the referent control theory, and they thus represent the barriers that a theory should overcome to be considered as a valuable alternative or a modification of the referent theory. In contrast, computational theories failed under the scrutiny of these three criteria. Instead of solving problems, computational theories create a new set of problems such as the problem of inverse-dynamic computations, the posture-movement problem, and the mapping problem. The validity of different models and views can be evaluated not only on the basis of the above criteria but also by experimental testing. This has been done in several studies (Foisy and Feldman 2006; Ilmane et al. 2013; Raptis et al. 2010; Sangani et al. 2011; Turpin et al. 2016; Zhang et al. 2017, 2018) with results inconsistent with the notion of preprogramming of the motor outcome, as illustrated in Fig. 6.

The following metaphor may help illustrate the empirical nature of referent control. A car can be considered as a spatial FR in which the range of motor actions of the driver is limited, but this does not prevent the driver (brain) from using available means to move the FR (car) and bring him/herself to the desired destination. The point is that referent control restricts the set of all possible motor actions to those consistent with the task demands such that the motor goal can be reached by simply shifting the FR in an appropriate direction.

It might be helpful to explain why computational control strategies works well for robotics but are inappropriate for biological motor control. In robotics, forces (torques) required for a preplanned motion of an artificial arm can be precomputed on the basis of the known equations of motion (“internal model”) and, by inverting the input/output characteristics of robot actuators (electrical motors), to determine and produce the requisite electrical currents to drive the robot arm along the desired trajectory. In contrast, input/output functions of MNs with their threshold properties are irreversible, and unlike electrical motors, each muscle is associated with a family of force-length characteristics (Fig. 1C), which also was emphasized by Bernstein (1967). Even if motor commands are precomputed, one cannot determine which force-length characteristic is chosen for each muscle and which synaptic currents should be delivered to MNs to produce the required motor commands (Ostry and Feldman 2003; see also Sergio et al. 2005).

Georgopoulos and Carpenter (2015) consider brain-robot and brain-computer interfaces as supporting the notion that M1 neurons predetermine kinematic characteristics of motor actions. No doubt such interfaces are helpful in improving the everyday life of paralyzed individuals. They also demonstrate the capacity of the brain to learn novel motor skills. Interfaces allow paralyzed individuals to modify brain activity to control electrical motors of artificial arms and legs or computer cursors, which can also be achieved by using other biological signals, e.g., EMG activity of nonparalyzed muscles. However, as follows from the present analysis, brain activity in normal conditions cannot and does not predetermine kinematics and/or motor commands that MNs and muscles should produce. Therefore, despite impressive engineering imitations of biological motor actions, robotics and computational framework in general are not helpful and are even misleading in the understanding of how motor actions are controlled in biological systems. The opposite is true: the use of some control principles underlying biological motion can be helpful in robotics and brain-machine interfaces (e.g., Bicchi et al. 2002; Schwartz 2016).

Can computational strategies be employed during specification of referent variables? While trying to answer this question, one should also have in mind that referent, noncomputational control might be sufficient for explanations of motor actions, including learning (e.g., Turpin et al.2016; Zhang et al. 2018). Regardless, before the limits of referent control and the role of motor memory in it are investigated, the notion of computational control of referent variables can hardly be discussed productively without maintaining the fashion of seeing computer programs in every aspect of brain activity.

Conclusions

Directional tuning of neurons, including M1 neurons, can be considered a natural consequence of their functioning within spatial frames of reference that are shifted to produce intentional motor actions but remain motionless during involuntary, uncorrected reactions to external perturbations. Thereby, neurons are primarily tuned to the referent direction of a movement or an isometric force production, whereas the actual motor direction depends not only on referent shifts but also on external conditions. Indirect, referent control of posture and movement is a departure from conventional views based on direct preprogramming of the motor outcome with or without internal models. Referent control also challenges conventional views on the integration of central and peripheral (reflex) mechanisms in the control of posture and movement.

GRANTS

This work was supported by the Natural Sciences and Engineering Research Council of Canada and the Heart and Stroke Foundation of Canada.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author.

AUTHOR CONTRIBUTIONS

A.G.F. conceived and designed research; A.G.F. performed experiments; A.G.F. analyzed data; A.G.F. interpreted results of experiments; A.G.F. prepared figures; A.G.F. drafted manuscript; A.G.F. edited and revised manuscript; A.G.F. approved final version of manuscript.