Generalized Bayesian Factor Analysis for Integrative Clustering with Applications to Multi-Omics Data

Abstract

Integrative clustering is a clustering approach for multiple datasets, which provide different views of a common group of subjects. It enables analyzing multi-omics data jointly to, for example, identify the subtypes of diseases, cells, and so on, capturing the complex underlying biological processes more precisely. On the other hand, there has been a great deal of interest in incorporating the prior structural knowledge on the features into statistical analyses over the past decade. The knowledge on the gene regulatory network (pathways) can potentially be incorporated into many genomic studies.

In this paper, we propose a novel integrative clustering method which can incorporate the prior graph knowledge. We first develop a generalized Bayesian factor analysis (GBFA) framework, a sparse Bayesian factor analysis which can take into account the graph information. Our GBFA framework employs the spike and slab lasso (SSL) prior to impose sparsity on the factor loadings and the Markov random field (MRF) prior to encourage smoothing over the adjacent factor loadings, which establishes a unified shrinkage adaptive to the loading size and the graph structure. Then, we use the framework to extend iCluster+, a factor analysis based integrative clustering approach. A novel variational EM algorithm is proposed to efficiently estimate the MAP estimator for the factor loadings. Extensive simulation studies and the application to the NCI60 cell line dataset demonstrate that the propose method is superior and delivers more biologically meaningful outcomes.

I. Introduction

Rapid advances in technologies have led to the generation of massive amounts of multi-omics data. This has led to a great deal of interest in the integrative analysis of multiple datasets. As the multiple datasets provide information on the subjects and/or the features from many different perspectives, the integrative analysis can help us better understand complex biological underpinnings of many diseases and health problems.

Integrative clustering is the integrative analysis approach that aims to cluster the subjects from which multiple datasets have been gathered. By capturing the underlying biological variants governing the variations of all datasets, we are able to obtain more accurate subtyping, uncover new disease subtypes, understand disease progression, or develop tailored treatment and personalized medicine. For example, while the classification of cancers is typically based on the tissue/cell-type origin and pathogens [1], the biological mechanism of diseases actually builds upon several biological molecular processes [2]. By aggregating the information of the molecular processes at different levels, the integrative clustering can identify new disease subtypes whose clinical outcomes are distinct from the traditional cancer subtypes [3, 4] and help us understand better the survival and mortality risk differences.

Several approaches for integrative clustering have been proposed and applied to multi-omics data [1]. Many approaches are based on the low-rank matrix factorization such as the nonnegative matrix factorization [5] and the factor analysis [6, 7, 4]. Kim et al. [8] utilizes the hierarchical structure among the multi-omics data. Kiselev et al. [9] applies the consensus clustering approach to the single-cell RNA-seq data. Shen et al. [6] introduces iCluster, which is a Bayesian factor analysis based integrative clustering approach. In the framework of iCluster, the low-dimensional latent factors are assumed to carry sufficient information about the underlying biological variations among the subjects, and the posterior distribution of the latent factors are considered much less noisy and more reliable than the original data. Therefore, they perform the K-means clustering on the posterior mean of the latent factors, which are imputed by the EM algorithm. iCluster+ [4] extends iCluster allowing for dealing with more data types such as binary and Poisson in addition to Gaussian. Mo et al. [10] proposes the full Bayesian approach of iCluster.

On the other hand, many techniques of incorporating biological structural information have been developed over the past decade. It is well-known that gene expressions are governed by the gene regulatory network (GRN), which includes various pathways. A gene pathway can be represented by a directed acyclic graph (DAG) where the nodes represent pathway members (genes) and the edges represent production dependencies between the gene pairs. The knowledge on such graphical structure of genes can potentially improve statistical analyses of gene expression data, and is constantly growing fed by various data sources [11]. Some pathway databases are publicly available [12].

The existing statistical approaches capable of incorporating graph information include Li and Li [13] and Pan et al.[14], which propose network-based penalties from the frequentist perspectives. In the Bayesian framework, Li and Zhang [15] and Stingo et al. [16] use the spike and slab prior in combination with the Markov random field (MRF) prior. Chang et al. [17] and Rockova and Lesaffre [18] incorporate graph information by smoothing shrinkage parameters under Bayesian lasso framework. The basic principle behind these works is that the penalties or the shrinkage priors encourage group-wise selection of features that are adjacent on the graph structure or belong to a same pathway. In addition to the biological qualitative motivation offered by the GRN, Yu and Liu [19] provides a quantitative justification of the group-wise selection. However, all of the aforementioned approaches are developed for the regression framework. For clustering, we note that the PARADIGM [20] uses the pathway level activities instead of the individual gene expression data, but no clustering method has been proposed to utilize the pathway graph information, to the best of our knowledge.

In this paper, we propose a novel integrative clustering method that can incorporate the graph information. We first build the generalized Bayesian factor analysis (GBFA) framework, and use the framework to extend iCluster+ [4]. Our GBFA framework employs the spike and slab lasso (SSL) prior to impose sparsity on factor loadings and the MRF prior [15] or the Ising prior to incorporate network information. The combination of the SSL and MRF (or Ising) priors achieves doubly adaptive L₁ shrinkage on factor loadings; the level of shrinkage is adaptive to the corresponding loading size and its neighboring shrinkage levels. The adaptivity to loading sizes alleviates the bias caused by the L₁ shrinkage and the adaptivity to neighboring shrinkage parameters encourages the group-wise selection among the adjacent factor loadings, which are the first innovation of our work. Plus, the SSL prior allows the Maximum a Posteriori (MAP) estimates of the factor loadings to attain exact zeros unlike the traditional spike and slab Gaussian prior. This leads to more accurate estimation of other parameters involving the latent factors, which the subsequent clustering procedure will be based on.

Similar approaches have been proposed by Klami et al. [21], Virtanen et al. [22], which they call the group factor analysis. Note that, while their approaches incorporate the group membership information, our GBFA takes into account the network graph information, which contains finer interaction knowledge beyond the membership. Also, while their approaches can deal with continuous variables only, our GBFA can support multiple data types including discrete variables such as binomial, negative binomial, and Poisson. This is the second innovation of our work.

The third innovation is that we propose an efficient variational EM algorithm for the MAP estimator of the factor loadings, where the posterior mean and covariance of the latent factors are imputed by minimizing the Kullback-Leibler divergence to the original posterior distribution. Owing to the latent variable augmentation [23], all relevant expectations are completely tractable, and therefore we can avoid the Monte Carlo approximation used in [4]. The imputed posterior mean of the latent factors are then used for clustering via the K-means clustering method.

The paper is organized as follows. In the following section, we propose the GBFA framework and the integrative clustering method. Section III presents the variational EM algorithm. Extensive simulation studies are conducted in Section IV, followed by the application to the NCI60 dataset in Section V. Section VI includes conclusions and discussion.

II. Methodology

In this section, we first establishes the generalized Bayesian factor analysis framework. Then, we propose an integrative clustering algorithm based on the GBFA framework.

A. Notation

Vectors are denoted by bold and lowercase letters. Matrices are denoted by uppercase letters if not greek. For a p × n matrix A, a_ji stands for the (j, i) entry of A, a_i = (a_1i,..., a_pi)^T stands for the i-th column vector of A, and ã_j = (a_j1,..., a_jn)^T stands for the j-th row vector of A. For a vector b, b_i stands for the i-th element of b and D_b denotes the diagonal matrix diag(b).

B. Generalized Bayesian Factor Analysis Framework

Suppose we have H multi-modal data generated from various technologies, say X¹, ..., X^H, each of which is a ph × n matrix for 1 ≤ h ≤ H where n is the sample size. Let X be their vertical concatenate, which is of size p × n where $p={\sum }_{h=1}^H\mathit{ph}$.

$$X=\left[\begin{array}{c}\hfill X^1\hfill \\ \hfill ⋮\hfill \\ \hfill X^H\hfill \end{array}\right]\in {\mathbb{R}}^{p\times n}.$$

Let z_i be the L-dimensional latent factor for the i-th subject and w̃_j be the factor loadings for the j-th feature. Let μ = m1^T + WZ where m is the location vector, Z = [z₁,...,z_n] ∈ ℝ^L×n be the latent factor matrix, and W = [w̃₁,..., w̃_p]^T ∈ ℝ^p×L be the factor loading matrix. GBFA assumes that the distribution of X is governed by the parameter matrix μ, which takes a low-rank representation, i.e., L ≪ p.

Suppose {x_ji}_1≤i≤n belong to the same distribution family and the distribution of X, parameterized by μ, has the following form of likelihood.

$$\pi (X\mid \mu )=\prod _j\prod _i{\pi }_j(x_{\mathit{ji}}\mid {\mu }_{\mathit{ji}}),$$

where π_j is the density function for the j-th distribution family.

Note that it is critical to support various and heterogeneous data types in accommodating multi-omics data. Our framework allows for analyzing heterogeneous data types including binomial, negative binomial, Poisson, and Gaussian distributions, and is more flexible than iCluster+ [4], which admits Bernoulli, Poisson, and Gaussian distributions only. Suppose {x_ji}_1≤i≤n follow the binomial distribution with parameters n_j and p_ji. We use the logit link function for p_ji and the likelihood is given by

$${\pi }_j(x_{\mathit{ji}}\mid {\mu }_{\mathit{ji}})=\left(\begin{array}{c}\hfill n_j\hfill \\ \hfill x_{\mathit{ji}}\hfill \end{array}\right)\frac{e^{{\mu }_{\mathit{ji}}{x}_{\mathit{ji}}}}{{(1+e^{{\mu }_{\mathit{ji}}})}^{n_j}},0\le x_{\mathit{ji}}\le n_j.$$ (1)

If {x_ji}_1≤i≤n follow the negative binomial distribution with parameters r_j and p_ji, for which we use the logit link function, the likelihood is given by

$${\pi }_j(x_{\mathit{ji}}\mid {\mu }_{\mathit{ji}})=\left(\begin{array}{c}\hfill r_j+x_{\mathit{ji}}-1\hfill \\ \hfill x_{\mathit{ji}}\hfill \end{array}\right)\frac{e^{{\mu }_{\mathit{ji}}{x}_{\mathit{ji}}}}{{(1+e^{{\mu }_{\mathit{ji}}})}^{r_j+x_{\mathit{ji}}}},x_{\mathit{ji}}\ge 0.$$ (2)

If {x_ji}_1≤i≤n follow the Poisson distribution with mean e^μ_ji, the likelihood is given as follows.

$${\pi }_j(x_{\mathit{ji}}\mid {\mu }_{\mathit{ji}})=e^{-e^{{\mu }_{\mathit{ji}}}}\frac{e^{{\mu }_{\mathit{ji}}{x}_{\mathit{ji}}}}{x_{\mathit{ji}}!},x_{\mathit{ji}}\ge 0.$$ (3)

If {x_ji}_1≤i≤n follow the Gaussian distribution with mean μ_ji and precision ρ_j, we have the likelihood as follows.

$${\pi }_j(x_{\mathit{ji}}\mid {\mu }_{\mathit{ji}})=\frac{{\rho }_j^{1∕2}}{\sqrt{2\pi }}{e}^{-{\rho }_j{(x_{\mathit{ji}}-{\mu }_{\mathit{ji}})}^2∕2},x_{\mathit{ji}}\in \mathbb{R}.$$

Binomial, negative binomial, and Gaussian distributions have extra parameters n_j, r_j, and ρ_j, respectively. The parameters n_j and r_j must be provided with the data. We assign the gamma distribution $\mathcal{G}\left({\zeta }_j/2,{\zeta }_j/2\right)$ as the prior for ρ_j. A typical choice for ϛ_j is 1, which gives the most uninformative prior. We marginalize out ρ_j and the actual (marginal) distribution of x_ji becomes the Student t-distribution.

Of note, the Bernoulli distribution is a special case of the binomial distribution with n_j = 1 and the geometric distribution is a special case of the negative binomial distribution with r_j = 1 .

C. Priors for W and Z

We consider the L₁ shrinkage spike and slab prior on W,

$$\text{log}\pi (W\mid \gamma )=C+\sum _{j,l}\text{log}{\lambda }_{\mathit{jl}}-\sum _{j,l}{\lambda }_{\mathit{jl}}\mid w_{\mathit{jl}}\mid ,$$

where λ_jl = (1 − γ_jl)λ₀+γ_jlλ₁ with 0 ≤ λ₁ < λ₀ and γ_jl is a binary variable indicating nonzero-ness of w_jl. This spike and slab lasso (SSL) prior, which has been introduced in [24, 25], administers two levels of shrinkage depending on the size of loadings. If |w_jl| is close to zero, γ_jl turns off and triggers higher level of shrinkage λ₀ for w_jl. Conversely, if |w_jl| is far from zero, γ_jl turns on and w_jl receives lower level of shrinkage λ₁. Furthermore, combined with EM algorithm, the SSL prior imposes continuously adaptive shrinkage on w_jl, as elaborated in Section III.

An important advantage of SSL prior against the traditional spike and slab Gaussian prior [26] is that the elements in the MAP estimator Ŵ can take exact zero values. Having exact zero values for true zeros in W leads to more accurate estimation of other parameters including the ones related to the latent factors Z. As the clustering algorithm, presented in Section II-E, is based on the posterior mean of Z, it makes a crucial improvement.

Following the standard orthonormality assumption on the latent factors, we assign the standard Gaussian prior for Z.

$$\text{log}\pi (Z)=C-\frac{1}{2}\sum _{l,i}{z}_{\mathit{li}}^2.$$

D. Prior for γ: Incorporating Network Information

Suppose the graphs G_h = ⟨P_h,E_h⟩ are given where P_h = {1,...,p_h} represents the set of variables in the h-th dataset and E_h is the set of edges among them, where the presence of edge indicates the correlation between the relevant pair of variables. We incorporate this network information into the generalized factor analysis framework by encouraging to match the correlation structure. Since X^h are vertically concatenated, we first combine H graphs into a single graph G = ⟨P,E⟩ by setting P = {1, ...,p} and E = {(ι(h,j),ι(h,k)) : (j, k) ∈ E_h, 1 ≤ h ≤ H} where ι(h,j) is the index in the matrix X of the j-th variable in the h-th dataset. Let G be the adjacency matrix for G.

Consider two Gaussian variables x_j and x_k. Note that, under the assumption that the latent factors z_li are independent with zero mean and unit variance, the covariance of x_j and x_k given W is as follows.

$$\text{Cov}(x_j,x_k)=\sum _l{w}_{\mathit{jl}}{w}_{\mathit{kl}}.$$

This implies that, in order for x_j and x_k to be correlated, they must load at least one common factor. This argument easily extends to non-Gaussian variables as well. If the latent factors are independent, the only way a pair of variables can be correlated is that they must load at least one common factor.

Therefore, it is reasonable to encourage the pairs of adjacent variables to share common factors. If one variable loads any factor, its adjacent variables are encouraged to load the factor as well. In other words, if x_j and x_k are adjacent in G and if w_jl ≠ 0 for some l, then we promote w_kl ≠ 0.

To this end, we employ the Markov random field (MRF) prior, as introduced in Li and Zhang [15].

$$\text{log}\pi (\gamma )=C_{\delta ,\eta }-\delta \sum _{j,l}{\gamma }_{\mathit{jl}}+\eta \sum _{j,k,l}{G}_{\mathit{jk}}{\gamma }_{\mathit{jl}}{\gamma }_{\mathit{kl}},$$ (4)

where δ is the parameter that controls of the sparsity of factor loadings. The MRF prior helps achieve our goal because γ_kl = 1 is encouraged if γ_jl = 1 and vice versa, when x_j and x_k are adjacent (G_jk = 1). Here, η ≥ 0 is the smoothing parameter that controls the strength of the encouragement.

We also propose using the Ising prior for γ_jl as follows.

$$\text{log}\pi (\gamma )=C_{\delta ,\eta }-\delta \sum _{j,l}{\gamma }_{\mathit{jl}}+\eta \sum _{j,k,l}{G}_{\mathit{jk}}\mathbb{I}({\gamma }_{\mathit{jl}}={\gamma }_{\mathit{kl}}).$$ (5)

The key difference between (4) and (5) is that the former encourages γ_jl = γ_kl = 1 only while the latter promotes γ_jl = γ_kl. The two-way smoothing in (5) can enhance specificity depending on the specified graph structure.

E. Clustering

In the GBFA framework, the high-dimensional data matrix X is represented by the low-rank parameter matrix μ. In particular, the low-dimensional latent factors Z are shared by all data sets and assumed to capture all biological variations among the subjects. Since Z is not observed, we retrieves the cluster membership based on the posterior mean 𝔼(Z|X). When the model assumptions are true, 𝔼(Z|X) is considered much less noisy and more reliable than the original data matrix X. In Section III, we develop the variational EM algorithm, where 𝔼(Z|X) is approximated by μ_Z. We then conduct the K-means clustering on the estimate of μ_Z to retrieve the membership of clusters. We call the resulting clustering method GBFA_CL.

III. Computation

We propose the Maximum A Posteriori (MAP) estimator for W marginalizing Z and γ out. Unfortunately, the classical EM approach involves an intractable conditional expectation of the loglikelihood. To address the problem, we use the latent variable augmentation technique and the variational EM approach. For binomial and negative binomial likelihood functions, we use the following identity [23].

$$\frac{e^{{\mu }_{\mathit{ji}}{x}_{\mathit{ji}}}}{{(1+e^{{\mu }_{\mathit{ji}}})}^{b_{\mathit{ji}}}}=2^{-b_{\mathit{ji}}}{e}^{{\kappa }_{\mathit{ji}}{\mu }_{\mathit{ji}}}{\int }_0^{\infty }{e}^{-{\rho }_{\mathit{ji}}{\mu }_{\mathit{ji}}^2∕2}{\pi }_{\mathit{ji}}({\rho }_{\mathit{ji}})d{\rho }_{\mathit{ji}},$$

where k_ji = x_ji − b_ji/2 and π_ji(ρ_ji) is the density of the Polya-Gamma class $\mathcal{P}\mathcal{G}(b_{ji},0)$. Applying this identity to (1), (2), and (3) offers a unified form of likelihood for Gaussian, binomial, and negative binomial variables as follows.

$${\pi }_j({\tilde{\mathbf{x}}}_j,{\tilde{\rho }}_j\mid {\tilde{\mu }}_j)\propto e^{-\frac{1}{2}\sum \begin{array}{c}\hfill \\ i\hfill \end{array}{\rho }_{\mathit{ji}}{({\mu }_{\mathit{ji}}-{\psi }_{\mathit{ji}})}^2+\sum \begin{array}{c}\hfill \\ i\hfill \end{array}{\kappa }_{\mathit{ji}}{\mu }_{\mathit{ji}}}{\pi }_j^{\ast }({\tilde{\rho }}_j),$$ (6)

where the unknown components are summarized in Table I. There is no ρ_ji associated with a Poisson variable x_ji. But, for succinct notations, we use ${\pi }_j({\tilde{\mathbf{x}}}_j,{\tilde{\rho }}_j\mid {\tilde{\mu }}_j)={\pi }_j({\tilde{\mathbf{x}}}_j\mid {\tilde{\mu }}_j){\pi }_j^{\ast }({\tilde{\rho }}_j)$ with any ${\pi }_j^{\ast }$. Then, the full likelihood can be written as

$$\pi (\gamma ,\rho ,W,Z,X\mid \mathbf{m})=\pi (W\mid \gamma )\pi (\gamma )\pi (Z)\prod _j{\pi }_j({\tilde{\mathbf{x}}}_j,{\tilde{\rho }}_j\mid {\tilde{\mu }}_j).$$

TABLE I.

Parameters for unified likelihood in (6).

Type	ψji	kji	${\pi }_j^{\ast }({\rho }_j)$
Gaussian	xji	0	${\rho }_{\mathit{ji}}\equiv {\rho }_j\sim \mathcal{G}\left(\frac{{\zeta }_j+n}{2},\frac{{\zeta }_j}{2}\right)$
Binomial	0	xji − nj/2	${\rho }_{\mathit{ji}}\sim \mathcal{P}\mathcal{G}(n_j,0)$
Neg. Bin.	0	(xji − rj)/2	${\rho }_{\mathit{ji}}\sim \mathcal{P}\mathcal{G}(x_{\mathit{ji}}+r_j,0)$

A. Variational EM Algorithm

Let π̃(·) be a measure on γ, ρ, and Z and $\tilde{\mathbb{E}}(\cdot )$ denotes the expectation with respect to π̃. The EM algorithm yields the MAP estimator by maximizing

$$Q(\mathbf{m},W,\tilde{\pi })=\tilde{\mathbb{E}}\text{log}\pi (\gamma ,\rho ,W,Z,X\mid \mathbf{m})-\tilde{\mathbb{E}}\text{log}\tilde{\pi }(\gamma ,\rho ,Z),$$

which is maximized when π̃(·) = π(·|m, W, X) and Q(m, W, π̃) = log π(W, X|m).

Unfortunately, there is no analytic solution to the conditional expectations involving γ, ρ, and Z given W. Therefore, we use the variational EM approach [27], which limits the domain of π̃ within tractable. We consider a product measure on individual γ_jl;, ρ, and Z. Let π̂(γ, ρ, Z) = π̂(γ)π̂(ρ)π̂(Z) where

$$\begin{array}{cc}\hfill \widehat{\pi }(\gamma )& =\prod _{j,l}{\theta }_{\mathit{jl}}^{{\gamma }_{\mathit{jl}}}{(1-{\theta }_{\mathit{jl}})}^{1-{\gamma }_{\mathit{jl}}},\hfill \\ \hfill \widehat{\pi }(\rho )& \propto \prod _j{e}^{-\frac{1}{2}\sum \begin{array}{c}\hfill \\ i\hfill \end{array}{\rho }_{\mathit{ji}}{\phi }_{\mathit{ji}}^2}{\pi }_j^{\ast }({\tilde{\rho }}_j),\hfill \\ \hfill \widehat{\pi }(Z)& \propto \prod _i{e}^{-\frac{1}{2}{({\mathbf{z}}_i-{\mu }_{z,i})}^T{\Sigma }_{z,i}^{-1}({\mathbf{z}}_i-{\mu }_{z,i})},\hfill \end{array}$$

and 𝔼̂ be the expectation operator under π̂. Note that {ρ_ji}_1≤i≤n associated with a Poisson variables x_j are completely independent, for which we freely fix φ_ji = 0.

Then, our MAP estimator is obtained by maximizing the evidence lower bound (ELBO) with respect to m, W, θ, φ, and {μ_z,i, ∑_z,i}_1≤i≤n

$$\begin{array}{cc}\hfill Q(\mathbf{m},W,\theta ,& \phi ,{\{{\mu }_{z,i},{\Sigma }_{z,i}\}}_{i=1}^n)=\widehat{\mathbb{E}}\text{log}\pi (\gamma ,\rho ,W,Z,X\mid \mathbf{m})\hfill \\ \hfill & -\widehat{\mathbb{E}}\text{log}\widehat{\pi }(\gamma )-\widehat{\mathbb{E}}\text{log}\widehat{\pi }(\rho )-\widehat{\mathbb{E}}\text{log}\widehat{\pi }(Z),\hfill \end{array}$$ (7)

which lower-bounds the log evidence log π(W, X |m).

Each of E- and M-steps will be detailed in the following sections. A single iteration of our EM algorithm takes O(npL² + eL) time complexity where e = |E| is the number of edges in the graph, assuming L ≪ min(p, n). The EM approach has an advantage over MCMC in that the number of iterations that EM algorithm requires is generally much smaller than the number of samples that MCMC needs. It is worth noting that E-step for Z and M-step for W are the bottleneck but can be obviously parallelized. Finally, we note that any coordinate ascent algorithm would be inappropriate because the objective function is not concave and the solution will depend on the order of the variables.

B. E-steps

E-steps optimize (7) with respect to the parameters of π̂(Z), π̂(ρ), and π̂(γ), alternately.

1). E-step for γ:

Let ${\alpha }_{\mathit{jl}}=\text{log}\frac{{\theta }_{\mathit{jl}}}{1-{\theta }_{\mathit{jl}}}$. We make a quasi-Newton update for α_l with backtracking line search for each l. As the Hessian matrix is huge if p is large, we make use of only the diagonal elements of the Hessian matrix following Becker and Le Cun [28]. This alleviates the gradient vanishing problem of the sigmoid (expit) function.

As alluded to in Section I, we can see that the SSL and MRF priors indeed achieve the doubly adaptive shrinkage for W. The KKT condition yields, for each α_jl,

$${\alpha }_{\mathit{jl}}=-\delta +\eta \sum _k{G}_{\mathit{jk}}{\theta }_{\mathit{kl}}+\text{log}\frac{{\lambda }_1}{{\lambda }_0}-\mid w_{\mathit{jl}}\mid ({\lambda }_1-{\lambda }_0).$$ (8)

Section III-C1 and (8) show that L₁ shrinkage for w_jl depends on the loading size |w_jl| and the shrinkage for adjacent loadings (θ_kl).

Algorithm 1: EM algorithm for GBFA
P ← {j : xj is Poisson}.
Initialize m, W, ρ, and θ.
$$\begin{array}{c}\mathbf{repeat}\hfill \\ \mid \begin{array}{c}\mathbf{for}\underset{¯}{l=1,\dots ,L}\mathbf{do}∕\star \text{E}-\text{step for}\gamma \star ∕\hfill \\ \mid \begin{array}{c}{\alpha }_{\mathit{jl}}\leftarrow {\alpha }_{\mathit{jl}}+s_l(-\delta +\eta \sum \begin{array}{c}\hfill \\ k\hfill \end{array}{G}_{\mathit{jk}}{\theta }_{\mathit{kl}}+\text{log}({\lambda }_1∕{\lambda }_0)-\mid w_{\mathit{jl}}\mid ({\lambda }_1-{\lambda }_0)-{\alpha }_{\mathit{jl}})\text{for all}j\text{where}{s}_l\text{is determined by the}\hfill \\ \text{backtracking line search}.\hfill \\ {\theta }_{\mathit{jl}}\leftarrow 1∕(1+e^{-{\alpha }_{\mathit{jl}}});{\lambda }_{\mathit{jl}}\leftarrow (1-{\theta }_{\mathit{jl}}){\lambda }_0+{\theta }_{\mathit{jl}}{\lambda }_1\text{for all}j.\hfill \end{array}\phantom{\mid }\hfill \\ \mathbf{end}\hfill \\ \mathbf{if}\underset{¯}{\mathcal{P}=\varnothing }\mathbf{then}\text{update}{\mu }_{z,i}\text{and}{\Sigma }_{z,i}\text{as in (9) for}1\le i\le n.∕\star \text{E}-\text{step for}Z\star ∕\hfill \\ \mathbf{else}\hfill \\ \mid \mathbf{for}\underset{¯}{i=1,\dots ,n}\mathbf{do}\text{update}{\mu }_{z,i}\text{and}{\Sigma }_{z,i}\text{by the gradient ascent method with the backtracking line search}.\hfill \\ \mathbf{end}\hfill \\ \mathbf{for}\underset{¯}{j=1,\dots ,p}\mathbf{do}\text{update}{\phi }_{\mathit{ji}},{\rho }_{\mathit{ji}},\text{and}{\rho }_j\text{as in Section III-B2}.∕\star \text{E}-\text{step for}\rho \star ∕\hfill \\ \mathbf{for}\underset{¯}{j=1,\dots ,p}\mathbf{do}∕\star \text{M}-\text{step for}W\star ∕\hfill \\ \mid \begin{array}{c}\mathbf{if}\underset{¯}{j\notin \mathcal{P}}\mathbf{then}{\tilde{\mathbf{w}}}_j\leftarrow {\text{argmin}}_{\mathbf{w}}(\frac{1}{2}{\mathbf{w}}^T{A}_j\mathbf{w}-{\mathbf{b}}_j^T\mathbf{w}+\sum \begin{array}{c}\hfill \\ l\hfill \end{array}{\lambda }_{\mathit{jl}}\mid w_l\mid \text{where}{A}_j\text{and}{\mathbf{b}}_j\text{are given by (10)}.\hfill \\ \mathbf{else}\text{update}{\tilde{\mathbf{w}}}_j\text{by the proximal gradient ascent method}.\hfill \end{array}\phantom{\mid }\hfill \\ \mathbf{end}\hfill \end{array}\phantom{\mid }\hfill \\ \mathbf{until}\underset{¯}{\text{convergence}}.\hfill \end{array}$$

2). E-step for ρ:

For a non-Poisson variable x_j, we have

$${\phi }_{\mathit{ji}}^2\leftarrow {(m_j+{\tilde{\mathbf{w}}}_j^T{\mu }_{z,i}-{\psi }_{\mathit{ji}})}^2+{\tilde{\mathbf{w}}}_j^T{\Sigma }_{z,i}{\tilde{\mathbf{w}}}_j.$$

For a non-Poisson discrete variable x_j, we have by Poison et al. [23]

$$\widehat{\mathbb{E}}({\rho }_{\mathit{ji}})=\frac{b_{\mathit{ji}}(e^{{\phi }_{\mathit{ji}}}-1)}{2{\phi }_{\mathit{ji}}(e^{{\phi }_{\mathit{ji}}}+1)},1\le i\le n,$$

with b_ji = n_j if x_j is a binomial variable and b_ji = x_ji + r_j if x_j is a negative binomial variable. For a Gaussian variable x_j, we have

$$\widehat{\mathbb{E}}({\rho }_j)=\frac{{\zeta }_j+n}{{\zeta }_j+\sum _i{\phi }_{\mathit{ji}}^2}.$$

3). E-step for Z:

Exact solutions exist for μ_z,i and ∑_z,i if there is no Poisson variable in data. For each i, we update

$${\Sigma }_{z,i}\leftarrow {(W^T{\mathcal{D}}_{{\rho }_i}W+I)}^{-1},{\mu }_{z,i}\leftarrow {\Sigma }_{z,i}{W}^T{\mathbf{c}}_i,$$ (9)

where C = κ + ρ○(ψ − m1^T). Here, ○ denotes the Hadamard product.

The gradient ascent updates with backtracking line search are performed if at least one Poisson variable is included in data.

C. M-steps

M-steps optimize (7) with respect to W (and m jointly).

M-step for W:

For a non-Poisson variable x_j, we solve

$${\tilde{\mathbf{w}}}_j\leftarrow \underset{\mathbf{w}}{\text{argmin}}\left(\frac{1}{2}{\mathbf{w}}^T{A}_j\mathbf{w}-{\mathbf{b}}_j^T\mathbf{w}+\sum _l\widehat{\mathbb{E}}({\lambda }_{\mathit{jl}})\mid w_l\right),$$

where $\widehat{\mathbb{E}}({\lambda }_{\mathit{jl}})={\theta }_{\mathit{jl}}{\lambda }_1+(1-{\theta }_{\mathit{jl}}){\lambda }_0$, and

$$\begin{array}{cc}\hfill A_j& =-\frac{d^2\widehat{\mathbb{E}}\text{log}{\pi }_j({\tilde{\mathbf{x}}}_j,{\tilde{\rho }}_j\mid {\tilde{\mu }}_j)}{d{\tilde{\mathbf{w}}}_{j}d{\tilde{\mathbf{w}}}_j^T},\hfill \\ \hfill {\mathbf{b}}_j& =A_j{\tilde{\mathbf{w}}}_j+\frac{d\widehat{\mathbb{E}}\text{log}{\pi }_j({\tilde{\mathbf{x}}}_j,{\tilde{\rho }}_j\mid {\tilde{\mu }}_j)}{d{\tilde{\mathbf{w}}}_j}.\hfill \end{array}$$ (10)

Note that A_j and b_j do not depend on the current value of w̃_j, and this is an adaptive lasso problem where the penalties are adaptive to both the corresponding loading sizes and the graph structure, as so are θ_jls. We use the DWL algorithm [29], which efficiently computes the exact solution. This guarantees the monotone increase of Q.

For a Poisson variable x_j, w̃_j cannot be solved by lasso. Instead, we use the proximal gradient ascent method.

2). M-step for m (jointly with W):

If m_j is fitted rather than fixed, we update m_j and w̃_j jointly. For a non-Poisson variable x_j, we can update (m_j, w̃_j)^T with extended A_j and b_j as follows.

$$A_j=-\left[\begin{array}{cc}\hfill \frac{d^2\widehat{\mathbb{E}}\text{log}{\pi }_j({\tilde{\mathbf{x}}}_j,{\tilde{\rho }}_j\mid {\tilde{\mu }}_j)}{{\mathit{dm}}_j^2}\hfill & \hfill \frac{d^2\widehat{\mathbb{E}}\text{log}{\pi }_j({\tilde{\mathbf{x}}}_j,{\tilde{\rho }}_j\mid {\tilde{\mu }}_j)}{{\mathit{dm}}_{j}d{\tilde{\mathbf{w}}}_j^T}\hfill \\ \hfill \frac{d^2\widehat{\mathbb{E}}\text{log}{\pi }_j({\tilde{\mathbf{x}}}_j,{\tilde{\rho }}_j\mid {\tilde{\mu }}_j)}{d{\tilde{\mathbf{w}}}_j{\mathit{dm}}_j}\hfill & \hfill \frac{d^2\widehat{\mathbb{E}}\text{log}{\pi }_j({\tilde{\mathbf{x}}}_j,{\tilde{\rho }}_j\mid {\tilde{\mu }}_j)}{d{\tilde{\mathbf{w}}}_{j}d{\tilde{\mathbf{w}}}_j^T}\hfill \end{array}\right],$$

$${\mathbf{b}}_j=A_j\left[\begin{array}{c}\hfill m_j\hfill \\ \hfill {\tilde{\mathbf{w}}}_j\hfill \end{array}\right]+\left[\begin{array}{c}\hfill \frac{d\widehat{\mathbb{E}}\text{log}{\pi }_j({\tilde{\mathbf{x}}}_j,{\tilde{\rho }}_j\mid {\tilde{\mu }}_j)}{{\mathit{dm}}_j}\hfill \\ \hfill \frac{d\widehat{\mathbb{E}}\text{log}{\pi }_j({\tilde{\mathbf{x}}}_j,{\tilde{\rho }}_j\mid {\tilde{\mu }}_j)}{d{\tilde{\mathbf{w}}}_j}\hfill \end{array}\right].$$

Note that m_j receives no shrinkage. Again, for a Poisson variable x_j, w̃_j cannot be solved by lasso. Instead, we use the proximal gradient ascent method.

D. Initialization

Let Y be a matrix approximating μ, which is defined as

$$y_{\mathit{ji}}=\{\begin{array}{cc}{x}_{\mathit{ji}},\hfill & \text{if}{x}_j\text{is}\text{Gaussian},\hfill \\ \text{logit}\left(\frac{x_{\mathit{ji}}+1}{n_j+2}\right),\hfill & \text{if}{x}_j\text{is binomial},\hfill \\ \text{logit}\left(\frac{x_{\mathit{ji}}+1}{r_j+x_{\mathit{ji}}+2}\right),\hfill & \text{if}{x}_j\text{is negative binomial},\hfill \\ \text{log}(x_{\mathit{ji}}\vee 1∕2),\hfill & \text{if}{x}_j\text{is Poisson}.\hfill \end{array}\phantom{\}}$$

For the location m_j, one can choose the (trimmed) mean of ỹ _j, the median of ỹ _j, or any fixed vector. One way to initialize W would be the (reduced) singular value decomposition of Y − m1^T = U DV^T and W = U D. We initialize φ_ji = 0 and θ_jl = 0.5. The algorithm is summarized in Algorithm 1.

IV. Simulation Study

We conduct simulation study to evaluate performance of our proposed method. We compare its performance to other methods; the K-means clustering applied to separate and concatenated data, and iCluster+ [4].

A. Simulation Design

We generate 100 Monte Carlo datasets. For each dataset, we generate H = 3 data matrices mimicking multi-omics data, each of which has p₁ = p₂ = p₃ = 300 features of homogeneous data types varying with h. For each h, we have μ^h = m^h1^T + W^hZ where μ^h ∈ ℝ^Ph×n, m^h ∈ ℝ^Ph×1, W^h ∈ ℝ^Ph×L, and Z ∈ ℝ^L×n.

We have L = 3 latent factors. The true loading matrix W^h is generated as follows.

$$\begin{array}{cc}\hfill w_{\mathit{jl}}^1& =\{\begin{array}{cc}\mathcal{U}(1.5,2.5),\hfill & \text{if}\{l=1,j=1,\dots ,20\},\hfill \\ \hfill & \text{or}\{l=2,j=281,\dots ,300\},\hfill \\ 0,\hfill & \text{otherwise},\hfill \end{array}\phantom{\}}\hfill \\ \hfill w_{\mathit{jl}}^2& =\{\begin{array}{cc}\mathcal{U}(1.5,2.5),\hfill & \text{if}\{l=1,j=281,\dots ,300\},\hfill \\ \hfill & \text{or}\{l=3,j=1,\dots ,20\},\hfill \\ 0,\hfill & \text{otherwise},\hfill \end{array}\phantom{\}}\hfill \\ \hfill w_{\mathit{jl}}^3& =\{\begin{array}{cc}\mathcal{U}(1.5,2.5),\hfill & \text{if}\{l=2,j=1,\dots ,20\},\hfill \\ \hfill & \text{or}\{l=3,j=281,\dots ,300\},\hfill \\ 0,\hfill & \text{otherwise},\hfill \end{array}\phantom{\}}\hfill \end{array}$$

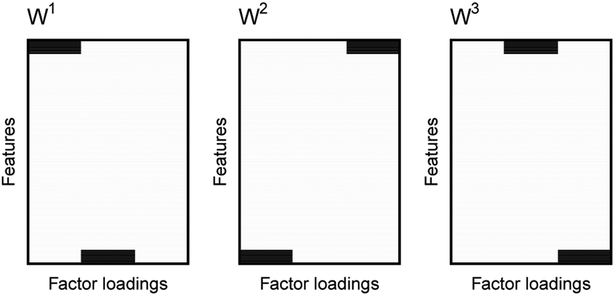
where U stands for the uniform distribution. All nonzero entries of W^h flip their signs with probability 1/2. Figure 1 illustrates the form of W.

Fig. 1.

Regions of nonzero elements in W¹, W², and W³ shown in black.

We consider two cases for the true number of clusters; K = 4 and K = 6. When K = 4, there are n = 160 subjects. When K = 6, there are n = 180 subjects. All subjects are grouped to into K equally sized disjoint clusters. If the i-th subject belongs to k-th cluster, the latent factor for the i-th subject is generated as follows.

$${\mathbf{z}}_i={\nu }_k+{\sigma }_z\times \mathcal{N}(0,\mathbf{I}),$$

where, when K = 4, we use σ_z = 0.3 and

$$\begin{array}{cc}{\nu }_1={(1∕2,1∕\sqrt{2},0)}^T,\hfill & {\nu }_2={(1∕2,-1∕\sqrt{2},0)}^T,\hfill \\ {\nu }_3={(-1∕2,0,1∕\sqrt{2})}^T,\hfill & {\nu }_4={(-1∕2,0,-1∕\sqrt{2})}^T,\hfill \end{array}$$

and when K = 6, we use σ_z = 0.2 and

$$\begin{array}{cc}{\nu }_1={(1∕\sqrt{2},0,0)}^T,\hfill & {\nu }_2={(-1∕\sqrt{2},0,0)}^T,\hfill \\ {\nu }_3={(0,1∕\sqrt{2},0)}^T,\hfill & {\nu }_4={(0,-1∕\sqrt{2},0)}^T,\hfill \\ {\nu }_5={(0,0,1∕\sqrt{2})}^T,\hfill & {\nu }_6={(0,0,-1∕\sqrt{2})}^T.\hfill \end{array}$$

We consider three scenarios, each of which has a different combination of data types as described in Table II. Any Gaussian variable is sampled from $\mathcal{N}({\mu }_{\mathit{ji}}^h,{\sigma }_e^2)$. When K = 4, we use σ_e = 3, and when K = 6, we use σ_e = 2. Any binary variable has the success probability $p_{\mathit{ji}}^h=1∕(1+\text{exp}(-{\mu }_{\mathit{ji}}^h))$. Any Poisson variable has the mean $\text{exp}(-{\mu }_{\mathit{ji}}^h)$ with $m_j^h=2.5$. For any binomial variable, the number of trial parameter n_j is randomly selected between 1 and 15 and the success probability is given by $p_{\mathit{ji}}^h=1∕(1+\text{exp}(-{\mu }_{\mathit{ji}}^h))$. We use $m_j^h=0$ for all data types except for Poisson.

TABLE II.

Combinations of data types explored in each simulation scenario.

Scenario	X1	X2	X3
1	Gaussian	Gaussian	Gaussian
2	Gaussian	Bernoulli	Poisson
3	Gaussian	Binomial	Poisson

In all three scenarios, we assume that every 20 consecutive genes in X¹ and X² form a pathway and we randomly generate 50 edges within each pathway.

B. Tuning Strategy and Performance Measure

To select the GBFA model, we use the Bayesian information criteria (BIC). We select the model that gives the minimum value of the BiC defined as follows.

$$\text{BIC}=-2\sum _h{l}_h(X^h,{\widehat{\mu }}^h)+\text{log}(n)\times \mathit{df},$$

where l_h is the log-likelihood of h-th data and df is the number of nonzero elements in Ŵ.

For a given η, we select the tuning parameter combination (L, λ₀, δ) that gives the minimum BIC value. In all simulations, we use the Ising prior for smoothing, and fix λ₁ = λ₀/5 and m at the trimmed mean of ỹ _j (see Section III-D).

We conduct the K-means clustering on the estimated posterior mean μ_Z of the latent factors. To select the optimal number of clusters, there are several widely used methods such as the elbow method [30], the silhouette method [31], gap statistics [32], and so on. We use the silhouette analysis for our proposed method and the K-means clustering method.

For iCluster+, we use the R package iClusterPlus and perform the most extensive search to choose the best tuning parameters and the best number of clusters K (and of latent factors L = K − 1), as suggested by [4].

In order to measure the similarity between the estimated clustering and the true clustering, we use the Jaccard index [33] and the Rand index [34], both of which have values between 0 and 1. The higher the value is, the more similar the clusterings are.

C. Results

The summary of all simulation results is shown in Table III. In all aspects of performance measures, GBFA_CL outperforms other methods in all scenarios. In particular, the ability to choose the right number of clusters of the proposed method is by far superior to that of other methods.

TABLE III.

Summary of the performance in the simulation study. The competing methods are the K-means clustering applied to the concatenated data and separated data, iCluster+, the integrative clustering proposed by Mo et al. [4]; and GBFA_CL, the proposed method. Rate indicates the rate of choosing the right number of clusters (K). Averages of Jaccard and Rand indexes out of 100 Monte Carlo datasets are reported. The corresponding standard errors are shown in the parentheses.

K = 4
		Scenario 1			Scenario 2			Scenario 3
Method		Rate	Jaccard	Rand	Rate	Jaccard	Rand	Rate	Jaccard	Rand
con K-means		0.52	0.441(.011)	0.763(.010)	0.19	0.322(.007)	0.606(.014)	0.19	0.308(.006)	0.559(.014)
	H = 1	0.04	0.289(.005)	0.622(.007)	0.03	0.288(.004)	0.623(.006)	0.02	0.291(.004)	0.620(.007)
sep K-means	H = 2	0.05	0.287(.004)	0.618(.006)	0.01	0.408(.007)	0.715(.008)	0.00	0.550(.008)	0.811(.007)
	H = 3	0.03	0.283(.003)	0.599(.004)	0.16	0.318(.007)	0.606(.014)	0.21	0.311(.006)	0.583(.015)
iCluster+		0.17	0.321(.007)	0.674(.008)	0.37	0.603(.012)	0.877(.006)		-	-
	η = 0	0.91	0.648(.001)	0.893(.000)	0.76	0.704(.002)	0.880(.001)	0.77	0.792(.001)	0.931(.001)
GBFA_CL	η = 0.5	0.97	0.675(.001)	0.903(.000)	0.77	0.706(.002)	0.879(.001)	0.82	0.807(.001)	0.938(.001)
	η =1	0.98	0.684(.001)	0.906(.000)	0.78	0.709(.002)	0.883(.001)	0.84	0.810(.001)	0.940(.001)
K = 6
		Scenario 1			Scenario 2			Scenario 3
Method		Rate	Jaccard	Rand	Rate	Jaccard	Rand	Rate	Jaccard	Rand
con K-means		0.01	0.261(.003)	0.618(.004)	0.02	0.288(.006)	0.635(.014)	0.02	0.303(.007)	0.663(.014)
	H=1	0.00	0.218(.001)	0.581(.003)	0.00	0.217(.002)	0.579(.003)	0.00	0.215(.001)	0.570(.002)
sep K-means	H=2	0.00	0.212(.002)	0.570(.002)	0.13	0.174(.003)	0.643(.010)	0.00	0.238(.002)	0.592(.002)
	H=3	0.00	0.214(.002)	0.578(.003)	0.00	0.298(.006)	0.659(.014)	0.02	0.306(.007)	0.670(.014)
iCluster+		0.28	0.341(.010)	0.825(.004)	0.25	0.508(.006)	0.825(.001)		-	-
	η = 0	0.85	0.580(.012)	0.907(.004)	0.62	0.647(.020)	0.897(.010)	0.91	0.811(.011)	0.963(.003)
GBFA_CL	η = 0.5	0.89	0.631(.010)	0.922(.003)	0.69	0.687(.017)	0.919(.009)	0.87	0.809(.011)	0.962(.003)
	η =1	0.92	0.650(.011)	0.927(.003)	0.63	0.667(.017)	0.913(.009)	0.85	0.798(.012)	0.960(.003)

GBFA_CL we obtains improved results when η ≠ 0 in general compared to when η = 0, which proves the usefulness of the ability to incorporate the network graph information in the GBFA framework. However, the observed improvement is subtle when the result is already very good without incorporation of the graph information.

Note that the concatenated K-means clustering is not necessarily better than the separate K-means clusterings. In fact, we observe each separate K-means clustering works better in many cases. This is due to the fact that the errors are accumulated in the concatenated data, and suggests that a naïve concatenation of data is not a good practice of the integrative analysis. On the other hand, GBFA_CL and iCluster+ outperform the K-means clustering, which demonstrates the effectiveness of the low-dimensional factor analysis when the model assumptions are applicable.

It is surprising that GBFA_CL substantially outperforms iCluster+ even when the graph information is not incorporated. Our understanding is that it is largely owing to our variational EM algorithm being accurate and efficient. Of note, iCluster+ uses Monte Carlo Newton-Raphson type of algorithm due to intractability of the relevant expectations in the EM approach. Finally, we note that iCluster+ is not feasible in scenario 3 because it does not support binomial variables, while GBFA_CL works seamlessly.

V. Real Data Analysis

A. NCI60 Cell Line Data

The NCI60 is a panel of 60 diverse human cancer cell lines used by the Developmental Therapeutics Program (DTP) of the U.S. National Cancer Institute (NCI) to screen over 100,000 chemical compounds and natural products. It consists of 9 kinds of cancerous cell lines; leukemia, melanomas, ovarian, renal, breast, prostate, colon, lung, and CNs origin. There are various -omics datasets available for those cell lines including gene expression data from various platforms, protein abundance data, and methylation data. We download three datasets from CellMiner [35], two of which are gene expression data and the other one is protein abundance data.

The first data is a transcript profile data based on Affymetrix HG-U133 chips [36]. The second data is a mRNA expression data based on Agilent Whole Human Genome Oligo Microarray technology [37]. The last one is a proteomics profiling data using high-density reverse-phase lysate microarrays [38]. We use 59 cell line data consisting of 9 subgroups which are common to all three datasets. As a preprocessing [39], we select the top 5% of genes with high variance, which results in 491 genes in the affymetrix data, 488 genes in the agilent data, and 94 proteins in proteomics data.

We incorporate the pathway graph information from the Kyoto Encyclopedia of Genes and Genomes (KEGG) pathway database [40] in GBFA_CL. For the pathway enrichment data analysis, we use ToppGene Suite [41], a portal for the enrichment analysis.

B. Results

We apply GBFA_CL and iCluster+ to NCI60 data. Various combinations of tuning parameters are explored for both methods and the optimal model is selected in the same manner as in section IV.

We compare the estimated clusterings with the true cell line clustering. The results are shown in Table V. iCluster+ chooses L = 8 (and K = 9) and GBFA_CL chooses similarly between L = 8, 9 and K = 8, 9, 10. In terms of the similarity of the clustering, all versions of GBFA_CL show better results except for the case with η = 0.5, in which case the result is comparable to that of iCluster+. Overall, the incorporation of the pathway graph knowledge improves the similarity of the estimated clustering to the truth.

TABLE V.

NCI60 data analysis results from iCluster+ and 4 different versions of GBFA_CL (η = 0, 0.5, 1, 1.5). For each method, the chosen number of latent factors and the chosen number of clusters are listed. Two similarity measures are also listed.

Method	η	L	K	Jaccard	Rand
iCluster+	-	8	9	0.348	0.896
GBFA_CL	0	9	10	0.496	0.930
	0.5	8	8	0.367	0.886
	1	9	9	0.521	0.933
	1.5	9	10	0.527	0.933

We also conduct the pathway enrichment analysis to identify the pathways significantly enriched among the genes selected by GBFA factor loadings. We compare the genes selected from GBFA_CL with η = 0 and η = 1.5, and the pathways that are related with cancers are listed in in Table IV. “Pathways in cancer” is enriched in most of the factors (factor loadings). Other cancer related pathways such as breast cancer, melanoma, lung cancer, and prostate cancer are also enriched in several factors. “Hemostatis” and “Melanogenesisis” are also related to leukemia [42] and melanoma [43, 44] cancers, respectively. These facts indicate that GBFA successfully captures the underlying biological variations.

TABLE IV.

Pathway enrichment analysis result for NCI60 data analysis results of the GBFA. Source means the database that has information about corresponding pathway, and q-value is the Bonferroni adjusted p-value. L is the index of the factor loading that includes the genes of the enriched pathway. REACTOME is another biological pathway database like KEGG pathway database.

Name	Source	η = 0		η = 1.5
		L	q-value	L	q-value
Pathways in cancer	REACTOME	2	8.11e–10	2	1.27e–09
Non-small cell lung cancer	KEGG	4	1.09e–05	4	1.16e–05
Bladder cancer	KEGG	4	8.46e–05	4	8.88e–05
Melanogenesis	KEGG	4	1.77e–04	2	4.15e–04
Breast cancer	KEGG	2	1.13e–03	2	1.36e–03
Chronic myeloid leukemia	KEGG	4	8.37e–03	4	8.78e–03
Prostate cancer	KEGG	6	1.42e–02	6	1.62e–02
Hemostasis	REACTOME	1	3.71e–02	1	2.57e–02
Neurotrophin signaling pathway	KEGG	-	-	6	2.77e–02
Chemokine signaling pathway	KEGG	-	-	6	3.23e–02

We observe that there are two pathways enriched only in GBFA_CL with graph information incorporated; the neurotrophin signaling pathway and the chemokine signaling pathway. It is known that the neurotrophins regulate the cancer stem cells [45] and the chemokine signaling pathway governs cancer progression [46]. Figure 2 shows the edges between the genes in our data which belong to the neurotrophin signaling pathway. Incorporating this graph information has lead to the conclusion that can potentially be biologically meaningful.

Fig. 2.

Network of Neurotrophin signaling pathway. Each node are genes selected by GBFA incorporating the network information.

VI. Conclusion and Discussion

We have proposed the generalized Bayesian factor analysis framework, which is a generalization of the sparse factor analysis framework in two ways; the incorporation of the network graph information and the accommodation of multiple data types. We have also proposed the very efficient variational EM algorithm for the MAP estimator. Then, GBFA has been applied to the integrative clustering analysis. The newly proposed integrative clustering method has been proven to be flexible, accurate, and efficient throughout the simulation studies and the application to the NCI60 datasets. Moreover, we have shown that the use of the proposed method on the analysis of multi-omics data with incorporation of the pathway graph information can deliver more biologically meaningful outcomes.

Note that the applications of our GBFA framework is not limited to the integrative clustering only. We believe that GBFA can extend many other existing statistical methods and can potentially address plenty of problems where the structural graph information exists.

Another future work will include the extension of the proposed framework for more complicated forms of data. Due to the advances of the mobile businesses and technologies, various biomedical data such as the electronic health record (EHR) are available in great abundance. Such data often involve not only graphical structure but also hierarchical structure, multi class categorical variables, missing values, and distributed repositories.