Combining Old and New for Better Understanding and Predicting Dyslexia

Abstract

Despite decades of research, it has been difficult to achieve consensus on a definition of common learning disabilities such as dyslexia. This lack of consensus represents a fundamental problem for the field. Our approach to addressing this issue is to use model-based meta-analyses and Bayesian models with informative priors to combine the results of a large number of studies for the purpose of yielding a more stable and well-supported conceptualization of reading disability. A prerequisite to implementing these models is establishing informative priors for dyslexia. We illustrate a new approach for doing so based on the known distribution of the difference between correlated variables, and use this distribution to determine the proportion of poor readers whose poor reading is unexpected (i.e., likely to be due to dyslexia) as opposed to expected.

Learning disabilities including dyslexia are difficult to diagnose reliably (Waesche et al., 2011; Wagner et al., 2011). A large part of the difficulty results from measurement error, which becomes increasingly problematic when (a) the category of having the condition relies on which side an individual falls on a cut-point put arbitrarily on a continuous distribution (Francis et al., 2005), (b) the condition has a relatively low base-rate (e.g., under 10 percent), and (c) the diagnosis relies primarily on a single criterion as opposed to multiple criteria.

Waesche, Schatschneider, Mane, Ahmed, and Wagner (2011) documented the poor agreement when alternative operational definitions of dyslexia are applied to the same sample. The agreement between an aptitude-achievement discrepancy definition and response to instruction or intervention (RTI) definition was only 31 percent. The agreement between an aptitude-achievement discrepancy definition and a low-achievement based definition was only 32 percent. In addition to poor agreement among alternative operational definitions, the longitudinal stability of all the definitions was poor: One-year stabilities for diagnosis based on the alternative operational definitions of dyslexia were 24, 34, and 41 percent for the discrepancy, RTI, and low achievement operational definitions respectively. Others have reported similarly poor levels of agreement and longitudinal stability (Barth et al., 2008; Fuchs, Fuchs & Compton, 2004; Wagner et al., 2011). All of these operational definitions primarily relied on a single criterion (e.g., poor decoding or inadequate response to intervention). Understanding the reason for unreliable diagnosis helps point the way to improved models that combine multiple sources of information (Wagner, 2018).

Improving Diagnosis by Incorporating More Sources of Information

Hybrid models use multiple indicators or criteria, which can reduce the effects of measurement error (Wagner et al., 2011). We refer to the hybrid model we have been investigating as a constellation model because it incorporates a constellation of symptoms and indicators (Wagner, Spencer, Quinn, & Tighe, 2013). The constellation model differentiates causes, consequences, and correlates of dyslexia. The model includes three causes: Impaired phonological processing, genetic risk, and environmental influences. Impaired phonological processing has been found to be related to the development of dyslexia regardless of the written script to be learned (Branum-Martin et al., 2012; Song et al., 2016; Swanson et al., 2003). Genetic risk for dyslexia has been shown by behavioral genetic studies. It also is the case that a family history of reading problems, which can include both genetic and environmental components, increases the probability of having dyslexia by a factor of four (Snowling & Melby-Lervag, 2016). For an example of environmental influences, good reading instruction coupled with effective intervention when required reduces the incidence and severity of cases of dyslexia (VanDerHeydan, Witt, & Gilbertson, 2007).

Turning to potential correlates, ADHD co-occurs with reading disability from 30 to 50 percent of the time (Willcutt et al., 2003). Having math disability more than doubles the chances of having co-occurring dyslexia (Joyner & Wagner, in press). The incidence of severe reading disability also is greater for males than females, with the ratio of males to females increasing with the severity of the reading problem. Quinn and Wagner (2015) reported the results of a large-scale study of reading impairment among 491,103 beginning second graders. Because they had data on all participants, no referral or ascertainment bias was possible. Sex differences increased with greater severity of the reading impairment, peaking at a ratio of 2:4 to 1 for a broader measure of fluency and at a ratio of 1:6 to 1 for a narrower measure of decoding, with an average ratio of 2 to 1. The correspondence between identification as having a reading impairment by our study criteria and school identification as learning disabled was poor overall and worse for girls than for boys. Only 1 out of 4 boys and 1 out of 7 girls identified as reading impaired in our study was school identified as learning disabled, even after we matched the percentage of students identified by both methods so that the poor correspondence was not a result of differences in numbers of students identified.

Turning to consequences, which also serve as indicators of the latent construct of reading disability in our model, four proximal consequences are included: Poor decoding (e.g., nonword decoding accuracy and fluency) (Hermann, Matyas, & Pratt, 2006; Lyon, Shaywitz, & Shaywitz, 2003; Stanovich, 1988); impoverished sight-word vocabulary (e.g., real words that are decoded automatically) (Ehri, 1988); poor response to instruction and intervention (Fletcher & Vaughn, 2009); and listening comprehension better than reading comprehension (Badian, 1999; Stanovich, 1991; Spencer et al., 2014).

In a large-scale study (N = 31,339) of students who were followed longitudinally from first to second grade, Spencer et al. (2014) implemented two versions of a model of reading disability based on the four consequences just mentioned. The first dimensional version of the model included reading disability as a latent variable with the four consequences as observed indicators. Confirmatory factor analysis yielded an excellent model fit (χ²(2) = 263.4; Comparative Fit Index = .99; Tucker Lewis Index = .97; Root Mean Square Error of Approximation = .065 with a 95% confidence interval between .058 and .071). The one-year stability of this dimensional version of the model was substantial with a standardized structure coefficient of 0.88. This means that over three-fourths of the variance in the latent variable representation of reading disability in second grade was accounted for by first grade performance. The second model was categorical rather than dimensional to be more comparable to existing alternative categorical models. The implementation was based on the number of indicators that were present instead of their continuous levels as in the first version of the model. The one-year stability of various versions of this model exceeded that of traditional, single-indicator models, with the best performing versions of the model approaching twice the stability of single-indicator traditional models.

One issue that arises for models that rely on multiple sources of information is how to combine them. One approach that can be used is a Bayesian model. Bayesian models are commonly used in medical diagnosis and policy (Spiegelhalter, Abrams, & Myles, 2004). Bayesian models are flexible models that can incorporate multiple kinds of information. They are particularly useful when informative priors are available. In the present context, informative priors are baseline probabilities that represent the prevalence of something in the population in general. This population prevalence or prior probability is then updated based on information for particular individuals.

For an example of using a Bayesian model to estimate the probability of the presence of dyslexia, we operationally defined dyslexia as scoring at or below the 5^th percentile on a factor score representing the constellation model described previously. The four indicators of the factor were poor decoding, impoverished sight word vocabulary, poor response to instruction, and listening comprehension better than reading comprehension. Because we chose the 5^th percentile, the prior probability or chance of having dyslexia is 5 percent. We can then update this probability on the basis of whether an individual is male or female, because boys are about 2 times more likely to have severe cases of dyslexia than girls are. If the individual is female, the chance of having dyslexia goes down, from 5 to 3 percent; if male, the chance goes up, from 5 to 7 percent. Scoring at or below the 20^th percentile on a battery of first-grade predictors triples the chances of having dyslexia, from 5 to 15 percent. Co-occurring ADHD increases the chances of having dyslexia fourfold, from 5 to 19 percent. Having an affected parent or sibling increases the chances fivefold, from 5 to 26 percent. Combinations of risk factors have an even larger effect on risk. For example, being male with ADHD increases the chances from 5 to 24 percent. Add in an affected parent or sibling and the chances increase to 76 percent. Finally, add in scoring low on the predictor battery and chances increase to 92 percent!

These probabilities were generated by applying Bayes theorem sequentially to data from the large-scale database used by Spencer et al. (2014). Doing so required making two simplifying assumptions. The first simplifying assumption, which only affects the probabilities from combinations of risk factors, was that the predictors are independent. This assumption is necessitated because Bayes theorem was applied sequentially without regard to possible correlations among the predictors. For example, the combined risk of dyslexia for males with ADHD of 24 percent came from first applying Bayes theorem to the base rate of 5 percent to account for the risk factor of being male, which resulted in a probability of 7 percent. This then was updated using Bayes theorem to account for the risk factor of having ADHD, resulting in a probability of 24 percent. The simplifying assumption of independent predictors is not tenable in this case given the known greater incidence of ADHD for males. Fortunately, the assumption of independent predictors can be relaxed by using either Bayesian multiple regression for dyslexia as a continuous outcome or Bayesian logistic regression for dyslexia as a categorical outcome. For these models, Markov Chain Monte Carlo (MCMC) is used to generate parameter estimates and probabilities.

The second simplifying assumption is that the incidence rate of dyslexia is known, and that it is a discrete number. Quite a few prevalence rates have been proposed for dyslexia, ranging from a low of 2 percent to a high of 10 percent (Hoeft, McCardle, & Pugh, 2015; Moll, Kunze, Neuhoff, Bruder, & Schulte-Korne, 2014). Differences in proposed prevalence rates reflects differences across studies in (a) the severity of the reading problem required to be called dyslexia or reading disability, (b) the definition used for dyslexia or reading disability, and (c) characteristics of the orthography, such as whether it is deep or shallow.

The goal of the present study is to present a new approach for determining the incidence rate of dyslexia. How common dyslexia is has implications for policy and funding decisions. It also is prerequisite to using a Bayesian approach to diagnose dyslexia. Although there is a consensus that prevalence depends upon severity of the reading problem—with lower rates for more severe problems—this consensus has not been incorporated in prevalence estimates; rather, it has been used to justify differences in proposed estimates. A more direct way to incorporate the fact that prevalence varies as a function of severity is to reject the idea of a single prevalence estimate and replace it with a distribution of prevalence as a function of severity. The task then becomes one of estimating a distribution rather than a single number. To illustrate our approach for doing this, we first have to describe our operational definition of dyslexia for present purposes.

A common feature of nearly all conceptualizations of dyslexia is the concept of unexpectedness. The idea is that performance in reading is unexpectedly poor relative to expectations. This distinguishes dyslexia from poor reading, which may be expected if the performance on reading is consistent with performance in other domains such as language or achievement in other academic subjects. At some level, the concept of unexpectedness implies some kind of a discrepancy-based definition. Because of problems associated with an IQ-achievement discrepancy definition, a number of researchers have proposed replacing IQ-achievement discrepancy with a difference between listening and reading comprehension (Aaron, 1991; Badian, 1999; Beford-Fuell, Geiger, Moyse, & Turner, 1995; Erbelli, Hart, Wagner, & Taylor, 2018; Spring & French, 1990; Stanovich, 1991). Poor reading comprehension relative to listening comprehension would seem to have a functional use in the context of assistive technology. Assistive technology in the form of text to speech improves reading comprehension for individuals with reading disability or dyslexia (Wood, Moxley, Tighe, & Wagner, 2018). However, because text-to-speech essentially turns a reading comprehension task into a listening comprehension task, there is no reason to expect improvement for an individual whose listening comprehension is no better than reading comprehension.

To estimate the distribution of the prevalence of dyslexia, we take advantage of the fact that if the correlation between two variables is known, then the standard deviation of the difference between the two variables also is known. When converted to standard scores, the standard deviation of the difference between two variables equals two minus two times the correlation between the variables.

To get the best estimate of the correlation between listening comprehension and reading comprehension, we carried out a model-based meta-analysis (Quinn & Wagner, 2018). The meta-analysis included 155 studies and over one million students. The average weighted correlation between listening and reading comprehension was .495. Plugging this correlation into the equation gives a standard deviation for the difference between listening and reading comprehension of 1.01. To verify that the formula works, we used the correlation of .495 as a population estimate and created a simulated dataset of 1,000 individuals. The distribution of listening comprehension minus reading comprehension is presented in Figure 1. The observed standard deviation of 1.005 when rounded to two decimal places is equal to the predicted standard deviation of 1.01.

Figure 1.

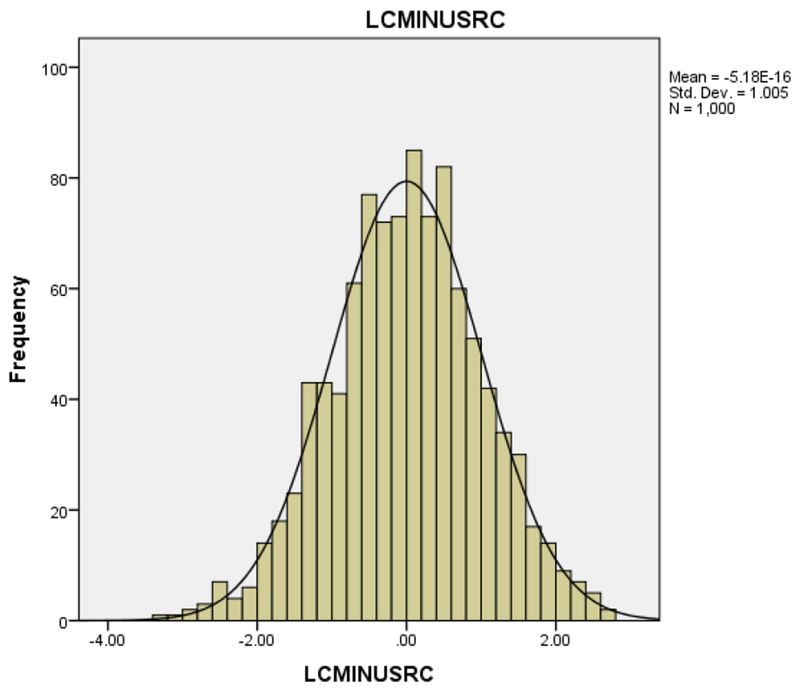
The distribution of the difference between listening comprehension and reading comprehension.

Having verified the distribution, it can be used in several ways. The first is to calculate how the prevalence of various degrees of discrepancy between listening and reading comprehension. For example, a difference between listening and reading comprehension of 1 standard deviation or larger occurs 16 percent of the time. A difference of 1 and ½ standard deviations or larger occurs 7 percent of the time. Finally, a difference of 2 standard deviations or larger occurs only 2 percent of the time.

By including decoding in the dataset, we can ask what percentage of poor decoders has a discrepancy between listening and reading comprehension of a given size. For example, if poor decoding is operationally defined as the bottom 20th percent of all decoders, what proportion of the poor decoders are unexpected? If we define unexpected as belonging to the 20th percent of individuals with the largest discrepancy between listening and reading comprehension, only 28 percent of the poor decoders are unexpected as opposed to expected. If we focus on more severe decoding problems by operationally defining poor decoders as the bottom 5^th percent of all decoders, what proportion of these poor decoders are unexpected? Keeping the definition of unexpected as the same criterion of the 20^th percent with the largest discrepancy, only 7 percent of the poor decoders are unexpected.

A scatterplot of listening and reading comprehension is presented in Figure 2. If we take, for example, reading comprehension (RC) at a standard score of .00 or average, the distribution of listening comprehension minus reading comprehension is represented by the points on an imaginary vertical line drawn at the point representing a score of .00 for reading comprehension. The normal distribution of listening comprehension minus reading comprehension can be seen by the concentration of points in the center of the distribution of the points on the imaginary line relative to the lower and upper tails. Notice the vertical and angled line drawn on the scatterplot. Beginning with the vertical line, points to the left represent poor reading as defined by scoring at or below the 20^th percentile in reading comprehension. Turning to the angled line, points above this line represent unexpected poor reading as defined by a difference between listening and reading comprehension falling at or above the 80^th percentile. The scatterplot provides a visual representation of two important points. First, looking only at poor readers, or individuals represented by points to the left of the vertical line, more of them are expected than unexpected (i.e., below rather than above the angled line). Second, looking only at unexpected poor reading, or individuals represented by points above the angled line, it occurs at all levels of reading and more fall above the poor reading cutoff than below it (i.e., to the right rather than to the left of the vertical line).

Figure 2.

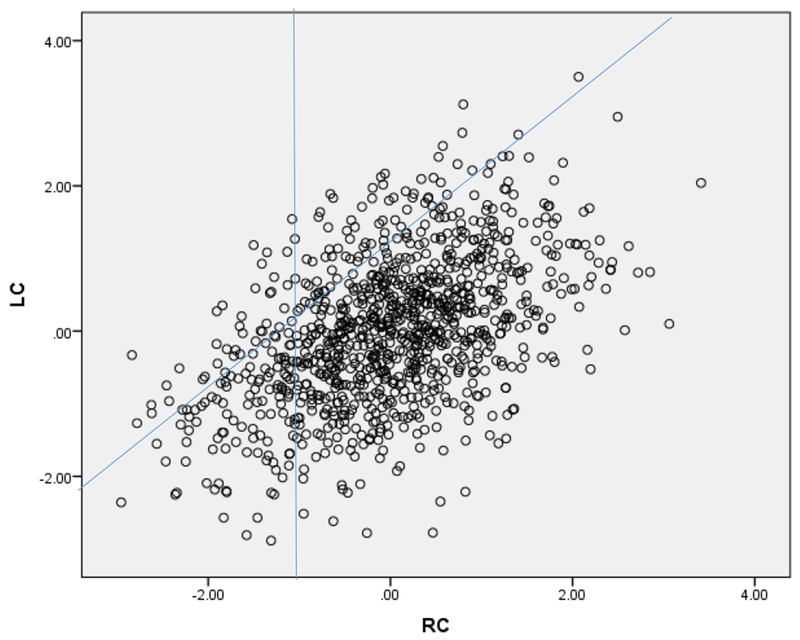
Scatterplot of listening comprehension and reading comprehension. Points to the left of the vertical line represent poor reading (i.e., at or below the 20^th %-ile). Points above the slanted line represent listening comprehension better than reading comprehension (i.e., at or above the 80^th %-ile).

Turning to some implications of this study, the results call into question efforts to screen for individuals with dyslexia that focus only on poor reading. Although such an approach can make sense as a screen for poor readers, most individuals identified will be expected poor readers and a majority of unexpected poor readers will be missed by the screen. Turning to identification approaches based on poor response to instruction or intervention, the same situation is likely to be present. Poor responders to instruction and intervention will represent a mixture of expected and unexpected poor responders, with expected poor responders likely to be in the majority.

A second important implication of a known distribution for dyslexia is that it can be used as an informative prior distribution for a Bayesian predictive model. Recall that expanding operational definitions of dyslexia to include multiple indicators should improve the reliability of diagnosis. Moving to Bayesian models with informative priors should result in additional improvement in diagnosis.

There are important limitations to acknowledge. The first is that predictions from the model need to be verified by studies using empirical rather than simulated datasets. A second limitation is that assumptions that were made need to be verified. For example, we assumed that both listening comprehension and reading comprehension are multivariate normally distributed variables. A consequence of this assumption is that the distribution of the difference between listening and reading comprehension is normally distributed and therefore symmetrical. This means there should be as many individuals whose reading comprehension exceeds their listening comprehension as there are whose listening comprehension exceeds their reading comprehension. The rationale for individuals whose listening comprehension exceeds their reading comprehension is that dyslexia prevents them from reading the words on the page fluently. The rationale for individuals whose reading comprehension exceeds their listening comprehension is less obvious. Limitations in attention might explain reading comprehension better than listening comprehension if listening comprehension places more demands on attention than does reading comprehension, perhaps because you can refer back to text when reading. Or it may be that the distribution in not normal and symmetric and that the model needs to be adjusted for this fact. Finally, implementation of the present approach would likely identify a different subset of readers as having dyslexia relative to use of a DSM-5 or RTI-based definitions which rely on poor absolute performance in decoding or in response to instruction and intervention, respectively.

In summary, we have used model-based meta-analysis and mathematical properties of the distributions of differences between correlated variables to identify a distribution of dyslexia as a function of severity as opposed to a single prevalence estimate. By using reading comprehension poorer than listening comprehension as our operational definition of dyslexia, examining the distribution reveals two important points: Samples of poor readers will contain more expected poor readers than unexpected or dyslexic readers; and dyslexic readers can be found across the reading spectrum. These points have implications for screening and diagnosis, calling into question approaches that rely on absolute as opposed to relative poor reading.