Maternal and fetal genetic effects on birth weight and their relevance to cardio-metabolic risk factors

Abstract

Birth weight variation is influenced by fetal and maternal genetic and non-genetic factors, and has been reproducibly associated with future cardio-metabolic health outcomes. In expanded genome-wide association analyses of own birth weight (n=321,223) and offspring birth weight (n=230,069 mothers), we identified 190 independent association signals (129 novel). We used structural equation modelling to decompose the contributions of direct fetal and indirect maternal genetic effects, and then applied Mendelian randomization to illuminate causal pathways. For example, both indirect maternal and direct fetal genetic effects drive the observational relationship between lower birth weight and higher later blood pressure: maternal blood pressure-raising alleles reduce offspring birth weight, but only direct fetal effects of those alleles, once inherited, increase later offspring blood pressure. Using maternal birth weight-lowering genotypes to proxy for an adverse intrauterine environment provided no evidence that it causally raises offspring blood pressure, indicating that the inverse birth weight-blood pressure association is attributable to genetic effects, and not to intrauterine programming.

Birth weight is an important predictor of newborn and infant survival, a key indicator of pregnancy outcomes, and is observationally associated with future risk of adult cardio-metabolic diseases in the offspring. These observational associations are often assumed to reflect adaptations made by a developing fetus in response to an adverse intrauterine environment, a concept termed the Developmental Origins of Health and Disease (DOHaD)¹. Support for DOHaD is primarily from animal models (reviewed in ²). Observational studies of famine-exposed populations support prenatal programming in relation to type 2 diabetes (T2D), but not other cardio-metabolic health measures (reviewed in ³). However, DOHaD cannot provide a complete explanation for the relationship between lower birth weight and increased risk of cardio-metabolic disease. Other likely contributing factors are (i) environmental confounding, leading to phenotypic associations across the life-course⁴, and (ii) shared genetic effects operating at the population level⁵. Genetic associations between birth weight and later cardio-metabolic diseases may arise from the direct effects of the same inherited genetic variants at different stages of the life-course⁶. However, consideration of an individual’s own genotype in isolation cannot exclude potential confounding by any indirect effects of the correlated maternal genotype (r≈0.5) on the intrauterine, and possibly postnatal, environment. Evidence for maternal indirect effects on birth weight and later offspring disease risk could implicate the intrauterine environment in later-life disease etiology.

To date, 65 genetic loci have been associated with birth weight in genome-wide association studies (GWAS), implicating biological pathways that may underlie observational associations with adult disease^5,7–9. However, most of those studies did not distinguish between maternal and fetal genetic influences. Evidence from monogenic human models¹⁰ and variance components analyses¹¹ demonstrate that birth weight is influenced both by genotypes inherited by the fetus and by maternal genotypes that influence the intrauterine environment. To date, GWAS of own birth weight⁵, and maternal GWAS of offspring birth weight⁷, have produced overlapping signals due to the correlation between maternal and fetal genotypes. Identified birth weight variants might have (i) a direct fetal effect only, (ii) an indirect maternal effect only, or (iii) some combination of the two. Performing separate GWAS analyses of own or offspring birth weight precludes full resolution of the origin of the identified genetic effects.

To address these issues, we performed greatly-expanded GWAS of own (n=321,223) and offspring birth weight (n=230,069 mothers) using data from the EGG Consortium and the UK Biobank (2017 release). We applied a structural equation model that we recently developed to partition genetic effects on birth weight into maternal and fetal components at genome-wide significant loci^7,12. We then extended the method to estimate maternal- and fetal-specific genetic effects across the genome in a computationally efficient manner, and used the results for downstream analyses. Our ability to resolve maternal and fetal genetic contributions provides substantial insights into the underlying biological regulation of birth weight and into the origins of observational relationships with T2D and blood pressure.

Results

Meta-analyses of fetal and maternal GWAS

We conducted GWAS meta-analyses of own (fetal) genetic variants on own birth weight (Supplementary Figure 1, Supplementary Tables 1, 2) and maternal genetic variants on offspring birth weight (Supplementary Figure 2, Supplementary Tables 3, 4) in individuals of European ancestry. We then performed approximate conditional and joint multiple-SNP analysis (COJO¹³) and a trans-ethnic meta-analysis to identify further independent SNPs (Methods). The GWAS meta-analysis of own birth weight (N=321,223) identified 146 independent single nucleotide polymorphisms (SNPs) at genome-wide significance (P<6.6x10^-9; Supplementary Figures 3, 4, 5a, Supplementary Table 5a, Methods). The GWAS meta-analysis of offspring birth weight (N=230,069 mothers) identified 72 independent SNPs (P<6.6x10^-9; Supplementary Figures 3, 4, 5b, Supplementary Table 5a, Methods). Applying the more lenient significance threshold used previously (P<5x10^-8)^5,7, 211 SNPs and 105 SNPs reached significance for own and offspring birth weight, respectively (Supplementary Table 5b).

SNPs at 30 genome-wide significant loci (within 500Kb and r² ≥ 0.1) were identified in the GWAS of both own and offspring birth weight. Of these, 9 loci had the same lead SNP and 21 loci had fetal and maternal lead SNPs correlated with r² ≥ 0.1. Colocalization analysis indicated 19/21 of these correlated lead SNP pairs were likely tagging the same birth weight signal (posterior probability > 0.5). Therefore, we identified a total of 190 independent association signals, represented by 209 lead SNPs (Supplementary Figure 4, Supplementary Table 5a). Of the 209 lead SNPs, 146 were novel representing 129 independent association signals, three are rare (minor allele frequency (MAF)<1%) and 13 are low-frequency (1%≤MAF<5%). The three rare variants (at the YKT6/GCK, ACVR1C and MIR146B loci) alter birth weight by more than double the effect (>100g per allele) of the first common variants identified⁹. In the independent Norwegian MoBa-HARVEST study (N=13,934 mother-offspring duos), the lead SNPs explained 7% of the variance in birth weight, calculated as the sum of variances explained by the fetal genotype (6%), maternal genotype (2%), plus twice the covariance (-0.5%). Maternal genome-wide complex trait analysis (M-GCTA¹¹), which estimates SNP-heritability and partitions this quantity into maternal and fetal components, estimated that 39.8% of the variance in birth weight could be explained by tagged fetal genetic variation (28.5%), tagged maternal genetic variation (7.6%) and twice the covariance (3.7%).

We integrated data from several sources to highlight possible causal genes underlying the identified associations, including gene-level expression data across 43 tissues (from GTEx v6p¹⁴), placental expression quantitative trait loci (eQTL)¹⁵, topologically associating domains (TADs) identified in human embryonic stem cells^16,17 and non-synonymous SNPs (see Supplementary Tables 5a, 5b; Methods). Several genes were highlighted by multiple approaches; however, further functional studies are required to confirm causality.

Structural equation model to estimate maternal and fetal effects

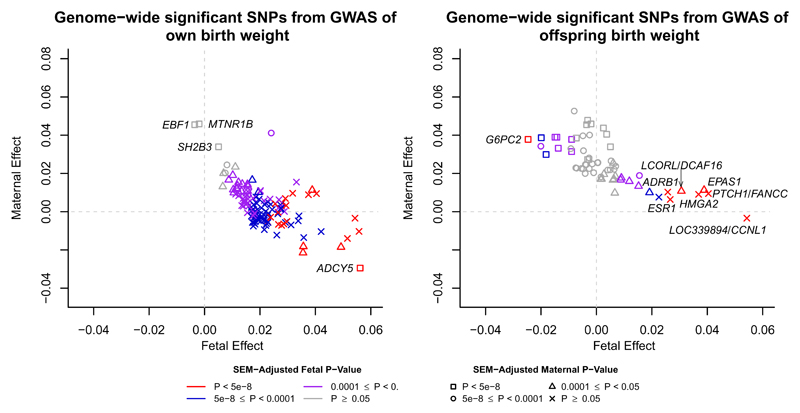
We next partitioned the 209 lead SNPs into five categories based on their maternal and/or fetal genetic contributions to birth weight. To achieve this, we used structural equation modelling (SEM) that accounts for the correlation between fetal and maternal genotypes and thereby provides unbiased estimates of the maternal and fetal genetic effects on birth weight¹² (see Methods and Supplementary Figure 6a for details). The results are presented in Figure 1, Supplementary Figures 4, 7 and Supplementary Table 5. Using the confidence intervals around the SEM-adjusted maternal and fetal effect estimates, we identified 64 SNPs with fetal-only effects, 32 SNPs with maternal-only effects, 27 SNPs with directionally-concordant fetal and maternal effects, and 15 SNPs with directionally-opposing fetal and maternal effects (Supplementary Figure 8). For example, rs10830963 at MTNR1B was identified in both the own birth weight (P=2.8x10^-11) and offspring birth weight (P=9.1x10^-39) GWAS, but the SEM analysis revealed that its effect was exclusively maternal (P_SEMfetal=0.7, P_SEMmaternal=4.6x10^-19). In contrast, rs560887 at G6PC2 was identified only in the GWAS of offspring birth weight (P=1.2x10^-14), but was found to have directionally-opposing maternal and fetal effects (β_SEMfetal=-0.03, P_SEMfetal=2.8x10^-8; β_SEMfetal=0.04, P_SEMmaternal=5.4x10^-14). At present, these categories are suggestive as the current sample size has insufficient statistical power to detect small genetic effects, particularly maternal effects. There were 71 unclassified SNPs, and some that were classified as fetal only, for example, may have had a small, undetected maternal effect. Asymptotic power calculations showed we had 80% power to detect fetal (maternal) effects that explained 0.006% (0.008%) of the variance in birth weight (α=0.05). However, there was strong consistency with traditional conditional linear regression modelling in N=18,873 mother-offspring pairs (Supplementary Table 6, Methods), and overall, the method gave a clear indication as to which genetic associations are driven by the maternal or fetal genomes.

Figure 1. Structural equation modelling (SEM)-adjusted fetal and maternal effects for the 193 lead SNPs that were identified in the GWAS of either own birth weight (left panel) or offspring birth weight (right panel) with minor allele frequency greater than 5%.

The SEM included 85,518 individuals from the UK Biobank with both their own and offspring’s birth weight, 178,980 and 93,842 individuals from the UK Biobank and the EGG consortium with only their own birth weight or offspring’s birth weight respectively. The colour of each point indicates the SEM-adjusted fetal effect on own birth weight association P-value and the shape of each point indicates the SEM-adjusted maternal effect on offspring birth weight association P-value. P-values for the fetal and maternal effect were calculated using a two-sided Wald test. SNPs which are labelled with the name of the closest gene are those which were identified in the GWAS of own birth weight but whose effects are mediated through the maternal genome (left panel) and SNPs that were identified in the GWAS of offspring birth weight but whose effects are mediated through the fetal genome (right panel). SNPs are aligned to the birth weight increasing allele from the GWAS.

To extend the estimates of adjusted maternal and fetal effects genome-wide, we developed a weighted linear model (WLM) (see Methods), which yields a good approximation to the SEM with equivalent estimates for the 209 lead SNPs (Supplementary Figure 9). This was necessary because the SEM is too computationally intensive to fit across the genome. The adjusted fetal and maternal genotype effect estimates on birth weight from the WLM are hereafter referred to as WLM-adjusted estimates. Using linkage disequilibrium (LD) score regression¹⁸, we observed that the genetic correlation between the WLM-adjusted maternal and fetal effects (r_g=0.10, P=0.12) was substantially lower than that between the unadjusted effects from the original GWAS (r_g=0.82, P<0.01), indicating that the WLM largely accounts for the underlying correlation between fetal and maternal genotypes. No additional novel loci were identified, but we used the WLM-adjusted estimates in downstream analyses to identify fetal- and maternal-specific mechanisms that regulate birth weight and to investigate the genetic links between birth weight and adult traits.

Maternal- and fetal-specific tissues and mechanisms underlying birth weight regulation

Tests of global enrichment of birth weight SNP associations across tissues sampled from the GTEx project¹⁴ using LD-SEG¹⁹ are presented in Supplementary Figure 10. Only enrichment for maternal-specific SNP associations for genes expressed in connective/bone tissues was detected after Bonferroni correction. Integration of epigenetic signatures defined by the Roadmap Epigenomics project highlighted a significant enrichment of maternal-specific effects in the ovary for histone modification marks (H3K4me1) and regions of open chromatin (Supplementary Table 7); no significant enrichment was detected for other signatures. Gene-set enrichment analysis implicated different fetal-specific (Supplementary Table 8) and maternal-specific (Supplementary Table 9) gene sets.

A major determinant of birth weight is the duration of gestation. Using LD score regression¹⁸, we found a substantial genetic correlation between published maternal genetic effects on gestational duration²⁰ and the WLM-adjusted maternal effects on offspring birth weight (r_g=0.63; P=2.1x10^-5; Supplementary Table 10; Methods), but not with the WLM-adjusted fetal effects on own birth weight (r_g=-0.10, P=0.34). Gestational duration was unavailable for >85% of individuals in the birth weight GWAS analyses, so it is possible that some identified association signals influence birth weight primarily by altering gestational duration. We looked up the 209 lead birth weight-associated SNPs in the published maternal GWAS of gestational duration²⁰ (Supplementary Table 11) and followed up 7 associated SNPs (P<2.4x10^-4, corrected for 209 tests, Methods) in 13,206 mother-child pairs. Meta-analysis with summary data from 23andMe²⁰ strengthened associations with gestational duration at 5/7 loci (EBF1, AGTR2, ZBTB38, KCNAB1 and KLHL25/AKAP13; Supplementary Table 12). The precise causal relationship between fetal growth and gestational duration at these loci requires further investigation, however, the majority of associations with birth weight do not appear to be driven by associations with gestational duration.

Maternal- and fetal-specific genetic correlations between birth weight and adult traits

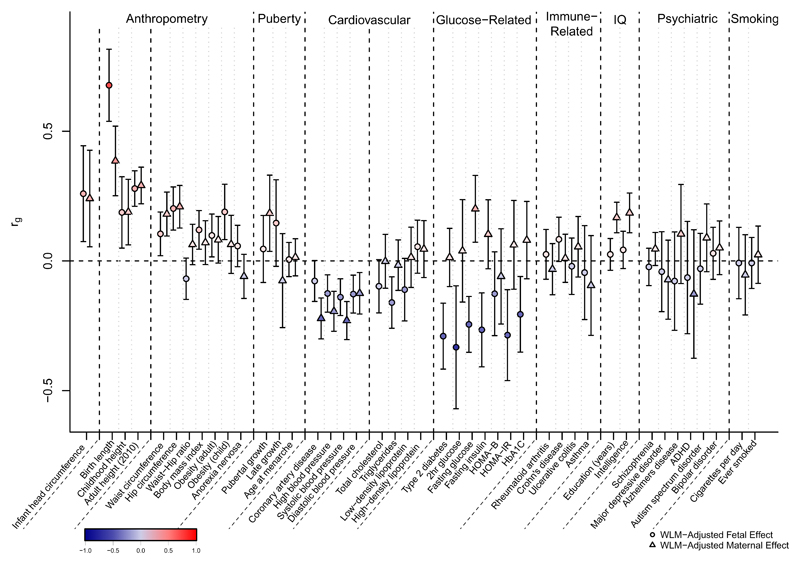
The 209 lead birth weight-associated SNPs were associated with other phenotypes in previously-published GWAS and the UK Biobank (Supplementary Table 13, Methods). At the genome-wide level, we previously reported genetic correlations between own birth weight and several adult cardio-metabolic traits⁵ but were unable to distinguish the direct fetal genotype contribution from the indirect contribution of maternal genotype. To understand these distinct contributions, we calculated genetic correlations using LD score regression¹⁸ between WLM-adjusted fetal and maternal SNP effect estimates and GWAS estimates for a range of traits (Figure 2, Supplementary Table 10, Methods). For many traits (e.g. adult height), the fetal-specific genetic correlation was similar to the maternal-specific genetic correlation, but for some traits, the fetal-specific and maternal-specific genetic correlations were different in magnitude (e.g. SBP) or even in direction (e.g. T2D). For several glycemic traits, (e.g. fasting glucose) the genetic correlations estimated using the WLM-adjusted effects were substantially different from those estimated using the unadjusted effects, demonstrating the importance of accounting for the maternal-fetal genotype correlation.

Figure 2. Genome-wide genetic correlation between birth weight and a range of traits and diseases in later life.

Genetic correlation (r_g) and corresponding 95% confidence intervals between birth weight and the traits were estimated using linkage disequilibrium (LD) score regression in LD Hub. Genetic correlations were estimated from the summary statistics of the weighted linear model (WLM)-adjusted fetal genome-wide association study (GWAS; WLM-adjusted fetal effect on own birth weight) and the WLM-adjusted maternal GWAS (WLM-adjusted maternal effect on offspring birth weight). The total sample size included in the WLM-adjusted GWAS is 406,063 individuals with their own and/or their offspring’s birth weight. The genetic correlation estimates are colour coded according to their intensity and direction (red for positive correlation and blue for negative correlation). HOMA-B/IR, homeostasis model assessment of beta-cell function/insulin resistance; HbA1c, hemoglobin A1c; ADHD, attention deficit hyperactivity disorder. See Supplementary Table 10 for the references for each of the traits and diseases displayed and the genetic correlation results for other traits and diseases.

Using genetics to estimate causal effects of intrauterine exposures on birth weight

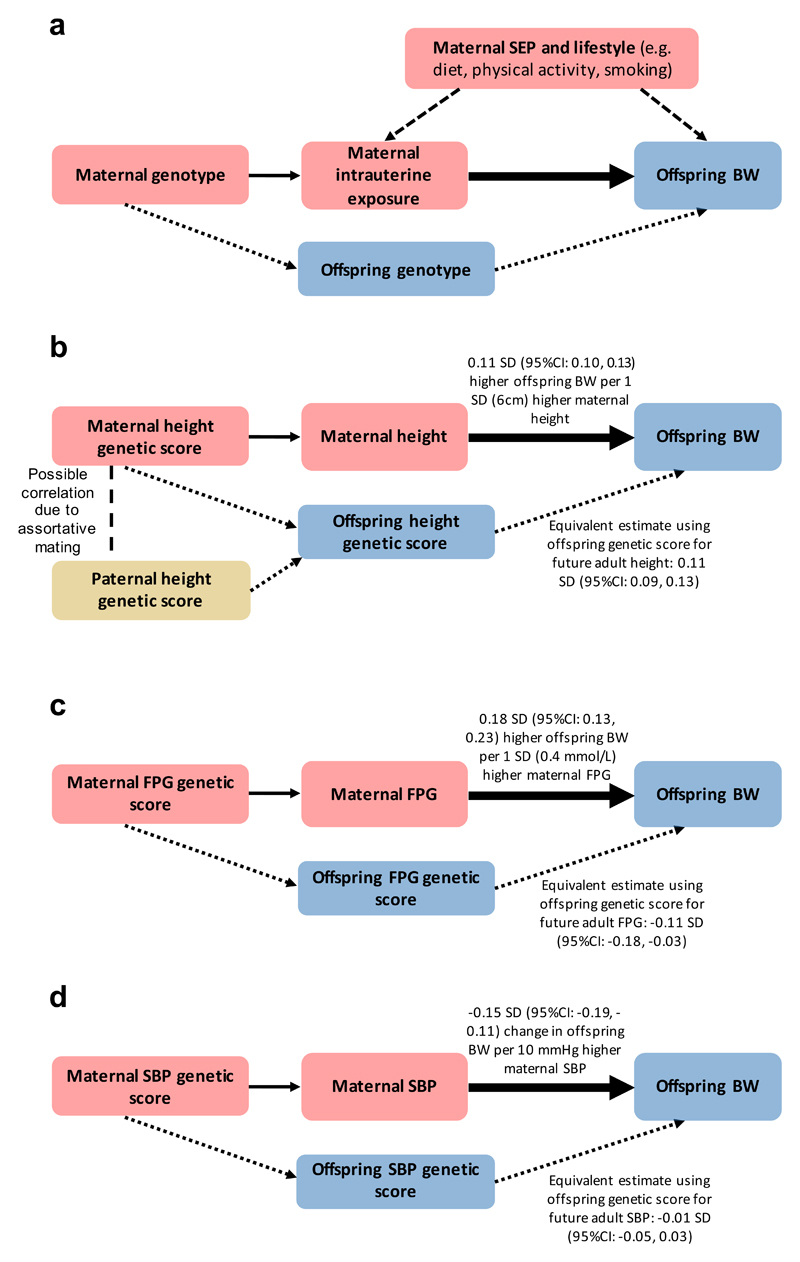
The separation of direct fetal genotype effects from indirect maternal genotype effects on birth weight offers the novel opportunity to estimate unconfounded causal influences of intrauterine exposures using Mendelian randomization (MR) analyses. The principle of MR is similar to that of a randomized controlled trial: parental alleles are randomly transmitted to offspring and are therefore generally free from confounding^21,22. Consequently, an association between a maternal genetic variant for an exposure of interest, and offspring birth weight, after accounting for fetal genotype, provides evidence that the maternal exposure is causally related to offspring birth weight (Figure 3a). Previous attempts to estimate causal effects of maternal exposures on offspring birth weight were limited by an inability to adjust for fetal genotype in adequately-powered samples²³, which can now be overcome by using WLM-adjusted estimates. We applied two-sample MR²⁴ to estimate causal effects of maternal exposures on offspring birth weight, focusing on height, glycemic traits and blood pressure. We selected SNPs known to be associated with each exposure, and regressed the WLM-adjusted maternal effects on birth weight for those SNPs against the effect estimates for the maternal exposure, weighting by the inverse of the variance of the maternal exposure effect estimates. In the same way, we used the WLM-adjusted fetal effects to estimate the casual effect of the offspring’s genetic potential on their own birth weight, and compared the results with the estimated maternal causal effects.

Figure 3. Mendelian randomization (MR) to assess the causal effect of maternal intrauterine exposures on offspring birth weight (adapted from Lawlor et al. ⁴⁴).

a. Since maternal and fetal genotypes are correlated, it is essential to account for offspring genotype in this analysis. The continuous, thin arrow represents the relationship between the genetic instrument and intrauterine exposure. The dashed arrows represent potential confounding via maternal characteristics which, under MR assumptions, are not associated with the genetic instrument. The dotted arrows represent potential violation of MR assumptions via offspring genotype. The thick arrow represents the causal effect of interest.

b. Higher offspring birth weight is caused by direct fetal genetic effects of height-raising alleles and indirect effects of maternal height-raising alleles. Maternal indirect effects of height-raising alleles may increase offspring birth weight by increasing the space available for growth, but we cannot rule out alternative explanations e.g. assortative mating.

c. Higher maternal fasting glucose levels increase offspring birth weight. Conversely, direct fetal genetic effects of glucose-raising alleles reduce birth weight. This is likely due to their effects on insulin: variants that lower maternal insulin levels increase maternal glucose, which crosses the placenta and stimulates fetal insulin-mediated growth. However, the same variants in the fetus cause lower fetal insulin levels, and consequently, reduced fetal insulin-mediated growth.

d. Higher maternal SBP is causally associated with lower offspring birth weight. After adjusting for maternal effects, there was no evidence of an effect of offspring’s own SBP genetic score on their own birth weight.

SEP, socio-economic position; BW, birth weight; FPG, fasting plasma glucose; SBP, systolic blood pressure. 1 SD of BW = 484g⁹,⁴²

Height and birth weight

Classical animal experiments²⁵ demonstrated that larger maternal size can support greater fetal growth. This is supported by observational human data showing that offspring height shifts from being closer to maternal than paternal height percentile in infancy towards mid-parental height in adulthood, the latter reflecting the predominant role of inherited genetic variation²⁶. However, several observational studies have provided mixed evidence regarding correlations between maternal or paternal height and offspring birth weight: some studies show a stronger correlation with maternal than paternal height^27,28, which would be consistent with a role for intrauterine effects, while others show that maternal and paternal height are both strongly correlated with offspring birth weight^29–31. The MR analysis, using 693 height-associated SNPs³² (Supplementary Table 14), estimated that a 1 SD (6cm) higher maternal height is causally associated with a 0.11 SD (95%CI: 0.10, 0.13) higher offspring birth weight (Figure 3b), independent of the direct fetal effects. A similar estimate was obtained using the WLM-adjusted fetal effects on own birth weight (0.11 SD (95%CI: 0.09, 0.13)), reflecting the role of inherited height alleles (Supplementary Table 15). Both a previous study³³ and complementary analysis using transmitted and non-transmitted height alleles in mother-offspring pairs estimated a much larger contribution of direct fetal effects than indirect maternal effects to offspring birth weight (Supplementary Table 16, Methods), but with relatively small sample sizes. Contrary to a previous report³³, there was little supportive evidence that the maternal height effect on birth weight was via prolonged gestation, (P=0.12; Supplementary Table 15). These MR results are consistent with the hypothesis that greater maternal height causally increases birth weight, and that this effect is independent of the direct birth weight-raising effect of height alleles inherited by the fetus. Although greater availability of space for fetal growth is a possible explanation, we cannot rule out other causal pathways. For example, causal associations between greater height and more favourable socio-economic position³⁴ could enhance maternal nutritional status and result in higher offspring birth weight. We also cannot exclude the contribution of assortative mating³⁵ to these results: correlation between maternal and paternal height genotypes could lead to similar maternal and fetal MR estimates.

Glycemic traits and birth weight

Maternal glucose is a key determinant of fetal growth: it crosses the placenta, stimulating the production of fetal insulin which promotes growth³⁶, and as a consequence, strong, positive associations are seen between maternal fasting glucose, fetal insulin levels, and offspring birth weight³⁷. In a randomized clinical trial of women with gestational diabetes mellitus, glucose control was shown to reduce offspring birth weight³⁸. Therefore, we anticipated detecting a positive causal effect of maternal glucose on offspring birth weight, as previously observed using MR in a smaller sample²³. Indeed, the MR analysis using 33 fasting glucose-associated SNPs (Supplementary Table 14), estimated an 0.18 SD (95%CI: 0.13, 0.23) higher offspring birth weight due to 1 SD (0.4mmol/L) higher maternal fasting glucose, independent of the direct fetal effects (Supplementary Table 15, Figure 3c). A large part of the genetic variation underlying fasting glucose levels is implicated in pancreatic beta cell function and thus overlaps with the genetics of insulin secretion. To estimate the causal effect of insulin secretion on birth weight, we used 18 SNPs associated with disposition index, a measure of insulin response to glucose, adjusted for insulin sensitivity. Alleles that increase insulin secretion in the mother tend to decrease her glucose levels, which consequently reduces insulin-mediated growth of the fetus. This was reflected in the negative causal estimate from the MR analysis of the effect of maternal disposition index on offspring birth weight (-0.17 SD per 1 SD higher maternal disposition index (95%CI: -0.26, -0.08); Supplementary Table 15). In contrast, we estimated that birth weight was 0.10 SD (95%CI: 0.02, 0.19) higher per 1 SD genetically higher fetal disposition index (Methods), highlighting that genetic variation underlying insulin secretion plays a key role in fetal growth, and suggesting that the genetic effects on disposition index are similar in fetal and adult life.

Birth weight associations with previously-reported GWAS SNPs for fasting glucose, T2D, insulin secretion and insulin sensitivity loci were directionally consistent with the overall genetic correlations and supported the opposing contributions of fetal versus maternal glucose-raising alleles on birth weight (Supplementary Figures 11-14). Taken together with the WLM-adjusted genetic correlations, the MR results underline the importance of fetal insulin in fetal growth and demonstrate that fetal genetic effects link lower birth weight with reduced insulin secretion and higher T2D risk in later life⁶. However, further work is needed to investigate the role of maternal indirect genetic effects in the relationship between high birth weight and higher future risk of T2D.

Blood pressure and birth weight

Observational studies of the relationship between birth weight and later life blood pressure have produced mixed findings: some studies indicate that lower birth weight is associated with higher later life blood pressure and related comorbidities³⁹, whereas others have shown that this relationship could be driven by a statistical artifact due to adjusting for current weight^40,41. We have previously shown that genetic factors account for a large proportion of an association between lower birth weight and higher blood pressure⁵, but it was not clear whether this was due to direct fetal genotype effects, or indirect maternal effects, or a combination of the two. We explored this association further using several complementary analyses. The estimate of the birth weight-SBP covariance explained was higher when using the maternal genotyped SNP associations with offspring birth weight (65% (95%CI: 57, 74%)), than when using the fetal genotype associations with own birth weight (56% (95%CI: 48, 64%); Supplementary Table 17). A similar pattern was seen with the birth weight-diastolic blood pressure (DBP) covariance (maternal: 72% (95%CI: 58, 85%); fetal: 56% (95%CI: 46, 67%); Supplementary Table 17). Together with the larger maternal than fetal genetic correlation for SBP (Figure 2), these results point to the importance of indirect maternal effects of blood pressure on offspring birth weight (Supplementary Figures 15, 16). In line with this, MR analyses indicated that a 1SD (10mmHg) higher maternal SBP is causally associated with a 0.15 SD (95%CI: -0.19, -0.11) lower offspring birth weight, independent of the direct fetal effects. In contrast, there was no fetal effect of SBP on their own birth weight, after adjusting for the indirect maternal effect (-0.01 SD per 10mmHg, 95% CI: -0.05, 0.03; Figure 3d; Supplementary Tables 14, 15). Similar results were seen in the WLM-adjusted MR analyses of DBP on offspring and own birth weight.

Estimating the causal effect of birth weight-lowering intrauterine exposures on offspring SBP

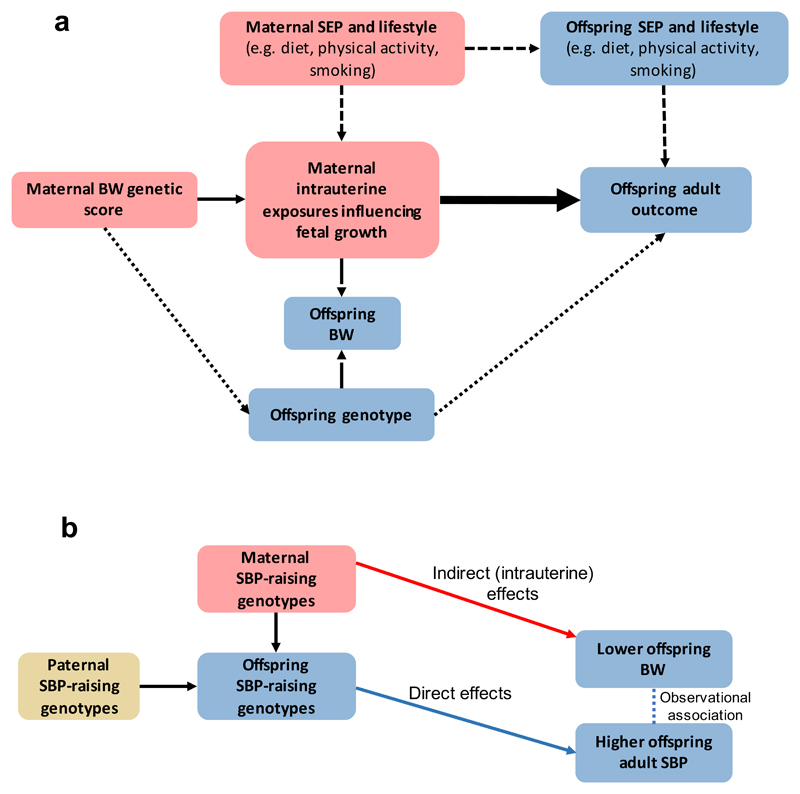
A key question is whether maternal SNPs that reduce offspring birth weight through intrauterine effects are also associated with higher SBP in their adult offspring. Such an association would suggest that the maternal intrauterine effects cause the later SBP effect (i.e. through developmental adaptations) (Figure 4a, Supplementary Figure 17). To investigate this possibility, we tested the conditional association between maternal and offspring genetic scores for birth weight and offspring SBP as measured in 3,886 mother-offspring pairs in the UK Biobank, with sensitivity analyses in 1,749 father-offspring pairs. The fetal genetic score for lower birth weight was associated with higher offspring SBP, even after adjustment for maternal (or paternal) birth weight genotypes. However, when adjusted for fetal genotypes, the maternal genetic score for lower birth weight was associated with lower (not higher) offspring SBP (Supplementary Table 18). Taken together, our results demonstrate that the observed negative correlation between birth weight and later SBP is driven by (i) the causal effect of higher maternal SBP on lower offspring birth weight (Figure 3d), in combination with (ii) the subsequent transmission of SBP-associated alleles to offspring, which then increase offspring SBP (Figure 4b), rather than by long-term developmental compensations to adverse in utero conditions.

Figure 4. Mendelian randomization (MR) to assess the causal effect of intrauterine growth on offspring adult outcomes, using maternal intrauterine exposures that influence fetal growth.

a. Maternal genotype should be associated with offspring birth weight independently of offspring genotype, so it is essential to adjust the analysis for offspring genotype.

The continuous, thin, arrow represents the relationship between the genetic instrument and intrauterine exposure. The long-dashed arrows denote the (maternal and possibly fetal) genotype associations with birth weight; these arrows highlight the assumption that genetic variation influences offspring adult outcome via intrauterine growth, not birth weight. The short-dashed arrows represent potential confounding via maternal and offspring characteristics. The dotted arrow represents potential violation of assumptions of the MR analysis via offspring genotype. The thick arrow represents the causal effect of interest.

We have not estimated the size of the causal effect as we do not have effect estimates for the SNP-maternal intrauterine exposures influencing fetal growth. However, we have used the presence/absence and direction of association in 3,886 mother-offspring pairs to indicate whether the intrauterine environment causes changes in adult offspring SBP (see Supplementary Table 18 for full results).

b. Our results demonstrate that the observed negative correlation between birth weight and later SBP may be driven by the causal effect of higher maternal SBP on lower offspring birth weight (red arrow), in combination with the subsequent transmission of SBP-associated alleles to offspring (blue arrow), which then increase offspring SBP, rather than by long-term developmental compensations to adverse intrauterine conditions.

SEP, socio-economic position; BW, birth weight; SBP, systolic blood pressure.

Discussion

In greatly-expanded GWAS and follow-up analyses of own and offspring birth weight, we have identified 129 novel association signals and partitioned the genetic effects on birth weight into direct fetal and indirect maternal (intrauterine) effects. Using these partitioned effects, we identified fetal- and maternal-specific mechanisms and tissues involved in the regulation of birth weight, and mechanisms with directionally-opposing effects in the fetus and mother (e.g. insulin secretion, fasting glucose).

MR analyses using the WLM-adjusted estimates showed (i) both direct fetal and indirect maternal effects of height-raising genotypes contribute to higher offspring birth weight, (ii) fetal, and not maternal, genotype effects explain the negative genetic correlation between birth weight and later T2D, and (iii) the negative genetic correlation between birth weight and adult SBP is the result of both indirect SBP-raising effects of maternal genotypes reducing offspring birth weight, and direct effects of fetal genotypes on higher adult SBP. The resolution of maternal vs. fetal effects was higher in these MR analyses than has previously been achieved using analyses of available mother-child pairs²³, due to greater statistical power. Recently, a number of studies have attempted to use MR methodology to investigate causal links between birth weight and later T2D^43–45. However, such naïve MR analyses using two-sample approaches in unrelated sets of individuals, which do not properly account for the correlation between maternal and fetal genotype effects, may result in erroneous conclusions regarding causality. Future investigations into causal links between birth weight and later T2D or other disease outcomes will require larger samples than are currently available, with maternal and offspring genotypes and offspring later life disease outcomes.

There are some limitations to this study (see Supplementary Note for a full discussion). First, the MR results concern birth weight variation within the normal range and do not necessarily reflect the effects of extreme environmental events (e.g. famine), which may exert qualitatively different effects. Additionally, we have assumed a linear relationship between birth weight and later life traits, which may be an oversimplification for some traits such as T2D. Second, birth weight is the end marker of a developmental process, with critical periods during the process that may make the fetus particularly sensitive to environmental influences. The MR analyses could therefore be masking effects at certain critical periods. Third, we have assumed that genetic variants identified in large GWAS of SBP and glycemic traits in males and non-pregnant females are similarly associated in pregnant women. Fourth, we have not investigated the potential gender difference in the associations between birth weight and later life traits. Fifth, we have assumed that the critical period of exposure to maternal indirect genetic effects is pregnancy, and that the estimates do not reflect pre-pregnancy effects on primordial oocytes or post-natal effects⁴². Sixth, we have not considered paternal genotypes, and it is possible that this omission has biased the results of some of our analyses. Finally, although we were able to fit the full SEM at the 209 lead SNPs, we were unable to fit the SEM, including the two degree of freedom test (i.e. where maternal and fetal paths are constrained to zero), at all SNPs across the genome.

To conclude, the systematic separation of fetal from maternal genetic effects in a well-powered study has enhanced our understanding of the regulation of birth weight and of its links with later cardio-metabolic health. In particular, we show that the association between lower birth weight and higher adult blood pressure is attributable to genetic effects, and not to intrauterine programming. In successfully separating fetal from maternal genetic effects and using them in Mendelian randomization analyses, this work sets a precedent for future studies seeking to understand the causal role of the intrauterine environment in later life health.

Online Methods

Ethics statement

All human research was approved by the relevant institutional review boards and conducted according to the Declaration of Helsinki. Participants of all studies provided written informed consent. The UK Biobank has approval from the North West Multi-Centre Research Ethics Committee (MREC), which covers the UK. Ethical approval for the ALSPAC study was obtained by the ALSPAC Ethics and Law Committee and the local Research Ethics Committees. Ethical approval for the EFSOCH study was given by the North and East Devon Local Ethics Committee. Approval for access to data and biological material for MoBa-HARVEST was granted by the Scientific Management Committee of MoBa and the Regional Committee for Medical and Health Research Ethics.

Statistical tests

Details of statistical tests used in the various analyses are reported under the appropriate headings below. All tests were two-sided, unless otherwise stated.

GWAS of own birth weight

European ancestry meta-analysis

The European ancestry GWAS meta-analysis of own birth weight consisted of two components (Supplementary Figure 1): (i) 80,745 individuals from 35 studies participating in the EGG Consortium from Europe, USA and Australia; and (ii) 217,397 individuals of white European origin from the UK Biobank (see Supplementary Note for details on phenotype preparation and GWAS analyses). We combined the summary statistics from the EGG meta-analysis with the UK Biobank summary statistics using a fixed-effects meta-analysis in GWAMA⁴⁶ (max N=297,142). Variants failing GWAS quality control filters, reported in less than 50% of the total sample size in the EGG component, or with MAF<0.1%, were excluded. We also performed a fixed-effects meta-analysis of the association summary statistics for 16,095 directly genotyped SNPs on the X-chromosome from the UK Biobank and the EGG meta-analysis using GWAMA⁴⁶ (max N=270,929). Genome-wide significance was defined as P<6.6x10^-9 as calculated by Kemp et al.⁴⁷, which was similar to the thresholds calculated using permutations by Jones el al.⁴⁸. A locus was defined as one or more SNPs reaching genome-wide significance within a region of the genome; two genome-wide significant SNPs are defined as belonging to two separate loci if the distance between them is ≥500kb. The lead SNP within each locus was the SNP with the smallest P-value.

Several sensitivity analyses were conducted to confirm the quality of our meta-analysis results (see Supplementary Note for details). Univariate LD score regression⁴⁹ estimated the genomic inflation as 1.08, indicating that the majority of genome-wide inflation of the test statistics was due to polygenicity. To assess the impact of this inflation, we re-calculated the association P-values after adjusting the test statistics for the LD score regression intercept (Supplementary Table 5).

Approximate conditional and joint multiple-SNP (COJO) analysis to identify additional independent signals

Approximate COJO analysis¹³ was performed in GCTA⁵⁰ using the European ancestry meta-analysis summary statistics to identify independent association signals attaining genome-wide significance (P<6.6x10^-9). The LD reference panel was made up of 344,246 unrelated UK Biobank participants defined by the UK Biobank as having British ancestry and SNPs were restricted to those present in the HRC reference panel. At each locus, only SNPs labelled by GCTA as “independent” and not in LD with the original lead SNP (R²<0.05) were listed as secondary SNPs.

Trans-ethnic meta-analysis

To identify any further independent birth weight-associated SNPs, we conducted a trans-ethnic meta-analysis combining three components (Supplementary Figure 1): (i) 80,745 individuals from the European ancestry component within EGG; (ii) 12,948 individuals from nine studies within EGG from diverse ancestry groups: African American, Afro-Caribbean, Mexican, Chinese, Thai, Filipino, Surinamese, Turkish and Moroccan; and (iii) 227,530 individuals of all ancestries from the UK Biobank. The same strategy and variant filtering criteria were applied as in the European meta-analysis (Supplementary Figure 1). Univariate LD score regression⁴⁹ estimated the genomic inflation as 1.08. P-values after adjustment of the test statistics for the LD score regression intercept are presented in Supplementary Table 5.

GWAS of offspring birth weight

European ancestry meta-analysis

The European ancestry GWAS meta-analysis of offspring birth weight consisted of three components (Supplementary Figure 2): (i) 12,319 individuals from 10 European GWAS imputed up to the HapMap 2 reference panel; and (ii) 7,542 individuals from two European GWAS imputed up to the HRC panel; and (iii) 190,406 individuals of white European origin from the UK Biobank (see Supplementary Note for details on phenotype preparation and GWAS analyses). We conducted a European ancestry fixed-effects meta-analysis to combine the association summary statistics from the three components using GWAMA⁴⁶ (max N=210,267). We also performed a fixed-effects meta-analysis of the association summary statistics for 18,137 directly genotyped SNPs on the X-chromosome from the UK Biobank and the EGG meta-analysis using GWAMA⁴⁶ (max N=197,093). The same strategy and variant filtering criteria were applied as in the meta-analysis of own birth weight and the same sensitivity analyses were conducted (Supplementary Note).

Univariate LD score regression⁴⁹ estimated the genomic inflation as 1.05. We recalculated the P-values after adjusting the test statistics for this LD score intercept (Supplementary Table 5).

Approximate COJO analysis to identify additional independent signals

We performed approximate COJO analysis¹³ using the European ancestry meta-analysis summary statistics of offspring birth weight, using the same reference panel as in the own birth weight analysis and listed any secondary “independent” SNPs associated with offspring birth weight.

Trans-ethnic meta-analysis

We conducted a trans-ethnic meta-analysis combining three components (Supplementary Figure 2): (i) 12,319 individuals from 10 European GWAS imputed up to the HapMap 2 reference panel; and (ii) 7,542 individuals from two European GWAS imputed up to the HRC panel; and (iii) 210,208 individuals of all ancestry from the UK Biobank. The same strategy and variant filtering criteria were applied as in the European meta-analysis (Supplementary Figure 2) and the same sensitivity analyses were conducted (Supplementary Material). Univariate LD score regression⁴⁹ estimated the genomic inflation as 1.04 and the recalculated P-values after adjusting the test statistics for this LD score intercept are presented in Supplementary Table 5.

Colocalization methods

For each signal where we identified different lead SNPs in the GWAS of own birth weight and offspring birth weight, we performed co-localization analysis using the "coloc" R package⁵¹. For each signal, we input the regression coefficients, their variances and SNP minor allele frequencies for all SNPs 500kb up and downstream of the lead SNP from the European meta-analysis. We used the coloc.abf() function, with its default parameters, to calculate posterior probabilities that the own birth weight and offspring birth weight lead SNPs were independent (H₃) or shared the same associated variant (H₄). We called variants the same signal if the H₄ posterior probability was greater than 0.50, and different signals if the H₃ posterior probability was greater than 0.50.

Estimation of genetic variance explained

Firstly, we estimated the proportion of birth weight variance explained by fetal genotypes, maternal genotypes and the covariance between the two at the 190 genome-wide significant signals in the Norwegian Mother and Child Cohort Study (MoBa-HARVEST; https://www.fhi.no/en/studies/moba/). This sample was independent of samples contributing to the discovery meta-analyses, apart from a small potential overlap with mothers from the MoBa-2008 sample that was included in the GWAS of offspring birth weight (<0.07% of the meta-analysis sample). For the 19 signals that had different maternal and fetal lead SNPs, the fetal SNP (and not the maternal SNP) was used in the analysis to avoid collinearity in the model. We excluded multiple births, babies of non-European descent, born before 37 weeks of gestation, born with a congenital anomaly or still-born. Birth weight was Z-score transformed and all models were adjusted for sex, gestational duration and the first 4 ancestry informative principal components. We conducted a linear regression analysis in R⁵² using 13,934 mother-offspring pairs where offspring birth weight was regressed on the maternal and fetal genotypes at all 190 SNPs simultaneously. The proportion of variance explained by fetal genotypes at the 190 genome-wide significant signals was calculated as:

$${\displaystyle \sum _{i=1}^{190}\frac{2p_i\left(1-p_i\right){\widehat{\beta }}_{f_i}^2}{var\left(BW\right)}}$$

Where p_i is the effect allele frequency of the i^th SNP, ${\widehat{\beta }}_{f_i}$ is the regression coefficient for the effect of the offspring’s genotype at the i^th SNP on offspring birth weight and var(BW) is the variance of offspring birth weight (which is approximately 1 as birth weight was Z-score transformed). A similar formula was used to calculate the variance explained by maternal genotypes, using :

$${\displaystyle \sum _{i=1}^{190}\frac{2p_i\left(1-p_i\right){\widehat{\beta }}_{m_i}^2}{var\left(BW\right)}}$$

Where ${\widehat{\beta }}_{m_i}$ is the regression coefficient for the effect of the maternal genotype at the i^th SNP on offspring birth weight. The following formula was used to calculate twice the covariance:

$${\displaystyle \sum _{i=1}^{190}\frac{2p_i\left(1-p_i\right){\widehat{\beta }}_{f_i}{\widehat{\beta }}_{m_i}}{var\left(BW\right)}}$$

Secondly, we used maternal genome-wide complex trait analysis¹¹ (M-GCTA) to estimate the proportion of variance explained in birth weight by genome-wide SNPs, or SNPs they tag, in the fetal genome, the maternal genome, the covariance between the two or environmental factors in MoBa-HARVEST. The same phenotype was used as in the previous analysis and the model was adjusted for sex and gestational duration. Mothers or offspring were excluded if they were related to others in the sample, using a genetic relationship cut-off 0.025, leaving N=7,910 mother-offspring pairs available for analysis.

Identifying eQTL linked genes

We used FUSION⁵³ with the v6p release of the GTEx data¹⁴ to identify eQTL linked genes. FUSION incorporates information from gene-expression and GWAS data to translate evidence of association with a phenotype from the SNP-level to the gene. Only gene level results from the adjusted model were taken forward for consideration. Each of the genes implicated by this analysis survived multiple testing correction (Bonferroni corrected P<6x10^-7, after adjusting for 44 tissues) and were independent from other proximal genes tested in a joint model.

Placenta eQTL look ups

We annotated genome-wide significant birth weight-associated SNPs with gene expression data (200/209 SNPs available) from European ancestry placental samples in the Rhode Island Child Health Study¹⁵ (RICHS; N=123 with fetal genotype, including 71 with birth weight appropriate for gestational age, 15 small for gestational age, and 37 large for gestational age). SNPs were annotated if they had genome-wide empirical FDR<0.01 for association with one or more transcripts and r²>0.7 with a lead eQTL SNP.

TAD pathways

Topologically associating domains (TAD) pathway analysis was performed using software described in Way et al.¹⁶. Briefly, the software uses publicly available TAD boundaries, identified in human embryonic stem cells and fibroblasts using a Hidden Markov Model¹⁷, to prioritize candidate genes at GWAS SNPs. These TAD boundaries are stable across different cell types and can be used to identify genomic regions where non-coding causal variants will most likely impact tissue-independent function.

Structural equation model for estimating adjusted maternal and fetal effects of the genome-wide significant variants

The structural equation modelling (SEM) approach used to estimate adjusted maternal and fetal effects has been described elsewhere¹² (for additional details, see Supplementary Note).

The SEM was fit to data from 146 genome-wide significant lead fetal SNPs and 72 lead maternal SNPs from the GWAS meta-analysis (Supplementary Figure 4). In order to identify a subset of unrelated individuals in the UK Biobank (as the SEM cannot easily account for relatedness), we generated a genetic relationship matrix in the GCTA software package⁵⁰ (version 1.90.2) and excluded one of every pair of related individuals with a genetic relationship greater than 9.375%. After the same exclusions were made as in the GWAS, 85,518 unrelated individuals of European ancestry with their own and their offspring’s birth weight, 98,235 individuals with their own birth weight only, and 73,981 with their offspring’s birth weight only were available for analysis. We fit linear regression models to birth weight and offspring birth weight in this subset of unrelated, European ancestry individuals adjusting for sex (own birth weight only), assessment centre and the top 40 ancestry informative principal components provided by the UK Biobank to account for any remaining population substructure. The residuals from these regression models were Z-score transformed for analysis. Because we included the summary statistics from the meta-analysis of the EGG studies, rather than the individual level data, we were unable to account for the small subset individuals who contributed to both the own birth weight and offspring birth weight GWAS meta-analyses. Based on the results from simulations (not shown), we expect that this non-independence will result in very slightly smaller standard errors and increased type 1 error rate, particularly for the fetal effect which is estimated from a larger sample size than was available to estimate the maternal effect. Therefore, we conducted a sensitivity analysis that first excluded EGG studies from the meta-analysis of own birth weight that contributed to both GWAS meta-analyses of own and offspring birth weight (e.g. ALSPAC), and then refitted the non-overlapping data in the SEM; these results are presented in Supplementary Table 19. For SNPs identified on the X chromosome, we fit a slightly different SEM due to males having double the expected genetic variance at X linked loci compared to females. We did not incorporate summary statistics from the EGG consortium as the GWAS results were not stratified according to sex (additional details on the X chromosome analysis are provided in the Supplementary Note and Supplementary Figure 6b).

We used the estimates from the SEM to classify the lead SNPs into the following five categories; 1) fetal only: the 95% confidence interval surrounding the fetal effect estimate does not overlap zero and does not overlap the 95% confidence interval around the maternal effect estimate. Additionally, the 95% confidence interval surrounding the maternal effect estimate overlaps zero; 2) maternal only: the 95% confidence interval surrounding the maternal effect estimate does not overlap zero and does not overlap the 95% confidence interval around the fetal effect estimate. Additionally, the 95% confidence surrounding the fetal effect estimate overlaps zero; 3) fetal and maternal, effects going in the same direction: the 95% confidence intervals around both the maternal and fetal effect estimates do not overlap zero, and their effect is in the same direction; 4) fetal and maternal, effects going in opposite direction: the 95% confidence intervals around both the maternal and fetal effect estimates do not overlap zero, and their effects are in opposite directions; and 5) unclassified: SNPs that do not fall into any of these categories, and therefore the 95% confidence intervals around the maternal and fetal effect estimates overlap, and at least one overlaps zero.

Meta-analysis of maternal and fetal effects from a conditional regression analysis in mother-offspring pairs

We conducted conditional association analyses for all 209 lead SNPs in 18,873 mother-offspring pairs from three studies (MoBa-HARVEST, ALSPAC and EFSOCH) adjusting for both maternal and offspring genotype and combined the summary statistics for each SNP in a fixed effects meta-analysis using METAL⁵⁴. We compared the estimates of the maternal and fetal effects of this meta-analysis to the SEM-adjusted maternal and fetal effects using a heterogeneity test (Supplementary Table 6).

Approximation of the SEM for genome-wide analyses

The SEM is computationally intensive to fit, making it difficult to run on all SNPs across the genome. Therefore, we developed an approximation of the SEM using a linear transformation and ordinary least squares linear regression, which we refer to as the weighted linear model adjusted (WLM-adjusted) analyses. The full details of the derivation are provided in the Supplementary Note. Briefly, from ordinary least squares regression we know that the estimated fetal effect size from the GWAS of own birth weight, ${\widehat{\beta }}_{f_{\mathit{\text{unadj}}}}$, is calculated by dividing the sample covariance between birth weight and SNP by the sample variance of the SNP. Similarly, the estimated maternal effect from the GWAS of offspring birth weight, ${\widehat{\beta }}_{m_{\mathit{\text{unadj}}}}$, is calculated by dividing the sample covariance between offspring birth weight and SNP by the sample variance of the SNP. It follows that an estimate of the fetal effect adjusted for the maternal genotype is (see Supplementary Note for full derivation):

$${\widehat{\beta }}_{f_{adj}}=-\frac{2}{3}{\widehat{\beta }}_{m_{unadj}}+\frac{4}{3}{\widehat{\beta }}_{f_{unadj}}$$

and an estimate of the maternal effect adjusted for the fetal genotype is:

$${\widehat{\beta }}_{m_{adj}}=\frac{4}{3}{\widehat{\beta }}_{m_{unadj}}-\frac{2}{3}{\widehat{\beta }}_{f_{unadj}}$$

If the model is truly linear, then the same estimates can be obtained by transforming the reported birth weights rather than the regression coefficients⁵⁵. See the Supplementary Note and Supplementary Figure 18 for a flow diagram of the full analysis pipeline. A comparison of the results using this WLM method and the full SEM for the lead SNPs is presented in Supplementary Figure 9.

Gene expression integration

To identify which tissue types were most relevant to genes involved in birth weight, we applied LD score regression to specifically expressed genes (“LDSC-SEG”)¹⁹. We used the summary statistics from the GWAS meta-analysis of own and offspring birth weight and the WLM-adjusted meta-analyses. Briefly, the method takes each tissue, ranking genes by a t-statistic for differential expression, using sex and age as covariates, and excluding all samples in related tissues. It then takes the top 10% of ranked genes, and makes a genome annotation including these genes (exons and introns) plus 100kb on either side. Finally, it uses stratified LD score regression to estimate the contribution of this annotation to per-SNP birth weight heritability, adjusting for all categories in the baseline model. We computed significance using a block jackknife over SNPs, and corrected for the number of tissues tested.

Gene-set enrichment analysis (MAGENTA)

Pathway-based associations using summary statistics from the GWAS meta-analysis of own and offspring birth weight and WLM-adjusted meta-analysis were tested using MAGENTA⁵⁶. Briefly, the software maps each gene to the SNP with the lowest P-value within a 110kb upstream and 40kb downstream window. This P-value is corrected for factors such as SNP density and gene size using a regression model. Genes within the HLA region were excluded. The observed number of gene scores within a given pathway with a ranked gene score above a given threshold (95^th or 75^th percentile) was calculated. This statistic was compared with 1,000,000 randomly permuted pathways of the same size to calculate an empirical P-value for each pathway. We considered pathways with false discovery rate (FDR) < 0.05 to be of interest. The 3,230 biological pathways tested were from the BIOCARTA, Gene Ontology, KEGG, PANTHER and READTOME databases along with a small number of custom gene-sets.

Gestational duration associations

We extracted the 209 lead birth weight-associated SNPs from the summary statistics provided by 23andMe and published in a recent GWAS of gestational duration²⁰. Any birth weight-associated SNP that was also associated with gestational duration (P<2.4x10^-4, corrected for 209 tests) was followed-up in 13,206 mother-child pairs from the MoBa-HARVEST, ALSPAC and EFSOCH studies. Preterm births (gestational duration <37 weeks) were removed before analysis, and gestational duration and birth weight were both z-score transformed. We conducted linear regression analyses to test the association between maternal or fetal genotype (both unadjusted and adjusted genotype effects) and gestational duration, birth weight or gestational duration adjusted for birth weight. The association analysis results were combined using inverse variance weighted meta-analysis. We also combined the unadjusted maternal SNP-gestational duration associations with the 23andMe summary statistics²⁰ using P value based meta-analysis implemented in METAL⁵⁴.

Association between birth weight-associated SNPs and a variety of traits

We performed GWAS on 78 traits in the UK Biobank using BOLT-LMM in an analogous way to analysis of own birth weight. Phenotype definitions for the 78 traits are described in Frayling et al.⁵⁷. Association statistics for the 209 lead birth weight-associated SNPs were then extracted from the results (Supplementary Table 13). Additionally, we searched the NHGRI GWAS catalog (https://www.ebi.ac.uk/gwas/; accessed 16th January 2018) for the 209 lead birth weight-associated SNPs, or SNPs in high LD with the 209 lead SNPs (r²>0.8), and reported associations with other traits (Supplementary Table 13).

Linkage-Disequilibrium (LD) score regression

LD score regression, which has been described in detail elsewhere¹⁸, was used to estimate the genetic correlation between birth weight and a range of traits/diseases. We used LDHub⁵⁸ (ldsc.broadinstitute.org/) to perform the LD score regression analyses. Due to the different LD structure across ancestry groups, the summary statistics from the European only birth weight analyses were uploaded to LDHub and genetic correlations were calculated with all available phenotypes. We conducted four separate analyses in LDHub using: (1) GWAS meta-analysis of own birth weight, (2) GWAS meta-analysis of offspring birth weight, (3) WLM-adjusted fetal effect and (4) WLM-adjusted maternal effect.

To calculate the genetic correlation between the maternal and fetal effect estimates from the unadjusted and WLM-adjusted analyses, and also between gestational duration and the WLM-adjusted maternal and fetal effects, we used the scripts provided by the developer (https://github.com/bulik/ldsc).

Mendelian randomization analyses of maternal and fetal exposures on offspring birth weight

Two-sample Mendelian randomization analyses were performed with own or offspring birth weight as outcomes. The exposures included height, fasting glucose, disposition index of insulin secretion⁵⁹, insulin sensitivity and systolic (SBP) and diastolic blood pressure (DBP). The SNP-exposure associations were taken from external studies (Supplementary Table 14). The SNP-outcome associations were taken from the current European GWAS meta-analyses of own birth weight, offspring birth weight, WLM-adjusted fetal effect and WLM-adjusted maternal effect. Two-sample Mendelian randomization regresses effect sizes of SNP-outcome associations against effect sizes of SNP-exposure associations, with an inverse-variance weighted (IVW) analysis, giving similar results to the two-stage least squares analysis in a single sample⁶⁰. We performed several sensitivity analyses to assess the impact of genetic pleiotropy on the causal estimates including MR-Egger⁶¹, Weighted Median (WM)⁶² and Penalized Weighted Median (PWM)⁶² (see Supplementary Table 15 for results). Details of the R code for the MR analyses are provided elsewhere^61,62.

Due to the strong negative correlation between estimates of the maternal and fetal genetic effects on birth weight, we conducted simulations to confirm that this correlation did not bias the results of downstream MR analyses; these simulations are described in the Supplementary Note.

Transmitted/non-transmitted allele scores in ALSPAC

Allelic transmission was determined for 4,962 mother/offspring pairs in ALSPAC. We first converted maternal and fetal genotypes into best guess genotypes where SNPs of interest had been imputed. Where one or both of the mother/offspring pair were homozygous, allelic transmission is trivial to determine. Where both mother and offspring were heterozygous for the SNP of interest we used phase imputation generated using SHAPEIT2⁶³ to examine the haplotypes in the region of the SNP of interest to determine allelic transmission. Weighted allele scores were generated for maternal non-transmitted, shared (maternal transmitted) and paternally inherited fetal alleles for SBP, DBP, fasting glucose, insulin secretion and insulin sensitivity. Associations were tested between the weighted allele scores and birth weight.

Covariance between birth weight and adult traits explained by genotyped SNPs

The genetic and residual covariance between birth weight and several quantitative/disease phenotypes was calculated in the UK Biobank using REML in BOLT-LMM⁶⁴. We included 215,444 individuals of European ancestry with data on own birth weight and 190,406 with data on offspring birth weight. SNPs with minor allele frequency < 1%, evidence of deviation from Hardy-Weinberg equilibrium (P≤1x10^-6) or overall missing rate > 0.015 were excluded, resulting in 524,307 genotyped SNPs for analysis. Ninety-five per cent confidence intervals for the proportion of covariance explained by genotyped variants were calculated as gcov/(gcov+rcov) ± 1.96*gcovSE/abs(gcov+rcov) where gcov is genetic covariance, rcov is residual covariance, gcovSE is the standard error for gcov and abs is the absolute value. Details of the phenotype preparation for the adult traits is provided in the Supplementary Note.

Association between maternal SNPs associated with offspring birth weight and later life offspring systolic blood pressure

Using the UK Biobank, we tested whether maternal SNPs associated with offspring birth weight were also associated with offspring SBP in later life. The UK Biobank released kinship information generated in KING⁶⁵, which included kinship coefficients and IBS0 estimates. We defined parent/offspring pairs using the kinship coefficient and IBS0 cut-offs recommended in Manichaikul et al.⁶⁵. There were 5,635 unique parent/offspring pairs of European ancestry with SBP data (for parents who had multiple offspring with SBP data, only the oldest offspring was included in the analysis); 3,886 mother/offspring pairs and 1,749 father/offspring pairs. We tested the relationship between unweighted allelic scores of birth weight-associated SNPs in mothers/fathers and offspring SBP (see Supplementary Note for SBP phenotype preparation) before and after adjusting for offspring genotypes at the same loci. We examined unweighted allelic scores consisting of all autosomal lead birth weight-associated SNPs available in the UK Biobank (205 SNPs), 72 autosomal SNPs that showed evidence of a maternal effect, and 31 autosomal SNPs that showed evidence only of maternal effects on birth weight. We also looked at the SNPs previously associated with SBP (Supplementary Table 14) as a sensitivity analysis to rule out the possibility of postnatal pleiotropic effects contaminating our results. All analyses were adjusted for offspring age at SBP measurement, sex and assessment center.

Reporting Summary

Further information on research design is available in the Nature Research Reporting Summary linked to this article

Editorial summary.

An expanded GWAS of birth weight and subsequent analysis using structural equation modeling and Mendelian randomization decomposes maternal and fetal genetic contributions and causal links between birth weight, blood pressure and glycemic traits.