Enhancing Automatic Closed-Loop Glucose Control in Type 1 Diabetes with an Adaptive Meal Bolus Calculator – In Silico Evaluation under Intra-Day Variability

Abstract

Background and Objective

Current prototypes of closed-loop systems for glucose control in type 1 diabetes mellitus, also referred to as artificial pancreas systems, require a pre-meal insulin bolus to compensate for delays in subcutaneous insulin absorption in order to avoid initial post-prandial hyperglycemia. Computing such a meal bolus is a challenging task due to the high intra-subject variability of insulin requirements. Most closed-loop systems compute this pre-meal insulin dose by a standard bolus calculation, as is commonly found in insulin pumps. However, the performance of these calculators is limited due to a lack of adaptiveness in front of dynamic changes in insulin requirements. Despite some initial attempts to include adaptation within these calculators, challenges remain.

Methods

In this paper we present a new technique to automatically adapt the meal-priming bolus within an artificial pancreas. The technique consists of using a novel adaptive bolus calculator based on Case-Based Reasoning and Run-To-Run control, within a closed-loop controller. Coordination between the adaptive bolus calculator and the controller was required to achieve the desired performance. For testing purposes, the clinically validated Imperial College Artificial Pancreas controller was employed.

The proposed system was evaluated against itself but without bolus adaptation. The UVa-Padova T1DM v3.2 system was used to carry out a three-month in silico study on 11 adult and 11 adolescent virtual subjects taking into account inter-and intra-subject variability of insulin requirements and uncertainty on carbohydrate intake.

Results

Overall, the closed-loop controller enhanced by an adaptive bolus calculator improves glycemic control when compared to its non-adaptive counterpart. In particular, the following statistically significant improvements were found (non-adaptive vs. adaptive). Adults: mean glucose 142.2±9.4 vs. 131.8±4.2 mg/dl; percentage time in target [70, 180] mg/dl, 82.0±7.0 vs. 89.5±4.2; percentage time above target 17.7±7.0 vs. 10.2±4.1. Adolescents: mean glucose 158.2±21.4 vs. 140.5±13.0 mg/dl; percentage time in target, 65.9±12.9 vs. 77.5±12.2; percentage time above target, 31.7±13.1 vs. 19.8±10.2. Note that no increase in percentage time in hypoglycemia was observed.

Conclusion

Using an adaptive meal bolus calculator within a closed-loop control system has the potential to improve glycemic control in type 1 diabetes when compared to its non-adaptive counterpart.

1. Introduction

Type 1 diabetes mellitus (T1DM) is an autoimmune condition characterized by elevated blood glucose levels due to the lack of endogenous insulin production. People with T1DM require exogenous insulin delivery to regulate glucose. Current therapies for T1DM management include the administration of multiple daily injections or continuous insulin infusion with pumps. However, such therapies are still suboptimal and require constant adjustment by the person with T1DM and carers. A closed-loop control system consisting of a continuous glucose sensor, an insulin pump and an algorithm that computes the required insulin dose at any instant [Trevitt 2015], has the potential to improve glucose control in people with T1DM.

Recent studies evaluating a closed-loop system for automatic glucose control in type 1 diabetes mellitus (T1DM), also referred to as artificial pancreas, have demonstrated safety and efficacy during in-clinic and ambulatory trials [Thabit 2015].

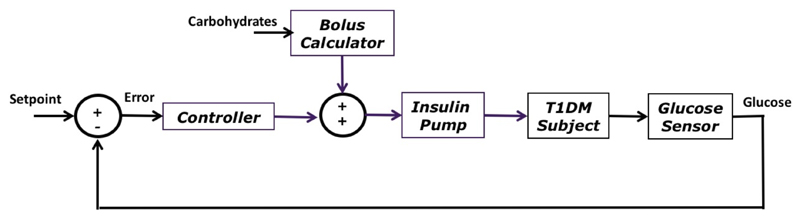
Ideally, a completely automated closed-loop control system would not require any user intervention, for example to announce meals, and would react in real-time to changes in blood glucose. However, delays in subcutaneous insulin absorption have led many investigators to include the use of a pre-meal insulin bolus within the artificial pancreas [Doyle 2014] (Figure 1). The calculation of such pre-meal insulin bolus is usually done by means of a simple bolus calculator [Schmidt 2014], found in most insulin pumps. However, accurately computing a meal bolus remains a challenging task due to the high variability of insulin requirements in T1DM [Visentin 2015] and the uncertainty in carbohydrate estimations [Brazeau 2013].

Figure 1.

Block diagram of a closed-loop system for glucose control incorporating a meal bolus calculator.

The utilisation of an adaptive meal-priming bolus within an artificial pancreas has previously been proposed by El-Khatib et al. [El-Khatib 2015] showing some encouraging clinical results relative to an entirely reactive system with no meal-priming boluses. Such adaptive meal-priming insulin bolus consists of automatically adjusting the size of breakfast, lunch, and dinner doses by administering 75% of the average prandial insulin provided for previous meals at that time of day. However, this method has the limitation that assumes that carbohydrate intakes are fairly similar every day, which is not always the case. It also does not take into consideration intra-subject insulin variability due to factors such as exercise, alcohol, stress, weather, hormones, and variation in macronutrient meal composition.

Recent work by Wang and colleges presents a clinical evaluation of a combination of Iterative Learning Control (ILC) and Model Predictive Control (MPC), referred to as learning-type MPC (L-MPC), to exploit the repetitive nature of glucose-meal-insulin dynamics [Wang 2017]. However, the L-MPC controller does not require user intervention (e.g. meal announcement), hence it is not directly comparable to the approach proposed in this manuscript.

Outside the context of the artificial pancreas, the concept of an adaptive bolus calculator has been proposed by Palerm et al. [Palerm 2007] by means of Run-to-Run control [Wang 2009]. Although showing some promising preliminary clinical results, this approach has the limitation of being very sensitive to meal composition due to the employed control law. In [Tuo 2015], Tuo et al. propose a similar technique based on a high order Run-to-Run control scheme. The problem with this approach is that the employed control law does not account for hypoglycemia. Similar to the work proposed by El-Khatib et. al [El-Khatib 2015], these two approaches do not consider factors affecting insulin requirements, other than circadian variations.

In this paper, we present a novel technique to automatically adjust the meal-priming bolus within an artificial pancreas. For this purpose, a Run-to-Run algorithm incorporating a new control law, which avoids some of the limitations of previously proposed techniques, is introduced. Then, Case-Based Reasoning [Aamodt 1994], an artificial intelligence technique which solve new problems based on the solutions of similar past problems, is employed to account for intra-subject insulin sensitivity variability.

The proposed technique is based on an existing adaptive bolus calculator, referred to as Advanced Bolus Calculator for Diabetes (ABC4D) [Herrero 2015a, Herrero 2015b, Pesl 2016a], which has been modified to fulfill the requirements of a closed-loop system for blood glucose control.

For evaluation purposes, a novel version of the clinically validated Imperial College Bio-inspired AP controller [Herrero 2012, Reddy 2014, Reddy 2015] (see Appendix A) and the UVa-Padova T1DM v3.2 system (T1DMS) simulation platform [Kovatchev 2009] were employed.

2. Materials and Methods

2.1. Insulin Bolus Calculator

A standard insulin bolus calculator [Schmidt 2014] is defined by the equation

$$B=\frac{CHO}{ICR}+\frac{\left(G_M-G_T\right)}{ISF}-IOB,$$ (1)

where B (U) is the total calculated bolus, CHO (g) is the estimated amount of ingested carbohydrates, ICR (g/U) is the insulin-to-carbohydrate-ratio, G_M (mg/dl) is the measured glucose at meal time, G_T (mg/dl) is the glucose target to be achieved, ISF (mg/dl/U) is the insulin sensitivity factor, and IOB (U) is the insulin-on-board, which represents an estimation of the remaining active insulin in the body [Schmidt 2014].

The parameters of a bolus calculator (ICR, ISF) can be manually adjusted based on the time of the day (i.e. breakfast, lunch, dinner), exercise, or variation in hormonal cycles. However, these adjustments are often crude approximations and are rarely revised by the users (subject with T1DM or carer) on a regular basis.

In order to provide the required adaptability within a bolus calculator to be able to cope with the significant intra-subject variability in T1DM management, a Case-Based Reasoning approach [Aamodt 1994] was proposed by Herrero and colleagues [Herrero 2015a].

2.2. An Adaptive Insulin Bolus Calculator

The proposed adaptive meal bolus calculator for closed-loop control is based on an existing technique referred to as Advanced Bolus Calculator for Diabetes Management (ABC4D) [Herrero 2015a, Herrero 2015b]. ABC4D has previously been validated in silico [Herrero 2015a, Herrero 2015b] and tested in clinical trials [Pesl 2016b, Reddy 2016].

ABC4D enhances currently existing bolus calculators by means of a combination of Case-Based Reasoning [Aamodt 1994] and Run-To-Run Control [Wang 2009]. Periodic use of continuous glucose monitoring (CGM) data is required in order to perform a retrospective optimization of the bolus calculator parameters as described in [Herrero 2015b].

Case-Based Reasoning

Case-Based Reasoning (CBR) is an artificial intelligence problem solving framework that solves a newly encountered problem, based on the information obtained from previously solved problems and stored as cases in a case-base. A case is defined by

$$Cas{e}_i=\left\{Proble{m}_i,Solutio{n}_i,Outcom{e}_i\right\}\text{,}$$ (2)

where Problem_i is the description of the problem to be solved (insulin dosing for a breakfast with 70g of carbohydrates and planned moderate exercise); Solutioni is the solution to Problemi (administered insulin dose, i.e. parameters ICR and ISF of the bolus calculator); and Outcome_i is the outcome resulting of applying Solution_i to Problemi (post-prandial excursion without hypoglycemia and mild hyperglycemia).

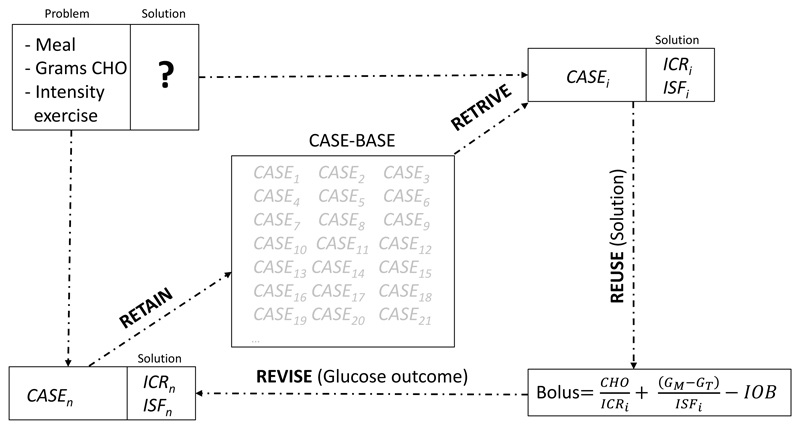
CBR is usually described in four steps: Retrieve the most similar cases to the problem to be solved from the case-base; Reuse the solutions of retrieved cases; Revise the outcome of the applied solution to the new problem; and Retain the new problem if its solution is considered useful for solving future problems [Aamodt 1994]. Figure 2 show the four steps of the CBR cycle (Retrieve, Reuse, Revise, Retain) applied to the problem of meal insulin dosing using a bolus calculator.

Figure 2.

CBR cycle (Retrieve, Reuse, Revise, Retain) applied to the problem of meal insulin dosing using a bolus calculator.

In ABC4D, cases are stored in a subject-specific case-base representing meal scenarios with significantly different insulin requirements (e.g. breakfast after exercise vs. dinner after watching a movie) and therefore, requiring a different meal insulin dose.

Cases are retrieved from the case-base by computing the Euclidian distance between the current problem and all the cases in the case-base and by selecting the case with the shorter distance [Herrero 2015a].

If the retrieved case is different from the current scenario (e.g. breakfast with exercise vs. breakfast with exercise), its solution is reused (Reuse step) by applying a set of simple rules to guarantee that the applied solution is safe (e.g. increase ICR and ISF by 30%) and a new case is created for the new scenario. If the retrieved case is equal to the current scenario, then no new case is created.

In order to perform the Revision step, the Run-to-Run algorithm proposed by Herrero et al. [Herrero 2015b] is employed, which adapt the solution of the retrieved, or newly created, case (i.e. ICR and ISF) when the glucose outcome is considered sub-optimal based on the analysis of the postprandial CGM measurements.

Note that, unlike the traditional CBR approach [Aamodt 1994] where the solutions of the cases in the case-base are static, in ABC4D, such solutions (ICR and ISF) can be adapted if considered to be sub-optimal. This strategy partially solves the so-called problem of cold-start in CBR [Quijano-Sánchez 2012] (i.e. insufficient cases in the case-base) by initializing the case-base with a small set of sub-optimal, but safe, cases and letting the system converge towards an optimal solution while adapting solutions of existing cases and adding new cases to the case-base.

Run-To-Run Algorithm

Run-To-Run (R2R) is a control methodology designed to exploit repetitiveness in the process that is being controlled [Wang 2009]. Its purpose is to enhance performance, using a mechanism of trial and error. The simplest formulation of R2R may be,

$$u_{k+1}=u_k+K\cdot error,$$ (3)

where u is the control action, K is a tuning gain and error is the tracking error defined as the difference between a measurement from the process and a set-point.

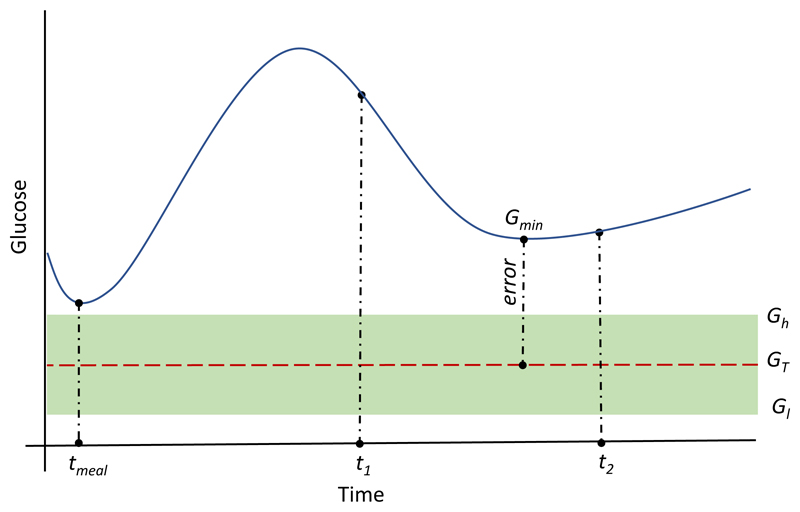
The R2R algorithm used in revision step of the CBR algorithm in ABC4D is based on the hypothesis that, if the meal insulin bolus is not optimal, this is going to be reflected on the minimal glucose value achieved over the postprandial period, which in subjects with T1DM lasts around 5–6 h after a meal [ADA 2001]. Then, the meal insulin bolus can be adjusted based on the error between the minimal post-prandial glucose concentration (G_min), obtained with a continuous glucose monitor over a predefined time window [t1, t2] (see Figure 3), and a glucose target (G_T) preselected by the user or healthcare professional, which corresponds to the same glucose target in the bolus calculator (Equation (1)).

Figure 3.

Graphical representation of the calculation of the error term (G_min- G_T) in Equation (4). t_meal corresponds to meal ingestion time.

Therefore, the adjusted bolus is calculated as

$$B_{k+1}=B_k+K\cdot \left(G_{\mathit{\text{min}}}-G_T\right),$$ (4)

where K·(G_min- G_T) is the extra insulin (B_extra1) that needs to be added (or subtracted) to the original bolus (B_k) in order to bring blood glucose levels back to the target (G_T), and K is a tuning gain defined as K=1/ISF.

In order to avoid unnecessary adaptations due to the inherent uncertainty in glucose management (e.g. sensor noise and carbohydrate estimation), a glucose target range [G_l, G_h] is defined where no adaptation is required if G_min falls within this range (see Figure 3). For the same reason, the second term of Equation (1) (i.e. correction bolus) is set to zero if the glucose measurement at meal time (G_M) falls within the glucose range [G_l, G_h]. Figure 3 graphically represents how the error term (G_min- G_T) in Equation (4) is calculated.

The proposed R2R algorithm for meal bolus adaptation is based on a second hypothesis that sustains that insulin-to-carbohydrate-ratio (ICR) and insulin sensitivity factor (ISF) are correlated [Walsh 2011] by the expression

$$ISF=\frac{1960ICR}{2.6W},$$ (5)

where W is the weight of the subject (lbs).

Thus, from Equation (1), the ICR parameter can be updated according to the equation

$$IC{R}_{k+1}=\frac{CHO+\frac{G-G_T}{(1960/2.6W)}}{(B_k+B_{extra1})+IOB}\cdot$$ (6)

However, Equation (6) is not fully suited to be used within the context of a closed-loop (CL) system for blood glucose control. Note that the CL controller can compensate for the lack of meal-priming bolus and bring glucose levels within the target range [G_l, G_h] over the time window [t1, t2], but the post-prandial glucose peak can still be significantly sub-optimal. Nonetheless, assuming that the CL controller is correctly tuned, the ABC4D R2R metric is still valid when G_min falls below the target range. If G_min falls within or above the target range, a new metric for adjusting ICR is required.

The new proposed metric is based on the hypothesis that, assuming that the CL controller is appropriately tuned, the insulin delivered by the CL controller during the postprandial period over the basal insulin, is insulin that should have been delivered by the meal-priming bolus. Thus, the bolus calculator parameters can be updated based on this additional insulin.

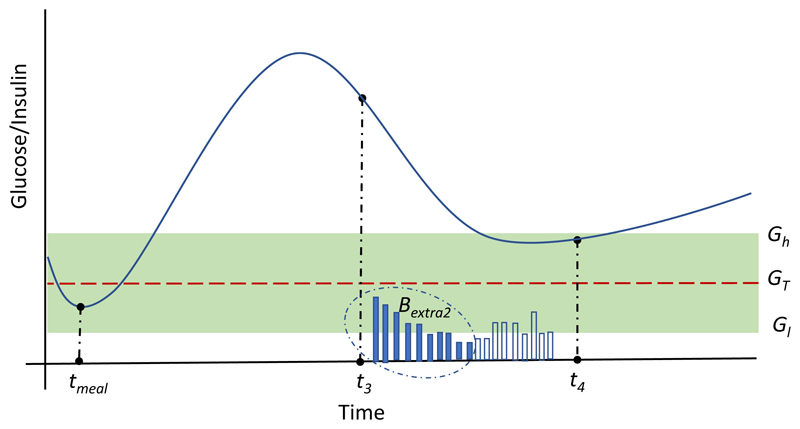
Let the insulin delivered by the CL controller over the basal insulin during a predefined postprandial time window [t3, t4] be defined as

$$B_{\mathit{\text{extra}}2}=\mathit{\text{min}}\left({\displaystyle {\sum }_{t3}^{t4}D(k)},k_2\cdot B\right),$$ (7)

where D(k) are the insulin doses delivered by the CL controller when glucose levels G(k) are above the glucose target range (G(k)>Gh), and K₂ a tunable gain used to saturate B_extra2 to a maximum allowed dose of K₂·B. Figure 4 graphically represents how B_extra2 in Equation (7) is calculated. Note that postprandial time windows [t1, t2] and [t3, t4] are tunable parameters and might have different lengths.

Figure 4.

Graphical representation of the calculation of the term B_extra2 in Equation (7). Solid and empty vertical bars represent insulin doses D(k) delivered by the CL controller when G(k)>Gh and G(k)<Gh respectively.

Then, the updated ICR (ICR_k+1), and consequently ISF_k+1, can be easily obtained by replacing B_extra1 by B_extra2 in Equation (6). Note that, since the objective is to bring glucose levels within the target range [G_l, G_h], only the insulin delivered over G>G_h is considered in Equation (7). Finally, to filter potential outliers, the new ICR is obtained by computing the average of two consecutive ICR adaptations and the current value. Therefore, actual adaptations are only carried out every two adaptations for the same meal case.

Finally, in order to integrate the presented adaptive meal bolus calculator (ABC) within a closed-loop (CL) controller two additional considerations need to be taken into account. First, since both the CL controller and the ABC include mechanisms to prevent insulin overdosing (i.e. insulin-on-board), the insulin-on-board (IOB) term from Equation (1) and Equation (6) were omitted. Second, since the CL controller is meant to correct hyperglycemia during fasting condition, the correction bolus term from Equation (1) (second term) was omitted when G_M> G_l.

The reader is referred to Appendix A for details about the Imperial College Artificial Pancreas controller employed in this study.

2.3. In Silico Evaluation under intra-day variability

The latest version of the UVa-Padova T1DM simulator (v3.2) [Kovatchev 2009] was used to evaluate the proposed adaptive bolus calculator for closed-loop controllers. 11 adult subjects and 11 adolescent subjects were used for this purpose. The chosen basal insulin infusion rate for the virtual subjects was the one provided by the default insulin therapy of the simulator. The selected CGM and insulin pump models to perform the simulations were the Dexcom G4 and Deltec Cozmo. A three-month scenario was selected in order to leave enough time to the meal bolus adaptation mechanism to converge. The selected daily pattern of carbohydrate dose intake was 7am (60g), 12pm (100g) and 6pm (80g).

In order to test the benefits of the proposed technique, the Imperial College Artificial Pancreas (AP) controller with the adaptive meal bolus calculator (ABC-AP) was evaluated against the same controller without meal bolus adaptation (AP).

Intra-day variability

Intra-day variability was introduced to the simulator by modifying some of the parameters of the model described in [Dalla Man 2007]. In particular, meal variability was emulated by introducing meal-size variability (CV=10%), meal-time variability (STD=20) and uncertainty in the carbohydrate estimation (uniform distribution between -30% and +20%) [Brazeau 2013]. Meal absorption rate (k_abs) and carbohydrate bioavailability (f) were considered to be ±30% and ±10% respectively. The 11 meals corresponding to each cohort were randomly assigned at each meal intake. Intra-subject variability in insulin absorption model parameter (k_d, k_a1, k_a2) was assumed ±30% [Haidar 2013]. Insulin sensitivity parameters (V_mx, K_p3) were assumed to vary along the day following the sinusoidal pattern

$$p\left(t\right)=p_0+0.3\cdot p_0\mathit{\text{sin}}\left(2\frac{\pi }{24.60}\right)t+2\pi \cdot \mathit{\text{RND}},$$ (7)

where p(t) is the corresponding time varying parameter (i.e. V_mx or k_p3); p0 is the default parameter value in the simulator; and RND is a randomly uniformly generated number between 0 and 1.

Note that despite all the variability introduced in the simulator, only three different cases were required within the CBR algorithm (i.e. breakfast, lunch and dinner).

Controller tuning

For this in silico study, the following tuning values were considered for the evaluation of the proposed algorithm: G_l = 80mg/dl; G_h=120 mg/dl; G_sp=100 mg/dl; t₁=2h; t₂=5h, t₃=2h; t₄=4h, K₂=0.2. The rational for choosing such time windows was the fact that it usually takes about 2 hours to be able to say that a meal bolus is not enough to cover a meal due to the slow insulin pharmacokinetics (i.e. insulin-on-board), and that a postprandial glucose excursion for a standard mixed meal lasts around 5 hours [ADA 2001]. Note that these values could be individualized and such individualization could lead to superior glycemic outcomes. However, we wanted to prove that the proposed technique is still valid for a generic tuning.

Regarding the CBR algorithm, since only three scenarios (i.e. cases) were considered (breakfast, lunch and dinner), the potential benefit of this algorithm could not be fully evaluated. Finally, the Imperial College Artificial Pancreas (AP) controller was tuned as described in Appendix A.

Evaluation metrics

The following glycemic metrics, which are widely accepted by the artificial pancreas community to evaluate glucose controllers [Maahs 2016], were selected for comparison purposes: mean blood glucose (BG); percentage time in glucose target range [70,180] mg/dl (%inT); percentage time below target (i.e. hypoglycemia) (%<T); percentage time above target (i.e. hyperglycemia) (%>T); glycemic variability indices: low blood glycemic index (i.e. risk of hypoglycemia) (LBGI), high blood glycemic index (i.e. risk of hyperglycemia) (HBGI), risk index (RI=LBGI+HBGI); and daily average of insulin delivered in units of insulin (TDI).

3. Results

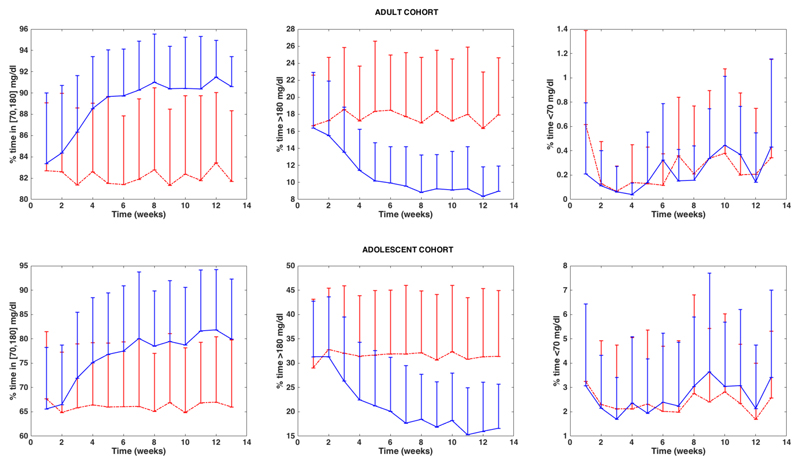
Table 1 and Table 2 show the results corresponding to the 11 adults and 11 adolescents for each one of the evaluated control strategies (AP vs. ABC-AP). Figure 2 shows a comparison between AP and ABC-AP of the weekly evolution of three of the evaluated glycemic metrics (%inT, %<T and %>T) for the two studied cohorts.

Table 1. Glycemic results corresponding to the 11 adult subjects.

	BG	%inT	%<T	%>T	RI	LBGI	HBGI	TDI
AP	142.2±9.4	82.0±7.0	0.21±0.36	17.7±7.0	3.7±1.3	0.14±0.12	3.6±1.3	45.8±10.1
ABC-AP	131.8±4.2	89.5±4.2	0.21±0.18	10.2±4.1	2.4±0.69	0.19±0.06	2.2±0.6	48.5±10.4
p	<0.001	<0.001	0.99	<0.001	<0.005	0.12	<0.005	0.002

Table 2. Glycemic results corresponding to the 11 adolescent subjects.

	BG	%inT	%<T	%>T	RI	LBGI	HBGI	TDI
AP	158.2±21.4	65.9±12.9	2.2±2.7	31.7±13.1	7.8±3.9	0.73±0.82	7.0±3.9	35.0±8.8
ABC-AP	140.5±13.0	77.5±12.2	2.5±2.4	19.8±10.2	5.2±3.1	0.94±0.84	4.2±2.4	38.3±10.2
p	<0.001	<0.001	0.6446	<0.001	<0.001	0.4	<0.001	<0.001

Figure 2.

Weekly evolution of the glycemic metrics %inT, %<T and %>T for the adult cohort (above) and the adolescent cohort (below) corresponding the AP controller without meal bolus adaptation (dashed red line) and the AP controller with meal bolus adaptation (ABC-AP) method (solid blue line). Error bars represent the standard deviation.

4. Discussion

Integrating an adaptive meal bolus calculator within the Imperial College Artificial Pancreas controller (ABC-AP) significantly improves all the evaluated glycemic outcomes in a virtual T1D population (11 adults + 11 adolescents) when compared against the Imperial College AP without bolus adaptation over a three-month scenario with intra-day variability. It is important to note that the proposed adaptive meal bolus calculator is independent of the closed-loop controller employed and could be used within other artificial pancreas systems. It is also worth noting that the significant reduction in hyperglycemia was achieved without any increase in hypoglycemia – indeed in both the adult and adolescent there was a non-significant reduction in time spent below target.

Despite the significant intra-subject variability and uncertainty in carbohydrate intake estimation, the closed-loop controller was able to cope avoid remarkably well with hypoglycemia. Therefore, the inclusion of the adaptive meal bolus calculator did not introduce any improvement regarding time spent in hypoglycemia.

Although statistically significant, the increase in total daily insulin delivered was not dramatically relevant (i.e. 3 U per day on average). This is an indicator that for this study, the most important factor for improving glycemic control is the way insulin was delivered and not the total amount.

When analyzing the weekly evolution of the evaluated glycemic metrics, it was observed that glycemic metrics take about 8 weeks to converge without significant oscillations towards a steady state value and remain fairly stable along the simulation. This convergence rate could be increased by using a less conservative strategy when saturating/filtering the insulin-to-carbohydrate ratio adaptation.

In a real-life scenario, the convergence rate might take longer due to the consideration of more cases representing other scenarios such as exercise, alcohol consumption, hormone cycles or stress.

Thanks to the additional intra-day variability introduced in the simulator, it was possible to evaluate the robustness of the proposed technique under conditions which might be not too far from a real-life scenario. Clinical trials to evaluate such a technique are currently in preparation.