Tuning the Circumference of Six-Porphyrin Nanorings

Abstract

Most macrocycles are made from a simple repeat unit, resulting in high symmetry. Breaking this symmetry allows fine-tuning of the circumference, providing better control of the host–guest behavior and electronic structure. Here, we present the template-directed synthesis of two unsymmetrical cyclic porphyrin hexamers with both ethyne (C2) and butadiyne (C4) links, and we compare these nanorings with the symmetrical analogues with six ethyne or six butadiyne links. Inserting two extra carbon atoms into the smaller nanoring causes a spectacular change in binding behavior: the template affinity increases by a factor of 3 × 10⁹, to a value of ca. 10³⁸ M^–1, and the mean effective molarity is ca. 830 M. In contrast, removing two carbon atoms from the largest nanoring results in almost no change in its template-affinity. The strain in these nanorings is 90–130 kJ mol^–1, as estimated both from DFT calculation of homodesmotic reactions and from comparing template affinities of linear and cyclic oligomers. Breaking the symmetry has little effect on the absorption and fluorescence behavior of the nanorings: the low radiative rates that are characteristic of a circular delocalized S₁ excited state are preserved in the low-symmetry macrocycles.

Introduction

Symmetry confers beauty and simplicity. Most large synthetic macrocycles are constructed from a repeating monomer unit, resulting in a highly symmetric structure (C_n or D_nh), which expedites their synthesis and spectroscopic characterization; for example, it gives simple NMR spectra.¹ Conversely, a less symmetrical design brings structural versatility: it allows the diameter of the macrocycle to be adjusted in smaller increments in order to optimize binding to a specific guest. In π-conjugated macrocycles, if the singlet electronic excited state is delocalized over the whole ring, high symmetry makes the S₀–S₁ transition forbidden; thus, reducing the symmetry is expected to increase the radiative rate and increase the fluorescence quantum yield.^2,3 Previously, we reported the template-directed synthesis of two 6-fold symmetric cyclic porphyrin hexamers, c-P6[b₆] and c-P6[e₆], linked via butadiyne (C4) and ethyne (C2) bridges, using templates T6 and T6*, respectively (Figure 1).⁴⁻⁶ Here, we show that low-symmetry (C_2v) versions of these macrocycles, c-P6[b₅e] and c-P6[be₅], can be synthesized using the same T6 and T6* templates. We demonstrate that the ability to adjust the circumference, by adding or removing two carbon atoms, has a dramatic effect on the binding behavior of these nanorings. In contrast, the changes in symmetry are too subtle to have a strong effect on the radiative rates of the singlet excited states, and the photophysical behavior of the parent structures is preserved.

Figure 1.

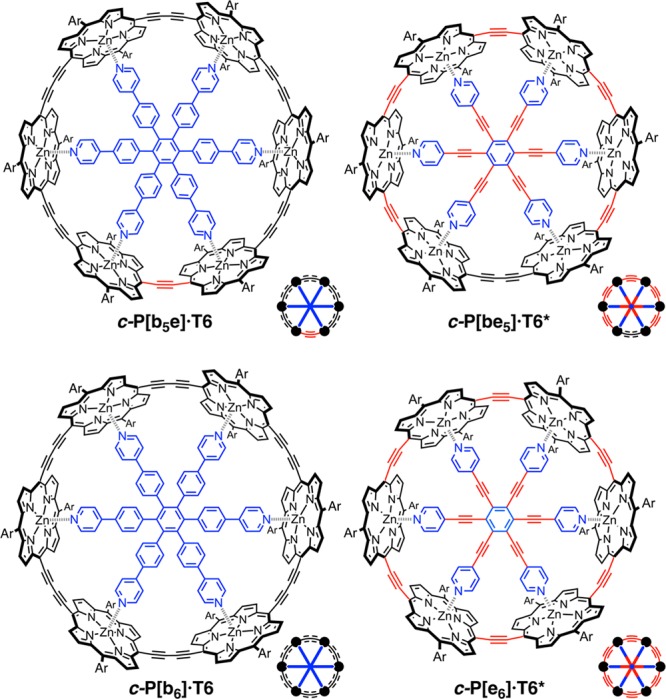
Molecular structures, schematic representation and labels of the porphyrin nanorings used throughout this study. The label in brackets indicates the number of butadiyne [b_x] or ethylene [e_y] linkages present in the nanoring. Ar = 3,5-bis(trihexylsilyl)phenyl.

Results and Discussion

Molecular Modeling

Density functional theory (DFT; B3LYP, 6-31G* basis set, in vacuum) was used to calculate optimized geometries of the free nanorings and their template complexes, to estimate the level of strain, and to predict which templates would be effective for nanoring synthesis.⁷ The strain in each nanoring (ΔH_strain) was estimated by calculating the free energy change for a homodesmotic reaction:⁸ cyclic hexamer + linear dimer → linear octamer. The results (Table 1) show a gradual reduction in strain with ring expansion.

Table 1. Calculated Strains and Geometries from DFT^a.

molecule	ΔHstrain (kJ mol–1)	RZn (Å)	RN,ideal (Å)	RN – RN,ideal (Å)
c-P6[e6]	131	10.33	7.81	0.49 (T6*)
c-P6[be5]	115	10.72	8.20	0.10 (T6*)
c-P6[b5e]	105	12.38	9.86	0.17 (T6)
c-P6[b6]	100	12.82	10.30	–0.27 (T6)

^aB3LYP/6-31G*; aryl groups replaced by H to facilitate calculations.

The complementarity of the templates was estimated from the average distances of the six zinc atoms from the centroid (R_Zn) for the template-free nanorings (Table 1). The ideal template radius (R_N,ideal) for each nanoring was calculated by subtracting the crystallographic out-of-plane distance of the zinc atom (0.37 Å) and the Zn–N(pyridine) bond length (2.15 Å) from R_Zn.⁵ The calculated radii of T6 and T6* (R_N) are 10.03 and 8.30 Å, respectively, allowing us to calculate the misfit (R_N – R_N,ideal) as listed in Table 1. These data lead to the surprising conclusion that, if we ignore the angular deviation from D_6h symmetry in the low-symmetry nanorings, then T6* and T6 are expected to fit the unsymmetrical rings better than the symmetrical rings for which they were originally designed.^4,6T6 is slightly too small for c-P6[b₆] and slightly too big for c-P6[b₅e], while T6* is slightly too big for c-P6[be₅] and substantially too big for c-P6[e₆].

The DFT-optimized geometries of the nanoring–template complexes (Figure 2) show that when the template is too large for the cavity, it adopts a domed conformation, rising above the plane of the nanoring, as seen clearly in c-P6[e₆]·T6* and to a more subtle extent in c-P6[b₅e]·T6.

Figure 2.

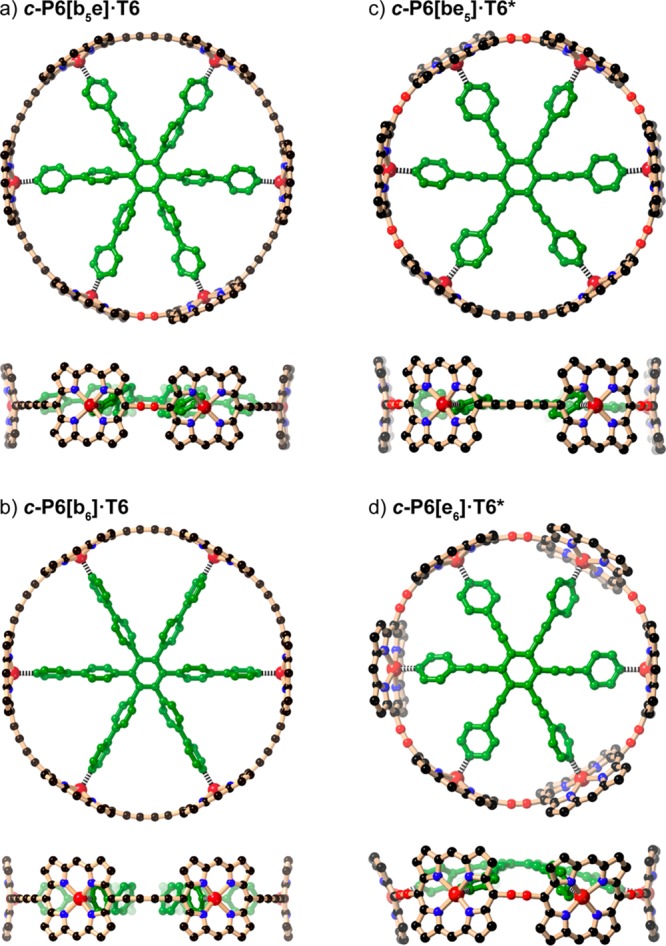
DFT-calculated geometries of (a) c-P6[b₅e]·T6, (b) c-P6[b₆]·T6, (c) c-P6[be₅]·T6*, and (d) c-P6[e₆]·T6* (two orthogonal views of each complex; B3LYP/6-31G*, aryl groups replaced by H to facilitate geometry optimization).

Synthesis

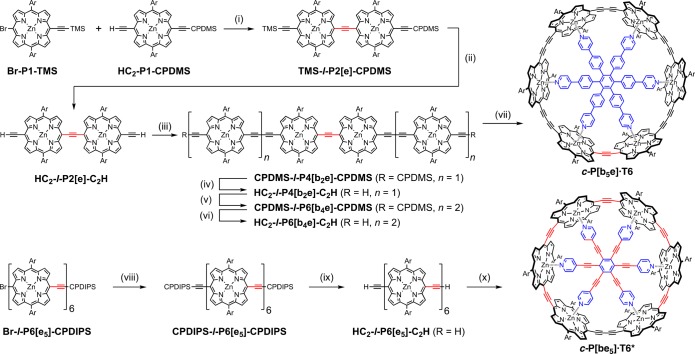
The unsymmetrical nanorings were prepared from linear porphyrin hexamers, as summarized in Scheme 1. The key intermediate in the synthesis of c-P6[b₅e] is the C2-linked porphyrin dimer TMS-l-P2[e]-CPDMS, which was prepared by Sonogashira coupling of monomers Br-P1-TMS and HC₂-P1-CPDMS. This combination of silicon protecting groups with different polarities⁹ was used to enable the C2-linked dimer to be separated from any C4-linked dimer byproduct, CPDMS-l-P2[b]-CPDMS, produced by oxidative Glaser coupling of HC₂-P1-CPDMS. Traces of the butadiyne-linked byproduct must be removed, otherwise they lead to contamination of c-P6[b₅e] with symmetric c-P6[b₆], which is inseparable. Complete deprotection of TMS-l-P2[e]-CPDMS followed by palladium-catalyzed oxidative coupling with excess HC₂-P1-CPDMS yielded porphyrin tetramer CPDMS-l-P4[b₂e]-CPDMS in 50% yield. This deprotection/coupling sequence was repeated to give porphyrin hexamer CPDMS-l-P6[b₄e]-CPDMS in good yield (68% over two steps). Deprotection of the hexamer followed by palladium-catalyzed oxidative coupling in the presence of T6 template gave the target porphyrin nanoring c-P6[b₅e]·T6 in 37% yield.

Scheme 1. Synthesis of c-P6[b₅e]·T6 and c-P6[be₅]·T6*.

Reaction conditions: (i) Pd₂(dba)₃, AsPh₃, 64%; (ii) TBAF, 94%; (iii) HC₂-P1-CPDMS, Pd(PPh₃)₂Cl₂, CuI, 1,4-benzoquinone, 50%; (iv) TBAF, 100%; (v) HC₂-P1-CPDMS, Pd(PPh₃)₂Cl₂, CuI, 1,4-benzoquinone, 68%; (vi) TBAF, 100%; (vii) T6, Pd(PPh₃)₂Cl₂, CuI, 1,4-benzoquinone, 37%; (viii) CPDIPS-acetylene, Pd(PPh₃)₂Cl₂, CuI, 95%; (ix) TBAF, 96%; (x) T6*, Pd(PPh₃)₂Cl₂, CuI, 1,4-benzoquinone, 25%. Ar = 3,5-bis(trihexylsilyl)phenyl. TMS = SiMe₃. CPDMS = SiMe₂(CH₂)₃CN. CPDIPS = Si(i-Pr)₂(CH₂)₃CN. The syntheses of the starting materials are detailed in the SI.

The smaller unsymmetrical nanoring c-P6[be₅]·T6* was synthesized in 25% yield by palladium-catalyzed oxidative coupling of the linear C2-linked hexamer HC₂-l-P6[e₅]-C₂H in the presence of the T6* template. This linear hexamer was prepared from a known bromoporphyrin hexamer⁶ by Sonogashira coupling as shown in Scheme 1. The unsymmetrical nanoring c-P6[be₅] is easier to synthesize than c-P6[e₆] both because oxidative Glaser coupling is a more efficient reaction than Sonogashira coupling, for the final cyclization step, and because the T6* template matches the cavity of c-P6[be₅] better than that of c-P6[e₆] (Table 1).

NMR Spectroscopy

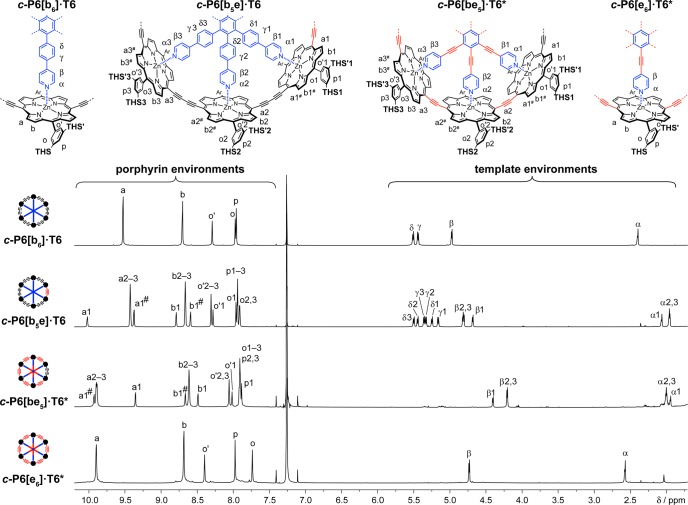
The ¹H NMR spectra of the four nanoring–template complexes are compared in Figure 3. Resonances from β-pyrrole protons nearest to an ethyne bridge are easy to identify by virtue of their high chemical shifts (ca. 10 ppm).¹⁰ The spectra were fully assigned using 2D NMR techniques (as detailed in the SI). The complexes c-P6[b₆]·T6 and c-P6[e₆]·T6* have D_6h symmetry on the NMR time scale, as reported previously,⁴⁻⁶ whereas c-P6[b₅e]·T6 and c-P6[be₅]·T6* have effective C_2v symmetry, resulting in splitting of the porphyrin and template resonances, as expected. The shielding of the α- and β-pyridine template protons is substantially greater in c-P6[be₅]·T6* than in c-P6[e₆]·T6*, which probably reflects the tighter N–Zn interaction and less distorted geometry of c-P6[be₅]·T6* (Figure 2c,d).

Figure 3.

Partial ¹H NMR spectra of c-P6[b₆]·T6, c-P6[b₅e]·T6, c-P6[be₅]·T6*, and c-P6[e₆]·T6* (700 MHz, CDCl₃, 298 K).

Stabilities of Template Complexes: UV–vis–NIR and NMR Titrations

The stabilities of the nanoring–template complexes c-P6[b₆]·T6, c-P6[b₅e]·T6, c-P6[be₅]·T6*, and c-P6[e₆]·T6* were determined by UV–vis–NIR titration, in toluene at 298 K, and compared with the corresponding complexes of linear porphyrin hexamers HC₂-l-P6[b₅]-C₂H·T6, HC₂-l-P6[b₄e]-C₂H·T6, and HC₂-l-P6[e₅]-C₂H·T6*. All of the formation constants, K_f, are too high to be determined by direct titration, so they were measured by denaturation titrations using a monovalent ligand to displace the template (pyridine or N-methylimidazole; for details, see the SI).^4,11 Some examples of denaturation titration curves are plotted in Figure 4, showing that the stabilities of the nanoring complexes increase in the order c-P6[e₆]·T6* < c-P6[b₅e]·T6 < c-P6[b₆]·T6 < c-P6[be₅]·T6*. Nonlinear curve fitting of the titration data gave the values of log K_f listed in Table 2 (see the SI for details). The nanorings all bind the templates much more strongly than the corresponding linear hexamers. Inserting two carbon atoms into c-P6[e₆] to give c-P6[be₅] results in a colossal increase in affinity for T6*; log K_f increases from 29.0 to 38.5.

Figure 4.

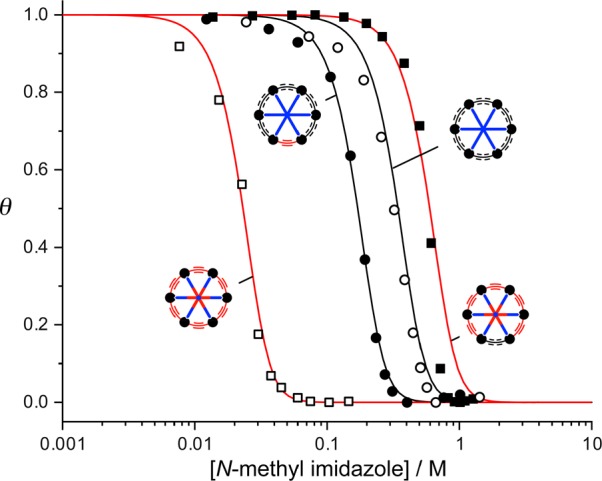
Denaturation curves for titration of c-P6[b₆]·T6, c-P6[b₅e]·T6, c-P6[be₅]·T6*, and c-P6[e₆]·T6* with N-methyl imidazole. θ is the mole fraction of nanoring bound to the template, estimated as θ = (A – A_f)/(A_i – A_f), where A, A_i, and A_f are absorption, initial absorption, and final absorption, respectively. Titrations were carried out in toluene at 298 K with a nanoring concentration of ca. 1 μM.

Table 2. Thermodynamic Parameters from UV–vis–NIR Titrations.

porphyrin hexamer	ligand	log Kf	log EM	ΔGf (kJ mol–1)	ΔGstrain (kJ mol–1)
HC2-l-P6[e5]-C2H	T6*	15.8 ± 0.3	–1.6 ± 0.1	–90 ± 2
HC2-l-P6[b4e]-C2H	T6	19.9 ± 0.3	–1.7 ± 0.1	–113 ± 2
HC2-l-P6[b5]-C2H	T6	20.8 ± 0.3	–1.5 ± 0.1	–119 ± 2
c-P6[e6]	T6*	29.0 ± 0.3	1.0 ± 0.1	–166 ± 2	76 ± 3 (cf. HC2-l-P6[e5]-C2H)a
c-P6[be5]	T6*	38.5 ± 0.3	2.9 ± 0.1	–220 ± 2	130 ± 3 (cf. HC2-l-P6[e5]-C2H)
c-P6[b5e]	T6	35.6 ± 0.3	1.4 ± 0.1	–203 ± 2	90 ± 3 (cf. HC2-l-P6[b4e]-C2H)
c-P6[b6]	T6	37.0 ± 0.3	1.7 ± 0.1	–211 ± 2	92 ± 3 (cf. HC2-l-P6[b5]-C2H)

^aThe poor complementary between c-P6[e₆] and T6* means that this value does not accurately reflect the strain in c-P6[e₆].

The level of chelate cooperativity^12,13 in the porphyrin hexamer template complexes was evaluated by calculating the effective molarities, EM, by comparing the stability of each complex with that of a single-site reference interaction, using eq 1

1

where EM is the geometric mean of the effective molarities for five intramolecular interactions, K_chem is the statistically corrected formation constant of the hexamer–template complex (K_chem = K_f/768), and K₁ is the statistically corrected binding constant of a monovalent reference ligand for a zinc porphyrin monomer. We use 4-phenylpyridine (K₁ = 1.7 × 10⁴ M^–1) as a reference for T6 and 4-phenylethynylpyridine (K₁ = 3.2 × 10³ M^–1) as a reference for T6*. The values of log EM listed in Table 2 highlight the exceptionally high chelate cooperativity of the c-P6[be₅]·T6* complex; log EM = 2.9 ± 0.1; EM = 830 ± 190 M. This is among the highest effective molarities found for any noncovalent supramolecular complex.¹³⁻¹⁵

The difference in formation constant between c-P6[b₆]·T6 and c-P6[b₅e]·T6 is surprisingly subtle. Presumably, the weaker binding of c-P6[b₅e] reflects its lack of D_6h symmetry because, according to our DFT calculations, its size-complementarity is better than that of c-P6[b₆] (Table 1). We carried out a ¹H NMR experiment to check the relative affinities of c-P6[b₆] and c-P6[b₅e] for T6 in CDCl₃. The competition equilibrium constant K_C is defined as shown in Figure 5 and eq 2. The data from UV–vis–NIR denaturation titrations (Table 2) indicate that log K_C = 1.4 ± 0.4 in toluene at 298 K.

2

A 1:1 mixture of c-P6[b₆]·T6 and c-P6[b₅e] was dissolved in CDCl₃ and N-methylimidazole was added to catalyze exchange of the template between the two nanorings. After equilibrium had been established, the ratio of c-P6[b₆]·T6 to c-P6[b₅e]·T6 was estimated by integration of the ¹H NMR spectrum (see the SI for details). Within experimental error, the same mole ratio of complexes was formed by starting from a 1:1 mixture of c-P6[b₆] and c-P6[b₅e]·T6, confirming that this ratio reflects the position of thermodynamic equilibrium. At equilibrium, the [c-P6[b₆]·T6]/[c-P6[b₅e]·T6] ratio is 1.23 ± 0.10, giving K_C = 1.5 ± 0.2 (in CDCl₃ at 298 K).

Figure 5.

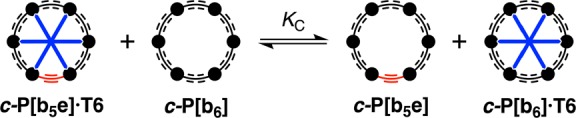
Position of this equilibrium was probed by ¹H NMR spectroscopy to measure the relative affinities of c-P6[b₆] and c-P6[b₅e] for T6.

The strain energy in a porphyrin nanoring (ΔG_strain) can be estimated from the difference in binding energy of the template with the corresponding cyclic and linear oligomers, as expressed by eqs 3.^4,16

3

The values of ΔG_strain calculated in this way for c-P6[be₅], c-P6[b₅e], and c-P6[b₆] (Table 2) are similar to the strain enthalpies from DFT (ΔH_strain, Table 1), indicating that the main cause for the weaker binding of the linear oligomers is the enthalpy cost of bending the linear oligomer into a cyclic conformation. This analysis assumes that there is no significant change in conformation, or increase in strain, when the nanoring binds the template and that the strain in the bound linear oligomer is essentially the same as the strain in the nanoring. Equation 3 does not provide a good estimate of the strain if the template and/or nanoring undergo deformation on complexation, as is the case when c-P6[e₆] binds T6*; here, the low value of ΔG_strain reflects the poor shape complementarity between the nanoring and the template.

Photophysical Behavior

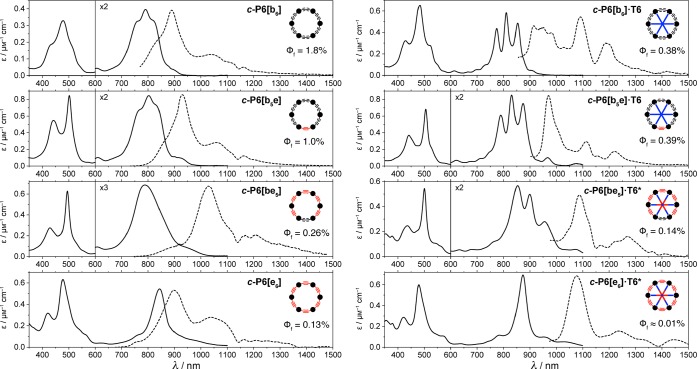
The absorption and fluorescence spectra of the nanorings and their template complexes are compared in Figure 6. Fluorescence lifetimes, quantum yields, and radiative rates are listed in Table 3.¹⁷ The spectra of c-P6[b₆] and c-P6[b₅e] are very similar (with and without bound T6). There is a larger difference between the spectra of c-P6[e₆] and c-P6[be₅], which probably reflects the greater strain in these complexes and the severe dome-shaped distortions in c-P6[e₆]·T6* (Figure 2d). Data for a typical linear hexamer, THS-l-P6[b₅]-THS, are also included in Table 3, for comparison. Linear conjugated porphyrin oligomers of this type generally have high radiative rates and fluorescence quantum yields.^17,18 All of the nanorings have much lower fluorescence quantum yields and radiative rates than linear oligomers, as would be expected for a forbidden S₁–S₀ transition in a symmetrical circular π-system.^2,3,17 Comparison of the radiative rates for c-P6[e₆] and c-P6[be₅] suggests, that in this case, lowering the symmetry increases the oscillator strength, but in general, the reduction in symmetry seems to be too subtle to have a strong effect on the photophysical behavior.

Figure 6.

Absorption (black lines) and fluorescence (dashed lines) spectra at 298 K of (left) c-P6[b₆], c-P6[b₅e], c-P6[be₅], c-P6[e₆] in toluene containing 1% pyridine and (right) c-P6[b₆]·T6, c-P6[b₅e]·T6, c-P6[be₅]·T6*, and c-P6[e₆]·T6* in toluene. Fluorescence quantum yields (Φ_f) are given in %. The dip in the fluorescence spectra at around 1140 nm is due to absorption by the solvent.

Table 3. Fluorescence Lifetimes, Quantum Yields, and Radiative Rates^a.

compd	τf (ns)	Φf	krad (μs–1)
c-P6[e6]	0.49	0.0013	2.6
c-P6[be5]	0.28	0.0026	9.4
c-P6[b5e]	0.44	0.010	23
c-P6[b6]	0.51	0.018	35
c-P6[be5]·T6*	0.22	0.0014	6.3
c-P6[b5e]·T6	0.32	0.0039	12
c-P6[b6]·T6	0.34	0.0038	11
THS-l-P6[b5]-THS	0.70	0.28	400

^aAll measurements were carried out in toluene (containing 1% by volume of pyridine for the template-free nanorings to suppress aggregation). Fluorescence lifetimes were measured using excitation at 810 nm and detection at 1050 nm. Fluorescence quantum yields were measured using THS-l-P6[b₅]-THS as a standard.¹⁷ Radiative rates are calculated as k_rad = Φ_f/τ_f.

Conclusions

The template-directed synthesis of unsymmetrical porphyrin nanorings, with both ethyne (C2) and butadiyne (C4) links, opens up a new dimension in the investigation of conjugated porphyrin arrays.^10,19,20 Inserting two carbon atoms into the smallest nanoring, c-P6[e₆], causes a spectacular increase in its affinity for the template T6*. The binding constant increases by a factor of 3 × 10⁹ to a value of ca. 10³⁸ M^–1, and the mean effective molarity is ca. 830 M. Changing the size and symmetry has little effect on the absorption and fluorescence behavior of the nanorings. All the nanorings have much lower radiative rates than the corresponding linear oligomers, which implies that the S₁ excited state is delocalized around the circular π-system.

This work provides a dramatic demonstration of the importance of structural complementarity and preorganization in multivalent molecular recognition.^11,21 Nanoring–template binding constants can be tremendously sensitive to a geometrical mismatch, particularly if the template is too big for the cavity, as in c-P6[e₆]·T6*. Even though T6* does not fit well in the cavity of c-P6[e₆], it is still an effective template for directing the formation of this nanoring, probably because a template needs to be complementary to the transition state for cyclization, rather than complementary to the product.⁷ This study also illustrates a new approach to estimating the strain in macrocyclic receptors by comparing their guest affinities with those of acyclic analogues. Strain-free energies determined by this method (ΔG_strain, Table 2) agree remarkably well with strain enthalpies from DFT calculation of homodesmotic reactions (ΔH_strain, Table 1) in every case except that of the c-P6[e₆]·T6* complex where there is poor shape complementarity. This shows that the main barrier for bending a linear oligomer into a circular conformation is enthalpic rather than entropic.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.9b02965.

• Synthetic procedures and characterization data; assignment of NMR spectra; UV–vis–NIR titrations; NMR competition experiments; photophysical characterization; computational chemistry (PDF)

• DFT calculations (ZIP)

Author Contributions

^§ R.H., L.T., H.-W.J., and M.R. contributed equally.

The authors declare no competing financial interest.