Elastography of multicellular spheroids using 3D light microscopy

Abstract

We have demonstrated a new method of 3D elastography based on 3D light microscopy and micro-scale manipulation. We used custom-built micromanipulators to apply a mechanical force onto multicellular tumor spheroids (200-300 µm in size) and recorded the induced compression with a differential interference contrast (DIC)/confocal microscope to obtain a 4D (x, y, z, and indentation steps) image sequence. Deformation analysis made through 3D pattern tracking without using fluorescence revealed 3D structural and spatial heterogeneity in tumor spheroids. We observed a 20-30 µm-sized spot of locally-induced large deformation within a tumor spheroid. We also found solid fibroblast cores formed in a tumor-fibroblast co-culture spheroid to be stiffer than surrounding cancer cells, which would not have been discovered using only conventional fluorescence. Our new method of 3D elastography may be used to better understand structural composition in multicellular spheroids through analysis of mechanical heterogeneity.

1. Introduction

Elastography is an imaging modality used to visualize the internal elasticity distribution of tissues. It is most commonly realized with ultrasound imaging platforms and is used to correlate the tissue elasticity with diagnostic information about the presence or status of disease [1]. Elastography can be divided into two main types: strain-imaging and shear wave. Strain-imaging elastography, or strain elastography, can determine relative differences in stiffness by measuring the displacement resulting from compression stimuli [2]. This method is based on the idea that the distribution of strain (percentage of deformation to the initial dimension) under known mechanical stress is an indication of the internal elasticity map, where softer tissue regions show larger strains than stiffer regions. Shear wave elastography can determine the absolute modulus of elasticity of a sample by measuring the velocity of an applied shear wave. One state-of-the-art shear wave elastography method, which uses a vibrating micropipette to mechanically induce elastic waves, has demonstrated the ability to map internal cell structures of a mouse oocyte, but requires the use of a high-speed camera to record images at 200,000 frames per second [3]. Current imaging methods, other than ultrasound imaging, include optical coherence tomography (OCT) [4] and magnetic resonance imaging (MRI) [5,6]. In particular, the elastography based on OCT is termed optical coherence elastography (OCE) [7,8], and can achieve a resolution to the level of single cells. OCE has enabled the characterization of the three-dimensional elastic modulus of a mouse aorta at an ultrahigh resolution of 15 µm in a 1 mm field of view [9], as well as the rapid response of multicellular spheroids under osmo-mechanical stress [10].

In this paper, we propose a new method of elastography based on 3D light microscopy, which uses a differential interference contrast (DIC)/confocal microscope to study the internal strain distribution in multicellular tumor spheroids. This method allows for the mapping of 3D internal strains within microscale tissues with a resolution comparable to that of the advanced OCE, and has the benefit of compatibility with standard commercial DIC/confocal microscopes. Microscale tissues in the size range of 100 μm - 1 mm are considered to be the smallest functional unit of tissues that maintain the basic physiology [11]. Therefore, the study of multicellular clusters in such size range, including tumor spheroids and cellular organoids, is of scientific and clinical importance. Tumor spheroids are a 3D platform that have been used to test drug delivery systems [12,13], study molecular changes [14], and analyze 3D tumor formation [15,16]. Cellular organoids that represent the morphology and behavior of organs are of recent interest [17–19] in the field of regenerative medicine as well. By studying the physical properties of microscale tissues, we can obtain insight into cell differentiation, morphogenesis, and cancer invasion in 3D models.

The application of mechanical force is an essential step in strain imaging-based elastography. In order to induce internal strains, the use of manual indentation, ultrasound-induced acoustic radiation [20], and internal physiologic motion [21] have been studied. Here we use a custom-built micromanipulator to apply mechanical forces onto samples. In our previous study, we demonstrated the first successful measurement of the elastic modulus of a spheroid using the micromanipulator [22]. Now, we can both image the 3D deformation of microtissues with a DIC/confocal microscope, and analyze the 3D strain distribution as well. We have developed a system that synchronizes the manipulator indentation and the 3D DIC/confocal microscopic imaging to acquire a 4D image sequence. The obtained data was processed by a custom MATLAB program that uses 3D cross-correlation to track the displacement of points in the spheroid and calculate the strain distribution. With the capability to image micro/mesoscale samples, our unique elastography has the potential to open up new applications in cell/tissue biology and engineering.

2. Materials and methods

2.1 Multicellular spheroid preparation

We prepared multicellular tumor spheroids with known cellular composition as a reference. We used a spheroid seeded from a breast tumor cell line (BT474) and a co-culture spheroid seeded from breast tumor cells (T47D) and human dermal fibroblast cells (HDFa). BT474 spheroids were cultured in agarose gel-coated 96 well plates. The seeding density was 1000 cells/150 µl basal media/well. After 5 days, the spheroids were harvested and incubated with Nile Red (Sigma Aldrich) for 60 minutes before confocal imaging. The co-culture of T47D and HDFa allows for the growth of spheroids containing areas with different structural characteristics. Prior to seeding, human breast cancer cells (T47D) and human dermal fibroblasts (HDFa) were stained with 1 μL of 1 μg/μL CellTracker CM-DiI (Molecular Probes) per 1 mL of cell suspension in PBS, and 10 μL of 5 μg/μL SP-DiOC18(3) (Molecular Probes) per 1 mL of cell suspension in PBS, respectively. The cell tracker dyes were added to the cell suspension, incubated for 5 minutes at 37 °C, then at 4 °C for 15 minutes. Cells were washed with PBS and resuspended in DMEM. T47D and HDFa were cultured in DMEM, 10% FBS and 1% Pen/Strep (Life Technologies). A 96-well, U-bottom plate (Thermo Fisher Scientific) was coated with 50 μL per well of 1.6% agarose and sterilized under UV light for 10 minutes. Monolayer cultures of T47D and HDFa were grown to confluency and counted via hemocytometer. T47D were plated at a concentration of 600 cells/150 µL DMEM per well. After 7 days of T47D spheroid formation, HDFa were added at a concentration of 900 cells/50 µL DMEM per well. An additional incubation period of 4 days was allowed before harvesting for confocal imaging.

2.2 Microindentation and 4D image acquisition

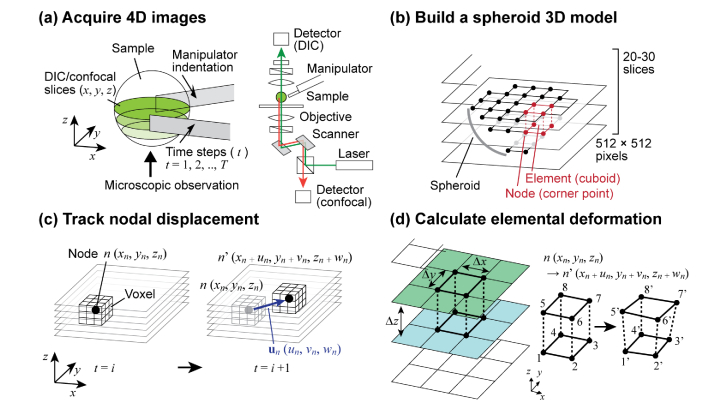
We used the same custom-built micromanipulation system as in the spheroid mechanical characterization experiment we reported in [22]. The manipulator tips are made of photolithographically patterned SU-8, at a size of 1600 µm (L) × 100 µm (W) × 15 µm (T). The tips are attached to a 3D-printed nylon flexure, which is actuated by a single bimorph piezoelectric actuator (Steminc, FL) with driving signals ranging from 0 V to typically ~40 V. See [22] for the detailed description of the manipulator. We obtained 4D (x, y, z, and indentation steps) images for deformation analysis. Figure 1(a) illustrates the experimental setup. The manipulators were installed on the Nikon A1R Spectral Confocal Microscope with a 20x (NA = 0.5) microscope objective. Stepwise indentation was applied to the spheroid, and 3D DIC and confocal fluorescence slices were obtained for each indentation step. While the laser illumination (488 and 561 nm) was scanned using galvanometer mirrors in the x- and y-axes, the DIC signal and the fluorescence emission (green: 500 - 550 nm, red: 575 - 625 nm) were collected simultaneously through different detection pathways (Fig. 1(a)). Each layer was 512 × 512 pixels, and a total of 20 - 30 (typ.) z-axis slices were obtained. We assumed the spheroids to be a sphere, and imaged the bottom half to reduce the data size. With shorter imaging light paths, the bottom half of the spheroid shows a better quality for confocal imaging. With the 20x objective, the field of view was typically 512 µm × 512 µm and the z-distance between two adjacent layers was set to 3 - 5 µm (typ.). Using the microscope’s optical zooming function, the xy field of view can be adjusted to obtain higher resolution images in the area of interest. The maximum achievable resolution is given by the wavelength of light and NA of the objective for fluorescence, in addition to the NA of the condenser for DIC. For 561 nm imaging, the resolution in the x/y-axes is 0.62 µm for fluorescence and 0.7 µm for DIC. The z-axis resolution, defined by the focal depth of the objective, is approximately 1.5 µm. The displacement of the manipulators is controlled by the voltage applied to the integrated piezoelectric actuator. The indentation of 30 - 40 µm (typ.) was applied by 15 - 20 actuation steps (typ.) at a rate of 2 - 3 µm/step (typ.). A custom-built digital controller programmed on a microcomputer board, Arduino Leonardo, was used to synchronize the mouse-click signal to trigger the image acquisition with the microscope imaging software (Nikon NIS Elements) and the control signal sent to the high-voltage piezo driver. A typical measurement takes 2 - 3 s × 20 - 30 layers × 15 - 30 indentation steps = ~20 minutes.

Fig. 1.

Image tracking and deformation analysis. (a) The bottom half of the spheroid was imaged by the Nikon DIC/confocal microscope as it was gently compressed by a pair of tweezers. (b) A meshed model was built based on the obtained 3D image. (c) Nodal displacement was found by image-tracking a voxel. (d) The strain vector of each element was found from the displacement vectors of the eight nodes.

2.3 Deformation analysis

We developed a custom MATLAB 3D deformation analysis program by expanding the 2D analysis we reported in [23]. The analysis steps are illustrated in Fig. 1. After the image acquisition, we modeled the spheroid as an assembly of cuboidal elements, as shown in Fig. 1(b). The size of the element was ∆x × ∆y × ∆z = 5 × 5 × 1 pixels. The meshed model was created layer-by-layer by selecting the areas of pixelated spheroid images. The displacement vectors of the nodes ( = corner points of elements) were found by tracking the voxel that represents each node n (x_n, y_n, z_n), as shown in Fig. 1(c). The size of voxels were typically 16 × 16 × 4 pixels. Three-dimensional cross-correlation was calculated and interpolated to obtain the displacement vector u_n = (u_n, v_n, w_n) in real numbers. The position of the voxel to be tracked was updated for each step of indentation. As illustrated in Fig. 1(c), once we track the movement of node n at t = i to n’ at t = i + 1, the point n’ is used as the new point to find the position of the node at t = i + 2. The strain is found from the displacement vectors of the eight nodes u₁, u₂, …, u₈. The cumulative strain between the initial image i₀ (beginning of indentation) and image i₀ + n (the indentation step of interest) was typically considered. Steps of n = 5 - 10, corresponding to the indentation depth of 10 - 30 µm, are usually sufficient to obtain visible strain patterns. Detailed mathematical expressions used in the analysis are described in [23] for the 2D model. Here, the equations are simply expanded to 3D. The strain vector $\left\{\epsilon \right\}$ at the center point of the element was calculated in the following way:

$$\left\{\epsilon \right\}=\left[B\right]\left\{u\right\}$$

where,

$$\left\{\epsilon \right\}=\left\{{\epsilon }_x;{\epsilon }_y;{\epsilon }_z;{\gamma }_{xy};{\gamma }_{zx};{\gamma }_{yz}\right\},$$

$$\left[B\right]=\left[\begin{array}{ccc}{N}_X& O& O\\ O& N_Y& O\\ O& O& N_Z\\ N_Y& N_X& O\\ N_Z& O& N_X\\ O& N_Z& N_Y\end{array}\right]$$,

$$N_X=\frac{2}{\Delta x}\cdot \left[\begin{array}{cccccccc}\mathrm{1/8}& \mathrm{1/8}& -\mathrm{1/8}& -\mathrm{1/8}& \mathrm{1/8}& \mathrm{1/8}& -\mathrm{1/8}& -\mathrm{1/8}\end{array}\right]$$

$$N_Y=\frac{2}{\Delta y}\cdot \left[\begin{array}{cccccccc}-\mathrm{1/8}& \mathrm{1/8}& \mathrm{1/8}& -\mathrm{1/8}& -\mathrm{1/8}& \mathrm{1/8}& \mathrm{1/8}& -\mathrm{1/8}\end{array}\right]$$

$$N_Z=\frac{2}{\Delta z}\cdot \left[\begin{array}{cccccccc}-\mathrm{1/8}& -\mathrm{1/8}& -\mathrm{1/8}& -\mathrm{1/8}& \mathrm{1/8}& \mathrm{1/8}& \mathrm{1/8}& \mathrm{1/8}\end{array}\right]$$

$$O=\left[\begin{array}{cccccccc}0& 0& 0& 0& 0& 0& 0& 0\end{array}\right]$$

$$\left\{u\right\}=\left\{u_1;u_2;u_3;\cdots ;u_8;v_1;v_2;v_3;\cdots ;v_8;w_1;w_2;w_3;\cdots ;w_8\right\}$$

For visualization, it is practical to use the Von Mises strain, which is a scalar value calculated from the six components of $\left\{\epsilon \right\}$:

$${\epsilon }_{\text{VM}}=\frac{2}{3}\cdot \sqrt{\frac{3({e_{xx}}^2+{e_{yy}}^2+{e_{zz}}^2)}{2}+\frac{3({{\gamma }_{xy}}^2+{{\gamma }_{zx}}^2+{{\gamma }_{yz}}^2)}{4}},$$

where,

$$e_{xx}=(2{\epsilon }_{xx}-{\epsilon }_{yy}-{\epsilon }_{zz})/3;e_{yy}=(-{\epsilon }_{xx}+2{\epsilon }_{yy}-{\epsilon }_{zz})/;e_{zz}=(-{\epsilon }_{xx}-{\epsilon }_{yy}+2{\epsilon }_{zz})/3.$$

3. Results

3.1 Tumor spheroid

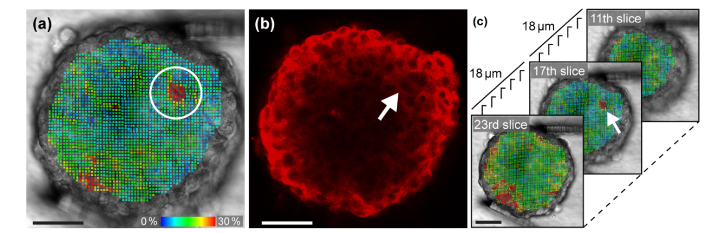
Figure 2 shows the analysis of a BT474 tumor spheroid. A total of 27 z-slices, 37,251 elements, and 42,168 nodes were studied in this analysis. Figure 2(a) shows the distribution of the Von Mises strains of the 17th layer from the bottom. Each colored dot represents an element composed of eight nodes. Figure 2(b) is the fluorescence image of the same layer. The strain plot in Fig. 2(a) shows a spot that experienced a substantially larger deformation than its surrounding areas. The size of the spot is similar to that of a cell observed in the fluorescence image shown in Fig. 2(b). The area that corresponds to the spot is indicated by the white arrow. The same spot was also visible in neighboring z-slices, but was not observed in z-layers distant from it (see Fig. 2(c)), showing that it is a small, localized spot rather than a line that spans the entire spheroid. This result demonstrates our ability to discover a single-cell sized spot that has mechanical characteristics distinctively different from the surrounding areas.

Fig. 2.

(a) A cell-sized spot with a localized, large deformation was visualized in the strain analysis of a tumor spheroid. (b) Fluorescence image of the same layer. The white arrow indicates the position of the soft spot. (c) The soft spot was not observed in distant layers. Scale bars = 50 µm. A movie clip (Visualization 1 ^{(440.6KB, mp4)} ) is available.

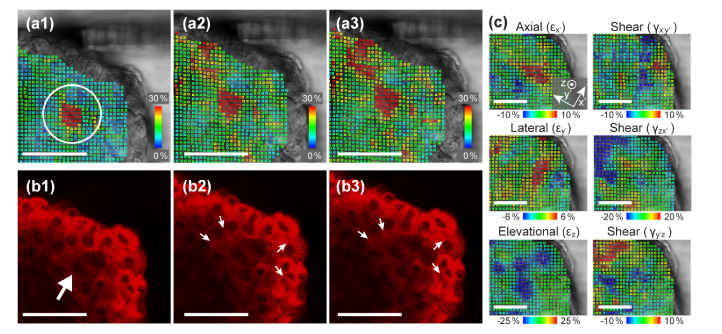
After careful observation of the further compression that was added beyond the relatively mild indentation shown in Fig. 2, we found that the cells around the soft spot were easily displaced. Figures 3 (a1-a3) and (b1-b3) show the sequence of the further compression. We observed that the right side of the area shown in Figs. 3(b2) and (b3) rapidly inflated as the left side of the area shrunk in response to the compression. The movement is more clearly visible in a motion video (see Visualization 1 ^{(440.6KB, mp4)} ). This could mean that there is a loose cell-cell connection or an intercellular space that resulted in a larger local displacement. In order to study the motion of the individual cells visualized in the confocal images, we conducted a detailed strain analysis based on the last 6 steps of the sequence with the confocal images overlaid on the DIC images. Figure 3(c) shows calculated components of axial, lateral, elevational and shear strains. The strain tensor was transformed to show the components in the x’- y’ plane, where the direction parallel to the indentation force was chosen as the axial (x’) direction. Compressive (negative) strains, indicated by blue dots, are visible in the top left of the ε_z plot, while tensile (positive) strains, indicated by red dots, are shown in the area around the observed inflation in the plots of ε_x’ and ε_y’. This may indicate that the fluid in the intercellular space was pushed from one side to the other by surrounding cells.

Fig. 3.

(a1-a3) Von Mises strain analysis and (b1-b3) corresponding fluorescence images of the further indentation sequence. When a large compression was added, cell displacement is observed as the balloon-like deflation and inflation from (b2) to (b3). The strain analysis detected the displacement at an early step of indentation in (a1). (c) Analysis of axial (x’), lateral (y’), and elevational (z) and shear (x’y’, zx’, and y’z) strain components. The direction of the indentation was chosen as the x’ axis. Scale bars = 50 µm. See also Visualization 1 ^{(440.6KB, mp4)} and Visualization 2 ^{(236.6KB, mp4)} .

3.2 Tumor-fibroblast co-culture spheroid

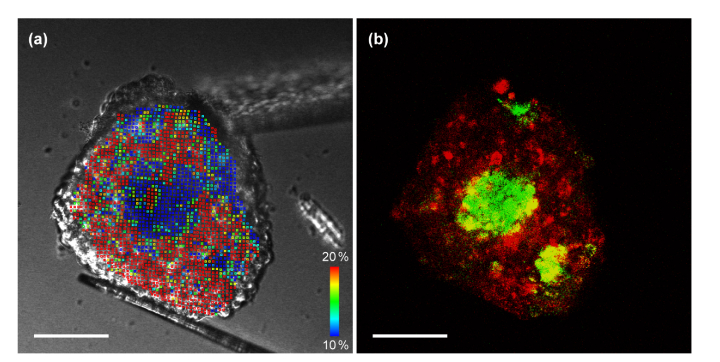
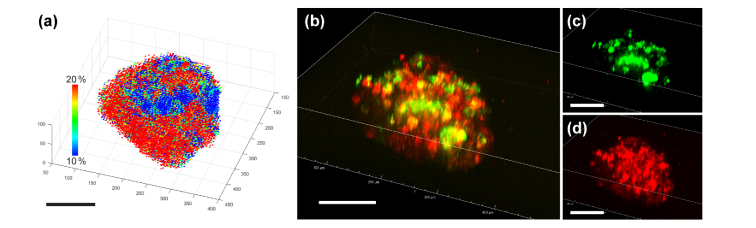
We imaged a co-culture spheroid seeded from breast tumor cells (T47D) and human dermal fibroblast cells (HDFa) to study a structure containing areas with different mechanical characteristics. Figure 4 shows a comparison of the deformation analysis and the confocal fluorescence image. Figure 4(a) is the Von Mises distribution calculated from the DIC images. Figure 4(b) is an overlay fluorescence image of fibroblast cells (DiO: green) and tumor cells (DiI: red) stained with tracking dyes to identify cell types. Both correspond to the 14th layer from the bottom of the total 19 slices we imaged for the co-culture spheroid. Although fibroblast cells were added after the formation of the tumor spheroid, it is apparent that the fibroblast cells migrated into the center of the tumor spheroid, which corresponds to the observation reported in [24]. The strain distribution in the left panel shows a clear correlation with the fluorescence image, which shows the cellular composition of the co-cultured spheroid. There are three distinctive fibroblast regions, which are visible in both panels. Note that the strain distribution in the left panel was calculated only from the DIC images without using fluorescence. It has been newly discovered in our study that in T47D/HDFa co-cultured spheroids, fibroblast cells can form a stiff inner core surrounded by softer tumor cells. This conclusion could not be drawn from fluorescent images alone. Based on the calculated strain of the 3D model, we can construct the 3D map of elasticity. Figure 5(a) shows the 3D scatter plot of the Von Mises strains. For each element, the center point found from the average of the eight nodes was used in the 3D plot. The positions of the nodes were found from voxel tracking. A total of 18,609 elements and 22,219 nodes were studied in this analysis. Figure 5(b) is a reconstructed fluorescence overlay of the fibroblast cells (Fig. 5(c)) and the tumor cells (Fig. 5(d)). The formation of fibroblast cores inside the spheroid is seen in both the deformation analysis and the fluorescence overlay.

Fig. 4.

Analysis of tumor-fibroblast co-culture spheroid. HDFa cells were added to the T47D spheroid at day 7 of incubation, allowing for fibroblast infiltration, and imaged at day 11. (a) Von Mises strain calculated from DIC images. (b) Overlay fluorescence image of tracking dyes used to identify cell types (T47D: red, HDFa: green). Three distinctive regions of fibroblast cells are visible in both images. The strain analysis indicates that fibroblast regions are stiffer than cancer cells. Scale bars = 100 µm. A movie clip (Visualization 3 ^{(488.4KB, mp4)} ) is available.

Fig. 5.

Analysis of the fibroblast-infiltrated tumor spheroid with (a) 3D strain map and (b) 3D fluorescence overlay of (c) fibroblast (green) and (d) tumor cells (red). Scale bars = 100 µm. Movie clips (Visualization 4 ^{(2.3MB, mp4)} andVisualization 5 ^{(1.1MB, mp4)} ) are available.

4. Discussion and conclusion

4.1 Significance of 3D microtissue imaging

We demonstrated that mechanical deformation analysis based on 3D light microscopy and image tracking can successfully generate a 3D strain map that showed a heterogeneous distribution of elasticity within a spheroid. Multiple mechanical assays for single cell analysis have been previously published. For example, atomic force microscopy (AFM) has been used to differentiate between cancerous and normal cells [25]. One more modern method demonstrates how a pulsed opto-acoustic microscope, which uses pulsed lasers to generate broadband acoustic waves, allows for non-invasive observation of stiffness and adhesion of single cells [26]. Another method uses particle tracking to characterize the viscoelastic properties of a single cell subjected to stress induced by shear flow [27]. However, it is believed that monolayer cell cultures do not represent the mechanisms associated with drug resistance in tumor microenvironments [12,28,29]. Therefore, the analysis of 3D microtissues is necessary to more accurately mimic in vivo conditions. It has been pointed out that 3D structural and spatial heterogeneity, characterized by unique degrees and locations of stiffness within a microtissue, contributes to the mechanisms of cancer cell proliferation, tumor metastasis, and drug responses [30,31]. The drug resistance acquired through interaction with cancer-associated fibroblast cells is also a topic of recent interest [32,33]. An in vitro assay that adequately visualizes the 3D microscale internal structure will have a significant impact on cancer studies. Through the image analysis of a co-cultured spheroid, we have visualized the presence of structural areas with significantly different relative elasticity than that of neighboring regions, which were shown by fluorescence to correspond with the composition of fibroblast and tumor cells in the given area. Fibroblast cells added to the tumor spheroid formed distinctively stiff inner areas, which was visualized through our strain analysis. Fluorescence analysis alone will not quantify such mechanical characteristics. Molecular analysis and immunoassay have been the predominant methods to characterize 3D models. However, tumor growth involves mechanical interaction between tumor cells and surrounding tissues. Our 3D analysis method can reveal the internal formation of cancer spheroids through strain mapping, which will complement typical immunoassays and molecular analysis. Another important aspect is that the strain analysis was made without using fluorescent images. We demonstrated that an application of simple mechanical indentation visualizes mechanical deformability within a microtissue.

4.2 Future directions and limitations

We used the image correlation technique to evaluate the displacement field. The use of interpolation allows for the resolution of displacement measurement to be well below the pixel size [7]. Our optical tracking showed ~0.1-pixel resolution by three sigma [23], and Sun et al. reported the resolution of 0.01 pixels [34]. On the other hand, the cross-correlation analysis of a 3D volume (16 × 16 × 4 pixels) reduces the spatial resolution [7]. When we consider that the obtained displacement is the average of all the pixels within the volume, the obtained displacement map gives the low-pass filtered values of the actual pixel displacements. In our system, the spatial resolution can be estimated to be about 32 × 32 × 8 pixels, because spatial contrast patterns at this frequency retain the optical contrast higher than 60% after being filtered by the 16 × 16 × 4 pixel averaging. The actual spatial resolution depends on the optics used. In the case of our experiment (20x, NA = 0.5), 32 × 32 × 8 pixels corresponds to 32 µm × 32 µm × 40 µm. When we use a high-resolution water immersion objective available for the Nikon confocal microscope (60x, NA = 1.3), the optical resolution is more than twice higher, and thus a spatial resolution as high as ~15 µm may be achieved. In this study, we used a simple image correlation method for displacement analysis. Algorithms to improve processing efficiency have been actively studied in the field of OCE, and may be used in our future analysis. One issue is the potential of the numerical derivative operation in digital image correlation to induce noise. The use of model-based algorithms, where the process is converted to a parameter optimization problem without using a derivative operator, has demonstrated the efficacy [34,35].

The evaluation of elastic modulus is an important next step to quantitatively assess a tissue’s mechanical characteristics. Essential in the process of determining elastic modulus is the evaluation of the internal stress distribution, which requires us to know the boundary conditions, including the external loads. Our method is advantageous in this respect because the external loads can be found by measuring the bending of the manipulator tips through image analysis [22]. Given the applied external forces, mechanical models based on finite element analysis (FEM) can be built to find the stress distribution as discussed in previous OCE studies [36–38]. We typically considered the cumulative strain between the initial indentation step and the step of interest. Non-linear effect may become significant when the indentation is deeper. By tracking the displacement throughout the indentation steps, we can obtain the non-linear components of deformation. It is also possible to calculate strain between any indentation steps to consider tangent modulus.

In conclusion, we have demonstrated a label-free, image-based deformation analysis to measure 3D maps of local elasticity that visualize distinct areas. Our method will open up a new class of in vitro 3D assays to quantify characteristics of multicellular tumor spheroids such as cellular adhesions, extracellular matrix, and density.

Funding

National Science Foundation (NSF) (IDBR1555986, CCSS1809047).

Disclosures

The authors declare that there are no conflicts of interest related to this article.