Skip to main content
PMC home page
Biomedical Optics Express logoLink to Biomedical Optics Express
. 2019 Apr 22;10(5):2504–2512. doi: 10.1364/BOE.10.002504

Photoacoustic computed tomography with lens-free focused fiber-laser ultrasound sensor

Xue Bai 1, Yumeng Qi 1, Yizhi Liang 1, Jun Ma 1,2, Long Jin 1,3, Bai-ou Guan 1
PMCID: PMC6524584  PMID: 31143500

Abstract

Optical detection of ultrasound is attractive to photoacoustic imaging due to its high sensitivity per unit area, broad bandwidth, and electromagnetic immunity. To enhance the sensitivity, previous optical transducers commonly necessitate bulk acoustic lenses to achieve focused ultrasound detection. Here, we proposed and demonstrated a novel lens-free focused optical ultrasound sensor by mechanically bending a flexible fiber laser. At a curvature radius of 30 mm, the curved fiber laser well conformed to the spherical wavefront of ultrasound exhibiting ~5 times higher sensitivity compared with the straight one. The focused fiber laser ultrasound sensor (FUS) presented a minimum detectable pressure of ~36 Pa with a working distance equal to its curvature radius. The sensor was applied to circular scanning photoacoustic computed tomography (PACT), which showed a ~70 μm in-plane resolution and a ~500 μm elevational resolution. In vivo imaging of a zebrafish and mouse brain shows the potential of this focused FUS for photoacoustic imaging in biological/medical studies.

1. Introduction

Photoacoustic tomography (PAT) is a rapidly developing noninvasive imaging modality with potential applications in areas of vascular biology [1,2], dermatology [3,4], and neurology [5,6]. Based on the detection of ultrasound waves emitted from biological tissues irradiated by an optical or electromagnetic pulse, PAT combines advantages of pure optical imaging and sonography featuring optical contrast and deep penetration. Endogenous contrast agents in biological tissues such as hemoglobin, melanin, lipids can provide rich anatomic and functional information for biomedical/clinical studies [7]. Compared with optical-resolution photoacoustic microscopy (OR-PAM) that uses tightly focused laser light to excite photoacoustic (PA) signals for shallow tissues imaging [8], photoacoustic computed tomography (PACT) employing diffusive light allows whole-body imaging of small animals with a tens of micrometers spatial resolution [9].

PACT commonly uses state-of-the-art piezoelectric transducers (PZTs) to acquire PA signals emitted from the region of interest (ROI) by mechanically scanning a single transducer [10] or by using linear [11], ring-shaped [12] or spherical [13] array transducers. These widely used PZTs, however, are sensitive to electromagnetic interference (EMI) and confront a tradeoff between detector size and sensitivity. And transducers with a large size might suffer from spatial averaging effects, which would degrade the image resolution especially for high-frequency ultrasound detection. Optical ultrasound sensors with advantages of high sensitivity per unit area, wide frequency bandwidth, electromagnetic immunity and optical-transparency offer a promising alternative to existing PZTs [14,15]. For example, a charge-coupled device (CCD) camera was used to capture snapshots of spatially encoded pressure field for fast three-dimensional (3-D) PAT [16]. An optical Fabry–Pérot (FP) etalon, formed by a polymer film spacer sandwiched between a pair of highly reflective mirrors, was demonstrated for studying cellular and genetic processes in deep mammalian tissues [17]. By constructing a plano-concave FP etalon on an optical fiber tip, the same group recently developed a miniature ultrasensitive fiber-optic ultrasound sensor, which is flexible, lightweight and tolerable to mechanical bending [18]. In fact, utilization of optical fibers for ultrasound detection can be dated back to several decades ago [19–21]. When subjected to ultrasound, an optical fiber can strongly scatter the impinging ultrasonic waves at frequency of tens of megahertz. The acoustic scattering, in analogy to Mie scattering in optics, establishes a discrete set of mechanical modes over fiber cross section. This acoustic interaction vibrates the fiber and induces a detectable response in optical phase change, which can be readily read out by fiber-optic Michelson, Mach-Zehnder interferometry or phase-shift fiber grating. Nevertheless, these two-beam interferometers and optical resonators are sensitive to ambient temperature drift and mechanical vibration especially during in vivo biological imaging. Servo-control based stabilization scheme and heterodyne detection can effectively reduce these disturbances [22,23]. To obtain more robust performance, pulse interferometry was also developed to demodulate a phase-shift fiber grating for clinical endoscopic imaging [24]. Recently, fiber-laser ultrasound sensors (FUSs) interrogated using mature I/Q demodulation technique exhibited a strong immunity to environmental disturbances [25]. The FUS also showed great potential for in vivo OR-PAM imaging of vasculature in mouse ears [26]. However, the mouse ear needed to be placed extremely close to the fiber surface during the imaging process because the FUS sensitivity rapidly decayed with increasing working distance. This phenomenon was caused by the wavelength-scale equivalent interaction length of a straight fiber subjected to spherical ultrasound waves [27] and might limit the potential of FUS for deep penetration PACT imaging.

In this work, we demonstrated a novel lens-free focused FUS with greatly increased sensitivity at long working distance. The focus capability was obtained by simply bending the straight FUS along its axial direction to conform the spherical wavefront of ultrasound. At a curvature radius of 30 mm, the focused FUS showed a ~5 times higher sensitivity compared with the straight one, and was demonstrated for in vivo PACT of a zebrafish and mouse brain. In contrast to traditional PZTs, the proposed focused FUS is lens-free, optical transparent and focus-tunable, making it promising for PA imaging in biological/medical studies as well as clinical applications.

2. Theory

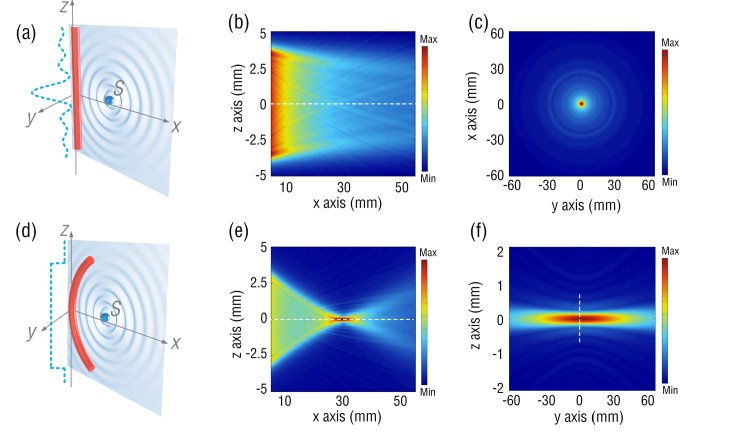
To illustrate the sensitivity enhancement by bending the straight FUS, we studied the spatial ultrasound responses of the FUS in both straight and curved geometries. The acoustic response of the FUS can be obtained by treating the forward problem [14]. As shown in Figs. 1(a) and (d), a point ultrasound source S located at position (x, y, z) is assumed to emit spherical pressure waves. The location of receiver is (x’, y’, z’). The ultrasound wave is described by p0exp(ikar)/r, where p0 denotes the initial pressure amplitude, r is equal to (x−x')2+(y−y')2+(z−z')2, ka=ω/c is the ultrasound wavenumber, and c is the ultrasound velocity in the surrounding medium (common water). When spherical ultrasound waves impinge on the FUS with an ultrasound-sensitive length of L, the response of the FUS can be obtained by,

Ru=Γp0A(ω)∫Lexp(ikar)rdL (1)

where Г is a coefficient accounting for the absorption or scattering experienced by the sound when travelling from source S to FUS, A(ω) is normalized frequency response of a straight FUS to plane ultrasound waves [27] and the ultrasound-sensitive length L is approximately equal to the laser cavity length of the FUS. By varying the location (x, y, z) of the point source S, 3-D spatial responses of the FUS to ultrasound can be calculated. Figures 1(b) and (c) show the spatial sensitivities of a straight FUS with a laser cavity length L of 8 mm. The ultrasound response weakens as the distance to the FUS along x axis increases, which is caused by the phase mismatch of spherical ultrasound waves impinging on the straight fiber as shown in dashed line in Fig. 1(a). This substantial reduction in the sensitivity at long working distance limits the straight FUS to shallow imaging applications. In contrast, spherical ultrasound waves arrive at the curved FUS surface have identical phases due to the matched shape of FUS and wavefront of ultrasound, as illustrated by the dashed line in Fig. 1(d). Figures 1(e)-(f) show the responses of a curved FUS with a curvature radius of 30 mm. The FUS sensitivity maximizes at the arc center or the focal spot as shown in Fig. 1(e) and is ~5 times higher than that of a straight one. From the dashed line in Fig. 1(f), the waist of the focal zone along z axis is estimated to be ~350 μm, which is determined by the FUS bending curvature. Compared with the straight FUS, the curved FUS can greatly boost up the ultrasound sensitivity at long working distance, which is important to large-area and deep-tissue PACT imaging.

Fig. 1.

Fig. 1

Open in a new tab

(a) and (d): Schematic of a straight and a curved FUSs subjected to a point ultrasound source, respectively. The dashed lines plot the phase distribution of the ultrasound waves along the fiber. (b-c): Calculated spatial sensitivities of a straight FUS in x-z plane and x-y plane. (e-f) Calculated spatial sensitivities of a curved FUS in x-z plane and y-z plane.

3. Focused FUS

3.1 Work principle

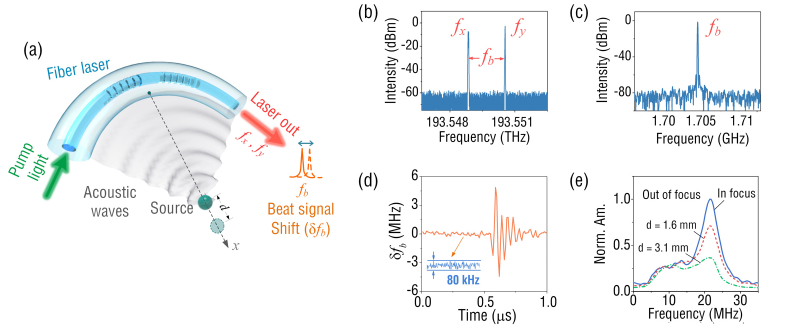
Figure 2(a) shows the working principle of a curved FUS for ultrasound waves detection. The laser cavity, with two high-reflectivity fiber Bragg gratings (FBGs) as mirrors, has an effective length of 8 mm. The FBGs are inscribed in the core of a rare-earth doped fiber (EY305, CorActive) by a 248 nm excimer laser with a beam diameter of 1 mm. The fiber has a core/cladding diameter of 8/125 μm, a numerical aperture of 0.18 and a cutoff wavelength of 1277 nm. During the grating inscription, the laser beam passes through an optical phase mask and induces periodic refractive index modulation in the fiber core. By slowly scanning the laser beam along the fiber longitudinal axis, two FBGs with the grating lengths of 7 and 9 mm can be fabricated. The FBG-incorporated laser cavity absorbs the pump light at 980 nm with a coefficient 1337 dB/m and generates the laser light at 1550 nm as shown in Fig. 2(a). Figure 2(b) shows that the laser has two orthogonal polarized outputs (fx = 193.548843 THz and fy = 193.550547 THz) as a result of the intrinsic fiber birefringence, which generates a radio-frequency (RF) beat signal at fb = | fx - fy | = 1.704 GHz (Fig. 2(c)). When the FUS is subjected to ultrasound waves, the pressure impinging onto the laser cavity drives it into vibration, which has a maximum amplitude at a frequency of ~22 MHz. This frequency corresponds to the eigen vibration mode (l = 2, n = 1), where l and n denote the azimuthal and radial order numbers of the in-plane vibration modes of the fiber, according to our previous study [27]. For ultrasound with the frequency far below the central frequency of the vibration mode, the sensor shows much weaker response, which is similar to the widely used PZT transducers and differs from previously reported optical ultrasound sensors [14,17]. The ultrasound-induced vibration changes the fiber birefringence, and subsequently causes the shift in the laser beat frequency that can be interrogated by a RF demodulation unit [25]. Figure 2(d) presents the temporal response of the curved FUS with a radius curvature of 30 mm at its focus. Based on the measured sensitivity of 2.25 MHz/kPa [27] and a noise floor of ~80 kHz estimated from Fig. 2(d), the corresponding noise-equivalent pressure (NEP) is ~36 Pa at a 50 MHz acquisition bandwidth. To show the focus-enabled sensitivity enhancement more clearly, the frequency responses at locations deviating from the focal spot along the x axis (see Fig. 2(a)) were studied. As shown in Fig. 2(e), as the distance to the focal spot d increases, the sensitivity continues to decrease due to the mismatch of the fiber curvature with the spherical wavefront of ultrasound.

Fig. 2.

Fig. 2

Open in a new tab

(a) Schematic of ultrasound detection by using a curved fiber-laser sensor; (b) output laser spectrum; (c) beat frequency spectrum; (d) temporal response to an ultrasound pulse; (e) frequency responses to ultrasound sources in and out of focus, Norm. Am.: normalized amplitude.

3.2 Spatial sensitivity

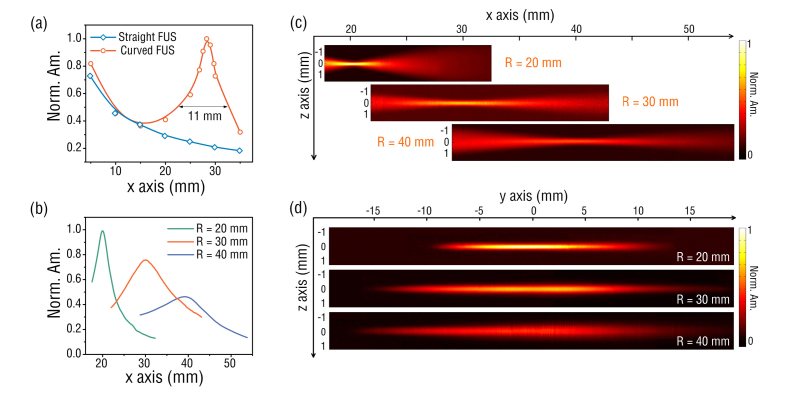
To characterize the spatial sensitivity of the FUS, a 532 nm pulsed laser was used to illuminate a black tape for generation of ultrasound waves via PA effect. The laser beam was focused by an objective lens (NA = 0.1) to obtain nearly spherical ultrasound waves. Meanwhile, the FUS was bent to desired curvature and subsequently mounted onto a custom-made arc-shape alumina holder. To map the spatial ultrasound response, the distance between the sensor and the laser spot was changed by scanning the curved FUS with a 3-D linear stage. Figure 3(a) shows the profiles of measured ultrasound responses along x axis for a straight FUS and a curved one with a curvature radius of 30 mm. At location close to the fiber surface, the responses of the straight and curved FUSs follow similar trend as 1/r [27]. As the distance increases, the response of straight FUS continues to reduce whereas the curved FUS features a maximum response at a distance of ~30 mm or at the focus, similar to the calculated results as shown in Figs. 1(b) and (e). The curved FUS has a depth of focus (DOF) of ~11 mm, which is estimated based on the full width at half maximum (FWHM) of the PA amplitude profile in Fig. 3(a), and more importantly, shows a ~5 times higher sensitivity than that of the straight FUS.

Fig. 3.

Fig. 3

Open in a new tab

(a) Measured acoustic responses of the straight and curved FUSs as a function of the distance along x axis, respectively; dots: measured results, curves: fit results. (b) Measured responses at curvatures of 20, 30 and 40 mm. (c-d) 2-D distribution of the ultrasound sensitivity in x-z plane and y-z plane, respectively.

We further measured the ultrasound responses of FUS at different curvature radii. As shown in Fig. 3(b), the focal lengths of all FUSs are close to their curvature radii, and a larger curvature radius corresponds to an extended DOF but a reduced sensitivity. Figures 3(c) and (d) show the two-dimensional (2-D) spatial ultrasound responses of FUS in x-z plane and y-z plane, respectively. By plotting the profiles along the z axis at the focus in Fig. 3(c), the z-axial FWHMs of FUSs with curvature radii of 20, 30, and 40 mm are estimated to be 230 μm, 400 μm, 500 μm, respectively. This z-axial FWHM determines the elevational resolution of imaging if the curved FUS is employed for circular scanning PACT system [28]. It is also found that the measured y-axial FWHM is smaller than the theoretical value estimated from Fig. 1(f). This is because the FUS mechanically resonating in an asymmetry mode has an ultrasound acceptance angle following a relationship of |cos2θ| in the x-y plane [27]. For deep-tissue imaging, a long focal length is desired and can be obtained by using a FUS with a larger curvature radius as shown in Fig. 3(c). However, the sensitivity of the FUS at the focus will also reduce. One effective way to address this issue is to use a fiber-laser with longer cavity length or effective ultrasound detection zone. At a given curvature radius, a longer cavity length gives a larger NA, capable of improving both the sensitivity and the elevational resolution. We attempted to write long-cavity fiber-laser, but the multiple longitudinal modes competed and caused the instability of laser output. Currently, the maximum length of the fiber cavity with stable imaging performance is limited to ~10 mm, which sets the upper boundary of the laser cavity length. In the future, we will try to insert in-line fiber-optic filters, such as phase-shift fiber Bragg gratings into the laser cavities to develop long-cavity single-longitudinal-mode lasers.

In another aspect, the smallest curvature radius of the curved FUS is ~20 mm. Further bending of the fiber might increase the fiber loss and the risk of the fiber-laser breakage. Recently, polymer fibers featuring high flexibility and low bending loss have been exploited for solutions to low-cost optical link as well as wearable devices [29,30]. For example, a bended polymer fiber with a curvature radius down to 10 mm has been demonstrated for high-performance fiber-optic interferometric sensor [31]. By optimizing the fiber material and structure parameters, the polymer fibers made of soft materials such as polymethyl methacrylate (PMMA) might be a potential alterative to build more flexible FUSs.

4. PACT using focused FUS

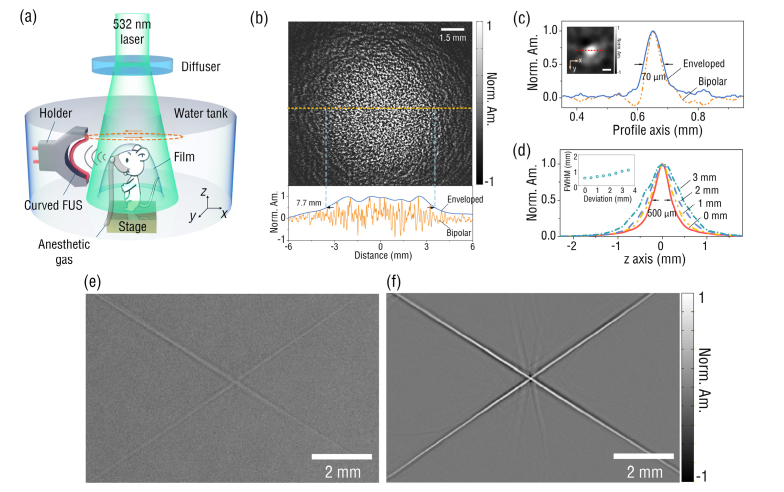
Figure 4(a) shows the schematic of the curved FUS based PACT system. A 532 nm Nd:YAG laser (Dawa 100, Beamtech) with a pulse width of 6.5 ns and a repetition rate of 10 Hz was used to excite PA signals. The laser beam with a single pulse energy of 30 mJ was homogenized and expanded by a beam diffuser (DG10-120, Thorlabs) to a 1.5 cm-diameter illumination spot. The corresponding optical fluence of the laser was ~16 mJ/cm2, lower than the American National Standards Institute (ANSI) safety limit. The sample located at the focus of the curved FUS with a radius curvature of 30 mm, absorbed the illumination light and generated PA signals. Then the FUS was scanned around the sample via a computer-controlled rotary motor and collected the PA signals at each scanning position. The sampling frequency for the PA signal acquisition is 100 MHz. The scanning step was 0.36 degree, which corresponded to 1000 sampling points for a full circular scanning. All collected data was then used to reconstruct image with 2-D back-projection (BP) algorithm [32]. To evaluate the field of view (FOV) of the system, we imaged a phantom prepared by adding black-dyed microspheres into the agar solution. From Fig. 4(b), the FOV for the system with a FUS of a 30 mm curvature radius was estimated to be ~7.7 mm. This FOV is smaller than the DOF (~11 mm) of the sensor, which might be caused by the unperfect alignment of the rotation axis with the z axis during the imaging process (see Fig. 4(a)). By plotting the PA amplitude profile along a single 10 μm-diameter microsphere as shown in Fig. 4(c), the in-plane resolution was estimated to be ~70 µm. We further scanned the sensor across a ~100 µm-diameter human hair along z axis (Fig. 4(a)) to characterize its elevational resolution, which is estimated to be ~500 µm at the center of the FOV, as shown in Fig. 4(d). We also quantified the elevational resolution of the system at different locations along the x axis. At distances of 1 mm, 2mm, and 3 mm to the FOV center, the elevational resolutions are 601 μm, 706 μm and 936 μm, respectively. The resolution degrades with the distance to the FOV center, in agreement with the spatial ultrasound response of the FUS in x-z plane as shown in Fig. 3(c). To testify the improvement in the image quality using the curved FUS, PA images of a hair cross acquired by the straight and curved FUSs were compared in Figs. 4(e) and (f). The curved FUS provides an image with contrast much higher than that of the straight, due to its focusing-enhanced ultrasound sensitivity.

Fig. 4.

Fig. 4

Open in a new tab

(a) Schematic of a PACT system employing a curved FUS with a curvature radius of 30 mm; (b) the PA image of a phantom prepared by mixing black-dyed microspheres into agar (up) and the PA amplitude profile along the dashed line (bottom); (c) the normalized PA amplitude profile across a single 10 μm-diameter microsphere (the scale bar is 50 μm); (d) the normalized PA amplitude profiles across a human hair along z axis at different x locations (the inset figure summarizes the elevational resolutions at different x locations); (e) and (f) are the reconstructed images of a hair-cross with a straight (left) and a curved (right) FUSs, respectively.

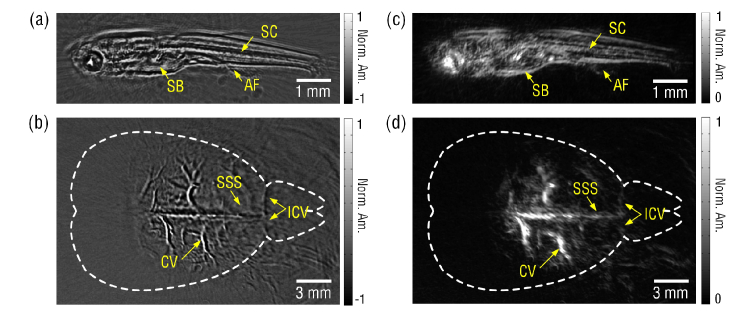
In vivo anatomical imaging capability of the curved fiber based PACT system was also demonstrated by imaging a 25 days-post-fertilization (dpf) zebrafish and an 8-week-old male mouse. To minimize the movement of the alive zebrafish, it was covered with low-melting-point agar. Image of the 8 mm-long zebrafish with clear anatomical features such as the internal organ boundary was shown in Fig. 5(a). We further imaged a mouse brain in vivo. The mouse was hair-removed and hold beneath the water tank as shown in Fig. 4(a). Ultrasound gel was applied between the intact scalp of the mouse and the covered plastic film. During the imaging, the mouse was anesthetized with 1.5% isoflurane, and the mouse head was secured with its cortical surface aligned with the focal plane of the curved FUS. All procedures were conducted in accordance to the Institutional Animal Care and Use Committee at Jinan University. As shown in Fig. 5(b), main blood vessels in the cortex can be clearly observed due to the high sensitivity and high resolution of the curved FUS based PACT system. To avoid the possible misleading to physicians or biologists caused by the bipolar pixel values, the above in vivo images (Figs. 5(a) and (b)) were further processed by Hilbert transformation following the procedures described in [33,34]. Features of the biological structures in the unipolar images as shown in Figs. 5(c) and (d) match well with those in bipolar ones. To reduce impulse noise in the images, the median filter with a 2 × 2 window size has been applied to all of the above images. For the observed streak artifacts, pulse lasers with higher repetition rates (>10 Hz) can be employed to diminish them by increasing the sampling density without much compromise of the imaging time.

Fig. 5.

Fig. 5

Open in a new tab

In vivo images of (a) a zebrafish and (b) a mouse brain obtained by the FUS based PACT system. (c) and (d) are the unipolar images of (a) and (b), respectively, obtained by performing Hilbert transformation. SB: swim bladder, SC: spinal cord, AF: anal fin, CV: cortical vessels, SSS: superior sagittal sinus, ICV: inferior cerebral vein.

5. Summary

In summary, a flexible lens-free focused FUS was demonstrated for PACT imaging. Without using bulk acoustic lens, the focused FUS realized a ~5 times sensitivity enhancement at focus by mechanical bending the fiber. PACT based on the FUS at a curvature radius of 30 mm showed an in-plane resolution of ~70 µm and a ~500 μm elevational resolution. In vivo imaging of a zebrafish and a mouse brain were also demonstrated. The focus capability of the FUS might also reduce the section thickness or increase the elevational resolution of 3-D images acquired by 2-D image stacking in the future. This flexible lens-free focused FUS will be of great interest to photoacoustic imaging for fundamental biological/medical studies as well as clinical applications.

Funding

National Natural Science Foundation of China (NSFC) (61705082, 61775083, 61805102); Natural Science Foundation of Guangdong Province (2017A030313361, 2018030310587).

Disclosures

The authors declare that there are no conflicts of interest related to this article.

References

  • 1.Yao J., Kaberniuk A. A., Li L., Shcherbakova D. M., Zhang R., Wang L., Li G., Verkhusha V. V., Wang L. V., “Multiscale photoacoustic tomography using reversibly switchable bacterial phytochrome as a near-infrared photochromic probe,” Nat. Methods 13(1), 67–73 (2016). 10.1038/nmeth.3656 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.Lin L., Hu P., Shi J., Appleton C. M., Maslov K., Li L., Zhang R., Wang L. V., “Single-breath-hold photoacoustic computed tomography of the breast,” Nat. Commun. 9(1), 2352 (2018). 10.1038/s41467-018-04576-z [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Aguirre J., Schwarz M., Garzorz N., Omar M., Buehler A., Eyerich K., Ntziachristos V., “Precision assessment of label-free psoriasis biomarkers with ultra-broadband optoacoustic mesoscopy,” Nat. Bio. Eng. 1, 0068 (2017). [Google Scholar]
  • 4.Berezhnoi A., Schwarz M., Buehler A., Ovsepian S. V., Aguirre J., Ntziachristos V., “Assessing hyperthermia-induced vasodilation in human skin in vivo using optoacoustic mesoscopy,” J. Biophotonics 11(11), e201700359 (2018). 10.1002/jbio.201700359 [DOI] [PubMed] [Google Scholar]
  • 5.Hu S., Wang L. V., “Neurovascular Photoacoustic Tomography,” Front. Neuroenergetics 2, 10 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Yao J., Xia J., Maslov K. I., Nasiriavanaki M., Tsytsarev V., Demchenko A. V., Wang L. V., “Noninvasive photoacoustic computed tomography of mouse brain metabolism in vivo,” Neuroimage 64(1), 257–266 (2013). 10.1016/j.neuroimage.2012.08.054 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Wang L. V., Yao J., “A practical guide to photoacoustic tomography in the life sciences,” Nat. Methods 13(8), 627–638 (2016). 10.1038/nmeth.3925 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Maslov K., Zhang H. F., Hu S., Wang L. V., “Optical-resolution photoacoustic microscopy for in vivo imaging of single capillaries,” Opt. Lett. 33(9), 929–931 (2008). 10.1364/OL.33.000929 [DOI] [PubMed] [Google Scholar]
  • 9.Jeon M., Kim J., Kim C., “Multiplane spectroscopic whole-body photoacoustic imaging of small animals in vivo,” Med. Biol. Eng. Comput. 54(2-3), 283–294 (2016). 10.1007/s11517-014-1182-6 [DOI] [PubMed] [Google Scholar]
  • 10.Wang X., Pang Y., Ku G., Xie X., Stoica G., Wang L. V., “Noninvasive laser-induced photoacoustic tomography for structural and functional in vivo imaging of the brain,” Nat. Biotechnol. 21(7), 803–806 (2003). 10.1038/nbt839 [DOI] [PubMed] [Google Scholar]
  • 11.Zhang P., Li L., Lin L., Hu P., Shi J., He Y., Zhu L., Zhou Y., Wang L. V., “High-resolution deep functional imaging of the whole mouse brain by photoacoustic computed tomography in vivo,” J. Biophotonics 11(1), e201700024 (2018). 10.1002/jbio.201700024 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Li L., Zhu L., Ma C., Lin L., Yao J., Wang L., Maslov K., Zhang R., Chen W., Shi J., Wang L. V., “Single-impulse panoramic photoacoustic computed tomography of small-animal whole-body dynamics at high spatiotemporal resolution,” Nat. Biomed. Eng. 1(5), 0071 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Kruger R. A., Lam R. B., Reinecke D. R., Del Rio S. P., Doyle R. P., “Photoacoustic angiography of the breast,” Med. Phys. 37(11), 6096–6100 (2010). 10.1118/1.3497677 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Dong B., Sun C., Zhang H. F., “Optical detection of ultrasound in photoacoustic imaging,” IEEE Trans. Biomed. Eng. 64(1), 4–15 (2017). 10.1109/TBME.2016.2605451 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Wissmeyer G., Pleitez M. A., Rosenthal A., Ntziachristos V., “Looking at sound: optoacoustics with all-optical ultrasound detection,” Light Sci. Appl. 7(1), 53 (2018). 10.1038/s41377-018-0036-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Nuster R., Slezak P., Paltauf G., “High resolution three-dimensional photoacoutic tomography with CCD-camera based ultrasound detection,” Biomed. Opt. Express 5(8), 2635–2647 (2014). 10.1364/BOE.5.002635 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Jathoul A. P., Laufer J., Ogunlade O., Treeby B., Cox B., Zhang E., Johnson P., Pizzey A. R., Philip B., Marafioti T., Lythgoe M. F., Pedley R. B., Pule M. A., Beard P., “Deep in vivo photoacoustic imaging of mammalian tissues using a tyrosinase-based genetic reporter,” Nat. Photonics 9(4), 239–246 (2015). 10.1038/nphoton.2015.22 [DOI] [Google Scholar]
  • 18.Guggenheim J. A., Li J., Allen T. J., Colchester R. J., Noimark S., Ogunlade O., Parkin I. P., Papakonstantinou I., Desjardins A. E., Zhang E. Z., Beard P. C., “Ultrasensitive plano-concave optical microresonators for ultrasound sensing,” Nat. Photonics 11(11), 714–719 (2017). 10.1038/s41566-017-0027-x [DOI] [Google Scholar]
  • 19.Paltauf G., Nuster R., Haltmeier M., Burgholzer P., “Photoacoustic tomography using a Mach-Zehnder interferometer as an acoustic line detector,” Appl. Opt. 46(16), 3352–3358 (2007). 10.1364/AO.46.003352 [DOI] [PubMed] [Google Scholar]
  • 20.Rosenthal A., Razansky D., Ntziachristos V., “High-sensitivity compact ultrasonic detector based on a pi-phase-shifted fiber Bragg grating,” Opt. Lett. 36(10), 1833–1835 (2011). 10.1364/OL.36.001833 [DOI] [PubMed] [Google Scholar]
  • 21.Guan B. O., Tam H. Y., Lau S. T., Chan H. L. W., “Ultrasonic hydrophone based on distributed Bragg reflector fiber laser,” IEEE Photonics Technol. Lett. 17(1), 169–171 (2005). 10.1109/LPT.2004.838141 [DOI] [Google Scholar]
  • 22.Gatti D., Galzerano G., Janner D., Longhi S., Laporta P., “Fiber strain sensor based on a π-phase-shifted Bragg grating and the Pound-Drever-Hall technique,” Opt. Express 16(3), 1945–1950 (2008). 10.1364/OE.16.001945 [DOI] [PubMed] [Google Scholar]
  • 23.Eom J., Park S. J., Lee B. H., “Noncontact photoacoustic tomography of in vivo chicken chorioallantoic membrane based on all-fiber heterodyne interferometry,” J. Biomed. Opt. 20(10), 106007 (2015). 10.1117/1.JBO.20.10.106007 [DOI] [PubMed] [Google Scholar]
  • 24.Rosenthal A., Kellnberger S., Bozhko D., Chekkoury A., Omar M., Razansky D., Ntziachristos V., “Sensitive interferometric detection of ultrasound for minimally invasive clinical imaging applications,” Laser Photonics Rev. 8(3), 450–457 (2014). 10.1002/lpor.201300204 [DOI] [Google Scholar]
  • 25.Liang Y., Jin L., Wang L., Bai X., Cheng L., Guan B. O., “Fiber-Laser-Based Ultrasound Sensor for Photoacoustic Imaging,” Sci. Rep. 7(1), 40849 (2017). 10.1038/srep40849 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Liang Y., Liu J. W., Jin L., Guan B. O., Wang L., “Fast-scanning photoacoustic microscopy with a side-looking fiber optic ultrasound sensor,” Biomed. Opt. Express 9(11), 5809–5816 (2018). 10.1364/BOE.9.005809 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Bai X., Liang Y., Sun H., Jin L., Ma J., Guan B. O., Wang L., “Sensitivity characteristics of broadband fiber-laser-based ultrasound sensors for photoacoustic microscopy,” Opt. Express 25(15), 17616–17626 (2017). 10.1364/OE.25.017616 [DOI] [PubMed] [Google Scholar]
  • 28.Gamelin J., Maurudis A., Aguirre A., Huang F., Guo P., Wang L. V., Zhu Q., “A real-time photoacoustic tomography system for small animals,” Opt. Express 17(13), 10489–10498 (2009). 10.1364/OE.17.010489 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Ziemann O., Krauser J., Zamzow P. E., Daum W., POF-polymer Optical Fibers for Data Communication (Springer Science & Business Media, 2002). [Google Scholar]
  • 30.Ishigure T., Aruga Y., Koike Y., “High-bandwidth PVDF-clad GI POF with ultra-low bending loss,” J. Lightwave Technol. 25(1), 335–345 (2007). 10.1109/JLT.2006.886666 [DOI] [Google Scholar]
  • 31.Bauer-Marschallinger J., Höllinger A., Jakoby B., Burgholzer P., Berer T., “Fiber-optic annular detector array for large depth of field photoacoustic macroscopy,” Photoacoustics 5, 1–9 (2017). 10.1016/j.pacs.2017.01.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Xu M., Wang L. V., “Time-domain reconstruction for thermoacoustic tomography in a spherical geometry,” IEEE Trans. Med. Imaging 21(7), 814–822 (2002). 10.1109/TMI.2002.801176 [DOI] [PubMed] [Google Scholar]
  • 33.Li L., Zhu L., Shen Y., Wang L. V., “Multiview Hilbert transformation in full-ring transducer array-based photoacoustic computed tomography,” J. Biomed. Opt. 22(7), 07617 (2017). 10.1117/1.JBO.22.7.076017 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 34.Li G., Li L., Zhu L., Xia J., Wang L. V., “Multiview Hilbert transformation for full-view photoacoustic computed tomography using a linear array,” J. Biomed. Opt. 20(6), 066010 (2015). 10.1117/1.JBO.20.6.066010 [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Biomedical Optics Express are provided here courtesy of Optica Publishing Group

RESOURCES