Abstract
We propose a joint segmentation and classification deep model for early glaucoma diagnosis using retina imaging with optical coherence tomography (OCT). Our motivation roots in the observation that ophthalmologists make the clinical decision by analyzing the retinal nerve fiber layer (RNFL) from OCT images. To simulate this process, we propose a novel deep model that joins the retinal layer segmentation and glaucoma classification. Our model consists of three parts. First, the segmentation network simultaneously predicts both six retinal layers and five boundaries between them. Then, we introduce a post processing algorithm to fuse the two results while enforcing the topology correctness. Finally, the classification network takes the RNFL thickness vector as input and outputs the probability of being glaucoma. In the classification network, we propose a carefully designed module to implement the clinical strategy to diagnose glaucoma. We validate our method both in a collected dataset of 1004 circular OCT B-Scans from 234 subjects and in a public dataset of 110 B-Scans from 10 patients with diabetic macular edema. Experimental results demonstrate that our method achieves superior segmentation performance than other state-of-the-art methods both in our collected dataset and in public dataset with severe retina pathology. For glaucoma classification, our model achieves diagnostic accuracy of 81.4% with AUC of 0.864, which clearly outperforms baseline methods.
1. Introduction
Glaucoma is the leading cause of irreversible blindness [1], and the early detection of glaucoma is of great significance to cure this disease. Elevated intraocular pressure (IOP), visual field (VF) defect and glaucomatous optic neuropathy (GON) yield three main clinical symptoms for glaucoma diagnosis [2]. Retinal nerve fiber layer (RNFL) thinning is an early signal of glaucoma [2]. The advantages of Optical Coherence Tomography (OCT), such as fast scanning speed, non-invasiveness, high resolution and repeatability, make it widely used in eye disease diagnosis. In clinical practice, ophthalmologists make use of OCT to measure the RNFL thickness of peripapillary regions [3] to diagnose glaucoma. Current clinical OCT machines give high-resolution cross sectional structure of retina, but rough retinal layer segmentation.
One striking characteristic of retina is the strict biological topology, i.e., the distinctive retinal layers reflected in OCT image. Retina has been partitioned into ten layers [4] in medical imaging according to components of cells and biological functions. Retinal layers are naturally distributed in a fixed order. Overlapping or intercross of layers does not exist. Keeping the accurate topology of retina in segmentation is necessary, and also challenging. Previous works [5, 6] proposed using an additional network with the same architecture of segmentation net to rectify the topology error of OCT image segmentation, which was at the price of much more parameters. Another work [7] introduced a new loss measuring the similarity of topological features to restrict the topology error when delineating road maps. We observe that the boundaries between retinal layers are also in a fixed order and thus can be complementary to the retinal layer segmentation. Therefore, our network is designed to detect retinal boundaries and to segment retinal layers simultaneously in a sequential way where the former predicted boundaries give complementary information to guide the latter layer segmentation. And a novel post processing step is added to fuse both results and ensures to obtain topology-correct segmentation results.
Our network adopts fully-convolutional design considering that fully convolutional network (FCN) has shown state-of-the-art performance on pixel-wise labeling in semantic segmentation [8–10] and boundary detection [7, 11]. Convolutional network has strong representation ability of image features and shows state-of-the-art performance in many computer vision tasks such as image classification [12] and object detection [13]. Fully convolutional network takes advantage of convolutional networks to complete the label predictions pixels-to-pixels. Ronneberger et al. [14] proposed a U-shape FCN called U-net to deal with very small training set, especially biomedical images. U-net has been successfully implemented in many tasks of biomedical images segmentation [15]. For OCT segmentation, He et al. [5] proposed a modified U-net called S-net to segment retinal layers combined with an additional identical net to correct topology error of the segmented mask. Other state-of-the-art approaches for retina segmentation include combining graph search with convolutional neural network (CNN-GS) [16, 17] or with recurrent neural network (RNN-GS) [18], however, researches show that these patch-based methods are comparable or slightly inferior to FCN-based model on segmentation performance and take more time for inference [18]. Hence we design our network in a fully-convolutional way.
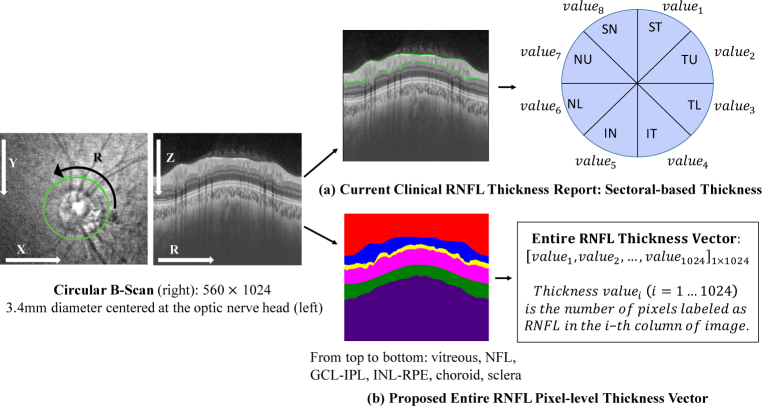
Most of previous machine learning methods used in glaucoma diagnosis adopt either the vertical cup to disc ratio (CDR) or RNFL thickness as the feature [1, 19] via super pixel segmentation, which is inevitably incomprehensive compared with pixel-wise segmentation. What is worse, current RNFL thickness measurements in clinical OCT reports are summarized in 4 quadrants, 8 quadrants or 12 clock hours [19, 20], or in thickness maps [21]. RNFL is split into 4 or 8 or 12 equal parts and average thickness of each part is reported, which loses local or pixel-level information. However, sectoral-based RNFL thickness report still remains the basis to diagnose glaucoma in clinical practice (see Fig. 1(a)). We claim that it is beneficial for the algorithm to have access to the pixel-level thickness instead of a sectoral-based thickness, as more information can be used and automatically learned by the network. Thickness is defined as the number of pixels of a certain retinal layer at a certain position in this paper (see Fig. 1(b)).
Fig. 1.
Our collected data are circular B-Scans performed in a 3.4mm diameter circle centered at the optic nerve head with depth of 1.9mm. (a) Current clinical RNFL thickness report uses sectoral-based RNFL thickness obtained from automatic segmentation of OCT machine; (b) Entire RNFL thickness vector is adopted in this paper calculated from segmentation results by our proposed approach. We segment the whole circular B-Scan into six layers (from top to bottom): vitreous, NFL (nerve fiber layer), GCL + IPL (ganglion cell layer and inner plexiform layer), INL-RPE (from inner nuclear layer to retinal pigment epithelium), choroid and sclera.
In this paper, we propose a joint segmentation-diagnosis pipeline to detect retinal layer boundaries, segment retinal layers and diagnose glaucoma (see Fig. 2). We achieve topology-correct layer segmentation and complete layer boundaries. Accuracy of glaucoma diagnosis outperforms baseline models. Our main contributions are as follows:
Fig. 2.
The workflow of segmentation-diagnosis pipeline: BL-net for segmentation, refinement process and classification net.
We design a sequential multi-task fully convolutional neural network called BL-net to detect boundaries and to segment layers. BL-net utilizes the detected boundaries to facilitate the layer segmentation.
We propose a topology refinement strategy called bi-decision to improve the results of layer segmentation. Also, combination strategy is proposed to fuse both layer segmentation and boundary detection results to obtain topology consistent segmentation mask.
We design a classification network with an interpretable module to diagnose glaucoma based on the entire RNFL thickness vector calculated from segmentation results.
The rest of this paper is structured as follows. Section 2 details the proposed OCT segmentation and glaucoma diagnosis pipeline. Section 3 presents experimental setting, including details of the dataset, implementation details, baseline models and evaluation metrics. Section 4 shows experimental results, including layer segmentation and boundary detection, glaucoma classification as well as analysis of classification results. Section 5 discusses our method and results compared with current approaches. Conclusions are included in Section 6.
2. Method
Our method consists of three components, the first is proposed BL-net for joint boundary detection and layer segmentation. The coarse results of BL-net are delivered to the second component for refinement. Finally, classification net takes the RNFL thickness vector extracted from segmentation result as feature to diagnose glaucoma.
2.1. BL-net
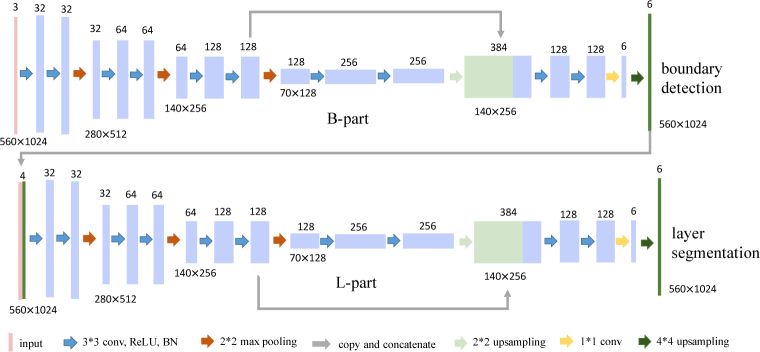
BL-net consists of two consecutive parts with identical network architecture as shown in Fig. 3: the first is for pixel-wise retinal boundary detection noted as B-part and the second is for pixel-wise retinal layer segmentation noted as L-part. The only difference is the input. OCT image alone is the input of B-part, while the predicted boundary masks from the B-part and OCT image are concatenated together as the input of the L-part. BL-net is the first to simultaneously implement retinal boundary detection and retinal layer segmentation in OCT image. BL-net fuses the information of retinal boundaries with OCT image to facilitate the retinal layer segmentation. This sequential multi-task design is more direct to utilize complementary information of boundaries than Chen et al. [22] using two parallel decoders. The network architecture adopts an encoder-decoder design (See Fig. 3). Encoder of the network consists of four contracting blocks to extract feature. Each block consists of two 3 × 3 convolutions, each convolution is followed by a rectified linear unit (ReLU) and batch normalization [23]. A 2 × 2 max pooling operation with stride 2 connects blocks for downsampling. After each downsampling the number of feature channels is doubled. Decoder of the network consists of a 2 × 2 bilinear upsampling followed by concatenation with the feature map of the third block of encoder and two aforementioned convolutions. The second to last layer is a 1 × 1 convolution to map final feature vectors to the desired retinal layer. And the last layer is an upsampling operation to map the logits into the same size of the input image followed by a softmax operation. Here the final output is a volume. For B-part, it is corresponding to the probability maps of five boundaries between neighboring layers and background; and for L-part, it represents six layers: vitreous, NFL, GCL-IPL, INL-RPE, choroid and sclera.
Fig. 3.
The architecture of BL-net.
BL-net is trained end-to-end and parameters of B-part (wb) and L-part (wl) are updated for the two tasks jointly. Therefore, B-part and L-part learn feature representation and segmentation independently, while the detected boundary from B-part is as extra information to guide the following layer segmentation except for OCT image. The objective function for segmentation consists of two unweighted cross-entropy losses and L2 regularization: = + + L2, where is for per-pixel boundary detection and is for pixel-wise layer segmentation. More clearly, we optimize the following function during training BL-net:
| (1) |
where the first two terms are pixel-wise error loss for boundary detection and layer segmentation, and the last term is L2 regularization. x is the pixel position in image space χ, and is the predicted softmax probability of x with the true boundary label ; similarly, denotes the predicted softmax probability of x with the true layer label . α denotes the weight coefficient of regularization. All parameters w are updated with standard back propagation.
2.2. Refinement
It exists that coarse predictions of boundaries and layers are discontinuous and topology-wrong. Hence we propose three strategies to tackle these situations.
2.2.1. Interpolation
Interpolation is adopted to refine incomplete boundaries. Given n pairs of detected boundary coordinates (xj, yj), our goal is to recover the missing boundary height from 1 to 1024 along the width. We adopt the interpolation method proposed in [24], which uses all the observed samples to recover the missing sample as shown in Eq. 2:
| (2) |
where interpolation parameters A, α and β are set as 3.2, 1, and -1 respectively. This setting shows good visual effects when interpolating discontinuous boundaries. Except for this approximate neural network (nn) interpolation, we also employ linear interpolation as comparison.
2.2.2. Bi-decision strategy
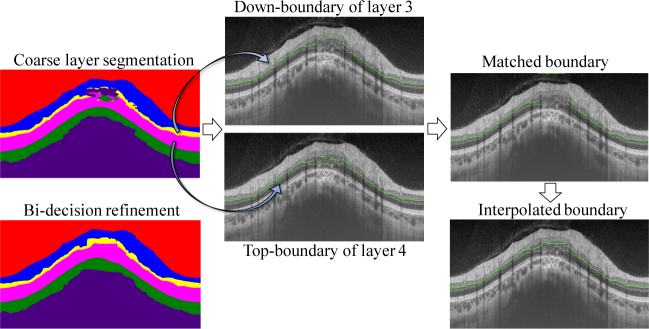
We devise bi-decision strategy to decide the exact location of boundary in the layer segmentation masks via its two adjacent layers. Take the first boundary as an example: it is the down-boundary of layer 1 and simultaneously the top-boundary of layer 2. If the layer segmentation is perfect, they should completely match each other; otherwise, any noise with these two labels would lead to mismatch. To this end, we propose the location of boundary should be assured if and only if the top- and down- layers touch each other seamlessly.
Our bi-decision strategy can be formulated as Algorithm 1:
Algorithm 1.
Bi-decision strategy
| Input: coarse layer mask: L | |
| Output: boundary location matrix: Ml; mask of boundary location matrix: | |
| 1: | Initialize Ml as 0 with size 5 × 1024; |
| 2: | Initialize as 0 with size 5 × 1024; |
| 3: | for do column of L |
| 4: | for do label of layer |
| 5: | v1 = all indexes of layer l in column c |
| 6: | v2 = all indexes of layer l+1 in column c |
| 7: | if max{v1 } + 1 == min{v2 } then matched boundary index |
| 8: | Ml[l, c] = min{v2 } assign index to boundary location matrix |
| 9: | [l, c] = 1 assign 1 to valid mask entry |
| 10: | end if |
| 11: | end for |
| 12: | end for |
The returns a vector of locations of layer l in column c. The output Ml records the exact boundary locations and records the validity of each entry of Ml.
2.2.3. Combination strategy
We employ combination strategy to combine the results of boundary detection and layer segmentation, and ensures the final results to be topology correct. In our experiment, we observe that the predicted boundaries by B-part are accurate but have a low recall. On the other hand, boundaries from masks of layer segmentation are complete but lack accuracy. For simplicity, we transfer both the segmentation results into two 5 × 1024 boundary location matrices Ml, Mb, where 5 corresponds to the number of boundaries, 1024 is the image width, and each entry of the matrix represents the height of the boundary in the original segmentation map. If a boundary is missing at a certain region, then the matrix will be invalid at the corresponding entry. To cope with this situation, we also generate a binary mask for each matrix, whose entry is 1 if that boundary location is valid and 0 otherwise (see Alg. 2.2.2). Intuitively, we can use interpolation or fill in the missing values by the complementary matrix. On the other hand, since we have ground-truth boundary locations, we can also learn to complement the incomplete boundary location matrix with the complete one.
We formulate the complementary strategy with a shallow convolutional network (see Fig. 4):
| (3) |
| (4) |
where Mb, Ml and M are the boundary location matrix from predicted boundary mask, predicted layer mask and the final predicted location matrix, respectively. Mark denotes element-wise multiplication, and are weighted matrices functioning on Mb and Ml, respectively. This process can be understood as a simplified implementation of attention. is the concatenation of masked Mb and Ml in the channel dimension, followed by a convolutional operation. The convolution combines these two matrices according to the learned weights to get final boundary location matrix.
Fig. 4.

Network for combination strategy. Mb is the boundary location matrix from coarse predicted boundary mask of B-part, and Ml is the one from the predicted layer mask of L-part refined by bi-decision. This network outputs the final learned location matrix M taking Mb and Ml as inputs.
The way to get Mb is straightforward: the height of the detected boundary in each column is its location. Ml is from refined layer segmentation. In layer segmentation mask, the fact that two adjacent pixels with different labels indicate boundary enables the transformation from layer mask to boundary mask and boundary location matrix. We use Huber loss [25] as the objective function:
| (5) |
where y is the ground-truth location matrix, is the predicted location by the network with parameters , and δ is a threshold determining the point of intersection of different sections. This loss function is quadratic for predicted locations near the ground-truths, and linear for those far away from each other. Here we set δ as 1 in a general way [26].
2.3. Classification net
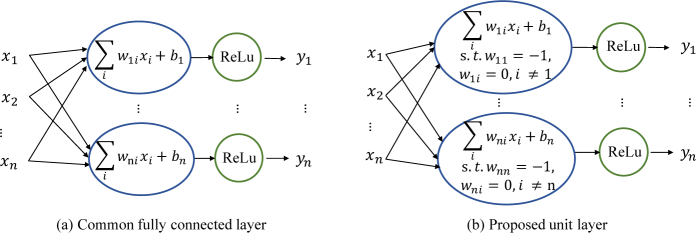
Classification net mimics the process of how ophthalmologists diagnose glaucoma: given the OCT report of sectoral-based RNFL thickness in 8 quadrants or 12 clock hours, if there is a thinning, then there is likely a glaucoma lesion. We formulate this process as a standard inner-product layer with a ReLU unit called unit layer (see Fig. 5) in the neural network, using the entire thickness vector instead of sectoral thickness vector:
| (6) |
where ( - ) is the inner product layer, is the bias to be learned, and I is an identity matrix that is fixed during training. Operation max is the ReLU activation. Only the entries of thickness values below the threshold can be activated and passed to following layers, while other entries are zero cleared. In this way, the classification net is no longer a black-box classifier, as we can directly inspect the learned threshold to see if it is meaningful and comparable to the average thickness of glaucomatous patients. This layer is followed by three hidden fully connected layers with 300, 100, and 50 neurons, respectively. Then the output layer predicts the probability of glaucoma with a sigmoid function. Moreover, the classification net can be optimized with BL-net end-to-end, even though they are separately trained in this paper.
Fig. 5.
Common fully connected layer (a) versus proposed unit layer (b).
The objective function of classification is also a cross-entropy loss:
| (7) |
where ti is the RNFL thickness vector of i-th sample in n samples of training set, and is the sigmoid probability of the sample with the ground-truth disease label. We guarantee that all images both in training set and testing set are at the same scale proportion to physical retina structures, and also RNFL thickness vector calculated in pixels are proportional to the true thickness in the real world.
3. Experiments
3.1. Data and preprocessing
Our collected dataset is comprised of 1004 OCT optic nerve scans from Zhongshan Ophthalmic Center of Sun Yat-sen University. Totally 234 subjects with or without glaucoma were enrolled at one to seven visits over a 20-month period in our study. Each subjects provided two to fourteen scans. Images were acquired by peripapillary circular scan using a Topcon DRI-OCT device. The scan was performed in a 3.4mm diameter circle centered at the optic nerve head with depth of 1.9mm. Each scan was automatically segmented by built-in software into six layers: vitreous, NFL (retinal neural fiber layer), GCL-IPL (ganglion cell layer and inner plexiform layer), INL-RPE (from inner nuclear layer to retinal pigment epithelium), choroid and sclera. These images were also manually delineated by three professional doctors in the same way. Correspondingly, the boundaries between layers were extracted as the boundary detection ground-truths. The boundary ground-truth map is also with six labels, i.e., five boundaries and background. We adopted 3-fold cross-validation in our experiments with the intention of obtaining an accurate estimation of the generalizability of our network to unseen data. We randomly split subjects into three subsets: 48 subjects of 341 scans (132 health and 209 glaucoma) in subset1, 66 subjects of 330 scans (120 health and 210 glaucoma) in subset2, and 120 subjects of 333 scans (123 health and 210 glaucoma) in subset3. Of the three subsets, each of them was retained as the validation data for testing the model, and the remaining two subsets were used as training data. After repeating three times, the three results were averaged to produce a final estimation. There is no overlap of subjects among subset1, subset2 and subset3. The resolution of OCT image is about 1.92 microns per pixel in height, and all the scans and ground-truth segmentations are cropped into the size of 560 × 1024.
Except for our collected dataset, we also applied our method to a public dataset [27]. This dataset was acquired using a Spectralis HRA+OCT (Heidelberg Engineering, Heidelberg, Germany). It is comprised of 10 OCT volumes obtained from 10 patients with diabetic macular edema (DME) containing large visible intraretinal cysts. More details were described in [27].
3.2. Implementation details
We trained all networks using Adam [28] implemented in Python 2.7 using TensorFlow [29] with a fixed learning rate of 0.0001 and momentum of 0.9 on GeForce GTX 1080. Adjusting weight balance between glaucoma and healthy images did not bring much improvement, even though the number of glaucoma images is bigger than that of health images.
3.3. Baseline models
For retina segmentation, we compared the performance of our model with the automatic segmentation of OCT device. Also we compared our BL-net with the backbone network separately trained for layer segmentation or boundary detection. Further, we compared our model with other two fully convolutional networks, i.e., U-net [14] which was widely used in medical image segmentation, and S-net + T-net [5] which was exactly designed for retinal layer segmentation. Two baseline models were trained from scratch for layer segmentation on our collected dataset. All the models adopted padded convolutions and reached convergence when stopping training. Even though there are other state-of-the-art methods for retina layer segmentation such as RNN-GS [18] and CNN-GS [16], these patch-based approaches have intrinsic drawbacks. Patch-based approaches involve pre-processing of splitting image into patches around each pixel, make classification decision according to the local features (patch) regardless of global features, and consume much time to predict segmentation. Moreover, fully-convolutional based approach is proven to be comparable and even slightly superior to patch-based approaches [18]. Considering these factors, we compared our approach with other two FCN models. In addition, to further assure the fairness and to show the generalizability of our approach, we trained our model on a public dataset for both seven retinal layers segmentation and total retina thickness segmentation to compare with existing algorithms [27, 30–32] for the same task on the same dataset.
For glaucoma diagnosis, to show the effectiveness of our classification net, SVM [33] was adopted as a baseline. SVM was often used in glaucoma classification [20]. SVM with linear kernel was used as we found it achieved much better results than other kernels such as rbf. To demonstrate the validity of using entire RNFL thickness vector to diagnose glaucoma, VGG16 [34] using OCT images as inputs was adopted as the other baseline. VGG16 was pre-trained with ImageNet and fine-tuned on our collected dataset. In addition, our classification net with sectoral-based thickness was also compared as another baseline.
3.4. Evaluation metrics
To evaluate the layer-based segmentation similarity, we adopt the average Jaccard index J [35] defined as the mean intersection-over-union (mIoU) of each estimated layer and the ground-truth. To evaluate the boundary-based accuracy, we employ average Dice coefficient (F-score) [35] as the metric. Dice coefficient reflects the trade-off between precision and recall. J and are defined as follows using TP (true positive), FP (false positive), TN (true negative) and FN (false negative):
| (8) |
| (9) |
where L and are the predicted mask and ground-truth of layer segmentation, l and b are the number of layers to segment and the number of boundaries to detect, respectively. To show the segmentation result of each retinal layer, we provide Dice coefficient for each layer and the average unsigned distance (in pixels) [30] between the ground-truth and computed boundaries of bi-decision for each retinal boundary. For the public dataset, to compare our method to existing algorithms, we also calculate Dice coefficient for each layer and unsigned boundary localization errors (U-BLE) [30] for each boundary. In addition, we use accuracy and area under ROC curve (AUC) to evaluate the performance of classification.
4. Results
4.1. Layer segmentation and boundary detection
Results on our collected dataset are shown in Table 1 and Fig. 6. Results of our models include coarse results from BL-net and refined results: bi-decision for coarse layer masks, interpolation for coarse boundary masks, and combination strategy for boundary location matrices from bi-decision result and coarse boundary masks. Our model and baseline models outperformed the built-in algorithm of OCT device with a large margin. Both J and of BL-net are higher than those of separately trained backbone network (see Table 1). Paired T-test shows that the improvement of is statistically significant (pvalue=0.014 for L-part, pvalue=0.018 for B-part). These verify the advantage of our proposed sequential architecture. The following presents the comparison between our model and baseline models.
Table 1.
Average segmentation results using 3-fold cross-validation on our collected dataset. Jaccard index J is used as the region-based metric and Dice coefficient is used as the contour-based metric. ‡: Boundary masks are transformed from predicted layer segmentation. †: Layer masks are transformed from predicted boundaries. *: Statistically significant improvement compared with S-net+T-net (pvalue ≤ 0.1).
| OCT device | J | Paras.(M) | |||
|---|---|---|---|---|---|
| 0.841 | 0.585 | - | |||
| U-net [14] | 0.896 ± 0.014 | 0.694 ± 0.035 | 53.7 | ||
| S-net [5] | 0.918 ± 0.001 | 0.709 ± 0.008 | 13.4 | ||
| S-net+T-net [5] | 0.919 ± 0.000 | 0.716 ± 0.013 | 26.8 | ||
| backbone | layer segmentation | 0.926 ± 0.005 | 0.710 ± 0.009 | 2.8 | |
| backbone | boundary detection | 0.681 ± 0.058 | 0.721 ± 0.009 | 2.8 | |
| BL-net(ours) | B-part | coarse | 0.690 ± 0.019 | 0.010 | 5.6 |
| linear-interpolation | 0.916 ± 0.003 | 0.008 | |||
| nn - interpolation | 0.912 ± 0.006 | 0.008 | |||
| L-part | coarse | 0.928 ± 0.004 | 0.717 ± 0.009 | ||
| bi-decision | 0.003 | 0.719 ± 0.009 | |||
| two parts | combination | 0.005 | 0.720 ± 0.013 |
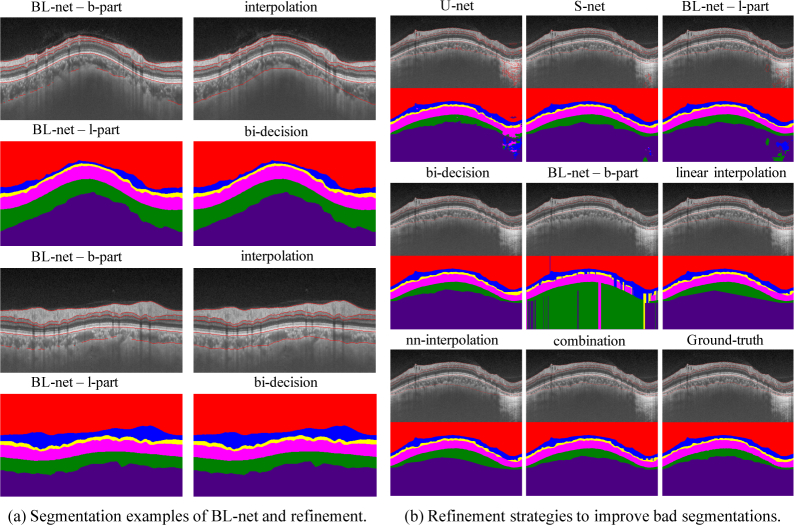
Fig. 6.
Qualitative results of segmentation on our collected dataset. (a) shows examples of segmentations from BL-net and refinement strategies. (b) shows the refinement process of a bad case’s detected boundaries and segmented layers. U-net and S-net are two baseline models, bi-decision is proposed to refine outputs of the l-part of BL-net, interpolation is proposed to refine outputs of the b-part of BL-net and combination strategy is to fuse the two refined results. Refinement strategies correct topology error of bad segmentations.
Table 2.
Dice coefficient for each retinal layer and unsigned boundary localization errors (mean ± standard deviation in pixels) for each retinal boundary of bi-decision.
| vitreous | NFL | GCL-IPL | INL-RPE | choroid | sclera |
|---|---|---|---|---|---|
| Dice | |||||
| 0.999 ± 0.001 | 0.960 ± 0.004 | 0.897 ± 0.008 | 0.979 ± 0.001 | 0.941 ± 0.002 | 0.990 ± 0.001 |
| vitreous/NFL | NFL/GCL | IPL/INL | RPE/choroid | choroid/sclera | |
| U-BLE | |||||
| 0.20 ± 0.15 | 1.07 ± 0.35 | 0.50 ± 0.31 | 0.59 ± 0.22 | 3.72 ± 0.26 | |
Coarse results of L-part, with J = 92.8% and = 71.7%, were superior to the performance of S-net with increase of 1.0% and 0.8%, respectively. This demonstrated the effectiveness of detected boundaries on facilitating layer segmentation. Still coarse results of L-part achieved better results than S-net + T-net. Further S-net outperformed U-net with more than 2% and 1.5% improvement at these two metrics. In addition, BL-net showed superiority in the load of network with just 5.6 million parameters, less than half of those of S-net. Coarse predicted boundaries by B-part were accurate but incomplete with = 73.2% and J = 69.0%, where was higher but J was much lower compared with results of L-part. In addition, coarse predicted boundaries had a high precision of 75.3% and a relatively low recall of 71.9%, which also reflected the accuracy and discontinuity of direct predicted boundaries.
Bi-decision strategy improved the coarse results of L-part, increasing both J and by 0.2%. It surpassed S-net + T-net by 1.1% on metric J and 0.3% on metric . Bi-decision refined the topology of retina segmentation by removing intra-layer noise. The process of bi-decision is illustrated in Fig. 7. Take the third boundary for example. It is the down-boundary of layer 3 (marked as yellow in layer masks) and the top-boundary of layer 4 (marked as purple in layer masks). The destroyed topology of layer 3 and layer 4 in layer masks leads to the separation between them, causing the incomplete matched boundary. Then interpolation produces the final third boundary. The Dice for each retinal layer and the unsigned boundary localization errors (in pixels) for each retinal boundary are shown is Table 2, which also verifies the effectiveness of bi-decision strategy. In a word, bi-decision strategy effectively rectifies the topology error by utilizing two adjacent layers to decide the boundary.
Fig. 7.
Illustrations of bi-decision strategy removing the topology error. Take the third boundary for example. The third boundary is the down-boundary of layer 3 and the top-boundary of layer 4. The matched of these two boundaries is assured as the true boundary which is followed by interpolation to produce the final complete one.
Table 3.
Comparison of Dice coefficient for each retinal layer on a public dataset. The best performance is shown by bold and the second best is shown by .
| NFL | GCL-IPL | INL | OPL | ONL-ISM | ISE | OS-RPE | |
|---|---|---|---|---|---|---|---|
| manual expert 2 [30] | 0.86 ± 0.07 | 0.89 ± 0.05 | 0.80 ± 0.06 | 0.72 ± 0.09 | 0.88 ± 0.06 | 0.86 ± 0.05 | 0.84 ± 0.05 |
| Chiu [27] | 0.86 ± 0.05 | 0.88 ± 0.06 | 0.73 ± 0.08 | 0.73 ± 0.09 | 0.86 ± 0.08 | 0.86 ± 0.05 | 0.80 ± 0.06 |
| Chakravarty [30] | 0.86 ± 0.07 | 0.89 ± 0.05 | 0.80 ± 0.06 | 0.72 ± 0.09 | 0.88 ± 0.06 | 0.86 ± 0.05 | 0.84 ± 0.05 |
| Roy [31] | 0.93 | ||||||
| bi-decision (ours) | 0.86 ± 0.01 | 0.90 ± 0.00 | 0.78 ± 0.01 | 0.78 ± 0.01 | 0.01 | 0.90 ± 0.00 | 0.86 ± 0.01 |
Both interpolation methods, i.e., nn and linear interpolation, brought a surprisingly large improvement (from 0.690 to 0.912) of the J score of B-part prediction. This makes sense because the predicted boundaries are accurate but discontinuous, which can be further refined by interpolation. On the other hand, the coefficient dropped accordingly by 1.0%, which we think is acceptable. In addition, combination strategy, learning the combination of the results of B-part and L-part, increased J by 1.0% and increased by 0.4% compared with S-net + T-net.
A complete layer segmentation was produced in only 0.32 seconds per image on average during test for l-part in our BL-net. The average time per image combining with bi-decision strategy was 0.94 seconds. This definitely outperforms the results in existing algorithms such as 145 seconds in [18], 43.1 seconds in [16] and 11.4 seconds in [27].
Results on public dataset for seven retinal layers segmentation are shown in Table 3, Table 4 and Fig. 8(a). Our method performed best in one of the seven retinal layers in terms of Dice, and second best in five retinal layers compared with other three recently published papers [27, 30, 31]. Compared with the manual expert 2, our method got higher Dice coefficient in five retinal layers. In addition, our method outperformed both manual expert 2 and paper [30] in delineating all eight retinal boundaries in terms of the unsigned boundary localization errors (see Table 4). For total retina segmentation, the proposed bi-decision strategy with BL-net achieved 0.991 on Dice, surpassing both the method in [32] with 0.969 and the method in [27] with 0.985. Examples of segmentation results are shown in Fig. 8(b).
Table 4.
Comparison of unsigned boundary localization errors (in pixels) for each retinal boundary on a public dataset. The best performance is shown by bold.
| ILM | NFL/GCL | IPL/INL | INL/OPL | OPL/ONL | IS/OS | RPE in | RPE out | |
|---|---|---|---|---|---|---|---|---|
| manual expert 2 [30] | 1.27 ± 0.41 | 1.77 ± 0.69 | 2.12 ± 1.66 | 2.21 ± 1.46 | 2.49 ± 1.63 | 1.25 ± 0.53 | 1.27 ± 0.50 | 1.25 ± 0.46 |
| Chakravarty [30] | 1.22 ± 0.44 | 3.35 ± 2.14 | 3.27 ± 2.73 | 3.84 ± 3.61 | 4.44 ± 3.81 | 1.44 ± 0.70 | 1.34 ± 0.43 | 1.09 ± 0.39 |
| bi-decision (ours) | 0.05 | 0.09 | 0.08 | 0.08 | 0.19 | 0.07 | 0.02 | 0.15 |
Table 5.
Diagnosing results (testing set). †: Initialization of bias of the unit layer of classification net. *: Average RNFL thickness in training.
Fig. 8.
Examples of seven retinal layers and total retina segmentation on public dataset. (a) For seven retina layers, the first column shows segmented layers, and the second column shows computed boundaries. (b) shows segmentation results for total retina. All segmentations are from l-part of BL-net combined with bi-decision strategy.
4.2. Glaucoma classification
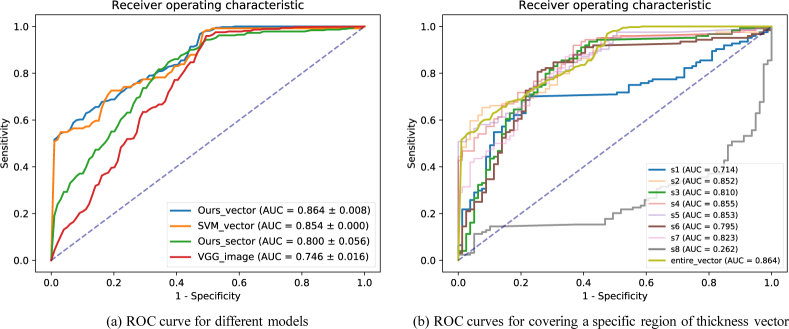
The classification results of glaucoma are shown in Table 5 and ROC curves are shown in Fig. 9(a). Our model achieved diagnostic accuracy of 0.814 with AUC of 0.864. The accuracy surpassed SVM by 5.5% and VGG16 by 6.0%. The AUC surpassed SVM by 1.0% and VGG16 by 11.8%. This result indicates that using RNFL thickness vector to diagnose glaucoma was more efficient than using the whole OCT images. In addition, our model using entire RNFL thickness vector outperformed using RNFL thickness sectors (eight quadrants). This verified that the entire RNFL thickness information is necessary for the diagnose of glaucoma.
Table 6.
Classification results using the RNFL thickness vector covering a specific region.
| section | s 1 | s 2 | s 3 | s 4 | s 5 | s 6 | s 7 | s 8 | entire-vector |
|---|---|---|---|---|---|---|---|---|---|
| acc. | 0.793 | 0.788 | 0.783 | 0.803 | 0.793 | 0.788 | 0.778 | 0.798 | 0.814 |
| AUC | 0.852 | 0.855 | 0.853 | 0.823 | 0.864 |
Fig. 9.
ROC curves for glaucoma classification. (a) shows the performance of different models. (b) shows the performance of our classification net using RNFL thickness vector when covering a specific region. S1, S2 .. S8 sequentially denote each of the region of eight splitting on the vector.
4.3. Analysis of classification
We verify that our idea using the entire RNFL thickness vector is better than the traditional sectoral-based thickness to diagnose glaucoma. As Table 5 shows, our net using entire thickness vector outperformed using sectoral-based thickness by 2.9% on accuracy and 6.4% on AUC. Further, we investigated whether some regions of RNFL are more critical than others to diagnose glaucoma. So we equally divided the thickness vector into 8 sections (noted as s1, s2 .. s8), and evaluated the classification performance by randomly setting one section of the vector to 0 during testing. The results are shown in Table 6 and Fig. 9(b). Turning off regions s1, s3, s6 and s8 caused obvious decline of AUC. From a doctor’s view, these regions correspond to those near the temporal quadrant, where glaucomatous optic neuropathy usually starts.
5. Discussion
In this paper, we design a novel fully convolutional network called BL-net to segment retinal layers and to detect retinal boundaries simultaneously, propose novel post-processing strategies including bi-decision strategy and combination strategy to improve segmentation results, and leverage the ophthalmologists’ diagnostic strategy to design a simple but interpretable classification network to diagnose glaucoma according to the entire RNFL thickness calculated from segmentation results. Our segmentation-diagnosis pipeline combines retina segmentation and glaucoma diagnosis in a consecutive way, predicting both retina layer and boundary segmentation as well as giving glaucoma diagnosing result. Experimental results on our collected dataset of 234 subjects (1004 images) demonstrate the effectiveness of the proposed segmentation-diagnosis pipeline, and experimental results on public dataset of 10 patients (110 images) with diabetic macular edema show the generalizability of our method.
Our BL-net, a fully convolutional network, is a full image-based approach. Experimental results verify the discussion in [18] that FCN-based approaches are much faster than patch-based approaches. BL-net takes only 0.32 seconds on average to predict a complete retina segmentation for an OCT image, and BL-net plus post-processing take less than 1 second. Since FCN-based approaches are comparable or even slightly superior to patch-based approaches on accuracy and consistency as shown in [18], baseline models for retina segmentation in this paper are all FCN-based models. One baseline model, S-net + T-net, was proposed by He et al. [5] where T-net was designed as an additional net to correct topology error of the segmented mask from S-net to improve the performance. They flattened OCT images and subdivided them into small overlapping patches to train the net. Superior to He et al. [5] and other retina segmentation algorithms [36, 37], our model accepts the whole image as input with no need to flatten or subdivide image, which simplifies the data pre-processing and speeds the inference process. Also BL-net has relatively less parameters (5.6 million) than S-net + T-net (26.8 million).
We design the BL-net as a multi-task FCN to segment retinal layers and to detect retinal boundaries simultaneously. Our idea is inspired by the work of Chen et al. [22], which detects gland objects and contours simultaneously with multi-level features. Different from Chen et al. [22] which mainly aimed at accurately segmenting touching glands, our BL-net is designed to keep the accurate topology of retina in final layer segmentation by leveraging complementary information of layer and boundary. Also instead of just concatenating the up-sampling results of multi-level features with different receptive field sizes, we adopt a skip connection similar with U-net [14] to concatenate features in down-sampling way with up-sampling results. This connection enables our network to learn multi-scale features. Another difference lies in the architecture of network, Chen et al. [22] adopted two branches to implement multi-task, while we design a tandem structure with two consecutive parts to employ two different tasks. In addition, we propose novel refinement strategies, including bi-decision for layer refinement and combination strategies. Bi-decision is proved to be efficient in removing topology errors and achieves good performance in both private and public datasets. Note that the combination strategy does not surpass the bi-decision, the reason lies in the difficulty to learn a proper convolutional filter which fits every point of the retinal boundaries. However, the combination strategy provides a feasible and novel idea to leverage both the boundary location matrix from detected boundaries of B-part and the boundary location matrix from bi-decision of L-part. And the combination net is actually small with only 11 parameters (when the size of convolutional filter set as 1 × 5), so there is little computation. We think this should be of interest and inspiration for future study.
For glaucoma diagnosis, we design a simple classification network with several fully connected layers where the first layer learns the thickness thresholds to keep thinning signals. The input of classification network is the entire RNFL thickness vector calculated from pixel-wise segmentation results. Different from super pixel segmentation adopted by current methods of automatic glaucoma diagnosis [1, 19], pixel to pixel labeling keeps complete and accurate information. Muhammad et al. [38] used convolutional neural network to extract features from OCT images to diagnose glaucoma. Their research focused on the whole image but lacked medical interpretations. Experimental results show our simple classification network using RNFL thickness outperforms deep convolutional neural networks like VGG16 using the whole image. We analyzed the learned thickness thresholds which presented min of 30.7μm, median of 53.8μm, max of 78.7μm, mean of 52.1μm, and standard deviation of 7.27. The learned thickness threshold varied along the RNFL. This verifies that the design of the unit layer in classification network is efficient to learn a unique thickness threshold at each point of RNFL.
More researches directly took conventional RNFL thickness measurements from OCT reports to train a classifier to diagnose glaucoma [39], however, conventional RNFL thickness measurements are often summarized in 4 quadrants, 8 quadrants or 12 clock hours [19,20], or in thickness maps [21], these sectoral-based measurements or maps lose thickness information in more detailed level. Therefore, to avoid problems of using incomprehensive thickness information and getting hardly interpretable diagnosing results [38], we develop a segmentation-diagnosis pipeline for joint pixel-wise retinal layer segmentation, retinal boundary detection and glaucoma diagnosis. Different from [40] which also conducted segmentation of OCT images and diagnosis of general sight-threatening retinal diseases, we utilize the intermediate results (RNFL thickness) of segmentation masks while they directly use the segmentation masks, and we focus on the assistant diagnosis of glaucoma which is not included in [40]. From the segmentation result, we can get the RNFL thickness at each column in the OCT image. Then we use this entire RNFL thickness vector instead of current sectoral-based thickness to train our model to diagnose glaucoma.
It should be noted that BL-net and classification net have not been trained in an end-to-end way due to the intermediate refinement strategies. Actually BL-net and classification net can be optimized end-to-end if without the proposed refinement strategies which are not differentiable. And we have tried fine-tuning the pre-trained BL-net directly combined with the classification net, and found the performance of B-part in BL-net improved, especially the region metric J of coarse prediction increased 9.7%. However, the performance of classification declined 1.3% on AUC compared with separately trained classification net. Future work may investigate the special network design to take place of additional refinement process, thus making the end-to-end training of segmentation-diagnosis possible.
6. Conclusion
We propose a segmentation-diagnosis pipeline for joint retina segmentation and glaucoma diagnosis. Our BL-net outputs retinal boundary mask and retinal layer mask in a sequential way. Proposed bi-decision strategy rectifies the topology error to improve both region connectivity and boundary correctness. Proposed combination strategy utilizes complementary information from both detected boundaries and segmented layers to boost segmentation performance. Our classification net verifies that using entire RNFL thickness vector from segmentation maps is more effective than using sectoral-based RNFL thickness to diagnose glaucoma. Our BL-net combined with refinement strategies achieves state-of-the-art segmentation performance on both our collected dataset and the public dataset. And our method also achieves the best diagnostic accuracy of glaucoma.
Funding
National Key Research and Development Project (2018YFC010302); Science and Technology Program of Guangzhou, China (201803010066); Industrial Collaboration Project (Y9Z005); Shenzhen Research Program (JCYJ20170818164704758, JCYJ20150925163005055).
Disclosures
The authors declare that there are no conflicts of interest related to this article.
References
- 1.Bechar M. E. A., Settouti N., Barra V., Chikh M. A., “Semi-supervised superpixel classification for medical images segmentation: application to detection of glaucoma disease,” Multidimens Syst. Signal Process. pp. 1–20 (2017). [Google Scholar]
- 2.Usman M., Fraz M. M., Barman S. A., “Computer vision techniques applied for diagnostic analysis of retinal oct images: a review,” Arch. Comput. Methods Eng. 24, 449–465 (2017). 10.1007/s11831-016-9174-3 [DOI] [Google Scholar]
- 3.Medeiros F. A., Zangwill L. M., Alencar L. M., Bowd C., Sample P. A., Susanna R., Weinreb R. N., “Detection of glaucoma progression with stratus oct retinal nerve fiber layer, optic nerve head, and macular thickness measurements,” Investig. ophthalmology & visual science 50, 5741–5748 (2009). 10.1167/iovs.09-3715 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Shi F., Chen X., Zhao H., Zhu W., Xiang D., Gao E., Sonka M., Chen H., “Automated 3-d retinal layer segmentation of macular optical coherence tomography images with serous pigment epithelial detachments,” IEEE transactions on medical imaging 34, 441–452 (2015). 10.1109/TMI.2014.2359980 [DOI] [PubMed] [Google Scholar]
- 5.He Y., Carass A., Yun Y., Zhao C., Jedynak B. M., Solomon S. D., Saidha S., Calabresi P. A., Prince J. L., “Towards topological correct segmentation of macular oct from cascaded fcns,” in Fetal, Infant and Ophthalmic Medical Image Analysis, (Springer, 2017), pp. 202–209. 10.1007/978-3-319-67561-9_23 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.He Y., Carass A., Jedynak B. M., Solomon S. D., Saidha S., Calabresi P. A., Prince J. L., “Topology guaranteed segmentation of the human retina from oct using convolutional neural networks,” arXiv preprint arXiv:1803.05120 (2018).
- 7.Mosinska A., Marquez Neila P., Kozinski M., Fua P., “Beyond the pixel-wise loss for topology-aware delineation,” in Conference on Computer Vision and Pattern Recognition (CVPR), (2018), CONF. [Google Scholar]
- 8.Long J., Shelhamer E., Darrell T., “Fully convolutional networks for semantic segmentation,” in Proceedings of the IEEE conference on computer vision and pattern recognition, (2015), pp. 3431–3440. [DOI] [PubMed] [Google Scholar]
- 9.Chen L. C., Papandreou G., Kokkinos I., Murphy K., Yuille A. L., “Semantic image segmentation with deep convolutional nets and fully connected crfs,” Comput. Sci. pp. 357–361 (2014). [DOI] [PubMed]
- 10.Chen L.-C., Papandreou G., Kokkinos I., Murphy K., Yuille A. L., “Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs,” IEEE transactions on pattern analysis machine intelligence 40, 834–848 (2018). 10.1109/TPAMI.2017.2699184 [DOI] [PubMed] [Google Scholar]
- 11.Xie S., Tu Z., “Holistically-nested edge detection,” in Proceedings of the IEEE international conference on computer vision, (2015), pp. 1395–1403. [Google Scholar]
- 12.Krizhevsky A., Sutskever I., Hinton G. E., “Imagenet classification with deep convolutional neural networks,” in Advances in neural information processing systems, (2012), pp. 1097–1105. [Google Scholar]
- 13.Girshick R., Donahue J., Darrell T., Malik J., “Rich feature hierarchies for accurate object detection and semantic segmentation,” in Proceedings of the IEEE conference on computer vision and pattern recognition, (2014), pp. 580–587. [Google Scholar]
- 14.Ronneberger O., Fischer P., Brox T., “U-net: Convolutional networks for biomedical image segmentation,” in International Conference on Medical image computing and computer-assisted intervention, (Springer, 2015), pp. 234–241. [Google Scholar]
- 15.Çiçek Ö., Abdulkadir A., Lienkamp S. S., Brox T., Ronneberger O., “3d u-net: learning dense volumetric segmentation from sparse annotation,” in International Conference on Medical Image Computing and Computer-Assisted Intervention, (Springer, 2016), pp. 424–432. [Google Scholar]
- 16.Fang L., Cunefare D., Wang C., Guymer R. H., Li S., Farsiu S., “Automatic segmentation of nine retinal layer boundaries in oct images of non-exudative amd patients using deep learning and graph search,” Biomed. optics express 8, 2732–2744 (2017). 10.1364/BOE.8.002732 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hamwood J., Alonso-Caneiro D., Read S. A., Vincent S. J., Collins M. J., “Effect of patch size and network architecture on a convolutional neural network approach for automatic segmentation of oct retinal layers,” Biomed. Opt. Express 9, 3049–3066 (2018). 10.1364/BOE.9.003049 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kugelman J., Alonso-Caneiro D., Read S. A., Vincent S. J., Collins M. J., “Automatic segmentation of oct retinal boundaries using recurrent neural networks and graph search,” Biomed. Opt. Express 9, 5759–5777 (2018). 10.1364/BOE.9.005759 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Xu J., Ishikawa H., Wollstein G., Bilonick R. A., Folio L. S., Nadler Z., Kagemann L., Schuman J. S., “Three-dimensional spectral-domain optical coherence tomography data analysis for glaucoma detection,” PloS one 8, e55476 (2013). 10.1371/journal.pone.0055476 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Bizios D., Heijl A., Hougaard J. L., Bengtsson B., “Machine learning classifiers for glaucoma diagnosis based on classification of retinal nerve fibre layer thickness parameters measured by stratus oct,” Acta ophthalmologica 88, 44–52 (2010). 10.1111/j.1755-3768.2009.01784.x [DOI] [PubMed] [Google Scholar]
- 21.Vermeer K., Van der Schoot J., Lemij H., Boer J. De, “Automated segmentation by pixel classification of retinal layers in ophthalmic oct images,” Biomed. optics express 2, 1743–1756 (2011). 10.1364/BOE.2.001743 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Chen H., Qi X., Yu L., Heng P.-A., “Dcan: deep contour-aware networks for accurate gland segmentation,” in Proceedings of the IEEE conference on Computer Vision and Pattern Recognition, (2016), pp. 2487–2496. [Google Scholar]
- 23.Ioffe S., Szegedy C., “Batch normalization: Accelerating deep network training by reducing internal covariate shift,” arXiv preprint arXiv:1502.03167 (2015).
- 24.Llanas B., Sainz F., “Constructive approximate interpolation by neural networks,” J. Computat. Appl. Math. 188, 283–308 (2006). 10.1016/j.cam.2005.04.019 [DOI] [Google Scholar]
- 25.Huber P. J., et al. , “Robust estimation of a location parameter,” The annals mathematical statistics 35, 73–101 (1964). 10.1214/aoms/1177703732 [DOI] [Google Scholar]
- 26.Olut S., Sahin Y. H., Demir U., Unal G., “Generative adversarial training for mra image synthesis using multi-contrast mri,” arXiv preprint arXiv:1804.04366 (2018).
- 27.Chiu S. J., Allingham M. J., Mettu P. S., Cousins S. W., Izatt J. A., Farsiu S., “Kernel regression based segmentation of optical coherence tomography images with diabetic macular edema,” Biomed. optics express 6, 1172–1194 (2015). 10.1364/BOE.6.001172 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kingma D. P., Ba J., “Adam: A method for stochastic optimization,” arXiv preprint arXiv:1412.6980 (2014).
- 29.Abadi M., Barham P., Chen J., Chen Z., Davis A., Dean J., Devin M., Ghemawat S., Irving G., Isard M., et al. , “Tensorflow: a system for large-scale machine learning,” in OSDI, vol. 16 (2016), pp. 265–283. [Google Scholar]
- 30.Chakravarty A., Sivaswamy J., “A supervised joint multi-layer segmentation framework for retinal optical coherence tomography images using conditional random field,” Comput. methods programs biomedicine 165, 235–250 (2018). 10.1016/j.cmpb.2018.09.004 [DOI] [PubMed] [Google Scholar]
- 31.Roy A. G., Conjeti S., Karri S. P. K., Sheet D., Katouzian A., Wachinger C., Navab N., “Relaynet: retinal layer and fluid segmentation of macular optical coherence tomography using fully convolutional networks,” Biomed. optics express 8, 3627–3642 (2017). 10.1364/BOE.8.003627 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Venhuizen F. G., van Ginneken B., Liefers B., van Grinsven M. J., Fauser S., Hoyng C., Theelen T., Sánchez C. I., “Robust total retina thickness segmentation in optical coherence tomography images using convolutional neural networks,” Biomed. optics express 8, 3292–3316 (2017). 10.1364/BOE.8.003292 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Suykens J. A. K., Vandewalle J., “Least squares support vector machine classifiers,” Neural Process. Lett. 9, 293–300 (1999). 10.1023/A:1018628609742 [DOI] [Google Scholar]
- 34.Simonyan K., Zisserman A., “Very deep convolutional networks for large-scale image recognition,” Comput. Sci. (2014).
- 35.Perazzi F., Pont-Tuset J., McWilliams B., Van Gool L., Gross M., Sorkine-Hornung A., “A benchmark dataset and evaluation methodology for video object segmentation,” in The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), (2016). [Google Scholar]
- 36.Lang A., Carass A., Hauser M., Sotirchos E. S., Calabresi P. A., Ying H. S., Prince J. L., “Retinal layer segmentation of macular oct images using boundary classification,” Biomed. optics express 4, 1133–1152 (2013). 10.1364/BOE.4.001133 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Chiu S. J., Li X. T., Nicholas P., Toth C. A., Izatt J. A., Farsiu S., “Automatic segmentation of seven retinal layers in sdoct images congruent with expert manual segmentation,” Opt. express 18, 19413–19428 (2010). 10.1364/OE.18.019413 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Muhammad H., Fuchs T. J., Cuir N. De, Moraes C. G. De, Blumberg D. M., Liebmann J. M., Ritch R., Hood D. C., “Hybrid deep learning on single wide-field optical coherence tomography scans accurately classifies glaucoma suspects,” J. glaucoma 26, 1086–1094 (2017). 10.1097/IJG.0000000000000765 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Omodaka K., An G., Tsuda S., Shiga Y., Takada N., Kikawa T., Takahashi H., Yokota H., Akiba M., Nakazawa T., “Classification of optic disc shape in glaucoma using machine learning based on quantified ocular parameters,” PloS one 12, e0190012 (2017). 10.1371/journal.pone.0190012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Fauw J. De, Ledsam J. R., Romera-Paredes B., Nikolov S., Tomasev N., Blackwell S., Askham H., Glorot X., O’Donoghue B., Visentin D., et al. , “Clinically applicable deep learning for diagnosis and referral in retinal disease,” Nat. medicine 24, 1342 (2018). 10.1038/s41591-018-0107-6 [DOI] [PubMed] [Google Scholar]